Coulomb effect in hybrid double quantum dot-metal nanoparticle systems considering the wetting layer

Abstract

Many body effects in the wetting layer (WL)-double quantum dot (DQD)-metal nanoparticle (MNP) structure have been studied by modeling the Coulomb scattering rates in this structure. The strong coupling between WL-DQD-MNPs was considered. An orthogonalized plane wave (OPW) is assumed between WL-QD transitions. The transition momenta are calculated accordingly to specify the normalized Rabi frequency on this structure, considering the strong coupling between the WL-DQD-MNP structures. This approach is important for realizing scattering rates, including in-and-out capture and relaxation rates, which are essential for specifying the type of structure used depending on the optimum value of the scattering time required to fit the application. The QD hole capture rate is the highest, and the hole capture times are the shortest. The relaxation times are less than the electron capture times by one order, while they are half of the hole capture times. The capture rates increase with increasing distance R between the DQDs and the MNP. High tunneling increases hole-capture rates and changes the relaxation rates, showing the importance of tunneling in controlling the scattering rates.

1 Introduction

Quantum dot (QD) nanostructures are promising for future devices [1]. The development of nano growth methods has made aligning QDs with metal nanoparticles (MNPs) easy. As strong coupling in MNP-QD systems has been proven, controlling the dynamics and parameters of MNP-QD systems has become desirable [2–4]. The MNP surface plasmonic field and QD excitons interact via Coulomb interactions with energy transfer [5]. The frequency-dependent absorption and scattering, i.e., near-field enhancement, are detected in the strong coupling regime. This enables the spectroscopy of the enhanced surface used in many applications, such as Raman spectroscopy and biochemical sensors [6]. He and Zho [5] studied the strong coupling in a double MNP-QD system via quantum electrodynamics and canonical transformations. The importance of Fano resonance is determined. Trügler and Hohenester used quantum mechanics to describe surface-plasmon-polaritons and molecular dynamics and demonstrated strong coupling in an MNP-QD hybrid system [2]. In the quasistatic regime, where the light wavelength is much larger than the MNP size, and the MNP-QD distance, Hohenester and Trügler used the Green function as an essential couple between classical Maxwell and quantum electrodynamics. These methods separate the decay rate into radiative and nonradiative components [6]. Both [2] and [6] use the boundary element approach to calculate the decay rates. Refs. [1, 5, 6] exploit the Drude model to describe the electrons in an MNP.

Many-body effects affect the optical properties of QD nanostructure devices. The simple rate equations cannot represent the essential dynamics in a nonequilibrium case [7]. The density matrix theory simulates QD, DQD, and MNP-DQD systems [8]. Such modeling is adequate for describing the interaction between states well through the density element $\rho _{ij}$, which cannot be calculated with rate equations. Modeling of QD and DQD systems under many-body effects has been performed [9]. However, modeling the many-body effect in MNP-QDs has not been achieved.

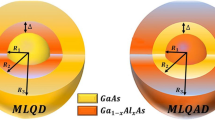
The QD nanostructure was grown conventionally on a wetting layer (WL) in Stranaska–Krastanov growth mode (by molecular beam epitaxy). It is an ordinary quantum well (QW) layer, a two-dimensional layer quantized in one dimension (1D). As shown in Fig. 1, carrier transitions from WL to QDs are inevitable in the WL-QD structures. This is because the WL is a reservoir of carriers, and if there is an injection in the device (laser or light emitting diode device), the injection occurs on the WL, and then the carriers can reach the QD state. WL is only quantized in 1D, while QDs are quantized in total (3D). Physically, the transitions occur only between the states of the same quantized numbers. Therefore, transitions between the in-plane (two dimensions) WL and the QDs are impossible. The orthogonalized plane wave (OPW) approximation is required in the WL-QD simulation to satisfy this reality. In OPW, the plane wavefunction of the WL is orthogonalized on the QD state wavefunctions. Then, the transitions occur only between quantized states of the same quantum numbers. This formulation is not easy to apply and is only used in a limited number of works [8, 9]; simplified approximations are employed. Earlier works [10, 11] used OPW and considered the QD wavefunction as a simple harmonic oscillator and the quantum well (QW) WL an infinite structure that oversimplified the problem. However, one must refer to their high work on putting the main points on modeling.

Figure 1

Schematic diagram of the DQD and MNP hybrid system, where $r_{d1}$ and $r_{d2}$ are the radii of DQD and the radius $r_{m}$ of MNP, respectively

The InAs/GaAs DQD system was detected experimentally by Tarasov et al. [12]. The attachment of QDs to MNPs via bimolecular centers was described in many articles [13, 14]. Zhang et al. clarified the alignment of MNPs to QDs via molecular beam epitaxy through strain-driven nucleation [15]. Therefore, preparing such a hybrid structure was possible.

The WL-DQD-MNP structure was studied in our earlier works [8, 16] by applying the OPW (which has not been involved before in QD-MNP works). However, the Coulomb effect has never been discussed in these works or others dealing with WL-QD-MNPs in the strong coupling case. Each work addresses QD-MNPs or semiconductor nanostructure-MNPs; one can see the direct lines in their sketches, referred to as the Coulomb effect. However, no one has studied this phenomenon, and the real problem of strong coupling (in the case here, where MNP is nearest to QDs) has been approximated and not solved.

This work models the many-body effects in the WL-DQD-MNP structure considering the OPW, which is inevitable in WL-QD transitions. In addition to this modeling, this work has many perspectives. The effect of MNP was evaluated by normalization of the Rabi frequency. The carrier occupation probability is computed through the density matrix theory by modeling the scattering rates. The literature uses experimental data from materials different from those in the understudy or normalized values for energies and momenta. In this work, the WL and QD energies are calculated and subsequently used to estimate the momenta, which calculates the Rabi frequency. The capture rates increase with increasing distance R between the DQDs and the MNP.

The paramount importance of such modeling is to specify the scattering (capture and relaxation) rates. Therefore, one can determine if the scattering is strong (one of the results here is increasing the scattering with MNP-DQD distance). For example, high scattering is required for high-speed frequency modulation. Then, one can desire the structure necessary depending on the needed application. A comparison with the results of other works (with WL-QD structures) provides insight into the correctness of the results obtained here.

2 DQD-MNP structure

The case of study here is the hybrid DQD-MNP structure with DQDs of two InAs QDs, a quantum disk shape, each with $r_{d1}$ ($=13\ nm$) and $r_{d2}$ ($=11\ nm$) radii and $h_{d1}$ ($=2\ \mathrm{nm}$) and $h_{d2}$ ($=3\ nm$) heights, for QD1 and QD2, respectively. The MNP is a sphere with a radius $r_{m}$ ($=8\ nm$), the distance between the DQDs and the MNP is denoted by R ($=7\ \mathrm{nm}$); see Fig. 1. A Coulombic study assumes strong coupling; of course, $R < r_{m} < r_{d1}$ and $r_{d2}$ must be fulfilled [17] as strong coupling conditions. The dielectric constants $\varepsilon _{\mathrm{s}}$ and $\varepsilon _{\mathrm{M}}$ are defined as those of the QD and MNP, respectively. WL is the QW on which the QDs are grown.

3 Theoretical model

3.1 Wave function

The QD wavefunction is defined in cylindrical coordinates $( \rho ,\phi , z )$ as follows [9],

$$ \varphi _{QD} ( \overset{\rightharpoonup}{r} ) = \varphi _{d} ( \overset{\rightharpoonup}{\rho} ) \varphi _{QD} ( \overset{\rightharpoonup}{z} ) u ( \overset{\rightharpoonup}{r} ) $$

(1)

The in-plane QD envelope function $\varphi _{d} ( \overset{\rightharpoonup}{\rho} )$ is defined by $J_{m} (p \overset{\rightharpoonup}{\rho} )$, the first kind of Bessel function [9],

$$ \varphi _{d} ( \overset{\rightharpoonup}{\rho} ) = C_{nm} J_{m} ( p \overset{\rightharpoonup}{\rho} ) $$

(2)

where $C_{nm}$ is the normalization constant, and the constant p is defined by,

$$ p = \frac{\sqrt{2 m_{d}^{*} (E_{\rho} - V_{d} )}}{\hslash} $$

(3)

$E_{\rho}$ is the QD-energy state in the in-plane direction, and $V_{d}$ and $m_{d}^{*}$ are the potential and the effective mass of the QD, respectively. $V_{d}$ is taken as zero inside the disk. The QD is defined by the conduction CB (valence VB) band offset $\Delta E_{c} (\Delta E_{v} )$. The QD envelope function in the z-direction resembles that of the QW [9],

$$ \varphi _{QD} ( z ) = A_{ZQD} \cos ( k_{z} z ) $$

(4)

where $A_{ZQD}$ is the normalization constant of the QD function in the z-direction. $u ( \overset{\rightharpoonup}{r} )$ is the periodic part of the Bloch function in the QD crystal. The QW-WL wavefunction is written as [18],

$$ \varphi _{w} ( \vec{r} ) = \varphi _{k}^{0} ( \overset{\rightharpoonup}{\rho} ) \varphi _{w} ( z ) u ( \vec{r} ) $$

(5)

where $\varphi _{k}^{0} ( \overset{\rightharpoonup}{\rho} )$ is the in-plane ($\overset{\rightharpoonup}{\rho}$-direction) WL wavefunction and the superscript (⁰) distinguish it from the orthogonalized wavefunction. It is defined by [18],

$$ \varphi _{k}^{0} ( \overset{\rightharpoonup}{\rho} ) = A_{w_{\rho}} exp ( i \vec{k}_{w_{\rho}}. \overset{\rightharpoonup}{\rho} ) $$

(6)

In the in-plane WL, $\vec{k}_{w_{\rho}}$ is the wavevector, and $A_{w_{\rho}}$ is the normalization constant. In the z-direction [18],

$$ \varphi _{w} ( z ) = A_{w_{z}} \cos ( k_{zw} z ) $$

(7)

$A_{w_{z}}$ is the normalization constant, and $k_{zw}$ is the WL wavevector in the z-direction.

3.2 Coulomb potential

According to [19], the Hamiltonian in the second quantization for carrier–carrier scattering is written for the DQD–WL–MNP hybrid system (Fig. 2) as follows,

$$ H_{sys} = H_{kin} + H_{C} = \sum _{b} \varepsilon _{b} a_{b}^{\dagger} a_{b} + V_{C} (DQD - WL - MNP) $$

(8)

Figure 2

Energy band diagram of the DQD-WL-MNP hybrid system. Note that $\mathrm{k}_{1}$, $\mathrm{k}_{2}$, $\mathrm{k}_{3}$ are three wave vectors in the WL (in the z-direction), which are chosen depending on the WL energy states in the CB while $\mathrm{k}_{1\mathrm{h}}$, $\mathrm{k}_{2\mathrm{h}}$, $\mathrm{k}_{3\mathrm{h}}$ are those in the VB

The parts define the Hamiltonian $H_{kin}$ as the kinetic contribution and $H_{C}$ as the Coulomb interaction. The electron creation and annihilation operators are $a_{x}$ and $a_{x}^{\dagger}$ at energy $\varepsilon _{x}$ in the $| x \rangle$ state. The bare Coulomb potential of the DQD-WL-MNP Coulomb interaction is,

$$ V_{C} ( DQD - WL - MNP ) = \frac{1}{2} \sum _{bfgh} \bigl\{ V_{bfgh} a_{b}^{\dagger} a_{f}^{\dagger} a_{g} a_{h} \bigr\} + V_{M} $$

(9)

The MNP potential is $V_{M}$. Additionally, note that b, f, g, and h in the sum denote all possible electron states. For the QD structure [19, 20],

$$ V_{bfgh} = \iint dr \,dr ' \varphi _{b}^{*} ( r ) \varphi _{f}^{*} \bigl( r ' \bigr) \frac{e_{0}^{2}}{4 \pi \epsilon _{0} \epsilon _{QD} \vert r - r ' \vert } \varphi _{g} \bigl( r ' \bigr) \varphi _{h} ( r ) $$

(10)

$\varphi _{x} ( r )$ is the wave function of the single particle. The permittivity of the vacuum and background are given by $\epsilon _{0}$ and $\epsilon _{QD}$, respectively, and $- e_{0}$ is the elementary electronic charge. The wave functions are separated into an in-plane a⃗-dimensional part and a z-dimensional part. Then, under a Fourier transform, the bare Coulomb potential as a function of the 2D wavevector q⃗ is [20]

$$ V_{c} \bigl( \vert \vec{r}_{1} - \vec{r}_{2} \vert \bigr) = \sum_{q} e^{- i \vec{q} .( \vec{\rho} - \vec{\acute{\rho}} )} V ( \vec{q}, z - \acute{z} ) $$

(11)

Under [14]

$$ V ( \vec{q}, \vec{z} - \vec{\acute{z}} ) = \frac{e_{0}^{2}}{2 \epsilon _{0} q} e^{- q \vert z - \acute{z} \vert } $$

(12)

In Eq. (10), the Coulomb potential, including the screening effect (through $\epsilon _{0} \epsilon _{QD}$), is defined. Equations (11) and (12) define the bare Coulomb potential. To formulate the problem to the $DQD - WL - MNP$ system under study, with disk shape QDs (in-plane ρ⃗, and z⃗-dimensions quantized) and 2D WL (z⃗-dimension quantized only), the bare Coulomb potential is separated according to the ρ⃗, and z⃗-dimensions dependence wave functions as follows,

$$ V_{v v_{2} v_{3} v_{1}} = \frac{1}{A} \sum_{q} V_{\sigma \sigma _{2} \sigma _{3} \sigma _{1}}^{b_{,} b_{2}} ( \vec{q} ) \delta _{b, b_{1}} \delta _{b_{2,} b_{3}} \times \bigl\langle \varphi _{d}^{b} \bigl\vert e^{-i \vec{q}. \vec{\rho}} \bigr\vert \varphi _{k_{1}}^{b_{1}} \bigr\rangle \bigl\langle \varphi _{k_{2}}^{b_{2}} \bigl\vert e^{i \vec{q}. \vec{\rho}} \bigr\vert \varphi _{k_{3}}^{b_{3}} \bigr\rangle $$

(13)

A is the WL area, and the available carrier states are $v v_{2} v_{3} v_{1}$, while the z-direction quantum numbers are σ, $\sigma _{2}$, $\sigma _{3}$, $\sigma _{1}$. The DQD states are referred to here by d, while $k_{i}$ ($i=1,2,3$) refers to the wavevectors in the in-plane direction of the WL. In the 2D-momentum (q⃗), the Coulomb potential is given by [19]

$$ V_{\sigma \sigma _{2} \sigma _{3} \sigma _{1}} ( \vec{q} )= \frac{e_{0}^{2}}{2 \epsilon _{0} q} \iint d z \,d \acute{z} \varphi _{\sigma}^{*} ( z ) \varphi _{\sigma _{2}}^{*} ( \acute{z} ) e^{- q \vert z - \acute{z} \vert } \varphi _{\sigma _{1}} ( z ) \varphi _{\sigma _{3}} ( \acute{z} ) $$

(14)

Considering the approximation [9, 21],

$$\begin{aligned}& \vert z - \acute{z} \vert \approx z - \frac{\vec{z} \vec{\acute{z}}}{z}\\& e^{- q \vert z - \acute{z} \vert } \approx e^{- q ( z - \frac{\vec{z} \vec{\acute{z}}}{z} )} \end{aligned}$$

Then, set $q \frac{\vec{z}}{z} \cong \vec{\acute{q}}$. The Coulomb potential in the z-direction is then written as,

$$ V_{\sigma \sigma _{2} \sigma _{3} \sigma _{1}} ( \vec{q} ) = \frac{e_{0}^{2}}{2 \epsilon _{0} q} \biggl\{ \biggl[ \int d z \varphi _{\sigma}^{*} ( z ) e^{-qz} \varphi _{\sigma _{1}} ( \acute{z} ) \biggr] \biggl[ \int d \acute{z} \varphi _{\sigma _{2}}^{*} ( \acute{z} ) e^{\acute{q} \acute{z}} \varphi _{\sigma _{3}} ( \acute{z} ) \biggr] \biggr\} $$

(15)

3.3 The screened Coulomb matrix element

The screening effect can be introduced through the 2D static limit of the dynamic Lindhard equation [9–11, 19, 22]. In the DQD-WL-MNP hybrid system, the screened Coulomb matrix element is given by

$$ \begin{aligned}[b] W ( DQD - WL - MNP ) ( \vec{q} )&= \frac{V_{C} ( DQD - WL - MNP ) ( \vec{q} )}{\epsilon ( q )} \\ &\rightarrow \frac{V_{C} ( DQD - WL - MNP ) ( \vec{q} )}{\frac{1+ k_{0}}{k_{v v_{1}}}} \end{aligned} $$

(16)

The 2D dielectric function $\epsilon ( q )$ is defined through the 2D inverse screening length $k_{0}$, given by [10],

$$ k_{0} = \sum_{b = e, h} \frac{2 m_{b} e^{2}}{\epsilon _{0} \epsilon _{QD} \hslash ^{2}} \biggl[ 1 - \exp \biggl( - \frac{\hslash ^{2} \pi w_{b}}{k_{B} T m_{b}} \biggr) \biggr] $$

(17)

The thermal energy is $k_{B} T$, the effective mass and the frequency of the carrier are $m_{b}$ and $w_{b}$, respectively.

3.4 DQD-MNP applied fields

To calculate Eq. (16), one needs to compute the MNP potential, as shown in Eq. (9). It is estimated from the integration over the DQD-MNP distance R as

$$ V_{M} = - \int _{0}^{R} E_{MNP}.dR $$

(18a)

According to Ref. [23], the DQD-MNP hybrid system has a total field inside the MNP, as shown in Fig. 2, given by,

$$ E_{MNP} = \frac{1}{\varepsilon _{eff m}} \biggl[ \frac{E_{02}^{(0)}}{2} + \frac{S_{a} P_{QD}}{\varepsilon _{eff s} R^{3}} \biggr] $$

(18b)

The screening effect is considered for both MNP and DQD fields as [23],

$$ \varepsilon_{ effi =} \frac{(2\varepsilon_{ 0}+ \varepsilon _{i})}{ 3\varepsilon_{ 0}} $$

(18c)

where $\varepsilon _{i}$ is either $\varepsilon _{s}$ for the dielectric constant of the semiconductor DQD or $\varepsilon _{m}$ for the MNP. The probe amplitude is $E_{02}^{0}$, and the polarization in the DQD is $P_{QD}$ ($= \mu _{20} (\rho _{20} + \rho _{02} )$). Considering the probe field applied between QD states $(v,v_{1})$, the potential of the MNP reads,

$$ V_{M_{v v_{1}}} = - \frac{1}{\varepsilon _{eff m}} \biggl[ \frac{E_{02}^{(0)}}{2} R - \frac{S_{a} \mu _{v v_{1}} \rho _{v v_{1}}}{2 \varepsilon _{eff s} R^{2}} \biggr] $$

(18d)

where $\mu _{v v_{1}}$ and $\rho _{v v_{1}}$ are the momentum and the density matrix elements, respectively, between QD states $v,v_{1}$.

The probe field between the states $| 0 \rangle \leftrightarrow | 2 \rangle$ of the DQD-MNP system was applied. This field is written as $\mathrm{E}_{02} ( \mathrm{t} ) = \frac{E_{02}^{0}}{2} e^{- i \omega _{02} t} +\text{c.c.}$ with a transition frequency $\omega _{02}$. Considering the MNP effect, the total QD field is [23],

$$ E_{QD} = \frac{1}{2} \frac{E_{02}^{(0)}}{\varepsilon _{eff \mathrm{s}}} + \frac{S_{a} P_{MNP}}{\varepsilon _{eff \mathrm{s}} R^{3}} $$

(19)

The direction of the electric field is specified by $S_{a}$, where $S_{a} =2$ is the z-axis polarization and $S_{a} =-1$ is the parallel direction. The MNP-induced polarization is $P_{MNP}$ ($= \beta E_{MNP}$). β ($= \gamma a^{3}$) defined by [23],

$$ \gamma = \frac{\varepsilon _{m} ( w ) - \varepsilon _{0}}{ \varepsilon _{m} ( w ) +2 \varepsilon _{0}} $$

(20)

Using the $P_{MNP}$ definition in Eq. (19) and then substituting into Eq. (18b), the total QD field becomes,

$$ E_{QD} = \frac{1}{2} \frac{E_{02}^{(0)}}{\varepsilon _{effs}} + \frac{1}{ 2} \frac{E_{02}^{(0)}}{\varepsilon _{effs}} \frac{S_{a} \gamma a^{3}}{ R^{3}} + \frac{S_{a}^{2} \gamma P_{QD}}{\varepsilon _{effs}^{2}} \frac{a^{3}}{R^{6}} $$

(21)

The second and third terms in Eq. (21) define the normalized Rabi frequency [16],

$$ \Omega _{20}^{(r)} = \Omega _{20}^{(1)} -\eta \rho _{20} $$

(22a)

where

$$ \Omega _{20}^{(1)} =\Omega _{20}^{(0)} \biggl( 1+ \frac{S_{a} \gamma a^{3}}{ R^{3}} \biggr) $$

(22b)

and

$$ \eta = \frac{S_{a}^{2} \gamma \mu _{20}^{2}}{\hslash \varepsilon _{eff1}^{2}} \frac{a^{3}}{R^{6}} $$

(22c)

The definitions in Eq. (22a)–(22c) are attained at strong coupling [16]. Note that the unnormalized Rabi frequency of the probe field is $\Omega _{20}^{(0)} = \frac{\mu _{12} E_{02}^{(0)}}{2 \hslash \varepsilon _{effs}}$ [23]. The dielectric function of the MNP is defined by [24],

$$ \varepsilon _{m} ( w ) = \varepsilon _{d} ( w ) + \varepsilon _{s} ( w ) $$

(23a)

where $\varepsilon _{s} ( w )$ gives the electrons of the s-state contribution to the dielectric constant. It is defined in the Drude model by [24]

$$ \varepsilon _{s} ( w ) =1- \frac{w_{p}^{2}}{w^{2} +iw ( \gamma _{bulk} + \frac{A v_{f}}{r_{m}} )} $$

(23b)

where $\gamma _{bulk}$ is the damping constant of the metal bulk structure, $v_{f}$ is the Fermi energy electron velocity, $w_{p}$ is the metal plasma frequency, A is related to the MNP electron scattering, and $\varepsilon _{IB} ( w )$ is the d-state contribution of electrons in the MNP and is defined for the gold-plasma frequency $w_{p} =2.5\ (eV)$ by [24],

$$ \varepsilon _{d} ( w ) =1.15+i10.5 $$

(23c)

Using the Drude model to describe electrons in the MNP is a common assumption with a strong coupling regime. Such behavior results from the high electron concentration even with MNP [25–28].

3.5 The processes in the DQD-WL-MNP system under the Coulomb effect

The QD-WL carrier scattering rates are listed in Ref. [11]. For the hybrid DQD-WL-MNP system, shown in Fig. 2, the carrier scattering rate can be written as,

$$ \begin{aligned}[b] S_{b,M,d} &= \frac{2 \pi}{\hslash} \sum _{k_{1}, k_{2}, k_{3}, b '} \bigl[ 2 \vert W_{M,d k_{2} k_{3} k_{1}} \vert ^{2} - W_{M,d k_{2} k_{3} k_{1}} W_{M,d k_{3} k_{2} k_{1}}^{*} \bigr] \delta \bigl( \varepsilon _{d}^{b} - \varepsilon _{k_{1}}^{b} + \varepsilon _{k_{2}}^{b '} - \varepsilon _{k_{3}}^{b '} \bigr) \\ &\quad {}\times \bigl\{ \bigl( 1 - f_{d}^{b} \bigr) f_{k_{1}}^{b} \bigl(1 - f_{k_{3}}^{b '} \bigr) f_{k_{2}}^{b '} - ( f \rightarrow 1 - f )\bigr\} \end{aligned} $$

(24)

In Eq. (24), the direct and exchange partners (the first and second terms in the square brackets) determine the screened Coulomb matrix element. The spin degeneracy causes a factor of 2 in the direct Coulomb process. This factor is discarded in the exchange electron-hole process. Accordingly, seven possible scattering processes for the WL-QD-MNP hybrid system are listed in Table 1 (the fifth process is an exchange process added to processes 3 and 4). These processes are diagrammed in Fig. 3.

Figure 3

Scattering processes in the WL-DQD system. Each process has two lines of the same color for two carrier processes (ee and eh or he and hh with e: electron and h: hole). Only the exchange process (black line), contributed to by other processes, appears lonely. Cap: capture, relax: relaxation, mix: mixed, and exch: exchange processes. The processes are numbered according to their appearance in Table 1. For example, p1 refers to the process no. 1 in Table 1

Table 1 QD states where capture and relaxation processes can occur. Note that an assistant process is associated with each process (capture or relaxation) as a four-carrier Coulomb process

For the 1st scattering rate in Table 1 (Fig. 3), an electron is captured from the WL electron $| k_{1} \rangle$ to the $| 12 \rangle$ electron state in QD₁ with the assistance of the WL transition $| k_{2} \rangle \rightarrow | k_{3} \rangle$. It is written as,

$$ \begin{aligned}[b] S_{M,e, c_{12}}^{cap} &= S_{M,ee, c_{12}}^{cap} + S_{M,e h, c_{12}}^{cap} \\ &= \frac{2 \pi}{\hslash} \delta \bigl( E_{c_{12}}^{e} - E_{k_{1}}^{e} + E_{k_{3}}^{e} - E_{k_{2}}^{e} \bigr) \\ &\quad {}\times W_{M, c_{12} k_{3} k_{2} k_{1}} \bigl[ 2 W_{M, c_{12} k_{3} k_{2} k_{1}}^{*} -W_{M, c_{12} k_{3} k_{1} k_{2}}^{*} \bigr] \\ &\quad {}\times \bigl\{ ( 1 - f_{c_{12}} ) f_{k_{1}} ( 1 - f_{k_{3}} ) f_{k_{2}} - f_{c_{12}} ( 1 - f_{k_{1}} ) f_{k_{3}} ( 1 - f_{k_{2}} ) \bigr\} \\ &\quad {}+ \frac{2 \pi}{\hslash} \delta \bigl( E_{c_{12}}^{e} - E_{k_{1}}^{e} + E_{k_{3 h}}^{h} - E_{k_{2 h}}^{h} \bigr) \times 2 \vert W_{M, c_{12} k_{3 h} k_{2 h} k_{1}} \vert ^{2} \\ &\quad {}\times \bigl\{ ( 1 - f_{c_{12}} ) f_{k_{1}} ( 1 - f_{k_{3 h}} ) f_{k_{2 h}} - f_{c_{12}} ( 1 - f_{k_{1}} ) f_{k_{3 h}} ( 1 - f_{k_{2 h}} ) \bigr\} \end{aligned} $$

(25)

The Coulomb scattering matrix element is $W_{M, c_{12} k_{3} k_{2} k_{1}}$ of the four-carrier DQD interaction under the MNP effect, where M refers to the MNP, $c_{12}$ refers to the $| 12 \rangle$ QD CB state, and $k_{i}$ and $k_{i h}$ refer to the WL states according to the quantum numbers in the CB and VB, respectively. $E_{c_{ij}}^{e}$ is the QD electron energy of the $| ij \rangle$ QD CB state, $E_{k_{i}}^{e}$ and $E_{k_{2 h}}^{h}$ are, respectively, that of WL CB electron and VB hole energies corresponding, respectively, to their wave numbers $k_{i}$ and $k_{2 h}$. $f_{i}$ refers to the Fermi function of the referred state in the QD or WL in the CB or VB. All these states and wave numbers are clarified in Fig. 2 above. $\delta (E)$ refers to the delta function. The Coulomb matrix element for the e-e interaction is [10],

$$ W_{M, c_{12} k_{3} k_{2} k_{1}} ( \vec{q} )= \frac{V_{c_{12} k_{3} k_{2} k_{1}} ( \vec{q} )}{\epsilon ( q )} \rightarrow \frac{V_{c_{12} k_{3} k_{2} k_{1}} ( \vec{q} )}{\frac{1+ k_{0}}{k_{c_{12}}}} $$

(26a)

With the $V_{c_{12} k_{3} k_{2} k_{1}}$ is the interaction matrix element of the bare Coulomb potential and $\epsilon ( q )$ is the dielectric function. To determine the Coulomb interactions for QD-WL-MNPs, we have the following integrations:

$$ \begin{aligned}[b] V_{c_{12} k_{3} k_{2} k_{1}} &=\bigl\{ V_{c_{12} k_{3} k_{2} k_{1}} ( \vec{z} ) \times \bigl\langle \Phi _{c_{12}} ( \vec{\rho} ) \bigl\vert e^{- i \vec{q}. \vec{\rho}} \bigr\vert \Phi _{k_{1}} ( \vec{\rho} ) \bigr\rangle \bigl\langle \Phi _{k_{3}} ( \vec{\rho} ) \bigl\vert e^{i \vec{q}. \vec{\rho}} \bigr\vert \Phi _{k_{2}} ( \vec{\rho} ) \bigr\rangle \bigr\} \\ &\quad {}+ V_{M 02} \end{aligned} $$

(26b)

In the z-direction, we have

$$ V_{c_{12} k_{3} k_{2} k_{1}} ( \vec{z} ) = \frac{e_{0}^{2}}{2 \epsilon _{0} k_{z}} \times \bigl\langle \Phi _{c_{12}} ( \vec{z} ) \bigl\vert e^{- \vec{q}. \vec{z}} \bigr\vert \Phi _{k_{1}} ( \vec{z} ) \bigr\rangle \bigl\langle \Phi _{k_{3}} ( \vec{z} ) \bigl\vert e^{\vec{q}. \vec{z}} \bigr\vert \Phi _{k_{2}} ( \vec{z} ) \bigr\rangle $$

(26c)

With $\Phi _{c_{ij}} ( \vec{\rho} )$ and $\Phi _{k_{i}} ( \vec{\rho} )$ in Eq. (26b) are, respectively, the in-plane $( \vec{\rho} )$ wave functions of the QD and WL in the CB. Also $\Phi _{c_{12}} ( \vec{z} )$ and $\Phi _{k_{1}} ( \vec{z} )$ in Eq. (26c) are their corresponding in the z-direction. $V_{M 02}$ is the MNP potential between QD states $| 0 \rangle$ and $| 2 \rangle$ where the field is applied. For the WL-DQD system with QDs of a quantum disk shape, it is written (in the z-direction) as,

$$ \begin{aligned}[b] V_{d_{1} k_{3} k_{2} k_{1}} ( \vec{z} ) &= \frac{e^{2}}{2\epsilon _{0} k_{w}} \times \int _{0}^{z_{w}} A_{QD_{z}} \cos ( k_{z c_{12}} z ) \exp (- k_{1} z ) A_{w} \cos ( k_{1} z ) \,dz \\ &\quad {}\times \int _{0}^{z_{w}} A_{w} \cos ( \acute{k_{3}} \acute{z} ) \exp ( \acute{k_{2}} \acute{z} ) A_{w} \cos ( k_{2} \acute{z} ) \,d \acute{z} \end{aligned} $$

(26d)

where $k_{z c_{12}}$ is the QD wavenumber for the QD state, and $\acute{k_{3}}$ is the WL wavevector in the QW sublevel, which is slightly different from that represented by $k_{3}$.

3.6 OPW in the QD-WL interaction

In the ρ⃗-dimension, some difficulty arises from considering the OPW, which is inevitable in WL-QD transitions. In the ρ⃗-dimension, each WL-WL integration has eight integrations due to the consideration of OPW according to [9],

$$ \begin{aligned}[b]& \bigl\langle \Phi_{k_{2}} \bigl\vert e^{i \vec{q}. \vec{\rho}} \bigr\vert \Phi_{k_{3}} \bigr\rangle \\ &\quad= \frac{1}{ N_{k_{2}} N_{k_{3}}} \biggl\{ \bigl\langle \Phi_{k_{2}}^{\circ} \bigr\vert - \sum_{i} \bigl\langle \Phi_{d}^{i} \bigr\vert \bigl\langle \Phi_{k_{2}}^{\circ} \big\vert \Phi_{d}^{i} \bigr\rangle \biggr\} \bigl\vert e^{i \vec{q}. \vec{\rho}} \bigr\vert \biggl\{ \bigl\vert \Phi_{k_{3}}^{\circ} \bigr\rangle - \sum _{j} \bigl\vert \Phi_{d '}^{j} \bigr\rangle \bigl\langle \Phi_{d '}^{j} \big| \Phi_{k_{3}}^{\circ} \bigr\rangle \biggr\} \\ &\quad= \frac{1}{N_{k_{2}} N_{k_{3}}} \biggl\{ \bigl\langle \Phi_{k_{2}}^{\circ} \bigl\vert e^{i \vec{q}. \vec{\rho}} \bigr\vert \Phi_{k_{3}}^{\circ} \bigr\rangle - \sum_{i} \bigl\langle \Phi_{k_{2}}^{\circ} \bigl\vert e^{i \vec{q}. \vec{\rho}} \bigr\vert \Phi_{d}^{i} \bigr\rangle \bigl\langle \Phi_{d}^{i} \bigl\vert \Phi_{k_{3}}^{\circ} \bigr\rangle \\ &\qquad {}- \sum_{i} \bigl\langle \Phi_{d}^{i} \bigr\vert e^{i \vec{q}. \vec{\rho}} \bigl\vert \Phi_{k_{3}}^{\circ} \bigr\rangle \bigl\langle \Phi_{k_{2}}^{\circ} \bigr\vert \Phi_{d}^{i} \bigr\rangle + \sum_{ij} \bigl\langle \Phi_{d}^{i} \bigl\vert e^{i \vec{q}. \vec{\rho}} \bigr\vert \Phi_{d '}^{j} \bigr\rangle \bigl\langle \Phi_{k_{2}}^{\circ} \bigl\vert \Phi_{d}^{i} \bigr\rangle \bigl\langle \Phi_{d '}^{j} \bigr\vert \Phi_{k_{3}}^{\circ} \bigr\rangle \biggr\} \end{aligned} $$

(27)

with $N_{k_{2}} = \sqrt{1- \vert \sum_{i} \langle \Phi_{d}^{i} | \Phi_{k_{2}}^{\circ} \rangle \vert ^{2}}$. Also, $\Phi_{d}^{i}$ and $\Phi_{d '}^{j}$ are the QD wave functions for states $| i \rangle$ and $| j \rangle$ and $\Phi_{k_{j}}^{\circ}$ is the WL wave function before using OPW.

3.7 Scattering rates in the WL-DQD-MNP hybrid system

The other scattering rates in the WL-DQD-MNP hybrid system are listed in Table 1 and shown in Fig. 3. Process no. 2 in Table 1 is defined as,

$$ \begin{aligned}[b] S_{M, h, v_{32}}^{cap} &= S_{M, hh, v_{32}}^{cap} + S_{M, h e, v_{32}}^{cap} \\ &= \frac{2 \pi}{\hslash} \delta \bigl( E_{v_{32}}^{h} - E_{k_{1 h}}^{h} + E_{k_{3 h}}^{h} - E_{k_{2 h}}^{h} \bigr) \\ &\quad {}\times W_{M, v_{32} k_{3 h} k_{2 h} k_{1 h}} \bigl[ 2 W_{M, v_{32} k_{3 h} k_{2 h} k_{1 h}}^{*} -W_{M, v_{32} k_{3 h} k_{1 h} k_{2 h}}^{*} \bigr] \\ &\quad {}\times \bigl\{ ( 1 - f_{v_{32}} ) f_{k_{1 h}} ( 1 - f_{k_{3 h}} ) f_{k_{2 h}} - f_{v_{32}} ( 1 - f_{k_{1 h}} ) f_{k_{3 h}} ( 1 - f_{k_{2 h}} ) \bigr\} \\ &\quad {}+ \frac{2 \pi}{\hslash} \delta \bigl( E_{v_{32}}^{h} - E_{k_{1 h}}^{h} + E_{k_{3}}^{e} - E_{k_{2}}^{e} \bigr) \times 2 \vert W_{M, v_{32} k_{3} k_{2} k_{1 h}} \vert ^{2} \\ &\quad {}\times \bigl\{ ( 1 - f_{v_{32}} ) f_{k_{1 h}} ( 1 - f_{k_{3}} ) f_{k_{2}} - f_{v_{32}} ( 1 - f_{k_{1 h}} ) f_{k_{3}} ( 1 - f_{k_{2}} ) \bigr\} \end{aligned} $$

(28)

hh and he in the S rates are, respectively, refer to the hole-hole and hole-electron interactions. Please return to Fig. 2 to know the numbering of states in this equation. Process no. 3 in Table 1 is defined as,

$$ \begin{aligned}[b] S_{M,e, c_{01}}^{relax} &= S_{M,ee, c_{01}}^{relax} + S_{M,e h, c_{01}}^{relax} \\ &= \frac{2 \pi}{\hslash} \times 2 \vert W_{M, c_{01} k_{3} k_{2} c_{02}} \vert ^{2} \delta \bigl( E_{c_{01}}^{e} - E_{c_{02}}^{e} + E_{k_{3}}^{e} - E_{k_{2}}^{e} \bigr) \\ &\quad {}\times \bigl\{ ( 1 - f_{c_{01}} ) f_{c_{02}} ( 1 - f_{k_{3}} ) f_{k_{2}} - f_{c_{01}} ( 1 - f_{c_{02}} ) f_{k_{3}} ( 1 - f_{k_{2}} ) \bigr\} \\ &\quad {} + \frac{2 \pi}{\hslash} \times 2 \vert W_{M, c_{01} k_{3 h} k_{2 h} c_{02}} \vert ^{2} \delta \bigl( E_{c_{01}}^{e} - E_{c_{02}}^{e} + E_{k_{3 h}}^{h} - E_{k_{2 h}}^{h} \bigr) \\ &\quad {}\times \bigl\{ ( 1 - f_{c_{01}} ) f_{c_{02}} ( 1 - f_{k_{3 h}} ) f_{k_{2 h}} - f_{c_{01}} ( 1 - f_{c_{02}} ) f_{k_{3 h}} ( 1 - f_{k_{2 h}} ) \bigr\} \end{aligned} $$

(29a)

Process no. 4 in Table 1 is defined as,

$$ \begin{aligned}[b] S_{M,e, c_{01a}}^{relax} &= S_{M,ee, c_{01a}}^{relax} + S_{M,e h, c_{01a}}^{relax} \\ &= \frac{2 \pi}{\hslash} \times 2 \vert W_{M, c_{01} k_{3} c_{11} k_{2}} \vert ^{2} \delta \bigl( E_{c_{01}}^{e} - E_{k_{2}}^{e} + E_{k_{3}}^{e} - E_{c_{11}}^{e} \bigr) \\ &\quad {}\times \bigl\{ ( 1 - f_{c_{01}} ) f_{k_{2}} ( 1 - f_{k_{3}} ) f_{c_{11}} - f_{c_{01}} ( 1 - f_{k_{2}} ) f_{k_{3}} ( 1 - f_{c_{11}} ) \bigr\} \\ &\quad {}+ \frac{2 \pi}{\hslash} \times 2 \vert W_{M, c_{01} k_{3 h} v_{31} k_{2}} \vert ^{2} \delta \bigl( E_{c_{01}}^{e} - E_{k_{2}}^{e} + E_{k_{3 h}}^{h} - E_{v_{31}}^{h} \bigr) \\ &\quad {}\times \bigl\{ ( 1 - f_{c_{01}} ) f_{k_{2}} ( 1 - f_{k_{3 h}} ) f_{v_{31}} - f_{c_{01}} ( 1 - f_{k_{2}} ) f_{k_{3 h}} ( 1 - f_{v_{31}} ) \bigr\} \end{aligned} $$

(29b)

Process no. 5 in Table 1, which is a Coulomb exchange contribution process, is defined as,

$$ \begin{aligned}[b] S_{M, e, c_{01b}}^{relax} &= S_{M,ee, c_{01b}}^{relax} + S_{M,e h, c_{01b}}^{relax} \\ & = \frac{2 \pi}{\hslash} \times 2\operatorname{Re} \bigl[ W_{Mc_{01} k_{3} k_{2} c_{02}} W_{Mc_{01} k_{3} c_{02} k_{2}}^{*} \bigr] \delta \bigl( E_{c_{01}}^{e} - E_{c_{02}}^{e} + E_{k_{3}}^{e} - E_{k_{2}}^{e} \bigr) \\ &\quad {} \times \bigl\{ ( 1 - f_{c_{01}} ) f_{c_{02}} ( 1 - f_{k_{3}} ) f_{k_{2}} - f_{c_{01}} ( 1 - f_{c_{02}} ) f_{k_{3}} ( 1 - f_{k_{2}} ) \bigr\} \\ &\quad {}+ \frac{2 \pi}{\hslash} \times 2\operatorname{Re} \bigl[ W_{Mc_{01} k_{3 h} k_{2 h} c_{02}} W_{Mc_{01} k_{3 h} c_{02} k_{2 h}}^{*} \bigr] \delta \bigl( E_{c_{01}}^{e} - E_{c_{02}}^{e} + E_{k_{3 h}}^{h} - E_{k_{2 h}}^{h} \bigr) \\ &\quad {}\times \bigl\{ ( 1 - f_{c_{01}} ) f_{c_{02}} ( 1 - f_{k_{3 h}} ) f_{k_{2 h}} - f_{c_{01}} ( 1 - f_{c_{02}} ) f_{k_{3 h}} ( 1 - f_{k_{2 h}} ) \bigr\} \end{aligned} $$

(29c)

$Re()$ refers to the real part. Note that the relaxations in processes 3 and 4 are used with the Coulomb exchange part as follows,

$$ S^{relax} = S_{M,e, c_{01}}^{relax} + S_{M,e, c_{01a}}^{relax} - S_{M, e, c_{01b}}^{relax} $$

(29d)

Additionally, define,

$$\begin{aligned}& S_{M, ee,a}^{relax} = S_{M,ee, c_{01}}^{relax} + S_{M,ee, c_{01a}}^{relax} - S_{M,ee, c_{01b}}^{relax} \end{aligned}$$

(29e)

$$\begin{aligned}& S_{M, eh,a}^{relax} = S_{M,e h, c_{01}}^{relax} + S_{M,e h, c_{01a}}^{relax} - S_{M,e h, c_{01b}}^{relax} \end{aligned}$$

(29f)

The subscripts a and b are used to recognize these terms from the above terms that began with the same QD state. Process no. 6 in Table 1 is a mixed process and is defined by

$$ \begin{aligned}[b] S_{M,e h, c_{01}}^{mixed} &= \frac{2 \pi}{\hslash} \times 2 \vert W_{M, c_{01} k_{3 h} v_{21} k_{1}} \vert ^{2} \delta \bigl( E_{c_{01}}^{e} - E_{k_{1}}^{e} + E_{k_{3 h}}^{h} - E_{v_{21}}^{h} \bigr) \\ &\quad {}\times \bigl\{ ( 1 - f_{c_{01}} ) f_{k_{1}} ( 1 - f_{k_{3 h}} ) f_{v_{21}} - f_{c_{01}} ( 1 - f_{k_{1}} ) f_{k_{3 h}} ( 1 - f_{v_{21}} ) \bigr\} \end{aligned} $$

(30)

Process no. 7 in Table 1 is defined as,

$$ \begin{aligned}[b] S_{M, e, c_{12}}^{cap} &= S_{M,ee, c_{12a}}^{cap} + S_{M,e h, c_{12a}}^{cap} \\ &= \frac{2 \pi}{\hslash} \delta \bigl( E_{c_{12}}^{e} - E_{k_{1}}^{e} + E_{c_{11}}^{e} - E_{c_{01}}^{e} \bigr) \\ &\quad {}\times W_{Mc_{12} c_{11} c_{01} k_{1}} \bigl[ 2 W_{Mc_{12} c_{11} c_{01} k_{1}}^{*} -W_{Mc_{12} c_{11} k_{1} c_{01}}^{*} \bigr] \\ &\quad {}\times \bigl\{ ( 1 - f_{c_{12}} ) f_{k_{1}} ( 1 - f_{c_{11}} ) f_{c_{01}} - f_{c_{12}} ( 1 - f_{k_{1}} ) f_{c_{11}} ( 1 - f_{c_{01}} ) \bigr\} \\ &\quad {}+ \frac{2 \pi}{\hslash} \delta \bigl( E_{c_{12}}^{e} - E_{k_{1}}^{e} + E_{v_{31}}^{h} - E_{v_{21}}^{h} \bigr) \times 2 \vert W_{Mc_{12} v_{31} v_{21} k_{1}} \vert ^{2} \\ &\quad {}\times \bigl\{ ( 1 - f_{c_{12}} ) f_{k_{1}} ( 1 - f_{v_{31}} ) f_{v_{21}} - f_{c_{12}} ( 1 - f_{k_{1}} ) f_{v_{31}} ( 1 - f_{v_{21}} ) \bigr\} \end{aligned} $$

(31)

Process no. 8 in Table 1 is defined as,

$$ \begin{aligned}[b] S_{M, b, m}^{relax}& = S_{M,ee, c_{01a}}^{relax} + S_{M,e h, c_{01a}}^{relax} \\ &= \frac{2 \pi}{\hslash} \delta \bigl( E_{c_{01}}^{e} - E_{c_{02}}^{e} + E_{k_{1}}^{e} - E_{c_{11}}^{e} \bigr) \\ &\quad {}\times W_{Mc_{01} k_{1} c_{11} c_{02}} \bigl[ 2 W_{Mc_{01} k_{1} c_{11} c_{02}}^{*} -W_{Mc_{01} k_{1} c_{02} c_{11}}^{*} \bigr] \\ &\quad {}\times \bigl\{ ( 1 - f_{c_{01}} ) f_{c_{02}} ( 1 - f_{k_{1}} ) f_{c_{11}} - f_{c_{01}} ( 1 - f_{c_{02}} ) f_{k_{1}} ( 1 - f_{c_{11}} ) \bigr\} \\ &\quad {}+ \frac{2 \pi}{\hslash} \delta \bigl( E_{c_{01}}^{e} - E_{c_{02}}^{e} + E_{k_{1 h}}^{h} - E_{v_{31}}^{h} \bigr) \times 2 \vert W_{Mc_{01} k_{1 h} v_{31} c_{02}} \vert ^{2} \\ &\quad {}\times \bigl\{ ( 1 - f_{c_{01}} ) f_{c_{02}} ( 1 - f_{k_{1 h}} ) f_{v_{31}} - f_{c_{01}} ( 1 - f_{c_{02}} ) f_{k_{1 h}} ( 1 - f_{v_{31}} ) \bigr\} \end{aligned} $$

(32)

4 Calculation scenario

Each of the scattering rates of these eight processes in Eqs. (25), (28)-(32) is defined by two types of parameters: the screened Coulomb matrix element W (for direct or exchange process or both) and the Fermi distribution functions $f_{c_{ij}}$ (or $f_{v_{ij}}$). The first type, W, is defined by Eq. (26a) for electrons (and a similar equation for holes), which is calculated through Eq. (26b) and their related integrations in Eqs. (26c), (26d) and the OPW defined in Eq. (27). For the Fermi distribution functions, they are calculated by the distribution functions ($\rho _{ii}$) for their states ($| 0 \rangle \dots | 5 \rangle$), see Fig. 2. The distributions are defined in Appendix B through the density matrix system equations. The first five equations in Appendix B define these distributions as the occupation probabilities of the WL-DQD states. The rest of the equations in Appendix B define the density operators ($\rho _{ij}$) for the interactions between WL-DQD states ($| i \rangle$ and $| j \rangle$).

The screened Coulomb matrix elements here obey the Markov approximation in the time scale. Thus, the carrier population of the WL-DQD states is cast into the equation $\rho ^{\boldsymbol{\cdot}} = S^{in} ( 1-\rho ) - S^{out} \rho$ [10]. Then, the scattering rates are prepared to this form in Appendix A before introducing them into the density matrix system, Appendix B.

5 Results and discussion

MAOUD-37 software written in the MATLAB environment [9] was built in our laboratory to interact with the optical properties of QDs, and it is used in many of our articles. Plasmonic structures are also studied by this software [8]. This work involved strong coupling between DQDs and MNPs. It has material properties. The calculations began with QD energy levels, transition momenta, and Rabi frequencies. In the literature, QD energy states and momenta are taken from experimental values for materials different from those under study. This simulation has another property. The Coulomb interaction between QDs and MNPs is considered here, but this interaction is implicitly taken only through the Rabi frequency in the literature. QD energy states are calculated via the quantum disk model [29] and compared with experimental results [8]. The QD-WL-MNP scattering rates are defined in Eqs. (25) and (28)-(32). These equations are introduced to the density matrix system equations in Appendix B, which are then solved via the Runge–Kutta method in the MAOUD-37 software. The resulting energy states and momenta are listed in Table 2 for easy results. The pump and probe powers are defined by $I_{i} =c \sqrt{\varepsilon _{b}} \varepsilon _{0} \vert E_{i} \vert ^{2} / 10^{4}$, where $i=0,1$ is the probe and pump power, and $E_{i}$ is the intensity. The data used are listed in Table 2.

Table 2 The parameters used in the calculations

5.1 DQD-MNPs in the presence of WL (OPW)

Figure 4 shows the capture and relaxation rates of the WL-DQD-MNP hybrid system. For the in-capture rates, as shown in Fig. 4 (a), the WL hole in-capture rate $S_{h}^{5}$ (magenta curve) is the highest. The peak rate is $0.135\ ps^{-1}$ and occurs at the WL occupation of electrons $\rho _{44} =0.4$. This result is acceptable because the quantum well WL has many energy states and becomes a carrier reservoir for QDs [33]. As a result, more carriers can enter the WL, and a high carrier scattering rate is obtained. The QD electron rate $S_{e}^{1}$ (the red curve) is less by one order, where its peak is $0.01\ ps^{-1}$. After that, the QD hole rate $S_{h}^{3}$ appears (the black curve). The QD in-capture rates of $S_{e}^{0}$ and $S_{h}^{2}$ are very low. For the out-capture rate, as shown in Fig. 4 (b), the QD hole rate $S_{h}^{3}$ is the highest, and its peak is $0.135\ ps^{-1}$. After that, the QD electron rate $S_{e}^{1}$ is $0.01\ ps^{-1}$. The WL hole rate $S_{h}^{5}$ then appears and is reduced by two orders of magnitude from $S_{h}^{3}$. The values of $S_{e}^{0}$ and $S_{h}^{2}$ are very small. Figure 4 (c) shows the in-relaxation rates, which are the same for all the states. This is because of the calculation method, which is abstracted in Eqs. (A.2g), (A.2h) in Appendix A below. The in-relaxation peak occurs at $\rho _{44} \sim 0.4$ and is reduced at complete WL occupation. Figure 4 (d) shows that the out-relaxation rate is one order longer than the in-relaxation rate. Additionally, all the states have the same relaxation for the same reason. The results in Fig. 4 are consistent with those in [34], where the $S_{h}$ in-and-out-capture rates are the higher rates, having a peak, and the $S_{h}$ out-rate peaked at $0.12\ ps^{-1}$. The excited-state in-capture rate for holes is also the highest in [35]. The Pauli blocking is evident in the scattering rate behavior in all panels of Fig. 4, where the rates vanish at complete occupation ($\rho _{44} =0.4$).

Figure 4

(a) In-capture rates, (b) out-capture rates, (c) in-relaxation rates, and (d) out-relaxation rates of the DQD-MNP hybrid system. These figures are plotted at $T_{10} =150 \gamma _{0}$, $I_{1} =8\times 10^{-12} W$, and $I_{0} = 10^{-15} W$. The MNP radius is $\mathrm{r}_{\mathrm{m}} =8\ \mathrm{nm}$, and the distance between the DQDs and the MNP is $\mathrm{R}=7\ \mathrm{nm}$

Figure 5 shows the scattering times. Figure 5 (a) illustrates the electron capture time $\tau _{e}^{1}$. Figure 5 (b) shows that the hole capture time $\tau _{h}^{3}$ is shorter than the electron capture time in Fig. 5 (a) by one order. This result is with [36]. The electron capture time $\tau _{e}$ is longer than the hole in [11] by more than one order of magnitude. The electron capture time $\tau _{e}$ in [11] is more significant than our results by ∼ one order, demonstrating the ability of MNP to shorten the scattering time. The excited-state capture time for holes in [11] doubles our results. Figure 5 (c) shows the relaxation times for electrons and holes, respectively. As the relaxation rates are similar (in relation), their times are identical. At zero and full WL occupation, the relaxation times are high, while a dip occurs at $\rho _{44} \sim 0.45$. The relaxations are less than the hole (electron) capture time by one (two) order(s). The QD relaxation times in [11] are shorter than the capture times, coinciding with our results.

Figure 5

(a) Electron capture times, (b) hole capture times, and (c) electron relaxation time of the DQD-MNP hybrid system. These figures are plotted at $T_{10} =150 \gamma _{0}$, $I_{1} =8\times 10^{-12} W$, and $I_{0} = 10^{-15} W$. The MNP radius is $\mathrm{r}_{\mathrm{m}} =8\ \mathrm{nm}$, and the distance between the DQDs and the MNP is $\mathrm{R}=7\ \mathrm{nm}$

Figure 6 shows the effect of changing the distance R between the DQDs and the MNP on the scattering rate. Figure 6 (a) indicates that the $S_{e}^{1}$ in-capture rate is increased by $0.021\ ps^{-1}$ and peaks at $\rho _{44} =0.65$ when R is increased by $1\ nm$. Figure 6 (b) shows that the $S_{h}^{5}$ in-capture rate is increased by $0.04\ ps^{-1}$, corresponding to a more significant increase in the hole capture rate. Figure 6 (c) shows that the $S_{e}^{1}$ out capture rate is increased by $0.004\ ps^{-1}$. Figure 6 (d) shows that the $S_{h}^{3}$ out capture rate increment is $0.05\ ps^{-1}$. Figure 6 (e) shows that the in-relaxation $S_{h}^{5}$ rate increment is $0.05\ ps^{-1}$. Figure 6 (f) shows that the out-relaxation rate $S_{e}^{0}$ is $0.02\ ps^{-1}$ at the complete occupation of $\rho _{44}$. It was shown [37] that QD-MNP properties develop with increasing interparticle distance R. Except for Fig. 6 (f), the scattering rates peak at moderate WL occupation, while the difference between the two curves is maximized at the peak.

Figure 6

Scattering rates at two different DQD-MNP distances: (a) $S_{e}^{1}$ in-capture rate, (b) $S_{h}^{5}$ in-capture rate, (c) $S_{e}^{1}$ out-capture rate, (d) $S_{h}^{3}$ out-capture rate, (e) $S_{h}^{5}$ in-relaxation rate, and (f) $S_{e}^{0}$ out-capture rate of the DQD-MNP hybrid system. These figures are plotted at $T_{10} =150 \gamma _{0}$, $I_{1} =8\times 10^{-12} W$, and $I_{0} = 10^{-15} W$. The MNP radius is $\mathrm{r}_{\mathrm{m}} =8\ \mathrm{nm}$

Figure 7 shows the scattering rates at two values of tunneling $\mathrm{T}_{10} =150 0\gamma _{0}$ (blue curve) and $\mathrm{T}_{10} =15{,}000\gamma _{0}$, (red curve). The in–and–out–scattering rates with shallow values are not shown here. The $S_{e}^{1}$ in-capture rate, Fig. 7 (a), is not changed under increased tunneling; this is also the case for $S_{e}^{1}$ out-capture rate, Fig. 7 (c). This result occurs due to the vast distance (in energy) between DQD states in the CB, see Fig. 2, and the high relaxation rate from states (greater by one order). So, even high tunneling does not change the situation. The vast energy distance between CB QD states is assigned [29, 38]. The $S_{h}^{5}$ in-capture rate increases under increased tunneling, Fig. 7 (b). When tunneling is increased by one order, $S_{h}^{5}$ in-capture rate is (approximately) doubled. Similar behavior for $S_{h}^{3}$ out-capture rate is shown in Fig. 7 (d). This can be reasoned to the nearest VB QD energy states [29, 38], see Fig. 2. As the relaxations are taken similarly, $S_{e}^{0}$ in-relaxation and $S_{h}^{2}$ out-relaxation rates are shown in Fig. 7 (e) and (f), respectively. It is shown that $S_{h}^{2}$ out-relaxation rate, Fig. 7 (f), is reduced under tunneling; all other scattering rates contradict the behavior. The reason for this is that with increasing tunneling, the carriers can be distributed between DQD states, and then, there is a possibility of filling new carriers in these states. This behavior means increasing in-relaxation and reducing out-relaxation.

Figure 7

Scattering rates at two values of tunneling component: $T_{10} =150 0\gamma _{0}$ (blue curve) and $T_{10} =150 00\gamma _{0}$, (red curve). (a) $S_{e}^{1}$ in-capture rate, (b) $S_{h}^{5}$ in-capture rate, (c) $S_{e}^{1}$ out-capture rate, (d) $S_{h}^{3}$ out-capture rate, (e) $S_{e}^{0}$ in-relaxation rate, and (f) $S_{h}^{2}$ out-capture rate of the DQD-MNP hybrid system. These figures are plotted at $I_{1} =8\times 10^{-12} W$, and $I_{0} = 10^{-15} W$. The MNP radius is $\mathrm{r}_{\mathrm{m}} =8\ \mathrm{nm}$

Figure 8 shows the scattering rates at two values of MNP radius. Figure 8 (a) for $S_{e}^{1}$ in-capture rate and Fig. 8 (b) for $S_{h}^{3}$ out-capture rate. In both figures, the change in scattering rate is marginal and occurs at moderate WL electron occupation $\rho _{44}$. Such behavior occurs because of the strong coupling, and then the system behaves as a whole, and the change under structure parameters is small.

Figure 8

Scattering rates at two values of MNP radius: $\mathrm{r}_{\mathrm{m}} =4.5\ \mathrm{nm}$ (blue curve) and $\mathrm{r}_{\mathrm{m}} =10.5\ \mathrm{nm}$ (red curve). (a) $S_{e}^{1}$ in-capture rate, (b) $S_{h}^{3}$ out-capture rate of the DQD-MNP hybrid system. These figures are plotted at $T_{10} =150 \gamma _{0}$, $I_{1} =8\times 10^{-12} W$, and $I_{0} = 10^{-15} W$

The eh and he (e: electron and h: hole) processes are essential in most of the processes studied here and also to satisfy the stringent energy conservation conditions. Figure 9 shows the scattering rates under the approximation of neglecting these processes to see their importance. The $S_{e}^{0}$ in-capture rate is shown in Fig. 9 (a) and $S_{h}^{3}$ out-capture rate is shown in Fig. 9 (b). Also, the eh and he processes effect is marginal. Such behavior is also shown in [39]. This work deals with the WL-DQD-MNP hybrid structure under strong coupling. In both Figs. 8 and 9, the marginal change lies under the main effect of the MNP potential.

Figure 9

Comparison of scattering rates with the case of neglecting mixed processes (red line): $\mathrm{r}_{\mathrm{m}} =4.5\ \mathrm{nm}$ (blue curve) and (red curve). (a) $S_{h}^{3}$ out-capture rate and (b) $S_{e}^{0}$ in-relaxation rate of the DQD-MNP hybrid system. These figures are plotted at $T_{10} =150 \gamma _{0}$, $I_{1} =8\times 10^{-12} W$, $I_{0} = 10^{-15} W$ and $\mathrm{r}_{\mathrm{m}} =8\ \mathrm{nm}$

6 Conclusions

In this work, Coulomb scattering rates in the WL-DQD-MNP structure are modeled considering the MNP potential, which was not modeled earlier. The strong coupling and the OPW are considered. The Rabi frequency is normalized by considering strong coupling. It is then solved in the density matrix theory, where the modeled capture and scattering rates are introduced. The highest capture rate occurs for the QD hole states with the shortest capture times. The electron capture times are more significant than the one-order-of-magnitude relaxation times. The capture rates increase with increasing distance R between the DQDs and the MNP. Tunneling is of great importance in controlling the scattering rates. From a physical point of view, the scattering rates of the WL-DQD-MNP hybrid structure studied here lie under the Pauli-blocking behavior in filling the states, the energy distance between states, and the effect of the MNP potential under strong coupling.

Appendices

Appendix A: Capture and relaxation rates

For some DQD states, there is more than one rate (capture or relaxation). Therefore, one needs to introduce the total rate of entering the states. The occupation probability for the states included in the Coulomb matrix element is defined as shown in Eq. (24). Taking the matrix element $W_{M,d k_{2} k_{3} k_{1}}$, the occupations associated with the in-scattering rate are $f_{k_{1}}^{b} (1 - f_{k_{3}}^{b '} ) f_{k_{2}}^{b '}$, while those associated with the out-scattering rate are $(1-f_{k_{1}}^{b} ) f_{k_{3}}^{b '} (1 - f_{k_{2}}^{b '} )$. Then, the capture rate that comes from the mixing process in Eq. (30) is written as

$$\begin{aligned}& S_{M,e h,4}^{cap,in} = S_{M,e h, c_{01}}^{mixed} \bigl( \rho _{44} \times ( 1 - \rho _{55} ) \times \rho _{22} \bigr) \end{aligned}$$

(A.1a)

$$\begin{aligned}& S_{M,e h,4}^{cap,out} = S_{M,e h, c_{01}}^{mixed} \bigl( ( 1 - \rho _{44} ) \times \rho _{55} \times ( 1 - \rho _{22} ) \bigr) \end{aligned}$$

(A.1b)

The electron and hole occupation probabilities are $\rho _{ii}$ for the $| i \rangle$ state of the DQD. Note that $\rho _{44}$ and $\rho _{55}$ refer to the WL CB and VB (states $| 4 \rangle$ and $| 5 \rangle$) respectively, see Fig. 2. Additionally, there are many relaxation processes. The total relaxation rate must be collected. Using Eqs. (29b) and (29c), one can write,

$$\begin{aligned}& S_{M,ee,4}^{rel,in} = S_{M, ee,a}^{relax} \bigl( \rho _{00} \times ( 1 - \rho _{44} ) \times \rho _{44} \bigr) \end{aligned}$$

(A.1c)

$$\begin{aligned}& S_{M,ee,4}^{rel,out} = S_{M, ee,a}^{relax} \bigl( ( 1 - \rho _{00} ) \times \rho _{44} \times ( 1 - \rho _{44} ) \bigr) \end{aligned}$$

(A.1d)

$$\begin{aligned}& S_{M,e h,5}^{rel,in} = S_{M, eh,a}^{relax} \bigl( \rho _{00} \times ( 1 - \rho _{55} ) \times \rho _{55} \bigr) \end{aligned}$$

(A.1e)

$$\begin{aligned}& S_{M,e h,5}^{rel,out} = S_{M, eh,a}^{relax} \bigl( ( 1 - \rho _{00} ) \times \rho _{55} \times ( 1 - \rho _{55} ) \bigr) \end{aligned}$$

(A.1f)

Where $S_{M,ee,4}^{rel,in}$, $S_{M,ee,4}^{rel,out}$, $S_{M,e h,5}^{rel,in}$, $S_{M,e h,5}^{rel,out}$ are the in-and out-scattering relaxation rates for electrons and holes from states $| 4 \rangle$, $| 5 \rangle$, respectively. Collecting Eqs. (A.1c) with (A.1e) and (A.1d) with (A.1f) to get,

$$\begin{aligned}& S_{M,e,WD,0}^{rel,in} = S_{M,ee,4}^{rel,in} +S_{M,e h,5}^{rel,in} \end{aligned}$$

(A.1g)

$$\begin{aligned}& S_{M,e,WD,0}^{rel,out} = S_{M,ee,4}^{rel,out} + S_{M,e h,5}^{rel,out} \end{aligned}$$

(A.1h)

Where the subscript WD is WL-QD transition. Additionally, there is another relaxation transition. Using Eq. (29b) and (29c),

$$\begin{aligned}& S_{M,ee,1}^{rel,in} = S_{M, ee,a}^{relax} \bigl( \rho _{00} \times ( 1 - \rho _{44} ) \times \rho _{11} \bigr) \end{aligned}$$

(A.2a)

$$\begin{aligned}& S_{M,ee,1}^{rel,out} = S_{M, ee,a}^{relax} \bigl( ( 1 - \rho _{00} ) \times \rho _{44} \times ( 1 - \rho _{11} ) \bigr) \end{aligned}$$

(A.2b)

$$\begin{aligned}& S_{M,e h,3}^{rel,in} = S_{M, eh,a}^{relax} \bigl( \rho _{00} \times ( 1 - \rho _{55} ) \times \rho _{33} \bigr) \end{aligned}$$

(A.2c)

$$\begin{aligned}& S_{M,e h,3}^{rel,out} = S_{M, eh,a}^{relax} \bigl( ( 1 - \rho _{00} ) \times \rho _{55} \times ( 1 - \rho _{33} ) \bigr) \end{aligned}$$

(A.2d)

By combining equations (A.2a) with (A.2b) and (A.2c) with (A.2d), we obtain

$$\begin{aligned}& S_{M,e,DD,0}^{rel,in} = S_{M,ee,1}^{rel,in} + S_{M,e h,3}^{rel,in} \end{aligned}$$

(A.2e)

$$\begin{aligned}& S_{M,e,DD,0}^{rel,out} = S_{M,ee,1}^{rel,out} + S_{M,e h,3}^{rel,out} \end{aligned}$$

(A.2f)

Where the subscript DD is for QD-QD transitions. Now, the total relaxation rate is,

$$\begin{aligned}& S_{M,e,0,tot}^{rel,in} = S_{M,e,WD,0}^{rel,in} + S_{M,e,DD,0}^{rel,in} \end{aligned}$$

(A.2g)

$$\begin{aligned}& S_{M,e,0,tot}^{rel,out} = S_{M,e,WD,0}^{rel,out} + S_{M,e,DD,0}^{rel,out} \end{aligned}$$

(A.2h)

Where the subscript “tot” refers to the total rate. Also have, for the contributions to the $\rho _{11}$ from Eq. (25),

$$\begin{aligned}& S_{M,ee, c_{12}}^{cap,in} = S_{M,ee, c_{12}}^{cap} \bigl( \rho _{44} \times ( 1 - \rho _{44} ) \times \rho _{44} \bigr) \end{aligned}$$

(A.3a)

$$\begin{aligned}& S_{M,ee, c_{12}}^{cap,out} = S_{M,ee, c_{12}}^{cap} \bigl( ( 1 - \rho _{44} ) \times \rho _{44} \times ( 1 - \rho _{44} ) \bigr) \end{aligned}$$

(A.3b)

$$\begin{aligned}& S_{M,e h, c_{12}}^{cap,in} = S_{M,e h, c_{12}}^{cap} \bigl( \rho _{44} \times ( 1 - \rho _{55} ) \times \rho _{55} \bigr) \end{aligned}$$

(A.3c)

$$\begin{aligned}& S_{M,e h, c_{12}}^{cap,out} = S_{M,e h, c_{12}}^{cap} \bigl( ( 1 - \rho _{44} ) \times \rho _{55} \times ( 1 - \rho _{55} ) \bigr) \end{aligned}$$

(A.3d)

By collecting equations (A.3a) with (A.3c) and (A.3b) with (A.3d), one gets,

$$\begin{aligned}& S_{M,e,W,4}^{cap,in} = S_{M,ee, c_{12}}^{cap,in} + S_{M,e h, c_{12}}^{cap,in} \end{aligned}$$

(A.3e)

$$\begin{aligned}& S_{M,e,W,4}^{cap,out} = S_{M,ee, c_{12}}^{cap,out} + S_{M,e h, c_{12}}^{cap,out} \end{aligned}$$

(A.3f)

Additionally, from Eq. (31),

$$\begin{aligned}& S_{M,ee,c_{12a}}^{cap,in} = S_{M,ee, c_{12a}}^{cap} \bigl( \rho _{44} \times ( 1 - \rho _{11} ) \times \rho _{00} \bigr) \end{aligned}$$

(A.4a)

$$\begin{aligned}& S_{M,ee, c_{12a}}^{cap,out} = S_{M,ee, c_{12a}}^{cap} \bigl( ( 1 - \rho _{44} ) \times \rho _{11} \times ( 1 - \rho _{00} ) \bigr) \end{aligned}$$

(A.4b)

$$\begin{aligned}& S_{M,e h,c_{12a}}^{cap,in} = S_{M,e h, c_{12a}}^{cap} \bigl( \rho _{44} \times ( 1 - \rho _{33} ) \times \rho _{22} \bigr) \end{aligned}$$

(A.4c)

$$\begin{aligned}& S_{M,e h, c_{12a}}^{cap,out} = S_{M,e h, c_{12a}}^{cap} \bigl( ( 1 - \rho _{44} ) \times \rho _{33} \times ( 1 - \rho _{22} ) \bigr) \end{aligned}$$

(A.4d)

By collecting Eqs. (A.4a) with (A.4c) and (A.4b) with (A.4d), one gets,

$$\begin{aligned}& S_{M,e,D,4}^{cap,in} = S_{M,ee, c_{12a}}^{cap,in} + S_{M,e h, c_{12a}}^{cap,in} \end{aligned}$$

(A.4e)

$$\begin{aligned}& S_{M,e,D,4}^{cap,out} = S_{M,ee, c_{12a}}^{cap,out} + S_{M,e h, c_{12a}}^{cap,out} \end{aligned}$$

(A.4f)

With the total capture rates,

$$\begin{aligned}& S_{M,e,1,tot}^{cap,in} = S_{M,e,W,4}^{cap,in} + S_{M,e,D,4}^{cap,in} \end{aligned}$$

(A.4g)

$$\begin{aligned}& S_{M,e,1,tot}^{cap,out} = S_{M,e,W,4}^{cap,out} + S_{M,e,D,4}^{cap,out} \end{aligned}$$

(A.4h)

For $\rho _{22}$

$$\begin{aligned}& S_{M,e,2}^{cap,in} = S_{M,e h,4}^{cap,out} \end{aligned}$$

(A.5a)

$$\begin{aligned}& S_{M,e,2}^{cap,out} = S_{M,e h,4}^{cap,in} \end{aligned}$$

(A.5b)

For $\rho _{33}$, using Eq. (28),

$$\begin{aligned}& S_{M, hh, v_{32}}^{cap,in} = S_{M, hh, v_{32}}^{cap} \bigl( \rho _{55} \times ( 1 - \rho _{55} ) \times \rho _{55} \bigr) \end{aligned}$$

(A.6a)

$$\begin{aligned}& S_{M, hh, v_{32}}^{cap,out} = S_{M, hh, v_{32}}^{cap} \bigl( ( 1 - \rho _{55} ) \times \rho _{55} \times ( 1 - \rho _{55} ) \bigr) \end{aligned}$$

(A.6b)

$$\begin{aligned}& S_{M, h e, v_{32}}^{cap,in} = S_{M, h e, v_{32}}^{cap} \bigl( \rho _{55} \times ( 1 - \rho _{44} ) \times \rho _{44} \bigr) \end{aligned}$$

(A.6c)

$$\begin{aligned}& S_{M, h e, v_{32}}^{cap,out} = S_{M, h e, v_{32}}^{cap} \bigl( ( 1 - \rho _{55} ) \times \rho _{44} \times ( 1 - \rho _{44} ) \bigr) \end{aligned}$$

(A.6d)

Collecting Eqs. (A.6a) with (A.6c) and (A.6b) with (A.6d), one gets,

$$\begin{aligned}& S_{M,e,5,tot}^{cap,in} = S_{M, hh, v_{32}}^{cap,in} + S_{M, h e, v_{32}}^{cap,in} \end{aligned}$$

(A.6e)

$$\begin{aligned}& S_{M,e,5,tot}^{cap,out} = S_{M, hh, v_{32}}^{cap,out} + S_{M, h e, v_{32}}^{cap,out} \end{aligned}$$

(A.6f)

Therefore, for $\rho _{33}$ and $\rho _{55}$

$$\begin{aligned}& S_{M,e,3}^{cap,in} = S_{M,e,5,tot}^{cap,in}\quad \text{and}\quad S_{M,e,5}^{cap,in} = S_{M,e,5,tot}^{cap,out} \end{aligned}$$

(A.6g)

$$\begin{aligned}& S_{M,e,3}^{cap,out} = S_{M,e,5,tot}^{cap,out}\quad \text{and}\quad S_{M,e,5}^{cap,out} = S_{M,e,5,tot}^{cap,in} \end{aligned}$$

(A.6h)

Now, for $\rho _{44}$ in Eqs. (A.1a), (A.1b), (A.3e), (A.3f), and (A.4e), (A.4f),

$$\begin{aligned}& S_{M,e,4,tot}^{cap,in} = S_{M,e,W,4}^{cap,out} + S_{M,e h,4}^{cap,out} + S_{M,e,D,4}^{cap,out} \end{aligned}$$

(A.7a)

$$\begin{aligned}& S_{M,e,4,tot}^{cap,out} = S_{M,e,W,4}^{cap,in} + S_{M,e h,4}^{cap,in} + S_{M,e,D,4}^{cap,in} \end{aligned}$$

(A.7b)

Appendix B: Density matrix of the DQD-MNP system under Coulomb scattering with OPW

Applying the density matrix formalism for the WL-DQD-MNP structure, as shown in Fig. 2, under the rotating wave approximation, the change in occupation probability under the probe and pump applied fields with Rabi frequencies $\Omega _{02}$ and $\Omega _{13}$ and the tunneling component $T_{10}$ with time is written as

$$\begin{aligned}& \begin{aligned} \dot{\rho _{00}} &= S_{M,e,0,tot}^{rel,in} ( 1 - \rho _{00} ) - \bigl( S_{M,e,0,tot}^{rel,out} \rho _{00} \bigr) + S_{M,e h,4}^{cap,in} ( 1 - \rho _{00} ) - \bigl( S_{M,e h,4}^{cap,out} \rho _{00} \bigr) \\ &\quad {}+i T_{10} ( \rho _{10} - \rho _{01} ) +i ( \Omega _{02} - \eta \rho _{20} ) ( \rho _{20} - \rho _{02} ) +i \beta _{03} ( \rho _{30} - \rho _{03} ) +i \beta _{04} ( \rho _{40} - \rho _{04} )\end{aligned} \\& \begin{aligned} \dot{\rho _{11}} &= S_{M,e,0,tot}^{rel,in} ( 1 - \rho _{11} ) - \bigl( S_{M,e,0,tot}^{rel,out} \rho _{11} \bigr) + S_{M,e,1,tot}^{cap,in} ( 1 - \rho _{11} ) - \bigl( S_{M,e,1,tot}^{cap,out} \rho _{11} \bigr)\\ &\quad {} +i T_{10} ( \rho _{10} - \rho _{01} ) +i \beta _{12} ( \rho _{21} - \rho _{12} ) +i \Omega _{13} ( \rho _{31} - \rho _{13} ) +i \beta _{14} ( \rho _{41} - \rho _{14} )\end{aligned} \\& \begin{aligned} \dot{\rho _{22}} &= S_{M,e,0,tot}^{rel,in} ( 1 - \rho _{22} ) - \bigl( S_{M,e,0,tot}^{rel,out} \rho _{22} \bigr) - S_{M,e,2}^{cap,in} ( 1 - \rho _{00} ) + \bigl( S_{M,e,2}^{cap,out} \rho _{00} \bigr) \\ &\quad {}+i \beta _{23} ( \rho _{32} - \rho _{23} ) +i ( \Omega _{02} - \eta \rho _{20} ) ( \rho _{02} - \rho _{20} ) +i \beta _{12} ( \rho _{12} - \rho _{21} ) +i \beta _{25} ( \rho _{52} - \rho _{25} )\end{aligned} \\& \begin{aligned} \dot{\rho _{33}} &= S_{M,e,0,tot}^{rel,in} ( 1 - \rho _{33} ) - \bigl( S_{M,e,0,tot}^{rel,out} \rho _{33} \bigr) + S_{M,e,3}^{cap,in} ( 1 - \rho _{33} ) - \bigl( S_{M,e,3}^{cap,out} \rho _{33} \bigr) \\ &\quad {}+i \beta _{30} ( \rho _{03} - \rho _{30} ) +i \Omega _{13} ( \rho _{13} - \rho _{31} ) +i \beta _{23} ( \rho _{23} - \rho _{32} ) +i \beta _{35} ( \rho _{53} - \rho _{35} )\end{aligned} \\& \begin{aligned} \dot{\rho _{44}}& = S_{M,e,0,tot}^{rel,in} ( 1 - \rho _{44} ) - \bigl( S_{M,e,0,tot}^{rel,out} \rho _{44} \bigr) - S_{M,e,4,tot}^{cap,in} ( 1 - \rho _{11} ) + \bigl( S_{M,e,4,tot}^{cap,out} \rho _{11} \bigr)\\ &\quad {} +i \beta _{40} ( \rho _{04} - \rho _{40} ) +i \beta _{41} ( \rho _{14} - \rho _{41} )\end{aligned} \\& \begin{aligned} \dot{\rho _{55}} &= S_{M,e,0,tot}^{rel,in} ( 1 - \rho _{55} ) - \bigl( S_{M,e,0,tot}^{rel,out} \rho _{55} \bigr) - S_{M,e,5}^{cap,in} ( 1 - \rho _{33} ) + \bigl( S_{M,e,5}^{cap,out} \rho _{33} \bigr) \\ &\quad {}+i \beta _{52} ( \rho _{25} - \rho _{52} ) +i \beta _{53} ( \rho _{35} - \rho _{53} )\end{aligned} \\& \begin{aligned} \dot{\rho _{10}} &= - ( \gamma _{0} + \gamma _{1} ) \rho _{10} +i T_{10} ( \rho _{00} - \rho _{11} ) + ( i \beta _{12} \rho _{20} ) + ( i \Omega _{13} \rho _{30} ) + ( i \beta _{14} \rho _{40} ) \\ &\quad {}- i ( \Omega _{02} - \eta \rho _{20} ) \rho _{12} - i \beta _{30} \rho _{13} - i \beta _{40} \rho _{14}\end{aligned} \\& \begin{aligned} \dot{\rho _{20}} &= \bigl(\rho _{20} ( - i \Delta _{20} ) - ( \gamma _{0} + \gamma _{2} ) \bigr)+i ( \Omega _{20} - \eta \rho _{20} ) ( \rho _{00-} \rho _{22} ) + ( i \beta _{21} \rho _{10} ) +i \beta _{23} \rho _{30}\\ &\quad {} - ( i \beta _{40} \rho _{24} ) - i T_{10} \rho _{21} - ( i \beta _{30} \rho _{23} ) - i \beta _{52} \rho _{25}\end{aligned} \\& \begin{aligned} \dot{\rho _{30}} &= - ( \gamma _{0} + \gamma _{3} ) \rho _{30} +i \beta _{30} ( \rho _{00-} \rho _{33} ) + ( i \beta _{13} \rho _{10} ) +i \beta _{23} \rho _{20} \\ &\quad {}- i T_{10} \rho _{31} - i ( \Omega _{20} - \eta \rho _{20} ) \rho _{32} + ( i \beta _{35} \rho _{50} ) - ( i \beta _{40} \rho _{34} )\end{aligned} \\& \dot{\rho _{40}} = - ( \gamma _{0} + \gamma _{4} ) \rho _{40} - i ( \Omega _{20} - \eta \rho _{20} ) \rho _{42} +i \beta _{40} ( \rho _{00-} \rho _{44} ) + ( i \beta _{41} \rho _{10} ) - i T_{10} \rho _{14} - ( i \beta _{30} \rho _{43} ) \\& \begin{aligned} \dot{\rho _{21}} &= - ( \gamma _{2} + \gamma _{1} ) \rho _{21} +i \beta _{21} ( \rho _{11} - \rho _{22} ) +i ( \Omega _{20} - \eta \rho _{20} ) \rho _{01} +i \beta _{23} \rho _{31} + ( i \beta _{25} \rho _{51} ) \\ &\quad {}- i T_{10} \rho _{20} - ( i \beta _{41} \rho _{24} ) - ( i \Omega _{13} \rho _{23} )\end{aligned} \\& \begin{aligned} \dot{\rho _{31}} &= - ( \gamma _{3} + \gamma _{1} ) \rho _{31} +i \Omega _{13} ( \rho _{11-} \rho _{33} ) + ( i \beta _{30} \rho _{01} ) +i \beta _{23} \rho _{21} \\ &\quad {}- i T_{10} \rho _{30} - ( i \beta _{21} \rho _{32} ) + ( i \beta _{35} \rho _{51} ) - ( i \beta _{41} \rho _{34} )\end{aligned} \\& \dot{\rho _{41}} = - ( \gamma _{4} + \gamma _{1} ) \rho _{41} +i \beta _{41} ( \rho _{11-} \rho _{44} ) + ( i \beta _{40} \rho _{01} ) - i T_{10} \rho _{40} - ( i \beta _{21} \rho _{42} ) - ( i \Omega _{13} \rho _{43} ) \\& \begin{aligned} \dot{\rho _{23}} &= - ( \gamma _{2} + \gamma _{3} ) \rho _{23} +i \beta _{23} ( \rho _{33} - \rho _{22} ) +i ( \Omega _{20} - \eta \rho _{20} ) \rho _{03} - i \beta _{53} \rho _{25} + ( i \beta _{21} \rho _{13} ) \\ &\quad {}+ ( i \beta _{25} \rho _{53} ) - ( i \beta _{03} \rho _{20} ) - ( i \beta _{53} \rho _{25} ) - ( i \Omega _{13} \rho _{21} )\end{aligned} \\& \dot{\rho _{24}} = ( - \gamma _{2} + \gamma _{4} ) \rho _{42} +i ( \Omega _{20} - \eta \rho _{20} ) \rho _{04} +i \beta _{21} \rho _{41} - ( i \beta _{14} \rho _{21} ) - ( i \beta _{04} \rho _{20} ) +i \beta _{23} \rho _{34} \\& \begin{aligned} \dot{\rho _{25}} &= ( - \gamma _{2} + \gamma _{5} ) \rho _{25 } +i ( \Omega _{20} - \eta \rho _{20} ) \rho _{05} +i \beta _{25} ( \rho _{55} - \rho _{22} ) \\ &\quad {}+i \beta _{23} \rho _{25} - ( i \beta _{35} \rho _{23} ) + ( i \beta _{21} \rho _{15} )\end{aligned} \\& \dot{\rho _{35}} = - ( \gamma _{3} + \gamma _{5} ) \rho _{35 } +i \beta _{23} \rho _{25} +i \beta _{35} ( \rho _{55} - \rho _{33} ) + ( i \beta _{30} \rho _{05} ) + ( i \beta _{31} \rho _{15} ) - ( i \beta _{25} \rho _{32} ) \\& \dot{\rho _{43}} = - ( \gamma _{4} + \gamma _{3} ) \rho _{43 } +i \beta _{40} \rho _{03} + ( i \beta _{41} \rho _{13} ) - ( i \beta _{03} \rho _{40} ) - ( i \Omega _{13} \rho _{41} ) - i \beta _{23} \rho _{42} \\& \dot{\rho _{50}} = - ( \gamma _{5} + \gamma _{0} ) \rho _{50 } +i \beta _{52} \rho _{20} + ( i \beta _{53} \rho _{30} ) - i T_{10} \rho _{50} - i ( \Omega _{20} - \eta \rho _{20} ) \rho _{52} - ( i \beta _{30} \rho _{53} ) \\& \dot{\rho _{51}} = - ( \gamma _{5} + \gamma _{1} ) \rho _{51 } +i \beta _{52} \rho _{21} + ( i \beta _{53} \rho _{31} ) - i T_{10} \rho _{50} - ( i \beta _{21} \rho _{52} ) - ( i \Omega _{13} \rho _{53} ) \end{aligned}$$

(B.1)

The electron and hole occupation probabilities are $\rho _{ii}$ for the $| i \rangle$ state of the DQD, while the density operator $\rho _{ij}$ defines the interaction between DQD states $| i \rangle$ and $| j \rangle$. $\beta _{ij} = \frac{A_{ij}}{2} + \frac{1}{\tau _{t}}$, where $A_{ij}$ ($= \frac{\mu _{ij}^{2} \omega _{ij}^{2}}{3\pi \hslash \varepsilon _{s} c^{3}}$) is the Einstein coefficient, $\tau _{t}$ is the dipole dephasing time, and $\omega _{ij}$ is the transition frequency between the $| \mathrm{i} \rangle$ and $| \mathrm{j} \rangle$ states in the WL-DQD structure. The momentum of the transitions between the WL-QD and QD-QD transitions is $\mu _{ij}$. The momentum calculations are defined well in [16]. Based on the calculated momenta, the normalized Rabi frequency is computed from Eq. (22a)–(22c). Then, $\beta _{ij}$ is calculated depending on the computed momenta values.