1 Introduction

Hybridizing distinct physical systems possessing complementary charateristics is crucial for practical quantum information applications. In the past several years, hybrid quantum system based on magnonics has aroused much concern and gradually developed as a promising quantum information processing platform [1]. The magnon which generated by collective spin excitations in ferromagnetic crystals, can coherently interact with optical or microwave photons, as well as phonons through magneto-optical [2–9], magnetic dipole [10–14], and magnetostrictive interactions [15, 16] respectively. Besides, coherent effective coupling of the magnon and superconducting qubit in the cavity can be realized via the coupling of them to the same cavity modes [17] or the virtual photon excitation [14, 18, 19]. The successful development of the system has attracted considerable interest into this field. A variety of novel phenomena have been investigated, for instance, magnon gradient memory [20], level attraction [21–24], exceptional points [25–27], manipulation of Distant Spin Currents [28], bistability [29], nonreciprocity [30], magnon laser [31], etc.

Another attraction of cavity magnomechanical system is that it enables the exhibition of macroscopic quantum effects from the fundamental perspective. Therefore, a wide range of interests have been engaged to the generation of different types of macroscopic nonclassical states, including genuine tripartite [16] or bipartite entanglement between subsystems [32–42], squeezing of magnon and phonon [43, 44], magnon Fock states [45], among others. Recently, the proposal of optomagnonic Bell test [46] and entanglement between two orthogonally polarized optical modes [47] are also presented. Apart from the studies mentioned above, substantial attention has been attracted to the generation of quantum steering [48–52], which is essentially different from entanglement or Bell nonlocality for its asymmetric characteristics between the parties involved.

Here, inspired by the approach in Ref. [16], which has opened new perspectives for the realization of quantum interfaces among microwave, magnonic, and mechanical systems serving for the quantum information processing, we propose an effective approach for generating significant amount of photon-phonon entanglement and asymmetric steering in a cavity magnomechanical system which consists of a microwave cavity mode, macroscopic magnon and phonon modes. Light-mechanical [53–55] and mechanical-mechanical [56–58] quantum steering have been widely studied in cavity optomechanical systems, suggesting that one-way photon-phonon or phonon-phonon quantum steering can be achieved in such systems [55, 57, 58]. Primary researches also indicate that asymmetric steering between two magnons [48, 50] can be obtained in cavity magnonics. In particular, Tan etal. [51] proposed a deterministic scheme to generate long-distance hybrid entanglement and steering between a macroscopic mechanical oscillator and a magnon mode across about 10 GHz of frequency difference in a microwave-mediated magnomechanical interface. The strong stationary phonon-magnon entanglement and steering achieved are far beyond the sideband-resolved regime in the electromechanical subsystem. Nevertheless, whether asymmetric steering can be directly obtained in cavity magnomechanical system is still almost in blank. Recently, it is shown that one-way magnon-phonon steering can be remarkably enhanced by introducing a gain cavity mode in PT-symmetry system [49]. The studies pioneer a new way to seek the characteristics of asymmetric steering in magnomechanical interface. Unlike the proposal of Ref. [49], which concerned mainly about the enhancement of magnon-phonon asymmetric steering in PT-symmetry system, we show that significant amount of photon-phonon entanglement and asymmetric steering can be directly obtained in a cavity magnomechanical system. By applying a blue-detuned microwave driving field, we obtain a beam-splitter-like interaction Hamiltonian where the magnon mode acting as an engineered resevoir cools the Bogoliubov modes of microwave cavity mode and mechanical mode. By this means, the microwave cavity mode and mechanical mode can be driven to a two-mode squeezed state in the stationary limit. Particularly, strong two-way and one-way photon-phonon asymmetric quantum steering can be obtained with even equal dissipation. It is widely divergent with the conventional proposal, where additional unbalanced losses or noises should be imposed on the two subsystems. Our finding may be significant to expand our understanding of the essential physics of asymmetric steering as well as to extend the potential application of the cavity spintronics to quantum key distribution that are device-independent.

2 The model and dynamics

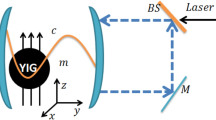
The cavity magnomechanical system is constituted by trapping a highly polished single-crystal yttrium iron garnet (YIG) sphere in a microwave cavity. The coupling between the microwave cavity mode a and magnon m (i.e., the quanta of collective motion of a large number of spins in YIG sphere) is mediated by the magnetic dipole interaction. The YIG sphere is also an excellent mechanical resonator b, which couple to magnons via magnetostrictive interaction. Therefore, a radiation pressure-like Hamiltonian similar to cavity optomechanical system can be used to describe the system [16],

$$\begin{aligned} H ={}& \omega _{a} a^{\dagger }a+\omega _{m} m^{\dagger }m+\omega _{b} b^{ \dagger }b+g\bigl(a+a^{\dagger} \bigr) \bigl(m+m^{\dagger}\bigr)+\eta m^{\dagger }m\bigl(b+b^{\dagger} \bigr) \\ &{}+ i E(t) \bigl(e^{-i\omega _{d}t}m^{\dagger }-e^{i\omega _{d}t}m\bigr), \end{aligned}$$
(1)

where \(\hbar =1\) is used. The parameter \(w_{j}\) is the resonance frequency of the bosonnics mode j (\(j=a, b\), and m), g and η respectively denotes the magnetic dipole interaction and magnetostrictive interaction strength. The last term of the Hamiltonian represents the driving term of the magnon mode with the time-dependent amplitude \(E(t)\) and frequency \(\omega _{d}\). A wide range of the magnon frequency \(w_{m}=\Upsilon H_{B}\) can be adjusted by altering the strength of the external bias magnetic field \(H_{B}\) with respect to the gyromagnetic ratio ϒ. The magnetic dipole interaction \(g\propto \sqrt{N}\) with N being the number of spins. Strong cavity-magnon coupling can be realized in recent experiments while the magnetostrictive interaction strength η is typically weak. Nevertheless, we can effectively enhance the magnetostrictive interaction by strong driving. The magnetic dipole interaction term \(g(a+a^{\dagger})(m+m^{\dagger})\) can be rewritten as \(g(am^{\dagger}+a^{\dagger }m)\) by adopting the rotating-wave approximation. Then, moving into a rotating frame with respect to \(\omega _{d} (m^{\dagger }m+a^{\dagger }a)\), we obtain

$$\begin{aligned} H_{R} ={}& \Delta _{a} a^{\dagger }a+ \Delta _{m} m^{\dagger }m+\omega _{b} b^{\dagger }b+g \bigl(am^{\dagger}+a^{\dagger }m\bigr)+\eta m^{\dagger }m \bigl(b+b^{\dagger}\bigr) \\ &{}+ i E(t) \bigl(m^{\dagger }-m\bigr), \end{aligned}$$
(2)

with \(\Delta _{a}=\omega _{a}-\omega _{d}\) and \(\Delta _{m}=\omega _{m}-\omega _{d}\).

In noisy environments, the coupling between the system and environment introduces damping channel into the system, which inevitably allows environmental noise to perturb the system. In this case, the system dynamics is described by the Heisenberg–Langevin equations (HLEs) [59]:

$$\begin{aligned} &\dot{a}=-(\kappa _{a}/2+i\Delta _{a})a-ig m +\sqrt{\kappa _{a}}a ^{ \mathrm{{in}}}(t), \end{aligned}$$
(3a)
$$\begin{aligned} &\dot{b}=-(\gamma /2+i\omega _{b})b-i\eta m^{\dagger }m+\sqrt{ \gamma}b^{ \mathrm{{in}}}(t) , \end{aligned}$$
(3b)
$$\begin{aligned} &\dot{m}=-(\kappa _{m}/2+i\Delta _{m})m-iga-i\eta m \bigl(b+b^{\dagger}\bigr)+E(t)+ \sqrt{\kappa _{m}}m ^{\mathrm{{in}}}(t). \end{aligned}$$
(3c)

Here, \(\kappa _{a}\), γ, and \(\kappa _{m}\) stand for the dissipation rates of the cavity mode, the phonon mode, and the magnon mode, respectively. \(a^{\mathrm{{in}}}(t)\), \(b^{\mathrm{{in}}}(t)\), and \(m^{\mathrm{{in}}}(t)\) are input noise operators of photon, phonon, and magnon modes, which obeying the auto-correlation functions:

$$\begin{aligned} &\bigl\langle {{a}^{\mathrm{{in}}}(t)} {a^{\mathrm{{in}\dagger}}\bigl(t' \bigr)}\bigr\rangle = \delta \bigl(t - t'\bigr), \end{aligned}$$
(4a)
$$\begin{aligned} &\bigl\langle {{a}^{\mathrm{{in}\dagger}}(t)} {a^{\mathrm{{in}}}\bigl(t' \bigr)} \bigr\rangle = 0, \end{aligned}$$
(4b)
$$\begin{aligned} &\bigl\langle {{b}^{\mathrm{{in}}}(t)} {b^{\mathrm{{in}\dagger}}\bigl(t' \bigr)}\bigr\rangle = (\bar{n}_{b}+1) \delta \bigl(t - t' \bigr), \end{aligned}$$
(4c)
$$\begin{aligned} &\bigl\langle {{b}^{\mathrm{{in}\dagger}}(t)} {b^{\mathrm{{in}}}\bigl(t' \bigr)} \bigr\rangle = \bar{n}_{b} \delta \bigl(t - t' \bigr), \end{aligned}$$
(4d)
$$\begin{aligned} &\bigl\langle {{m}^{\mathrm{{in}}}(t)} {m^{\mathrm{{in}\dagger}}\bigl(t' \bigr)}\bigr\rangle = \delta \bigl(t - t'\bigr), \end{aligned}$$
(4e)
$$\begin{aligned} &\bigl\langle {{m}^{\mathrm{{in}\dagger}}(t)} {m^{\mathrm{{in}}}\bigl(t' \bigr)} \bigr\rangle = 0, \end{aligned}$$
(4f)

with \(\bar{n}_{b}=(\exp (\hbar \omega _{b}/(k_{B}T))-1)^{-1}\) being the mean thermal phonon number at the environmental temperature T. Here, a Markovian approximation has been made and the system is at lower temperature that the mean thermal photon and magnon number are almost negligible.

The standard linearization technique [60] can be adopted in the presence of strong driving field. Since large amplitudes of the cavity and magnon modes are guaranteed due to the beamsplitter interaction between the cavity and the magnon mode, by substituting each system operators o (\(o=a, m\), and b) with the sum of classical steady-state mean values \(\langle o(t)\rangle \) and its surrounding quantum fluctuations δo, Eq. (2) is linearized as

$$\begin{aligned} {H^{{\mathrm{{lin}}}}} ={}& \Delta _{a} \delta a^{\dagger }\delta a + \tilde{\Delta}_{m} \delta m^{\dagger } \delta m +\omega _{b} \delta b^{ \dagger }\delta b+g\bigl(\delta a \delta m^{\dagger}+\delta a^{\dagger }\delta m\bigr) \\ &{}+\bigl(G(t)^{*}\delta m+G(t) \delta m^{\dagger}\bigr) \bigl( \delta b+\delta b^{\dagger}\bigr), \end{aligned}$$
(5)

where the effective detuning \(\tilde{\Delta}_{m}=\Delta _{m} +\eta (\langle b(t)\rangle +\langle b(t) \rangle ^{*})\simeq \Delta _{m}\) and the effective coupling \(G(t)=\eta \langle m(t)\rangle \). Here, we have dropped the small term just as standard linearization technique does.

After standard linearization techniques are applied to Eq. (3a)–(3c), we obtain the following differential equations for the classical steady-state mean values:

$$\begin{aligned} &\dot{\bigl\langle a(t)\bigr\rangle }=-(\kappa _{a}/2+i\Delta _{a})\bigl\langle a(t) \bigr\rangle -ig\bigl\langle m(t)\bigr\rangle , \end{aligned}$$
(6a)
$$\begin{aligned} &\dot{\bigl\langle b(t)\bigr\rangle }=-(\gamma /2+i\omega _{b})\bigl\langle b(t) \bigr\rangle -i\eta \bigl\vert \bigl\langle m(t)\bigr\rangle \bigr\vert ^{2}, \end{aligned}$$
(6b)
$$\begin{aligned} &\dot{\bigl\langle m(t)\bigr\rangle }=-(\kappa _{m}/2+i\Delta _{m})\bigl\langle m(t) \bigr\rangle -ig\bigl\langle a(t)\bigr\rangle -i\eta \bigl\langle m(t)\bigr\rangle \bigl(\bigl\langle b(t) \bigr\rangle +\bigl\langle b(t)\bigr\rangle ^{*}\bigr)+E(t), \end{aligned}$$
(6c)

and the linearized QLEs for the quantum fluctuation operators:

$$\begin{aligned} &\dot{\delta a}=-(\kappa _{a}/2+i\Delta _{a})\delta a-ig \delta m+ \sqrt{\kappa _{a}} a^{\mathrm{{in}}}(t), \end{aligned}$$
(7a)
$$\begin{aligned} &\dot{\delta b}=-(\gamma /2+i\omega _{b})\delta b-i\eta \bigl(\bigl\langle m(t) \bigr\rangle ^{*} \delta m+\bigl\langle m(t)\bigr\rangle \delta m^{\dagger }\bigr) +\sqrt{ \gamma}b^{\mathrm{{in}}}(t), \end{aligned}$$
(7b)
$$\begin{aligned} &\dot{\delta m}=-(\kappa _{m}/2+i\Delta _{m})\delta m-ig \delta a-i \eta \bigl[(\langle m\rangle \bigl(\delta b+\delta b^{\dagger} \bigr)+\delta m\bigl(\bigl\langle b(t) \bigr\rangle +\bigl\langle b(t)\bigr\rangle ^{*}\bigr) \bigr] \\ &\phantom{\dot{\delta m}=}{}+ \sqrt{\kappa _{m}}m^{\mathrm{{in}}}(t). \end{aligned}$$
(7c)

By applying the blue-detuned (\(\omega _{1}=\tilde{\Delta}_{m}+\omega _{b}\)) and red-detuned (\(\omega _{2}=\tilde{\Delta}_{m}-\omega _{b}\)) two-tone driving lasers

$$\begin{aligned} E(t)=\sum_{j = 1,2}E_{j}e^{-i\omega _{j}t}, \end{aligned}$$
(8)

the asymptotic solution \(\langle m(t)\rangle \) in the long evolution limit can be expressed as

$$\begin{aligned} \bigl\langle m(t)\bigr\rangle \approx \sum_{j = 1,2} \frac{E_{j}e^{-i\omega _{j}t}}{\kappa _{m}/2+i(\tilde{\Delta}_{m}\mp \omega _{j})+g^{2}/[\kappa _{a}/2+i(\Delta _{a}\mp \omega _{j})]}. \end{aligned}$$
(9)

By performing the unitary transformation \(U(t)=\exp [-it(\Delta _{a} \delta a^{\dagger }\delta a + \tilde{\Delta}_{m} \delta m^{\dagger }\delta m + \omega _{b} \delta b^{\dagger }\delta b)]\), the asymptotic Hamiltonian of Eq. (5) in the interaction picture becomes

$$\begin{aligned} {H^{{\mathrm{{asy}}}}} ={}& g\delta a\delta m^{\dagger }e^{-i(\Delta _{a}- \tilde{\Delta}_{m})t}+G_{1} \delta m^{\dagger}\delta b^{\dagger }+G_{1} \delta m^{\dagger}\delta b e^{-2i\omega _{b}t}+G_{2}\delta m^{\dagger} \delta b^{\dagger }e^{2i\omega _{b}t} \\ &{}+G_{2}\delta m^{\dagger}\delta b +h.c., \end{aligned}$$
(10)

with

$$\begin{aligned} &G_{1}= \frac{\eta E_{1}}{\kappa _{m}/2+i(\tilde{\Delta}_{m}-\omega _{1})+g^{2}/[\kappa _{a}/2+i(\Delta _{a}-\omega _{1})]}, \end{aligned}$$
(11a)
$$\begin{aligned} &G_{2}= \frac{\eta E_{2}}{\kappa _{m}/2+i(\tilde{\Delta}_{m}+\omega _{2})+g^{2}/[\kappa _{a}/2+i(\Delta _{a}+\omega _{2})]}. \end{aligned}$$
(11b)

If we set \(\Delta a =\tilde{\Delta}_{m}\), under the condition of weak coupling (i.e., \(G_{1},G_{2}\ll \omega _{b}\)), Eq. (10) becomes

$$\begin{aligned} {H^{{\mathrm{{eff}}}}} =g\delta a\delta m^{\dagger }+G_{1} \delta m^{\dagger} \delta b^{\dagger}+G_{2}\delta m^{\dagger}\delta b +h.c.. \end{aligned}$$
(12)

In the following, the cases of two-tone driving and blue-detuned driving only will be respectively discussed. Introducing three annihilation operators of Bogoliubove-mode

$$\begin{aligned} &\beta _{1}=S(r_{1})\delta bS^{\dagger}(r_{1})= \delta b \cosh r_{1}+ \delta b^{\dagger }\sinh r_{1}, \end{aligned}$$
(13a)
$$\begin{aligned} &\beta _{2}=S(r_{2})\delta aS^{\dagger}(r_{2})= \delta a \cosh r_{2}+ \delta b^{\dagger }\sinh r_{2}, \end{aligned}$$
(13b)
$$\begin{aligned} &\beta _{3}=S(r_{2})\delta bS^{\dagger}(r_{2})= \delta b \cosh r_{2}+ \delta a^{\dagger }\sinh r_{2}, \end{aligned}$$
(13c)

where the squeezing operators \(S(r_{j})\) and squeezing parameters \(r_{j}\) are defined as

$$\begin{aligned} &S(r_{1})=\exp \bigl[r_{1}\bigl(\delta b\delta b-\delta b^{\dagger }\delta b^{\dagger}\bigr)\bigr], \end{aligned}$$
(14a)
$$\begin{aligned} &S(r_{2})=\exp \bigl[r_{2}\bigl(\delta a\delta b-\delta a^{\dagger }\delta b^{\dagger}\bigr)\bigr], \end{aligned}$$
(14b)
$$\begin{aligned} &r_{1}=\tanh ^{-1}(G_{1}/G_{2}), \end{aligned}$$
(14c)
$$\begin{aligned} &r_{2}=\tanh ^{-1}(G_{1}/g). \end{aligned}$$
(14d)

The Hamiltonian of Eq. (12) is thus given by

$$\begin{aligned} {H_{1}^{{\mathrm{{eff}}}}} = g\delta a\delta m^{\dagger }+\tilde{G_{1}} \delta m^{\dagger}\beta _{1} +h.c., \end{aligned}$$
(15)

or

$$\begin{aligned} {H_{2}^{{\mathrm{{eff}}}}} = G_{2}\delta b \delta m^{\dagger }+\tilde{G_{2}} \delta m^{\dagger}\beta _{2} +h.c., \end{aligned}$$
(16)

with the effective coupling strengths

$$\begin{aligned} &\tilde{G_{1}}=\sqrt{G^{2}_{2}-G_{1}^{2}}, \end{aligned}$$
(17a)
$$\begin{aligned} &\tilde{G_{2}}=\sqrt{g^{2}-G_{1}^{2}}. \end{aligned}$$
(17b)

Both Eqs. (15) and (16) are Hamiltonian that consist of a group of beam-splitter-like interaction terms. It is well known that this type of Hamiltonian can be used for optomechanical sideband cooling [61, 62]. For small dissipation rate of the phonon mode, the dissipations of the cavity mode and the magnon mode can be exploited to cool the Bogoliubove-mode \(\beta _{1}\), generating single-mode squeezed state of δb. In other words, the coupling between δm and \(\beta _{1}\) induces the cooling process of \(\beta _{1}\), while the coupling between δa and δm is responsible for cooling the δm mode. The cooling process of \(\beta _{2}\) can be directly realized via the interaction term between the magnon mode δm and the Bogoliubove-mode \(\beta _{2}\) when \(G_{2}=0\). Therefore, under appropriate system parameters, it is possible to cool the Bogoliubove-mode \(\beta _{1}\) or \(\beta _{2}\) to near ground state. From Eq. (13a)–(13c), it was found apparently that the ground state of \(\beta _{1}\) is the single-mode squeezed state of δb while the ground state of \(\beta _{2}\) is two-mode squeezed state of δa and δb. We note that the scheme to generate single-mode squeezed state of δb has been proposed by applying a two-tone microwave fields in a cavity magnomehanical system [44]. The physical essence of the scheme is to adopt the cascaded dissipative cooling process, which can also be used to generate entanglement between two microwave fields [63]. Therefore, we will focus on the generation of entanglement and asymmetric quantum steering between the cavity mode δa and mechanical mode δb by applying the blue-detuned microwave driving only. Our proposal not only provide another way to comprehend the scheme in Ref. [44] but also expanded its contents in the field of entanglement and asymmetric quantum steering.

3 Evolution equation of the covariance matrix

Introducing column vectors of dimensionless quadrature operators and their input noises

$$\begin{aligned} &R=(q_{\delta a},p_{\delta a},q_{\delta b},p_{\delta b},q_{\delta m},p_{ \delta m})^{T}, \end{aligned}$$
(18a)
$$\begin{aligned} &N(t)=(\sqrt{\kappa _{a}}q_{a^{in}},\sqrt{\kappa _{a}}p_{a^{in}}, \sqrt{\gamma}q_{b^{in}},\sqrt{ \gamma}p_{b^{in}},\sqrt{\kappa _{m}}q_{m^{in}}, \sqrt{ \kappa _{m}}p_{m^{in}})^{T}, \end{aligned}$$
(18b)

which are related to bosonic modes o (\(o\in \{\delta a,\delta b, \delta m,a^{\mathrm{{in}}}(t),b^{\mathrm{{in}}}(t),m^{\mathrm{{in}}}(t)\}\)) via \(q_{o}=(o+o^{ \dagger})/\sqrt{2}\) and \(p_{o}=(o-o^{\dagger})/(i\sqrt{2})\), Eq. (7a)–(7c) is thus rewritten as

$$\begin{aligned} \dot{R}=MR+N, \end{aligned}$$
(19)

with

$$\begin{aligned} {\footnotesize M = \begin{pmatrix} -\kappa _{a}/2&0&0&0&0&g \\ 0&-\kappa _{a}/2&0&0&-g&0 \\ 0&0&-\gamma /2&0&f_{1I}+f_{2I}&f_{1R}-f_{2R} \\ 0&0&0&-\gamma /2&-f_{1R}-f_{2R}&f_{1I}-f_{2I} \\ 0&g&f_{2I}-f_{1I}&f_{1R}-f_{2R}&-\kappa _{m}/2&0 \\ -g&0&-f_{1R}-f_{2R}&-f_{1I}-f_{2I}&0&-\kappa _{m}/2 \end{pmatrix},} \end{aligned}$$
(20)

where we have used the asymptotic approximation Hamiltonian of Eq. (10), and \(f_{jR}\) and \(f_{jR}\) are independent the real parts and imaginary parts of \(f_{j}\) defined by

$$\begin{aligned} &f_{1}(t)=G_{2}+G_{1}e^{-2i\omega _{b}t}, \end{aligned}$$
(21a)
$$\begin{aligned} &f_{2}(t)=G_{1}+G_{2}e^{2i\omega _{b}t}. \end{aligned}$$
(21b)

When focus only on blue detuning laser driving, \(G_{2}=0\) in all the terms.

Due to the linearized Hamiltonian of the system, an initial Gaussian state of the system will remains Gaussian as it is stable [64]. To obtain the information-related properties of a Gaussian state, we introduce the \(6\times 6\) covariance matrix (CM) σ with entries defined as [64–66]

$$\begin{aligned} \sigma _{j,k}= &\langle R_{j}R_{k}+R_{k}R_{j} \rangle /2. \end{aligned}$$
(22)

Here, \(R_{j}\) represents the jth element of column vector R. It can be gained from Eqs. (4a)–(4f), (19), and (22) [67]

$$\begin{aligned} \dot{\sigma}=M\sigma +\sigma M^{T}+D, \end{aligned}$$
(23)

where D is a diffusion matrix. The components of D is relevant to the noise correlation functions in Eq. (4a)–(4f). Obviously,

$$\begin{aligned} D_{j,k}\delta \bigl(t-t'\bigr)=\bigl\langle N_{j}(t)N_{k}\bigl(t'\bigr)+N_{k} \bigl(t'\bigr)N_{j}(t) \bigr\rangle /2. \end{aligned}$$
(24)

It can be actually proved that D is diagonal

$$\begin{aligned} D=\mathrm{diag}\bigl[\kappa _{a}/2,\kappa _{a}/2,\kappa _{b}(2\bar {\mathrm{n}}_{b}+1)/2, \kappa _{b}(2\bar {\mathrm{n}}_{b}+1)/2,\kappa _{m}/2,\kappa _{m}/2\bigr]. \end{aligned}$$
(25)

In the following, Eq. (23) will be utilized to numerically simulate the time evolution of photon-phonon entanglement and asymmetric quantum steering.

For a Gaussian state of the two modes of interest, the logarithmic negativity \(E_{\mathrm{{N}}}\) [68–70] is used to gauge its level of entanglement. As for quantum steering, it is very convenient to introduce a computable criterion based on the form of quantum coherent information [71]. Both of the above measures can be calculated from the reduced CM \({\sigma _{R}}(t)\) for the photon and phonon modes

$$\begin{aligned} {\sigma _{R}}(t) = \begin{pmatrix} {{\sigma _{1}}}&{{\sigma _{\mathrm{{3}}}}} \\ {\sigma _{\mathrm{{3}}}^{\mathrm{{T}}}}&{{\sigma _{2}}} \end{pmatrix}, \end{aligned}$$
(26)

with each \(\sigma _{j}\) being a \(2\times 2\) subblock matrices of \({\sigma _{R}}(t)\). The amount of entanglement is given by

$$\begin{aligned} E_{\mathrm{{N}}} = \max \bigl[0, - \ln (2\vartheta )\bigr], \end{aligned}$$
(27)

with

$$\begin{aligned} \vartheta \equiv 2^{-1/2}\bigl\{ \Sigma _{-}-\bigl[\Sigma _{-}^{2}-4I_{4}\bigr]^{1/2} \bigr\} ^{1/2}, \end{aligned}$$
(28)

and

$$\begin{aligned} \Sigma _{-} \equiv I_{1} + I_{2} - 2I_{3}, \end{aligned}$$
(29)

where \(I_{1}=\det{\sigma _{1}}\), \(I_{2}=\det{\sigma _{2}}\), \(I_{3}=\det{\sigma _{\mathrm{{3}}}}\), and \(I_{4}=\det{\sigma _{R}}\) are symplectic invariants. The measure of steerability from photon to phonon can be expressed as

$$\begin{aligned} G_{A}\equiv G^{a\rightarrow b}({\sigma _{\mathrm{{R}}}}) = \max \biggl[0, \frac{1}{2} \ln \frac{I_{1}}{4I_{4}}\biggr], \end{aligned}$$
(30)

and the measure of steerability from phonon to photon can be computed by swapping the corresponding item of photon and phonon, i.e.,

$$\begin{aligned} G_{B}\equiv G^{b\rightarrow a}({\sigma _{\mathrm{{R}}}}) = \max \biggl[0, \frac{1}{2} \ln \frac{I_{2}}{4I_{4}}\biggr]. \end{aligned}$$
(31)

Since both the measures of entanglement and quantum steering introduced can be calculated by the symplectic invariants, it is convenient for both numerical simulation and comparison between then.

4 The results and discussion

In order to demonstrate the feasibility of the proposal, we plot in Fig. 1 the peak values of photon-phonon entanglement and asymmetric steering for each time period in the asymptotic regime as functions of mechanical dissipation rate γ and mean thermal phonon numbe \(\bar{n}_{b}\). On the one hand, it can be found from Fig. 1 that the maximal values of photon-phonon entanglement \(E_{\mathrm{{N}}}\) and asymmetric steering \(G_{A}\) as well as \(G_{B}\) all decrease with the increase of \(\bar{n}_{b}\). The phenomenon is obvious and easy to understand. From Eq. (13a)–(13c), we can find that the temperature of the Bogoliubov mode \(\beta _{2}\) is related to the temperature of the cavity mode δa and the mechanical mode δb. When the mechanical dissipation rate γ takes a fixed value, the interaction between the mechanical mode δb and its thermal bath accordingly maintains a constant intensity, the increase of \(\bar{n}_{b}\) (i.e., raising the temperature T of thermal bath) will raise the temperature of mechanical mode δb as well as Bogoliubov-mode \(\beta _{2}\). Since both photon-phonon entanglement and asymmetric steering are sensitive to the effective temperature of Bogoliubov-mode \(\beta _{2}\), the optimal values obtained are bound to decrease with the increase of \(\bar{n}_{b}\). However, the \(a\rightarrow b\) steering \(G_{A}\) drops faster than photon-phonon entanglement \(E_{N}\) and the \(b\rightarrow a\) steering \(G_{B}\), on account of the asymmetry of the system. As a consequence, the states that only have one-way quantum steering can be obtained under properly parameters. Figure 1, on the other hand, also displays that the maximal values of photon-phonon entanglement and asymmetric steering are nonmonotonic functions of γ and take a maximum for a specific γ. Peculiarly, entanglement and steering are more sensitive to γ with the increase of \(\bar{n}_{b}\). The larger of γ means stronger coupling of the mechanical mode δb and its thermal bath. When the mean thermal phonon number \(\bar{n}_{b}\) is not negligible, the enlarged γ will quickly raise the final effective temperature of Bogoliubov-mode \(\beta _{2}\). Therefore, entanglement and steering drop quickly. When \(\bar{n}_{b}\) is small, although the coupling of the mechanical mode δb and its thermal bath will be enhanced with increasing γ, the increase in effective temperature of \(\beta _{2}\) is not significant. Accordingly, entanglement and steering are less affected by the variation of γ. From the above analyses, it seems that the smaller of the dissipation rates γ of the phonon mode, the larger amount of entanglement and steering can be obtained. However, the mechanical resonator under the condition of larger dissipation will have a smaller steady-state mean phonon number, which is one of the conditions for acquisition of the Hamiltonian of Eq. (12) (i.e., \(\tilde{\Delta}_{m}=\Delta _{m} +\eta (\langle b(t)\rangle +\langle b(t) \rangle ^{*})\simeq \Delta _{m}\)). Taking all of the above into account, the maximal values of photon-phonon entanglement and asymmetric steering are nonmonotonic functions of γ and take a maximum for a specific γ. The physical mechanism is somewhat similar to that of earlier study [58]. As have been previously studied in Ref. [58], the modes dissipation as well as noises can affect the steerability from one mechanical mode to another mechanical mode simultaneously. It is also shown that the mechanical mode with smaller dissipation is more easy to be steered by the other one when the temperature of thermal baths are not negligible. Within the parameters that we are discussing about, \(\kappa _{a}\) is set to be 0.02. The \(a\rightarrow b\) steering \(G_{A}\) will be greater than the \(b\rightarrow a\) steering \(G_{B}\) only if both the conditions of larger γ and smaller \(\bar{n}_{b}\) are satisfied (e.g., \(\gamma =0.07\) and \(\bar{n}_{b}=0\)), otherwise, \(G_{B}\geq G_{A}\). The results enriches the earlier studies [72–75], where only the mode with larger dissipation rate can be steered by the other one. Besides, similar to that of Ref. [50], significant amount of two-way and one-way photon-phonon asymmetric steering can be obtained with even equal dissipation (e.g., \(\kappa _{a}=\gamma =0.02\)). Our scheme is quite different from the conventional proposal, where additional unbalanced losses or noises should be imposed on the two subsystems and irrevocably at the cost of reducing steerability.

Figure 1
figure 1

Maximum photon-phonon entanglement and asymmetric steering for each time period in the asymptotic regime as functions of γ and \(\bar{n}_{b}\). The parameters in units of \(\omega _{b}\) are chosen as: \(\Delta _{a}=\Delta _{m}=1000\), \(\kappa _{a}=0.02\), \(\kappa _{m}=0.3\), \(g=0.28\), \(\eta =2\times 10^{-8}\), \(G_{1}=0.21\), and \(G_{2}=0\)

Full size image

Finally, we give a brief discussion on the experimental feasibility of our scheme. In the first experimental work of a coupled phonon-magnon system based on ferrimagnetic spheres [15], the highly polished 250-mm-diameter YIG sphere is glued to a 125-mm-diameter supporting silica fiber and placed near the maximum microwave magnetic field (along the y direction) of the cavity mode. The experimental parameters are chosen as: \(\omega _{b}/2\pi =11.42\text{ MHz}\), \(\omega _{a}/2\pi \simeq \omega _{m}/2\pi =7.86\text{ GHz}\), \(\eta /2\pi \leq 9.9\) mHz, \(2\gamma /2\pi =300\text{ Hz}\), \(2\kappa _{a}/2\pi =3.35\text{ MHz}\), and \(2\kappa _{m}/2\pi =1.12\text{ MHz}\). On the one hand, a YIG sphere with a smaller diameter is favorable for achieving larger coupling strengths, which also results in a higher frequency for the phonon mode. On the other hand, the phonon linewidth due to clamping loss is a function of the supporting fiber diameter. As a consequence, relevant parameters can be adjusted within a certain range as required. In our scheme, the coupling strengths are not the key points, we only require an atypical cavity magnomechanical system, where the dissipation rates of the phonon mode and the magnon mode (especially the phonon mode) are larger than that of conventional cavity magnomechanical system. They should be relatively easy to satisfy experimentally. Nevertheless, the dissipation rate of the cavity mode that we used is relatively small, which means that a high quality factor microwave cavity would be ideal. Except for these, all the other parameters are chosen in terms of their achievability in current or future experiments.

5 Conclusions

In summary, a theoretical scheme has been proposed to achieve significant amount of steady-state photon-phonon entanglement and asymmetric steering in a cavity magnomechanical system. By applying a blue-detuned microwave driving field, we obtain an effective Hamiltonian where the magnon mode acting as an engineered resevoir cools the Bogoliubov modes of microwave cavity mode and mechanical mode via a beam-splitter-like interaction. By this means, the microwave cavity mode and mechanical mode can be driven to a two-mode squeezed state with asymmetric steering in the stationary limit. The numerical simulation results reveal that the maximal values of photon-phonon entanglement and asymmetric steering all decrease with the increase of \(\bar{n}_{b}\), but are nonmonotonic functions of γ and take a maximum for a specific γ. Peculiarly, entanglement and steering are more sensitive to γ with the increase of \(\bar{n}_{b}\). The underlying physical mechanism is analyzed in detail. Moreover, strong two-way and one-way photon-phonon asymmetric steering can be obtained with even equal dissipation. It is quite different from the conventional proposal, where additional unbalanced losses or noises should be imposed on the two subsystems. Our results may be significant to expand the understanding of the essential physics of asymmetric steering and extend the potential application of the cavity spintronics to device-independent quantum key distribution.