1 Introduction

These last years, optically pumped magnetometers (OPM) operating in very low magnetic fields have reached excellent sensitivities [1–3]. Thereby they have become serious candidates to replace SQUIDs, avoiding cryogeny in applications requiring ultra-low noise magnetic field measurements like magnetoencephalography [4, 5], magnetocardiography [6], magnetomyography [7] and magnetorelaxometry [8].

Among all the OPM configurations operating in low field, Hanle effect magnetometers have yield the best DC-to-low-frequency sensitivities [1, 9]. However a variant of these, called parametric resonance magnetometers (PRM), are often used instead, because they may operate with a single optical beam, which is very convenient for building arrays of sensors [10–12]. In PRM one or two RF fields modulate the magnetic moments of the atoms so as to obtain a measurement of one or several components of the magnetic field, with a single optical beam which both pumps and probes the atoms. This beam may be circularly polarized, yielding atomic orientation, a configuration thoroughly studied in the 1970’s [13–16].

In parallel, these last years, there is a renewed interest for optically pumped magnetometers based on linearly polarized light, yielding atomic alignment [17–21]. We recently worked on PRM based on linearly polarized light. For metastable helium-4 [22–24], this configuration is advantageous, showing better sensitivities in a multi-axis configuration, and no vector light-shifts [25].

Both for orientation and alignment-based PRM two approximations are usual for obtaining closed-form expressions for the photodetection signals:

  • The three step approach consists in modelling the magnetometer dynamics as if it happened in three sequential steps: (i) state preparation by optical pumping, (ii) evolution under a magnetic field and relaxation, and (iii) measurement of the system state. This approach introduces a steady-state polarization resulting from the pumping. This assumption is accurate as far as the pumping and probing light have sufficiently low intensities [26–28].

  • The rotating wave approximation (RWA) requires the RF frequencies to be much larger than other characteristic frequencies [16, 25], including the total spin relaxation rate and the precession rates corresponding to each component of the magnetic field e. g. \(\omega _{x}=\gamma B_{x}\), with γ the gyromagnetic ratio of the atomic species.

The conditions for these approximations are hardly fulfilled in practical magnetometers. The first one because it is well known that the best sensitivities are obtained with pumping rates much larger than the relaxation rates in the dark [14]. The second one because the slower RF field frequency Ω is usually just a few times larger than the relaxation rate. Indeed, it has to comply with \(\varOmega \ll \omega \), while the faster RF field frequency ω remains low enough so that the ratio \(\gamma B_{1}/\omega \) is near the optimum of sensitivity [16, 25]. For instance, with helium-4, choosing \(\omega =2\pi 100\text{ kHz}\) yields an optimal \(B_{1}\) of 3.5 μT, which is difficult to generate without increasing noise around DC.

It is important to have an exact picture of the consequences of the breakdown of these approximations. Indeed, optically pumped magnetometers are often used for applications requiring good accuracy in addition to ultra-low noise. Therefore the presence of offsets in the magnetic field readings, or the emergence of additional sources of noise, could seriously compromise the interest of OPMs. From the same perspective, pumping with linearly polarized light has the advantage of inducing no vector light-shifts, which could result in field offsets or increased noise [29]. However linearly-polarized light detuned from an optical transition causes tensor light-shifts (TLS) [30–32]. It is not clear if such TLS could also translate into systematic errors or increased noise for an alignment-based magnetometer operating in very low magnetic fields.

In this paper we aim to study these three second-order effects in order to clarify how they translate to metrological properties of optically pumped magnetometers based on atomic alignment.

We will start (in Sect. 2) by briefly recalling the Hanle effect and PRM schemes that we study. In Sect. 3 we show that the three-step approach results in inaccurate predictions for photodetection signals under high pump intensities, and how to refine it. In Sect. 4 we calculate the first correction terms to RWA and discuss on their impact on magnetic measurements. In Sect. 5 we analyze the impact of TLS on magnetic field measurements. Finally in Sect. 6 we discuss the results and conclude.

2 Overview of the schemes used for studying the Hanle effect and the parametric resonance magnetometer based on alignment

We will focus here on the metastable state of helium-4 (\(F=1\)) as magnetically-sensitive species. The spin polarization of this state can be prepared by optical pumping towards the \(F'=0\) state \(2^{3}P_{0}\) [33]. Both atomic orientation and alignment can be obtained in this way. We will focus here on alignment only, which has been shown to display interesting advantages [25]. Both these polarizations decay, notably due to the collisional relaxation of metastable state, at rates \(\varGamma _{e}\) of a few kHz in 5–10 mm sized cells [34].

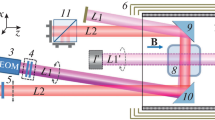
The setup for observation of the Hanle effect is represented in Fig. 1(a): a linearly polarized light beam is sent through a helium-4 cell along the z axis with the polarization electric field along the x axis. When the magnetic field transverse to x is not null, the alignment created by the pumping is partially suppressed and optical absorption increases [35]. The photodetection signals are even-symmetric in magnetic field, which is not convenient for measuring the magnetic field. However, like in the case of atomic orientation, dispersive (i.e. odd-symmetric) photodetection signals can be obtained by adding an independent probe beam [36].

Figure 1
figure 1

Null-field alignment-based magnetometry schemes. (a) Hanle effect on atomic alignment: a cell containing helium, with the metastable state populated by a high-frequency discharge, is subject to a linearly-polarized light-beam, with light electric field \(\vec{E}_{p}\). This beam is photodetected after the cell. (b) Parametric resonance magnetometer based on atomic alignment: in the addition to the elements of the former scheme, this one includes two RF fields set along the axes orthogonal to \(\vec{E}_{p}\). (c) Experimental setup which allows an implementation of both schemes

Full size image

Parametric resonance magnetometer scheme is shown in Fig. 1(b). Compared to the previous scheme, two RF fields are added along the z and y axes, both orthogonal to the linear polarization of the pump, with angular frequencies ω and Ω which comply with \(\omega \gg \varOmega \gg \varGamma \). The photodetection signal contains harmonics and inter-harmonics of ω and Ω. The first harmonic of each RF is sensitive to the \(B_{0}\) component parallel to the axis of the corresponding RF, and their first inter-harmonics (\(\omega \pm \varOmega \)) are sensitive to the third component of the magnetic field with lower sensitivity. It is usual to operate PRM in a closed-loop mode, where these three signals are used to cancel the measured field by applying opposite fields on compensation coils [37].

In both configurations, our experimental setup is composed of the elements shown in Fig. 1(c). The optical beam is generated by a fiber-coupled DFB laser diode (QD Laser QLD1061-8330) tuned to D0 line of helium-4 (at 1083.206 nm wavelength in the vacuum) with a linewidth <5 MHz and no wavelength stabilisation. Its intensity can be varied thanks to a variable fiber optical attenuator. The beam is collimated with a 5.7 mm \(1/e^{2}\) waist by a 3D-printed collimator. Although we use polarization-maintaining fibers, a linear polarizer is placed before the cell to improve the polarization extinction ratio. This beam is sent through a pyrex cell of 12 mm length and 10 mm diameter containing ultra-pure helium-4. Due to practical issues of availability, the setup for observing Hanle effect includes an aluminium mirror at the end of the cell, and the light, with 5∘ incidence angle, undergoes a double pass in the helium cell. The setup for parametric resonance does not include such a mirror, and the light undergoes a single pass in the cell. Under appropriate high-frequency excitation, the density of helium atoms excited to the metastable state is on the order of 1011 cm−3. The optical beam is photodetected by an InGaAs photodiode, connected to a home-made 25 kΩ transimpedance amplifier. Both DC and RF magnetic fields applied to the atoms are generated with the same tri-axial coils, also 3D printed, of 5 cm diameter. The whole setup is enclosed in a three-layer cylindrical magnetic shielding made of mu-metal, of 12 cm inner diameter.

3 Strong pumping toward aligned states: anisotropic relaxation and its dressing

The three-step approach is a useful method for describing the evolution of optically pumped systems. This approach is however known to be limited to low light intensities [26–28]. For depopulation pumping of a spin \(1/2\) system with circularly polarized light, it was shown long ago that this approach remains valid for higher light intensities if an additional relaxation term \(\gamma _{p}\) due to the pumping, and proportional to light intensity I is added to the natural relaxation \(\varGamma _{e}\).

Some authors have discussed if a similar approach may be valid for a \(\mbox{spin} >1/2\) pumped by linearly polarized light towards an aligned state [38]. We study here if adding well-chosen relaxation terms to the three-step approach model could yield accurate predictions for the photodetection signals of helium-4 interacting with linearly polarized light. We first study the simplest scheme which is the Hanle effect. Then we consider the case of parametric resonance magnetometers.

3.1 Hanle effect

We will consider here the situation sketched in Fig. 1(a). Let us recall the multipole decomposition of the density matrix on the irreducible tensor operators \(\hat{T}_{q}^{(k)}\) [39]:

$$ \hat{\rho }=\sum_{k,q}m_{q}^{(k)} \hat{T}_{q}^{(k)\dagger } $$
(1)

with \(m_{q}^{(k)}=\langle \hat{T}_{q}^{(k)}\rangle \). The order \(k=1\) corresponds to orientation and \(k=2\) to alignment. The latter can be described by a column matrix M with five components \(m_{-2}^{(2)}\), \(m_{-1}^{(2)}\), \(m_{0}^{(2)}\), \(m_{1}^{(2)}\), \(m_{2}^{(2)}\).

Within the three-step approach, the evolution of M is given by [25, 35]:

$$ \frac{\mathrm{d}}{\mathrm{d}t}M=\mathbb{H} (B_{0} ) \cdot M- \varGamma (M-M_{ss}) $$
(2)

with \(\mathbb{H} (B_{0} )\) the matrix describing the magnetic evolution, the total relaxation rate \(\varGamma =\varGamma _{e}+\gamma _{p}\) and the pumping steady-state is \(M_{ss}=\gamma _{p}/\varGamma (0,0,1/\sqrt{6},0,0)^{t}\). The optical pumping rate \(\gamma _{p}=\eta I\) with I the light intensity and η a constant. The evolution of M causes the light absorption to vary. For an input intensity \(I_{0}\), the intensity at the output of the cell will be \(I_{0}-\Delta I\) with [40]:

$$ \Delta I=I_{0} \alpha _{r} \biggl[\frac{m_{0}^{(0)}}{\sqrt{3}}+ \frac{m_{0}^{(2)}}{\sqrt{6}}-\Re \bigl(m_{2}^{(2)} \bigr) \biggr], $$
(3)

where \(\alpha _{r}\) a constant which depends on the optical transition, and the quantization axis is set along the propagation axis z.

In order to probe this approach we have recorded a set of Hanle-effect resonance curves for growing light intensities from 35 μW/cm2 up to 1.96 mW/cm2. For each light power, a quasi-static ramp of the \(B_{z}\) component of the magnetic field is applied to the cell, and the photodetection signals are recorded with a National Instruments DAQmx board at the output of the transimpedance amplifier. These Hanle resonance curves are shown in Fig. 2.

Figure 2
figure 2

Comparison of the three-step approach and the complete model for predicting Hanle resonances shapes at various optical powers. The five first plots show the photodetected optical power \(P_{pd}\) as a function of the magnetic field, in units of the magnetic linewidth. Experimental data (in black) is compared to the theoretical expectations resulting from the three-step approach comprising only with isotropic relaxation (blue line) and complete model including anisotropic relaxation resulting from the pumping (red line). The bottom right plot shows the dependence of the full-width at half maximum of the curves as a function of the optical power for the experiment and the two theoretical models. The optical powers are given with 10% systematic uncertainty coming from optical power calibration

Full size image

This data is compared to the theoretical predictions resulting from Eqs. (2) and (3). The only free parameters of this model are the proportionality constants η and \(\alpha _{r}\) which are common for the whole data set: we have fitted them on the resonance curve corresponding to the lowest light intensity. The resulting theoretical curves show a fair agreement fort the lowest light intensities, which is progressively degraded for larger light intensities. A qualitative explanation for these disagreements is the following. In this model the effective relaxation \(\gamma _{p}\) does only depend on the light intensity, and not on the system alignment M. This is only accurate as far as the system is far from a fully aligned state, i.e. as far as optical power remains very low.

For larger optical powers, the complete equations describing optical pumping [41, 42], suggest that it may be possible to refine the previous model by considering the anisotropic nature of the effective relaxation brought by the pumping. The equation of evolution thus becomes:

$$ \frac{\mathrm{d}}{\mathrm{d}t}M = \mathbb{H} (B_{0} ) \cdot M -\mathbb{R}\cdot M + \gamma _{p} M_{ss}, $$
(4)

where \(\mathbb{R}=\mathbb{R}^{(2)}+\varGamma _{e}\mathbb{I}\) with \(\mathbb{I}\) the identity matrix and \(\mathbb{R}^{(2)}\) is a \(5 \times 5\) matrix which accounts for relaxation due to the optical pumping. From the complete equations of optical pumping [42], this latter is found to be for \(D_{0}\) line of helium-4

$$ \mathbb{R}^{(2)}= \begin{pmatrix} 0 & 0 & 0 & 0 & 0 \\ 0 & \frac{3}{2}\gamma _{p} & 0 & 0 & 0 \\ 0 & 0 & 2\gamma _{p} & 0 & 0 \\ 0 & 0 & 0 & \frac{3}{2}\gamma _{p} & 0 \\ 0 & 0 & 0 & 0 & 0 \end{pmatrix} $$
(5)

and the pumping steady-state \(M_{ss}=(0,0,\sqrt{2/3},0,0)^{t}\), both with quantization axis parallel to the light polarization. The pumping rate is:

$$ \gamma _{p}=I_{0}\frac{2\pi ^{2}r_{e}cf}{\hbar \omega }\Re \bigl[ \mathcal{V} ( \omega -\omega _{0} ) \bigr] $$
(6)

with \(r_{e}\) the electron classical radius, f the oscillator strength of the transition, ω and \(\omega _{0}\) the angular frequencies of the light and of the transition respectively, ℜ is the real part and \(\mathcal{V}\) the complex Voigt profile function. Since the same beam is used as pump and probe, it is possible to write \(\alpha _{r}\) in terms of \(\gamma _{p}\): \(\alpha _{r}=3\alpha \gamma _{p}\) with \(\alpha =\omega l n \hbar /I_{0}\), where l is the inner cell length and \(n_{m}\) the density of atoms in the metastable state [40].

A first measurement at 9 μW optical power allows to deduce the metastable density \(n_{m}\) and a second one at 37 μW, the ratio between the effective pumping rate in the double-pass configuration and the \(\gamma _{p}\) given by Eq. (6). Except for these independently-measured parameters, the model contains no free parameters at all. We have calculated the resonance curves from Eq. (4) for the optical powers used in the experiments described above (Fig. 2). The agreement with experimental data is much better than with the previous model. Figure 2 also shows the widths of the Hanle resonances. For growing powers the experimentally measured widths become narrower than the three step approach prediction. Including an anisotropic relaxation term as explained above allows a very good agreement between the predicted widths and those observed.

3.2 Parametric resonance

We now consider the case of practical interest which is the PRM. Thanks to the dressed atom formalism, PRM equations of motion can be mapped to the ones of the Hanle effect of the atom dressed by the two RF fields [16, 25].

For optical powers larger than those described by the three step approach, this equivalence remains valid if, in addition to the usual conditions, all the elements of the \(\mathbb{R}\) matrix to remain much lower than the RF frequencies ω and Ω. If this condition is fulfilled, the dressed anisotropic relaxation matrix \(\mathscr{R}\) can be found to be [43]:

$$ \mathscr{R}_{q,q'}=\sum_{r=-\infty }^{{+\infty }}J_{r,q} \mathbb{R}_{q,q'}J_{r,q'}=J_{0, \vert q-q' \vert }\mathbb{R}_{q,q'}, $$
(7)

where the second equality comes from Graf’s theorem [44]. The PRM equations can then be solved as usual.

For single-RF parametric resonance (the scheme of Fig. 1(b) with \(B_{2}=0\)), the absorption signal at odd harmonics of the RF frequency ω is sensitive to the \(B_{z}\) component of the field. From Eq. (5), (7) and [25] one can find around null field:

$$ \Delta I=\frac{48 I_{0}\alpha }{2\varGamma _{e}+3\gamma _{p}}\times \frac{\gamma B_{z}\varGamma _{e}\gamma _{p}^{2}J_{0,2}J_{p,2}}{ (2\varGamma _{e}+\gamma _{p} ) (2\varGamma _{e}+3\gamma _{p} )-3\gamma _{p}^{2}J_{0,2}^{2}} \sin (p\omega t ), $$
(8)

where p is an odd integer and \(J_{q,q'}=J_{q}(q'\gamma B_{1}/\omega )\) with \(J_{q}(x)\) the Bessel function of first kind and order q.

To probe if this description of PRM is accurate we have acquired a set of parametric resonance dispersive response curves at different optical powers, in the presence of a single RF field. To do so we slowly varied the \(B_{z}\) component of the magnetic field in the presence of a RF field along the z axis, of 20 kHz frequency and \(B_{1}=\omega /(2\gamma )\). The photodetection signal at the output of the transimpedance amplifier was sent to the input of a Zurich MFLI lock-in amplifier. The output of this lock-in is then acquired with the same National DAQmx board used before.

The resulting resonance curves are plotted with crosses in Fig. 3(a). The theoretical predictions with no free parameters are superposed to this data set, and show an excellent agreement with the experimental data in the central null-field region. The agreement becomes slightly worse for high light intensities and larger magnetic field. We believe this may be due to slight imperfections on the cancellation of the transverse components of the magnetic field.

Figure 3
figure 3

Parametric resonance magnetometer response: comparison between the theoretical prediction (with no free parameters) and the experimental data. (a) Superposition of experimental measurements (color disks) for different optical powers (given in the inset, with 10% systematic uncertainty coming from optical power calibration) and theoretical predictions (solid lines). (b) Slopes of the dispersive response near the null magnetic field, as a function of the optical power: experimental data (blue crosses) and theoretical predictions (blue solid line)

Full size image

The Fig. 3(b) displays the slopes of the linear low-field portion of the Fig. 3(a). The agreement is very good for light power up to 1 mW (i.e. an intensity of 3.9 mW/cm2), which is well above the light power which optimizes the magnetometer signal [14]. For larger powers a disagreement is clearly visible, probably due to the incipient saturation of the optical transition. Indeed the saturation intensity in our system is 7.42 mW/cm2, corresponding to an integrated power of 2.1 mW.

The two RF case can be addressed in the very same way, dressing the atom with the faster RF field first, then rotating the quantization axis from z to y and finally dressing the atom with the slower RF field. The resulting relaxation matrix is \(\mathscr{R}=\varGamma _{e} \mathbb{I}+\gamma _{p} \mathbb{D}\), where \(\mathbb{D}\) is

$$ \begin{pmatrix} \frac{3}{4} (1+J_{0,2} ) & 0 & \sqrt{\frac{3}{32}} (1+J_{0,2} )\mathcal{J}_{0,2} & 0 & 0 \\ 0 & \frac{3}{8} (3-J_{0,2} ) & 0 & \frac{3}{8} (1+J_{0,2} )\mathcal{J}_{0,2} & 0 \\ \sqrt{\frac{3}{32}} (1+J_{0,2} )\mathcal{J}_{0,2} & 0 & \frac{1}{4} (5-3J_{0,2} ) & 0 & \sqrt{\frac{3}{32}} (1+J_{0,2} )\mathcal{J}_{0,2} \\ 0 & \frac{3}{8} (1+J_{0,2} )\mathcal{J}_{0,2} & 0 & \frac{3}{8} (3-J_{0,2} ) & 0 \\ 0 & 0 & \sqrt{\frac{3}{32}} (1+J_{0,2} )\mathcal{J}_{0,2} & 0 & \frac{3}{4} (1+J_{0,2} ) \end{pmatrix}. $$
(9)

4 Breakdown of the RWA

The dressed atom formalism relies on a RWA which requires \(\omega \gg \varOmega \), \(\gamma B_{1}\), \(\gamma B_{0}\), Γ and \(\varOmega \gg \gamma B_{0}\), Γ. In practice, this latter condition may not be well achieved. In the case of orientation-based PRM, the breakdown of RWA is somehow beneficial because it yields a resonance at the interharmonics \(\omega \pm \varOmega \) which is sensitive to the third component of the magnetic field, which otherwise cannot be measured [15, 16].

We study here the case of alignment-based PRM. The calculation can be performed in a very similar way as done for orientation [16]: after dressing the atom with the fast RF field, one obtains a set of differential equations for the dressed alignments \(\overline{M}=(\overline{m}_{-2}^{(2)}, \overline{m}_{-1}^{(2)}, \overline{m}_{0}^{(2)}, \overline{m}_{1}^{(2)}, \overline{m}_{2}^{(2)})^{t}\) as explained in [25]. For instance the equation for \(\overline{m}^{(2)}_{2}\) is:

$$ \frac{d}{dt}\overline{m}_{2}^{(2)}+ \bigl[\varGamma -2i \overline{\omega }_{y}-2i\overline{\varOmega }_{1}\cos ( \varOmega \tau ) \bigr]\overline{m}_{2}^{(2)}= \bigl(i \overline{\omega }_{+}\overline{m}_{1}^{(2)}+ \varGamma \overline{m}_{2,ss}^{(2)} \bigr), $$
(10)

where we kept the same notations used in [25] i.e. \(\overline{\omega }_{x,y}=\gamma J_{0,2} B_{x,y} \), \(\overline{\omega }_{z}=\gamma B_{z}\), \(\overline{\varOmega }_{1}=\gamma J_{0,2} B_{1}\), \(\overline{\omega }_{\pm }=\omega _{z}\pm i \omega _{x}\), with \(J_{q,q'}=J_{q}(q'\gamma B_{1}/\omega )\) and \(J_{q}(x)\) is the Bessel function of first kind of order q and argument x.

These equations can be written in an integral form, for instance Eq. (10) yields:

$$\begin{aligned} \overline{m}_{2}^{(2)} = & \exp \biggl[-\varGamma t+2i \overline{\omega }_{y}t+2i\frac{\overline{\varOmega }_{1}}{\varOmega }\sin (\varOmega t ) \biggr] \\ &{}\times \int _{-\infty }^{t}\exp \biggl[\varGamma \tau -2i \overline{\omega }_{y}\tau -2i\frac{\overline{\varOmega }_{1}}{\varOmega } \sin (\varOmega \tau ) \biggr] \times \bigl(i \overline{\omega }_{+}\overline{m}_{1}^{(2)}+ \varGamma \overline{m}_{2,ss}^{(2)} \bigr)\,\mathrm{d}\tau. \end{aligned}$$
(11)

Developing these equations to the first order in \(\gamma B_{x}/\varOmega \), \(\gamma B_{y}/\varOmega \), \(\gamma B_{z}/\varOmega \) and \(\varGamma /\varOmega \), and replacing the dressed alignments M̅ appearing in the integrals with the zero-order solutions of [25] we obtain:

$$ \begin{gathered} \overline{m}_{0}^{(2)} = \overline{m}_{0,ss}^{(2)}+ \sqrt{6} \biggl[ \biggl(\frac{\overline{\omega }_{z}}{\varOmega }\Re \overline{\overline{m}}_{1}^{(2)}+ \frac{\overline{\omega }_{x}}{\varOmega }\Im \overline{\overline{m}}_{1}^{(2)} \biggr)C_{0} \\ \hphantom{\overline{m}_{0}^{(2)} = }{}+ \biggl(\frac{\overline{\omega }_{x}}{\varOmega }\Re \overline{\overline{m}}_{1}^{(2)}- \frac{\overline{\omega }_{z}}{\varOmega }\Im \overline{\overline{m}}_{1}^{(2)} \biggr)N_{0} \biggr], \\ \Im \overline{m}_{1}^{(2)} = \biggl(\frac{\varGamma }{\varOmega } \overline{m}_{1,ss}^{(2)}-\sqrt{\frac{3}{2}} \frac{\overline{\omega }_{x}}{\varOmega }\overline{\overline{m}}_{0}^{(2)} \biggr)C_{1}+ \biggl(-\frac{\overline{\omega }_{x}}{\varOmega }\Re \overline{\overline{m}}_{2}^{(2)}+ \frac{\overline{\omega }_{z}}{\varOmega }\Im \overline{\overline{m}}_{2}^{(2)} \biggr)C_{3} \\ \hphantom{\Im \overline{m}_{1}^{(2)} =} {}+ \biggl(\frac{\overline{\omega }_{z}}{\varOmega }\Re \overline{\overline{m}}_{2}^{(2)}+ \frac{\overline{\omega }_{x}}{\varOmega }\Im \overline{\overline{m}}_{2}^{(2)} \biggr)N_{1}-\sqrt{\frac{3}{2}} \frac{\overline{\omega }_{z}}{\varOmega }\overline{\overline{m}}_{0}^{(2)}N_{2}, \\ \Re \overline{m_{2}^{(2)}} = \biggl( \frac{\overline{\omega }_{x}}{\varOmega } \Re \overline{\overline{m}}_{1}^{(2)}+ \frac{\overline{\omega }_{z}}{\varOmega }\Im \overline{\overline{m}}_{1}^{(2)} \biggr)N_{3}- \frac{\varGamma }{\varOmega }\overline{m}_{2,ss}^{(2)}N_{4} \\ \hphantom{\Re \overline{m_{2}^{(2)}} = } {}+ \biggl(\frac{\overline{\omega }_{x}}{\varOmega }\Im \overline{\overline{m}}_{1}^{(2)}- \frac{\overline{\omega }_{z}}{\varOmega }\Re \overline{\overline{m}}_{1}^{(2)} \biggr)C_{2}, \end{gathered} $$
(12)

where ℜ and ℑ are the real and imaginary parts, \(\overset{=}{m}_{0}^{(2)}\) are the doubly dressed alignments and the expressions of \(N_{i}\) and \(C_{i}\) are:

$$\begin{aligned}& N_{0} = \sum_{q>0}2\sin 2q\varOmega t \frac{\mathscr{J}_{2q,1}}{2q}, \\& N_{1} = \sum _{q,r>0}2\sin 2r\varOmega t \frac{\mathscr{J}_{q,1} (\mathscr{J}_{q-2r,1}-\mathscr{J}_{-q-2r,1} )}{q}, \\& N_{2} = \sum _{q,r>0}2\sin 2r\varOmega t \frac{\mathscr{J}_{q,1} (\mathscr{J}_{q+2r,1}-\mathscr{J}_{q-2r,1} )}{q}, \\& N_{3} = \sum _{q,r>0}2\sin 2r\varOmega t \frac{\mathscr{J}_{q,1} (\mathscr{J}_{q+2r,2}-\mathscr{J}_{q-2r,2} )}{q}, \\& N_{4} = \sum _{q,r>0}2\sin 2r\varOmega t \frac{\mathscr{J}_{q,2} (\mathscr{J}_{q+2r,2}-\mathscr{J}_{q-2r,2} )}{q}, \\& C_{0} = \sum_{q>0}2\cos (2q-1 )\varOmega t \frac{\mathscr{J}_{2q-1,1}}{2q-1}, \\& C_{1} = \sum _{q,r>0}2\cos (2r-1 )\varOmega t \frac{\mathscr{J}_{q,1} (\mathscr{J}_{q+2r-1,1}+\mathscr{J}_{q-2r+1,1} )}{q}, \\& C_{2} = \sum _{q,r>0}2\cos (2r-1 )\varOmega t \frac{\mathscr{J}_{q,1} (\mathscr{J}_{q+2r-1,2}+\mathscr{J}_{q-2r+1,2} )}{q}, \\& C_{3} = \sum _{q,r>0}2\cos (2r-1 )\varOmega t \frac{\mathscr{J}_{q,1} (\mathscr{J}_{-q+2r-1,1}+\mathscr{J}_{-q-2r+1,1} )}{q} \end{aligned}$$
(13)

with \(\mathscr{J}_{q,q'}=J_{q}(q'\gamma \overline{B}_{2}/\varOmega )\) with \(\overline{B}_{2}=J_{0,1} B_{2}\).

The variation of light intensity contains the following terms:

$$ 3 \biggl(\frac{\overline{m}_{0}^{(2)}}{\sqrt{6}}- \frac{\Re \overline{m}_{2}^{(2)}}{3} \biggr)\cos \frac{2\omega _{1}\sin \omega t}{\omega }- \frac{\overline{m}_{0}^{(2)}}{\sqrt{6}}+\Re \overline{m}_{2}^{(2)}-2 \sin \frac{2\omega _{1}\sin \omega t}{\omega }\Im \overline{m}_{1}^{(2)}. $$
(14)

Putting together Eqs. (12), (13) and (14) in a symbolic calculation software like Mathematica we have studied the non-secular terms which appear at the three frequencies ω, Ω, \(\omega \pm \varOmega \) which are used for magnetic field measurement.

The only term which is constant in magnetic field, and thus could cause a fixed offset, is \(\Re \overline{m}_{2}^{(2)}\). Expanding Eq. (14) with Jacobi-Anger relations [44] shows however that all the resulting terms are at even harmonics of ω.

All other terms have at least first-order dependence on the magnetic field. We have analyzed if these terms could bring spurious sensitivities to components other than \(B_{z}\), \(B_{y}\) and \(B_{x}\) for the three frequencies ω, Ω and \(\omega \pm \varOmega \) respectively. This is not the case. Indeed one can notice in Eqs. (13) that for all the ones with a \(\sin (p \varOmega t)\) time-dependence p is even and all the ones with a \(\cos (p \varOmega t)\) time-dependence p is odd. This is exactly the opposite for secular terms [25]. Therefore the terms resulting from RWA breakdown are in quadrature with the secular terms. An important example is the interharmonic term which allows the measurement of the \(B_{x}\) component of the magnetic field. The secular sensitivity to \(B_{x}\) has a time dependence \(\sin (\omega t)\sin (\varOmega t)\) [25]. The new term which appears here has a time dependence \(\sin (\omega t)\cos (\varOmega t)\).

We can therefore conclude that no systematic errors in magnetic field readings should result from the first order corrections of RWA.

5 Tensor light-shifts

The absence of vector light-shifts is often cited as an advantage of optical pumping with linearly instead of circularly polarized light [20, 25, 45]. However, a detuning between the linearly-polarized light and the atomic transition leads to a TLS. The effect of such a shift can be modelled by adding to the Hamiltonian a term [30, 31]:

$$ \hat{H}_{\mathrm{TLS}}=-\sqrt{6}Q_{2}\Delta E\hat{T}_{0}^{(2)} $$
(15)

with quantization axis along light polarization. \(Q_{2}=1\) for \(D_{0}\) and

$$ \Delta E=I_{0}\frac{\pi ^{2}r_{e}cf}{\hbar \omega }\Im \bigl[ \mathcal{V} (\omega - \omega _{0} ) \bigr]. $$
(16)

\(\hat{H}_{\mathrm{TLS}}\) is formally equivalent to the Hamiltonian of quadrupole effects [46]. For a scalar magnetometer based on atomic alignment [38] the \(\hat{H}_{\mathrm{TLS}}\) can be treated as a perturbation, like it is usually done for quadrupole effects [47]. At first order it causes a broadening of the magnetic resonance line, and to second order a shift of the center of the resonance. The resulting systematic error on scalar magnetometers of the ESA Swarm mission [20, 48, 49] is around 1 pT/mW in the worst case. This is negligible as compared to other systematic errors [50].

Our goal here is to study if there is a systematic error arising from TLS for the PRM. From Eq. (15) Ehrenfest theorem yields:

$$ \textstyle\begin{cases} \frac{d}{dt}m_{\pm 1}^{(1)}=-\mathrm{i} \langle [\hat{T}_{ \pm 1}^{(1)},\hat{H}_{\mathrm{TLS}} ] \rangle =\mp 3Q_{2} \mathrm{i}\Delta Em_{\pm 1}^{(2)}, \\ \frac{d}{dt}m_{\pm 1}^{(2)}=-\mathrm{i} \langle [\hat{T}_{ \pm 1}^{(2)},\hat{H}_{\mathrm{TLS}} ] \rangle =\mp 3Q_{2} \mathrm{i}\Delta Em_{\pm 1}^{(1)}. \end{cases} $$
(17)

These terms describe alignment-to-orientation conversion. Adding these terms in the differential equations of Hanle effect presented in [25], and calculating the new steady-state yields cumbersome equations, which can be developed to first-order in each magnetic field component, yielding the alignment:

$$ \begin{gathered} m_{0}^{(2)} = \sqrt{ \frac{1}{6}} \frac{\gamma _{p}}{\varGamma _{e}+2\gamma _{p}}, \\ m_{1}^{(2)} = \omega _{y} \frac{2\varGamma _{e}+3\gamma _{p}}{\varGamma _{e}+2\gamma _{p}} \frac{2\gamma _{p}}{ (2\varGamma _{e}+3\gamma _{p} )^{2}+36\Delta E^{2}}, \\ m_{2}^{(2)} = \gamma _{p} \frac{(2\varGamma _{e}+3\gamma _{p})(4i\omega _{z}+2\varGamma _{e}+3\gamma _{p})+36\Delta E^{2}}{(\varGamma _{e}+2\gamma _{p}) [(2\varGamma _{e}+3\gamma _{p})^{2}+36\Delta E^{2} ]}. \end{gathered} $$
(18)

Comparing these solutions to the one in the absence of TLS (\(\Delta E=0\)) one sees that TLS causes no field offset, since ΔE is only involved in the factors dividing the magnetic field. The resonance curve is therefore only widened in the presence of a non null TLS.

The effect of a TLS on PRM can be deduced from the above considerations. Indeed PRM can be modelled as the Hanle effect of the dressed atom. The tensor light-shift rate ΔE is dressed in the same way as the pumping rate \(\gamma _{p}\). Once dressed, the problem is formally equivalent to the Hanle effect problem considered above. The photodetection signal demodulated at the RF frequency has an expression analog to Eq. (18) showing a widening but no shift in the presence of a TLS.

6 Discussion and conclusion

We have studied above three effects which are disregarded in the usual analysis of parametric resonance magnetometers.

For optimizing the signal-to noise ratio of PRM it is usual to raise the pump intensity well above the limits of the three-step approach. This is a situation which has been broadly addressed in the field of non-linear magneto-optical rotation (NMOR) [51]. The most usual NMOR scheme is based on the Hanle effect observed in birefringence [27]. This system is usually modelled by calculating the evolution of the whole density matrix dynamics, including the excited state. This approach has been used with great success also for the non-linear Hanle effect observed in fluorescence [52].

Our starting point was the Hanle effect, but observed in the pump absorption signal. We probed a simpler model, which consists in refining the three-step approach by introducing an anisotropic relaxation resulting from optical pumping. This model, which contains no free parameters, is in good agreement with a set of experimental acquisitions on a broad range of optical powers, as long as optical saturation is not reached. This latter can indeed be let aside, since for our helium-4 magnetometers the best sensitivities are achieved for optical intensities lamost an order of magnitude lower than optical saturation.

A former work [53] on Hanle effect deals with a somehow complementary situation where an anisotropic relaxation is probed with low light intensities, yielding isotropic pump-induced relaxation.

From our model of the Hanle effect we calculated the PRM photodetection signals by studying how anisotropic relaxation can be treated in the dressed-atom formalism for RF. We also found an expression for the doubly-dressed anisotropic relaxation term, which should allow to perform further checks of the accuracy of this model on two-RF PRM.

A second aspect we studied is the breakdown of RWA in PRM. For double-resonance magnetometers it is well known that such breakdown causes a systematic error: the Bloch-Siegert shift [21]. For PRM based on orientation no such systematic errors appear, and these effects are even beneficial, since they provide an additional sensitivity to the third axis of the magnetic field [15]. We have shown that for alignment-based PRM neither systematic errors are expected to result from this effect.

Finally we studied TLS which appear when the linearly-polarized pumping light is not well tuned to the transition, We have shown that these TLS cause a widening of the resonance curves, but no shift of their center, in contrast with vector light-shifts. If this widening varies with time it can cause a measurement error when the PRM is operated in open loop, relying on an initial calibration of the response curve to deduce the field from the optical signals. However it is usual to operate helium-4 PRM in closed-loop mode [37], where a compensation field continuously cancels the three components of the magnetic field. In such a configuration, a slope variation does not cause an error in the measurement.

As a conclusion, a reasonably good model of the photodetection signals can be obtained by refining the previous model of alignment-based PRM with the three mechanisms treated here. None of these mechanisms has been found to cause systematic errors. Therefore, the origin and ultimate order of magnitude of the systematic errors in PRM remains an open question.