1 Introduction

There has been a lot of interest in the expansion of general relativity (GR) to higher dimensions in recent years. The Kaluza–Klein (KK) five-dimensional and higher manifolds are employed in a variety of gravitational theories that go beyond Einstein’s GR. A few decades after the development of special relativity, KK [1, 2] proposed the presence of an additional spatial dimension as an extension of the relativistic theory. They did this because they wanted to provide a five-dimensional metric that would describe electromagnetic and gravity together. They looked at the characteristics of matter in KK theories in the extensive study done in this field following the presentation of KK by Wesson’s [3]. The dependence of the theory of gravitation and cosmology in the fifth dimension on space-time matter theories has been increasing, as stated in reference [4]. In higher dimensions, Liu and Overduin [5] looked at the outcomes of light deflection and temporal delays for massless test particles.

The investigation of more than four-dimensional gravstars was also carried out by Rahaman et al. [6].

In general relativity, spherically symmetric solutions are significant for the investigation of compact objects. The Einstein field equations (EFEs), which are among the most straightforward and accurate models available, can be used to predict the gravitational fields of astronomical bodies. In fact, spherically symmetric exact solutions to EFEs have been investigated the most. The Schwarzschild solution estimates the gravitational field surrounding a stationary, spherical, compact object [7]. The Schwarzschild, Reissner–Nordström, and Kerr solutions were examined by Myers and Perry in the context of higher-dimensional space-times [8]. In higher dimensions, Wyman’s approach was discussed by You-Gen Shen and Zhung-Qiang Tan [9]. A spherically symmetric KK-type metric exterior solution was found by Chatterjee [10].

Oppenheimer and Snyder’s [11] ground breaking research encouraged scientists to explore the relativistic features of gravitating objects and their internal composition. This interest stems from the fact that GR is predicted to be a significant factor in the observable occurrence of massive star gravitational collapse (GC). Chodos and Detweiler [12] presented a spherically symmetric, time-independent solution to the five-dimensional vacuum EFEs in standard three-dimensional space. Their technique was based on the assumption that a killing vector existed in a higher dimension. Kerr [13] examined the real physical bodies form black holes, singularities were not present. Roger Penrose postulated that imprisoned surfaces produce light rays of finite affine length, which Hawking and Penrose later demonstrated to be genuine singularities. However, counterexamples in the Kerr metric, which are asymptotic to at least one event horizon, do not result in singularities.

Vaz [14] studied that there is no need for Hawking radiation to be pure for effective field theory to hold outside of a stretched horizon and for infalling observers to notice nothing out of the ordinary for the black hole complementarity paradox to hold. They contend that the firewall breaches quantum gravity’s CPT invariance and violates the equivalence principle. They provide evidence in favor of Hawking’s conclusion in a quantum gravitational model of dust collapse, demonstrating that two separate and complete solutions of the Wheeler–DeWitt equation must be combined to achieve continuous collapse to a singularity. Such a combination is prohibited by this interpretation, which results in a picture of matter condensing during quantum collapse on the apparent horizon.

Corda [15] developed the Schrödinger equation of the Schwarzschild black hole. The black hole is made up of an electron and a central field, and at the Schwarzschild scale, quantum gravity effects change the black hole’s semi-classical structure. The Schrödinger equation for the hydrogen atom’s states can be used to solve the equation. Like the Rydberg constant and fine structure constant, the quantum gravitational quantities have discrete spectra and are dynamical quantities. Often referred to as “gravitational hydrogen atoms,” black holes are precisely characterized by quantum gravitational systems. The gravitational energy of a spherically symmetric shell is the potential energy in the black hole Schrödinger equation; as a result, black holes lack horizons, singularities, and information loss through evaporation, complexity, and firewall paradox. Corda [16] also determines the black hole mass and energy spectra using a Schrodinger-like method, confirming Vaz’s conclusion that a compact “dark star” held up by quantum gravity, similar to conventional atoms, is the outcome of gravitational collapse. The generalized uncertainty principle is used to estimate the maximum density of Vaz’s shell.

The phenomenon of GC has also been studied in different theories of gravity. The stability of a limited class of anisotropic axial symmetrical compact geometry under f(R, T) gravity is investigated by Bhatti et al. [17], where T is the trace of the energy-momentum tensor, and R is the Ricci curvature. The collapse equation is assessed using a perturbation technique after field and non-conservation equations have been set up. In the Newtonian and post-Newtonian approximations, significant limits are provided for the stiffness parameter \(\Gamma\) to examine the dynamical instability of a stellar compact structure. The phenomenon of GC has also been studied in different theories of gravity. In the nonminimally connected f(R, T) theory of gravity, Bhatti et al. [18] investigate the dynamical instability of charged spherical fluid structures under anisotropic conditions. It looks at continuity equations and modified field equations, analyzing how minor adjustments to material and geometric features impact the fluid’s collapse structure. The study examines unstable eras using approximations based on Newtonian and post-Newtonian theories. Throughout the evolutionary process, unstable structures/phases are caused by dark source terms owing to f(R, T) gravity, and the stiffness parameter \(\Gamma\) has a substantial impact on identifying unstable phases.

The investigation conducted by Barnafoldi et al. [19] involved the study of neutron stars with higher dimensions that included compactified excitations in the fifth dimension. The study proposed a fundamental concept of a compact star, implying that neutron stars with extradimensional cores are similar entities. The stability region in the case of extra dimensions where KK models could be observed was found to have a well-defined and similarly structured shape, as predicted by the Tolman–Oppenheimer–Volkoff (TOV) equation.

In his research, Paul [20] examined compact star solutions in higher dimensions that maintained hydrostatic equilibrium with spherical symmetric space-time. His findings revealed that the star’s central density was directly influenced by the existence of higher dimensions. The density of a star’s core increases proportionally to the square of its spatial and temporal dimensions. Consequently, for stars possessing more than four dimensions of space-time, the central density is comparatively higher for a given radius. Moreover, it is apparent that if there are more than four dimensions of space-time, a compact star with greater mass can exist for a given radius. The incorporation of an extra-temporal dimension was initially introduced by Bars and Terning [21], who used gauge symmetry as the foundation for their solution. By utilizing an extra time-dependent coordinate, they established a comprehensive framework and discovered that the findings were in agreement with the conventional models of GR.

Chattopadhyay and Paul [22] conducted a study to investigate compact stars under hydrostatic equilibrium conditions in higher dimensions. To do this, they employed a pseudospheroidal space-time metric in their investigation. This observation suggests that in higher-dimensional space-times, the gravitational forces become stronger, which leads to a denser and more compact core for a star of a given radius. This result highlights the impact of the number of dimensions of space-time on the properties of compact objects and has significant implications for the understanding of gravity and the behavior of stars in higher dimensions.

In their research, Bhar et al. [23] put forth evidence that indicated the presence of anisotropic compact stars in dimensions exceeding those of commutative space-time. The authors noted that model parameters, including radial and transverse pressures, matter-energy density, and anisotropy, exhibited uniform physical behaviors across the entire star structure. Additionally, they noted that as the dimensions of space-time increased, the central densities of the stars decreased sharply, while the level of anisotropy gradually increased and peaked at five dimensions.

Despite the usefulness of the static or quasi-static (QS) approximation in studying self-gravitating compact objects, there are some phenomena that cannot be accurately described by this approach. For instance, when a neutron star undergoes a quick collapse, non-equilibrium effects must be taken into consideration. To address this issue, Herrera et al. [24] introduced the PQS approximation, which was later extensively used by Herrera and his colleagues [25]. The PQS approximation differs from the QS approximation in that it uses “effective” variables rather than physical ones, such as effective pressure and energy density. This technique can be viewed as an iterative process, with each step deviating from equilibrium in increasing proportions. One approach to implementing the PQS approximation is through the radiative Bondi approach, which immediately takes the system from a static to a PQS evolution. The QS approximation can be considered as an iterative process; nevertheless, because the effective variables are the same as the physical variables. As an example, in reference [26], the authors utilized a method to simulate the evolution of self-gravitating bodies, which eliminates the need for fully integrating the EFEs in the time dimension.

Numerical techniques have proved to be useful for mathematicians in studying complex systems that are challenging to analyze analytically [30]. In particular, they have been effective in investigating strong field scenarios and revealing unforeseen phenomena in general relativity [27]. However, it is generally more difficult to solve partial differential equations numerically than ordinary differential equations (ODEs). To investigate self-gravitating spheres, the authors used a numerical method to develop a system of ODEs with variables determined at the BS of the fluid distribution. The researchers began with a seed solution to the EFEs that were static and spherically symmetric [27]. The numerical solution obtained describes the dynamic evolution of self-gravitating compact objects, with the initial solution representing the results of the static limit.

The study of GC is of great importance in the framework of various gravity theories associated with the five-dimensional system with smooth junction conditions at the boundary surface with the external Vaidya space-time. In their research of gravitational junction conditions for f(G, T) gravity, Bhatti et al. [28] presented the theory in both its derived dynamically equivalent scalar–tensor representation and its standard geometric representation. The established junction conditions for smooth matching between two space-times across a separation hyper-surface, preventing thin-shells, and providing a foundation for smooth matching model searching at the surface of alternative compact structures supported by thin-shells. The “cut and paste” method for static thin-shell wormhole models is investigated by Bhatti et al. [29]. They analyze the stability and instability of these models under isotropic perfect fluid and polytropic equation of state while taking mass and parametric factors into account.

The study’s goal is to investigate how compact objects evolve in a five-dimensional space-time during the PQS regime. The researchers concentrate on a radiative fluid distribution where dissipative effects are brought about by photon and/or neutrino emission. Compact object evolution frequently involves dissipation, with neutrino emission being the most effective method of eradicating the binding energy created during the formation of a collapsing star. The analysis of radiative transport in stellar objects frequently makes use of two additional approximations, diffusion and streaming out. The diffusion approximation, like thermal conduction, assumes that the flux of energy radiation is roughly proportional to the gradient of temperature. This approximation is frequently accurate because the mean free path of particles involved in energy transfer within star interiors is usually much shorter than the normal length scale of the object. The average free path of photons in a star like the sun, for instance, is roughly 2 cm. For compact cores with densities near \(10^{12}\,{\text {g}}\,{\text {cm}}^{-3}\), trapped neutrinos have a mean free path that is smaller than the size of the star’s core, as reported in [31, 32]. Furthermore, observations from the 1987A supernova showed that the streaming out limit [33] is more distant from the dominating radiation transport regime during the emission phase than the diffusion approximation.

The significance of GR and its alignment within the wider context of gravitational collapse with stellar sources is also of great interest. The behavior of stellar structures is investigated by Malik et al. [34], applying the embedding approach in the modified theory of gravity. LMC X-4, Cen X-3, and EXO 1785-248 are the three stars selected to illustrate stellar structures. To compute unknown parameters, the study compares spherically symmetric space-time with Schwarzschild space-time. The study looks into the equation of state parameters, pressure components, energy density, and other graphical aspects of stellar spheres. The outcomes demonstrate the viability and stability of the embedding class one solution for anisotropic compact stars and are consistent with established physical features. Yousaf et al. [35] study static cylindrically symmetric thin-shell wormhole models with an electric charge in f(R, T) gravity. They use a cut-and-paste technique and boundary conditions to ensure consistent matching. The study explores the stability of charged models.

Rosa’s [36] study examines the conditions necessary for matching two space-times at a separation hyper-surface in the perfect-fluid model of f(R, T) gravity. The parameters take into account scalar–tensor representations that are geometrically and dynamically equivalent, as well as partial derivatives and constraints on stress-energy tensor trace continuity. All energy conditions must be fulfilled by spherically symmetric thin-shells with a positive energy density. The stability of a limited class of axially symmetric cosmic matter configuration in anisotropic settings under modified gravitational theory is examined by Bhatti et al. [37]. It includes mass functions, collapse equations, continuity equations, and dynamically changed equations. The impact of a minimally connected gravitational function and f(R, T) gravity is also investigated. It also takes into account metric and material functions and investigates the fluid’s stiffness parameter.

Thin-shell wormholes from charged static cylindrically symmetric space-times are analyzed under f(R, T) gravity by Bhatti et al. [38], utilizing Visser’s “cut and paste” method. The study of the dynamics of manufactured wormholes is made possible by the modified Chaplygin gas, which supports exotic matter in the shell. The impact of the charge on the stability of the models is examined, as well as their stability under linear perturbations. The analysis discovers stable and unstable solutions for a range of gravity shapes and parameters. This study focuses on the behavior of collapsing fluid systems that are spherically symmetric and confined within a spherical surface in five dimensions while dissipating through free streaming radiation. The structure of the paper is organized as follows: Sect. 2 explains the conventions used and presents the EFEs. The methodology is discussed in Sect. 3. Lastly, Sect. 4 provides the conclusion and discussion.

2 The Einstein field equations in higher dimension

In this study, we examine collapsing fluid distributions that are spherically symmetric, non-static, and dissipating through free streaming radiation while being confined within a spherical surface \(\sum\). The metric in five dimensions is expressed as follows [39]:

$$\begin{aligned} {\text {ds}}^2=e^{\nu (r,t)} {\text {dt}}^2- e^{\lambda (r,t)} dr^2-r^2(d\theta ^2+{\text {sin}}^2d\phi ^2)-e^{\mu (r,t)} dw^2, \end{aligned}$$
(1)

The space-time coordinates are \(x^0=t, x^1=r, x^2=\theta , x^3=\phi , x^4=w\). We will use geometrized units, i.e., \(c=G=1\). The tensorial form of the corresponding EFEs is as follows:

$$\begin{aligned} G^{\nu }_{\mu }=-8\pi T^{\nu }_{\mu }. \end{aligned}$$
(2)

The resulting set of equations are as follows:

$$\begin{aligned} -8\pi T^{0}_{0}= & {} -\frac{1}{r^2}+e^{-\lambda } \Bigg (\frac{\mu _{,r}}{r}-\frac{\lambda _{,r}}{r}+\frac{\mu _{,r}^2}{4}-\frac{\mu _{,r}\lambda _{,r}}{4}+\frac{\mu _{,rr}}{2}+\frac{1}{r^2}\Bigg )+e^{-\nu }\Bigg (\frac{\mu _{,t}\lambda _{,t}}{4}\Bigg ), \end{aligned}$$
(3)
$$\begin{aligned} -8\pi T^{1}_{1}= & {} -\frac{1}{r^2}+e^{-\lambda }\Bigg (\frac{\nu _{,r}}{r}+\frac{\mu _{,r}}{r}+\frac{\mu _{,r}\nu _{,r}}{4}+\frac{1}{r^2}\Bigg )-\frac{e^{-\nu }}{4}\Bigg ({{\mu _{,t}}^2}-{\mu _{,t}}{\nu _{,t}} +2{\mu _{,tt}}\Bigg ), \end{aligned}$$
(4)
$$\begin{aligned} -8\pi T^{2}_{2}= & {} -8\pi T^{3}_{3}=\frac{1}{4}\Bigg [-{e^{-\nu }}\Bigg \{\mu _{,t}^2-\mu _{,t}\nu _{,t}+\mu _{,t}\lambda _{,t}+2\mu _{,tt}+2\lambda _{,tt} +\lambda _{,t}^2-\lambda _{,t}\nu _{,t}\Bigg \}\nonumber \\{} & {} +{e^{-\lambda }}\Bigg \{\nu _{,r}^2+\mu _{,r}^2-\nu _{,r}\lambda _{,r}-\mu _{,r}\lambda _{,r}+\mu _{,r}\nu _{,r}+2\nu _{,rr}+2\mu _{,rr}\Bigg \}\Bigg ]+\frac{2}{r}\Bigg (\nu _{,r}-\lambda _{,r}+\mu _{,r}\Bigg ), \end{aligned}$$
(5)
$$\begin{aligned} -8\pi T^{4}_{4}= & {} \frac{1}{r^2}-e^{-\lambda }\Bigg (\frac{\nu _{,r}}{r}-\frac{\lambda _{,r}}{r}+\frac{\nu _{,rr}}{2}+\frac{\nu _{,r}^2}{4}-\frac{\nu _{,r}\lambda _{,r}}{4}+\frac{1}{r^2}\Bigg )+\frac{e^{-\nu }}{4}\Bigg (2\lambda _{,tt}+{{\lambda _{,t}}^2}-\nu _{,t}\lambda _{,t}\Bigg ), \end{aligned}$$
(6)
$$\begin{aligned} -8\pi T_{01}= & {} \Bigg (\frac{\mu _{,r}\mu _{,t}}{4}-\frac{\mu _{,t} \nu _{,r}}{4}-\frac{\mu _{,r}\lambda _{,t}}{4}+\frac{\mu _{,tr}}{2}-\frac{\lambda _{,t}}{r}\Bigg ), \end{aligned}$$
(7)

To attribute physical significance to the elements of the stress tensor \(T^{\mu }_{\nu }\), we utilize the Bondi method. This Bondi method focuses on the behavior of gravitational fields at great distances from the sources, particularly at null infinity. These are space-times that, at large distances from any sources of gravity, resemble flat Minkowski space. The method is particularly useful in analyzing such space-times. In accordance with Bondi, we thus suggest Minkowski coordinates \((\tau , x, y, z, q)\) in five dimensions. In this case, \(d\tau = e^{\nu /2}{\text {dt}}\), \(dx = e^{\lambda /2}dr\), \(dy = r d\theta\), \(dz = r {\text {sin}}\theta d\phi\), and \(dq = e^{\mu /2}dw\). A bar is used to symbolize the energy stress tensor’s higher-dimensional Minkowski coordinates which gives \(\bar{T}^{0}_{0}=T^{0}_{0}\), \(\bar{T}^{1}_{1}=T^{1}_{1}\), \(\bar{T}^{2}_{2}=T^{2}_{2}\), \(\bar{T}^{3}_{3}=T^{3}_{3}\), \(\bar{T}^{4}_{4}=T^{4}_{4}\), and \(\bar{T}_{01}=e^{-\frac{(\nu +\lambda )}{2}}T_{01}\). We then assume that the physical components of space consist of an isotropic fluid with an energy density of \(\rho\), an isotropic pressure of P, an energy density of \({\hat{\epsilon }}\), and an unpolarized radiation with that is propagating radially, as seen by an observer moving at a proper velocity of \(\omega\) about these coordinates. The higher-dimensional Lorentz transformation can be used to demonstrate that

$$\begin{aligned}{} & {} T^{0}_{0}=\bar{T}^{0}_{0}=\frac{\rho +P\omega ^2}{1-\omega ^2}+\epsilon , \end{aligned}$$
(8)
$$\begin{aligned}{} & {} T^{1}_{1}=\bar{T}^{1}_{1}=-\frac{P+\rho \omega ^2}{1-\omega ^2}-\epsilon , \end{aligned}$$
(9)
$$\begin{aligned}{} & {} T^{2}_{2}=\bar{T}^{2}_{2}=T^{3}_{3}=\bar{T}^{3}_{3}=T^{4}_{4}=\bar{T}^{4}_{4}=-P, \end{aligned}$$
(10)
$$\begin{aligned}{} & {} T_{01}=e^{\frac{(\nu +\lambda )}{2}} \bar{T}_{01}=-\frac{(\rho +P)\omega e^{\frac{(\nu +\lambda )}{2}}}{1-\omega ^2}-e^{\frac{(\nu +\lambda )}{2}}\epsilon , \end{aligned}$$
(11)

with

$$\begin{aligned} \epsilon \equiv {\hat{\epsilon }} \frac{(\omega +1)}{(1-\omega )}. \end{aligned}$$
(12)

It is important to mention that in the \((t, r, \theta , \phi , w)\) system, the coordinate velocity \(\frac{dr}{\text {dt}}\) can be related to \(\omega\) (proper velocity) as follows:

$$\begin{aligned} \omega = \frac{dr}{\text {dt}} e^{\frac{(\lambda -\nu )}{2}}. \end{aligned}$$
(13)

After applying Lorentz transformations to Eqs. 8–11, we can substitute them into the field Eqs. 3–7, resulting in

$$\begin{aligned} \frac{\rho +P\omega ^2}{1-\omega ^2}+\epsilon= & {} -\frac{1}{8\pi }\Bigg \{-\frac{1}{r^2}+e^{-\lambda } \Bigg (\frac{\mu _{,r}}{r}-\frac{\lambda _{,r}}{r}+\frac{\mu _{,r}^2}{4}-\frac{\mu _{,r}\lambda _{,r}}{4}+\frac{\mu _{,rr}}{2}+\frac{1}{r^2}\Bigg )\nonumber \\{} & {} +e^{-\nu }\Bigg (\frac{\mu _{,t}\lambda _{,t}}{4}\Bigg )\Bigg \}, \end{aligned}$$
(14)
$$\begin{aligned} \frac{P+\rho \omega ^2}{1-\omega ^2}+\epsilon= & {} -\frac{1}{8\pi }\Bigg \{\frac{1}{r^2}-e^{-\lambda }\Bigg (\frac{\nu _{,r}}{r}+\frac{\mu _{,r}}{r}+\frac{\mu _{,r}\nu _{,r}}{4}+\frac{1}{r^2}\Bigg )+\frac{e^{-\nu }}{4}\Bigg ({{\mu _{,t}}^2}-{\mu _{,t}}{\nu _{,t}} +2{\mu _{,tt}} \Bigg )\Bigg \}, \end{aligned}$$
(15)
$$\begin{aligned} P\,=\, &\, \frac{-1}{32\pi }\Bigg [{e^{-\nu }}\Bigg (\mu _{,t}^2-\mu _{,t}\nu _{,t}+\mu _{,t}\lambda _{,t}+2\mu _{,tt}+2\lambda _{,tt} +\lambda _{,t}^2-\lambda _{,t}\nu _{,t}\Bigg )\nonumber \\{} & {} -{e^{-\lambda }}\Bigg (\nu _{,r}^2+\mu _{,r}^2-\nu _{,r}\lambda _{,r}-\mu _{,r}\lambda _{,r}+\mu _{,r}\nu _{,r}+2\nu _{,rr}+2\mu _{,rr}\Bigg )\Bigg ]-\frac{2}{r}\Bigg (\nu _{,r}-\lambda _{,r}+\mu _{,r}\Bigg ), \end{aligned}$$
(16)
$$\begin{aligned} e^{\frac{\nu +\lambda }{2}}\Bigg (\frac{\rho +P }{1-\omega ^2}\omega +\epsilon \Bigg )= & {} -\frac{1}{8\pi }\Bigg \{-\frac{\mu _{,r}\mu _{,t}}{4}+\frac{\mu _{,t} \nu _{,r}}{4}+\frac{\mu _{,r}\lambda _{,t}}{4}-\frac{\mu _{,tr}}{2}+\frac{\lambda _{,t}}{r}\Bigg \}. \,\,\,\,\,\,\,\ \end{aligned}$$
(17)

The system of equations in Eqs. 14–17 is used to determine the values of \(\omega\), \(\rho\), P, and \(\epsilon\) for given functions \(\mu\), \(\nu\), and \(\lambda\). For higher dimensions, the corresponding Vaidya exterior geometry is expressed as follows [40]:

$$\begin{aligned} {\text {ds}}^2=\left( 1-\frac{2M(u)}{R^{2}}\right) du^2+2dudR-R^2\left( d\theta ^{2}_{1}+{\text {sin}}^2\theta _1\left( d\theta ^{2}_{2}+{\text {sin}}\theta ^{2}_{2}d\theta ^{3}_{2}\right) \right) , \end{aligned}$$
(18)

where u stands for the retarded time, and M(u) represents the system’s total mass, indicated as Sigma inside the BS. At and outside the BS, the two coordinate systems \((t, r, \theta , \phi , w)\) and \((u, R, \theta _1, \theta _2, \phi )\) are connected as

$$\begin{aligned} u=t-r-2M {\text {ln}}\left( \frac{r}{2M}-1\right) ,\,\ R=r_\Sigma , \end{aligned}$$
(19)

and certain sufficient and necessary conditions must be met for the two metrics in Eqs. 1 and 18 to match smoothly. These conditions are given as

$$\begin{aligned}{} & {} e^{\nu _\Sigma }=e^{-\lambda _\Sigma }=e^{-\mu _\Sigma }=1-\frac{2M}{R^{2}_{\Sigma }}, \end{aligned}$$
(20)
$$\begin{aligned}{} & {} [P]_\Sigma =0. \end{aligned}$$
(21)

In this study, we assume that the fluid is isotropic and dissipative, with free streaming radiation. The radiation density is denoted by \(\epsilon\) and is defined as follows:

$$\begin{aligned} T_{\mu \nu }=(\rho +P)u_\mu u_\nu -P g_{\mu \nu }+\epsilon l_\nu l_\mu , \end{aligned}$$
(22)

with

$$\begin{aligned} u_\mu= & {} \left( \frac{e^{\nu /2}}{\sqrt{(1-\omega ^2)}}, \frac{\omega e^{\lambda /2}}{\sqrt{(1-\omega ^2)}}, 0, 0, 0\right) , \end{aligned}$$
(23)
$$\begin{aligned} l_\mu= & {} \left( e^{\nu /2},\,\ e^{\lambda /2}, 0, 0, 0\right) . \end{aligned}$$
(24)

The five velocity of the fluid is denoted by \(u_\mu\), and a null outgoing vector in five dimensions is denoted by \(l_\mu\). The following equation is obtained by using the conservation law to calculate \(T^{\mu }_{\nu ;\mu }=0\), we obtained:

$$\begin{aligned} P_{,r}=-\left( \frac{\nu _{,r}+\mu _{,r}}{2}\right) \left( \rho +P\right) . \end{aligned}$$
(25)

The static form of the TOV equation is represented in the above equation. By setting \(\mu _{,r}=0\) in the TOV Eq. 25, we can obtain the standard TOV equations in four dimensions.

3 The methodology for higher dimension

The most basic case when dealing with compact self-gravitating objects is static equilibrium. This condition indicates that all time-dependent derivatives vanish, the quantities \(\omega\) and \(\epsilon\) are equal to zero, and we will get a modified TOV equation. The timescale for the sphere to respond to minor perturbations in hydrostatic equilibrium is, on average, significantly longer, consistent with the sphere’s slower evolution in QS regime. Therefore, in QS regime, the system remains consistently in the vicinity of hydrostatic equilibrium. Equation 17 connects a series of static models that represent the evolution of the sphere. This estimate makes sense because the hydrostatic time scale is brief during different phases of a star’s.

For instance, it takes around 27 min for the Sun, 4.5 s for a white dwarf, and \(10^{-4}\) s for a neutron star with a solar mass and a radius of 10 km [41]. The stars have been observed to change over periods that are significantly longer than their corresponding hydrostatic timescales. However, as noted earlier, in certain critical scenarios, this approximation becomes inaccurate, and deviations from quasi-equilibrium must be considered.

3.1 Approximation of effective variables and higher dimension PQS

The PQS approximation employs the following equation to define the effective variables:

$$\begin{aligned}{} & {} \tilde{\rho }=T^{0}_{0}=\frac{\rho +P\omega ^2}{1-\omega ^2}+\epsilon , \end{aligned}$$
(26)
$$\begin{aligned}{} & {} \tilde{P}=-T^{1}_{1}=\frac{P+\rho \omega ^2}{1-\omega ^2}+\epsilon . \end{aligned}$$
(27)

In the QS regime, the effective variables and the corresponding physical variables satisfy the same TOV Eq. 25. Therefore, the physical and effective variables have identical radial dependencies in both QS and static conditions. The mass function associated with the effective variables is given by

$$\begin{aligned} m=\int _{0}^{r}4\pi r^2 \tilde{\rho }dr. \end{aligned}$$
(28)

Substituting Eq. 27 into Eq. 15:

$$\begin{aligned} \nu\,=\,\, & \nu _\Sigma + \int _{r_\Sigma }^{r} \frac{2(8 \pi \tilde{P} r^4(r^2-2m)-2r^3m_{,r}+6r^2m-12m^2+4rmm_{,r})}{(2r^3(r^2-5m)+12rm^{2}+r^4m_{,r}-2r^2m m_{,r})}\nonumber \\{} & {} +\frac{r^2}{r^2-2m}\Big (\frac{m_{,tt}}{(r^2-2m)}+\frac{4( m_{,t})^2}{(r^2-2m)^2}\Big ) dr, \end{aligned}$$
(29)
$$\begin{aligned} \mu\,=\,\, & \mu _\Sigma + \int _{r_\Sigma }^{r} \frac{2(8 \pi \tilde{P} r^4(r^2-2m)+2r^3m_{,r}-2r^2m+4m^2-4rmm_{,r})}{(2r^3(r^2-3m)+4rm^{2}-r^4m_{,r}+2r^2mm_{,r})}\nonumber \\{} & {} +\frac{r^2}{r^2-2m}\Big (\frac{m_{,tt}}{(r^2-2m)}+\frac{4( m_{,t})^2}{(r^2-2m)^2}\Big ) dr. \end{aligned}$$
(30)

For a given radial dependency of \(\tilde{\rho }\) and \(\tilde{P}\), the metric functions radial dependency can be entirely determined. The \(\tilde{\rho }\) and \(\tilde{P}\) exhibit a radial dependency that is comparable to that of the corresponding physical variables when they are in equilibrium or quasi-equilibrium. On the other hand, the PQS regime metric functions that define the system have the same radial dependency as the static or QS regime metric functions. This formulation was developed with a simple goal in mind: to identify a regime that, while not in an equilibrium state, best simulates the evolution of a QS.

3.2 The higher-dimensional algorithm for PQS approximation

We will be using the following approach:

  1. 1.

    An equilibrium state of fluid distributed matter is represented by an analytical interior solution to the EFEs, which is defined as \(\rho _{st}=\rho (r)\) and \(P_{st}=P(r)\).

  2. 2.

    Assume that \(\tilde{P}\) and \(\tilde{\rho }\) have the same radial dependence as \(P_{st}\) and \(\rho _{st}\).

  3. 3.

    Using Eqs. 28, 29, and 30, as well as the radial dependency of \(\tilde{P}\) and \(\tilde{r}ho\), obtain m, \(\mu\), and \(\nu\) up to certain functions of t.

  4. 4.

    For these functions of t, there are three surface equations given by:

    • Evaluating Eq. 13 at \(r=r_\Sigma\).

    • The equation that depicts the connection between mass loss rate along the BS and energy flux \((\hat{E})\).

    • Determining the dynamic TOV equation at \(r=r_\Sigma\).

  5. 5.

    Additional information is needed to conclude the set of surface equations and highlight a few physical factors on the BS.

  6. 6.

    Once the system is closed, it can be integrated for any given set of initial conditions.

  7. 7.

    The expressions for m, \(\mu\), and \(\nu\) can be fully determined by inserting the integration results.

  8. 8.

    For every kind of fluid distribution, a system of equations for physical variables can be generated by appropriately describing metric functions with the EFEs.

3.3 Higher-dimensional surface equations

The preceding discussion highlights that the system of surface equations plays a crucial role in the algorithm. To address this, we introduce dimensionless variables as follows:

$$\begin{aligned} F=1-\frac{2M}{A^2},\,\,\ A=\frac{r_\Sigma }{m_\Sigma (0)},\,\,\ M=\frac{m_\Sigma }{m_\Sigma (0)}, \,\,\ \beta =\frac{t}{m_\Sigma (0)}, \,\,\ \Omega =\omega _\Sigma . \end{aligned}$$

The total mass \(m_\Sigma (0)\) for the first surface equation is derived by substituting \(r=r_\Sigma\) in Eq. 13. We obtained,

$$\begin{aligned} \frac{dA}{d\beta }=F\Omega , \end{aligned}$$
(31)

by applying the junction conditions to Eqs. 14, 17, and 20 evaluated at \(r=r_\Sigma\), we can obtain:

$$\begin{aligned} \frac{d M}{d\beta }=\frac{-F^2}{{\hat{S}}}\Big ((1+\Omega )-\frac{\Omega \rho _\Sigma }{2}+\Omega \rho _\Sigma {\hat{B}}\Big )\hat{E}, \end{aligned}$$
(32)

where

$$\begin{aligned}{} & {} \hat{E}=4 \pi r{^{2}_\Sigma }\hat{\epsilon }_\Sigma , \end{aligned}$$
(33)
$$\begin{aligned}{} & {} \hat{S}=m_{,r\Sigma }r_\Sigma (3+r{^2_\Sigma }-2m_\Sigma )-6m_\Sigma , \end{aligned}$$
(34)
$$\begin{aligned}{} & {} \hat{B}=\frac{r{^3_\Sigma }-12\pi r{^2_\Sigma }\rho _\Sigma +16\pi r{^4_\Sigma }+r{^2_\Sigma }-2m_\Sigma -16\pi r{^3_\Sigma }\rho _\Sigma \Omega }{3r_\Sigma (r{^2_\Sigma }-2m_\Sigma )}. \end{aligned}$$
(35)

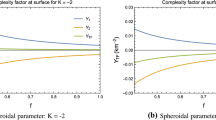
The right-hand side of Eq. 32 represents both the Doppler shift and gravitational redshift. The equation for defining the perceived luminosity at infinity as perceived by an observer is as follows:

$$\begin{aligned} L=-\frac{d M}{d\beta }. \end{aligned}$$
(36)

The following equation is the second surface equation:

$$\begin{aligned} \frac{dF}{d\beta }=\frac{2(1-F)F\Omega }{A}+\frac{2L}{A}. \end{aligned}$$
(37)

The evaluation of \(T^{\mu }_{\nu ;\mu }=0\) at the BS yields the following third surface equation:

$$\begin{aligned} \tilde{P}+(\tilde{\rho }+\tilde{P})\Big (\frac{\nu _{,r}+\mu _{,r}}{2}\Big )=\frac{e^{-\nu }}{4 \pi r(r^2-2m)}\Big (2m_{,tt}+\frac{7 (m_{,t})^{2}}{r^2-2m}- m_{,t} \nu _{,t}\Big )+\frac{2}{r}(P-\tilde{P}). \end{aligned}$$
(38)

When Eq. 38 is evaluated at the BS, the resulting equation is:

$$\begin{aligned} \frac{d\Omega }{d\beta }\,=\,\, & \Omega ^2\Bigg [\Big \{\frac{4\pi A^{5}\tilde{\rho }_{\Sigma } F-4\pi A^6\tilde{\rho }_\Sigma \Omega ^{2}F^{2}-3 A^{2} F m_{\Sigma }+6F m^{2}_{\Sigma }-2 A^{3}\tilde{\rho }_{\Sigma } \Omega F}{A^{5} -5A^{3} m_{\Sigma }+6 A m^{2}_{\Sigma }+2\pi A^{4}\tilde{\rho }_{\Sigma }-4\pi A^{4}m_{\Sigma }\tilde{\rho }_{\Sigma }}\Big \}\nonumber \\ {}{} & {} +6\pi \tilde{\rho }_\Sigma +16\pi ^2\tilde{\rho }^2_\Sigma \Omega ^2\Bigg ] -\frac{AF}{2\tilde{\rho }_\Sigma }\Bigg [R+\frac{2}{A}\Big (\tilde{\rho }_\Sigma \Omega ^2+\frac{\bar{E}(1+\Omega )}{4\pi r^2_\Sigma }\Big )\Bigg ] \end{aligned}$$
(39)

where

$$\begin{aligned}{} & {} R=\left[ \tilde{P}+\left( \tilde{\rho }+\tilde{P}\right) \left( \frac{\nu _{,r}+\mu _{,r}}{2}\right) \right] _\Sigma , \end{aligned}$$
(40)
$$\begin{aligned}{} & {} \bar{E}=\hat{E}(1+\Omega ). \end{aligned}$$
(41)

According to Eq. 31, this implies \(\Omega =0\), we get

$$\begin{aligned} \frac{d^2A}{d\beta ^2}=F\frac{d\Omega }{d\beta }. \end{aligned}$$
(42)

By applying \(\Omega =0\) on Eq. 39, we obtain

$$\begin{aligned} \frac{d\Omega }{d\beta }=-\frac{F}{\tilde{\rho }_\Sigma }\left[ \frac{AR}{2}+\frac{{\hat{E}}}{4\pi r^2_\Sigma }\right] . \end{aligned}$$
(43)

It can be observed that when there is a positive energy flux \({\hat{E}}\), the radius of the sphere tends to decrease, leading to object compactification, which is expected. Conversely, if the signs of these quantities are reversed, the opposite effect occurs. According to the following inequality, the sphere will only bounce at its surface if there is a positive energy flux and \(\Omega =0\).

$$\begin{aligned} \frac{d\Omega }{d\beta }\ge 0. \end{aligned}$$
(44)

This can be restated as per Eq. 43 to mean that

$$\begin{aligned} -\frac{AR}{2}(\Omega =0)\ge 0. \end{aligned}$$
(45)

The meaning of this equation is physical and can be explained as follows. When dealing with non-radiating and static configurations, the expression for R in Eq. 40 can be separated into two components. The gravitational and hydrodynamical forces are defined by the first and second terms of the expression given in Eq. 40, for non-radiating, static configurations. The force that results when r rises is precisely \(-\frac{AR}{2}\). The net acceleration of dynamic configurations in five dimensions can be shown using Eq. 45, indicating either an outward or inward acceleration depending on the direction of the force.

4 Summary and analysis

In this study, a non-comoving coordinate system similar to the five-dimensional Schwarzschild metric is employed to create a general framework for examining the GC of a spherical system. We extend the PQS approximation to five-dimensional space-time to explore the effects of GC. The additional spatial dimension enhances the gravitational interaction at small scales, leading to a more efficient collapse process. The EFEs are constructed using these coordinates, with the fifth coordinate representing the space-like element. In non-comoving coordinates, the velocity of any fluid element is considered a relevant physical variable. These variables are discussed in the context of higher-dimensional surface equations. A starting point was established by utilizing an analytical solution for the interior in the EFEs. This method proposes a collection of ODEs for quantities that are identified at the BS. By numerically solving these equations, it becomes possible to simulate self-gravitating spheres that are under consideration.

It is assumed that the fluid distribution in the inner region is isotropic and has a radiation factor that has dissipative effects on the field of gravitation. Dissipation is a stage in the evolution of giant stars, where massless particles are emitted, and neutrino emission is believed to be the only viable method for removing most of the binding energy during the collapse of a star, leading to the formation of a neutron star or black hole. Furthermore, the inclusion of the fifth dimension allows for a richer variety of isotropic, dissipative fluid dynamics, which are critical for accurately modeling the thermal properties of the collapsing matter. These effects are not adequately captured in four-dimensional models, thus justifying the need for higher-dimensional analysis. To ensure a smooth match at the boundary of the sphere, the outer region is considered as Vaidya space-time.

The TOV equation is obtained through the conservation law in higher dimensions. To develop the surface equation, we utilized a modified version of the TOV Eq. 22 that employs effective variables. Effective variables, including effective energy density and pressure, satisfy the TOV equation along with physical variables. Both physical and effective variables have identical radial dependencies in static and quasi-static equilibrium. This iterative process involves successive steps that reflect a profound understanding of the departure from the state of equilibrium. The PQS approximation has been defined to facilitate the analysis of GC in non-comoving coordinates. The justification and verification for the PQS method, which employs an approximate approach and “effective” variables, become evident in the context of a five-dimensional regime.

This investigation aimed to create a series of surface equations utilizing the PQS approximation methodology in higher dimensions, specifically in the context of the five-dimensional PQS framework. The study examined realistic characteristics of stars, such as gravitational redshift, Doppler shift, and total mass loss rate, which are associated with the energy flow of total mass loss over the BS. To gain an understanding of the nature of relativistic GC in five dimensions, it was necessary to establish a comprehensive framework for the PQS regime through the solution of nonlinear differential equations. The significance of dissipation in the process of GC was taken into account, as it is a highly energy-dissipating mechanism that plays a dominant role in star evolution and formation. The five-dimensional null outgoing vector represents the dissipative model in the diffusion approximation.

The existence of compact stars, such as neutron stars and hybrid stars, in higher-dimensional space-time, has prompted researchers to study GC in these dimensions. There is currently no model for GC in the PQS approximation for dimensions higher than four. This article examines the physical properties/aspects of the stellar structure of compact objects in five-dimensional coordinates. Three types of models can be utilized in relativistic astrophysical applications: Schwarzschild-type models, Tolman type-VI, and Lemaitre–Florides-type models. The above-mentioned models illustrate the relativistic gravitational effects resulting from the radial pressure discontinuity at the BS. This research could be expanded to GC for the PQS regime in comoving coordinates.