Mass and width of an unstable particle

Abstract

We show that the mass and width of an unstable particle are precisely defined by the pole in the complex energy plane, $\mu = m - (i/2)\Gamma$, by identifying the width, $\Gamma$, with the particle’s decay rate and the mass, m, with the oscillatory frequency. We find that the physical Z boson mass lies 26 MeV below its quoted value, while the physical W boson mass lies 20 MeV below. We also clarify the various Breit–Wigner formulae that are used to describe a resonance.

1 Introduction

The squared mass of a stable particle is equal to the pole in the particle’s propagator. For an unstable particle, the pole is complex, and is related to both the mass and the width of the particle. In this paper, we make this relation precise.

For simplicity, we consider a complex scalar field; the calculation also applies to the transverse part of a massive vector field, such as the W and Z bosons. We study the propagator, which in a free field theory is the amplitude for a particle to be created at the origin and destroyed at space-time point x (or an antiparticle to be created at x and destroyed at the origin),

$$\begin{aligned} \langle 0 | T \phi (x) \phi ^\dagger (0) |0\rangle = \int \frac{d^4p}{(2\pi )^4}\frac{ie^{-ip\cdot x}}{p^2-m^2+i\epsilon }\;. \end{aligned}$$

(1)

The squared mass of the particle is the pole in the momentum-space propagator.

We now include interactions to all orders in perturbation theory. Consider the self-energy corrections to the momentum-space propagator from the diagrams in Fig. 1, where the shaded circle denotes the bare one-particle-irreducible self-energy to all orders in perturbation theory, $i\Pi (p^2)$. Summing the series of diagrams gives

$$\begin{aligned}{} & {} \frac{i}{p^2 - m_B^2+i\epsilon }\left( 1-\frac{\Pi (p^2)}{p^2-m_B^2+i\epsilon }+\cdots \right) \end{aligned}$$

(2)

$$\begin{aligned}{} & {} =\frac{i}{p^2 - m_B^2 + \Pi (p^2)+i\epsilon } \end{aligned}$$

(3)

where $m_B$ is the bare mass. The pole of the full momentum-space propagator, $\mu ^2$, is the solution to equation

$$\begin{aligned} \mu ^2-m_B^2+\Pi (\mu ^2)=0\;. \end{aligned}$$

(4)

Combining Eqs. (3) and (4) yields

$$\begin{aligned} \langle 0 | T \phi (x) \phi ^\dagger (0) |0\rangle = \int \frac{d^4p}{(2\pi )^4}\frac{ie^{-ip\cdot x}}{p^2-\mu ^2+\Pi (p^2)-\Pi (\mu ^2)+i\epsilon } \end{aligned}$$

(5)

Since the unstable particle is not an asymptotic state it is not necessary to renormalize the field, although one may choose to do so.

Fig. 1

Self-energy corrections to the propagator

If the particle is unstable, $\Pi (\mu ^2)$ is complex, and hence, from Eq. (4), $\mu ^2$ is complex. The pole position is gauge invariant [1,2,3] and infrared safe [2, 3]. The fact that the pole is complex is a fundamental feature of an unstable particle, and will be used in the next section to derive the mass and width.

2 Width and mass

The width of an unstable state, whether it be a fundamental particle or a composite, is generally understood to be the decay rate of the particle, that is, $\Gamma = 1/\tau$, where $\tau$ is the lifetime. This provides an unambiguous definition of $\Gamma$, and is used in all branches of physics.

The scattering amplitude of a process with an intermediate unstable particle acquires a complex pole from the propagator,

$$\begin{aligned} S \sim \frac{1}{p^2-\mu ^2}\;. \end{aligned}$$

(6)

Going to the rest frame of the unstable particle (we consider a general frame in Appendix A), we can rewrite Eq. (6) as

$$\begin{aligned} S \sim \frac{1}{p_0^2-\mu ^2}=\frac{1}{(p_0 - \mu )(p_0 + \mu )}\;. \end{aligned}$$

(7)

To find the time dependence of the scattering amplitude, we Fourier transform from energy to time [4]:

$$\begin{aligned} S \sim \int _{-\infty }^\infty dp_0\; \frac{e^{-ip_0t}}{(p_0 - \mu )(p_0 + \mu )}\;. \end{aligned}$$

(8)

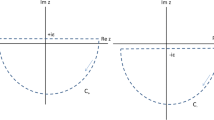
For $t>0$ we can close the contour in the lower-half complex $p_0$ plane, as shown in Fig. 2, since the integral along the large semicircle is exponentially damped. Using the residue theorem, we pick up the contribution of the pole at $p_0 = \mu$,

$$\begin{aligned} S \sim e^{-i\mu t} = e^{-i\textrm{Re}\,\mu t}e^{\textrm{Im}\,\mu t}\;. \end{aligned}$$

(9)

Fig. 2

Evaluating the Fourier transform of the propagator by closing the contour in the lower-half energy plane (for $t>0)$

The decay probability is given by the square of the scattering amplitude,

$$\begin{aligned} |S|^2 \sim e^{2\textrm{Im}\,\mu t}\;. \end{aligned}$$

(10)

This corresponds to exponential decay with $2\textrm{Im}\,\mu = -\Gamma$. Hence we learn that $\textrm{Im}\,\mu = - \Gamma /2$.

For $t<0$, we close the contour in the upper half complex $p_0$ plane and pick up the contribution of the pole at $p_0 = -\mu$. This pole is associated with antiparticle propagation. The residue theorem gives $S \sim e^{i\textrm{Re}\,\mu t}e^{-\textrm{Im}\,\mu t}$, and hence, $|S|^2 \sim e^{\Gamma t}$. This also corresponds to exponential decay since t is negative, and proves that the particle and antiparticle have the same lifetime.

The oscillatory frequency of the state is dictated by the particle energy, which in the rest frame is just its mass. Hence (from Eq. (9)) $\textrm{Re}\,\mu = m$, and we conclude that

$$\begin{aligned} \boxed {\mu = m - \frac{i}{2}\Gamma }\;. \end{aligned}$$

(11)

The same result has been obtained in Ref. [5] by different means, also using $\Gamma = 1/\tau$. Equation (11) is also used to define the mass and width of hadronic resonances (see Sec. 50 of Ref. [6]), and is used, in matrix form, in the analysis of neutral meson oscillations (see Sec. 13 of Ref. [6]). Equation (11) provides an unambiguous decomposition of $\mu$ into physically meaningful quantities. Note that nowhere did we make a nonrelativistic approximation.

Returning to Eq. (4), and using Eq. (11), we find

$$\begin{aligned} \textrm{Im}\,\mu ^2 = -m\Gamma = - \textrm{Im}\, \Pi (\mu ^2) \end{aligned}$$

(12)

or

$$\begin{aligned} \Gamma = \frac{1}{m}\textrm{Im}\, \Pi (\mu ^2)\;. \end{aligned}$$

(13)

This is an implicit formula for the decay rate, since $\mu = m - (i/2)\Gamma$, and can be solved iteratively. To next-to-next-to-leading order, we find

$$\begin{aligned} m\Gamma = \textrm{Im}\, \Pi (m^2)\left( 1-\textrm{Re}\, \Pi ^{\prime }(m^2)+(\textrm{Re}\, \Pi ^{\prime }(m^2))^2 -\frac{1}{2}\textrm{Im}\, \Pi (m^2) \textrm{Im}\, \Pi ^{\prime \prime }(m^2)-\frac{1}{4m^2}\textrm{Im}\, \Pi (m^2) \textrm{Im}\, \Pi ^{\prime }(m^2) + \cdots \right) \;. \end{aligned}$$

(14)

The leading term, $m\Gamma = \textrm{Im}\, \Pi (m^2)$, is the familiar tree-level expression.

The exponential decay of an unstable particle follows from the complex pole in the particle’s propagator. The propagator also has branch-point singularities, which we discuss in Appendix B. These singularities do not affect the exponential decay of the particle.

Some authors, going back to the original papers on the subject [7, 8], have expressed the opinion that the definition of the mass (and width) of an unstable particle is inherently ambiguous due to the uncertainty principle. A typical argument is that the energy-time uncertainty principle, $\Delta E \Delta t \ge 1$, restricts the accuracy with which the mass can be defined by $\Delta m\sim \Delta E \ge 1/\Delta t = 1/\tau = \Gamma$. This is faulty logic, as $\Delta E$ corresponds not to the uncertainty in the definition of the mass, but to the spread of energies that an unstable particle is produced with, i.e., the width. There is no uncertainty in the pole position in the complex energy plane, nor in the mass, which is the real part of the pole position. The same is true of the width.

3 Resonance formulae

In the energy region near the pole at $p_0 = \mu$, the amplitude of Eq. (7) can be approximated by neglecting the antiparticle pole at $p_0 = -\mu$,

$$\begin{aligned} S \sim \frac{1}{E - \mu } \end{aligned}$$

(15)

where $E=p_0$. The cross section in the resonance region is thus approximately

$$\begin{aligned} |S|^2 \sim \frac{1}{(E-m)^2 + \Gamma ^2/4} \end{aligned}$$

(16)

which is the well-known Breit–Wigner formula [9]. The resonance shape has a full width at half maximum of $\Gamma$, which is why $\Gamma$ is called the width. A similar formula may also be obtained from nonrelativistic quantum mechanics, such as in the original paper [9].

Another way to approximate the cross section in the resonance region is to start from Eq. (6). Making the approximation, valid for $\Gamma ^2 \ll m^2$,

$$\begin{aligned} \mu ^2 = \left( m-\frac{i}{2}\Gamma \right) ^2 \approx m^2-im\Gamma \end{aligned}$$

(17)

gives the propagator

$$\begin{aligned} S \sim \frac{1}{p^2 - m^2 + im\Gamma } \end{aligned}$$

(18)

and hence the cross section

$$\begin{aligned} |S|^2 \sim \frac{1}{(p^2 - m^2)^2 + m^2\Gamma ^2}\;. \end{aligned}$$

(19)

This is often referred to as a relativistic Breit–Wigner formula. The relativistic invariance follows from the inclusion of both particle and antiparticle poles.

The moral is that both versions of the Breit–Wigner formula, Eqs. (16) and (19), are approximations, and should be treated thusly. In addition, formula $\mu ^2 = m^2 - im\Gamma$ [see Eq. (17)], which has gained widespread currency, is also an approximation. The precise definition of the mass and width of an unstable particle is $\mu = m - (i/2)\Gamma$ [Eq. (11)].

Inserting Eq. (11) into Eq. (6) without making any approximations gives the propagator

$$\begin{aligned} S \sim \frac{1}{p^2 - \left( m - \frac{i}{2}\Gamma \right) ^2} \end{aligned}$$

(20)

and hence the cross section

$$\begin{aligned} |S|^2 \sim \frac{1}{(p^2 - m^2 + \Gamma ^2/4)^2+m^2\Gamma ^2}\;. \end{aligned}$$

(21)

It may seem unconventional to include the $\Gamma ^2/4$ term in the denominator of the above expression, but its presence follows from the precise definition of mass and width provided by Eq. (11). Equation (21) is the relativistic Breit–Wigner formula, Eq. (19), but without taking the limit $\Gamma ^2 \ll m^2$.

4 Weak boson masses

The Z and W boson masses have been extracted from experiment by using the resonance formula

$$\begin{aligned} |S|^2 \sim \frac{1}{(p^2 - M^2)^2 + (p^2{\varGamma }/M)^2} \end{aligned}$$

(22)

which corresponds to none of the Breit–Wigner formulae, Eqs. (16), (19), and (21). This formula is based on the propagator

$$\begin{aligned} \frac{1}{p^2 - M^2 + ip^2{\varGamma }/M} \end{aligned}$$

(23)

which has a troubled history. It was once thought that the mass of an unstable particle could be defined by

$$\begin{aligned} M^2-m_B^2+\textrm{Re}\,\Pi (M^2)=0\;. \end{aligned}$$

(24)

in contrast to Eq. (4). Combining Eqs. (3) and (24) yields the momentum-space propagator

$$\begin{aligned} \frac{1}{p^2 - M^2 + \Pi (p^2) - \textrm{Re}\,\Pi (M^2)} \approx \frac{1}{p^2 - M^2 + i\textrm{Im}\,\Pi (p^2)}\; \end{aligned}$$

(25)

For a weak boson coupled to massless fermions, the leading-order approximation gives $\textrm{Im}\,\Pi (p^2) = p^2{\varGamma }/M$, where ${\varGamma}$ is evaluated at tree level. Inserting this into Eq. (25) gives the propagator of Eq. (23). This is sometimes called the on-shell scheme for unstable particles.

The trouble with this scheme is not the aforementioned approximations, which can be improved; it is that the mass M is gauge dependent [10] and thus unphysical. All modern approaches to the resonance region (see Section 6 of Ref. [11]), including the complex-mass scheme [12, 13], use the pole position, Eq. (4), which is gauge invariant.

Although it has no good theoretical justification, Eq. (22) is widely used to model the resonance region. Fortunately, and despite appearances, the propagator of Eq. (23) is equivalent to that of Eq. (20), and gives exactly the same resonance shape. Both propagators have simple poles, and by equating the poles we can find the exact relation between the parameters M and ${\varGamma }$ and the physical mass and width of the particle,

$$\begin{aligned} m = M \left( \frac{r+1}{2r^2}\right) ^{\frac{1}{2}}\approx M\left( 1-\frac{3}{8}\left( \frac{{\varGamma }}{M}\right) ^2\right) \end{aligned}$$

(26)

$$\begin{aligned} \Gamma = 2M \left( \frac{r-1}{2r^2}\right) ^{\frac{1}{2}}\approx { \Gamma }\left( 1-\frac{5}{8}\left( \frac{{\varGamma }}{M}\right) ^2\right) \end{aligned}$$

(27)

where

$$\begin{aligned} r=\left( 1+\left( \frac{{\varGamma }}{M}\right) ^2\right) ^{\frac{1}{2}}\;. \end{aligned}$$

(28)

Going forward, it would be simpler to use the propagator of Eq. (20) to model the resonance region directly in terms of the physical mass and width.

The world-average values $M_Z = 91.1876 \pm 0.0021\; \textrm{GeV}$ and ${\varGamma }_Z = 2.4952 \pm 0.0023\; \textrm{GeV}$ [6] can be used to derive the physical Z boson mass and width from Eqs. (26) and (27),

$$\begin{aligned} m_Z = 91.1620 \pm 0.0021\; \textrm{GeV}\end{aligned}$$

(29)

$$\begin{aligned} \Gamma _Z = 2.4940 \pm 0.0023\; \textrm{GeV}. \end{aligned}$$

(30)

The physical Z boson mass is about 26 MeV less than the parameter $M_Z$, a result we derived long ago [14]; this is about ten times greater than the uncertainty in the mass. The Z boson width is the same as the parameter ${\varGamma }_Z$ within the uncertainty. This yields a Z boson lifetime of $\tau _Z = 2.6391 \pm 0.0024 \times 10^{-25}\; \textrm{s}$.

The world-average values $M_W = 80.379 \pm 0.012\; \textrm{GeV}$ and ${\varGamma }_W = 2.085 \pm 0.042\; \textrm{GeV}$ [6] yield the physical W boson mass and width

$$\begin{aligned} m_W = 80.359 \pm 0.012\; \textrm{GeV} \end{aligned}$$

(31)

$$\begin{aligned} \Gamma _W = 2.084 \pm 0.042\; \textrm{GeV}. \end{aligned}$$

(32)

The physical W boson mass is about 20 MeV less than the parameter $M_W$, which is nearly twice the uncertainty in the mass. The W boson width is the same as the parameter ${\varGamma }_W$ within the uncertainty, and yields $\tau _W = 3.158 \pm 0.064 \times 10^{-25} \; \textrm{s}$.

The top-quark mass and width are also extracted from experiment using the parameterization of Eq. (22). The world-average values are $M_t = 172.76 \pm 0.30\; \textrm{GeV}$ and ${\varGamma }_t = 1.42 + 0.19 - 0.15\; \textrm{GeV}$ [6]. The width is sufficiently narrow that these values are equal to the physical top-quark mass and width well within the uncertainties. In addition, the physical top-quark mass is ambiguous by an amount of order $\Lambda _{QCD}\sim 200\; \textrm{MeV}$ [15,16,17], just like any quark.

The Higgs boson width is expected to be so narrow ($\sim 4$ MeV) that the difference between the physical mass and the parameter $M_H$ is negligible.

5 Discussion

The relation $\mu = m - (i/2)\Gamma$ [Eq. (11)] is used to define the mass and width of hadronic resonances (see Sec. 50 of Ref. [6]) and is also used, in matrix form, in the analysis of neutral meson oscillations (see Sec. 13 of Ref. [6]). In the electroweak sector, an alternative decomposition of the pole position in terms of mass and width, $\mu ^2 = m^2 - im\Gamma$ [Eq. (17)], has gained widespread currency. How did this come to pass? Up until the discovery of the W and Z bosons, all particles that decayed via the electroweak interactions had widths that were many orders of magnitude less than their mass; the muon, for example, has $\Gamma _\mu /m_\mu = 3 \times 10^{-17}$. The formula $\mu ^2 = m^2 - im\Gamma$ is therefore an excellent approximation to $\mu = m - (i/2)\Gamma$. Over time it was forgotten that $\mu ^2 = m^2 - im\Gamma$ is an approximation, and it was taken to be exact. This approximation is sufficiently accurate for all particles that decay via the electroweak interaction except for the W and Z bosons, where $\Gamma _Z^2/m_Z^2\sim \Gamma _W^2/m_W^2\sim 0.0007$ is greater than the accuracy of the measurements of the masses ($\Delta m_Z/m_Z \sim 0.00002$, $\Delta m_W/m_W \sim 0.0002$).

The expression $\mu ^2 = m^2 -im\Gamma$ is often used as an intermediate step for the W and Z boson masses in precision electroweak analyses [18]. One could even view this as an alternative definition of m and $\Gamma$ [19]. The current standard definition of the W and Z boson masses is yet another alternative definition, $\mu ^2 = M^2/(1+i\frac{\varGamma }{M})$. These alternative definitions should be regarded as useful parameters, not as the fundamental mass and width of the W and Z bosons. Just as the electron has a unique mass, so do the W and Z bosons.

All modern approaches to the W and Z resonances, including the complex-mass scheme, are based on the complex pole position, $\mu$, which is gauge invariant. It appears that it does not matter for collider phenomenology how one defines the mass and width, as long as they are defined in terms of the complex pole position [20]. It remains to be seen whether the physical W and Z boson mass and width, $\mu = m - (i/2)\Gamma$, have any implications for current or future phenomenology.

Our goal in physics is not only to make precise measurements, but to also be precise about our concepts. With $\mu = m - (i/2)\Gamma$ as the definition of the mass and width, the time dependence of an unstable particle at rest is given by

$$\begin{aligned} e^{-imt}e^{-\frac{1}{2}\Gamma t} \end{aligned}$$

(33)

as desired, while any other definition leads to a bizarre time dependence. For example, the definition $\mu ^2 = m^2 -im\Gamma$ yields the time dependence

$$\begin{aligned} e^{-i\frac{1}{\sqrt{2}}m\left( 1+ \sqrt{1+\Gamma ^2/m^2}\right) ^{1/ 2}t} e^{-\frac{1}{\sqrt{2}}\Gamma \left( 1 + \sqrt{1+\Gamma ^2/m^2}\right) ^{-1/ 2}t}\;. \end{aligned}$$

(34)

With this definition, it is evident that $\Gamma$ is not the decay rate and m is not the mass. An even more bizarre time dependence is arrived at using the current standard definition of the W and Z boson masses,

$$\begin{aligned} e^{-i\frac{1}{\sqrt{2}}M\left( 1+ \sqrt{1+{\varGamma} ^2/M^2}\right) ^{1/ 2}\left( 1+{\varGamma} ^2/M^2\right) ^{-1/2}t} e^{-\frac{1}{\sqrt{2}} M\left( \sqrt{1+{\varGamma} ^2/M^2}-1\right) ^{1/ 2}\left( 1+{\varGamma} ^2/M^2\right) ^{-1/2}t}\;, \end{aligned}$$

(35)

again demonstrating that ${\varGamma}$ is not the decay rate and M is not the mass.

Appendices

Appendix A

In Eq. (8), we evaluated the Fourier transform of the scattering amplitude in the rest frame of the unstable particle. If we instead evaluate it in a frame where the particle has three-momentum $\textbf{p}$, we obtain [using $\mu = m - (i/2)\Gamma$]

$$\begin{aligned} S \sim \int _{-\infty }^\infty dp_0\; \frac{e^{-ip_0t}}{\left( p_0 - \sqrt{\textbf{p}^2+\mu ^2}\right) \left( p_0 + \sqrt{\textbf{p}^2+\mu ^2}\right) } \sim e^{-i\sqrt{\textbf{p}^2+\mu ^2}t} \sim e^{-iEt}e^{-(m/E)(\Gamma /2)t} \end{aligned}$$

(36)

where the energy E, identified by the oscillatory time dependence of the amplitude, is

$$\begin{aligned} E= \frac{1}{\sqrt{2}}\left( \textbf{p}^2+m^2-\Gamma ^2/4+\sqrt{\left( \textbf{p}^2+m^2-\Gamma ^2/4\right) ^2+m^2\Gamma ^2}\right) ^{1/2}\;, \end{aligned}$$

(37)

which reduces to m when $\textbf{p}=0$. As expected, the decay rate is reduced by a factor of m/E, which is the inverse of the usual time-dilation factor. This calculation generalizes that of Ref. [4], which is done using the approximation $\Gamma \ll m$.

Appendix B

The momentum-space propagator of an unstable particle has the analytic structure in the complex $p^2$ plane shown in Fig. 3 (see Sec. 50 of Ref. [6]). There is a branch point at the lowest threshold, with a branch cut extending to infinity along the positive real $p^2$ axis. There is a new branch point and branch cut for each new threshold, but we show only the lowest threshold for clarity of presentation. The physical axis lies on the first sheet, just above the branch cut. The pole in the propagator lies on the second sheet at $p^2 = \mu ^2$, which is accessed by passing downward through the branch cut from the physical axis. Since the self-energy $\Pi (p^2)$ satisfies the Schwarz reflection principle, there is also a pole on the second sheet at $p^2 = \mu ^{*2}$. This pole is much further from the physical axis than the pole at $p^2=\mu ^2$.

Fig. 3

Analytic structure of the propagator in the complex $p^2$ plane. The poles lie on the second sheet

The analytic structure of the momentum-space propagator in the complex energy ($p_0$) plane, with $\textbf{p} = 0$, is shown in Fig. 4. There is a branch point at the lowest threshold on the positive real axis as well as on the negative real axis. There is a particle pole on the second sheet below the branch cut on the positive real axis, and an antiparticle pole on the second sheet above the branch cut on the negative real axis. As in the $p^2$ plane, there are also poles at the complex conjugate positions, far from the physical axis. Also shown is the contour of integration for the Fourier transform of the propagator.

Fig. 4

Analytic structure of the propagator in the complex energy plane. The poles lie on the second sheet. The integration contour for the Fourier transform is also shown

The Fourier transform can be performed by closing the contour on the first sheet, as shown in Fig. 5. Since the poles lie on the second sheet, they are not shown in the figure, and are not enclosed by the contour. Let the momentum-space propagator be denoted by

$$\begin{aligned} G(p_0) = \frac{i}{p_0^2 - \mu ^2 + \Pi (p_0^2) - \Pi (\mu ^2)+i\epsilon } \;. \end{aligned}$$

(38)

Fig. 5

Evaluating the Fourier transform of the propagator by closing the contour in the lower-half energy plane (for $t>0)$ on the first sheet

Then, for $t>0$, the contour integration gives

$$\begin{aligned} \int _{-\infty }^\infty dp_0\; e^{-ip_0t}G(p_0) = \int _{thr}^\infty dp_0\; e^{-ip_0t}\;\textrm{Disc}\;G(p_0) \end{aligned}$$

(39)

where $\textrm{Disc}\;G(p_0)$ is the discontinuity of $G(p_0)$ across the branch cut running from threshold to infinity. Let us compare this with the Fourier transform of the Källen–Lehmann representation of the propagator (see Sec. 10.7 of Ref. [21]),

$$\begin{aligned} \int _{-\infty }^\infty dp_0\; e^{-ip_0t}G(p_0) = \int _{-\infty }^\infty dp_0\; e^{-ip_0t} \int _{thr^2}^\infty \frac{dM^2}{2\pi }\rho (M^2)\frac{i}{p_0^2-M^2+i\epsilon } \end{aligned}$$

(40)

where $\rho (M^2)$ is the spectral density. For $t>0$, we close the $p_0$ contour in the lower-half plane and pick up the residue of the pole at $p_0 = M-i\epsilon$, yielding

$$\begin{aligned} \int _{-\infty }^\infty dp_0\; e^{-ip_0t}G(p_0) = \int _{thr}^\infty dM\; e^{-iMt}\rho (M^2) \end{aligned}$$

(41)

Comparing with Eq. (39), we conclude

$$\begin{aligned} \rho (p_0^2) = \textrm{Disc}\;G(p_0) \end{aligned}$$

(42)

Note that the spectral function does not have a delta function contribution from the unstable particle, as it would from a stable particle, because the unstable particle is not part of the spectrum of asymptotic states.

To isolate the contribution from the unstable particle, it is necessary to close the contour on the second sheet, as shown in Fig. 6, rather than on the first sheet as was done above. One finds

$$\begin{aligned} \int _{-\infty }^\infty dp_0\; e^{-ip_0t}G(p_0) =-2\pi i (Re^{-i\mu t}-R^*e^{i\mu ^* t} ) - \int _{thr}^{-\infty } dp_0\; e^{-ip_0t}\;\textrm{Disc}\;G(p_0) \end{aligned}$$

(43)

Fig. 6

Evaluating the Fourier transform of the propagator by closing the contour in the lower-half energy plane (for $t>0)$ on the second sheet

where $R=[2\mu (1+\Pi ^\prime (\mu ^2))]^{-1}$ is the residue of the propagator pole, and where the discontinuity is between $G(p_0)$ on the first and second sheets. This alternative evaluation of the Fourier transform makes the exponential decay associated with the unstable particle pole explicit. The integral on the right-hand side also contributes to the time dependence of the Fourier transform of the propagator, but it does not yield exponential decay.

There may be other branch cuts that contribute to the time dependence of the Fourier transform of the propagator, but these also do not yield exponential decay. For example, consider the case of an unstable particle with electric or color charge. The self-energy has a contribution from the unstable particle emitting and then reabsorbing a virtual photon or gluon. The self-energy at one loop in the complex-mass scheme has terms proportional to [22]

$$\begin{aligned} \Pi (p^2) \sim (\mu ^2/p^2-1)\ln (1-p^2/\mu ^2)+\cdots \end{aligned}$$

(44)

which have a logarithmic branch point at the pole position, corresponding to an infrared singularity due to soft virtual photons or gluons. Since these terms vanish at the branch point, they do not affect the pole position. However, the residue of the propagator pole, R in Eq. (43), is infrared divergent. This divergence cancels against infrared divergences from the emission of soft real photons or gluons in physical processes in the usual way. The resulting analytic structure in the $p_0$ plane is shown in Fig. 7. The contour on the second sheet must avoid the branch cuts that emanate from the poles, but the small circles around the poles still pick up the residues of the poles, and one again arrives at Eq. (43), but with additional integrals on the right-hand side from the discontinuities across the photon or gluon branch cuts.

Fig. 7

Same as Fig. 6, but with additional branch cuts from a photon or gluon being emitted and reabsorbed by the unstable particle