1 Introduction

Nonlinear partial differential equations (PDEs) are a fascinating and challenging area of research, and their analysis and solution have far-reaching implications for understanding and predicting the behavior of complex systems across various scientific and engineering disciplines. Nonlinear PDEs have applications in several fields of study, such as physics [1, 2], engineering [3], biology [4], finance [5], and more. They are used to model phenomena like fluid flow [6], heat transfer [7], population dynamics [8], wave propagation [9], and reaction–diffusion systems [10]. Understanding and solving these equations play a crucial role in advancing scientific knowledge and engineering design. Some well-known examples include the Navier–Stokes equations [11] describing fluid flow, the nonlinear Schrödinger equation [12,13,14,15,16] modeling wave propagation, the Korteweg–de Vries equation [17], Lakshmanan–Porsezian–Daniel equation [18], Radhakrishnan–Kundu–Lakshmanan model [19, 20], Biswas–Milovic equation [21], and the reaction–diffusion equations like the Fisher’s equation [22].

The perturbed Schrödinger–Hirota (SH) equation is a nonlinear PDE that arises in the field of nonlinear optics and is taken advantage of in order to define the propagation of optical pulses in certain types of nonlinear media, such as self-phase modulation, cross-phase modulation, nonlinear pulse propagation, and modulation instability. These nonlinear effects have implications for various applications in optical communication, signal processing, sensing, and nonlinear optics. Understanding and managing these effects are essential for designing efficient and reliable optical fiber systems.

The main target of this paper is to peruse the perturbed SH equation [23] with anti-cubic law media in the presence of spatiotemporal dispersion, which is as follows:

$$\begin{aligned}&{i \Psi _t+\alpha \Psi _{xx}+\beta \Psi _{xt}+\left( \lambda _1|\Psi |^{-4}+\lambda _2|\Psi |^2+\lambda _3|\Psi |^4\right) \Psi } \nonumber \\&\quad {+i\left( \eta \Psi _{xxx}+\mu |\Psi |^2\Psi _{x}\right) =i\left( \gamma \Psi _{x}+a\left( |\Psi |^2\Psi \right) _{x}+b\left( |\Psi |^2\right) _{x}\Psi \right) }, \end{aligned}$$
(1)

where \(\Psi =\Psi (x,t)\) is a complex-valued function, representing the wave function, with x and t denoting the spatial and temporal variables, respectively. The first term on the left-hand side symbolizes the temporal evolution of the wave function, while \(\alpha\) and \(\beta\) represent the group velocity dispersion (GVD) and spatiotemporal dispersion (STD) terms, respectively. Besides, \(\lambda _{1},\lambda _{2},\lambda _{3}\) mean the coefficients of the anti-cubic nonlinearity term from self-phase modulation (SPM). \(\lambda _1\) stands for the effect of the anti-cubic term, and \(\lambda _2\) and \(\lambda _3\) are real-valued constants representing the effect of the cubic and quintic nonlinearity terms, respectively. If \(\lambda _1=0\), the form represented by Eq. (1) degenerates into the cubic-quintic form. \(\gamma\) and a stand also for intermodal dispersion and self-steepening. Furthermore, \(\eta\) is the coefficient of the third-order dispersion term [24], while b and \(\mu\) are the coefficients of the nonlinear dispersion terms.

A variety of SH equations have been examined, and an extensive investigation area has been constituted. Some of these can be itemized: In [25], conformable fractional SH equation was examined. In [26], the effect of power-law media was investigated for this equation by using the unified method. [27] presented optical solitons of perturbed SH equation by taking into consideration both the Kerr law and power-law nonlinearity. Tang [28] focused on dispersive soliton solutions and bifurcation with SH equation. In [29], the stochastic perturbation of optical solitons in SH model was investigated by utilizing inverse scattering transformation. The impact of Kerr law media was perused for the considered equation in [30]. The generalized SH model of the fourth order was considered using the simplest equation method in [31].The fractional SH equation including M-derivative was studied in [32]. The generalized SH equation with an arbitrary power of nonlinearity was perused in [33]. The SH model having parabolic law media was investigated in [34] by using a generalized Kudryashov scheme. Periodic and optical wave forms were analyzed to the fractional SH equation involving a truncated M-fractional derivative in [35]. The stochastic dispersive SH equation including parabolic law media with multiplicative white noise was investigated in [36]. The generalized SH equation was analyzed by the modified extended direct algebraic method in [37]. The governing SH equation was investigated in polarization-preserving fibers and birefringent fibers in [38]. In this paper, we have examined the dispersive optical soliton solutions of the perturbed SH model with anti-cubic law in the presence of STD and the effect of the coefficients of the anti-cubic law nonlinearity terms.

The presence of the anti-cubic nonlinearity [39,40,41,42,43,44,45,46,47,48] can significantly affect the dynamics of solutions to the corresponding partial differential equation. It can lead to the formation of singularities or influence the stability and propagation properties of certain types of waves or solitons. Analytical techniques and numerical methods are often employed to study the behavior and properties of solutions involving this type of nonlinearity. It is worth noting that the specific behavior and consequences of the anti-cubic nonlinearity depend on the context and the particular equation it appears in. Therefore, the study of anti-cubic nonlinearities involves a detailed analysis of the specific system and equation at hand.

The influence of anti-cubic parameters on soliton dynamics is indeed significant in various physical systems, particularly in nonlinear optics, condensed matter physics, and field theory. In nonlinear systems, the energy associated with the system can depend on the cubic and anti-cubic terms. While cubic terms promote dispersion and tend to spread out waves, anti-cubic terms counteract this effect by promoting focusing or compression of the wave. Anti-cubic terms can stabilize solitons against perturbations. In some cases, without these terms, solitons may be unstable and prone to decay or dispersion. By introducing anti-cubic effects, solitons can persist over longer distances and times. They can facilitate the formation of multi-soliton complexes or bound states. These complexes arise due to the interplay between cubic and anti-cubic effects, leading to intricate patterns of soliton interactions. By adjusting the anti-cubic parameters, one can control the propagation of solitons in a medium. This control enables the manipulation of soliton trajectories, allowing for applications in optical communications, signal processing, and other fields.

The article is structured with the main lines as follows: Sect. 2 involves the mathematical examination of the SH equation with anti-cubic media by taking advantage of the new Kudryashov method (nKM) and utilization of this method to the under consideration model which is presented by Eq. (1). The schematics of the acquired soliton solutions are demonstrated diagrammatically, and the outcomes that we gained are commented on in Sect. 3. The conclusion is attributed to Sect. 4.

2 Mathematical analysis of the method

2.1 Ordinary differential equation (ODE) structure of Eq. (1)

The following transmutation of Eq. (1) is taken into consideration as:

$$\begin{aligned} \Psi (x,t)=\Psi ({\zeta })e^{i(-k x+\omega t+\varphi _{0},)},\quad {\zeta }=x-v t, \end{aligned}$$
(2)

where \(v,k,\omega ,\) and \(\varphi _0\) are real numbers. Herein, v is the velocity, k expresses the wave number, \(\omega\) stands for the frequency, and \(\varphi _0\) indicates the phase number.

Inserting Eqs. (2)–(1), and splitting the produced relation into the real and imaginary parts, we acquire:

$$\begin{aligned} \left( 3k\eta +\alpha -v \beta \right) \Psi ^{3} \Psi ^{\prime \prime }+ \lambda _{3}\Psi ^{8}+\left( \left( \mu -a \right) k +\lambda _{2}\right) \Psi ^{6}+\left( k\left( \omega \beta -\gamma -\alpha \,k-\eta k^2\right) -\omega \right) \Psi ^{4}+\lambda _{1}=0, \end{aligned}$$
(3)

and

$$\begin{aligned} 3\eta \Psi ^{\prime \prime }+\left( \mu -3 a -2 b \right) \Psi ^{3}-3 \left( 3k^2\eta +\left( 2 \alpha -\beta v\right) k -\omega \beta +v +\gamma \right) \Psi =0, \end{aligned}$$
(4)

where \(\Psi =\Psi ({\zeta })\). From Eq. (4), we achieve the following constraints:

$$\begin{aligned} \eta= & {} 0, \end{aligned}$$
(5)
$$\begin{aligned} v= & {} \frac{2 \alpha k -\omega \beta +\gamma }{\beta k -1}, \end{aligned}$$
(6)
$$\begin{aligned} \mu= & {} 3a+2b. \end{aligned}$$
(7)

Now, let us consider Eq. (3) with Eqs. (10), (11) and utilize the homogeneous balance rule [49] between the terms \(\Psi ^{3}\Psi ^{\prime \prime }\) and \(\Psi ^{8}\). In this way, we get the balancing constant as \(n=\frac{1}{2}\). Since the balancing constant is considered a positive integer, to procure closed-form solutions, we should perform the following transmutation:

$$\begin{aligned} \Psi =H^{\frac{1}{2}}, \end{aligned}$$
(8)

which \(H=H({\zeta })\) and converts Eq. (3) to the following ODE:

$$\begin{aligned} {-}2\Upsilon _{1}H H^{\prime \prime }+\Upsilon _{1} \left( H^{\prime }\right) ^{2}+4 \lambda _{3}H^{4} +\left( \left( 8 a +8 b \right) k +4 \lambda _{2}\right) H^{3}+\Upsilon _{2} H^{2}+4 \lambda _{1}=0, \end{aligned}$$
(9)

where \(\Upsilon _{1}=\frac{\beta \left( 2 k \alpha -\omega \beta +\gamma \right) }{\beta k -1}-\alpha\), \(\Upsilon _{2}=-4 \alpha \,k^{2}+\left( 4 \omega \beta -4 \gamma \right) k -4 \omega\), and \(\beta k-1 \ne 0\).

By reapplying the balancing rule [49] between the terms \(HH^{\prime \prime }\) and \(H^4\), the balance constant is procured as \(n=1\).

2.2 Definition of the nKM

In this fragment, the cardinal stages of nKM [50, 51] are expressed. The undermentioned truncated series is paying attention to as a solution to Eq. (9):

$$\begin{aligned} H({\zeta })=\sum _{j=0}^{n}A_{j}R^{j}({\zeta }), \,\, A_n\ne 0, \end{aligned}$$
(10)

herein \(A_j\) are real numbers. \(R^{j}({\zeta })\) makes available to:

$$\begin{aligned} (R^{\prime }({\zeta }))^2=\delta ^2R^2({\zeta })[1-\chi R^2({\zeta })], \end{aligned}$$
(11)

in which \(\delta\) and \(\chi\) are nonzero real values to be specified later. Eq. (11) renders service to the presented solution as:

$$\begin{aligned} R({\zeta })=\frac{4 L}{4 L^2 e^{\delta {\zeta }} + \chi e^{-\delta {\zeta }}}, \end{aligned}$$
(12)

where L is a real constant. Equation (12) represents bright and singular solitons for \(\chi =4L^{2}\) and \(\chi =-4L^{2}\), respectively.

2.3 Application of the nKM to Eq. (1)

In this section, the soliton solutions of Eq. (9) are examined by way of nKM. Owing to \(n=1\), Eq. (10) is stated in the undermentioned form:

$$\begin{aligned} H({\zeta })= A_0+ A_1 R({\zeta }). \end{aligned}$$
(13)

Combination of Eqs. (13), (11), (9) gives rise to the undermentioned algebraic structure:


\(R^{0}\) coefficient:

$$\begin{aligned} \begin{array}{l} { \lambda _{3} A_{0}^{4}+\left( 2\left( a + b\right) k + \lambda _{2}\right) A_{0}^{3}+\left( \left( \beta \omega -\gamma \right) k- \alpha \,k^{2}- \omega \right) A_{0}^{2}+ \lambda _{1} = 0.} \end{array} \end{aligned}$$

\(R^{1}\) coefficient:

$$\begin{aligned} \begin{array}{l} {\left( \beta k -1\right) \left( 12 k \left( a +b \right) A_{0}-4 k \left( k \alpha +\gamma \right) +8 \lambda _{3} A_{0}^{2}+6 A_{0} \lambda _{2}-\alpha \,\delta ^{2}-8 \omega \right) }\\ \quad {+4 \omega \left( k^{2} \beta ^{2}-1\right) +\delta ^{2} \left( \beta \left( \beta \omega -\gamma \right) -2 \alpha \right) = 0.} \end{array} \end{aligned}$$

\(R^{2}\) coefficient:

$$\begin{aligned} \begin{array}{l} {\frac{\beta \,\delta ^{2} \left( -2 k \alpha +\beta \omega -\gamma \right) }{\beta k -1}+24 A_{0} \left( k \left( a +b \right) +\lambda _{3} A_{0}\right) +4 \omega \left( \beta k -1\right) +\alpha \,\delta ^{2}+12 A_{0} \lambda _{2}-4 \gamma k \left( k \alpha +\gamma \right) = 0.} \end{array} \end{aligned}$$

\(R^{3}\) coefficient:

$$\begin{aligned} \begin{array}{l} {\left( \left( 2 \left( a +b \right) k +4 A_{0} \lambda _{3}+\lambda _{2}\right) \left( \beta k-1\right) A_{1}^{2}+ A_{0}\delta ^{2} \chi (\alpha -\beta ^{2} \omega +\left( \alpha k +\gamma \right) \beta \right) = 0.} \end{array} \end{aligned}$$

\(R^{4}\) coefficient:

$$\begin{aligned} \begin{array}{l} {3 \left( \alpha -\beta ^{2} \omega +\left( \alpha k +\gamma \right) \beta \right) \chi \,\delta ^{2}+4 \lambda _{3} A_{1}^{2} \left( \beta k -1\right) = 0.} \end{array} \end{aligned}$$

Assaying the above algebraic system, the undermentioned sets are procured as:

Set 1:

$$\begin{aligned} \left\{ \begin{array}{l} {\omega =\frac{\left( \left( -6 \chi A_{0}^{2}+A_{1}^{2}\right) \left( \beta k +1\right) \delta ^{2}+4 k^{2} A_{1}^{2} \left( \beta k -1\right) \right) \lambda _{3}-3 \chi \,\delta ^{2} \gamma k}{3 \chi \,\delta ^{2}},\lambda _{1}=-\frac{A_{0}^{2} \lambda _{3} \left( \chi A_{0}^{2}-A_{1}^{2}\right) }{3 \chi },A_{0}=A_{0}} \\ {\alpha =\frac{\left( \left( \left( \delta ^{2}+4 k^{2}\right) A_{1}^{2}-6 \delta ^{2} \chi A_{0}^{2}\right) \beta ^{2}-8 \beta k A_{1}^{2}+4 A_{1}^{2}\right) \lambda _{3}-3 \beta \chi \,\delta ^{2} \gamma }{3 \chi \,\delta ^{2}},\lambda _{2}=\frac{\left( -6 a -6 b \right) k-8 A_{0} \lambda _{3}}{3},A_{1}=A_{1}} \end{array}\right\} . \end{aligned}$$
(14)

In Eq. (14), \(\chi ,\delta \ne 0\).

Set 2:

$$\begin{aligned} \left\{ \begin{array}{l} {\alpha =\frac{\left( \left( -\delta ^{2}-4 k^{2}\right) \lambda _{1} \beta ^{2}+\left( \delta ^{2} \gamma A_{0}^{2}+8 k \lambda _{1}\right) \beta -4 \lambda _{1}\right) A_{1}^{2}+\beta \left( -\gamma A_{0}^{2}+6 \beta \lambda _{1}\right) \chi \,\delta ^{2} A_{0}^{2}}{A_{0}^{2} \left( \chi A_{0}^{2}-A_{1}^{2}\right) \delta ^{2}} ,\lambda _{2}=\frac{-2 k \chi \left( a +b \right) A_{0}^{3}+2 k A_{1}^{2} \left( a +b \right) A_{0}+8 \chi \lambda _{1}}{A_{0} \left( \chi A_{0}^{2}-A_{1}^{2}\right) }} \\ {\omega =\frac{\left( \left( \beta k +1\right) \left( 6 \chi A_{0}^{2}-A_{1}^{2}\right) \lambda _{1}-k \gamma A_{0}^{2} \left( \chi A_{0}^{2}-A_{1}^{2}\right) \right) \delta ^{2}-4 k^{2} A_{1}^{2} \lambda _{1} \left( \beta k -1\right) }{A_{0}^{2} \left( \chi A_{0}^{2}-A_{1}^{2}\right) \delta ^{2}} ,\lambda _{3}=-\frac{3 \chi \lambda _{1}}{A_{0}^{2} \left( \chi A_{0}^{2}-A_{1}^{2}\right) },A_{0}=A_{0},A_{1}=A_{1}} \end{array}\right\} , \end{aligned}$$
(15)

where \(\delta ,A_{0},\lambda _{1} \ne 0\) and \(\chi A_{0}^{2}-A_{1}^{2} \ne 0\).

Set 3:

$$\begin{aligned} \left\{ \begin{array}{l} {\omega =\frac{\Pi _{1} k^{4}+\Pi _{2} k^{3}+\Pi _{3} k^{2}+\Pi _{4} k +\Pi _{5}}{8 \delta ^{2} A_{0}^{2}} ,\alpha =\frac{-8 \beta \,\delta ^{2} \gamma A_{0}^{2}+\Omega _{1} A_{0}^{3}+\Omega _{2}}{8 \delta ^{2} A_{0}^{2}},A_{0}=A_{0}} \\ {\lambda _{3}=\frac{\left( -6 a -6 b \right) k -3 \lambda _{2}}{8 A_{0}},A_{1}=-\frac{\sqrt{\left( 2 \left( a +b \right) k +\lambda _{2}\right) \left( \left( 2 \left( a +b \right) k +\lambda _{2}\right) A_{0}^{3}-4 \lambda _{1}\right) \chi A_{0}}}{\left( 2 \left( a +b \right) k +\lambda _{2}\right) A_{0}} } \end{array}\right\} , \end{aligned}$$
(16)

in which \(\delta ,A_{0} \ne 0\), \(\lambda _{2}+2\left( a+b\right) k \ne 0\) and

$$\begin{aligned}{} & {} \Pi _{1}=-8 \beta A_{0}^{3} \left( a +b \right) ,\\{} & {} \Pi _{2}=\left( -4 \beta \lambda _{2}+8 a +8 b \right) A_{0}^{3}+32 \beta \lambda _{1},\\{} & {} \Pi _{3}=\left( 10 \beta \left( a +b \right) \delta ^{2}+4 \lambda _{2}\right) A_{0}^{3}-32 \lambda _{1},\\{} & {} \Pi _{4}=\delta ^{2} \left( \left( 5 \beta \lambda _{2}+10 a +10 b \right) A_{0}^{3}-8 \gamma A_{0}^{2}+48 \beta \lambda _{1}\right) ,\\{} & {} \Pi _{5}=\left( 5 A_{0}^{3} \lambda _{2}+8 \lambda _{1}\right) \delta ^{2},\\{} & {} \Omega _{1}=-\left( 2 \left( a +b \right) k +\lambda _{2}\right) \left( 4+\left( -5 \delta ^{2}+4 k^{2}\right) \beta ^{2}-8 \beta k \right) ,\\{} & {} \Omega _{2}=8 \lambda _{1} \left( 4+\left( \delta ^{2}+4 k^{2}\right) \beta ^{2}-8 \beta k \right) \end{aligned}$$

Let we take into account Eq. (13) with Eqs. (2), (8), (12), then we derive:

$$\begin{aligned} \Psi (x,t)= \left( A_{0}+\frac{4 A_{1} L}{4 L^{2} {\mathrm e}^{\delta {\left( x -v t\right) }}+\chi \,{\mathrm e}^{-\delta {\left( x -v t\right) }}}\right) ^{1/2}{\mathrm e}^{\textrm{i} \left( -k x +\omega t +\varphi _{0}\right) }, \end{aligned}$$
(17)

where \(\omega ,A_{0},A_{1}\) are presented in Eqs. (14)–(16) and \(v=\frac{2 \alpha k -\omega \beta +\gamma }{\beta k -1}\) as given before by Eq. (6).

3 Results and discussion

This section involves a variety of diagrammatic sketches of Eq. (17) by using the sets in Eqs. (14)–(16). As we have put emphasis on before, our principle target is to acquire varied shapes of soliton solutions and to observe the impact of anti-cubic law parameters on soliton attitude in each circumstance. Before starting the graphic presentations, we would like to emphasize this point. The parameter selections for graphical presentations were chosen as a result of trials carried out in order to comply with the constraints of both the model and the applied method, not to create any mathematical contradictions, and to obtain a meaningful graphic in terms of soliton representation. The parameter selections given in the article are not limited to the parameters presented, and anyone who wishes can obtain similar graphic formations by selecting different parameter values.

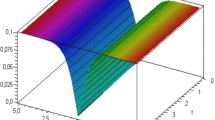
Figure 1 is pertinent to the aggregation of Set 1, \(\Psi (x,t)\) in Eq. (17) and the values decided as \(\varphi _{0}=1.21, \beta =0.65, \gamma =-2.2, \delta =-0.56, A_{0}=1.21, \chi =0.78, L=1.4, A_{1}=1.23, k=0.98, \lambda _{3}=0.78\). Figure 1a, b displays the 3D plots of \(|\Psi _{1}(x,t)|^2\) and \(Im(\Psi _{1}(x,t))\), while Fig. 1c, d demonstrates the 2D graphical representation, respectively. Figure (1a) exhibits a bright soliton character. Figure 1c is a 2D view that depicts the wave construction of \(|\Psi (x,t)|^2\) as it goes to the left (from solid purple line to dotted purple line) at \(t=1,2,3\) and the imaginary and real part of \(\Psi (x,t)\) at \(t=1\). Figure 1d is the 2D profile of \(|\Psi (x,t)|^2\) that shows the effect of the parameter \(\lambda _{3}\) (which represents the quintic nonlinearity effect) in Eq. (1) on soliton attitude. As is seen from Fig. 1d, if \(\lambda _{3}>0\) and increases, there is no change in the appearance and amplitude of the bright soliton, but it forms in different positions on the horizontal axis as a bright soliton formation. Based on the selected parameter values and the analysis made, the bright soliton shape formed due to the quintic nonlinearity parameter taking positive and increasing values is located on the horizontal axis, with each formation positioned to the left of the previous one. However, from the graphs given in Fig. 3, it can be seen that the soliton shape formed when \(\lambda _1<0\) gives a W-shape-like appearance. The consisted form, beyond being a W-shape-like soliton, reflects a degenerate form from the dark soliton. It is clear that the reason for this is due to the anti-cubic law form given by self-phase modulation. As is known, the formation and transmission of optical solitons depend on the interaction between group velocity dispersion and self-phase modulation, and this interaction requires a delicate balance. This is also a problem that requires proper management and control. Therefore, there are different forms for self-phase modulation (Kerr, power, parabolic, dual-power, cubic-quintic-septic, triple power, anti-cubic, generalized anti-cubic, Kudryashov’s law, log, etc.). Within the framework of the currently examined anti-cubic law form, when \(\lambda _1<0\), both the soliton degenerates from the dark soliton form to the W-shape-like form and a change in soliton amplitude is observed. This change can be clearly observed from the bright soliton form in the middle in the W-shape-like soliton view (Fig. 3e, blue to fushia lines).

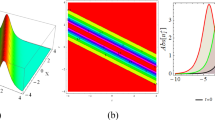
Figure 2 gives the multifold graphicals of \(\Psi (x,t)\) in Eq. (17) by taking advantage of Set 2. 3D projections of \(|\Psi (x,t)|^2\) and \(Im(\Psi (x,t))\) are made available to in Fig. 2a, b, respectively. Figure (2a) demonstrates the dark soliton character for \(\Psi (x,t)\) in Eq. (17) for Set 2 and \(\varphi _{0}=1.21, \beta =-1.65, \gamma =0.2, \delta =1.56, A_{0}=1.2, \chi =2.78, L=-2.4, A_{1}=1.21, k=-0.98, \lambda _{1}=-0.89\). Figure (2c) is the 2D soliton shape of \(|\Psi (x,t)|^2\) for \(t=1,2,3\) and \(Im(\Psi (x,t))\) at \(t=1\). It is said that as the value of t is raised, the soliton amplitude and its dark character continue the same, and the soliton also moves toward the right (from the solid fuchsia line to the dotted fuchsia line). In short, Fig. 2c reflects the time-dependent traveling wave feature of the dark soliton. Figure 2d is the 2D profile of \(|\Psi (x,t)|^2\) which indicates influence of the \(\lambda _{1}\) (which represents the anti-cubic nonlinearity effect) regarding the values as 0.5, 1.0, 1.5, 2.0. As is seen from Fig. 2d, if \(\lambda _{1}>0\) increases, then the soliton amplitude and its dark character continue the same. However, it is seen that the dark solitons formed for different \(\lambda _1\) parameter values at \(t=1\) are positioned on the horizontal axis, with each dark soliton form to the left of the previous one, depending on the increasing \(\lambda _1\) values. Therefore, the \(\lambda _1\) anti-cubic nonlinearity parameter affects the position of the formed soliton shape without causing any effect on the general character and amplitude of the soliton.

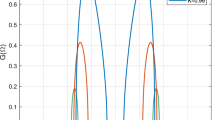
Figure 3 appertains to multifarious diagrammatic representations of \(\Psi (x,t)\) in Eq. (17) by making use of Set 3. Figure 3a is the 3D portraiture that depicts the W-shape soliton character for Set 3 and \(\varphi _{0}=-1.21, \beta =-1.65, \gamma =-1.2, \delta =1.56, A_{0}=1.2, \chi =2.28, L=2.4, A_{1}=1.21, k=-0.98, \lambda _{1}=-1.89, \lambda _{2}=-1.4, a=-0.43, b=-2.1\). Figure 3b, c presents the 3D view of \(Im(\Psi (x,t))\) and contour view of \(|\Psi (x,t)|^2\), respectively. Figure 3d means the 2D profile of \(|\Psi (x,t)|^2\) for \(t=1,2,3\). It is monitored that as the value of t is increased, the soliton also acts toward the left (from the solid blue line to the solid fuchsia line). Figure 3e is the 2D portrayal to demonstrate the influence of the \(\lambda _{1}\) taking into consideration the parameters as \(-4,-3,-2,-1\), respectively. Soliton sustains its W-shape-like soliton character, and the soliton also moves to the left (from the solid fuchsia line to the solid blue line). While the soliton has the dark soliton character at \(\lambda _{1}=1\), it is corrupted into the W-like soliton appearance for \(\lambda _{1}>0\). In this regard, the value of \(\lambda _{1}=0\) is a breaking point in regard to the examined circumstance and the determined parameter choice. Furthermore, its amplitude and magnitude decline because of the incremental values of \(\lambda _{1}\) while there is also a decrease in the wing pieces as they open in both directions. Figure 3f is the 2D diagrammatic simulation to show the influence of the \(\lambda _{2}\) (which represents the cubic nonlinearity effect) taking into account the parameters as 1, 2, 3, 4, respectively. Soliton perpetuates its W-shape-like soliton character, and the soliton also acts to the left (from a solid fuchsia line to a dotted fuchsia line). Besides, its amplitude declines and its W-shape-like soliton character degenerates by virtue of the increasing values of \(\lambda _{2}\).

Fig. 1
figure 1

Diagrammatic sketches of \(\Psi (x,t)\) in Eq. (17) for Set 1 and \(\varphi _{0}=1.21, \beta =0.65, \gamma =-2.2, \delta =-0.56, A_{0}=1.21, \chi =0.78, L=1.4, A_{1}=1.23, k=0.98, \lambda _{3}=0.78\)

Full size image
Fig. 2
figure 2

Schematic simulations of \(\Psi (x,t)\) in Eq. (17) for Set 2 and \(\varphi _{0}=1.21, \beta =-1.65, \gamma =0.2, \delta =1.56, A_{0}=1.2, \chi =2.78, L=-2.4, A_{1}=1.21, k=-0.98, \lambda _{1}=-0.89\)

Full size image
Fig. 3
figure 3

Graphics of \(\Psi (x,t)\) in Eq. (17) for Set 3 and \(\varphi _{0}=-1.21, \beta =-1.65, \gamma =-1.2, \delta =1.56, A_{0}=1.2, \chi =2.28, L=2.4, A_{1}=1.21, k=-0.98, \lambda _{1}=-1.89, \lambda _{2}=-1.4, a=-0.43, b=-2.1\)

Full size image

One of the points that should be emphasized here is that the parameter analyses given in Figs. 1d, 2d, 3e, f, which reflect the effects of the terms belonging to the anti-cubic law nonlinearity form, represent the position of the soliton in different positions on the horizontal axis. The question is whether these different positions where the soliton is located are related to the speed of the soliton. Because if the relevant graphs are taken into consideration again, only the \(\lambda _1,\lambda _2,\lambda _3\) coefficients of the anti-cubic law nonlinearity form are changed, while the parameter values selected for a certain time value are preserved in these graphs. In this context, let us consider the graph given by Fig. 1d. As can be seen from this graph, depending on the positive and increasing values of \(\lambda _3\), the bright soliton in each case is formed further to the left than the previous soliton without any change in its amplitude; in a sense, the soliton is displaced to the left. In this case, the question is: Is the reason for this change in position a change in the speed of the soliton at its different values? Or, in other words, does the quintic effect, represented by the \(\lambda _3\) coefficient, cause a change in the speed of the soliton? Let us remember the velocity relation obtained as a constraint condition with Eq. (6) and expressed as follows:

$$\begin{aligned}\begin{array}{l} { v=\frac{2 \alpha k -\omega \beta +\gamma }{\beta k -1}}. \end{array}\end{aligned}$$

As can be clearly seen from this equation, although the speed of the soliton does not seem to depend on the anti-cubic law nonlinearity coefficients (\(\lambda _1,\lambda _2,\lambda _3\)), considering Set 1 used in Fig. 1d representation and given by Eq. (14), this set depends on \(\omega\) and \(\alpha\).

It is clearly seen that both \(\omega\) and \(\alpha\) contain the quintic nonlinearity effect \((\lambda _3)\). Therefore, there is a linear relationship between the velocity of the soliton (v) and \(\omega\) and \(\alpha\) (and therefore \(\lambda _3\)). Additionally, in the specific solution set obtained, it is seen that \(\lambda _1\) and \(\lambda _2\) are obtained similarly depending on \(\lambda _3\) and have a linear relationship.

Similarly, the graph given by Fig. 2d and showing the anti-cubic nonlinearity effect is the graph of the solution function derived using Set 2 given by Eq. (15).

As can be clearly seen from this set expression, the parameters \(\omega ,\alpha ,\lambda _2,\lambda _3\) depend on \(\lambda _1\). So, in a sense, it is a function of \(\lambda _1\) and the dependence is linear. Therefore, the formations in the graph given by Figs. 1d and 2d, which show the effect of \(\lambda _3\) and \(\lambda _1\) parameters, respectively, indicate the existence of a linear relationship depending on the speed of the soliton (v). Just as an example, if \(\lambda -1 = 0.50, 1.00, 1.50,2.00\) are given in the graphical presentation for Fig. 2d showing the effect of \(\lambda _1\), considering the choices made for Eq. (6), Set 2 and other parameters, the values of the soliton’s speed are \(v = - 5.4128, -10.6256, -15.8384, -21.0512\), respectively. This indicates a linear relationship between \(\lambda _1\) and v.

4 Conclusion

In this paper, we have concentrated on acquiring new optical soliton solutions of the perturbed SH equation with anti-cubic law nonlinearity by using a very efficient analytical method, which is the nKM. From this point on, the technique has yielded efficient outcomes and has been applied to the given model for the first time. Multifold optical solitons such as W-shape-like, bright, and dark have been obtained. Deriving distinctive kinds of solitons is one of the targets of the study, and the second target, the impact of the anti-cubic parameters on soliton attitude, has been examined on the crest of a wave. The investigation was implemented individually for each soliton form acquired; the significant consequences given in this study were derived, assisted by graphical simulations in the related section, and commented in particular. The attained outcomes demonstrate that the anti-cubic parameters have an important impact on the soliton dynamics of the SH equation. This impact arises distinctly based on the kind of parameters. Besides, the impact of the parameters diverges with regard to the soliton forms. As it is known, NLS, as an equation with the best capacity to model soliton propagation in optical fibers, includes only GVD and SPM for picosecond light pulses. Considering that soliton transmission is a result of the delicate balance between GVD and SPM, different forms of SPM are important in maintaining this balance as well as having an impact on the form of the soliton. This impact, especially in the graphical representations presented in Fig. 3e showing the effect of the \(\lambda _{1}\), manifests itself as a change in the soliton form in the middle part, which can be considered a bright soliton appearance in a sense. We consider that the consequences acquired in this article will be practicable a great variety of perspectives, particularly the attitude of solitons in optics.