Background studies for the HOLMES experiment

Abstract

Determining the mass of neutrinos is one of the most compelling topics in particle physics. HOLMES, an experiment for a direct measurement of the neutrino mass, is addressing this subject through a calorimetric approach, exploiting arrays of Low-Temperature Transition-Edge Sensor Detectors (TESs) loaded with $^{163}$Ho. The experiment has entered its first phase in 2023, implanting approximately 1 Bq per pixel in an array of 64 detectors. In this work, I present the measurement made before this stage, in order to determine the expected background arising from natural radioactivity and cosmic rays. The significance of this background depends on the activity per pixel, which has yet to be defined based on the result of the first phase.

1 Direct neutrino mass measurement and HOLMES

The absolute mass of neutrinos is one of the most important riddles yet to be solved, since it has many implications in particle physics and cosmology. By tackling this issue, we will begin to shed light on a very crucial matter: what lies beyond the standard model (SM) of particle physics. In particular, its value will help to discriminate between many theories, from the ones related to the mass generation mechanisms to the one related to the cosmological evolution of large-scale structure. The only model-independent method of measuring the neutrino mass is based on the kinematic analysis of the beta or the electron capture (EC) decay [1], which only assumes momentum and energy conservation. Many experiments [2,3,4] are pursuing this goal, adopting a wide range of techniques and pushing each of them toward their technical limits. Having different techniques is necessary both to cross check the results of the current state-of-the-art experiment [5], removing the influence of any systematic effects in the measurement, and to define a legit way to probe sub-eV neutrino mass scale.

Thanks to the remarkable progress made by Low-Temperature Detector technologies, a calorimetric measurement of a suitable radioactive nuclide seems now a promising approach to tackle the hunt for the neutrino mass [6]. In an ideal calorimetric experiment, the radioactive source is embedded in the detector and, if the excitation of atomic or molecular levels is negligible compared with the detector time response, only the neutrino energy escapes the detection, avoiding most of source-related effects that characterize the spectrometric experiments. On the other hand, the whole spectrum is acquired, posing important limits on the source intensity and therefore on the statistics that can be accumulated. The activity of the source is also limited by the relation between the detector size and its energy resolution.

1.1 The HOLMES experiment

HOLMES [7] is an ambitious project that aims to verify the feasibility of the calorimetric approach to the neutrino mass determination. In doing so, it will also perform an exploratory measurement aiming to reach ${\mathcal {O}}$(1) eV sensitivity with hundreds of low-temperature TES [8] microcalorimeters, each implanted with an activity of ${\mathcal {O}}$(100) Bq of $^{163}$Ho.

In a calorimetric measurement of the electron capture (EC) decay of $^{163}$Ho, all the energy is measured except for the fraction carried away by the neutrino. The energy measured, indicated as de-excitation energy $E_c$, is mostly emitted in the form of Auger electrons from the relaxation of the excited daughter Dy atom.

$$\begin{aligned} ^{163}Ho + e^- \rightarrow ^{163}Dy^H + \nu _e \rightarrow ^{163}Dy + E_c \end{aligned}$$

(1)

H labels the H-shell from which the electron has been captured.

As shown in Fig. 1, the calorimetric spectrum of the $^{163}$Ho is composed of several Lorentzian-shaped peaks, each one with energy equal to the binding energy of the electron captured. Although the neutrino is not detected, the value of its mass affects the shape of the de-excitation spectrum [9], reducing also the end-point of the spectrum by an amount equal to $m_{\nu _e}$. The spectrum distortion is statistically significant only in a region close to the end-point, where the count rate is lowest and background can easily hinder the signal.

Fig. 1

$^{163}$Ho EC calorimetric spectrum per atom per half life as expected from first-order theory. O2 and P1 peaks have a negligible influence on the neutrino mass, and they are not depicted in this picture. On the right, the effect of different values of $m_{\nu }$ on the shape of the spectrum at the end-point is shown

In terms of achievable statistical sensitivity, $^{163}$Ho is one of the best candidates, given the combined effect of its low Q-value ($Q = 2833 \pm 30(stat) \pm 15(syst)$ eV [10]) and the proximity of the highest energy peak to the end-point of the spectrum. $^{163}$Ho also has a relatively short half life of $\tau _{1/2} \sim 4570$ years, which allows to embed a small number of nuclei in a small absorbing volume.

HOLMES will be a two-stage project. In the first phase of the experiment, started in June 2023, a low-dose implantation (max 1 Bq per pixel) of the 2 $\times$32 pixel array has been performed. The influence of the $^{163}$Ho on the detector response will be assessed for the HOLMES setup, and a resolute calorimetric spectrum of the $^{163}$Ho decay will be produced, helping to validate or disprove different theoretical models. A first limit on the neutrino mass of the order of ${\mathcal {O}}$(30) eV will be reached with three months of measurement time [11].

Upon the results of the first stage, it will be clear how much holmium could be embedded inside the detectors without spoiling their performances, and the high-dose, multi-channel phase will start. During this last phase, the challenges in running TES pixels with high activity will be defined and addressed, performing also a neutrino mass measurement of the order of ${\mathcal {O}}$(1) eV. At the end of HOLMES, it will be clear if the calorimetric approach can still be considered a feasible way to reach sub-eV sensitivity on the neutrino mass.

1.2 Expected background

Even with a single pixel activity of 300 Bq, the event rate is particularly low in the region of the holmium spectrum near the end-point, about 0.26 counts eV$^{-1}$ day$^{-1}$ det$^{-1}$ for the energy region [2650, 2833] eV is expected. Thus, to avoid artifacts that would inevitably impair the determination of the neutrino mass the fraction of background signals must be kept as low as possible. The expected background sources can be roughly divided into the following components:

• 1. Pile-up. We define a pile-up event a signal composed of two events of energies $E_1$ and $E_2$ which occur within a time interval shorter than the time resolution of the detector, producing a signal which is misinterpreted as a single signal with energy $E \simeq E_1 + E_2$. Thus, if not correctly identified, pile-up events will distort the decay spectrum of $^{163}$Ho, lowering the sensitivity to $m_{\nu }$.

• 2. Radionuclides in the detectors’ absorbers. $^{163}$Ho has been implanted inside the gold absorbers of the microcalorimeters with a custom ion implanter [12]. Radioactive contaminants from the embedding process are expected inside these absorbers. Among these, the $^{166m}$Ho ($\beta$ decay, $Q_{\beta } = 1854$ keV) represents the most dangerous one because it presents a ‘fast’ decay time of $\tau _{1/2} \sim 1200$ years, so even a small quantity can produce a flat but nonnegligible background spectrum in the ROI.

• 3. Natural radioactivity. Radioactive contaminants which are present in all the parts of the experimental setup, from the laboratory to the cryostat and the detector’s holder.

• 4. Cosmic rays. Muons from cosmic rays interacting directly with the detector will produce a signal which is theoretically indistinguishable from the $^{163}$Ho ones. Additionally, muons interacting with the experimental apparatus could create secondary products, increasing the total background rate.

The relative significance of these sources will vary according to the phase of the experiment. During the high activity phase, the pile-up will be the main background source. Offline analysis routine based on filters and unsupervised learning algorithms has been developed to this end, and the target time resolution, lower than the sampling time, has been achieved [13]. As regards the $^{166m}$Ho, Monte Carlo simulations show that with the ion implanter in the current configuration the $^{163}$Ho/$^{166m}$Ho separation is expected to be better than $10^6$, which results in a count rate contribution in the ROI of $< 0.01$ counts eV$^{-1}$ day$^{-1}$ det$^{-1}$ with 300 Bq of $^{163}$Ho. Also, considering that the HOLMES experiment is located at the cryogenic laboratory of the University of Milano-Bicocca at a depth of roughly 20 ms below ground, and that the TES have a sensitive area of the order of $5\times 10^{-8}$ m$^2$ and a thickness of a few micrometers, the background contributions due to both cosmic rays and natural radioactivity are expected to be negligible compared to pile-ups.

However, natural radioactivity and cosmic ray-induced events may become comparable or even overcome the pile-up rate if the $^{163}$Ho activity per pixel is too low. This will be the case during the low activity phase. Therefore, assessing the expected background rate and keeping it as low as possible are crucial for the success of the first stages of HOLMES.

2 Preliminary studies

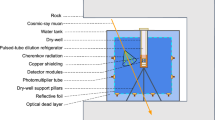
In general, radionuclides present in the environment can be grouped in three categories: primordial, cosmogenic, and anthropogenic (man-made). They are present in the air and laboratory building materials as well as in the cryostat components and in the detectors’ holder. Radionuclides which are naturally present on the surface of the detectors could also be enclosed in the bulk of the absorbers by the Au co-deposition process [14]. To quantify the concentration of radionuclides and the cosmic rays flux in the HOLMES laboratory, a six-day measurement was performed [15] with a HPGe close to the cryostat without the detectors holders, resulting in the energy spectrum shown in Fig. 2.

Fig. 2

HPGe gamma ray spectrum measured in Milano-Bicocca cryogenic laboratory. The CR spectrum is the difference between the measured and the simulated one

Through this measurement, we identified 84 peaks and, as expected due to the experiment location, the main radionuclides were primordial radionuclides, i.e., those from the radioactive decay chains of the $^{232}$Th and $^{238}$U, and $^{40}$K. Even if potassium has a $^{40}$K natural abundance of 0.01$\%$, its contribution is comparable to the ones from Th and U because of its greater abundance in the soil.

By removing from the measured spectrum the expected contribution of the radionuclides evaluated with a Monte Carlo, it was possible to achieve a preliminary estimation of the cosmic rays contribution to the total HPGe activity to 29$\%$.

2.1 Monte Carlo simulations

Each contribution of these radioactive sources to the actual background spectrum of our microcalorimeters is nontrivial to assess because as thermal detectors they are sensitive to all type of radiations but, due to their small volumes (180$\times$180$\times$2 $\mu$m for the gold absorber), they are almost transparent to gamma rays. In addition, the detectors are located in a “dirt” environment: they are installed inside a gold-plated copper holder at the bottom of the cryostat, in vacuum and surrounded by copper and aluminum shields at cryogenic temperature.

A Monte Carlo simulation was performed, using Geant4 10.3, with G4EmLivermorePhysics , Fluo, Auger, Pixe, CRY and Atomic Deexcitation. The detectors were approximated as cylinders of 0.226 mm diameter and 2 $\mu$m thickness above a holey Si substrate and inside a cylindrical copper holder (Fig. 3). Different energy spectra were generated by placing the radionuclides $^{238}$U, $^{232}$Th, $^{40}$K and $^{210}$Pb inside and on the surface of both the gold absorbers and the copper holder. Also a spectrum produced by a “cosmic ray source” above the detector was produced. Some of the resulting energy spectra are shown in Fig. 4.

Fig. 3

Detectors holder and chip configuration used for the MC simulations. Each simulated detector, depicted in pink, has an equivalent total area of the real TES ($180 \times 180 \ \upmu$m$^2$)

All the simulated background sources but the $^{40}$K produce a smooth and almost flat background in the ROI. The $^{210}$Pb presents a peak near the low energy (high statistic) edge of the ROI, and therefore, its contribution is expected to be negligible.

Due to the $^{40}$K peaks position in the region of interest, the impact of the contamination of $^{40}$K on the neutrino mass determination deserves to be further investigated, and this is carried out in Sect. 4.2.

Fig. 4

Resulting spectra of Geant4 Monte Carlo simulations. The green region highlights the HOLMES region of interest

3 Background measurement

A background measurement was performed with an array of 32 detectors inside the HOLMES $^{3}$He/$^{4}$/He dilution refrigerator (Triton by Oxford Instrument). Three scintillators were placed under the cryostat to assess the contribution of muons and muon-induced events. The measurement was performed during the month of August and lasted about 500 h. The purposes were to estimate the rate of background events and to determine the fraction of cosmic rays interactions.

3.1 Experimental setup

Three organic plastic scintillators were installed under the cryostat, as shown in Fig. 5, to mimic an experimental setup which could be employed during the actual physics runs: one directly below the cryostat, and two near the floor. The latter two are so close that they can be considered as one larger scintillator.

Fig. 5

Left: A side view of the experimental setup, in which the position of the three organic plastic scintillators below the cryostat is shown. Right: The schematic of the scintillator and detector holder positions. For ease, the scintillators slabs have been approximated as circle of equivalent area

Their relative distance and the distance from the detectors were chosen to cover an angle of 0.55 rad from the vertical. The cosmic rays flux angular distribution goes as $I\sim \cos (\theta )^2$, where theta is the zenith angle; thus, the scintillators setup should measure the muons hitting the detectors array with a geometric efficiency of roughly $50 \%$. The efficiency was evaluated by integrating the angular distribution of cosmic rays between 0 and 0.55 radians.

The logic chain was arranged to have the top scintillator in coincidence with bottom scintillators. A discriminator for each scintillator was employed, and the bias voltage for the scintillators was set to match the characteristics of the discriminators, while the discriminators threshold were set to remove the signals due to low energy natural radioactivity (around 8 MeV). The coincidence chain further reduces its contribution. The final measured rate of coincidence signals was approximately 7 Hz, corresponding to a cosmic ray vertical flux of approximately $I \simeq 0.2$ cm$^{-2}$ min$^{-1}$. This value is in agreement with the one expected with an overburden mass $m_{ob}$ of 18 m water equivalent, measured in previous studies [16]. Indeed, considering that the integral intensity of muons above 1 GeV/c at sea level is $I_{sea} \simeq 1$ cm$^{-2}$ min$^{-1}$ [17], the attenuation $A_{\mu }$ due to the location of the cryogenic laboratory is following the empirical relation [18]

$$\begin{aligned} A_{\mu }(m_{ob}) = I/I_{sea} = 10^{-1.32\log _{10}d-0.26(\log _{10}d)^2}\simeq 0.23 \ \ \ \; \ \ \ \ d = 1+ m_{ob}/10 \end{aligned}$$

(2)

which is comparable to the one we have measured. $m_{ob}$ is the overburden mass in mwe, and d can be interpreted as the total overburden (atmosphere included) measured in number of atmospheres.

Regarding the detectors, a spare array chip made of 32 TESs with different geometries and without $^{163}$Ho was employed. The detectors and the read-out chips ($\mu$mux17a, developed by NIST) were enclosed in a gold-plated copper holder, 10.5 $\times$ 7.5 $\times$ 0.85 cm$^3$, that was adopted in previous measurements with X-ray fluorescence sources [8], featuring an entrances closed by an aluminum film 6 $\mu$m thick. The holder without cover is shown in Fig. 6.

Fig. 6

Left: The detector holder box. In this measurement, only 32 of the 256 detectors are connected to the $\mu$MUX chips. Right: Zoom of the previous picture, in which the main components are highlighted: the TES chip in green, the bias (resistance) chip in cyan, the PCB in magenta, the $\mu$mux in blue, and the CPW in white

The holder was placed vertically, and it was thermally coupled to the coldest plate of the cryostat, which was heated and stabilized at a temperature of about 60 mK. The $\mu$-mux readout chip was also a spare one, used in many previous measurements. As a result of bad bonding and damaged resonances, of the 32 detectors only 16 were measurable.

3.2 Detector calibration

There were multiple factors that have led to a challenging calibration procedure for the whole array. First of all, these detectors were not previously characterized; secondly, they had different geometries alongside unwanted variations in the thermal conductance to the bath, resulting in different energy response. Moreover, the switchable calibration source was not ready at that time and no statistically significant peaks are expected in the energy interval that our detectors can cover with their dynamic range, from 0 to 10 keV.

To solve this daunting problem, it was necessary to make several approximations. I assumed that the microcalorimeter can be modeled as a single body connected to the thermal bath by one thermal conductance. Therefore, its thermal response to an energy deposition $E = \int P(t) dt$ is described by [19]

$$\begin{aligned} C \frac{dT}{dt} = P_J - P_{bath} + P \end{aligned}$$

(3)

Integrating the previous equation, I obtained the energy deposited in the absorber E as a function of the joule power $P_J$ and the power flowing from the TES to the thermal bath $P_{bath}$.

$$\begin{aligned} E = \int P_{bath}(t) dt + \int P_J(t) dt \end{aligned}$$

(4)

$P_j$ can be obtained by integration of the differential equation describing the electrical circuit

$$\begin{aligned} P_J(t) = I(t)^2 R_{TES} \simeq (R_0+R_L)I(t)^2 - R_L I(t)^2 \end{aligned}$$

(5)

The signal I(t) can be obtained from the measured signal s(t)

$$\begin{aligned} I(t) = -1 \times k_{\phi _0/A} \times s(t) + I_0 \end{aligned}$$

(6)

where $k_{\phi _0/A}$ is the known conversion factor from $\varPhi _0$ to Ampere, while $I_0$ and $R_0$ are the idle values of current and the resistance, which can be measured for each detector from their characteristic I–V curves; $R_L$ is the known value of the load resistances common for all the detectors.

On the other hand, $P_{bath} (t)$ can’t be measured because it requires the knowledge of the temperature variation of the detectors. I approximate its value by assuming that it doesn’t vary significantly during the energy deposition.

$$\begin{aligned} P_{bath} (t) \simeq P_{bath,0} = R_0 I_0^2 = cost \end{aligned}$$

(7)

In summary, with just the I–V curves from the measured signals s(t) it is possible to evaluate a parameter $E^*$ which is a good estimate of the true energy E released. The approximation holds for the low energy events, while for the higher energy events $E^*$ is an underestimation of E, as shown in Fig. 7 (Table 1)

Fig. 7

Trend of the $E^*$ parameter (black line) compared to the true simulated energy E. $E^*$ was evaluated using simulated pulses given an energy E. The red dotted line represents the case in which $E^* = E$. The higher the energy, the larger the error

$$\begin{aligned} E \simeq E^* = \int _{t_0}^{t_f} R_0 I_0^2 dt - \int _{t_0}^{t_f} R_0 I(t)^2 dt = R_0 I_0^2 \times (t_f - t_0) - \int _{t_0}^{t_f} R_0 I(t)^2 dt \end{aligned}$$

(8)

To test the goodness of this rough calibration procedure, I compared $E^*$ to $E^{cal}$ of an old ‘true’ calibrated measurement, where $E^{cal}$ was the energy obtained after a calibration procedure using an X-ray fluorescence sources.

Table 1 Comparison between the ’true’ measured signal energy ($E_{cal}$) and the energy estimated using this calibration procedure for an old dataset. The signals have been randomly taken from the dataset

The uncertainties reported in the following table are an estimation that take into account an uncertainty on the value of $R_0$ and $I_0$ of 10 $\%$ due to both the uncertainty related to the IV curve measurement and the temperature drift of the bath.

We can conclude that the calibration procedure described in this section cannot be used to a precise energy determination of the signals, but it can be used for an estimation of the number of events inside a sufficiently wide energy interval, fitting perfectly the first goal of this measurement: the evaluation of the background rate.

3.3 Expected background rate

To evaluate the expected background rate, nine separate measurements were performed, lasting for a total of 20 days. The signals were tagged as singles interactions or TES-TES coincidences.

Then, a calibration was performed using the detectors’ characteristic I–V curves, merging the data from each detectors to produce two different spectra, one for each tag.

To estimate the expected background rate in each energy interval, the posterior probability for the rate parameter was evaluated iteratively, using a Poisson distribution as likelihood given $x_j$ counts in the j-detector and a flat distribution as prior. Then, the probability for the background rate was updated using the resulting posterior as prior for the probability distribution of the rate for the ($j+1$)-th detector.

The resulting distribution for the rate r in the i-th bin is a gamma distribution

$$\begin{aligned} P(r |N,c) \propto r^c e^{-cN} \ \ \ \; \ \ \ \ c = \sum _{j=1}^N x_j \end{aligned}$$

(9)

with N the number of detectors and $x_j$ the counts of the j-th detector for that bin.

The data points in the rate plots represent the expected background rate in each bin expressed as the mean value of the gamma distribution while the error bars are the 95$\%$ credibility interval evaluated symmetrically from the median. If a bin has zero counts, the error represents the $95 \%$ upper limit.

The TES-TES background spectrum is composed of radiation that directly hits multiple absorbers or that interacts with the materials between the pixels. The latter case is the most probable, and the resulting signal is expected to have significant different shape compared to the direct interaction due to the different thermalization process of the TES thermometer, as shown in Fig. 8. Thus, they do not contribute to the final background rate; their energy spectrum is shown in Fig. 8.

Fig. 8

Left: example of the distribution of the signals amplitude respect to their rise time (RT). The signals tagged as TES-TES coincidences are shown in red. Right: the TES-TES coincidence energy spectrum

Single interactions produce a background spectrum as shown in Fig. 9. Between 0 and 10 keV, it seems to be monotonically decreasing¹ although the calibration procedure does not allow us to exclude the presence of low energy peaks. The background rate near the end-point of the spectrum is measured to be of the order of $0.5 \times 10^{-3}$ counts eV$^{-1}$ day$^{-1}$ det$^{-1}$.

Fig. 9

Left: (top) distribution of the signals energies in time for the singles interactions for all the detectors; (bot) the resulting background energy spectrum. Right: the same plots, but with only the bulk interactions

However, it is reasonable to believe that a great fraction of the events in the single interactions dataset are radiations which does not interact directly with the absorber but with the detector surroundings, the copper perimeter or the thermometer itself. As in the TES-TES case, these interactions should produce signals with different shape that can be easily recognized by our data reduction procedures.

The expected efficiency of these techniques is shown in Fig. 11, where the distribution of the rise time (RT) in one of the measured detectors is shown while the pink bands represent RT spread for direct interactions measured previously by similar detectors with an external calibration source. It can be clearly seen that it does not matter where pink band should actually be for the considered detector, as most of the events will be outside this narrow band and it will be discarded by simple cuts on the shape of the signal.

To quantify the efficiency of these techniques, the exact location of this band should be known, but without an external calibration source this seems impossible at first glance.

However, in previous measurements with the same array it was observed that signals from external X-ray sources show a RT distribution that can be modeled as a sum of gaussians with different means and intensities, as shown in Fig. 10. The difference in the relative intensity of the gaussians seems to decrease as the energy decrease and for energy above 6 keV just one peak is present. I believe that the signals in the low intensity peaks (smaller values of RT) are radiations which interact directly with the thermometer, resulting in faster RT, and the trend of the peaks’ intensity is motivated by the different attenuation lengths and dimensions in the absorber and in the thermometers.

Fig. 10

Left: example of the RT distribution at different energies intervals with an external calibration sources (Run 60). Right: the normalized area of the low RT peaks $A_{not \ abs}$ at different energies. As you can see, above 6 keV only the 5$\%$ of the signals presents a lower value of RT

Thus, the location of the RT band for the direct interactions in the absorber, i.e., for true Ho decays, can be found by looking at the RT of the high energy events (E > 6 keV) while the width of the band was conservatively defined as 3 $\mu$s, three times the expected one.

Thus, a similar cut as the one shown in Fig. 11 was applied to each detector, which results in the expected background spectrum presented in Fig. 9, presenting a background rate in the ROI $1 \times 10^{-4}$ counts eV$^{-1}$ day$^{-1}$ det$^{-1}$, five times lower than the one without the simple data reduction.

Fig. 11

Distribution of the signals energy respect to their rise time for the TES pixel 47. The pink bands are an example of the RT distribution from three different detectors for radiations that interact directly with the absorber (bulk interactions). The red dotted lines represent the region in which the bulk interaction is expected

4 Further studies

4.1 Muon induced background

To estimate the fraction of the background rate that is muon induced $f_{\mu }$ with the available data, I had to follow a procedure based on MonteCarlo simulations, that just allow me to have an idea of its order of magnitude. I divided the data in equal time intervals lasting 5 h. In each interval, the total counts recorded by the detector array $c_i$ follow a Poisson distribution

$$\begin{aligned} c_i = Poisson(c_i | N^{\mu }_i + N^b) \end{aligned}$$

(10)

where $N^{\mu }_i$ is the mean number of muon induced events and $N^b$ is the mean number events due to the natural radioactivity. The latter is assumed to be constant while $N^{\mu }_i$ in principle can vary during the measurement due to changes in atmospheric temperature and pressure above the laboratory.

The number of muon induced events in the array can be evaluated from the scintillators counts $N^s_i$ using MC simulations and some approximation to estimate the various geometrical efficiency. Calling P(A) the probability that a muon induced events hits the array while P(B) the probability that it hits the top and bottom plane of the scintillators

$$\begin{aligned} N^{\mu }_i= & {} k \times N^s_i \end{aligned}$$

(11)

$$\begin{aligned} k= & {} P(A|B) = P(B|A) \frac{P(A)}{P(B)} \simeq 0.5 \frac{2.97\times 10^{-5}}{0.86} = 1.75 \times 10^{-5} \end{aligned}$$

(12)

P(B|A) and P(B) are evaluated measuring the distance between the detector box and the scintillators $d_{bs}$and between the two scintillators plane $d_{ss}$ respectively and approximating the scintillators slabs as circle of radius $r_{top, bot}$ with equivalent area (see Fig. 5)

$$\begin{aligned} P(B|A)= & {} \frac{\int _0^{\alpha } cos(\theta )^2 d\theta }{\int _0^{\pi /2} cos(\theta )^2 d\theta } \ \; \ \ \alpha = \arctan {r_{top}/d_{bs}} \end{aligned}$$

(13)

$$\begin{aligned} P(B)= & {} \frac{\int _0^{\beta } cos(\theta )^2 d\theta }{\int _0^{\pi /2} cos(\theta )^2 d\theta } \ \; \ \ \beta = \arctan {r_{bot}/d_{ss}} \end{aligned}$$

(14)

P(A) was evaluated from MC simulations in which 100 milions muons were generated above the detector box from an area approximately infinite, but only $\sim 18\times 10^3$ interactions were recorded in the array composed of a matrix of $10 \times 10$ detectors.

From $N^b$, the posterior for $f_{\mu }$ was extracted, using for the prior of k a gamma distribution centered in (12) limited in a plausible interval of values and defining $f_{\mu }$ as

$$\begin{aligned} f_{\mu } = < f_{\mu }> = 1 - \frac{N \times N^b}{\sum _i=i^N c_i} \end{aligned}$$

(15)

The fraction of muon induced events was measured having a mean value of $E[f_{\mu }] = 0.460 \pm 0.002$, with a plausible interval of 90$\%$ between [0.28,0.59].

It’s worth noticing that with a slightly different scintillators configuration, a portion of the muon induced background could be easily recognized. The output of the scintillators logic chain could serve as a trigger for a signal generator. The resulting ad-hoc signal can then be sent as a custom input from room temperature to one of the SQUID of the multiplexing chip. In this way, the coincidence signals can be triggered by the HOLMES readout alongside the signals from the detectors, allowing to perform a coincidence measurement.

4.2 40K and neutrino mass sensitivity

$^{40}$K is the only natural occurring unstable potassium isotope, having a half-life of $1.3 \times 10^9$ years. It decays via beta decay (branching ratio $\sim 90\%$) to $^{40}$Ca or via electron capture (BR $\sim 10\%$) to an atomic and nuclear excited state of $^{40}$Ar, which in turn relaxes emitting X-rays, auger electron and the characteristic gamma of 1460 keV (Fig. 12).

Fig. 12

Scheme of the $^{40}$K decay

Both the gamma and the electron from beta decay produce a flat spectrum in the ROI region, while the EC produces de-excitation peaks with energy into and close to the ROI. If those peaks are present but not modeled in the final spectrum, they could potentially worsen the experimental sensitivity.

To have a preliminary idea of how severe this effect could be, I have studied qualitatively how the posterior of the neutrino mass changed if the likelihood did not include the $^{40}$K peaks by varying the number of counts B under those peaks.

I fixed the number of detectors $N_{det}$ to 32, the energy resolution to 5 eV, the time resolution $\tau _R$ to $1.5 \ \mu$s, the measurement time $T_{meas}$ to 3 years and I generated multiple toy ROI spectrum $S_{true}(E)$

$$\begin{aligned}{} & {} S_{true}(E) = S(E) + B \times m_{peaks}(E) \ \; \ \ \ \ S(E) = Ho(E) + f_{pp}\times ( Ho * Ho) (E) + bgk(E) \end{aligned}$$

(16)

$$\begin{aligned}{} & {} Ho(E) \propto \Big ( \sum _i I_i \times cauchy(E,x_{c,i},\gamma _i) \Big ) \times \Big ( (Q - E) \times \sqrt{(Q-E)^2 - m_{\nu }^2} \Big ) \end{aligned}$$

(17)

with Ho(E) being the de-excitation $^{163}$Ho spectrum,²$f_{pp}$ is the ratio of pile-up pulses to single pulses, which can be approximated³ from the single detector activity A as $f_{pp} = A \times \tau _R$, bkg(E) is the flat background and $m_{peaks}(E)$ are the de-excitations peaks due to the EC of $^{40}$K. The total number of generated events $n_{ev}$ for S(E) is given by the $^{163}$Ho activity per pixel A, $n_{ev} = T_{meas} A N_{det}$, while the total number of single pulse $n_s$ and pile-up pulses $n_p$ is given by

$$\begin{aligned} n_s = \frac{n_{ev}}{1+2f_{pp}} \ \ \ \; \ \ \ \ n_p = n_s f_{pp} \end{aligned}$$

(18)

The ROI region was defined as $E \in [2650,2900]$ eV, and the background activity for the bkg(E) spectrum was fixed at $2 \times 10^{-5}$ counts eV$^{-1}$ day$^{-1}$ det$^{-1}$, five times lower than the one measured in the previous section. For each value of B, ${\mathcal {O}}(10)$ different spectra were generated, following Eq. (16). The parameter estimation on $m_{\nu }, Q, f_{pp}, n_{single}$ and bkg was performed with STAN [20], choosing as likelihood

$$\begin{aligned} {\mathcal {L}} = Poisson(c_i | \lambda _i) \ \ \ \; \ \ \ \ \lambda _i = n_{single} \times \Big (S * normal (0,5/2.355) \Big ) (E_i) \end{aligned}$$

(19)

and a normal priors for $Q, f_{pp}, bkg$ and $n_{single}$, while for $m_{\nu }$ an exponential distribution with a slightly uninformative rate parameter of 0.01.

The samples generated from each Markov Chain Monte Carlo were merged to reduce the influence of the statistical fluctuation of each bin on the parameters posterior, and the resulting distribution of the “mean typical set” was summarized in a boxplot. The scheme for the followed procedure is depicted in Fig. 13, while Fig. 14 shows the final result for a single pixel activity of 1 Bq.

Fig. 13

Scheme of the simulations: first for a fixed value of B different spectra are generated; then, a parameters estimation is performed with STAN for each spectrum, using S(E) and not $S_{true}(E)$. The samples generated from the $m_{\nu }$ posteriors are merged to reduce the statistical fluctuations, and the resulting distribution is shown as a boxplot

Fig. 14

Distribution of the samples from the $m_{\nu }$ posteriors is shown with the variations in the total number of $^{40}$K decays (total peak counts), the B parameter. The boxplot lines approximately represent the 90$\%$ credible intervals, the orange (green) line the median (mean) of the distribution while inside the box there are 50$\%$ of the total entries

It is reasonable to assume that the only place from which the de-excitations product of $^{40}$K can reach the detectors are the internal cover of the detector’s holder and the surface of the gold absorbers, although the latter seems unlikely due to our fabrications procedures. Therefore, we used the MC simulations to convert B from total counts under the peaks to a surface density of K on the holder’s cover.

From that, we can conclude that with this configuration a surface contamination of 0.5 mg/cm$^2$ of K (corresponding to a number of counts under the $^{40}$K peaks of $\sim$ 1000) starts to affect the posterior distribution of $m_{\nu }$ and worsen the experimental sensitivity.

5 Conclusion

Studying the influence of $^{40}$K on the neutrino mass, I simulated the condition in which this effect should be more noticeable, i.e., with the lowest target pixel activity of HOLMES. Even with this setup, the amount of potassium required to produce a measurable effect on the final spectrum is quite large, and we can preliminary conclude that the influence of $^{40}$K on the experimental sensitivity will be negligible and that the shape of the expected background in the ROI will be smooth or approximately flat.

I measured a background rate in the ROI of $0.5\times 10^{-3}$ counts eV$^{-1}$ day$^{-1}$ det$^{-1}$, but I proved that with a rough first level data reduction this rate can be reduced by a factor of 5 to $1 \times 10^{-4}$ counts eV$^{-1}$ day$^{-1}$ det$^{-1}$. We believed that it can be further reduced by at least a factor two by using a more tight RT cuts in combination with second-level data reduction techniques based on optimum filter and unsupervised learning techniques.

The comparison between the background rate due to natural radioactivity and cosmic rays to the pile-up rate allows us to establish that the former is dominant in the hypothesis of an $^{163}$Ho activity of 1 Bq per detector (Fig. 15, left), while it becomes negligible compared to the pile-up above an activity of 50 Bq. The two have nearly the same magnitude at 10 Bq.

Fig. 15

A comparison between the expected pile-up spectrum and the measured background for different single pixel activity A. The green region represents the HOLMES region of interest

Due to the fact that the muon contribution to the final background rate is about the same order of magnitude as the natural one, it cannot be neglected. A further reduction in the total background rate of a factor of roughly 25$\%$ can be achieved by realizing an active muon veto similar to the one explained at the end of Sect. 4.1, enhancing the experimental sensitivity in the first phase of the HOLMES experiment.