Modulation instability spectrum and rogue waves of the repulsive lattices

Abstract

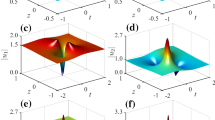
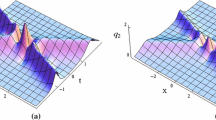
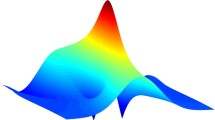
In this work, the modulation instability and solitonic rogue waves are addressed in the repulsive lattice formed by identical particles with nearest neighbor couplings. We use the multiple scale method to derive the extended nonlinear Schrödinger equation with fourth-order dispersion and cubic–quintic nonlinearity. To calculate the modulation instability growth rate, a linear stability analysis is used. Thereafter, we have demonstrated that both fourth-order dispersion and quintic nonlinearity can change the amplitude of the plane wave and bandwidth of the modulation instability in normal and anomalous dispersion regimes. The dynamics of the solitonic rogue waves have been pointed out to show an increasing amplitude with the variation of the free amplitude parameter of the chain of magnets. Via the numerical simulation, the modulated wave patterns have been exhibited to manifest the development of the modulation instability spectrum in the lattice, and the long-time evolution of the continuous waves has brought new features to show an increasing amplitude of the trains of pulses under the variation of the interaction interatomic parameters. These parameters are revealed to be a suitable tool to manipulate nonlinear objects in nonlinear media where higher-order dispersion competes with nonlinearity.

Appendix

It is essential to understand how Eq. (8) is generated. As a result, to derive Eq. (8), we use the method described in [7, 8, 12, 13]. We express the following equations using Taylor expansion in order 2 for the function $\psi (x,\tau )$ as follows:

$$ \begin{aligned} \Psi _n(t)&=\psi (x,\tau )e^{i\theta _n}+\psi ^*(x,\tau )e^{-i\theta _n},\\ \Psi _{n+1}(t)&=\Bigg (\psi +\frac{\partial \psi }{\partial x}+\frac{1}{2}\frac{\partial ^2\psi }{\partial x^2}+\frac{1}{6}\frac{\partial ^3\psi }{\partial x^3}+\frac{1}{24}\frac{\partial ^4\psi }{\partial x^4} \Bigg )e^{i\theta _n}e^{ik}\\&+\Bigg (\psi ^*+\frac{\partial \psi ^*}{\partial x}+\frac{1}{2}\frac{\partial ^2\psi ^*}{\partial x^2}+\frac{1}{6}\frac{\partial ^3\psi ^*}{\partial x^3}+\frac{1}{24}\frac{\partial ^4\psi ^*}{\partial x^4} \Bigg )e^{-i\theta _n}e^{-ik},\\ \Psi _{n-1}(t)&=\Bigg (\psi -\frac{\partial \psi }{\partial x}+\frac{1}{2}\frac{\partial ^2\psi }{\partial x^2}-\frac{1}{6}\frac{\partial ^3\psi }{\partial x^3}+\frac{1}{24}\frac{\partial ^4\psi }{\partial x^4} \Bigg )e^{i\theta _n}e^{-ik}\\&+\Bigg (\psi ^*-\frac{\partial \psi ^*}{\partial x}+\frac{1}{2}\frac{\partial ^2\psi ^*}{\partial x^2}-\frac{1}{6}\frac{\partial ^3\psi ^*}{\partial x^3}+\frac{1}{24}\frac{\partial ^4\psi ^*}{\partial x^4} \Bigg )e^{-i\theta _n}e^{ik}. \end{aligned}$$

(27)

By substituting Eq. (27) into Eq. (4), and collecting terms of order $e^{i\theta _n},$ we obtain the following equation:

$$ \begin{aligned}&\epsilon ^{4}\frac{\partial ^{2}\psi }{\partial {\tau }^{2}}-2\epsilon ^{3}v_{g}\frac{\partial ^{2}\psi }{\partial x\partial \tau }+\epsilon ^{2}\left( -2i\omega \frac{\partial \psi }{\partial \tau }+v_{g}^{2}\frac{\partial ^{2}\psi }{\partial {x}^{2}}\right) +2i\omega \epsilon {v_{g}}\frac{\partial \psi }{\partial x}-2\psi -\frac{1}{4}\frac{\partial ^{2}\psi }{\partial {x}^{2}}\\&\quad -\frac{1}{48}{\frac{\partial ^{4}\psi }{\partial {x}^{4}}}+48s_3(\psi )^{2}\psi ^*+3s_3\left( \frac{\partial \psi }{\partial x}\right) ^{2}{\frac{\partial ^{2}\psi ^*}{\partial {x}^{2}}}+6s_3\frac{\partial \psi }{\partial {x}}\frac{\partial ^{2}\psi }{\partial {x}^{2}}{\frac{\partial \psi ^*}{\partial x}}+640s_5(\psi )^{3}(\psi ^*)^{2}=0. \end{aligned}$$

(28)

In the upper frequencies, i.e., $k=\pi$ and $\omega =\sqrt{1+\Omega _{0}^2},$ considering the order terms only $\epsilon ^{0}$ and $\epsilon ^{2},$ we obtain

$$\begin{aligned} &i\frac{\partial \psi }{\partial \tau }+{\frac{1}{\epsilon ^{2}\sqrt{\Omega _{0}^{2}+1}}}\psi +\frac{1}{8\epsilon ^{2}\sqrt{\Omega _{0}^{2}+1}}\frac{\partial ^{2}\psi }{\partial {x}^{2}}+\frac{1}{96\epsilon ^{2}\sqrt{\Omega _{0}^{2}+1}}\frac{\partial ^{4}\psi }{\partial {x}^{4}}+\frac{\left( C+u_{{0}}\right) C}{u_{0}^{2}\epsilon ^{2}\sqrt{\Omega _{0}^{2}+1}}|\psi |^{2}\psi \\&\quad +\frac{2(C+3u_{0})(C+2u_{0})(C+u_{0})C}{3u_{0}^{4}\epsilon ^{2}\sqrt{\Omega _{0}^{2}+1}}|\psi |^{4}\psi +\frac{C(C+u_{0})}{16u_{0}^{2}\epsilon ^{2}\sqrt{\Omega _{0}^{2}+1}}\frac{\partial \psi }{\partial x}\left( \frac{\partial \psi }{\partial x}\frac{\partial ^{2}\psi ^*}{\partial {x}^{2}}+2\frac{\partial ^{2}\psi }{\partial {x} ^{2}}\frac{\partial \psi ^*}{\partial x}\right) =0. \end{aligned}$$

(29)