Abstract
We describe the behavior of a beam balance used for the measurement of small forces, in macroscopic samples, in tens of mHz frequency band. The balance, which works at room temperature, is the prototype of the cryogenic balance of the Archimedes experiment, aimed at measuring the interaction between electromagnetic vacuum fluctuations and the gravitational field. The balance described has a 50-cm aluminum arm and suspends an aluminum sample of 0.2 Kg and a lead counterweight. The read-out is interferometric, and the balance works in closed loop. It is installed in the low seismic noise laboratory of SAR-GRAV (Sardinia—Italy). Thanks to the low sensing and actuation noise and finally thanks to the low environmental noise, the sensitivity in torque \(\tilde{\tau _n}\) is about \(\tilde{\tau _n} \approx 2*10^{-12} \rm{Nm}/\sqrt {{\text{Hz}}}\) at 10 mHz and reaches a minimum of about \(\tilde{\tau _n} \approx 7*10^{-13} \rm{Nm}/\sqrt {{\text{Hz}}}\) at tens of mHz, corresponding to the force sensitivity \(\tilde{F_n}\) of \(\tilde{{F_{n} }} \approx 3*10^{{ - 12}} {\text{N/}}\sqrt {{\text{Hz}}}\). The achievement of this sensitivity, which turns out to be compatible with thermal noise estimation, on the one hand, demonstrates the correctness of the optical and mechanical design and on the other paves the way to the completion of the final balance. Furthermore, since the balance is equipped with weight and counterweight made of different materials, it is sensitive to the interaction with dark B-L photons. A first very short run made to evaluate constraints on B-L dark photon coupling shows encouraging results that will be discussed in view of next future scientific runs.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
One of the deepest problems of contemporary physics is the “cosmological problem” or rather the impossibility of reconciling the enormous value that quantum mechanics attributes to vacuum energy with the observation that the universe shows a value of cosmological constant enormously smaller than estimated by inserting this vacuum energy into Einstein’s equations [1,2,3].
In this context, we recently started the Archimedes experiment aimed at measuring the interaction of vacuum fluctuations with gravity. The experimental method is the measure of a change in weight due to the change in vacuum energy content at the transition of a high-Tc superconductor (with a mass of approximately 0.2 kg). The experimental apparatus will be a cryogenic balance, working at a temperature of about 90 K, modulating it around the transition temperature of the superconductor (GdBCO). The amplitude of the weight variations is expected to be of the order of few \(10^{-16}\) N modulated at a frequency of about 10 mHz [4,5,6].
Driven by the fact that the balance must be extremely sensitive, we realized a prototype intended above all to identify any experimental difficulties and develop the experimental techniques necessary for the final balance. The goal of the prototype is to reach a torque sensitivity \(\tilde{\tau _n}\), on an arm of half a meter, of the order (or better) of \(10^{{ - 12}} {\text{Nm/}}\sqrt {{\text{Hz}}}\) that could pave the way toward the final measurement, in which a sensitivity balance better than \(10^{-13} \rm{Nm}/\sqrt {{\text{Hz}}}\) is required, with a balance arm 1.4 m long, so to detect the signal in an integration time of the order of \(10^6\) s (about 2 weeks).
The prototype works at room temperature and shares with the final balance several critical features: the read-out of the arm tilt is interferometric, the balance works in closed loop, and it is installed in a very seismically quiet site, in the region of Sardinia (Italy).
The initial version of the prototype was presented in previous papers: having not suspended samples at its arm, it was tested, in particular, as ground tilt sensor, showing a remarkable sensitivity [7, 8]
Currently, the prototype has been equipped with a suspended sample with a mass of 0.2 kg, which mimics the final balance sample. With respect to previous works, the prototype has been also isolated from almost all possible sources of laboratory noise, and finally, the loop has been optimized by adding a temperature actuator that improved both the sensitivity and the lock duration.
The set of these improvements, which will be described and discussed in the rest of the article, led to the achievement of a sensitivity compatible with thermal noise, with a noise torque of the order (or slightly better) of \(10^{-12} \rm{Nm}/\sqrt {{\text{Hz}}}\) in the band of tens of mHz.
These achievements on the prototype constitute a solid step toward the final Archimedes balance: in particular, they demonstrate the robustness and sensitivity of the interferometric reading, of the control system, and the usefulness of carrying out the experiment in a very quiet site from a seismic point of view. Furthermore, we equipped the prototype with a weight and counterweight of different materials, to check what limits could be reached by this balance in the direct search of dark matter in the form of ultralight dark photon B-L, i.e., an ultra-light boson mass (ULBM) vector that couples with the B-L charge, being B the number of Baryons and L the number of Leptons.
In fact, among all possible dark matter candidates, recent attention has been posed in the search for bosonic ultralight fields with masses presently bounded in lower limits \(m \ge 10^{-22}\) eV and extending up to order of the eV [9,10,11,12,13].
Relevant in recent years has been the experimental research in the region of extremely low masses, on the order of \(m \approx 10^{-11}\) eV or less. Important constraints on the coupling of dark photons are reached through equivalent principle tests with EOT-WASH and MICROSCOPE experiments [14,15,16,17].
On the other hand, new constraints on dark photon coupling have been reached through direct search: the background of ultralight dark photons is expected to generate time-dependent forces on bodies, almost monochromatic, which in principle can be detected by measuring the spectrum of the position of a suspended body and searching for an almost monochromatic noise at the frequency \(f = m_A c^2/h\) of the dark photon field. This has prompted the dark photon direct search with very high-precision interferometry, particularly with gravitational-wave interferometers, such as LIGO, Virgo, GEO, and Kagra [18,19,20,21,22,23].
LIGO and Virgo, although not detecting any signal attributable to dark photons, have imposed remarkably stringent limits on the value of the coupling constant (both B coupled and B-L coupled dark photons) in the frequency region from a few kHz down to 10 Hz, corresponding to the mass region of \(O(10^{-14} - 10^{-11})\) eV [20], under the hypothesis that the whole dark matter mass is due to this particle. In a lower part of the frequency spectrum, the mHz, corresponding to the masses around \(f \approx 10^{-18}\) eV, direct search with torsion pendulums has led to new limits in B-L coupled dark photons [24]. With respect to these experiments, our balance can cover a frequency bandwidth not yet explored in direct search, in particular in the region from 20 mHz \(< f<\) 200 mHz (and above with lower sensitivity), corresponding to a mass decade above \(m_A \approx 10^{-16}\) eV. In the last part of the paper, we will show and discuss limits on the B-L dark photon coupling obtained with a short measurement run carried out with the present prototype. These limits are not yet more stringent than those obtained with the free fall experiments, but with a few months of integration time, a data taking with the prototype could close the gap and lead to a first direct search.
2 The experimental apparatus
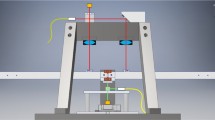
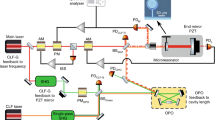
The experimental apparatus consists of a beam balance suspended with thin metallic joints, in a similar way to a rotation sensor originally realized by Venkateswara et al. [25]. Unlike the rotation sensor of Venkateswara (which has no additional suspended elements), our balance has a suspended element at one end of the arm, corresponding to the element in blue in Fig. 1. The length of the suspension wires is approximately 8 cm, compatible with the available space, and the wires are attached at the top in the vertical center of mass of the arm and at the bottom in the center of mass of the sample. This element mimics the similar suspended element of the final balance and is inserted to verify mainly the stability of the control loops and the sensitivity of the balance in this condition: the mass is 180 gr, very similar to the mass planned for the superconducting sample in the final experiment. On the same side of the arm balance, other aluminum weights for equilibrium tuning are installed. On the other side of the arm, a counterweight of lead is installed, sketched in yellow in Fig. 1, with its center of mass near the edge of the arm, actually at a distance of 0.24 m from the rotation center, with a mass of 0.210 kg. The balance arm is 0.5 m long, made of aluminum, and the total moment of inertia I = \(2.6*10^{-2}\) kgm\(^{2}\). The resonance frequency is \(f_0 = 26\) mHz in this measurement. The angular read-out is interferometric, through an equal-arms Michelson interferometer read in DC on the middle fringe, according to the scheme shown in Fig. 1 and also in the picture of Fig. 2 and described in detail in [8]. The apparatus is located in the site of Sos Enattos (Sardinia-Italy) to benefit from the extremely low seismic noise [8, 26]. The beam balance works in closed loop to keep the interferometer at the working point. Data are acquired, filtered, and sent to the actuators by a National Instruments C-RIO ADC/CPU/DAC system, acquiring data at 25 kHz and re-sampling them at 1 kHz before the filtering operations. The feedback loop corrects drifts in very low frequency, on the time scale of hours, mainly due to temperature drifts, and corrects the small angular fluctuations above the mHz. The feedback is a nested loop, also shown in Fig. 3: the control signal is sent to thermal actuators that act on the temperature of the chamber (covering the very low frequency range) and to electrostatic actuators that act directly on the beam balance arm and cover the frequency range above the mHz. In this way, the DC voltage sent to electrostatic actuators is reduced and the noise re-injected by electrostatic actuators in the interesting measurement band above 10 mHz, which is proportional to the DC voltage [7], is reduced to a negligible level.
The control signal, sent to electrostatic actuators, is calibrated with a 3-Hz injected line (more than one decade above the unity gain): the coupling constant \(\alpha\) of applied voltage to torque on the balance is \(\alpha = 3.4*10^{-8}\) Nm/V. The open-loop transfer function is reported in Fig. 4. The unity gain of the loop is set at 140 mHz. At 1.65 Hz and 2.3 Hz, two notches are visible, used to limit the resonant oscillations of the suspended sample. The torque sensitivity \(\tau _n\) is evaluated by acquiring the control signal sent to electrostatic actuators and corrected by the closed-loop transfer function \(\tau _n = \tau _{\rm{corr}}\frac{1 + GH}{GH}\) where H is the plant transfer function and G the correction filter transfer function. The signal \(\tau _{\rm{corr}}\) is the voltage applied to electrostatic actuators multiplied by the constant \(\alpha\).
3 Results on the sensitivity and perspective for the Archimedes experiment
The results we report correspond to an initial run. The total science mode time is 21000 s, selected in the night time. The reason for not having longer data taking is that the prototype balance is located in a section of the laboratory that is not thermally stabilized (fans thermalization is not usable in science mode because it is noisy due to the fans) and located in a peripheral part of the building so that there are considerable temperature fluctuations that cannot all be compensated for by the balance’s thermalization system. In addition, the hall is shared with the workshop operations still in place at the mine, and this severely limits the possibility of taking data during the day. In the immediate future, as will be discussed later, we plan to make other runs to study and eventually increase the sensitivity during working holiday periods of the mine workers. Nonetheless, even in a limited data-taking period, the results are very encouraging, especially as a demonstration of the sensitivity. Within the data taking, the 21000-s period is selected because it does not present high seismic or anthropogenic noise. In Fig. 5, we show the amplitude spectral density (ASD), i.e., the square root of the power spectral density (PSD) mediated over the selected period. The integration time of each pwelch is 5200 s. It has also been checked that the result is not affected by changing the integration time of the pwelch. In Fig. 5, referring to the left-hand scale, we read the amplitude spectral noise, reported to indicate the torque residual noise \(\tau _n\) of the measuring apparatus. In the region between about 20 mHz and 100 mHz, the spectrum is indeed compatible with thermal noise, whose equation is given by [27, 28]:
Here \(\tilde{\tau }_{\rm{tn}}\) is the amplitude spectral density of the thermal noise, \(K_B\) is the Bolzman constant, T is the temperature, the mechanical quality factor Q = 90 measured during balance free oscillations, and \(k = I (2\pi f_0)^2\) is the restoring constant. The lower limit is reached at about 60 mHz, and the value is \(7*10^{-13} \rm{Nm}/\sqrt {{\text{Hz}}}\). Indeed, the amplitude spectral density \(\tilde{\tau }\) of torque still depends on environmental conditions. In particular, during the quieter night hours, the spectrum is compatible with the thermal noise spectrum while in the evening and morning hours, the noise tends to rise above this level.
Looking ahead to the Archimedes experiment, these results are promising. The sensitivity necessary for the final experiment is of the order of \(\tau _n < 10^{-13} \rm{Nm}/\sqrt {{\text{Hz}}}\), at the frequency region around 10 mHz. The final design sensitivity is reported in Fig. 6: the horizontal blue line is the expected signal value. We point out that the signal is not present at all frequencies, but rather the blue line represents the value that the signal will have once the single modulation frequency has been chosen. From the figure, it is seen that the design sensitivity is limited by thermal noise and seismic noise. The thermal noise is evaluated using Eq. 1 with the expected parameters for the final balance: resonance frequency \(f0_f = 5\) mHz, moment of inertia \(I_f = 0.3\) kgm\(^2\), losses of the order of \(\phi _f = 1/Q_f = 10^-5\), and working temperature \(T_f = 77\) K. The seismic noise is assessed using the main formula that describes the coupling of the horizontal seism with the rotation of the suspended arm [7, 25]:
where \(M_t\) is the total suspended mass, \(\ddot{x}\) is the ground acceleration, and \(\delta\) is the distance between the center of mass and the rotation point. The final balance will have a total suspended mass (arm and samples) \(M_t = 1\) kg and an expected \(\delta \approx 5\, \upmu\)m. This value is rather conservative, because we have already demonstrated a value of \(\delta = 15\) \(\upmu\)m in the initial prototype used during the O3 Virgo run [7] and balance arm will be equipped for remote tuning. The seismic noise used to calculate the expected torque noise due to seism is measured in the Sos Enattos mine, and the period is the month of August 2023. The mine, although no longer used for mining, nevertheless sees the entry of miners for maintenance and safety work, except for a two-week holiday. For this reason, the estimation of noise due to the seism is reasonably conservative. In a future laboratory, access and work would be regulated according to the needs of the data taking.
The fact that the prototype has reached thermal noise is an excellent viaticum toward the final balance, in which the reduction in torque noise compared to the current thermal noise contribution is expected to be determined both by the cryogenic operation of the balance, 77 K compared to 300 K, and by the lower resonance frequency, designed to be 5 mHz. The suspension quality factor Q also needs to be much improved. The lowering of the temperature is expected to enhance it and various studies are underway within the Archimedes collaboration, which will be conducted both considering the Cu-Be joints themselves and possibly other materials with lower losses.
At frequencies below 20 mHz, the prototype is limited by ambient noise. Although the site is extremely quiet [8, 26], several factors must be considered. First of all, the prototype is installed in a peripheral room of the central building, so it is particularly exposed to wind and variations in ambient temperature. Furthermore, at the moment, for contingent reasons, not all instruments that generate seismic noise (typically through cooling fans) have been removed from the scale. In the next sensitivity studies of the prototype, these instruments will be removed and an improvement in sensitivity is expected even below 20 mHz. Finally, we point out that the final balance is installed in the central part of the building, protected from environmental noise and, in the latest version, it will be installed in the underground laboratory which is planned.
4 Dark photon field and torque on the beam balance
The beam balance used in the measurement is equipped with masses of different materials. Being more sensitive to dark photons coupled with B-L current \(J^\mu _D\), we restrict the analysis to this case. Here we use the units \(\hbar = c = \sqrt{\epsilon _0} = 1\) and we will recover the SI at the end of the section. The Lagrangian is given by [18]:
where \(F^{\mu \nu }F_{\mu \nu }\) is the field strength, \(m_A\) is the mass of the vector field, \(J_D\) is the B-L current, and \(\epsilon _D\) is the coupling constant normalized to the electromagnetic coupling constant e. The dark photon field is considered nonrelativistic so that \(A_t\) can be neglected with respect to \(\varvec{A}\) when evaluating the force on a charge \(q_D\). Following in the particular the analysis of [18, 19], the vector dark matter field at location \(\varvec{x}\) is given by
where \(\varvec{e}\) is polarization vector. The phase factor \(\phi (t)\) and the amplitude \(A_0\) can be regarded as constant within the coherent time scale \(\tau = 2\pi /(m_A v_0^2)\) (\(\tau = O(10^6)\) s for \(m_A = 10^{-15}\) eV), and the force can be written as:
Here \(q_D\) is the B-L total charge, which is equal to the number of neutron of the mass M. The amplitude of the field \(A_0\) is related to the dark photon energy density \(\rho _{DM}\) by: \(A_0 = \frac{\sqrt{2\rho _{DM}}}{m_A}\) By substituting and performing the mean over the direction of polarization, the standard deviation of the force along the X axis is [18]:
The evaluation of torque on the balance can be performed considering that for equal aluminum and lead mass \(M_Al = M_Pb = M\), difference \(\varDelta q_D\) of neutron numbers is given by
Thus, calling \(q= \frac{M}{mb}\) the total number of barion on each mass, the torque \(\tau _q\) acting on the balance is
where \(L_b = 0.24\) m is the force arm. The factor \(8.6\cdot 10^{-2}\) is the fraction of force produced by the photon field which is converted in useful signal in the detector.
The limit value of \(\epsilon _{B-L}\) is shown in Fig. 7. To obtain the coupling constant from the torque signal, first we perform a pwelch on the whole data set (with time length T), and we obtain the spectrum of the torque mean square deviation \(<\tau ^2>\), we then divide the ASD by the square root of T (\(\sqrt{\tau ^2} = ASD/\sqrt{T}\) to obtain the value of amplitude of the deviation in each frequency bin, and we multiply by 2 to obtain the \(95\%\) confidence value [29]; finally, we invert Eq. 8 to obtain the corresponding value of the coupling constant: (the simple division by \(\sqrt{T}\) is allowed by the coherence time of the dark photon wave that is longer than the measurement time [29]).
Limits on coupling \(\epsilon _{B-L}\) of the present experiment (blue curve) and expected limits with 2 weeks (red dashed) or one year (green dashed) integration time. The horizontal lines are the present limits from Eot-Wash (red) and MICROSCOPE (black) with free fall experiments and at low frequency limits from torsion balance direct search
Finally, in Fig. 8 the spectrogram of the correction signal over an entire night is reported. It can be appreciated again that no lines are visible and no glitches or other particular events.
5 Discussion and future developments
In this work, the sensitivity of a prototype balance was presented, useful for defining the last critical parameters of the Archimedes balance and for designing a balance for the direct search of the ultralight dark photon B-L in the mass band around \(10^{-16} eV\). Particularities of the balance are the interferometric reading, the closed-loop work, and the fact that it is installed in an extremely quiet site from a seismic point of view. The sensitivity of the prototype, in the tens of mHz band, is compatible with the thermal noise of the suspension. This result constitutes a first viaticum for the final Archimedes balance, which will have to achieve a torque sensitivity approximately 10 times higher, benefitting both from lowering the temperature and a necessary improvement in the quality factor of the suspension, currently under study. The prototype balance is equipped with a weight and counterweight of different materials, so as to be suitable for a direct search for the B-L dark photon. The sensitivity achieved made it possible to reach, even in a very limited run in time, a limit on the coupling close to the currently known limits and demonstrated that with a data taking of the order of months, it would be possible to undertake a direct search for dark photons with sensitivity to the best coupling of the current known limits. Motivated by these results, the next few months will be dedicated to the first scientific runs, in particular, for the direct search for the dark photon in the mass band of about a decade around \(10^{-16}\) eV.
Data Availability Statement
This manuscript has associated data in a data repository. [Authors’ comment: The data are available on our laboratory repository upon reasonable request to the corresponding author].
References
S. Weinberg, The cosmological constant problem. Rev. Mod. Phys. 61, 1–23 (1989)
J. Sola, Cosmological constant and vacuum energy: old and new ideas. J. Phys. Conf. Ser. 453, 012015 (2013)
C. Moreno-Pulido, J.S. Peracaula, Renormalizing the vacuum energy in cosmological spacetime: implications for the cosmological constant problem. Eur. Phys. J. C 82(6), 551 (2022)
G. Bimonte, E. Calloni, G. Esposito, L. Rosa, Energy-momentum tensor for a Casimir apparatus in a weak gravitational field. Phys. Rev. D 74, 085011 (2006)
E. Calloni, M. De Laurentis, R. De Rosa, L. Di Fiore, G. Esposito, F. Garufi, L. Rosa, C. Rovelli, P. Ruggi, F. Tafuri et al., Towards weighing the condensation energy to ascertain the Archimedes force of vacuum. Phys. Rev. D 90, 022002 (2014)
S. Avino, E. Calloni et al., Progress in a vacuum weight search experiment. MDPI Phys. 2(1), 1–13 (2020)
E. Calloni et al., High-bandwidth beam balance for vacuum-weight experiment and Newtonian noise subtraction. Eur. Phys. J. Plus 136(3), 335 (2021)
A. Allocca, E. Calloni et al., Picoradiant tiltmeter and direct ground tilt measurements at the Sos Enattos site. Eur. Phys. J. Plus 136(10), 1069 (2021)
M. Fabbrichesi, E. Gabrielli, G. Lanfranchi, The Physics of the Dark Photon. IN: Part of the book series: SpringerBriefs in Physics (SpringerBriefs in Physics)
B.J. Carr, K. Kohri, Y. Sendouda, New cosmological constraints on primordial black holes. Phys. Rev. D 86, 104019 (2010)
S.-R. Chen, H.-Y. Schive, T. Chiueh, Jeans analysis for dwarf spheroidal galaxies in wave dark matter. Mon. Not. R. Astron. Soc. 468(2), 1338 (2017)
L. Hui, J.P. Ostriker, S. Tremaine, E. Witten, Ultralight scalars as cosmological dark matter. Phys. Rev. D 95, 4 (2017)
E.G.M. Ferreira, Ultra-light dark matter. Astron. Astrophys. Rev. 29(1), 7 (2021)
S. Schlamminger, K.-Y. Choi, T. Wagner, J. Gundlach, E. Adelberger, Phys. Rev. Lett. 100, 041101 (2008). arXiv:0712.0607 [gr-qc]
T. Wagner, S. Schlamminger, J. Gundlach, E. Adelberger, Class. Quant. Grav. 29, 184002 (2012). arXiv:1207.2442 [gr-qc]
P. Touboul et al., Phys. Rev. Lett. 119, 231101 (2017). arXiv:1712.01176 [astro-ph.IM]
M. Pernot-Borràs, J. Bergé, P. Brax, J.P. Uzan., Phys. Rev. 101, 124056 (2020)
A. Pierce, K. Riles, Y. Zhao, Phys. Rev. Lett. 121(6), 061102 (2018)
H.-K. Guo, K. Riles, F.-W. Yang, Y. Zhao, Searching for dark photon dark matter in LIGO O1 data. Commun. Phys. 2, 155 (2019)
R. Abbott, LIGO and Virgo and Kagra Scientific Collaborations et al., Constraints on dark photon dark matter using data from LIGO. Phys. Rev. D. 105(6), 063030 (2022)
S.M. Vermeulen et al., Direct limits for scalar field dark matter from a gravitational-wave detector. Nature 600, 424–428 (2021)
Y. Michimura, T. Fujita, S. Morisaki, H. Nakatsuka, I. Obata, Ultralight vector dark matter search with auxiliary length channels of gravitational wave detectors. Phys. Rev. D 102(10), 102001 (2020)
S. Morisaki, T. Fujita, Y. Michimura, H. Nakatsuka, I. Obata, Improved sensitivity of interferometric gravitational wave detectors to ultralight vector dark matter from the finite light-traveling time. Phys. Rev. D 103(5), L051702 (2021)
E.A. Shaw, M.P. Ross et al., Torsion-balance search for ultralow-mass bosonic dark matter. Phys. Rev. D 105(4), 042007 (2022)
K. Venkateswara, C.A. Hagedorn, M.D. Turner, T. Arp, J.H. Gundlach, A high-precision mechanical absolute-rotation sensor. Rev. Sci. Instrum. 85, 015005 (2014)
L. Naticchioni et al., Characterization of the Sos Enattos site for the Einstein Telescope. J. Phys. Conf. Ser. 1468, 012242 (2020)
J. Harms, C.M. Mow-Lowry, Suspension-thermal noise in spring-antispring systems for future gravitational-wave detectors. Class. Q. Grav. 35, 025008 (2017)
P.R. Saulson, Thermal noise in mechanical experiments. Phys. Rev. D 42, 2437–2445 (1990)
Y. Michimura, T. Fujita, J. Kume, S. Morisaki, K. Nagano, H. Nakatsuka, A. Nishizawa, I. Obata, Ultralight dark matter searches with KAGRA gravitational wave telescope. J. Phys. Conf. Ser. 2156(1), 012071 (2021)
Acknowledgements
We are extremely grateful to Luca Loddo, Francesco Sedda, Alessandro Porcu, Mauro Porcu, Francesco Cossu, Giuseppe Lai, and Fabrizio Murgia; their generous work made ours possible. We are also in debt with Luca Francescon and Riccardo Machia for their precious support in vacuum equipment.
Funding
Open access funding provided by Università degli Studi di Napoli Federico II within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Allocca, A., Avino, S., Calloni, E. et al. Thermal noise-limited beam balance as prototype of the Archimedes vacuum weight experiment and B-L dark photon search. Eur. Phys. J. Plus 139, 158 (2024). https://doi.org/10.1140/epjp/s13360-024-04920-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjp/s13360-024-04920-x