A comparative study of different approaches for heavy quark energy loss, based on the latest experimental data

Abstract

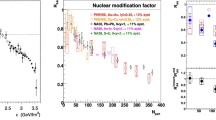
This paper examines collisional and radiative energy loss of heavy quarks in quark–gluon plasma and presents a comparative analysis of three different methods for energy dissipation. The study focuses on calculation of the nuclear modification factor ($R_{AA}$) of charm quarks in Pb–Pb collisions at $\sqrt{S_{NN}}=$ 5.02 TeV. All three methods are examined using the same numerical evolution based on the well-known Fokker–Planck equation by considering critical phenomena like a non-equilibrium state at the onset of heavy ion collisions. The outcomes of each approach are compared with the latest data from ALICE and ATLAS experiments spanning from 2018 to 2022. This study aims to compare the degree of agreement between each approach and recently obtained experimental data, in the intermediate and high $P_T$ regions.

Appendix

1.1 A: Energy loss

As mentioned before, in order to calculate drag and diffusion coefficients in the Fokker–Planck equation, we must calculate the energy loss of heavy quarks while passing through the plasma and consider both modes of energy loss through collisions and radiation. Here, we introduce three common approaches for calculating collisional energy loss and one of the most common approaches to calculating radiant energy loss.

The first calculation of collisional energy loss (Model A in our article) is proposed by Bjorken [23] which is:

$$\begin{aligned} -\frac{dE}{dx}=\frac{16\pi }{9}\alpha _s^2T^2\ln \left( \frac{4pT}{k_D^2}\right) \left[ \exp \left( -\frac{k_D}{T}\right) \left( 1+\frac{k_D}{T}\right) \right] \end{aligned}$$

(10)

P is the momentum of the particle, T is the temperature of the plasma, and $k_D = \sqrt{3} m_g$. We also have:

$$\begin{aligned} m_g^2 = \frac{4\pi \alpha _s T^2}{3}\left( 1+\frac{n_f}{6}\right) \end{aligned}$$

(11)

Another approach for calculating collisional energy loss is presented by Thoma and Gyulassy [24]. Through this approach which is our second model, we have:

$$\begin{aligned} -\frac{dE}{dx} = \frac{16\pi }{9} \alpha _s^2 T^2 \ln \left( \frac{k_{\text {max}}}{k_D}\right) \frac{1}{\nu ^2}\left[ \nu + \frac{\left( \nu ^2 - 1\right) }{2} \ln \left( \frac{1+\nu }{1-\nu }\right) \right] \end{aligned}$$

(12)

In which:

$$\begin{aligned} k_{\text {max}} \approx \frac{4pT}{\sqrt{p^2 + M^2} - p + 4T} \end{aligned}$$

(13)

Model C for collisional energy loss [26] involved calculating the energy loss of a quark with energy E in two different limits: $E \ll \frac{M^2}{T} \text { and } E \gg \frac{M^2}{T}$

A QED calculation has been used to determine contributions to the energy loss for some parts of the calculation. To achieve this, “e” in the QED calculations will be replaced by the $g_s=\frac{4}{3}\sqrt{4\pi \alpha _s}$ in the QCD calculations. The thermal photon mass $m=eT/3$ is also replaced by the thermal gluon mass which is $m_g=g_s T \sqrt{\frac{1+n_f/6}{3}}$

So for the $E \ll \frac{M^2}{T}$ limit we will have:

$$\begin{aligned} -\frac{dE}{dx} = \frac{8\pi \alpha _s^2 T^2}{3}\left( 1+\frac{n_f}{6}\right) \left[ \frac{1}{v}-\frac{1-v^2}{2v^2}\ln \left( \frac{1+v}{1-v}\right) \right] \ln \left( \frac{2^{n_f/(6+n_f)}B(v)ET}{m_g M}\right) \end{aligned}$$

(14)

B(v) is a smooth function that starts at $B(0)=0.604$, increases to $B(0.88)=0.731$, and then decreases to $B(1)=0.629$.

And in the $E \gg \frac{M^2}{T}$ limit, we have:

$$\begin{aligned} -\frac{dE}{dx} = \frac{8\pi \alpha _s^2 T^2}{3}(1+\frac{n_f}{6})\ln \left( 2^{\frac{n_f}{12+2n_f}} 0.920 \frac{\sqrt{ET}}{m_g}\right) \end{aligned}$$

(15)

A smooth connection between two limits is required for the intermediate region, E $\approx M^2/T$. Calculations indicate that we can use the first equation up to $E_{cross} = 1.8 M^2/T$ and then switch to the second one.

Also, the radiative energy loss of a heavy quark in a QGP is calculated as follows:

$$\begin{aligned} -\frac{dE}{dx}& {} = 24\alpha _s^3 \rho _{\text {QGP}} \frac{1}{\mu _g} (1-\beta _1) \left( \sqrt{\frac{1}{1-\beta _1} \ln \frac{1}{\beta _1}} - 1\right) F(\delta ) \end{aligned}$$

(16)

$$\begin{aligned} F(\delta )& {} = 2\delta - \frac{1}{2} \ln \left( \frac{1+\frac{M^2}{s}e^{2\delta }}{1+\frac{M^2}{s} e^{-2\delta }}\right) - \left( \frac{\frac{M^2}{s}\sinh (2\delta )}{1+2\frac{M^2}{s}\cosh (2\delta )+\frac{M^4}{s^2}}\right) \end{aligned}$$

(17)

$$\begin{aligned} \delta& {} = \frac{1}{2} \ln \left[ \frac{1}{1 - \beta _1} \ln \left( \frac{1}{\beta _1} \right) \left( 1 + \sqrt{1 - \frac{1 - \beta _1}{\ln (1/\beta _1)}} \right) ^2 \right] \end{aligned}$$

(18)

$$\begin{aligned} C& {} = \frac{3}{2} - \frac{M^2}{48E^2 T^2 \beta _0} \ln \left[ \frac{M^2+6ET(1+\beta _0)}{M^2+6ET(1-\beta _0)} \right] \end{aligned}$$

(19)

for more details see [27].

1.2 B: Hadronization

In order to find the $P_T$ distribution function for D meson, one can use the Peterson fragmentation function which is $D_c^D (z) = \frac{1}{{z\left( z - \frac{1}{z} + \frac{\epsilon }{{1-z}}\right) ^2}}$ [52]. Here, $z = \frac{P_D}{P_C}$ is the momentum fraction of the D meson which is fragmented from the charm quark.

We extend our calculations up to the hadronization stage for the ALICE 2022 dataset to assess the effect of hadronization on $R_{AA}$ shape. Figure 6 compares energy loss models before and after hadronization.

Fig. 6

Left panel a compares three energy loss models through $R_{AA}$ of D meson and right panel b compares these models through $R_{AA}$ of charm quark

It can be seen from Fig. 6 that the performance of the three models, in comparison to each other, remains relatively unchanged before and after hadronization. Therefore, the comparison of changes in dE/dx appears to be valid up to the pre-hadronization stage, aligning with the conventional assumption in other studies [37,38,39,40].

1.3 C: Hydrodynamic evolution equations of QGP

To consider the profile of temperature, it is important to note that we have solved the evolution equation using the Bjorken flow. Figure 7 shows the temperature profile resulting from Eq. (1).

We have constructed the hydrodynamic evolution equations of the QGP in the Milne coordinates ($\tau$,r,$\phi$,$\eta$) as Bjorken flow, where:

$$\begin{aligned} \begin{aligned} \tau = \sqrt{t^2 - z^2},&\quad \eta = \tanh ^{-1}\left( \frac{z}{t}\right) , \\ r = \sqrt{x^2 + y^2},&\quad \phi = \tan ^{-1}\left( \frac{y}{x}\right) . \end{aligned} \end{aligned}$$

(20)

in which r and $\phi$ express the transverse plane and $\eta$ is the rapidity (along the beam direction z).

According to the boost-invariance along the $\eta$, rotational and translational invariance in the transverse plane, as well as the reflection symmetry under $\eta \leftrightarrow -\eta$, the only flow due to these symmetries is $u^\mu = (u^\tau , u^x, u^y, u^\eta ) = (1, 0, 0, 0)$. This means that (r, $\phi$, $\eta$) are independent of the macroscopic physical quantities.

Considering dissipative hydrodynamics, the energy-momentum tensor can be defined as:

$$\begin{aligned} T^{\mu \nu } = \langle p^\mu p^\nu \rangle = \epsilon u^\mu u^\nu + P \Delta ^{\mu \nu } + \pi ^{\mu \nu } \end{aligned}$$

(21)

where $\epsilon$ and P are energy density and pressure, which are functions of the QGP temperature [13, 14]. Also we have $\Delta ^{\mu \nu } = g^{\mu \nu } + u^\mu u^\nu$ and $\mu ^{\mu \nu }$ is the shear stress tensor.

The evolution equations for the $\epsilon$ and $u^\mu$ are extracted through the $\partial _\mu T^{\mu \nu } = 0$ as follows:

$$\begin{aligned}{} & {} \dot{\epsilon } + (\epsilon + P)\theta + \pi ^{\mu \nu } \sigma _{\mu \nu } = 0 \end{aligned}$$

(22)

$$\begin{aligned}{} & {} (\epsilon + P) \dot{u}^\alpha + \nabla ^\alpha P + \Delta _\nu ^\alpha \partial _\mu \pi ^{\mu \nu } = 0 \end{aligned}$$

(23)

There are different expressions for the shear stress tensor. We have used the published expansion of the $\pi ^{\mu \nu }$ up to the third-order terms [13, 53, 54].

The time evolution of $\epsilon$ and $\pi$ are as follows:

$$\begin{aligned} \frac{d\epsilon }{d\tau }& {} = -\frac{1}{\tau }\left( \epsilon + P - \pi \right) \end{aligned}$$

(24)

$$\begin{aligned} \frac{d\pi }{d\tau }& {} = -\frac{\pi }{\tau _\pi } + \frac{1}{\tau }\left( \frac{4}{3}\beta _\pi - \lambda \pi - \chi \frac{\pi ^2}{\beta _\pi }\right) \end{aligned}$$

(25)

where $\beta _\pi = \frac{4P}{5}$, $\lambda = \frac{38}{21}$ and $\chi = \frac{72}{245}$ are third-order contribution coefficients of shear stress tensor expansion if we take $\epsilon = 3 P$.

Fig. 7

The profiles of temperature