Triad’s consonance and dissonance: combining roughness and compactness models

Abstract

Theories of consonance and dissonance based on the “roughness” approach are those that explain these perceptions as due to the primary beatings between harmonics. Originally proposed by Helmholtz, this approach has been very popular in the last century, being naturally associated to continuous functions of the frequency ratios, on the contrary of theories based on the “compactness” approach. In a previous work, we focused on the roughness consonance and dissonance indicators for dyads, showing the importance of including weight functions and especially secondary beatings. Here, we generalize the roughness indicators to describe the consonance and dissonance for triads. We compare our model predictions with perceptual data from a recent psychoacoustic test by means of a Chi-square analysis. The result is that roughness indicators provide a quite effective, but not fully satisfactory, description of consonance and dissonance for triads. We then study the effect of combining roughness and compactness models for triads: in this case, a very satisfactory agreement with perceptual data is achieved.

1 Introduction

The roughness approach to explain consonance and dissonance (C&D) in music was first proposed by H. Helmholtz [1] in the second part of the 19th century. His ideas of relating the perceptions of C&D to the presence of primary (or first order) beatings among the harmonics of simultaneous tones, met large favor. So large that the long-standing previous approach, based on some sort of compactness of the sound signal, either in terms of its period or its harmonic structure [2, 3], was nearly relegated to oblivion.¹ On the contrary of the compactness approach, the roughness one has the advantage of being associated with C&D indicators that are naturally continuous functions of the involved frequency ratios. The necessity of a continuous function to describe C&D had been stressed by A. Draghetti already in the late 18th century. In the first part of the 19th century F. Foderà experimentally determined a continuous curve for dyad’s C&D by means of pioneering psychoacoustic tests, and to fit his experimental curve, he introduced no less than seven rational algebraic formulae [6].

The roughness approach has been further refined in the second part of the 20th century by many studies. In particular, after the proposal of the connection with the critical bandwidth (CB) by Plomp and Levelt [7], many works followed, such as those of Hutchinson and Knopoff about dyads [8] and triads [9], those of Vos [10], Sethares [11], Purncutt and collaborators [12] and, more recently, refs. [13,14,15,16].

Focusing on dyads, in Ref. [17], we reviewed the main results of the previous literature models about C&D, for both roughness and compactness, and studied directions to improve them. In particular, we considered two directions for improving roughness models in the case of dyads: (1) introducing proper weight functions to describe the roughness suppression associated to higher harmonics with smaller amplitudes; (2) including the effect of secondary beatings, especially those of the mistuned octave and fifth intervals. The result is that roughness models reproduce the perceptual data more poorly than the compactness models in the case of dyads, but combined models with similar weights do perform very well [17, 18].

We worked out the extension of compactness models from dyads to triads in Ref. [19]: these models, when suitably extended to the continuum, turn out to account for triads perceptual data in a satisfactory way, but nevertheless seem to be incomplete. The aim of the present work is to extend roughness models from dyads to triads, and to study the effect of their combination with compactness models.

It has been stressed that roughness models for triads are not fully satisfactory, as they do not reproduce the standard expectations for the ordering of some well-known triads [20,21,22]. In order of decreasing consonance, the ordering is expected to be [22, 23]: major> minor> suspended> diminished> augmented. Roughness models instead predict diminished< augmented [9]. As a remedy, Cook [20, 21] proposed to complement the roughness approach for triads with the evaluation of quantities named tension and valence, while Ref. [22] proposed a dual-process theory that embeds roughness within tonal principles.

Here, we first refine the roughness models for triads to include the secondary beats and compare the associated predictions with psychoacoustics data: the most relevant ones for the sake of our analysis are the results of the psychoacoustic test by Bowling et al. [24], where all the 66 triads that can be formed within an octave using the just scale have been evaluated. The comparison between model predictions and observational data is carried out both by inspecting the predicted ordering of the various triads and by carrying out a chi square test. It turns out that the inclusion of secondary beats helps but does not completely solve the problem of the ordering between augmented and diminished triads. In addition, as was the case for dyads [17], roughness models for triads display a worse reduced Chi-square than compactness models [19]. This shows that, even including secondary beatings, roughness models are not fully satisfactory and call for the introduction of some other ingredient to effectively explain C&D.

We then combine our improved roughness models for triads with the compactness models for triads elaborated in Ref. [19]. The result is a systematic improvement in the reduced Chi-square, which is particularly evident when attributing equal weight to compactness and roughness, as was the case for dyads [17]. In addition, a fully satisfactory prediction for the ordering of all triads is achieved by the combined models. This shows that, also in the case of triads, roughness and compactness can together brilliantly explain the features of the perceived psychoacoustic sensations of C&D.

The paper is organized as follows. In Sect. 2, we review the results of some relevant psychoacoustic tests for triads. Section 3 reviews roughness models for dyads, together with the improvements proposed by us. In Sect. 4, we study the extension of roughness models to triads, while in Sect. 5, we explore the effect of combining roughness and compactness models. In Sect. 6, we draw our conclusions and comment on the impact of our results. The data of the psychoacoustics test by Bowling et al. [24] are displayed in Appendix 1.

2 Tests on triads

As discussed in [17], we define the C&D of two (or more) simultaneous tones according to their Greek and Latin literal meaning, that is whether the tones are perceived to mix well or not.

The most relevant psychoacoustic test for the sake of our analysis is the one conducted in 2018 by Bowling Purves and Gill [24], where all 66 triads that can be formed within an octave using the just scale and a piano timbre were considered, obtaining a score for the C&D of each triad, defined using the categories of pleasantness/unpleasantness. More comments about the methodology of this test and its results can be found in our previous work about compactness models for triads [19].

It is worth to emphasize that the test was performed with isolated (static) chords. In this case, the categories of pleasantness/unpleasantness and those of consonance/dissonance can reasonably be considered as equivalent. On the other hand, as already stressed by Galilei, Descartes and others, the distinction between these categories is an important issue in the musical language: when chords are heard in a dynamical sequence, a less consonant chord can indeed be perceived as more pleasing than a more consonant one.

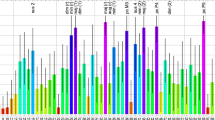
It is useful to normalize the Bowling et al. [24] test results to the range [0, 1], as done in Table 3 of Appendix 1. In such a way, C&D are complementary to unity. The normalized results are shown graphically in Fig. 1, introducing an alternative numbering for the triads of the test (upper horizontal axis), which we find more convenient than the one adopted in Ref. [24] (lower horizontal axis). In the latter triads are grouped into subgroups with the same value of $f_2/f_1$ and increasing value of $f_3/f_1$; here we rather display subgroups where $f_3/f_1$ is fixed and $f_2/f_1$ increases.

Fig. 1

Bowling et al. results [24] for the C&D of the 66 triads that can be formed within an octave using the just scale, normalized to the range [0, 1]. The error bars represent one standard deviation. The notation of most well-known triads is shown as well, see Table 3 in Appendix 1

Our numbering allows for instance to better see the trend of consonance attributed to the category with $f_3/f_1=2$, called power chords, that is triads 56-66 in our notation. The triads with a perfect fifth as largest interval, $f_3/f_1=\textrm{P5}$, are in the subgroup 16-21; they include the major and minor chords in the rest position. We can see that, apart from the power chords, the most consonant triads are in the subgroups with $f_3/f_1=$P5, M6, m6. The three most consonant triads are the major ones, in their various positions, maj (r) > maj (1) $\sim$ maj (2). Then, we find min (r)> sus (r)> min (1)> sus (1)> min (2) > dim (r) $\sim$ sus (2) > dim (1) $\sim$ dim (2)> aug .² The 38-44 subgroup is also notable, as it collects several voicings of common seventh shell chords .³

These results in general agree with and extend previous tests. In particular, this is the case for the first of the tests conducted in 1986 by Roberts [23], who assessed ⁴ the ordering maj> min> dim> aug. Another test has been conducted in 2012 by Johnson-Laird et al. [22]. In their first experiment, open position triads with a piano timbre and equal temperament were used; the answers to the test supported again the ordering maj> min> dim > aug. An interesting test has been carried out in 2014 by Rasmussen et al. [25], with the aim of comparing the consonance scores of dyads and triads, in order to show that dissonance cannot be merely seen as the result of combinatorially added roughness contributions.

3 Roughness models for dyads

It is useful to briefly review roughness models for dyads, before extending them to triads. We consider a dyad composed by two (pure or complex) tones with fundamental frequencies $f_1$ and $f_2$, with $f_2>f_1$. In case of complex tones, the spectrum is understood to be harmonic.

3.1 Primary beatings

Let assume first that $f_1$ and $f_2$ are pure tones. According to the data collected by Zwicker, Flottorp and Stevens (ZFS) [26], the CB associated to the mistuned unison is well fitted by the curve

$$\begin{aligned} b(\bar{f}) =( 0.003 \, {\bar{f}}^{1.47} + 90 ) \, \textrm{Hz} \,\,\, , \end{aligned}$$

(1)

where $\bar{f} =(f_1+f_2)/2$, and $f_1$, $f_2$ are the beating frequencies. As shown in Fig. 2, the CB is nearly constant and equal to 100 Hz in the range 100–500 Hz, and then it increases with frequency. Below middle C (that is $C_4$), even a M3 interval falls inside the CB.

Fig. 2

The solid thick curve is the CB, $b(\bar{f})$. The band associated to the maximum roughness (dashed) and the DL (dot-dashed) are also shown. The lines corresponding to the third and second (major and minor) intervals are shown for comparison

Plomp and Levelt (PL) [7] incorporated into the Helmholtz roughness approach the effect of the CB [27]. Relying on the ZFS data, PL found that the maximal roughness between two pure tones is not fixed at 33 Hz as assumed by Helmholtz, but it rather corresponds to intervals of about $25\%$of the CB, as shown in Fig. 2. PL modeled the dissonance of a dyad of pure tones by introducing a function (see Fig. 10 of Ref. [7]), to be called g(z),such that

$$\begin{aligned} d(f_1,f_2) = g(z),\,\,\,\, z= \frac{|f_1-f_2|}{b(\bar{f})}. \end{aligned}$$

(2)

The empirical curve g(z) vanishes in $z=0$,has a maximum at z = 0.25 and reaches smoothly zero at $z=1$.

Multiple parameterizations of such curve have been given by various authors [11, 12, 16], but none of them (including the PL original curve) takes into account the effect of the discrimination limen (DL), as they display a nonvanishing value for dg(z)/dz in $z=0$, which correspond to an unphysical spike. As can be seen in Fig. 2, the DL is approximately 1/30 of the CB, so that its effect has to be taken into account when $z \lesssim z_{DL}=1/30$. In order to account for the DL, as already done in refs. [17,18,19], we adopt a slight modification of the Dillon polynomial fit [16], that is

$$\begin{aligned} g(z) =0.761 \left( 1 - e^{-\frac{z^2}{0.06^2}} \right) \,\,\,\,\textrm{for}\,\,\,0 \le z \le 2 z_{DL} \,, \,\,\,g(z) = 4.906 \, z \, (1.2 -z)^4 \,\,\,\textrm{for}\,\, \,2 z_{DL} < z \le 1.2 \, , \end{aligned}$$

(3)

with $g(z) =0$ for $z > 1.2$. This function is explicitly shown in Fig. 3.

Fig. 3

The function g(z) according to PL (red), Dillon (dashed blue) and our modification to include the DL (solid blue). Left: full domain from 0 to 1. Right: zoom into the domain affected by the DL

3.2 Consonance indicators for dyads

Let us now consider complex tones for $f_1\,$ and $f_2$,in particular harmonic tones like those of musical instruments. We denote the harmonic series by $\{n_1 f_{1}\}$ and $\{n_2 f_{2}\}$, where $n_1$ and $n_2$ are integer numbers taking values from 1 up to $n_{\mathrm{{{max}}}}$.To describe the dyad’s pressure signal perceived by the ear as a function of time, let us introduce the following notation:

$$\begin{aligned} S_{f_1 f_2}(t)= s_{f_1}(t) +s_{f_2}(t), \quad s_{f_j}(t)= \sum _{n_{i}=1,2,...}^{n_{\mathrm{max}}}A^j_{n_i} \sin ( 2 \pi \, n_{i} \, f_j\, t +\theta ^j_{n_i}), \quad j=1,2 \,. \end{aligned}$$

(4)

Since the phases $\theta ^j_{n_i}$ disappear in the power spectral density, apart from specific circumstances, the ear is sensitive just to the frequencies and amplitudes that specify a particular timbre .⁵

Following the approach of Helmholtz [1], the dissonance of a dyad is obtained by adding the dissonance values due to the primary beatings between all pairs of harmonics .⁶ To describe a generic perceived timbre, we introduce weights for harmonics. The roughness dissonance indicator for the Y model is thus

$$\begin{aligned} D_Y^R (f_1,f_2)= \frac{1}{N_Y}\,\,\, {\displaystyle \sum _{n_1, n_2=1,2,...}^{n_{\mathrm{{{max}}}}} \, w^{Y}_{n_1} \,w^{Y}_{n_2} \,\, d( n_1 f_{1}, n_2 f_{2}) } \,\,\, , \end{aligned}$$

(5)

where Y is some parameter characterizing the weight function $w_n^{Y}$, and the denominator $N_Y$ is a proper normalization introduced such that $D^R_Y$ takes values in the range [0, 1]. According to the roughness approach, the consonance is thus entirely associated to the absence of roughness due to first-order beatings between all pairs of harmonics:

$$\begin{aligned} C_Y^R (f_1,f_2)=1-D_Y^R (f_1,f_2). \end{aligned}$$

(6)

The relation between the perceived timbre given by the weights in Eq. (5) and the actual timbre of the tones in Eq. (4) is unknown. Simple working hypothesis that may be formulated include taking $w_{n_i}^Y$ to be all equal, as done by PL; or rather taking $w_{n_i}^Y$ to be equal to the Fourier coefficients associated to the amplitude of the corresponding harmonics [17]. One should anyway be aware that the weight functions in Eq. (5) are of psychoacoustic type, as they encode all the processing done by the hearing system, also at neuronal level [28]. In Ref. [17], we explored various weight functions, with the property that the consonance results are stable with respect to the addition of more harmonics. We refer the interested reader to Ref. [17] for a review about the weight functions.

In the following, we discuss examples of weight functions that are suitable in the context of our analysis, where the theoretical predictions of roughness models are to be compared with the results of the psychoacoustic test of Ref. [24], obtained by using tones generated with a piano timbre. We consider for comparison two forms for the weight functions,

$$\begin{aligned} w^\alpha _n=\frac{1}{n^\alpha } \,\,\,, \,\,\, w^\beta _n=\frac{1}{\beta ^{n-1}}. \,\,\, \end{aligned}$$

(7)

They are shown in the left plot of Fig. 4 for $\alpha =1$ and $\beta =0.7$, values which are suitable to describe a spectrum extending up to $n_{\mathrm{{{max}}}}=8$; these weight functions are associated to a timbre that is respectively poorer and richer in the lowest harmonics.

The richer in lowest harmonics is the perceived timbre, the more the peaks of the consonance indicator $C^R_Y$ become sharp. This can be seen by looking at the right plot of Fig. 4: the upper (blue) and lower (green) dashed curves refer respectively to the models $C^R_\alpha$ and $C^R_\beta$, taking $\alpha =1$ ans $\beta =0.7$. The plot also shows for comparison the perceptual data (red) from the test conducted by Bowling et al. [24] about the 12 dyads that can be formed within an octave using the just scale. It can be seen that both models predict too much consonance around the peaks of the P8 and P5; this applies as well for the second octave [17].

Fig. 4

Left: The shape of the weight functions in Eq. (7), obtained taking $\alpha =1$, $\beta =0.7$ with $n_{\mathrm{{{max}}}}=8$. The choice of PL [7] is also shown for comparison. Right: Roughness models for dyads $C^R_\alpha$ and $C^R_\beta$, with $\alpha =1$ (blue) and $\beta =0.7$ (green). We take $n_{\mathrm{{{max}}}}=8$ and use the CB of ZFS. Dashed, solid and dotted lines refer respectively to $c_8=c_5=0$, $c_8=0.5$ and $c_5=0.25$, $c_8=0.7$ and $c_5=0.5$. The vertical (red) bars are the data from the test conducted by Bowling et al. [24] about the 12 dyads that can be formed within an octave using the just scale

3.3 Including secondary beatings

The problem with the too large consonance around the peaks of the P8 and P5 can be solved [17] by including secondary beatings of mistuned consonances [29], in particular those of the octave and the fifth. As discussed in Ref. [17], the inclusion can be made by adding to the dissonance associated to first-order beatings, $d(f_1,f_2)=g(z)$ of Eq. (2), also the dissonance associated to the second-order beatings, which we model by

$$\begin{aligned} d_{8}(f_1,f_2)= g(z|_{f_1 \rightarrow f_1/2}) +g(z|_{f_1 \rightarrow 2 f_1}) = g\left( \frac{|f_1/2-f_2|}{ b\left( \frac{f_1/2+f_2}{2}\right) } \right) + g\left( \frac{|2f_1-f_2|}{ b\left( \frac{2f_1+f_2}{2}\right) } \right) \end{aligned}$$

(8)

and

$$\begin{aligned} d_{5}(f_1,f_2)= g(2 z|_{f_1 \rightarrow 2/3 f_1}) +g(2 z|_{f_1 \rightarrow 3/2 f_1}) = g\left( 2 \frac{|2 f_1/3 -f_2|}{ b\left( \frac{2 f_1/3+f_2}{2}\right) } \right) + g\left( 2 \frac{|3 f_1/2-f_2|}{ b\left( \frac{3 f_1/2+f_2}{2}\right) } \right). \end{aligned}$$

(9)

Notice that, while the CB for the mistuned unison and the mistuned octave are experimentally comparable, the CB for the mistuned fifth is smaller.

As a result, the second-order beatings are associated to

$$\begin{aligned} d_{B2}(f_1,f_2)= c_8\,d_{8}(f_1,f_2) + c_5\, d_{5}(f_1,f_2), \end{aligned}$$

(10)

where $c_8$ and $c_5$ are real coefficients, to be determined experimentally. As discussed in Ref. [17], we performed a related perceptual test and found that reasonable values can be considered to be $c_8 \sim 1/2$ and $c_5 \sim 1/4$. The dissonance of complex tones can be evaluated by replacing d with $d+d_{B2}$ in Eq. (5) and properly normalizing the resulting function to the range [0, 1]:

$$\begin{aligned} D_{Y_{B2}}^R (f_1,f_2)= \frac{1}{N_Y}\,\,\, {\displaystyle \sum _{n_1, n_2=1,2,...}^{n_{\mathrm{{{max}}}}} \, w^{Y}_{n_1} \,w^{Y}_{n_2} \,\, \left( d( n_1 f_{1}, n_2 f_{2}) + d_{B2}( n_1 f_{1}, n_2 f_{2}) \right)}. \end{aligned}$$

(11)

To assess the impact of this extension, we consider the $\alpha =1$ and $\beta =0.7$ models, taking $n_{\mathrm{{{max}}}}=8$ and using the CB of ZFS. The right plot of Fig. 4 shows the predicted consonance for these models. The solid line refers to the representative values $c_8=0.5$and $c_5=0.25$;the dotted lines are obtained by taking $c_8=0.7$ and $c_5=0.5$,values which emphasize the contribution of secondary beatings. It can be seen that the dissonances around the P8 and P5 are now better accounted for.

4 Roughness models extended to triads

The simplest possibility to extend the roughness dissonance indicator to triads is to consider equal weights⁷ for the contributions associated to the three composing dyads,

$$\begin{aligned} \tilde{D}_Y^R (f_1,f_2,f_3) = D_Y^R (f_1,f_2) +D_Y^R (f_1,f_3) +D_Y^R (f_2,f_3). \end{aligned}$$

(12)

This dissonance indicator has to be normalized in a suitable way to compare the model predictions with the perceptual data.

Normalizing to the range [0, 1] the Bowling et al.[24] data about the consonance of the 66 triads that can be formed within the octave,the maximal consonance is attributed to the power chord, called cp P5 in Fig. 1. So, a suitable normalization for the dissonance indicator is

$$\begin{aligned} 1-C_Y^R (f_1,f_2,f_3)=D_Y^R (f_1,f_2,f_3)= \frac{ \tilde{D}_Y^R (f_1,f_2,f_3)- \tilde{D}_Y^R (f_1, 3/2 f_1, 2 f_1) }{\textrm{Max} (\tilde{D}_Y^R (f_1,f_2,f_3)- \tilde{D}_Y^R (f_1, 3/2 f_1, 2 f_1))} , \end{aligned}$$

(13)

where the maximum has to be taken among all the triads within one octave, that is $f_3 \le 2$. In this way, we are guaranteed that $C_Y^R (f_1,3/2 f_1, 2 f_1)=1$.

To make our computation faster, we have set $n_{\mathrm{{{max}}}}=8$. Larger values do not significantly affect the results as the contribution of such higher harmonics is minimal, adopting the $\alpha$ model with $\alpha =1$ and the $\beta$ model with $\beta = 0.7$. One might include in the dyad dissonance indicator only the unison primary beats, or also the secondary beats. In the following, we consider both cases and compare the results.

4.1 Primary beats

Considering the plane $f_2/f_1$ and $f_3/f_1$, in the upper panels of Fig. 5, we show the contour levels of the functions $C^R_\alpha$ with $\alpha =1$ (left) and $C^R_\beta$ with $\beta =0.7$ (right), including only primary beats and fixing $f_1$ to middle C. For both models, we see a large central bulk with a lot of consonance (indicated by cold colors); an even larger consonance is associated to the upper stripe where power chords lie. The dissonance region (indicated by hot colors) is relegated to the bottom, around the chromatic cluster chord, that is $(f_2/f_1,f_3/f_1)=$ (m2, M2), where unison beatings are dominant. These predictions are not satisfactory since, as well known, one should find more definite peaks of consonance, especially around triads which include P8 and P5 as composing intervals, and not such a large region of consonance.

There are slight differences between the two models. As an effect of the richer perceived timbre in the lower harmonics, the $\beta$ model predicts slightly larger dissonance regions than the $\alpha$ model.

Fig. 5

Roughness models for triads. Top (Middle and Bottom): without (with) secondary beatings

In the top panel of Fig. 6, we show the consonance predictions for the above two models: circles refer to the $\alpha =1$ model, triangles to the $\beta =0.7$ model. The results of the test by Bowling et al. [24] are superimposed for comparison (red bars). The agreement is not so satisfactory as the models fail to reproduce some features and in general they predict too much consonance. One can also see the already mentioned problem about the prediction that augmented triads are more consonant than diminished ones.

Fig. 6

Predictions for roughness models $\alpha =1$ and $\beta =0.7$. Top: considering only primary beatings. Middle and Bottom: Including secondary beatings as indicated. We consider our numbering for triads

To solve this issue, Cook [20, 21] proposed to complement the roughness approach for triads with a quantity called tension, which is by construction maximal for triads having $f_2/f_1=f_3/f_2$. This ad hoc approach does succeed in penalizing the augmented triad; however, the introduced correction does not seem to be based on physical grounds.

4.2 Adding secondary beats

We now turn to study the effect of including secondary beatings. In the middle panel of Fig. 5, the secondary beatings are added by taking the representative values $c_8=0.5$ and $c_5=0.25$. In the lower panels, the effect of further increasing these values is explored, taking $c_8=0.7$ and $c_5=0.5$. Dissonance regions are now larger and thin strips of consonance associated to triads including the P8 and P5 are now present. The agreement with perceptual data is thus expected to improve. There is not a significant difference between the middle and bottom plots, having respectively representative and extreme values for $c_8$ and $c_5$.

Notice that a sort of symmetry around the diagonal axis from the top-left to the bottom-right corner seems to appear, especially for the largest values of $c_8$ and $c_5$. We will comment about this later.

In the middle and bottom panels of Fig. 6, we show the consonance predictions for the above two models: circles refer to the $\alpha =1$ model, triangles to the $\beta =0.7$ model, now including secondary beatings with representative values $c_8=0.5$ and $c_5=0.25$ (middle) and extreme values $c_8=0.7$ and $c_5=0.5$ (bottom). The agreement is more satisfactory with secondary beatings. The ordering now has improved: it is dim (2) > aug $\sim$ dim (1) > dim (r). The fact that dim (r) is predicted to be more dissonant that the augmented triad is still however a problem of roughness models. In addition, the models still predict too much consonance without capturing the perceptual data.

This suggests that roughness models should be combined with some other ingredient. In the following, we will study the combination with compactness models.

4.3 Chi-square analysis

The reduced Chi-square is given by

$$\begin{aligned} \tilde{\chi }^2 = \frac{1}{66} \sum _{n=1,..., 66} \frac{ ( C^R_Y(n) - m(n))^2}{\sigma (n)^2} \,\,\, , \end{aligned}$$

(14)

where n stands for one of the 66 triads that can be formed within the octave using the just scale, while m(n) and $\sigma (n)$ are the normalized means and standard deviations of the test by Bowling et al. [24], and which are displayed in Table 3 of Appendix 1.

The reduced Chi-square for all these models is displayed in Table 1. The results of the Chi-square analysis confirm the previous observations. The reduced Chi-square values are satisfactory but not excellent, also considering that the test error bars are relatively large. We can see that the $\alpha =1$ model is slightly better than the $\beta =0.7$ model. In addition, we can see that it is relevant to include secondary beatings.

Table 1 Reduced Chi-square for indicated roughness models, calculated by using the 66 triads within one octave according to Bowling et al. [24]

Compactness models for triads have a better reduced chi square with respect to roughness models. For instance the values of the reduced chi square for the compactness models $C^P_1$, $C^P_3$, $C^{H}_{GP}$ are 1.16, 0.92, 0.81, respectively. These values are slightly better from those reported in Table 3 of Ref. [19], which are 1.26, 0.96, 0.81; the reason is that in Ref. [19] the reduced Chi-square was calculated before the procedure of extension to continuum. Here, we rather calculated the values after this procedure, which slightly improves the fit.

4.4 Considerations on symmetries and equally tempered triads

The upper plot of Fig. 7 shows the $C^R_\alpha$ model, with $\alpha =1$, $c_8=0.5$ and $c_5=0.25$. It can easily be seen that dim (r) is predicted to be less consonant than aug, as discussed previously. The plot shows two relevant (dashed) lines that naturally emerge when including secondary beats, those where $f_3/f_2$ is equal to a P5 and a P4. Other relevant consonance lines (not indicated) are the horizontal and vertical stripes corresponding to $f_3/f_1$ and $f_2/f_1$ equal to P5. Inside the triangular region whose contours are the three mentioned lines, a bulk of consonance is found. Inside it, there are the most common triads.

The dots displayed in the upper plot of Fig. 7 show the location of all triads formed by equally tempered tones, which are close to the just triads. As the roughness models are characterized by very smooth functions, the predictions for C&D do not differ significantly between equally tempered and just triads. This is contrary to common perception; for example, it is known that the tempered maj (r) is slightly more dissonant than its just version.

Fig. 7

Top: Roughness model $C^R_\alpha$, with $\alpha =1$, $c_8=0.5$ and $c_5=0.25$. Bottom: Compactness model $C^P_3$, as defined in Ref. [19]. Dots stand for equally tempered triads

It is interesting to establish a comparison with the predictions of compactness models, like the ones previously mentioned, whose C&D contour levels can be found in Fig. 5 of Ref. [19]. In particular, we reproduce in the bottom plot of Fig. 7 the model $C^P_3$. Consonance peaks emerge very sharply from the dissonance landscape at the locations of the just triads. In this case, most common equally tempered triads correctly feature a predicted consonance that is slightly worse with respect to just triads: similarly to the considerations in [17, 19], this is consistent with the choice of smoothing the consonance peaks with a Gaussian, whose standard deviation is identified with the DL.

Concerning the ordering maj> min> dim > aug, compactness models predict it correctly. Notice in particular that the dim (r) chord is predicted to be significantly more consonant than the aug one, as a result of its much higher fundamental bass. Compactness models have however some problematic predictions. As an example, the septimal minor third chord—which is the peak at the left of the min (r) and does not belong to the triads of the test [24]—is more consonant than the min (r) itself. Within the roughness approach instead, the septimal minor third chord is less consonant than the min (r), owing to its stronger beatings.

Compactness models have notable symmetry lines as well: they are nearly symmetric with respect to the line $f_2/f_2 +f_2/f_1 =3$. Peaks at the same distance with respect to this axis have the same fundamental bass. For instance, the symmetric of maj (r) is a 7no5 chord featuring the harmonic seventh interval, not present in the just scale; the symmetric of dim (1) is sus (2); the symmetric of sus (1) is maj7no3.

5 Combining roughness with compactness

To combine roughness and compactness models for triads, we introduce the parameter F, as we have done for dyads [17]. The expression for the consonance indicator of the combined model can thus be formulated as

$$\begin{aligned} C^{\mathrm{{{tot}}}}_{X,Y} = \frac{ F\, C^{C}_X + (1-F) \,C^R_Y}{N_{X,Y}} , \end{aligned}$$

(15)

where X and Yspecify the particular compactness and roughness models,respectively, F is the fractional contribution of compactness with respect to roughness, and $N_{X,Y}$is a normalization factor, so that $C^{\mathrm{{{tot}}}}_{X,Y}$takes values in the range [0, 1].

To provide explicit and representative examples, we focus on the combinations of three different compactness models with two roughness models, $C^R_\alpha$ and $C^R_{\alpha _{85}}$, respectively without and with secondary beatings. The selected compactness models are the two periodicity models $C^P_1$ and $C^P_3$ and the harmonicity model $C^H_{GP}$ [19]. $C^P_1$ is obtained by using the fundamental bass as an indicator, while $C^P_3$ is a generalization to triads of the Galileo-inspired model for dyads.

Fig. 8

Reduced Chi-square for combinations of compactness models with roughness model, with $\alpha =1$. Dashed $(c_8,c_5)=(0,0)$, solid $(c_8,c_5)=(0.5,0.25)$, dotted $(c_8,c_5)=(0.7,0.5)$

Similarly to Eq. (14), we calculated the reduced Chi-square for the above combined models, as a function of the parameter F. The results are shown in the panels of Fig. 8, indicating the combined models according to the notation of Eq. (15). The dashed curves represent the combinations of the three compactness models with the roughness model $C^R_\alpha$, the solid (dotted) curves stand for the combinations with $C^R_{\alpha _{85}}$, taking $c_8=0.5$ and $c_5=0.25$ ($c_8=0.7$ and $c_5=0.5$). One can see that the combined models perform better than single models, and that this holds for all combinations. The reduced Chi-square is minimized when the weights turn out to be similar, that is $F\approx 0.5$; significantly, this was the case also for the combined models for dyads [17]. The values of the reduced Chi-square obtained by taking $F=0.5$ are reported in Table 2.

Table 2 Reduced Chi-square for indicated combined models with $F=0.5$, calculated by using the 66 just triads within one octave according to Bowling et al. [24]

From the latter and Fig. 8 we can see that, although differences are marginal, the compactness model that gains most from the combination with roughness is $C^P_3$, whereas the harmonicity model $C^H_{GP}$, that was the best among compactness models, does not gain so much when combined with roughness. Again, this turned out to be the case also for dyads [17]. Notice that the data set used for the present analysis on triads [24] and the data set used in our analysis on dyads [17] have been obtained independently. All this supports the robustness of our findings, which apply for triads as well as for dyads, even using independent data sets.

Fig. 9

Combinations with $F=0.5$ and $\alpha =1$. Upper: $C^{\mathrm{{{tot}}}}_{1,\alpha }$ and $C^{\mathrm{{{tot}}}}_{1,\alpha _{85}}$, with $c_8=0.5$, $c_5=0.25$. Lower: $C^{\mathrm{{{tot}}}}_{3,\alpha _{85}}$ and $C^{\mathrm{{{tot}}}}_{GP,\alpha _{85}}$, both with $c_8=0.5$ and $c_5=0.25$. Color code as in the previous plots

We now turn to the inspection of the C&D contour levels in the plane $f_2/f_1$ and $f_3/f_1$, focusing on the previous combined models with $F=0.5$. In the upper plots of Fig. 9, we show the combinations of $C^{\mathrm{{{tot}}}}_{1,\alpha }$ and $C^{\mathrm{{{tot}}}}_{1,\alpha _{85}}$ with $c_8=0.5$, $c_5=0.25$. These two concrete examples show that, also in the combined case, the inclusion of secondary beatings helps to define the C&D structure and peaks. Notice also how the symmetric features of both roughness and compactness models, previously discussed in Sect. 4.4, are preserved in the combined models especially including secondary beatings. In the lower plots of Fig. 9, we show the combinations of $C^{\mathrm{{{tot}}}}_{3,\alpha _{85}}$ and $C^{\mathrm{{{tot}}}}_{GP,\alpha _{85}}$, taking $c_8=0.5$ and $c_5=0.25$ for both. As expected from their close value of the reduced Chi-square, these two models look very similar; the former however displays the most definite peaks.

Fig. 10

Consonance predictions for the model $C^{\mathrm{{{tot}}}}_{3,\alpha _{85}}$ with $\alpha =1$ and reference values for $c_8=0.5$ and $c_5=0.25$ and $c_8=0.7$ and $c_5=0.5$, obtained by taking $F=0.5$

In the following, we thus focus in particular on the combination $C^{\mathrm{{{tot}}}}_{3,\alpha _{85}}$ (always taking $F=0.5$, $\alpha =1$), which can be considered our best reference model among all the combined models discussed previously. In order to inspect also the dependence on the values of $c_8$ and $c_5$, in Fig. 10, we show the explicit predictions for C&D by taking $c_8=0.5$ and $c_5=0.25$ (circles), and $c_8=0.7$ and $c_5=0.5$ (triangles). First of all, one can see that the model predictions fit well the perceptual data, and that the difference between the models is not significant. Secondly, one realizes that the problem with the augmented triad is finally solved, as the predicted ordering turns out to be: dim (r)> dim (2) > dim (1) $\sim$ aug. Notice also the very large scores attributed to maj (r), maj (1) and min (r), with respect to the combined model predictions, while the predictions for all other triads essentially lie within the $1\,\sigma$ error bar. We consider this overestimate as likely due to cultural effects, as those triads are very common in Western music and might be easily identified.

Fig. 11

Combination of the roughness model with $\alpha =1$ and reference values for $c_8=0.5$ and $c_5=0.25$ with the periodicity model $C^P_3$, obtained by taking $F=0.5$

In order to provide a visual representation summarizing our findings about combined models for triads, in Fig. 11, we show a larger plot of the C&D contour levels of our representative model $C^{\mathrm{{{tot}}}}_{3,\alpha _{85}}$, (taking $F=0.5$, $\alpha =1$, $c_8=0.5$ and $c_5=0.25$). Here, the grid shows also some relevant microtonal intervals. The previously discussed symmetry lines are reported and the superimposed dots indicate the positions of the equally tempered triads. This allows for an easy estimate of the C&D difference between just and equally tempered triads. For instance, one can notice that tempered triads including a seventh, such as 7no5, maj7no5 and 7no3, are predicted as remarkably more dissonant than their closest peaks, corresponding to just triads. This is supported by common experience, as in Western music tempered seventh chords are known to introduce musical tension. The same consideration applies to tempered diminished triads, whereas the consonance of tempered major triads does not significantly differ from their just counterparts.

6 Conclusions and outlook

The goal of explaining on physical grounds the aesthetical perceptions of C&D has puzzled generations of natural philosophers, physicists, mathematicians and scientists over centuries, from Pythagoras to Galileo and Helmholtz, just to mention the most popular ones. The irresistible fascination exerted by this challenge is well expressed by one of them, F. Foderà, who declared about his own research that “although he might have been wrong in the invention of the true principle of harmony, this nevertheless had been such a highly remarkable attempt, that even in the error one would have recognized the greatness of his inventive ingenuity” [6].

The musical language originates from a wise interplay of C&D. So, researchers should first of all understand the C&D of the alphabet of the musical language, whose elements are dyads and triads; only after a successful description of an isolated (static) chord, can one turn to the issue of chords sequences (dynamics).

But, to which extent the program of rooting the musical language on mathematical expressions can be considered a realistic one? At which stage subjectiveness and creativity prevail in the choice of the sonorous material to be used in music composition? All these questions have to be raised in order to understand the potential and limit of the present and past researches about C&D. After all, the most famous composers were skilled in music theory, but not necessarily in mathematics. In addition, the musical languages of the various cultures are objectively geographically and historically different; this implies that also aspects from neurosciences are heavily involved, such as cultural exposition and musical training.

On the other hand, one has also to admit that, within the Western music culture, C&D for isolated chords are objective features. Indeed, the ordering of the C&D scores attributed to chords by (geographically and historically separated) people are essentially concordant, especially for the ratings of the more consonant and dissonant chords, see e.g. [17, 22,23,24]. It is undeniable that musically exposed or trained people might attribute a score more easily and precisely than unexposed or untrained ones. However, this does not mean that C&D are just the result of exposure or training in some musical language [31]; the idea that they might be universal perceptions⁸ is nowadays acquiring an increasing consensus, especially for roughness [32].

These considerations show the strong roots that the psychoacoustic perceptions of C&D have on Biology, that is on the functioning of the hearing system and information processing by the brain. Still, has Physics something interesting and robust to reveal about C&D? On the basis of the previous literature and our findings, we are convinced that this is the case. After all, the hearing system and the brain have to deal with some physical characteristics objectively present in the acoustic wave signal to be detected and processed, in order to discriminate sounds according to their degree of C&D. The role and the goal of Physics is precisely to understand which are the objective physical characteristics of the sound signal that (upon decoding by the ear and brain) are associated to C&D, and to describe them by using the mathematical language. Let us review and circumstantiate the findings in the Physics domain.

First of all, the approaches to C&D based on the physical characteristics called compactness and roughness—which have been pioneered respectively by Galilei (building on long-standing arguments from antiquity) and Helmholtz and later improved by many others—proved themselves to be relevant and to represent valuable directions for further explorations and insights. Secondly, by embarking ourselves along these two directions, we achieved the following results:

i) Compactness can be phrased both in terms of periodicity, that is the shortness of the period of the wave signal with respect to its components (also corresponding to the height of the fundamental bass of a chord), and equivalently in terms of harmonicity, that is the melting of the structure of the harmonics (see Ref. [17] for dyads and Ref. [19] for triads);

ii) Roughness is associated not only to first-order beatings, but also to secondary ones (see Ref. [17] for dyads and the present work for triads);

iii) For all combinations of a compactness and a roughness model, the reduced Chi-square of the equal weight combination is significantly lower than for individual models. This non trivial fact suggests that the two physical characteristics of compactness and roughness equally cooperate in accounting for the observational data (see Ref. [17] for dyads and the present work for triads).

We thus have shown that the psychoacoustic perceptions of C&D for dyads and triads can be effectively and successfully modeled by taking into account with equal weights both the compactness and the roughness properties, which objectively characterize a sound signal; and these physical characteristics are quantitatively described by means of mathematical expressions.

The combined models not only successfully explain the absolute scores and orderings of the observational data from the psychoacoustic tests [24] conducted adopting the just scale, but can be used for a full visual exploration of the C&D chords parameter space, as shown in Fig. 11, which is one of our main results. Predictions of the level of consonance for some chords not commonly used in Western music can be made, further corroborating our findings.

In our opinion, these considerations also useful to shed some light on the evolution of the empirical “rules” of the Western theory of music. With the aim of representing perfection, the Western musical language historically originated in the early centuries from the deliberate choice of selecting only the best consonances and accurately avoiding dissonances⁹ (with the constraint of having 12 notes per octave). This long period was followed by successive stages of exploration of the interplay between established consonances and ever increasing dissonances. In the last century, this exploration process led for example to the randomness of dodecaphony and to languages such as jazz where some dissonances are privileged.

Summarizing, the perceptions of C&D for isolated chords are physically rooted on the mathematically well-defined properties of compactness and roughness characterizing a sound signal, properties that can be turned into elegant equations. It is up to the artistic act of musical creation to decide how to exploit these perceptions to communicate and rise emotions on the audience. Visual representations of our results, such as the one in Fig. 11, are likely not directly useful to music composers, who already know very well their alphabet by the hearing experience; however, we think that scientifically trained musicians (or musically trained scientists) will appreciate our results as providing a complementary understanding and deeper awareness of which objective characteristics of the sound signal are relevant in the musical language.

Appendix 1: Results of the Bowling et al. test

The Bowling et al. [24] test results, normalized to the range [0, 1], are reproduced in Table 3.¹⁰ The last column shows the values of $(n,m,\ell )$, according to Eq. (5) of [19], that is $f_0=f_1/n=f_2/m=f_3/\ell$, where $f_0$ is the fundamental bass.

Table 3 Triad ratings according to Bowling et al. [24], rescaled to the range [0, 1]