Overtaking interactions in a strongly coupled inhomogeneous dusty plasma: the role of polarization force

Abstract

The nonlinear propagation of dust-acoustic waves (DAWs) is considered in a collisionless, inhomogeneous, weakly and strongly coupled dusty plasma composed of negatively charged dust, electrons, and ions. The reductive perturbation method is used to derive a Korteweg–de Vries equation (KdV). It is found that the KdV solitons are affected by the plasma parameters, whereas only rarefactive DAWs are obtained. Hirota’s bilinear approach is used to investigate the overtaking collision of two and three-soliton solutions. Physical parameters such as polarization, and the ions and electrons density gradient scale lengths have a significant impact and cause alterations in the behaviour of the solitons. Notably, as the polarization and ion density gradient scale length increase, the amplitude and width of the solitons decrease. Furthermore, the system parameters also affect the phase shifts of the solitons. The findings presented here have potential applications in the study of acoustic waves in compact astrophysical systems, where quantum polarization and inhomogeneity effects cannot be ignored, as well as in laboratory plasmas.

1 Introduction

Nonlinear dust-acoustic waves (DAWs) have received a lot of interest in an effort to better understand the properties of localized electrostatic disturbances in space and laboratory dusty plasmas [1,2,3,4]. Recent work on nonlinear DAWs has been studied theoretical [5, 6] and experimental [7, 8]. Strongly coupled plasmas may be found in jovian planets, laser heating of materials, and star interiors. The kinetic energy of the particles in the strongly coupled plasma is higher than the potential energy created by their Coulombic interaction. Laser irradiation of buried layer targets has been historically employed to produce strongly coupled plasma in the laboratory [9], preventing the target material from expanding. With simple single-layer planar targets and advances in capillary discharge laser technology [10,11,12,13], it is now possible to directly generate strongly coupled plasma on a picosecond time scale.

The coupling between particles may be shown using the coupling parameter, $\Gamma$ = $(Q^{2}e^{2}/4\pi \varepsilon _{0}aT_{\text {d}})$. Here, a stands for the distance between dust particles, $Q=Z_{\text {d}}e$, with the dust charge $Z_{\text {d}}$ and electron charge e for the charge on each dust particle with $\varepsilon _{0}$ is the vacuum permittivity, and $T_{\text {d}}$ for the dust grains’ temperature. The strongly coupled phase can be attained by raising the plasma density, lowering the plasma temperature, or raising the charge. The dust charge ranges from a few to $10^{4}$ times the elementary charge. As a result, it is easy to increase $\Gamma$ to order one or higher. The dust grains form crystalline forms for $\Gamma$ > $\Gamma _{\text {c}}$ (the crucial value) in strongly coupled dusty plasma when $\Gamma$ $>1$.

When the system is in a quasi-crystal state, the latter may accept a variety of dust lattice wave modes [14, 15], whereas the former can accommodate both longitudinal [16, 17] and transverse modes [18]. In laboratory plasmas, charged dust particles are frequently strongly coupled and can exist in either a liquid or solid phase [19]. Strongly coupled plasma is important to research because it can be used to examine the interiors of giant planets, and manufacture plasmas by compressing matter with a laser for use in industry [20]. On the other hand, a number of theoretical studies on the nonlinear propagation of dust acoustic (DA) and double layer waves in strongly coupled dusty plasmas have been conducted [21,22,23,24,25,26,27]. The reductive perturbation approach was used to make progress in understanding the nonlinear properties of DAWs that follow a collisional strongly and weakly coupled unmagnetized dusty plasma containing Boltzmann distributed electrons, ions, and negatively charged mobile dust [26, 27].

In a homogeneous plasma, the shape, amplitude, and speed of the DA solitons remain unchanged [28, 29]. In practice, plasma inhomogeneities can be caused by density [30], temperature gradients [31], or both can occur at the system’s limits. In contrast to the homogenous scenario, soliton propagation exhibits distinctive characteristics. The shape, amplitude, and speed of the soliton can be affected by the plasma inhomogeneities. These inhomogeneities may be found in abundance in equilibrium plasma states, including discharges in space and in laboratories. The influence of spatial inhomogeneity on nonlinear processes faced by a dusty plasma system has received relatively little attention in the literature [32,33,34,35,36,37,38]. The analysis of DAWs propagations in inhomogeneous dusty plasmas, taking into consideration the gradients of the plasma number density, was reported by Singh and Rao [32]. It was discovered that the amplitude of the nonlinear DAWs is proportional to $N_{{\text {d}}0}^{-1/4}$, whereas the amplitude of the linear DAWs is inversely related to the square root of the equilibrium dust density, $N_{{\text {d}}0}^{-1/2}$ [32]. Additionally, Singh and Bharuthram [39] demonstrated in case of inhomogeneity, both the nonthermal electrons and particle density have an impact on the propagation of nonlinear DAWs. Nonlinear DA solitary waves are significantly altered by the inhomogeneity brought on by nonuniform equilibrium values of particle densities, fluid velocities, and electrostatic potential. The numerical analysis showed how the plasma inhomogeneities affect the soliton’s amplitude, width, and velocity [40].

These studies are all valid only if the effects of the polarization force [41,42,43], which results from the polarization of plasma particles surrounding the dust grain, and the effective dust temperature [44,45,46], which results from the electrostatic interactions between highly negatively charged dust and from the dust thermal pressure, are minimal. However, it has been demonstrated that these effects [41,42,43,44,45,46] are crucial in a variety of space and laboratory dusty plasma settings in order to comprehend different DAWs propagation properties. In a recently published study, Mamun et al. [47] examined the impact of effective dust temperature and polarization force on the DA solitary and shock waves in a strongly coupled homogeneous dusty plasma. They demonstrated how the impacts of polarization and effective dust temperature greatly alter all of the fundamental characteristics of the DA solitary and shock waves.

Single waves interact in two different ways. The first is a head-on collision, whereas the second is an overtaking collision [48]. The head-on collision, defined as the angle between the two propagation directions of two solitary waves equals $\pi$, the two solitary waves propagating in the opposite direction, that was investigated by many researchers. The overtaking collision, defined as the angle between two propagation directions of two solitary waves equals 0 [49]. Hirota’s bilinear method (HBM) was employed to examine overtaking collisions between solitons. In fact, the HBM is a widely used algebraic method for creating N-soliton (or multi-solitons) solutions to integrable nonlinear evolution equations like the Korteweg-de Vries (KdV) equation [50,51,52,53]. Phase changes in solitons upon collision as well as the merging amplitude of two solitons were presented. The overtaking collision was investigated by several researchers in various plasma media [54,55,56,57,58,59,60,61]. The phase shift resulting from the ion-acoustic multi-solitons’ overtaking collision was determined by Roy et al. [55]. The overtaking collision of electrostatic N-solitons in electron–hole quantum plasmas was studied by El-Shamy and Mahmoud [56]. In an ultrarelativistic degenerate dense magnetoplasma, overtaking collisions of oblique isothermal ion-acoustic multi-solitons were investigated. The HBM was used to examine the oblique isothermal ion-acoustic multi-soliton overtaking collisions [57]. The exchange of energy brought on by overtaking collisions is influenced by physical factors [58].

Many researchers [54, 59,60,61] expanded their studies of the overtaking collision to include the collision of dust-acoustic solitary waves. A theoretical investigation has been made into the interaction of two dust-acoustic solitary waves (DASWs) in a three-dimensional magnetized dusty plasma. The overtaking collision and phase changes in N-solitons of DASWs in dusty plasmas were investigated by Mandal et al. [59]. They discovered that the larger soliton moves more quickly towards the smaller ones, and overtaking collision occures. Both solitons return to their initial shapes and speeds after collision. Consequently, the purpose of the current work is to investigate the impacts of polarization and inhomogenity on the overtaking collision of N-soliton. Moreover, this work is relevant for compact objects such as white dwarfs and neutron stars where polarization plays a significant rule.

The paper is structured as follows. Section 2 gives the model equations. Section 3 presents the nonlinear analysis (i.e. the KdV equation). In Sect. 4, HBM is used to obtain N-soliton solutions. In Sect. 5, we discuss the numerical results. The conclusions are presented in Sect. 6.

2 Basic equations of the model

We take into account the weakly inhomogeneous and strongly coupled dusty plasma composed of negatively charged dust, electrons, and ions [62]. As a result, when all that is in equilibrium, $n_{i0}=Z_{{\text {d}}}n_{{\text {d}}0}+n_{{\text {e}}0}$, where $n_{{\text {d}}0}$, $n_{{\text {e}}0}$, and $n_{{\text {i}}0}$ are the equilibrium dust, electron, and ion number density, respectively. It is assumed that the dusty plasma has a density gradient in the x-direction. Because of their higher temperatures and lower electric charges, electrons and ions are assumed to be weakly coupled, whereas dust particles are assumed to be strongly coupled due to their lower temperature and greater electric charge. The electrons and ions number densities that follow the Maxwellian distribution in the presence of low phase velocity DAWs, and their densities $n_{{\text {e}}}$ and $n_{{\text {i}}}$ are, respectively, given by

$$\begin{aligned} n_{{\text {e}}}\left( x\right)&=n_{{\text {e}}0}\left( x\right) \exp \left[ \frac{e\psi }{T_{{\text {e}}}}\right] , \end{aligned}$$

(1)

$$\begin{aligned} n_{{\text {i}}}\left( x\right)&=n_{i0}\left( x\right) \exp \left[ -\frac{e\psi }{T_{{\text {i}}}}\right] , \end{aligned}$$

(2)

where $T_{{\text {e}}}$ ($T_{{\text {i}}}$) is the electron (ion) temperature. According to other research [40, 63], it is assumed that the electron and ion equilibrium densities have the following forms: $n_{{\text {i}}\left( {\text {e}}\right) 0}\left( x\right) =n_{i\left( {\text {e}}\right) 0}\left( 0\right) \exp \left[ -s_{{\text {i}}\left( {\text {e}}\right) }x/L\right]$, where L denotes the density scale and is considered to be 200 of normalized length [64]. The density gradient scale length in this case, $s_{{\text {i}}\left( {\text {e}}\right) }$ for the ions (electrons). For a simple representation, we will write $n_{{\text {i}}\left( {\text {e}}\right) 0}\$instead of $n_{{\text {i}}\left( {\text {e}}\right) 0}\left( 0\right)$.

Additionally, we take into account the polarization force ($\textbf{F}_{\text {p}}$), which results from the interaction of thermal ions with strongly negatively charged dust particles. This effect, mathematically, is defined as $\textbf{F}_{\text {p}}=-Z_{\text {d}}eR\left( n_{\text {i}}/n_{{\text {i}}0}\right) ^{1/2}\bigtriangledown \psi$ [41,42,43], where $R=e^{2}Z_{\text {d}}/4T_{\text {i}}\lambda _{\text {Di}0}$ is a parameter determining the effect of polarization force, $\psi$ being the electrostatic potential, and $\lambda _{Di0}$ is the equilibrium ion Debye radius.

The polarization of plasma ions around the dust grain is the primary cause of the polarization force in the dusty plasma with substantially negatively charged dusts. The component R may be expressed as $R=\beta _{T}/4$ [43] where $\beta _{T}$ is the ratio of the Coulomb radius of contact between thermal ions and the dust grain. This is important to keep in mind when considering the limit $T_{\text {e}}\gg T_{\text {i}}$. This factor is taken into account in our dusty plasma model, with a range of $0<R<1$, which is in line with the actual experimental data. As grain size rises, the impact of polarization becomes increasingly significant since the grain charge is roughly proportional to grain radius. The following well-known generalized hydrodynamic equations control the dynamics of the nonlinear DAWs in such strongly coupled dusty plasma [65, 66]

$$\begin{aligned}{} & {} \partial _{t}n_{d}+\partial _{x}\left( n_{d}\textbf{u}_{d}\right) =0, \end{aligned}$$

(3)

$$\begin{aligned}{} & {} D_{\tau }\left[ m_{d}n_{d}D_{t}\textbf{u}_{d}-Z_{d}en_{d}\frac{\partial \psi }{\partial x}+Z_{d}en_{d}R\left( \frac{n_{i}}{n_{i0}}\right) ^{1/2} \frac{\partial \psi }{\partial x}+T_{ef}\frac{\partial n_{d}}{\partial x}\right] =0, \end{aligned}$$

(4)

$$\begin{aligned}{} & {} \frac{\partial ^{2}\psi }{\partial x^{2}}=4\pi e\left[ n_{e}-n_{i}+Z_{d} n_{d}\right] , \end{aligned}$$

(5)

where $u_{d}$ is the dust fluid velocity, $n_{d}$ is the dust number density, x (t) space (time) variable, $m_{d}$ is the dust grain mass,

$D_{t}=1+\tau _{m}\partial /\partial t+u_{d}\partial /\partial x$, $\tau _{m}$ is the viscoelastic relaxation time. Here, $T_{ef}=\left( \mu _{d}T_{d}+T_{*}\right)$ is the effective dust-temperature consisting of two parts: one ($\mu _{d}T_{d}$) arising from dust thermal pressure and another $\left( T_{*}\right)$ coming from the repelling force of similarly charged dust grains, $\mu _{d}$ is the compressibility. The Yukawa coupling energy between a particle and its closest neighbours is a good approximation for the crystalline term $T_{*}$. These have received a lot of literature-based discussion [65,66,67,68,69]. The compressibility $\mu _{d}$ and the viscoelastic relaxation time $\tau _{m}$ are provided by [66, 68, 44, 45].

$$\begin{aligned} \tau _{m}= & {} \frac{\eta _{1}}{n_{d0}T_{d}}\left[ 1-\mu _{d}+\frac{4}{15}u\left( \Gamma \right) \right] ^{-1}, \end{aligned}$$

(6)

$$\begin{aligned} \mu _{d}= & {} 1+\frac{1}{3}u\left( \Gamma \right) +\frac{\Gamma }{9}\frac{\partial u\left( \Gamma \right) }{\partial \Gamma }. \end{aligned}$$

(7)

Here, the excess internal energy of the system is measured by $u\left( \Gamma \right)$, which is estimated for weakly coupled plasmas ($\Gamma <1$) as $u\left( \Gamma \right) \simeq -\sqrt{3/2}\Gamma ^{3/2}$ [66, 69]. Slattery et al.’s relation [67] for $u\left( \Gamma \right)$ for a range of $1<\Gamma <100$, $u\left( \Gamma \right) =-0.89\Gamma +0.95\Gamma ^{1/4}+0.19\Gamma ^{-1/4}-0.81$, where a minor correction term owing to finite number of particles is omitted, that was analytically determined. The other transport coefficient’s reliance $\eta _{1}$ on $\Gamma$ is a bit more complicated, and therefore cannot be given in a closed analytical form. However, there are several statistical models and tabular graphical findings of their functional behaviour resulting from molecular dynamic simulations accessible in the literature [65].

3 KDV equation and solitary waves

We employ the reductive perturbation approach, which calls for the expansion of dependent variables like density, velocity, and potential about their equilibrium values in a small parameter, $\epsilon$ to discover the potential modes and develop a dynamical equation for the propagation of DA solitary waves. The degree of the disturbance is determined by the size of $\epsilon$, and smaller values of $\epsilon$ suggest that the physical quantity changes more quickly than those on which larger values of $\epsilon$ are present. We therefore asymptotically extend the perturbed variables $n_{d}$, $u_{d}$, and $\psi$ in powers series of approximately their equilibrium values as

$$\begin{aligned} n_{d}&=n_{d0}\left( x\right) +\epsilon n_{d1}\left( x,t\right) +\epsilon ^{2}n_{d2}\left( x,t\right) ,\nonumber \\ u_{d}&=u_{d0}\left( x\right) +\epsilon u_{d1}\left( x,t\right) +\epsilon ^{2}u_{d2}\left( x,t\right) ,\nonumber \\ \psi&=\psi _{0}\left( x\right) +\epsilon \psi _{1}\left( x,t\right) +\epsilon ^{2}\psi _{2}\left( x,t\right) . \end{aligned}$$

(8)

The aforementioned equations demonstrate that the disturbed quantities are functions of both space and time while the unperturbed values are simply functions of space coordinates. In a spatially inhomogeneous plasma, the independent variables are stretched as [32]

$$\begin{aligned} X=\epsilon ^{\frac{1}{2}}\left( \int _{0}^{x}\frac{\text {d}x}{v\left( x\right) }-t\right) ,\ \ \ \ \ \ \ \ T=\epsilon ^{\frac{3}{2}}t. \end{aligned}$$

(9)

It is possible to determine the unaltered densities that satisfy the neutrality criterion using the quantities v, the phase velocity, and $n_{d0}\left( x\right)$:

$$\begin{aligned} Z_{d}n_{d0}\left( x\right) +n_{e0}\left( x\right) -n_{i0}\left( x\right) =0. \end{aligned}$$

(10)

The zero-order values are exclusively a function of space due to the inhomogeneity of the plasma through space. Substitute Eqs. (8) and (9) into (1–5) and collecting the terms in the different powers of $\epsilon$, to the lowest order in $\epsilon$, we obtain the following phase velocity

$$\begin{aligned} v=u_{d0}\pm \sqrt{\gamma _{*}+\left( 1-R\right) \frac{\left( 1-\alpha \right) }{\left( 1+\alpha \sigma \right) },} \end{aligned}$$

(11)

where $\gamma _{*}=T_{ef}/Z_{d0}T_{i}$, $\alpha =n_{e0}/n_{i0}$ and $\sigma =T_{i}/T_{e}$. Equation (11) demonstrates that two types of waves, fast and slow waves, with phase velocities of $v_{f}$ and $v_{s}$, respectively, may be feasible in such  dusty plasma. It is clear that the R, or polarization force, enhances the phase velocity of the slow mode, and $T_{ef}$, or effective temperature, also increases it. This is fairly consistent with the outcome in Ref. [47]. The rise in phase velocity with dust temperature is also consistent with findings by Singh and Rao [32] for an inhomogeneous dusty plasma without electrostatic interaction between strongly negatively charged dust grains and the ions through polarization force $\textbf{F}_{p}$.

We constructed the pertinent KdV equation for the current dusty plasma in order to examine the rapid and slow single wave propagation. The equations in the second-order perturbed quantities are first obtained in order to perform that. We employ a variety of relationships between zeroth and first-order quantities as well as phase velocity relations to remove the second-order disturbed quantites, and then we follow the steps in ref. [70] to derive the KdV equation shown as follows:

$$\begin{aligned}{} & {} \frac{\partial \psi _{1}}{\partial T}+A\psi _{1}\frac{\partial \psi _{1}}{\partial X}+B\frac{\partial ^{3}\psi _{1}}{\partial X^{3}}=0, \end{aligned}$$

(12)

$$\begin{aligned}{} & {} A=\frac{a_{2}}{n_{d0}va_{1}},B=\frac{a_{3}}{a_{1}}, \end{aligned}$$

(13)

where

$$\begin{aligned} a_{1}&=Z_{d}en_{d0}v\left( 2+\frac{u_{d0}}{v-u_{d0}}\right) \left( R-1-\frac{1+\alpha \sigma }{1-\alpha }\gamma _{*}\right) -\frac{m_{d}n_{d0} }{T_{i}}evu_{d0}\left( v-u_{d0}\right) \frac{1+\alpha \sigma }{1-\alpha },\\ a_{2}&=\frac{Z_{d}e^{2}n_{d0}}{T_{i}}\left( 1-R\right) \left( \frac{1-\alpha \sigma ^{2}}{1+\alpha \sigma }+\frac{3\left( 1+\alpha \sigma \right) }{1-\alpha }\right) -\frac{Z_{d}e^{2}Rn_{d0}}{2T_{i}} +\frac{Z_{d}e^{2}n_{d0}}{T_{i}}\frac{\left( 1+\alpha \sigma \right) ^{2} }{1-\alpha }\left( 2\gamma _{*}-u_{d0}\left( v-u_{d0}\right) \right) ,\\ a_{3}&=\frac{T_{i}\left( 1-\alpha \right) \left( 1-R\right) }{4\pi ev^{2}\left( 1+\alpha \sigma \right) }. \end{aligned}$$

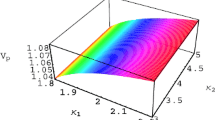
The plasma space is the major determinant of coefficients A and B. Figure 1a depicts that the nonlinearity increases as R increases and decreases as dust effective temperature increases. This is physically attributed to the inertia provided by the mass density of the dust species, where as its temperature increases or it becomes strongly coupled, these lead to sustained waves with higher amplitude. Figure 1b shows that when density gradient scale length associated with the ions increases or that for electrons decreases it leads to an increase in the nonlinearity through increasing of A. As a result of this explanation, $n_{i0}\left( x\right)$ decreases as x/L or $s_{i}$ increase.

Accordingly, as dust density decreases leads to decreasing inertia. This sustains waves with lower amplitude and width. While increasing of $s_{e}$ leads to increasing of dust density that leads to increasing inertia and decreasing nonlinearity. The dispersive term also decreases as dust’s effective temperature and density ( associated with larger $s_{e}$) increase or as dust becomes strongly coupled. While it increases as $s_{i}$ and R increase as depicted in Figs. 1c, d.

The KdV equation’s stationary solution is obtained by transforming the independent variables X and T to $\chi =\left( X-\lambda T\right)$, where $\lambda$ is the frame velocity travels perpendicular to the wave. The stationary solitonic solution is thus deduced to be [4, 61].

$$\begin{aligned} \psi _{1}=\psi _{m}{\text {sech}}^{2}\left( \frac{\chi }{\Delta }\right) , \end{aligned}$$

(14)

which presents DASWs of amplitude $\psi _{m}$ $=3\lambda /A$ and width $\Delta =\sqrt{4B/\lambda }$ [49, 50].

Figure 2 examines how coupling, polarization, ions,and electrons density gradients affect the properties of DAWs. It has been found that the amplitude and width of DA solitons decreases as $s_{i}$, and R increase or as $s_{e}$, and $\gamma _{*}$ decrease. This attributed to the effect of these parameters on the nonlinear and dispersive terms as shown in Fig. 1.

Fig. 1

The variation of a the nonlinear term, A, represented by Eq. (13), against R for different values of $\gamma _{*}$ at $s_{i}$ $=s_{e}=0.4$, b A against $s_{e}$ for different values of $s_{i}$ at $\gamma _{*}=0.7$, and $R=0.3$, c the dispersive term, B represented by Eq. (13), against R for different values of $\gamma _{*}$ at $s_{i}$ $=s_{e}=0.4$, d B against $s_{e}$ for different values of $s_{i}$ at $\gamma _{*}=0.4$, and $R=0.3$, for $n_{_{e0}}=4\times 10^{7}$, $n_{_{i0}}=7\times 10^{7}$, $T_{i} =0.3$, $Z_{_{d}}=3\times 10^{3}$, $\sigma =0.3$, $x/L=2$

Fig. 2

The variation of the potential, $\psi _{1}$, represented by Eq. (14) against $\chi$ for $n_{_{e0}}=4\times 10^{7}$, $n_{_{i0}}=7\times 10^{7}$, $T_{i}=0.3$, $Z_{_{d} }=3\times 10^{3}$,$\sigma =0.7$, and $u_{d0}=0.8$ a for different values of $\gamma _{*}$ at $R=0.3$, $x/L=0$ b for different values of R at $\gamma _{*}=0.7$, $x/L=0$ c for different values of $s_{i}$ at $s_{e} =0.4$, $\gamma _{*}=0.7$, $R=0.3$, $x/L=2$ d for different values of $s_{e}$ at $s_{i}=0.1$, $\gamma _{*}=0.7$, $R=0.3$, $x/L=2$

4 N-Soliton collision

The HBM [61] is used in this part to find multi-solitons solutions. To do this, the variables are adjusted to be $\tau \longrightarrow t$, $\zeta \longrightarrow xB^{\frac{1}{3}}$ and $B_{z}^{(1)}\longrightarrow 6\psi B^{\frac{1}{3}}/A$.

$$\begin{aligned} \frac{\partial \psi }{\partial t}+6\psi \frac{\partial \psi }{\partial x} +\frac{\partial ^{3}\psi }{\partial x^{3}}=0. \end{aligned}$$

(15)

The two-soliton and three-soliton solutions must be taken into account while researching overtaking collisions between N-solitons. In order to add the transformation $\psi =2(\log \Psi )_{xx}$ to Eq. (15), the HBM method is used. Then, [59, 61] may be used to represent the bilinear feature of Eq. (15) as.

$$\begin{aligned} \Psi \Psi _{xt}-\Psi _{x}\Psi _{t}+\Psi \Psi _{xxxx}-4\Psi _{x}\Psi _{xxx}+3\Psi _{xx}^{2}=0. \end{aligned}$$

(16)

Using the Hirota-D operator, we may get the following results [50, 71]

$$\begin{aligned}{} & {} D_{x}D_{t}\left[ \Psi .\Psi \right] =2\left( \Psi \Psi _{xt}-\Psi _{x}\Psi _{t}\right) , \end{aligned}$$

(17)

$$\begin{aligned}{} & {} D_{x}^{4}\left[ \Psi .\Psi \right] =2\left( \Psi \Psi _{xxxx}-4\Psi _{x} \Psi _{xxx}+3\Psi _{xx}^{2}\right) . \end{aligned}$$

(18)

Equations (17) and (18) are substituted into equation (16) to provide the following result

$$\begin{aligned} D_{x}\left( D_{t}+D_{x}^{3}\right) \left[ \Psi .\Psi \right] =0. \end{aligned}$$

(19)

Two DA solutions are built using the HBM, and the expression $\Psi$ is enlarged in terms of $\epsilon$ as $\Psi =1+\epsilon \Psi _{1}+\epsilon ^{2} \Psi _{2}+...$ where $\Psi _{1}=e^{\theta _{1}}+e^{\theta _{2}}$, $\theta _{1,2}=R_{1,2}x+\omega _{1,2}t+\gamma _{1,2}$. In order to formulate the linear dispersion relation as $\omega _{1,2}=-R_{1,2}^{3}$, where $\gamma _{1,2}$ is a constant capable of offsetting the impact of $\epsilon$, and $\Psi _{2} =\rho _{_{12}}e^{\theta _{1}+\theta _{2}}$ we then replace the resultant term, $\Psi$, into Eq. (19). The phase changes following the overtaking collision may be calculated using the formula $\rho _{_{12}}=\left( R_{1}-R_{2}\right) ^{2}/\left( R_{1}+R_{2}\right) ^{2}$. Thus, by taking $\epsilon =1$ into account, we can write down the two DA solutions of Eq. (15) as follows:

$$\begin{aligned} \psi =2\frac{R_{1}^{2}e^{\theta _{1}}+R_{2}^{2}e^{\theta _{2}}+\rho _{_{12} }e^{\theta _{1}+\theta _{2}}\left( R_{2}^{2}e^{\theta _{1}}+R_{1}^{2} e^{\theta _{2}}\right) +2\left( R_{1}-R_{2}\right) ^{2}e^{\theta _{1} +\theta _{2}}}{\left( 1+e^{\theta _{1}}+e^{\theta _{2}}+\rho _{_{12}} e^{\theta _{1}+\theta _{2}}\right) ^{2}}. \end{aligned}$$

(20)

The two DA solitons of equation (12) have the following solution:

$$\begin{aligned} \varphi ^{(1)}=\frac{12B^{\frac{1}{3}}}{A}\left[ \frac{R_{1}^{2}e^{\Theta _{1} }+R_{2}^{2}e^{\Theta _{2}}+\rho _{_{12}}e^{\Theta _{1}+\Theta _{2}}\left( R_{2}^{2}e^{\Theta _{1}}+R_{1}^{2}e^{\Theta _{2}}\right) +2\left( R_{1} -R_{2}\right) ^{2}e^{\Theta _{1}+\Theta _{2}}}{\left( 1+e^{\Theta _{1} }+e^{\Theta _{2}}+\rho _{_{12}}e^{\Theta _{1}+\Theta _{2}}\right) ^{2}}\right] , \end{aligned}$$

(21)

$\Theta _{1,2}=\frac{R_{1,2}}{B^{\frac{1}{3}}}\zeta +\omega _{1,2}\tau +\gamma _{1,2}$ is an expression incorporates the linear dispersion relation $\omega _{1,2}$. The terms $e^{-\left( \Theta _{1}+\Theta _{2}\right) }$, $e^{-\left( 2\Theta _{1}+\Theta _{2}\right) }$ and $e^{-\left( \Theta _{1}+2\Theta _{2}\right) }$ for the condition, $\tau$ $\gg 1$ are non-dominant and could be disregarded. In order to create a superposition, the two-DA solution, Eq. (22), combine two single-DA solitons [72].

$$\begin{aligned} \varphi ^{(1)}=\frac{12B^{\frac{1}{3}}}{A}\left( \frac{\rho _{_{12}}R_{1} ^{2}e^{-\Theta _{1}}}{\left( e^{-\Theta _{1}}+\rho _{_{12}}\right) ^{2}} +\frac{\rho _{_{12}}R_{2}^{2}e^{-\Theta _{2}}}{\left( e^{-\Theta _{2}} +\rho _{_{12}}\right) ^{2}}\right) . \end{aligned}$$

(22)

We can obtain the asymptotic solution of Eq. (12) as a two-soliton solution superposition as

$$\begin{aligned} \varphi ^{(1)}\approx \frac{6B^{\frac{1}{3}}}{A}\left[ \frac{R_{1}^{2}}{2}{\text {sech}}^{2}\left( \frac{R_{1}}{2B^{\frac{1}{3}}}\left( \zeta -B^{\frac{1}{3}}R_{1}^{2}\tau +\Delta _{1}\right) \right) +\frac{R_{2}^{2}}{2}{\text {sech}}^{2}\left( \frac{R_{2}}{2B^{\frac{1}{3}} }\left( \zeta -B^{\frac{1}{3}}R_{2}^{2}\tau +\Delta _{2}\right) \right) \right] . \end{aligned}$$

(23)

Following collisions between two single DA solitons cause phase changes that can be described by $\Delta _{1,2}=\pm \frac{2B^{\frac{1}{3}}}{R_{1,2}} \ln \left| \sqrt{\rho _{_{12}}}\right|$. We can modify two identically moving single DA solitons in accordance with Eq. (23). To analyse the overtaking collision of three DA solitons, similar methods can be used. The nonlinear three-soliton solution of Eq. (12) has the following formula:

$$\begin{aligned} \varphi ^{(1)}=1+e^{\Theta _{1}}+e^{\Theta _{2}}+e^{\Theta _{3}}+\eta _{12} ^{2}e^{\Theta _{1}+\Theta _{2}}+\eta _{23}^{2}e^{\Theta _{2}+\Theta _{3}}+\eta _{31}^{2}e^{\Theta _{3}+\Theta _{1}}+\eta _{123}^{2}e^{\Theta _{1}+\Theta _{2}+\Theta _{3}}, \end{aligned}$$

(24)

where $\eta _{12}^{2}=\left( R_{1}-R_{2}\right) ^{2}/\left( R_{1} +R_{2}\right) ^{2},\eta _{23}^{2}=\left( R_{2}-R_{3}\right) ^{2}/\left( R_{2}+R_{3}\right) ^{2},\eta _{31}^{2}=\left( R_{3}-R_{1}\right) ^{2}/\left( R_{3}+R_{1}\right) ^{2},\eta _{123}^{2}=\eta _{12}^{2}\eta _{23}^{2}\eta _{31}^{2}$ and $\Theta _{1,2,3}=\frac{R_{1,2,3}}{B^{\frac{1}{3}} }\zeta -R_{1,2,3}^{3}\tau +\gamma _{1,2,3}$. For $\tau$ $\gg 1$ the solution of Eq. (12) is simplified into a three-soliton solution superposed as

$$\begin{aligned} \varphi ^{(1)}\approx \sum _{i=1}^{3}\frac{3B^{\frac{1}{3}}R_{i}}{A} {\text {sech}}^{2}\left[ \frac{R_{i}}{2B^{\frac{1}{3}}}\left( \zeta -B^{\frac{1}{3}}R_{i}^{2}\tau +\Gamma _{i}\right) \right] , \end{aligned}$$

(25)

where the amplitude is $3B^{\frac{1}{3}}R_{i}/A$ and the phase changes brought on by three single DA solitons colliding with each other are $\Gamma _{1} =\pm \frac{2B^{\frac{1}{3}}}{R_{1}}\ln \left| \eta _{123}/\eta _{23} \right|$, $\Gamma _{2}=\pm \frac{2B^{\frac{1}{3}}}{R_{2}}\ln \left| \eta _{123}/\eta _{31}\right|$, $\Gamma _{3}=\pm \frac{2B^{\frac{1}{3}} }{R_{3}}\ln \left| \eta _{123}/\eta _{12}\right|$. Three distinct DA solitons are travelling in the same direction, as shown by Equation (25). Additionally, in (23) and (25), the wave numbers $R_{1}$, $R_{2}$, and $R_{3}$ stand for the wave numbers that defined the linear dispersion relation, polarity, and amplitude of the two and three DA solitons.

5 Results and Discussion

The overtaking collisions of two and three single DA solitons are investigated in the current work using the well-proven HBM method in a weakly inhomogeneous and strongly coupled dusty plasma consisting of negatively charged dust, electrons, and ions. We have studied the effects of polarization force on dust-acoustic solitary waves in a strongly coupled inhomogeneous dusty plasma. This study demonstrates that these effects, along with the inhomogeneity of dust grains, are responsible for the DASWs properties. The physical properties of the DA solitons during overtaking collision events are carefully examined. Then, the dynamical process involved in the collision of two and three single DA solitons that propagate in the same direction is numerically simulated. The following lines summarise our results and recommendations:

• 1. Our investigation has explored the influence of $s_{i}$, $s_{e}$, $\gamma _{*}$, and R on the nonlinear and disprtsive terms, and the results are presented in Figs. 1. The analysis revealed that A is negative in this plasma system. The negative values of A result in the formation of rarefactive DA solitons. It has been established that the nonlinearity increases as $s_{i}$, and R increase, while it decrease as $s_{e}$, and $\gamma _{*}$ increase. The dispersive term also increases as $\gamma _{*}$, $s_{e}$, and R increase, while it decreases as $s_{i}$ increases.

• 2. The DASWs can carry more energy as $s_{e}$, and $\gamma _{*}$ increase where these solitons become longer, while they become smaller as $s_{i}$, and R increase in case of slow mode.

• 3. An energy exchange between the N-solitons takes place during the overtaking collisions, causing phase changes in their trajectories. Our examination of the DA solitons’ overtaking collision dynamics has been expanded to look at how the system parameters $s_{i}$, $s_{e}$, $\gamma _{*}$, and R affect the variation of the resulting solitons’ phase shifts, $\Delta _{1,2}$, as illustrated in Figs. 3a–d. Our analysis has revealed that both phase shifts increase as $s_{i}$, and R increase, while they decrease as $\gamma _{*}$, and $s_{e}$, increase. This result can be attributed to the dependence of both phase shifts on the dispersive term, B, which is influenced by these parameters.

• 4. The temporal dynamics of two rarefactive solitons are depicted in Figs. 4 and 5 are against varying time values, $\tau$, while taking into account the impacts of R, and $s_{i}$ change, respectively. For $\tau =-4$, the smaller, slower amplitude soliton comes before the bigger, quicker soliton. The two solitons combine to form one soliton with an amplitude that is smaller than the sum of the amplitudes of the two single soliton as time rises to $\tau =0.4$. The lower amplitude soliton falls behind the bigger amplitude one when they diverge at $\tau =4$.

• 5. Also Figs. 4 and 5 depict that as R, and $s_{i}$ increase, the amplitude of the two solitons decreases, and the distance between them decreases (increases) on the $\zeta$ scale for $\tau =4$ ($\tau =-4$). In our plasma model, some physical explanation should be achieved. To gain a physical insight into the observed behaviour, we note that the numerical values of both the nonlinear and dispersive terms play a critical role in determining the phase shifts and amplitudes of the two solitons as described in Eq. (23). The nonlinear term, A, becomes dominant since B is raised to the power of 1/3, which depends on R, and $s_{i}\$as mentioned in Eq. (13). We further observe that solitons with larger amplitudes exhibit larger phase shifts, which is consistent with prior findings [61, 73].

• 6. The current work shows how to evaluate the overtaking collisions of three nonlinear solitons versus space over time and for a range of R, and $s_{i}$ values. It is also investigating how these characteristics affect the phase shifts brought on by DA multi-solitons overtaking one another in collisions. The three solitons are initially far away, then they gradually get closer to one another. The three solitons will ultimately return to their original forms as shown in Figs. 6 and 7, with different phase shifts, as predicted by Hirota [50].

Fig. 3

The variation of the solitons phase shifts, for $n_{_{e0}}=4\times 10^{7}$, $n_{_{i0}}=7\times 10^{7}$, $T_{i}=0.3$, $Z_{_{d}}=3\times 10^{3}$,$\sigma =0.7$, and $u_{d0}=0.8$ a $\Delta _{1} =\frac{2B^{\frac{1}{3}}}{R_{1}}\ln \left| \sqrt{\rho _{_{12}}}\right|$against R for different values of $\gamma _{*}$ at $s_{i}=0.4$, $s_{e}=0.4$, b $\Delta _{1}$ against $s_{e}$ for different values of $s_{i}$ at $\gamma _{*}=0.7$, and $R=0.3$ c $\Delta _{2}=\frac{2B^{\frac{1}{3}} }{R_{2}}\ln \left| \sqrt{\rho _{_{12}}}\right|$ gainst R for different values of $\gamma _{*}$ at $s_{i}=0.4$, $s_{e}=0.4$, d $\Delta _{2}$ against $s_{e}$ for different values of $s_{i}$ at $\gamma _{*}=0.7$, and $R=0.3$

Fig. 4

The overtaking collision profiles represented by Eq. (23) at different values of the time between two nonlinear DA solitons for two values of R at $s_{i} =0.4$, $n_{_{e0}}=4\times 10^{7}$, $n_{_{i0}}=7\times 10^{7}$, $T_{i}=0.3$, $Z_{_{d}}=3\times 10^{3}$, $\sigma =0.7$, $\gamma _{*}=0.7$, $s_{e}=0.4$, $u_{d0}=0.8$ and $x/L=2$

Fig. 5

The overtaking collision profiles represented by Eq. (23) at different time intervals between two nonlinear DA solitons for two values of $s_{i}$ at $R=0.3$, $n_{_{e0} }=4\times 10^{7}$, $n_{_{i0}}=7\times 10^{7}$, $T_{i}=0.3$, $Z_{_{d}} =3\times 10^{3}$, $\sigma =0.7$, $\gamma _{*}=0.7$, $s_{e}=0.4$, $u_{d0}=0.8$ and $x/L=2$

Fig. 6

The overtaking collision profiles represented by Eq. (25) at different values of the time between three nonlinear DA solitons for two values of R at $s_{i} =0.4$, $n_{_{e0}}=4\times 10^{7}$, $n_{_{i0}}=7\times 10^{7}$, $T_{i}=0.3$, $Z_{_{d}}=3\times 10^{3}$, $\sigma =0.7$, $\gamma _{*}=0.7$, $s_{e}=0.4$, $u_{d0}=0.8$ and $x/L=2$

Fig. 7

The overtaking collision profiles represented by Eq. (25) at different time intervals between three nonlinear DA solitons for two values of $s_{i}$ at $R=0.3$, $n_{_{e0} }=4\times 10^{7}$, $n_{_{i0}}=7\times 10^{7}$, $T_{i}=0.3$, $Z_{_{d}} =3\times 10^{3}$, $\sigma =0.7$, $\gamma _{*}=0.7$, $s_{e}=0.4$, $u_{d0}=0.8$ and $x/L=2$

6 Conclusions

In this work, we presented the nature of the nonlinear propagation and interaction of DA two solitons and three solitons in a weakly inhomogeneous and strongly coupled dusty plasma consisting of negatively charged dust, electrons, and ions. The KdV equation is derived using the reductive perturbation approach, and it is transformed into the standard KdV equation with the help of suitable transformation. We found two-soliton and three-soliton solutions to the KdV equation using the HBM. The propagations of two and three solitons have been thoroughly explored. It has been noted that the larger soliton goes faster, approaches the smaller one, and then both soliton sizes and speeds return to their original values following an overtaking collision. It should be emphasized depending on the initial circumstances that, the KdV equation represents multi-soliton solutions. Hirota’s method is a novel, effective approach that allows us to theoretically get any number of solutions for several nonlinear partial differential equations. The results are in accordance with the experimental model [74] that investigated the overtaking of quantum semiconductor plasma, according to which the magnitudes of phase shifts decrease as the ratio of density parameters rises. The results agree with those [57, 61] that recognize Hirota’s approach as a practical way to identify many answers.

The new information could help us understand DAWs in a strongly coupled dusty plasma more thoroughly. They demonstrate how the structure of the solitary waves is altered depending on these effects when the density gradient, polarization force, and effective dust temperature are present in such a dusty plasma. The nonlinear characteristics of localized DASWs in space and laboratory dusty plasma may also be understood using these findings.