Shadows and rings of a de Sitter–Schwarzschild black hole

Abstract

We study the optical appearance of a de Sitter–Schwarzschild black hole and its distinguishability from a Schwarzschild black hole. By exploring various accretion models and emission profiles, we investigate the impact of different parameters on the observed shadows and intensity profiles. Our analysis reveals that the outer edge of the shadow, corresponding to the apparent radius of the photon sphere, remains consistent regardless of the spherical accretion details or the size of the black hole. However, subtle differences in the overall brightness and intensity distribution can arise between these two black holes, especially for emission models with sharp peaks near the event horizon. We find that the de Sitter–Schwarzschild black hole tends to exhibit a slightly darker appearance in certain scenarios, while in others, it can appear slightly brighter than the Schwarzschild black hole. These distinctions become more prominent as the radial emission decreases more rapidly. Nevertheless, the size of the shadow alone is not sufficient to differentiate the potential differences in the optical appearance between the de Sitter–Schwarzschild black hole and the Schwarzschild black hole. Instead, distinctions may be observed in the overall brightness of the image.

Appendices

Appendix 1: Review of the de Sitter–Schwarzschild spacetime

The de Sitter–Schwarzschild spacetime was considered to be a solution of Einstein field equations with the following density profile [6]

$$\begin{aligned} \rho (r)=\frac{3}{8\pi r_0^2} \exp \left( -\frac{r^3}{r_0^2 r_g}\right) \,. \end{aligned}$$

(42)

One could define the mass function as

$$\begin{aligned} \mathcal {M}(r)=4\pi \int _{0}^{r} \rho (x)x^2\textrm{d}x\,, \end{aligned}$$

(43)

with which the metric (1) could be written as

$$\begin{aligned} -g_{00}=g_{11}^{-1}= 1-2\mathcal {M}/r\,. \end{aligned}$$

(44)

Depending on the ratio of $r_g/r_0$, the metric (1) can describe either a black hole or a gravitational object without an event horizon. In the case where there is no event horizon, the object is referred to as a G-lump, a term coined by Dymnikova [62]. For a given $r_0$, the critical value of $r_{g.\textrm{cr}}$ could be found by solving the following equations

$$\begin{aligned} g_{00}(r_{\textrm{cr}})=0 \,, \end{aligned}$$

(45a)

$$\begin{aligned} g_{00}'\Big | _{r=r_{\textrm{cr}}}=0\,, \end{aligned}$$

(46b)

where the prime denotes the derivative with respect to r and where $r_{\textrm{cr}}$ is location of the horizon. Equation (A4) reduce to

$$\begin{aligned} r_{\textrm{cr}}^2/r_0^2&=1/3+\ln (3r_{\textrm{cr}}^2/r_0^2) \,, \end{aligned}$$

(47a)

$$\begin{aligned} r_{g.\textrm{cr}}&=\frac{r_{\textrm{cr}}^3/r_0^3}{\ln (3r_{\textrm{cr}}^2/r_0^2)}\,. \end{aligned}$$

(48b)

The numerical physical solution for this equation yields $r_{\textrm{cr}}\approx 1.49571 r_0$ and $r_{g.\textrm{cr}}\approx 1.75759 r_0$. For $r_g>r_{g.\textrm{cr}}$, the metric (1) describes a black hole with two event horizons and these two horizons degenerate at $r_g=r_{g.\textrm{cr}}$. For $r_g<r_{g.\textrm{cr}}$, the metric describes the G-lump. Examples of different de Sitter–Schwarzschild metric are shown in Fig. 12.

Fig. 12

${t-t}$ component of de Sitter–Schwarzschild metric for different ratio $r_g/r_0$

Appendix 2: Geodesics of de Sitter–Schwarzschild black hole

For a static spherically symmetric metric which has the form:

$$\begin{aligned} \textrm{d}s^2=-B(r)\textrm{d}t^2 + B(r)^{-1}\textrm{d}r^2+r^2(\textrm{d}\theta ^2+\sin ^2\theta \textrm{d}\phi ^2)\,, \end{aligned}$$

(49)

the static Killing vector field $(\partial /\partial t)^{\mu }$ and the rotational Killing vector field $(\partial /\partial \phi )^{\mu }$ yield the following constants of the motion for geodesics, respectively:

$$\begin{aligned} E&=-g_{\mu \nu }\left( \frac{\partial }{\partial t}\right) ^{\mu }\left( \frac{\partial }{\partial \lambda }\right) ^{\nu }\,, \end{aligned}$$

(50a)

$$\begin{aligned} J&=g_{\mu \nu }\left( \frac{\partial }{\partial \phi }\right) ^{\mu }\left( \frac{\partial }{\partial \lambda }\right) ^{\nu }\,, \end{aligned}$$

(51b)

where $\lambda$ being the proper time for massive particle or the affine parameter for massless particle. Without loss of generality, we shall restrict our attention to the equatorial geodesics, i.e., $\theta =\pi /2$.

With the help of Eq. (B2), the geodesic equations

$$\begin{aligned} \frac{\textrm{d}^2x^{\mu }}{\textrm{d}\lambda ^2} +\Gamma ^{\mu }_{\rho \sigma }\frac{\textrm{d}x^{\rho }}{\textrm{d}\lambda }\frac{\textrm{d}x^{\sigma }}{\textrm{d}\lambda }=0 \end{aligned}$$

(52)

can be simplified to

$$\begin{aligned} \frac{E}{B(r)}&=\frac{\textrm{d}t}{\textrm{d}\lambda } \,, \end{aligned}$$

(53)

$$\begin{aligned} \frac{E^2}{2}&=\frac{1}{2}\left( \frac{\textrm{d}r}{\textrm{d}\lambda }\right) ^2 +\frac{B(r)}{2} \left( \frac{J^2 }{r^2}+N \right) \,, \end{aligned}$$

(54)

$$\begin{aligned} \frac{J}{r^2}&=\frac{\textrm{d}\phi }{\textrm{d}\lambda }\,, \end{aligned}$$

(55)

with constant $N=0$ for a massless particle and $N=1$ for a massive particle.

Note that Eq. (B4b) has the same form of the equation for a particle with unit effective mass and energy $E^2/2$ moving in a one-dimensional effective potential

$$\begin{aligned} V_{\textrm{eff}}=\frac{B(r)}{2} \left( \frac{J^2 }{r^2}+N \right) \,. \end{aligned}$$

(56)

Combining Eqs. (B4b) and (B4c), we obtain

$$\begin{aligned} \left( \frac{\textrm{d}r}{\textrm{d}\phi }\right) ^2-\frac{E^2 r^4}{J^2}+B(r)\left( r^2+\frac{Nr^4}{J^2}\right) =0\,. \end{aligned}$$

(57)

Fig. 13

Effective potential for massless particles in de Sitter–Schwarzschild spacetime with various values of $r_g$

Fig. 14

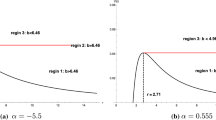
Left panel: Effective potential for massive particles with angular momentum $J=\sqrt{12}M$ in de Sitter–Schwarzschild spacetime, considering various values of $r_g/r_0$. For comparison purposes, we also include the corresponding results for the Schwarzschild spacetime, represented by dashed line. All these effective potentials have a local minimal at $r\approxeq 6M$, which corresponds to a stable circular orbits. Right panel: Effective potential for massive particles with different values of angular momentum J in a de-SBH with $r_g/r_0=1.76$

For null geodesics ($N=0$), the effective potential is given by

$$\begin{aligned} V_{\mathrm{eff-null}}=\frac{J^2 B(r) }{2r^2}\,. \end{aligned}$$

(58)

For a de-SBH, we have

$$\begin{aligned} B(r)=1-\frac{r_g}{r} \left( 1-\mathrm{{e}} ^{-r^3/r_0^2 r_g}\right) \,. \end{aligned}$$

(59a)

The equation for the effective potential and ${\textrm{d}r}/{\textrm{d}\phi }$ are given by

$$\begin{aligned} V_{\mathrm{eff-null}} =&\frac{J^2}{2r^2}-\frac{J^2r_g}{2r^3}+\frac{J^2r_g}{2r^3}\mathrm{{e}} ^{-r^3/r_0^2 r_g}\,, \end{aligned}$$

(60b)

$$\begin{aligned} 0=&\left( \frac{\textrm{d}r}{\textrm{d}\phi }\right) ^2-\frac{E^2 r^4}{J^2}+r^2-r_g r\left( 1-\mathrm{{e}} ^{-r^3/r_0^2 r_g}\right) \,, \end{aligned}$$

(61c)

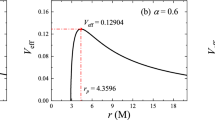
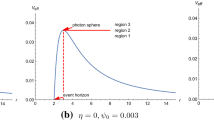
which are Eqs. (5) and (7), respectively. Figure 13 show the effective potential for massless particles in de Sitter–Schwarzschild spacetime.

For timelike geodesics, $N=1$, and the effective potential of a de-SBH is given by

$$\begin{aligned} V_{\mathrm{eff-massive}} =&\frac{J^2}{2r^2}-\frac{J^2r_g}{2r^3}+\frac{J^2r_g}{2r^3}\mathrm{{e}} ^{-r^3/r_0^2 r_g}+\frac{1}{2}-\frac{r_g}{2r}+\frac{r_g}{2r}\mathrm{{e}} ^{-r^3/r_0^2 r_g}\,. \end{aligned}$$

(62)

Examples of the effective potential are plotted in Fig. 14. The location of the stable circular orbits can be denoted by $r_{\textrm{SCO}}$ ($r_{\textrm{SCO}}>r_{h}$), which corresponds to the local minimal of the effective potential outside the event horizon. Note that $r_{\textrm{SCO}}$ is J dependent, and the minimal $r_{\textrm{SCO}}$ gives the location of the innermost stable circular orbits $r_{\textrm{ISCO}}$. The innermost stable circular orbits for de-SBHs is nearly equal to that of the SBH, i.e., $r_{\textrm{ISCO}}\approxeq 6\,M$.