1 Introduction

Two-dimensional (2D) nanomaterials, including graphene, boron nitride, and transition metal disulfide compounds, have been extensively studied due to their excellent physical properties and promising applications in the next generation of nanoelectronic devices [1,2,3]. Scientists have been dedicated to creating and enhancing a diverse array of 2D materials, each with its unique physical properties [4,5,6,7,8]. In order to realize the practical application of 2D materials in the field of electronics and spintronics, it is crucial to have a large adjustable band gap and high Curie temperature [9, 10]. Researchers have made numerous attempts and efforts to engineer the band gap and induce magnetism in 2D materials, such as through the utilization of asymmetric grating [11], doping [12], and surface functionalization (including hydrogenation, fluorination, oxygenation, etc.) [13,14,15,16,17]. Indeed, chemical functionalization is a widely adopted and effective method to tailor and modify the electronic and magnetic properties of 2D materials [18,19,20]. For example, in graphene, functionalization with hydrogen, fluorine, or other elements can effectively open a band gap, transforming it from a semimetal to a semiconductor [21,22,23,24]. The hydrogenation process has also induced ferromagnetism in the graphene surface [25,26,27,28].

The successful experimental production of ultrathin Cr2O3 nanosheets through rapid thermal annealing has provided evidence for the viability of synthesizing 2D Cr2O3 [29]. Building on these findings, Hashmi et al. were motivated to study the stability, electronic, and magnetic properties of the Cr2O3 monolayer using first-principle calculations [30]. In their systematic investigation, Hashmi et al. revealed that the honeycomb-kagome lattice of the Cr2O3 monolayer is thermodynamically stable at room temperature. This unique structure exhibits a kagome band with an unusually large gap in one spin channel, making it a highly interesting system for further exploration. Additionally, they found that the Cr2O3 monolayer displays stable intrinsic Ising ferromagnetism, as evidenced by the magnetocrystalline anisotropy energy (MAE). The calculations of the magnetic anisotropy further unveiled a remarkable perpendicular MAE of approximately 0.9 meV, which exceeds the values reported for experimentally realized 2D layers [31,32,33,34]. Moreover, the simulations for the Curie temperature (Tc) indicated that the Cr2O3 monolayer exhibits a Tc estimated to be 185 K, which highlights its potential for magnetic applications even at relatively high temperatures. In addition to its intriguing magnetic properties, Hashmi et al. explored the spin transport properties of the Cr2O3 monolayer using the nonequilibrium Green's function method. Their investigation demonstrated that the Cr2O3 monolayer exhibits excellent spin filtering behavior, further enhancing its potential for spintronics applications.

This article is based on first-principles calculations and aims to investigate a method to improve the electronic, and magnetic properties of the Cr2O3 monolayer honeycomb-kagome surface. Specifically, we study the effect of hydrogen and oxygen atom adsorption on the electronic and magnetic properties of the Cr2O3 monolayer surface. We demonstrate that the electronic properties can vary in a wide range. In addition, the Curie temperature in the Cr2O3 monolayer can be significantly improved by the adsorption of hydrogen and oxygen atoms, which can be attributed to the interaction between direct exchange and superexchange interactions. These findings provide a promising path for tuning electronic properties and optimizing Curie temperature in Cr2O3 monolayers, bringing this material closer to potential applications in nanoelectronic and spintronic devices.

2 Method of calculation

In this study, the first-principles calculations were conducted using the Quantum Espresso (QE) electronic structure code [35, 36], which is a simulation package based on the density-functional theory (DFT) approach [37, 38]. The Kohn–Sham (KS) formulation [37, 38] within the plane-wave (PW) basis set was resolved to efficiently describe the electronic structure of the material. The calculation adopted the scalar-relativistic projector-augmented wave (PAW) method [39], utilizing pseudopotentials to treat the Cr-3d and O-2p electrons as valence orbitals. To find the most stable configuration of the materials, we performed complete optimization of the unit cell volume, shape, and atomic positions. The optimization process was carried out using the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm, which efficiently converges to the optimal geometry [40]. The kinetic energy cut-off for the valence orbitals was set to 60 Ry, determining the accuracy and efficiency of the wave function expansion. Furthermore, the Brillouin Zone (BZ) sampling used a 5 × 5 × 1 k-point grid. In addition, a smearing parameter of 0.01 Ry was considered for the electron population function, implementing the Methfessel-Paxton smearing technique to improve the convergence of certain electronic properties [41]. The cell relaxation process continued until the force on each atom reached a threshold of 1 × 10−6 eV Å−1 and the total energy was 1 × 10−5 eV Å−1. To investigate the electronic properties in detail, band structure, and projected density of states (PDOS) calculations were performed. Both self-consistent field (SCF) and non-self-consistent (NSCF) calculations were carried out using different Monkhorst–Pack mesh sizes for Brillouin Zone sampling 9 × 9 × 1 and 33 × 33 × 1, respectively.

To simulate an infinite 2D plane, we employed a periodic cell in both the x- and y-directions for our 2D models. Additionally, to prevent any interaction between adjacent layers, a vacuum spacing of 25 Å was introduced in the z-direction. This avoids any potential false interactions and ensures the accuracy of our calculations.

For the 3d electron systems, the presence of strong Coulomb interaction between the localized 3d electrons of transition metals can significantly affect their properties. To account for this interaction, the Hubbard correction term is often used. In this calculation, the effective Hubbard parameters U = 2.0 eV with J = 0.7 eV were employed to describe the 3d electrons of the Cr atom, as employed in a previous study [30]. The Heyd–Scuseria–Ernzerhof (HSE) hybrid exchange–correlation functional calculations were performed to obtain an accurate electronic band structure.

3 Results and discussion

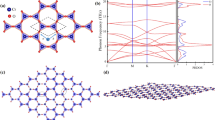
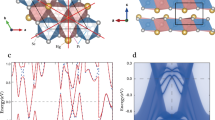
The study begins by conducting the optimization of the geometric structures of a pristine honeycomb-kagome Cr2O3 monolayer. In the original unit cell, there are two Cr atoms and three O atoms in one plane. The Cr atoms are bonded to three neighboring O atoms through covalent bonding, resulting in a Cr–O interatomic distance of approximately 1.79 Å. The hexagonal lattice parameters of the single layer have been optimized, with both the ɑ and ƅ parameters equal to 6.187 Å. These optimized values are found to be in good agreement with previous studies [30]. For completeness, Fig. 1 displays different views of the 3 × 3 × 1 supercell atomic structures of the pristine honeycomb-kagome Cr2O3, providing a visual representation of the arrangement of atoms in the material.

Fig. 1
figure 1

Atomic structure of the 3×3 Cr2O3 supercell monolayer. The area marked by black dashed lines indicates the unit cell

Full size image

Figure 2 displays the electronic band structure along the high-symmetry points ΓKMΓ and the corresponding total density of state (DOS) of a pristine Cr2O3 monolayer. As shown, the monolayer Cr2O3 is a half-metallic 2D material with a large spin gap of ~ 4.1 eV at Γ-point and this also agrees with the previous result [30]. The observation of typical kagome band characteristics in the electronic band structure is indeed intriguing. Below the Fermi level, the band structure exhibits a linearly dispersive band that forms a Dirac point at the high symmetry K-point in the Brillouin zone. Around this Dirac point, two flat bands are seen to quadratically contact with the Dirac bands at the Γ-point, which are located both above and below the Fermi level. This specific arrangement of bands with Dirac points and flat bands at specific high symmetry points in the Brillouin zone is a hallmark feature of the Kagome band structure.

Fig. 2
figure 2

The electronic band structures and corresponding DOS of a pristine Cr2O3 monolayer. The spin-up bands are represented by the blue line and the spin-down bands are represented by the red line

Full size image

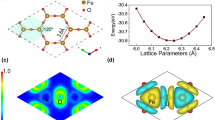
The investigation of the hydrogenation and oxygenation properties of the Cr2O3 monolayer is the main focus of our research. To begin our study, we examined the adsorption of hydrogen and oxygen on the Cr2O3 monolayer. In Fig. 3, we depict four distinct adsorption sites, namely top-on Cr (TCr), top-on O (TO), hollow (H), and bridge (B). These adsorption sites serve as crucial locations for the interaction between the Cr2O3 monolayer and hydrogen or oxygen atoms. By studying the behavior of hydrogen and oxygen adsorption at these sites, we can gain important insights into the reactivity and catalytic properties of the Cr2O3 monolayer.

Fig. 3
figure 3

The four different adsorption sites of a Cr2O3 monolayer surface

Full size image

Therefore, we performed full surface relaxation for each adsorption site and calculated the adsorption energy (Ea) for each site using the relevant equation provided in the study.

$$ E_{a} = E_{{Cr_{2} O_{3} + n\left( {H/O} \right)}} - E_{{Cr_{2} O_{3} }} - n E_{{\left( {H/O} \right)}} $$
(1)

where \(E_{{Cr_{2} O_{3} + n\left( {H/O} \right)}}\) is the total energy of the relaxed H/O-Cr2O3 system, \(E_{{Cr_{2} O_{3} }}\) is the total energy of pristine Cr2O3 layer, \(E_{{\left( {H/O} \right)}}\) is the total energy of an isolated H/O atom, and \(n\) is the total number of adatom H/O in the system. Figure 4 shows the adsorption energy (Ea) for an H/O adatom on the Cr2O3 surface for each site. Among the four possible adsorption sites for hydrogen atom, the top-on O (TO) adsorption became the most stable configuration. While for the oxygen atom, the top-on Cr (TCr) adsorption became the most stable configuration. Thus, we will focus on this adsorption configuration. Figure 5a–b shows the optimized atomic structure of a single H/O impurity adsorbed system on top of the O/Cr atom, respectively.

Fig. 4
figure 4

Adsorption energy in the four different adsorption sites of a Cr2O3 monolayer surface

Full size image
Fig. 5
figure 5

Optimized atomic structure of 2 × 2 Cr2O3 supercell with a 1H-Cr2O3, and b 1O-Cr2O3 systems

Full size image

3.1 Structure characterization

The adsorbed H/O atom is covalently bonded to one O/Cr atom and is located right above this atom. The O/Cr atom in the adsorption site extrudes out of the surface plane to form the σ H–O/O–Cr bond of distance d equal to 0.97 and 1.59 Å, respectively. We found that the bond lengths between the adsorptive O atom and its nearest neighbors were slightly increased to 2.00 Å while the adsorptive Cr atom and its nearest neighbors distance was 1.76 Å.

3.2 Dynamical and thermal stability

Structural stability is a primary requirement for two-dimensional materials in experimental preparation and applications. Therefore, the dynamic and thermal stability of the three different adsorption sites of a Cr2O3 monolayer surface were evaluated through calculations. Firstly, the phonon spectrum of the three different systems (1H-Cr2O3, 1O-Cr2O3, and 2O-Cr2O3) were calculated, as shown in Fig. 6. Throughout the entire Brillouin zone, no imaginary phonon modes were found, indicating its excellent dynamic stability. Consequently, these structures exhibit dynamic stability and can exist as independent two-dimensional crystals.

Fig. 6
figure 6

Vibrational phonon spectra of the a 1H-Cr2O3, b 1O-Cr2O3, and c 2O-Cr2O3 systems

Full size image

Furthermore, Fig. 7 shows the fluctuations in the total energy of the three different systems during AIMD simulation at 300 K, as well as the crystal structure after an 8 ps simulation. The MD method was used for temperature control during the calculations, with a time step of 1 fs in the canonical ensemble. From Fig. 7, it can be observed that throughout the entire simulation, both the energy and system temperature fluctuations are small, and all atoms vibrate near their equilibrium positions, maintaining the two-dimensional periodic structure. These calculations indicate that all the different systems exhibit good thermal stability and are predicted to remain stable at room temperature. The corresponding atomic structures after the AIMD simulation are presented in Fig. 7c, f, and i.

Fig. 7
figure 7

AIMD simulations of the temperature (left panels), total energy (middle panels), and atomic structures after an AIMD simulation (right panels) period of 8 ps for (a, b, c) 1H-Cr2O3, (d, e, f) 1O-Cr2O3, and (g, h, i) 2O-Cr2O3 systems

Full size image

3.3 Electronic structure

Figure 8a shows the electronic band structure of the hydrogenated Cr2O3 monolayer. As shown, the monolayer hydrogenated Cr2O3 is a half-metallic material with a large spin gap of ~ 4.18 eV at Γ-point. The exploration of electronic properties extends to the oxygenated Cr2O3 monolayer, as shown in Fig. 8b. In stark contrast to its hydrogenated counterpart, the band structure of the oxygenated monolayer takes on the form of a semiconductor. Notably, a narrow direct bandgap of 0.39 eV is distinctly present at the Γ-point. This alteration in electronic behavior upon oxygenation is a testament to the pivotal role played by oxygen in modulating the monolayer electronic properties.

Fig. 8
figure 8

The electronic band structures of the a 1H-Cr2O3, b 1O-Cr2O3, and c 2O-Cr2O3 systems using PBE + U and d 1H-Cr2O3, e 1O-Cr2O3, and f 2O-Cr2O3 systems using HSE

Full size image

Furthermore, as we delve deeper into the influence of oxygenation, Fig. 8c illustrates the electronic band structure of the oxygenated Cr2O3 monolayer, featuring the presence of two oxygen atoms. Notably, the bandgap is observed to expand to 0.65 eV, discernible at the K-point. This observation underscores the dynamic interplay between oxygen content and the material bandgap, offering intriguing prospects for the tailoring of its electronic properties.

In the HSE calculations, the band gap values for the 1O-Cr2O3 and 2O-Cr2O3 systems are 0.43 eV and 0.72 eV, respectively, and they closely align with the values obtained using the PBE + U method.

In the analysis of the projected density of states (PDOS), we gain valuable insights into the orbital contributions at the Fermi level (EF) within the Cr2O3 monolayer. The result reveals that at EF, the principal contributions originate from the d-orbitals of the Cr atoms and the p-orbitals of the O atoms. Notably, the d-orbitals of the Cr atom significantly outweigh the contribution of the p-orbitals of the O atoms, as shown in Fig. 9a. This dominance of Cr d-orbitals at the EF is a key factor in maintaining the half-metallic behavior observed in the electronic band structure. Interestingly, when exploring the influence of hydrogen and oxygen adatoms, we find that hydrogen adatoms do not contribute significantly through their s-orbital, and there is no noteworthy change in the electronic band structure, which continues to exhibit half-metallic behavior, as shown in Fig. 9b.

Fig. 9
figure 9

Partial density of states (PDOS) of a Cr2O3, b 1H-Cr2O3, c 1O-Cr2O3, and d 2O-Cr2O3 systems

Full size image

In contrast, oxygen adatoms attached to Cr atoms introduce a distinct behavior. The electronic band structure changes from its initial half-metallic state to a semiconducting nature, featuring a small direct band gap of 0.39 eV. This change can be understood by considering the contribution of the p-orbitals originating from the oxygen adatoms at the EF, as shown in Fig. 9c. With the introduction of two oxygen adatoms on the Cr2O3 surface, this band gap further increases to 0.65 eV. This is due to the elevated dominance of the p-orbitals from the two oxygen adatoms, which contribute significantly to both the p-orbitals of oxygen atoms and the d-orbitals of Cr atoms at the EF, as shown in Fig. 9d.

These observations highlight the significant role of oxygen adatoms in tailoring the electronic properties of the Cr2O3 monolayer, demonstrating the potential for precise band gap engineering in this material.

3.4 Magnetic properties

This section aims to study the magnetic properties of the pristine, hydrogenated, and oxygenated Cr2O3 monolayer by investigating the magnetic state, and Curie temperature. To calculate the magnetic state, we perform spin-polarized DFT calculations for a 2 × 2 supercell of ferromagnetic (FM) and various antiferromagnetic (AFM) phases, such as AFM Néel (AFM-N), AFM-zigzag (AFM-ZZ), and AFM-stripy (AFM-SR), respectively, for Cr elements, as shown in Fig. 10. The exchange energy, Eex, is calculated using the formula Eex = (EAFM − EFM). The results reveal that the FM configuration is the most energetically favorable magnetic state and the next higher energy one is AFM-N for all systems. The results of the calculation are presented in Table 1, which lists the exchange energy (Eex) for each system.

Fig. 10
figure 10

Schematics of different magnetic configurations

Full size image
Table 1 Calculated exchange energies Eex, magnetic exchange coupling constant (J), and Curie temperatures (Tc)
Full size table

The Curie temperature is estimated using the VAMPIRE software package [42, 43] and a magnetization curve obtained from Metropolis Monte Carlo (MC) simulations [26]. The Hamiltonian describes the magnetic energy of the system and is a sum of all possible pairs of magnetic moments. It was described using the Heisenberg model with the equation:

$$ \hat{H} = - \mathop \sum \limits_{i,j} J\hat{m}_{i} \cdot \hat{m}_{j} $$
(2)

The first term represents the exchange interaction, where J is the magnetic exchange coupling constant and \(\hat{m}_{i}\) and \(\hat{m}_{j}\) are the magnetic moments of atoms i and j, respectively. The dot product between \(\hat{m}_{i}\) and \(\hat{m}_{j}\) represents the interaction between the two magnetic moments. The magnetic exchange coupling constant J was obtained using the formula \(J = \frac{{E_{ex} }}{{Nm^{2} }}\), where Eex is the exchange energy, N is the number of magnetic atoms per unit cell, and m is the magnitude of the magnetic moment. The simulation was performed using 50 × 50 supercells, which were considered sufficiently large to minimize the impact of periodic boundary conditions. In this simulation, the temperature-dependent magnetization curves were calculated using 60,000 equilibration steps and 60,000 averaging steps with critical damping (λ = 1) and a temperature step interval of 0.2 K. Subsequently, the obtained magnetization curves were fitted by using the Curie-Bloch equation in the classical limit, expressed as \(m\left( T \right) = \left[ {1 - \frac{T}{{T_{c} }}} \right]^{\beta }\) (represented by the solid red line in Fig. 11) where T is the temperature and Tc represents the Curie temperature. The calculated critical exponent was determined to be β = 0.48.

Fig. 11
figure 11

Magnetization curve for a Cr2O3, b 1H-Cr2O3, c 1O-Cr2O3, and d 2O-Cr2O3 systems

Full size image

The magnetic moment variations of pristine, hydrogenated, and oxygenated Cr2O3 monolayer as a function of temperature were calculated using MC simulations. The results of average magnetic moments as a function of temperature are shown in Fig. 11. As shown in the results, the magnetic moment curves decrease as the temperature increases, dropping to near zero at a certain temperature, referred to as the Curie temperature. The estimated Tc for the different monolayers is listed in Table 1, with values of 170, 410, 277, and 380 K for pristine Cr2O3, 1H-Cr2O3, 1O-Cr2O3, and 2O-Cr2O3 systems, respectively. To confirm the accuracy of the MC calculations, we calculated the Tc of the CrI3 monolayer, which was found to be 46 K. This value is in excellent agreement with the experimental CrI3 monolayer Tc value of 45 K, thereby verifying the accuracy of our MC calculations.

4 Conclusions

In summary, our study provides insights into the structural, electronic, and magnetic properties of pristine, hydrogenated, and oxygenated Cr2O3 monolayer honeycomb-kagome (HK) surfaces. Our findings indicate that both hydrogenated and oxygenated Cr2O3 monolayers exhibit stability, as confirmed by the calculated phonon dispersion spectrum and AIMD simulations. The optimized structures are energetically favorable structures due to the negative adsorption energy. The results found that hydrogen adatoms preferentially adsorb on top of O atoms, while the oxygen adatoms preferentially adsorb on top of Cr atoms presenting much higher adsorption energy. The electronic properties can also be tuned by the oxygenation of the Cr2O3 monolayer, transforming from the half-metallic to the semiconducting nature. The band gap varies from 0 to 0.65 eV and can be achieved by the adsorption of two O atoms on the Cr2O3 monolayer surface. With the oxygenation of the Cr2O3 monolayer, the O atoms are strongly hybridized with the Cr atoms in the Cr2O3 surface due to which a band gap can be achieved. Interestingly, we have predicted that the intrinsic ferromagnetism and corresponding Curie temperature can be largely enhanced by the adsorption of H and O atoms. These theoretical findings present an innovative strategy to elevate the electronic and magnetic performance of Cr2O3 layers, with the potential for broader applications across the realm of advanced 2D materials.