Integrability in $[d+1]$ dimensions: combined local equations and commutativity of the transfer matrices

Abstract

We propose new inhomogeneous local integrability equations–combined equations, for statistical vertex models of general dimensions in the framework of the Algebraic Bethe Ansatz (ABA). For the low-dimensional cases the efficiency of the step-by-step consideration of the transfer matrices’ commutation is demonstrated. We construct some simple 3D solutions with the three-state R-matrices of certain 20-vertex structure; the connection with the quantum three-qubit gates is discussed. New, restricted versions of 3D local integrability equations with four-state R-matrices are defined, too. Then we construct a new 3D analog of the two-dimensional star-triangle equations.

A Appendix

For the well-known eight-vertex models [17] with the matrix elements

$R_{ij}^{kr}(u),\quad i+j=k+r \; {mod}\; 2$, the defining relations for the solutions following from Eq. (2.14) start from the low dimensions $n=2,3$. At $n=2$ there are two relations, which appear to be sufficient for commutation of the transfer matrices (with two arbitrary constant parameters $d_0,\; a_0$)

$$\begin{aligned}{} & {} \frac{R_{00}^{11}(u)R_{01}^{10}(u)}{R_{11}^{00}(u)R_{10}^{01}(u)}=d_0, \quad \frac{\left( [R_{00}^{00}(u)]^2-[R_{11}^{11}(u)]^2+[R_{10}^{10}(u)]^2-[R_{01}^{01}(u)]^2\right) }{R_{11}^{00}(u)R_{01}^{10}(u)}=a_0. \end{aligned}$$

(A.1)

Let us now separately discuss the situations with symmetric (*) and non-symmetric matrices (**).

* Symmetric R-matrices.

The following symmetry relations $R_{00}^{00}(u)={R_{11}^{11}}(u)$, $R_{01}^{01}(u)={R_{10}^{10}}(u)$ and $R_{01}^{10}(u)={R_{10}^{01}}(u)$, $R_{00}^{11}(u)=d_0 {R_{11}^{00}}(u)$,

imply that Eq. (A.1) takes place automatically. Now $a_0=0$, and the equations in (A.1) are identities. One can always take $d_0=1$, as all the discussed equations (the commutativity of the transfer matrices, the ordinary and non-homogeneous Yang–Baxter equations) are defined up to the transformations: $R_{00}^{11}(u)\rightarrow R_{00}^{11}(u)/\sqrt{d_0}$, ${R_{11}^{00}}(u)\rightarrow \sqrt{d_0} {R_{11}^{00}}(u)$.

At the next steps, when $n=3$ and $n=4$ there are arisen the following constraints correspondingly

$$\begin{aligned}{} & {} \frac{(R_{00}^{00}(u)-R_{01}^{01}(u))^2-R_{01}^{10}(u)^2-d_0 {R_{11}^{00}(u)}^2}{R_{11}^{00}(u)}={\textrm{const}},\quad {\textrm{and}}\quad \frac{R_{00}^{00}(u)R_{01}^{01}(u)}{R_{11}^{00}(u)}={\textrm{const}}. \end{aligned}$$

(A.2)

** Non-symmetric matrices. Here $a_0\ne 0$

in (A.1) and at the next step $n=3$ the defining relations are the following ones.

$$\begin{aligned}{} & {} \frac{R_{00}^{00}(u)([R_{00}^{00}(u)]^2-[R_{01}^{01}(u)]^2)-R_{10}^{10}(u)([R_{11}^{11}(u)]^2-[R_{10}^{10}(u)]^2)}{ (R_{11}^{11}(u)+R_{01}^{01}(u))( R_{01}^{10}(u) R_{10}^{01}(u)+R_{00}^{11}(u)R_{11}^{00}(u))+(d_{+})R_{11}^{00}(u)R_{01}^{10}(u)(R_{00}^{00}(u)+R_{10}^{10}(u))}=1,\nonumber \\{} & {} \frac{R_{11}^{11}(u)([R_{11}^{11}(u)]^2-[R_{10}^{10}(u)]^2)-R_{01}^{01}(u)([R_{00}^{00}(u)]^2-[R_{01}^{01}(u)]^2)}{ (R_{00}^{00}(u)+R_{10}^{10}(u))(R_{01}^{10}(u) R_{10}^{01}(u)+R_{00}^{11}(u)R_{11}^{00}(u))+(d_{-})R^{11}_{00}(u)R_{10}^{01}(u)(R_{11}^{11}(u)+R_{01}^{01}(u))}=1. \end{aligned}$$

(A.3)

We can see that two relations above can be obtained one from other by the transformations of the matrix elements - $R_{ij}^{kr}\rightarrow R_{\bar{i}\bar{j}}^{\bar{k}\bar{r}}$, with $\bar{i}=(i+1)\; \textrm{mod}\; 2$. The constants $d_{\pm }$ also are connected one with other, as one can define ([72])

$d_{+}=\frac{3{R_{00}^{00}}'(0)-{R_{11}^{11}}'(0)-{R_{01}^{01}}'(0)-{R_{10}^{10}}'(0)- {R_{01}^{10}}'(0)-{R_{10}^{01}}'(0)}{{R_{11}^{00}}'(0)}$, $d_{-}=\frac{3{R_{11}^{11}}'(0)-{R_{00}^{00}}'(0)-{R_{01}^{01}}'(0)-{R_{10}^{10}}'(0)- {R_{01}^{10}}'(0)-{R_{10}^{01}}'(0)}{{R_{00}^{11}}'(0)}$.

For the cases of next n-s ($n\ge 4$) the commutativity of the transfer matrices $\tau _n$ also is ensured by obtained relations (A.1, A.2, A.3), so they entirely define the R-matrices for integrable models. The obtained relations intend that for the general non-homogeneous case there are four independent functions (one of them always can be taken as unity) and three arbitrary constants by means of which all the matrix elements can be expressed, as it was stated already by direct solving the YBE (see the works [71, 72] and the citations therein). As it is discussed therein, following YBE (2.6) $\bar{R}(u,v)R(u)R(v)=R(v)R(u)\bar{R}(u,v)$, define uniquely the intertwiner matrix $\bar{R}(u,v)$, and there are no additional constraints on $\bar{R}(u,v)$ and R(u), and it appears that $R(u)=\bar{R}(u,0)$. The familiar elliptic, trigonometric, and rational parameterizations can be obtained letting $\bar{R}(u,v)=\bar{R}(u-v)$.

Fig. 4

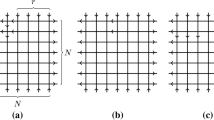
“Connected” (or combined) star-triangle relations: the corresponding transfer matrices and the plaquette weights; (i) product of two transfer matrices—darker stripes shifted by a link belong to two vertically disposed fragments of 2d transfer matrices, (ii) checkerboard arrangement of plaquette weights in a two-dimensional transfer matrix, (iii) the weight plaquettes on a fragment of the product of two transfer matrices—at the junctions between the plaquettes, the edges of horizontal or vertical intertwiner weights can be located