Skip to main content
SpringerLink
Log in

Deterministic and stochastic study of an eco-epidemic predator–prey model with nonlinear prey refuge and predator harvesting

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

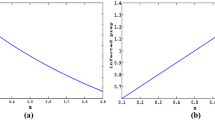
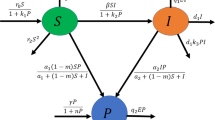
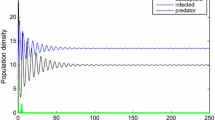
The present article deals with an eco-epidemic predator–prey model with infection in the prey population. The model system includes nonlinear prey refuges, harvesting in the predator, and assumes that the predator population preys on both prey populations following Holling type I functional response. After formulating the model system, the points of steady state are determined, and local stability and the global stability nature are discussed to examine the long-term behavior of the system. An expression for basic reproduction number is derived. By controlling the value of the basic reproduction number to be less than unity, it is found that the disease can be eradicated. Furthermore, Hopf-bifurcation with respect to important biological parameters and transcritical bifurcation are illustrated. An extension is introduced in the deterministic system by incorporating of environmental noise. Global positive solution as well as sufficient conditions for the extinction of species in the stochastic system are established. To validate the analytical findings of both the deterministic and stochastic model systems, we have executed numerical simulations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Data Availability Statement

This manuscript has associated data in a data repository. [Authors’ comment: The data that support the findings of this study are available from the corresponding author upon reasonable request.]

References

  1. T.R. Malthus, An Essay on the Principle of Population. J. Johnson in St. Paul’s Churchyard, London (1798)

  2. C.S. Holling, The components of predation as revealed by a study of small-mammal predation of the European Pine Sawfly. Can. Entomol. 91(5), 293–320 (1959)

    Article  Google Scholar 

  3. M. Haque, E. Venturino, An ecoepidemiological model with disease in predator: the ratio-dependent case. Math. Meth. Appl. Sci. 30(14), 1791–1809 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  4. M. Haque, A detailed study of the Beddington-DeAngelis predator-prey model. Math. Biosci. 234(1), 1–16 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  5. S. Jana, S. Guria, U. Das, T.K. Kar, A. Ghorai, Effect of harvesting and infection on predator in a prey-predator system. Nonl. Dyn. 81(1), 917–930 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  6. U. Kumar, P.S. Mandal, E. Venturino, Impact of Allee effect on an eco-epidemiological system. Ecol. Complex. 42, 100828 (2020)

    Article  Google Scholar 

  7. M. Haque, M.S. Rahman, E. Venturino, Comparing functional responses in predator-infected eco-epidemics models. Biosystems 114(2), 98–117 (2013)

    Article  Google Scholar 

  8. S. Sarwardi, S. Hossain, F. Al Basir, S. Ray, Mathematical analysis of an ecological system using a non-monotonic functional response: effects of gestation delay and predator harvesting. Int. J. Dyn. Cont. 11, 605–618 (2023)

    Article  MathSciNet  Google Scholar 

  9. W.O. Kermack, A.G. McKendrick, Contributions to the mathematical theory of epidemics. II. The problem of endemicity. Proceedings of the Royal Society of London. Series A, containing papers of a mathematical and physical character. 138(834), 55–83 (1932)

  10. K. Singh, K. Kaladhar, A mathematical study for the stability of two predator and one prey with infection in first predator using fuzzy impulsive control. Ann. Appl. Math. 39(1), 29–48 (2023)

    Article  MathSciNet  MATH  Google Scholar 

  11. M.S. Rahman, S. Islam, S. Sarwardi, Effects of prey refuge with Holling type IV functional response dependent prey predator model. Int. J. Model. Simul. 43, 1–19 (2023)

    Google Scholar 

  12. H. Molla, S. Sarwardi, M. Haque, Dynamics of adding variable prey refuge and an Allee effect to a predator-prey model. Alexandria Eng. J. 61(6), 4175–4188 (2022)

    Article  Google Scholar 

  13. H. Zhang, Y. Cai, S. Fu, W. Wang, Impact of the fear effect in a prey-predator model incorporating a prey refuge. Appl. Math. Comput. 356(1), 328–337 (2019)

    MathSciNet  MATH  Google Scholar 

  14. Y. Zhou, W. Sun, Y. Song, Z. Zheng, J. Lu, S. Chen, Hopf bifurcation analysis of a predator-prey model with Holling-II type functional response and a prey refuge. Nonl. Dyn. 97, 1439–1450 (2019)

    Article  MATH  Google Scholar 

  15. N. Sk, P.K. Tiwari, S. Pal, M. Martcheva, A delay non-autonomous model for the combined effects of fear, prey refuge and additional food for predator. J. Biol. Dyn. 15(1), 580–622 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  16. E. Gonzalez-Olivares, R. Ramos-Jiliberto, Dynamic consequences of prey refuges in a simple model system: more prey, fewer predators and enhanced stability. Ecol. Model. 166(1–2), 135–146 (2003)

    Article  Google Scholar 

  17. J.N. McNair, The effects of refuges on predator-prey interactions: a reconsideration. Theor. Popul. Biol. 29(1), 38–63 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  18. S. Thota, A mathematical study on a diseased prey-predator model with predator harvesting. Asian J. Fuzzy Appl. Math. 8(2), 16–21 (2020)

    Article  MathSciNet  Google Scholar 

  19. K. Chakraborty, S. Das, T.K. Kar, Optimal control of effort of a stage structured prey-predator fishery model with harvesting. Nonl. Anal.: Real World Appl. 12(6), 3452–3467 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  20. M. Manarul Haque, S. Sarwardi, Dynamics of a harvested prey-predator model with prey refuge dependent on both species. Int. J. Bifurc. Chaos 28(12), 1830040 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  21. J.D. Bairagya, S.S. Mondal, D. Chowdhury, S. Chakraborty, Game-environment feedback dynamics in growing population: Effect of finite carrying capacity. Phys. Rev. E 104(4), 044407 (2021)

    Article  ADS  MathSciNet  Google Scholar 

  22. D.V. Alexandrov, I.A. Bashkirtseva, L.B. Ryashko, Anomalous climate dynamics induced by multiplicative and additive noises. Phys. Rev. E 102(1), 012217 (2020)

    Article  ADS  MathSciNet  Google Scholar 

  23. G. Kozyreff, B. Seron, Dynamical elastic contact of a rope with the ground. Phys. Rev. Res. 3(2), L022026 (2021)

    Article  Google Scholar 

  24. X. Zhao, Z. Zeng, Stationary distribution and extinction of a stochastic ratio-dependent predator-prey system with stage structure for the predator. Physica A: Stats. Mech. Appl. 545, 123310 (2020)

    Article  MathSciNet  Google Scholar 

  25. A. Majumder, D. Adak, N. Bairagi, Persistence and extinction of species in a disease-induced ecological system under environmental stochasticity. Phys. Rev. E 103(3), 032412 (2021)

    Article  ADS  MathSciNet  Google Scholar 

  26. N. Sk, S. Pal, Dynamics of an infected prey-generalist predator system with the effects of fear, refuge and harvesting: deterministic and stochastic approach. The Eur. Phys. J. Plus. 137(1), 138 (2022)

    Article  Google Scholar 

  27. J.L. Callaham, J.C. Loiseau, G. Rigas, S.L. Brunton, Nonlinear stochastic modelling with Langevin regression. Proc. R. Soc. A 477(2250), 20210092 (2021)

    Article  ADS  MathSciNet  Google Scholar 

  28. N. Sk, S. Pal, Schooling behavior driven complexities in a fear-induced prey-predator system with harvesting under deterministic and stochastic environments. Sci. Rep. 13(1), 1234 (2023)

    Article  ADS  Google Scholar 

  29. M. Kang, F. Geng, M. Zhao, Dynamical behaviors of a stochastic predator-prey model with anti-predator behavior. J. Appl. Anal. Comput. 13(3), 1209–1224 (2023)

    MathSciNet  Google Scholar 

  30. S. Jana, T.K. Kar, Modeling and analysis of a prey-predator system with disease in the prey. Chaos, Solitons Fractals 47, 42–53 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  31. J. Hale, Ordinary Differential Equation (Klieger Publishing Company, Malabar, 1989)

    Google Scholar 

  32. T.C. Gard, T.G. Hallam, Persistence in food web-1, Lotka-Volterra food chains. Bull. Math. Biol. 41(6), 877–891 (1979)

    MathSciNet  MATH  Google Scholar 

  33. G. Birkhoff, G. Rota, Ordinary Differential Equations. Wiley, New York 342 QA372 B, 58 (1978)

  34. S. Wiggins, S. Wiggins, M. Golubitsky, Introduction to Applied Nonlinear Dynamical Systems and Chaos (Springer, New York, 1990)

    Book  MATH  Google Scholar 

  35. P.J. Pal, S. Sarwardi, T. Saha, P.K. Mandal, Mean square stability in a modified leslie-gower and Holling-type II predator-prey model. J. Appl. Math. Informatics. 29(3–4), 781–802 (2011)

    MathSciNet  MATH  Google Scholar 

  36. P.S. Mandal, M. Banerjee, Stochastic persistence and stationary distribution in a Holling-Tanner type prey-predator model. Physica A: Stats. Mech. Appl. 391(4), 1216–1233 (2012)

    Article  ADS  Google Scholar 

  37. S.R.J. Jang, H.C. Wei, Deterministic predator-prey models with disease in the prey population. J. Biol. Syst. 28(03), 751–784 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  38. A.K. Pal, A. Bhattacharyya, A. Mondal, Qualitative analysis and control of predator switching on an eco-epidemiological model with prey refuge and harvesting. Results Control Optim. 7, 100099 (2022)

    Article  Google Scholar 

Download references

Acknowledgements

The corresponding author Dr. Sarwardi is grateful to the Department of Mathematics and Statistics, Aliah University for providing necessary facilities to perform the present work. Mr. Islam is highly thankful to UGC (University Grants Commission), New Delhi, Govt. of India [NTA Ref. No.: 201610315672] for awarding doctoral scholarship. Mr. Nazmul is thankful to the Department of Mathematics, University of Kalyani for providing opportunity to do this research work.

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, Aliah University, IIA/27, New Town, Kolkata, 700160, India

    Md Sarijul Islam & Sahabuddin Sarwardi

  2. Department of Mathematics, University of Kalyani, Kalyani, 741235, India

    Nazmul Sk

Authors
  1. Md Sarijul Islam
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Nazmul Sk
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sahabuddin Sarwardi
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

The conceptualization and formal analysis of this research article were done by MSI and SS. The authors MSI, SS, and NS contributed equally to the main results and numerical simulations. All authors have read and approved the final manuscript for submission.

Corresponding author

Correspondence to Sahabuddin Sarwardi.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Islam, M.S., Sk, N. & Sarwardi, S. Deterministic and stochastic study of an eco-epidemic predator–prey model with nonlinear prey refuge and predator harvesting. Eur. Phys. J. Plus 138, 851 (2023). https://doi.org/10.1140/epjp/s13360-023-04476-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-023-04476-2

Search

Navigation