1 Introduction

For many years, both theoretically and experimentally, structure consisting of two superconductors connected via normal metal (SNS junctions) or via ferromagnet (SFS junctions) have been studied. Both their static properties (such as Josephson effect, proximity effect), and dynamic properties (current–voltage characteristic, conductance) are analized. Andreev reflection (AR) is a mechanism responsible for electron transport at normal metal/superconductor interface. Quasiparticle traveling throughout SNS and SFS junction experience variation of the order parameter along its path what is prerequisite for AR. Electron traveling from a normal metal to a superconductor is reflected back as a hole. In SNS junctions closed paths of electron–hole trajectories can be formed. In this way it is possible to achieve multiple Andreev reflections. This approach is commonly used to investigate stationary (without bias voltage) Josephson current in different junctions with superconducting electrodes [1,2,3,4,5,6,7,8]. Supercurrent in SNS junctions is mainly carried through these bound Andreev levels [9,10,11,12,13,14]. In non-stationary SNS junctions (bias-voltage applied) [15,16,17,18], the same mechanism is responsible for current flow. Dynamic characteristics are closely related to Andreev reflection as well. In voltage-biased SNS junction quasiparticle can be retroreflected through the normal region multiple times, as long as energy of quasiparticle remains within superconducting gap. Mechanism for current transport in which the quasiparticle can gain enough energy to leave the normal barrier and be transmitted into the superconductor is known as multiple Andreev reflection (MAR).

Resistively shunted junction method, which was widely used for description of current voltage characteristics (CVC) in SNS junctions turn out to be too simple to be able to explain some peculiarities observed in experiment: “foot” or “shoulder” at low voltage, negative differential conductivity and subharmonic gap structures. All these properties are well explained in Kümmel, Gunsenheimer and Nikolsky (KGN) theory [19]. This theory combines time-relaxation model and time-dependent Bogoliubov-de Gennes equations (BdGEs) to provide microscopic description of charge transport in SNS junction and is able to account the inelastic scattering and electron–hole asymmetry.

Hybrid structures that consist of ferromagnets and superconductors are promising candidate for application in high-tech electronic devices. Potential for practical application as well as multitude of effects arising from the mutual influence of superconductivity and ferromagnetism, have attracted attention of theorists and experimentalists. Current carrier energy and momentum near Fermi level is not altered in the moment of Andreev reflection. This is not the case for quasiparticle spin, when incident electron and reflected hole belong to opposite spin branches. The change of the spin branch due to Andreev reflection must be taken into account when studying heterostructures containing a ferromagnet. In this way, SFS junction enables study of the interplay between AR and spin polarization in F. Various experimental as well as theoretical groups studied static and dynamic properties of SF heterostructures [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35].

AR is suppressed by the exchange interaction in the ferromagnet. As a consequence spin-polarized quasiparticle transport in SFS junction is qualitatively and quantitatively different compared to SNS junction. Transport properties are significantly nonlinear, especially when AR suppression is not too strong. This low suppression occurs when exchange field in the barrier is smaller or comparable to the pair potential \(2\Delta\) in the superconducting electrodes. High-\(T_c\) superconductors are the most prominent candidates for superconductor/ferromagnet heterostructures in which exchange field is comparable with pair potential. This feature together with high transmissivity of FD interface made studies of transport properties in hybrid structures of ferromagnet and d-wave high-\(T_c\) superconductor (D) even more attractive for research. Several groups experimentally investigated layered DF heterostructures with manganite barriers (LSMO and LCMO): \(\check{S}\)trbík et al. [36], Chen et al. [37], Luo et al. [38], Schoop et al. [39], and others. Koren et al. [40] studied trilayers YBCO/SRO/YBCO, while Asulin et al. [41, 42] studied YBCO/SRO bilayers using itinerant ferromagnet \(SrRuO_3\) (SRO).

In DFD junction, exchange field is not the only mechanism for suppression of AR. For quasiparticles whose momentum directions is along the gap nodes [43] there is no AR. Therefore, quasiparticle current becomes reduced in comparison with isotropic s-wave case, and sharp CVC becomes broaden [44].

Motivated by the deficiency of qualitative comparison between experimental data and theoretical predictions for the MAR effect manifestation in dynamic conductance spectrum of ballistic high transparent SFS and DFD junctions we started this investigation ten years ago. We generalized the approach of KGN to calculate transport properties in this kind of junctions. First we solve the time dependent BdGEs for Andreev reflected quasiparticle in the case of ferromagnetic barrier. Then we extend this approach to anisotropic superconducting pairing. Also we study mutual influence of the exchange interaction in the barrier and symmetry of pair potential in the superconducting electrodes. There is prominent difference of CVC for isotropic and anisotropic superconducting pairing. We discuss the influence of misorientation of d-wave superconducting electrodes on transport properties. Details of calculation can be found in original KGN paper [19] for SNS junction, and in Refs. [44,45,46,47] for SFS and DFD junctions. In order to better understand results presented in this review article we will give brief review of our calculation.

In Sect. 2 we briefly present the model describing the quasiparticle dynamics, and in Sect. 3 current density. Results are discussed in Sects. 4, and 5 is devoted to the conclusion and future perspectives.

2 Model and formalism

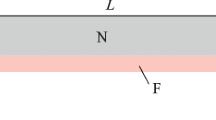
We consider a voltage biased superconductor/feromagnet/superconductor junction where superconductor could be s-wave or d-wave. The thickness of ferromagnetic layer is \(d=2a\), while the thickness of superconducting banks are \(L_z\), where \(L_z\gg 2a\), and cross section area is \(L_xL_y\). We assume fully transparent interfaces between layers. In the ferromagnet layer there is constant electric field due to the externally applied bias voltage V, \({\textbf{F}}=-\mathbf {e_z}(V/2a)\Theta (a-\mid z \mid )\), where \(\Theta (z)\) stands for the Heaviside step function. Therefore, the time-dependent vector potential is \({\textbf{A}}=-c{\textbf{F}}t=\mathbf {e_z}cVt/(2a)\Theta (a- \mid z \mid )\). We chose a gauge in which pair potential is real. Electric field penetration into the superconducting electrodes is negligible. In a case when superconducting electrodes are s-wave we describe them in the framework of the standard BCS formalism, while in a case of d-wave superconducting electrodes we use an anisotropic BCS model of superconductivity. Ferromagnet is described within the Stoner model, where between the spin sub-bands there is an exchange energy shift 2h.

To treat the quasiparticle motion we use the time-dependent Bogoliubov–de Gennes equations associated with the relaxation-time model for charge transport. Charge transport is affected by inelastic scattering and electric field, as well. We do not take into account elastic scattering, since we assume superconductor is in the clean limit. In relaxation-time model, the probability that the electric field will freely accelerate quasiparticle during time interval t is \(e^{-t/T_S}\), where \(T_S\) is the average scattering time. In order to calculate current density (see Sect. 3) which is given as a sum of time averages of all electron and hole momentum densities, it is necessary to take into account the rate \(1/t_c\) at which the quasiparticle start their motion [19], from the respective initial states k. Here \(t_c\) is the time interval between two quasiparticle “takeoffs” and for \(d>l\) (where \(l=v_zT_S\) is the inelastic scattering length of the electrons with velocity \(v_z\)) \(t_c=T_S\), while for \(d<l\) one has \(t_c=d/v_z\), which correspond to the ballistic transport that we will consider below.

Time dependent BdGEs for electron-like (ELQ) and hole-like (HLQ) quasiparticles with energy E are [19, 44, 45, 48]

$$\begin{aligned} i \hbar \frac{\partial }{\partial t}u_{\sigma }({\textbf{r}},t)= & {} \left[ \frac{1}{2m}\left[{\textbf{p}} +\frac{e}{c}{\textbf{A}}\right]^2-\mu -\rho _{\sigma }h\right] u_{\sigma }({\textbf{r}},t)+ \Delta (z) \Theta (\mid z \mid -a)v_{\sigma }({\textbf{r}},t),\nonumber \\ i \hbar \frac{\partial }{\partial t}v_{\sigma }({\textbf{r}},t)= & {} -\left[ \frac{1}{2m}\left[{\textbf{p}}-\frac{e}{c} {\textbf{A}}\right]^2-\mu -\rho _{\sigma }h\right] v_{\sigma }({\textbf{r}},t)+ \Delta (z) \Theta (\mid z \mid -a)u_{\sigma }({\textbf{r}},t), \end{aligned}$$
(1)

where \(\rho _{\sigma }=+1(-1)\) is connected with spin projection \(\sigma =\uparrow (\downarrow )\). The chemical potential is labeled by \(\mu\); \(e=\mid e \mid\). Fermi velocities are assumed to be equal in all regions, superconducting and ferromagnetic, and magnetic scattering is neglected.

When we consider superconducting electrodes as s-wave type, we approximate the spatial variation of the pair potential by step function \(\Delta \Theta (\mid z\mid -a)\), where \(\Delta\) is the bulk superconducting gap. The temperature dependence of \(\Delta\) is given by \(\Delta (T)=\Delta (0)\tanh (1.74\sqrt{T_c/T-1})\) [49]. In a case of anisotropic pairing in superconducting electrodes (d-wave type) the barrier is assumed to be perpendicular to the \({\hat{a}}\) axis in the \({\hat{a}}-{\hat{b}}\) plane of the left hand superconducting electrode \(D_L\) with pair potential \(\Delta =\Delta (T)\cos {2\varphi }\), where \(\varphi\) is the angle the quasiparticle momentum makes with the \({\hat{a}}\) axis. The right-hand superconducting electrode \(D_R\), could be misoriented by an angle \(\theta\). In d-wave case, the sign of pair potential is changing over Fermi surface, so the quasiparticle reflecting from the surface experience a sign change along its trajectory. The effective pair potentials in \(D_R\) for ELQ are \(\Delta _R^+(\varphi ,\theta )=\Delta (T)\cos {2(\varphi -\theta )}\) and for and HLQ are \(\Delta _R^-(\varphi ,\theta )=\Delta (T)\cos {2(\varphi +\theta )}\). Spatial variation of the pair potential is \(\Delta (z)=\Delta _L\Theta (-a-z)+\Delta _R\Theta (z-a)\).

The solutions of BdGEs, Eq. (1), are given by four component spinor wave function \(\Psi ({\textbf{r}},t)=[u_{\uparrow }({\textbf{r}},t), u_{\downarrow }({\textbf{r}},t), v_{\uparrow }({\textbf{r}},t),v_{\downarrow }({\textbf{r}},t)]^T\), which is in accordance with KGN approach. Since junction is translationally invariant in direction perpendicular to the z-axis, parallel component of wave vector \({\textbf{k}}_{\Vert }=k_x{\textbf{e}}_x+k_y{\textbf{e}}_y\) is conserved. Consequently, the wave function can be written in the following form \(\Psi ({\textbf{r}},t)=\psi (z,t)e^{i{\textbf{k}}_{\Vert }{\textbf{r}}}\), where \(\psi (z,t)=[u_{\uparrow }(z,t), u_{\downarrow }(z,t), v_{\uparrow }(z,t),v_{\downarrow }(z,t)]^T\).

In the following, we will briefly overview the calculation, in order to better understand the obtained results in Sect. 4. For details of these calculations, we refer the reader to Refs. [44,45,46], as well as Kümmel et al. [19].

In order to calculate current density, solutions of time dependent BdGE must be found in the ferromagnetic region. To calculate unknown coefficients in those solutions appropriate boundary conditions have to be satisfied. Electrons and holes with momentum in the same direction are coupled together by Andreev reflection, and are decoupled from electrons and holes with opposite momentum. The wave function in the ferromagnetic barrier and also in superconducting electrodes, separates into the two solutions which are independent and correspond to positive (\(+\)) and negative (−) z momentum [44, 45]

$$\begin{aligned} \psi _{F}^{\pm }(z,t,E_k)= & {} \begin{array}{ll} \left( \begin{array}{c} u_{k\uparrow }^{\pm }(z,t)\\ u_{k\downarrow }^{\pm }(z,t)\\ v_{k\uparrow }^{\pm }(z,t)\\ v_{k\downarrow }^{\pm }(z,t) \end{array}\right) \end{array} =\sum _{n=-\infty }^{+\infty }\left[ \begin{array}{ll} \left( \begin{array}{c} 1 \\ 0\\ 0\\ 0 \end{array}\right) u_{n\uparrow }^{\pm }(z,t,k) \end{array}+ \begin{array}{ll} \left( \begin{array}{c} 0\\ 1\\ 0\\ 0 \end{array}\right) u_{n\downarrow }^{\pm }(z,t,k) \end{array}\right. \nonumber \\{} & {} \left. \quad + \begin{array}{ll} \left( \begin{array}{c} 0\\ 0\\ 1\\ 0 \end{array}\right) v_{n\uparrow }^{\pm }(z,t,k) \end{array}+ \begin{array}{ll} \left( \begin{array}{c} 0\\ 0\\ 0\\ 1 \end{array}\right) v_{n\downarrow }^{\pm }(z,t,k) \end{array}\right] . \end{aligned}$$
(2)

Here the quasiparticle wave packets \(u_{k\sigma }^{\pm }\) and \(v_{k\sigma }^{\pm }\), moving in the electric field due to the applied voltage V, are \(u_{k\sigma }^{\pm }(z,t)=\Sigma _{n=-\propto }^{+\propto }u_{n\sigma }^{\pm }(z,t,k)\) and \(v_{k\sigma }^{\pm }(z,t)=\Sigma _{n=-\propto }^{+\propto }v_{n\sigma }^{\pm }(z,t,k)\), where \(u_{n\sigma }^{\pm }\) represents the wave packet of the quasiparticle which is an electron during the time interval between the 2nth and \(2n+1\)st Andreev reflection, then becomes a hole described by the wave packets \(v_{n\sigma }^{\pm }\) until the next Andreev reflection, which produces an electron again [19, 44, 45]. This can be seen in the proportionality of the solutions for \(u_{n\sigma }^{\pm }\) and \(v_{n\sigma }^{\pm }\) to the corresponding AR probability amplitudes, \(u_{n\sigma }^{\pm }(z,t,k)\propto \mid A_{2n}^{\pm }(E_k\pm eV/2+\rho _{\sigma }h) \mid\) and \(v_{n\sigma }^{\pm }(z,t,k)\propto \mid A_{2n+1}^{\pm }(E_k\pm eV/2-\rho _{\sigma }h) \mid\) [44, 45], where these multiple Andreev reflection probability amplitudes are defined as

$$\begin{aligned} A_{2n}^{\pm }(E)= & {} \prod _{r=1}^{2n}\gamma (E\pm reV\mp eV/2), \end{aligned}$$
(3)
$$\begin{aligned} A_{2n+1}^{\pm }(E)= & {} \prod _{r=1}^{2n+1}\gamma (E\pm reV\mp eV/2), \end{aligned}$$
(4)

and

$$\begin{aligned} A_0^{\pm }(E)=1, \end{aligned}$$
(5)

with

$$\begin{aligned} \gamma= & {} \frac{E-i(\Delta ^2-E^2)^{1/2}}{\Delta }\hspace{3mm} \textrm{for} \hspace{3mm} E<\Delta , \end{aligned}$$
(6)
$$\begin{aligned} \gamma= & {} \frac{E-(E^2-\Delta ^2)^{1/2}}{\Delta }\hspace{3mm} \textrm{for} \hspace{3mm} E>\Delta . \end{aligned}$$
(7)

It is important to notice that in the case of d-wave superconducting electrodes these probability amplitudes are angular dependent, since \(\Delta\) for arbitrary oriented d-wave electrodes can depend on angles \(\varphi\) and \(\theta\).

3 Current density

The averaged current density in the ferromagnetic barrier within the relaxation-time model, is given by [44,45,46]

$$\begin{aligned} \langle {\textbf{j}}\rangle= & {} -\frac{e}{4m}\hat{\sum _k}\Big \{f_0(E_k+h)\Big (\langle u_{k\uparrow }^{+*}{\textbf{P}}u_{k\uparrow }^{+}\rangle + \langle u_{k\uparrow }^{-*}{\textbf{P}}u_{k\uparrow }^{-}\rangle \Big ) \nonumber \\{} & {} \quad +f_0(E_k-h)\Big (\langle u_{k\downarrow }^{+*}{\textbf{P}}u_{k\downarrow }^{+}\rangle + \langle u_{k\downarrow }^{-*}{\textbf{P}}u_{k\downarrow }^{-}\rangle \Big ) \nonumber \\{} & {} \quad +(1-f_0(E_k+h))\Big (\langle v_{k\uparrow }^{+}{\textbf{P}}v_{k\uparrow }^{+*}\rangle + \langle v_{k\uparrow }^{-}{\textbf{P}}v_{k\uparrow }^{-*}\rangle \Big ) \nonumber \\{} & {} \quad +(1-f_0(E_k-h))\Big (\langle v_{k\downarrow }^{+}{\textbf{P}}v_{k\downarrow }^{+*}\rangle + \langle v_{k\downarrow }^{-}{\textbf{P}}v_{k\downarrow }^{-*}\rangle \Big )\Big \}, \end{aligned}$$
(8)

where \(f_0\) is the Fermi distribution function and \({\textbf{P}}=[-i\hbar \mathbf {\nabla }+e{\textbf{A}}/c]\), is the gauge-invariant momentum operator. The spatial and time integration in the averaged momentum densities are

$$\begin{aligned} \langle u_{k\sigma }^{\pm *}{\textbf{P}}u_{k\sigma }^{\pm }\rangle= & {} \frac{1}{2a}\frac{1}{t_c}\int _{-a}^{+a}dz \int _0^{\tau }dt e^{-t/T_S} u_{k\sigma }^{\pm *}(z,t){\textbf{P}}u_{k\sigma }^{\pm }(z,t), \end{aligned}$$
(9)
$$\begin{aligned} \langle v_{k\sigma }^{\pm }{\textbf{P}}v_{k\sigma }^{\pm *}\rangle= & {} \frac{1}{2a}\frac{1}{t_c}\int _{-a}^{+a}dz \int _0^{\tau }dt e^{-t/T_S} v_{k\sigma }^{\pm }(z,t){\textbf{P}}v_{k\sigma }^{\pm *}(z,t), \end{aligned}$$
(10)

where \(\tau\) is the time after which the quasiparticle has been accelerated to the edge of the pair potential well before leaving the F layer and entering one of the superconducting electrodes. It turns out that \(\tau\) contribute only to two negligible factors which can be omitted from momentum densities, Eqs. (9) and (10).

After extensive calculation, the details of which can be found in Refs. [44,45,46], the total current density \(\langle {\textbf{j}}\rangle\) can be written as a sum of two components. The first one is the ohmic current density

$$\begin{aligned} \langle {\textbf{j}}_N\rangle =-{\textbf{e}}_z\frac{V}{R_NL_xL_y}, \end{aligned}$$
(11)

where \(R_N\) is the normal resistance. The second component is the current density due to Andreev reflection \(\langle {\textbf{j}}_{AR} \rangle\). In order to calculate current due to AR one has to integrate over the density of states g(E), which is calculated numerically using the method of Ref. [50] for s-wave case and of Ref. [51] for d-wave case. As a result the finite integrand only exists in the range of nonvanishing scattering probabilities. When we are dealing with isotropic s-wave and d-wave superconducting electrodes without misorientation these probabilities can be approximated, after neglecting over the barrier reflection, in a same functional form by a step function product

$$\begin{aligned} \mid A_n^{\pm }((E\pm h)\pm \frac{1}{2}eV)\mid ^2\approx \Theta \Big (\Delta \pm (E\pm h)+eV\Big )\Theta \Big (\Delta \mp (E\pm h)-neV\Big ). \end{aligned}$$
(12)

Current density due to AR for s-wave superconducting electrodes becomes [44]

$$\begin{aligned}{} {} \langle {\textbf{j}}_{AR}\rangle =& -{\textbf{e}}_z\frac{e}{2m}\frac{\hbar }{\Omega _N} \sum _{n=1}^{\infty }e^{-\frac{2na}{l}}\nonumber \\{} & {} \quad\Bigg \{ \int _{B_1}^{C_1}dE g(E)\Big [\Big (f_0(E_k+h)k_{e\uparrow }-(1-f_0(E_k+h))k_{h\downarrow }\Big ) \nonumber \\{} & {} \quad + \Big (f_0(E_k-h)k_{e\uparrow }- (1-f_0(E_k-h))k_{h\downarrow }\Big )\Big ]\nonumber \\{} & {} \quad -\int _{B_2}^{C_2}dE g(E)\Big [\Big (f_0(E_k+h)k_{e\uparrow } -(1-f_0(E_k+h))k_{h\downarrow }\Big )\nonumber \\{} & {} \quad + \Big (f_0(E_k-h)k_{e\uparrow }- (1-f_0(E_k-h))k_{h\downarrow }\Big )\Big ]\nonumber \\{} & {} \quad +\int _{B_3}^{C_3}dE g(E)\Big [\Big (f_0(E_k-h)k_{e\downarrow } -(1-f_0(E_k-h))k_{h\uparrow }\Big )\nonumber \\{} & {} \quad +\Big (f_0(E_k+h)k_{e\downarrow }- (1-f_0(E_k+h))k_{h\uparrow }\Big )\Big ]\nonumber \\{} & {} \quad -\int _{B_4}^{C_4}dE g(E)\Big [\Big (f_0(E_k-h)k_{e\downarrow } -(1-f_0(E_k-h))k_{h\uparrow }\Big )\nonumber \\{} &\quad+\Big (f_0(E_k+h)k_{e\downarrow }- (1-f_0(E_k+h))k_{h\uparrow }\Big )\Big ]\Bigg \}, \end{aligned}$$
(13)

where

$$\begin{aligned} k_{e\sigma } &= {} k_{zf}+\frac{E_k+\rho _{\sigma } h}{\hbar v_{zf}}, \end{aligned}$$
(14)
$$\begin{aligned} k_{h\sigma }&= {} k_{zf}-\frac{E_k-\rho _{\sigma } h}{\hbar v_{zf}}, \end{aligned}$$
(15)

and limits of integrals are \(B_i\ge 0\), \(C_i>B_i\), \(i=1,\ldots ,4\), and \(B_1=0\), \(C_1=\Delta -neV-h\), \(B_2=neV-\Delta -h\), \(C_2=\Delta +eV-h\), \(B_3=-\Delta -eV+h\), \(C_3=\Delta +h-neV\), \(B_4=neV-\Delta +h\), \(C_4=\Delta +h+eV\).

For d-wave case without misorientation one obtains \(\langle {\textbf{j}}_{AR}\rangle\) in a similar form as previous relation but with additional integration, from \(-\pi /2\) to \(\pi /2\), over the angle \(\varphi\) of the quasiparticle propagation. The main difference is that in anisotropic case the integration limits for current density are angular dependent and given by angular dependent pair amplitude \(\Delta (\varphi )\).

For d-wave misoriented superconducting electrodes there is an extensive modification of the current calculation due to different pair potentials in the superconducting electrodes, as well as the angular dependent integration limits. Consequently, current density due to AR is [46]

$$\begin{aligned}{} {} \langle {\textbf{j}}_{AR} \rangle =& -{\textbf{e}}_z\frac{e}{2m}\frac{\hbar }{2aL_xL_y}\int _{-\pi /2}^{\pi /2} d\varphi \Bigg \{\sum _{n=1}^{\infty }e^{-\frac{2na}{l}}\nonumber \\{} & {} \qquad \Bigg [ \int _{B_1}^{C_1}dE g(E)f_0(E+h)k_{e\uparrow }-\int _{B_2}^{C_2}dE g(E)f_0(E+h)k_{e\uparrow }\nonumber \\{} & {} \quad +\int _{B_3}^{C_3}dE g(E)f_0(E-h)k_{e\downarrow }-\int _{B_4}^{C_4}dE g(E)f_0(E-h)k_{e\downarrow }\nonumber \\{} & {} \quad -\int _{B_5}^{C_5}dE g(E)(1-f_0(E+h))k_{h\uparrow }+\int _{B_6}^{C_6}dE g(E)(1-f_0(E+h))k_{h\uparrow }\nonumber \\{} & {} \quad -\int _{B_7}^{C_7}dE g(E)(1-f_0(E-h))k_{h\downarrow }+\int _{B_8}^{C_8}dE g(E)(1-f_0(E-h))k_{h\downarrow }\nonumber \\{} & {} \quad +\int _{B_9}^{C_9}dE(1-f_0(E-h))k_{h\uparrow }-\int _{B_{10}}^{C_{10}}dE g(E)(1-f_0(E-h))k_{h\uparrow }\nonumber \\{} & {} \quad +\int _{B_{11}}^{C_{11}}dE g(E)(1-f_0(E+h))k_{h\downarrow }-\int _{B_{12}}^{C_{12}}dE g(E)(1-f_0(E+h))k_{h\downarrow }\nonumber \\{} & {} \quad -\int _{B_{13}}^{C_{13}}dE g(E)f_0(E-h)k_{e\uparrow }+\int _{B_{14}}^{C_{14}}dE g(E)f_0(E-h)k_{e\uparrow }\nonumber \\{} & {} \quad -\int _{B_{15}}^{C_{15}}dE g(E)f_0(E+h)k_{e\downarrow }+\int _{B_{16}}^{C_{16}}dE g(E)f_0(E+h)k_{e\downarrow }\Bigg ]\Bigg \}, \end{aligned}$$
(16)

where integration limits \(B_i\) and \(C_i\) (\(B_i\ge 0\), \(C_i>B_i\)), \(i=1,\ldots ,16\) (they are given in Appendix of Ref. [46]), are found from scattering probabilities which can be approximated by step-function products [46]

$$\begin{aligned}{} & {} \prod _{r=1}^{\alpha }\mid \gamma _R^{\beta }(E\pm h+(2r-1)eV)\mid ^2\prod _{r=1}^{n}\mid \gamma _L(E\pm h+2reV)\mid ^2 \nonumber \\{} & {} \quad \approx \Theta \Big (\Delta _R^{\beta }(\varphi ,\theta )+E\pm h+eV\Big )\Theta \Big (\Delta _R^{\beta }(\varphi ,\theta )-E\mp h-(2n-1)eV\Big )\nonumber \\{} & {} \qquad \Theta \Big (\Delta _L(\varphi )+E\pm h+2eV\Big )\Theta \Big (\Delta _L(\varphi )-E\mp h-2neV\Big ),\nonumber \\{} & {} \prod _{r=1}^{n}\mid \gamma _R^{\bar{\beta }}(E\pm h-2reV)\mid ^2\prod _{r=1}^{\alpha }\mid \gamma _L(E\pm h-(2r-1)eV)\mid ^2 \nonumber \\{} & {} \quad \approx \Theta \Big (\Delta _R^{\bar{\beta }}(\varphi ,\theta )-E\mp h+2eV\Big )\Theta \Big (\Delta _R^{\bar{\beta }}(\varphi ,\theta )+E\pm h-2neV\Big ) \nonumber \\{} & {} \qquad \Theta \Big (\Delta _L(\varphi )-E\mp h+eV\Big )\Theta \Big (\Delta _L(\varphi )+E\pm h-(2n-1)eV\Big ), \nonumber \\{} & {} \prod _{r=1}^{\alpha }\mid \gamma _R^{\beta }(E\mp h-(2r-1)eV)\mid ^2\prod _{r=1}^{n}\mid \gamma _L(E\mp h-2reV)\mid ^2 \nonumber \\{} & {} \quad \approx \Theta \Big (\Delta _R^{\beta }(\varphi ,\theta )-E\pm h+eV\Big )\Theta \Big (\Delta _R^{\beta }(\varphi ,\theta )+E\mp h-(2n-1)eV\Big )\nonumber \\{} & {} \qquad \Theta \Big (\Delta _L(\varphi )-E\pm h+2eV\Big )\Theta \Big (\Delta _L(\varphi )+E\mp h-2neV\Big ), \nonumber \\{} & {} \prod _{r=1}^{n}\mid \gamma _R^{\bar{\beta }}(E\mp h+2reV)\mid ^2\prod _{r=1}^{\alpha }\mid \gamma _L(E\mp h+(2r-1)eV)\mid ^2 \nonumber \\{} & {} \quad \approx \Theta \Big (\Delta _R^{\bar{\beta }}(\varphi ,\theta )+E\mp h+2eV\Big )\Theta \Big (\Delta _R^{\bar{\beta }}(\varphi ,\theta )-E\pm h-2neV\Big ) \nonumber \\{} & {} \qquad \Theta \Big (\Delta _L(\varphi )+E\mp h+eV\Big )\Theta \Big (\Delta _L(\varphi )-E\pm h-(2n-1)eV\Big ), \end{aligned}$$
(17)

where \(\alpha =n[n+1]\) is related to \(\beta =+[-]\) and \(\bar{\beta }=-[+]\), and \(\gamma _L\) is given by Eqs. (6) and (7) with \(\Delta =\Delta _L(\varphi )\), while \(\gamma _R^{\pm }\) are given by

$$\begin{aligned} \gamma _R^{\pm }(\varphi , \theta )= & {}\, \frac{E-i(\Delta _R^{\pm }(\varphi , \theta )^2-E^2)^{1/2}}{\Delta _R^{\pm }(\varphi , \theta )}\hspace{3mm} \textrm{for} \hspace{3mm} E<\Delta _R^{\pm }(\varphi ,\theta ), \end{aligned}$$
(18)
$$\begin{aligned} \gamma _R^{\pm }(\varphi , \theta )= & {}\, \frac{E-(E^2-\Delta _R^{\pm }(\varphi , \theta )^2)^{1/2}}{\Delta _R^{\pm }(\varphi , \theta )}\hspace{3mm} \textrm{for} \hspace{3mm} E>\Delta _R^{\pm }(\varphi ,\theta ). \end{aligned}$$
(19)

The finite integrand exists only in the region where the scattering probabilities are non-vanishing.

4 Results and discussion

4.1 s-wave superconductor/ferromagnet/s-wave superconductor junctions

It is known [19] that CVCs of ballistic high-transparent SNS junction shows several characteristic features. One of them is a sudden increase of the current at low voltage, known as “foot” of the characteristics and is explained by large transfer of charge, which is made possible by the large number of Andreev reflections that each quasiparticle experience before it is scattered or leaves the pair potential well. Since the number of Andreev reflections at low voltages is specified by the inelastic scattering length l, as \(n\approx l/d\), “foot” emerges for sufficiently large l. It is also well-known [16,17,18,19, 52] that on the curve of the dynamic conductance \(G(V)=dI/dV\) there are a number of dips at certain bias voltages \(eV_n=2\Delta /n\), where n is the natural number, known as subharmonic gap structure (SGS). The arches of SGS and posible negative differential conductance associated with them are also true signature of multiple Andreev reflection.

Transport properties of SFS junctions strongly depend on value of the exchange energy h in F. We investigate this kind of junctions in Popović et al. [44] and here we present the most relevant results. In the following we will discuss the effects of different parameters such as d, l, h and temperature on CVC and conductance curves. We introduce the following reduced units: \(\tilde{h}=h/\Delta (T)\), \(\tilde{V}=eV/\Delta (T)\), \(\tilde{d}=d/\xi _0\) and \(\tilde{l}=l/\xi _0\). The total current is the sum of ohmic current and current due to the Andreev reflection, \(I=I_N+I_{AR}=L_xL_y(\langle j_N\rangle +\langle j_{AR}\rangle )\). This current is normalized by the temperature-dependent current \(I_0=2\Delta (T)/eR_N\). Our theoretical approach deals with junction in a clean regime, where parameters h and l for fixed d obeys the following inequalities: \(h>\hbar /T_S\), \(l>d\). Opposite inequalities correspond to a dirty regime [53].

Fig. 1
figure 1

a Current–voltage characteristic I(V) for \(T/T_c=0.05\), \(d/\xi _{0}=0.5\), \(l/\xi _{0}=4.5\), and three different values of the exchange energy \(h/\Delta (0):\) 0, 0.5 and 4 (from top to bottom). b Conductances G(V) for the same parameters as in (a)

Full size image

The influence of parameters l, d and T on CVCs shape in SNS and SFS case are similar, but in SFS case the effect of exchange field on transport properties is dominant. We found new h-induced structures in transport properties (CVCs and conductances), which are most pronounced for h not to large, \({\tilde{h}}\lesssim 1\), see red curve on Fig. 1. While for \({\tilde{h}}\gg 1\) there are no additional structures and CVCs are monotonous, see blue curve on Fig. 1. These new-induced structures for \({\tilde{h}}\lesssim 1\) are primarily affected by the effects of exchange field on Andreev reflection, and this influence is more visible in the bias voltage conductance dependence G(V). At low voltages, the effects of AR are still visible for h of the order of several \(\Delta\), for small barrier thickness d and relatively large l. The presence of exchange field affects the CVC and conductance curves in a way that curves have more nonlinear structures in the voltage range \({\tilde{V}}< {\tilde{h}}\), since this is the region of multiple ARs. Pronounced structures with one or two peaks between each pair of voltages \(\tilde{V}_{n+1}\) and \(\tilde{V}_n\) are present in the voltage range \(\tilde{V} > \tilde{h}\). For this voltage range our numerical calculation shows that CVC calculated with only a few n, coincide with those obtained with large n (\(n=100\) or more). Unlike the SNS case, one peak in CVC curve i.e. dip in corresponding conductance curve for \(\tilde{V} >2\) is always present in SFS junctions. This could be explained by analogy with SNS case [54]. After n Andreev reflections the energy received from the field in the barrier with potential V will be neV, and this energy is equal \(2\Delta\), since this is the maximum energy quasiparticle can absorb in the barrier. Therefore in SNS junction, at voltages \(eV=2\Delta (T)/n\) nonlinearities in transport curves will appear. In SFS junctions, since the energies are shifted by h, position of dips outside of MAR region in conductance curves (or peaks in CVC curves) are determined by relation \(neV\pm h=2\Delta (T)\).

Fig. 2
figure 2

Conductance spectra G(V) for \(h/\Delta (0)=0.5\), \(T/T_c=0.05\), \(d/\xi _{0}=0.5\), and l/d ratio variation (\(l/d=1, 2, 10, 15\))

Full size image

Also, we found that for higher voltages, the curves of CVC are moved to lower values of current with increasing h. This is expected since AR is affected by the polarization of the conduction electron in F [55, 56], in a way that with increasing h AR is reduced. Since, the exchange energy induces band splitting in F, electron and hole from process of AR lose their correlation and reduce the number of Cooper pairs that can be form and enter into S [57].

In the following we will discuss the effect of barrier thickness d and inelastic scattering length l on transport properties. This issue is important since l/d ratio in the KGN approach is considered as an input parameter. Most of the other theories [16, 17, 52, 58, 59], do not consider the finite ballistic condition.

All conductance curves from Fig. 2 have well visible dips at \(eV=(2\Delta \mp h)/n\). This formula determines position of dips at any temperature up to \(T_c\). The l/d ratio variation changes a dynamic conductance background, as well as the amplitudes and area of the Andreev minima. From Fig. 2, it can be also seen that change in l/d ratio does not change their position. The same conclusions exist in the case of SNS junction, as one can see in Popović et al. [60] where results for amplitudes of SNS Andreev dynamic conductance minima as a function of l/d ratio are presented. Also for the first time, comparison between experimental data obtained by “break-junction” technique and theoretical prediction in the framework of presented theory for temperature dependence of amplitudes and areas of Andreev features are presented, in high transparent SNS junction [60]. Break junction methodology [61] proved to be successful in comparison with our theoretical model. This experimental technique has the ability to provide CVC and conductance spectrum which enables it to study the gap anisotropy as well as the determination of the amplitude of the order parameter in multi gap superconductors based on the position of the Andreev minima. These will be the directions of our future theoretical research.

To emphasize the effect that barrier thickness has on CVCs we present on Fig. 3 curves for relatively large l and different barrier thicknesses. The shape of the curves depend on first place on d. We observe a sudden increase in CVCs at low voltage for thin F barrier. With increasing barrier thickness, CVCs shift down and becomes less structured. Since the number of irregularities is determined by h, structures of CVCs remarkably disappear particularly for large h.

Fig. 3
figure 3

a Current–voltage characteristic I(V) for \(h/\Delta (0)=1\), \(l/\xi _0=4.5\), \(T/T_c=0.05\) and three different values of the barrier thickness \(d/\xi _0=0.5, 1.5, 3\) (top down). Inset: The same as in (a) for \(h/\Delta (0)=0.5\) and \(l/\xi _0=7.5\). b Current–voltage characteristic I(V) for \(h/\Delta (0)=4\), \(l/\xi _0=4.5\), \(T/T_c=0.05\) and two values of the barrier thickness \(d/\xi _0=0.5, 1.5\) (top down). Taken from Ref. [44]

Full size image

The influence of the inelastic scattering length l on CVC is presented in Fig. 4. At low voltage, CVCs decrease with diminishing l. At higher voltages CVC curves are independent on value of l and h.

Fig. 4
figure 4

Current–voltage characteristic I(V) for \(T/T_c=0.05\), \(d/\xi _0=0.5\), and two values of the inelastic scattering length in the barrier \(l/\xi _0\): 4.5 (top) and 3.75 (bottom). a \(h/\Delta (0)=1\), b \(h/\Delta (0)=4\). Taken from Ref. [44]

Full size image

4.2 d-wave superconductor/ferromagnet/d-wave superconductor junctions

In DFD junctions, beside the parameters that are important in SFS case such as, barrier thickness d, inelastic scattering length l, temperature T, transport properties are determined by mutual influence of exchange field h in the barrier and pair potential anisotropy. We investigated this junction in Popović et al. [45,46,47] and here we review the most important results. We will present the influence of all above parameters in reduced units, \(\tilde{h}=h/\Delta (T)\), \({\tilde{V}}=eV/\Delta (T)\), \(\tilde{d}=d/\xi _{ab}\) (\(\xi _{ab}\) is the coherence length in the \({\hat{a}}-{\hat{b}}\) plane) and \({\tilde{l}}=l/\xi _{ab}\). Having in mind experiments with DFD trilayers where exchange energy is between 2 and 14 meV, barrier thickness vary between 4.5 and 45 nm, while in YBCO \(\Delta \sim 15\) meV and \(\xi _{ab}\) is about 1.5 nm [39, 40, 62,63,64], we illustrate our results by taking h and d of the same order of magnitude as in experiments meaning \(\tilde{h}\lesssim 1\) and \(\tilde{d}\approx 1\).

First we note that even for small h, while in isotropic s-wave case CVC curves show many nonlinear structures, in unconventional junctions with gap nodes in superconductor, CVCs becomes smooth. This is due to the fact that direction of quasiparticle momenta corresponding to the position of gap nodes, don’t participate in MAR. Only a subset of momenta directions participating in MAR will result in CVC nonlinearities, which leads to smoothing of previously found nonlinear structures in s-wave case, regardless of the value of h. This is presented in Fig. 5 where we compare the anisotropic cases: d-wave symmetry (\(\Delta =\Delta (T)cos2\varphi\)) and fully anisotropic s\(^A\)-wave (\(\Delta =\Delta (T)\mid cos2\varphi \mid\)) with isotropic s-wave one. Suppression of AR by gap nodes in anisotropic junctions is obvious and can be seen by comparison with CVC for isotropic s-wave case which shows prominent nonlinearities and higher current.

Fig. 5
figure 5

Current–voltage characteristic I(V) for \(T/T_c=0.05\), \(l/d=9\), \(h/\Delta (0)=1\) and three order parameter form: isotropic s-wave, fully anisotropic s\(^A\)-wave (\(\Delta =\Delta (T)\mid cos2\varphi \mid\) ) and d-wave for \(\theta =0\) (top down). Taken from Ref. [45]

Full size image

The angle of orientation of d-wave electrodes with respect to the FD interface influences transport properties of DFD junction. In order to study orientation effect we take (100) orientation of the left electrode, while for the right electrode we assume arbitrary orientation angle \(\theta\). With increasing \(\theta\), CVC is approaching the ohmic linear dependence without “foot”. “Foot” is present only at low voltage, due to MAR, for small misorientation, Fig. 6, which is connected with the orientation dependence of the proximity effect [46, 65]. Transport properties of DFD junction are significantly influence by proximity effect, as well as by misorientation angle \(\theta\). Namely, the superconducting order parameter (OP) in D decreases near the interface with increasing misorientation angle from \(\theta =0\) toward \(\theta =\pi /4\). For \(\theta =0\) order parameter show small decrease, while for \(\theta =\pi /4\) which means that x axis is a nodal direction of OP, order parameter in D has the biggest decrease. This is connected with a pronounced pair-breaking effect for strong proximity effect (for \(\theta =\pi /4\)) occurring due to spin-polarized electron injected from F to D. On the ferromagnetic side, since Cooper pairs are injected from D to F, there is a oscillation of superconducting OP due to the proximity of D, since ELQ and HLQ interfere with each other. The period of this oscillation for \(\theta =0\) is close to \(2\pi \xi _F\), where \(\xi _F=\hbar v_F/2h\) is the coherence length in ferromagnet, and is significantly longer than the corresponding period for \(\theta =\pi /4\) case [65].

Fig. 6
figure 6

Current–voltage characteristic I(V) for \(T/T_c=0.05\), \(l/\xi _{0}=27\), \({\tilde{d}}=d/\xi _{0}=3\), \({\tilde{h}}=h/\Delta (0)=0.5\) and four different values of misorientation angle \(\theta =0\) (black solid line), \(\pi /8\) (blue dotted line), \(\pi /4\) (pink dashed line) and \(\pi /2\) (orange dash-dotted line). Taken from Ref. [46]

Full size image

Interplay between decoherence mechanisms for propagation of Andreev pairs in barrier such as misorientation angle, exchange field induced pair breaking, temperature and bias voltage and phase-coherent propagation of Andreev pairs could be seen in exchange field dependence of the current and also in exchange field dependence of zero bias conductance \(\Gamma =dI/dV \mid _{V=0}\). These transport properties show nonmonotonic behavior as a function of h. The exchange field always breaks the induced Cooper pairs if we have strong enough ferromagnet. But more interesting situation happens in a case of weak exchange field in F when quasiparticle current can be even enhanced at low voltage which is connected with the possibility of multiple AR. We expect that mechanism for current enhancement is similar as in s-wave case [66,67,68,69]. Proximity effect in both D and F determine the form of I(h) curves, as well as \(\Gamma (h)\) curves.

For a weak exchange field, independently of the misorientation of superconducting electrodes (for any \(0\le \theta \le \pi /4\)) there is always a strong proximity effect in F, providing that thickness of barrier is smaller than magnetic coherence length, \(d<\xi _F(\theta )\), Fig. 7a. Consequently, in the whole ferromagnet OP is significantly induced. This leads to enhancement of current up to \(h\approx \Delta\), even for \(\theta =0\), with a possibility of small decrease for \(h<eV\). Minimum at I(h) curve for \(\theta =0\) occurs because the exchange field can not compensate the depairing effect of the applied bias voltage up to \(h=eV\) (see inset of Fig. 7a). In a similar way exchange field dependence of zero bias conductance (ZBC) in thin ferromagnetic barrier show enhancement up to \(h\approx \Delta\), for every angle \(\theta\), Fig. 8b.

For a weak exchange field and thick ferromagnetic barrier (Figs. 7b, 8a) proximity effect increase with \(\theta\) causes the current and ZBC to increase with exchange field up to \(h\approx \Delta\), except for \(\theta =0\) where proximity effect is weakest. ZBC can increase weakly with h up to \(h\approx \Delta\), even when the junction parameters approach the dirty limit case (inset of Fig. 8a).

Fig. 7
figure 7

The exchange field dependence of the current I(h) for \({\tilde{V}}=eV/\Delta (0)=0.2\), \(l/\xi _{0}=27\), \(T/T_c=0.05\), and three values of misorientation angle \(\theta =0\) (black solid line), \(\pi /8\) (blue dotted line) and \(\pi /4\) (pink dashed line). a \({\tilde{d}}=d/\xi _0=1\). b \({\tilde{d}}=d/\xi _0=3\). Inset: The same (a) for \(\theta =0\) and two values of the bias voltage \({\tilde{V}}=0.2\) and 0.3. Taken from Ref. [46]

Full size image
Fig. 8
figure 8

The exchange field dependence of ZBC \(\Gamma (h)\) for \(T/T_c=0.05\), \(l/\xi _0=27\) and two values of misorientation angle \(\theta =0\) (black dashed line), \(\pi /4\) (red solid line) and \(\pi /8\) (blue dash-dotted line). a \({\tilde{d}}=d/\xi _0=3\). b \({\tilde{d}}=d/\xi _0=1\). Inset: \(\Gamma (h)\) for non clean limit case \(l/\xi _0=3\), \({\tilde{d}}=d/\xi _0=3\), \(T/T_c=0.05\) and \(\theta =\pi /4\). Taken from Ref. [47]

Full size image

The influence of OP symmetry on phase coherent process of Andreev pairs propagation is better seen on conductance curves. In Fig. 9, we show comparison between s-wave, extended s-wave, d-wave, and misoriented d-wave case. In the low voltage region, \({\tilde{V}}\lesssim {\tilde{h}}\), where multiple Andreev reflection occur, curves have more nonlinear structure, which is confirmed by our numerical calculation. The nonlinear structure for d-wave superconductor is not as sharp as in isotropic s-wave case because of angular averaging. The shapes of G(V) are quite similar at higher voltages with few well defined dips. Position of dips are independent on misorientation angle in a case of d-wave superconductors and also independent on pair potential symmetry, but vary with exchange field and temperature according to formula \(neV=2\Delta (T)\mp h\), where \(n=0,1,\ldots\). Using this results, the value of exchange field in the barrier could be determined by measuring the location of conductance curve dip at given temperature.

Fig. 9
figure 9

Conductance G(V) for \(T/T_c=0.05\), \(d/\xi _{ab}=3\), \(l/\xi _{ab}=27\), \(h/\Delta (0)=0.5\) and four order parameter form: a s-wave, b extended s-wave (s*) superconductor (\(\Delta =(\Delta (T)/4)(1+3cos4\varphi )\)), c d-wave without misorientation \(\theta =0\), and d d-wave with misorinetation \(\theta =\pi /4\). Adopted from Refs. [45] and [46]

Full size image
Fig. 10
figure 10

Temperature dependence of ZBC \(\Gamma (T)\) for \(d/\xi _0=3\), \(l/\xi _0=27\) and two value of misorientation angle \(\theta =0\) (black dashed line) and \(\pi /4\) (red solid line). a \({\tilde{h}}=h/\Delta (0)=3\). b \({\tilde{h}}=h/\Delta (0)=0.8\). c \({\tilde{h}}=h/\Delta (0)=0.7\). Taken from Ref. [47]

Full size image

All conductance curves are presented for low temperature \(T/T_c=0.05\). With increasing temperature conductance curves becomes flatter, having more nonlinear structures in the MAR region at low voltage, and few nonlinearities at high voltages which position are independent of order parameter symmetry.

Analyzing the temperature dependence of \(\Gamma\) we found that it is a decreasing function of temperature independent on the exchange field and on the angle of misorientation, since Andreev reflection is suppressed for \(T\rightarrow T_c\). Note that current transport at zero voltage is determined by AR and the inelastic l/d ratio. While for large exchange field \(\Gamma\) is monotonically decreasing function of temperature, Fig. 10a, for small exchange field, \(h<\Delta (0)\), ZBC decreases with temperature and show clearly pronounced kink at temperature \(T^*\), Fig. 10b and (c). From our numerical results it follows that \(h=\Delta (T^*)\). This could be a useful way to extract the value of the exchange field in the experiment by observing kink at \(T^*\) in \(\Gamma (T)\) curve. Note that the value of h should be smaller or of the order of \(\Delta\).

Recently there is a progress in preparation of junction with weak ferromagnet materials [70, 71], which was followed by several suggested detection methods of measuring small exchange field. One of them follow from Ref. [72] where it is suggested to measure ZBC in several FD bilayers at given temperature, for different h. We believe that it is experimentally easier for given ferromagnetic barrier to change temperature and extract h from kink at \(T^*\). Also in SF bilayer with \(h<\Delta\) at zero temperature [66, 69], or DF bilayer with \(h\approx \Delta\) at low temperature and for all orientation of the superconducting electrodes [73], exchange field can be determined from the position of the peak on the subgap conductance at \(eV=h\).

5 Conclusions and future perspectives

We present our theoretical research of quasiparticle transport properties, such as current–voltage characteristic and conductance, in voltage-biased SFS and DFD junctions. Our main results correspond to influence of weak exchange field on transport properties. We proposed two methods for the experimental determination of weak exchange fields. Conductance curve (outside of MAR region), shows a regularities in the appearance of dips at higher voltages in accordance with \(eV=(2\Delta (T)\pm h)/n\), which could be a good way to experimentally determine the value of exchange field in weak ferromagnetic barrier. Also, temperature dependence of zero bias conductance in DFD junction with misoriented superconducting electrodes shows kink at some particular temperature \(T=T^*\). Observing temperature \(T^*\) one can determine the value of exchange field, since \(h\approx \Delta (T^*)\). These results are significant from the point of view of experimental efforts to synthesize ferromagnets with small exchange field. Another important result is the possibility to experimentally extract the value of superconducting gap, as well as order parameter nature. Our theoretical results come to the attention of experimental group, which was followed by joint research [60].

We are planing to generalize existing theory to the case when superconducting electrodes in a junction are in the dirty regime i.e. with the possibility of taking arbitrary value for the inelastic scattering length. Second direction is extension towards the study of gap anisotropy in superconductors.