Abstract
The next years will see the completion of several new facilities at Istituto Nazionale di Fisica Nucleare – Laboratori Nazionali del Sud (LNS) opening up new possibilities in the fields of nuclear structure, nuclear dynamics, nuclear astrophysics and applications. These include a new line for high-intensity cyclotron beams, a new facility for in-flight production of radioactive ion beams, the PANDORA plasma trap for multidisciplinary studies and a high-power laser for basic science and applied physics. The nuclear physics community has organized a workshop to discuss the new physics opportunities that will be possible in the middle term (5–7 years) by employing state-of-the-art detection systems. A detailed discussion of the outcome from the workshop is presented in this report.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Executive summary
The LNS is an user-oriented large-scale facility dedicated to basic nuclear and subnuclear physics studies and to the development of applications with important benefit for society. The LNS accelerator complex consists of a K-800 superconducting cyclotron (SC) and a 13.5 MV Tandem. To fulfill the requests of users aiming to study rare processes in nuclear physics, a significant upgrade of the entire setup is currently in progress. The availability of new beams and new facilities (discussed in Sect. 2) called for a thorough discussion on the midterm research plan to be carried out. The Nuclear Physics Mid Term Plan in Italy made it possible to trigger and coordinate new ideas proposed by the international community interested in such experimentations, in particular by younger nuclear physics researchers that will be the leading force in the exploitation of the new facilities. The LNS session of the workshop included four working groups on nuclear dynamics, nuclear structure, nuclear astrophysics and applications, involving experimentalists and theoretists.
This initiative follows the previous INFN Nuclear Physics Division joint works on nuclear astrophysics [1] and on particle identification [2].
1.1 Nuclear dynamics
Nuclear dynamics includes a large number of phenomena that allow to explore the relevant properties of the nuclear medium. Heavy-ion collisions (HIC) represent a powerful tool of investigation in this field, spanning a wide range of energies at LNS and creating different regimes of nuclear matter. In this way they could provide information on various aspects, from the features of nuclear equation of state (EOS) to the structure of nuclei and their decay modes, up to the dynamics of the nuclear reactions to produce nuclei in the region of “terra incognita”, far from the stability valley. In the framework of nuclear dynamics, three principal subjects “Heavy-Ion Collision and Equation of State” (Sect. 3.1), “Clustering” (Sect. 3.2) and “Fission Dynamics” (Sect. 3.3) were addressed.
Section 3.1 explores some new ideas and devices that, by using stable and radioactive beams at LNS in the Fermi energy domain, will improve the precision and the reliability of the symmetry energy constraints at densities below saturation (\(\rho \le 0.17 \textrm{fm}^{-3}\)). In particular, the symmetry energy will be investigated through the study of the dynamical dipole, an observable connected to the stiffness parameter, and by using advanced multidetectors such as CHIMERA, FARCOS and FAZIA, also coupling new devices for neutron detection. FraISe (Sect. 2.2.2) beams will be particularly important to span a broad isospin range.
The working group on “Clustering” (Sect. 3.2) proposes some new ideas to carry out very precise measurements of already known cluster states in a number of key nuclei and to search for new cluster structures and their decays, in previously unstudied nuclei or even new mass regions. Investigations of cluster states other than providing results on the clustering effects can also show the presence of neutron halos and skins, or \(\alpha\)-condensate structures, especially in medium–light nuclei. Tandem beams (including long-lived radioactive nuclei, see Sect. 5 and noble gas beams, Sect. 5.1.1) will be used in parallel to FraISe beams.
The “Fission Dynamics” working group (Sect. 3.3) has focused on shell effects in fission and quasifission (Sect. 3.3.1), on multinucleon transfer reactions to investigate “Terra Incognita” (Sect. 3.3.1), and on possible alternative paths to produce superheavy elements (Sect. 3.3.5), mostly using high-intensity cyclotron beams as cross sections can be as low as few pb. Besides the theoretical developments, new tools such as the addition of a time-of-flight arm to the MAGNEX spectrometer (Sect. 2.3) will be necessary to carry out the research program.
The time phases for the different physics programs are shown in Fig. 1, where A, B and C are used for the shorter to longer time intervals. The detailed timeline is presented in Table 4.
1.2 Nuclear structure
Nuclear structure (Sect. 4) addresses static properties of nuclei in their ground and excited states. These studies are characterized by important interfaces to nuclear dynamics. New ideas were gathered along two lines: the study of the nuclear matrix elements (NMEs) toward neutrinoless double-beta decay \(0\nu \beta \beta\)-decays (Sect. 4.1), with a synergistic work on the development of theoretical models and on the combined use of high-intensity beams and advanced spectrometry; and the study of collectivity in nuclei (Sect. 4.2).
The working group on NME focuses on single charge exchange (SCE) and double charge exchange (DCE) reactions (Sect. 4.1.2) induced by heavy ions as well as double \(\gamma\)-decay process (Sect. 4.1.6) to reduce uncertainties in the calculations of the NME. Indeed, the NME is a crucial ingredient in the expression of the \(0\nu \beta \beta\) half-life, describing the transition probability of nuclear processes. To date, results produced by different models to evaluate NME show a spread by a factor of three, leading to big uncertainties both on the amount of material required in the experiments and on the neutrino mass. To this purpose, state-of-the-art nuclear structure models (realistic SM, Skyrme-QRPA and IBMs, see Sect. 4.1.7 for details) will be developed to provide the input for direct and transfer heavy-ion SCE and DCE reactions.
As discussed in Sect. 4.1, the idea is to use heavy-ion DCE reactions to acquire information on the \(0\nu \beta \beta\) decay exploiting possible analogies between the two processes, as already pointed out for single CE excitations and \(\beta\) decay. To acquire experimental information on the \(0\nu \beta \beta\) NMEs, the NUMEN project proposes to use heavy-ion DCE reactions, with high-intensity beams and advanced spectrometry, as surrogates for \(0\nu \beta \beta\) decays. Although their different nature, these two processes, in fact, show possible analogies as discussed in Sect. 4.1.1.
Improved statistics using high-intensity beams from the LNS SC will make it possible to extend the studies to a larger number of systems presently not accessible due to the low cross sections. In the experimental approach to DCE reactions, a key tool will be the MAGNEX 2.3 magnetic spectrometer, with its upgrade to sustain high rates and at the same time to maintain the current resolution and sensitivity.
An additional topic is the investigation of collectivity in nuclei (Sect. 4.2), using FraISe (Sect. 2.2.2) beams in combination with the multidetectors available at LNS. In detail, FraISe day-one experiments will be devoted to Pigmy dipole resonance (PDR) search and then dynamical dipole studies in reactions induced by Ar isotopes on Ca or Ni isotope will be addressed. Phenomena linked with the giant dipole resonance (GDR), such as quenching of the GDR \(\gamma\)-ray yield and its disappearance with the liquid–gas phase transition will be also investigated, in connection with the nuclear dynamics working group.
The time phases for the different physics programs are shown in Fig. 2, with the same meaning for the three time steps. The detailed timeline is presented in Table 5.
1.3 Nuclear astrophysics
Nuclear astrophysics (Sect. 5) is an interdisciplinary field which connects astrophysics (mainly stellar physics and cosmological nucleosynthesis) to experimental techniques of low-energy cross section measurements and nuclear physics theory. In the last two decades, the measurements/calculations of many cross sections of astrophysical interest have been greatly improved. However, in several cases present uncertainties still affect the predictions for stellar characteristics and element nucleosynthesis. LNS has undoubtedly played a leading role within this framework with its stable and unstable beams.
In Sect. 5.1, “Nuclear and Atomic Inputs for Quiescent Stellar Evolution”, light elements depletion (Sect. 5.1.1) will be studied, in particular addressing the cosmological lithium problem, to date the most critical issue in our understanding of the early universe. Its investigation will benefit from the possibility of studying \(^{7}\)Be half-life (Sect. 5.1.2) in strongly ionized stellar environments by means of the PANDORA plasma trap (Sect. 2.3). Reaction involving heavier ions, taking place in advanced stellar evolutionary stages such as carbon and oxygen burning (Sect. 5.1.3) and NeNaAl cycle (Sect. 5.1.4), will be also studied using direct and indirect methods, especially thanks to the availability of the NESTOR source to be installed at the LNS Tandem. Also, nuclear reactions in hot and dense plasmas similar to the astrophysical ones will be studied thanks to the availability of the I-LUCE facility (Sect. 2.3).
Astrophysical most violent phenomena such as Novae, Supernovae, X-Ray Bursts and neutron-star mergers involve unstable nuclei (Sect. 5.2.2). As already tested using \(^{10}\)Be, at LNS it will be possible to accelerate long-lived isotopes at Tandem (\(^{26}\)Al,\(^{10}\)Be,\(^{44}\)Ti) at high intensities and angular/energy resolution, making it possible to understand, among others, the birth of the solar system. FraISe beams will be also used to access the isotopes far from the stability valley, exploring regions in the nuclear chart complementary to the ones reached by SPES.
Since nuclei heavier than iron are mostly produced through neutron captures (the so-called s- and r-processes), Sect. 5.3 is devoted to the direct and indirect studies of stellar neutron sources and neutron poisons (Sect. 5.3.1). A major role in shaping the path toward heavy ions is played by \(\beta\)-decays; PANDORA will allow very precise half-life/branching ratio measurements in stellar plasma for elements which are determinant for the s-process. Away from the stability valley, the POLYFEMO neutron detector will make it possible to characterize \(\beta\)-delayed neutron emission (Sect. 5.3.4). Along with the SC and the Tandem, laser beams will also make it possible to produce neutron beams for direct measurement of n-induced reactions (Sect. 5.3.2). Finally, the PANDORA facility may allow the measurement of opacities at electron densities and temperatures resembling some ejecta plasma conditions, sheddding light on r-process-generated metallic species at specific time stages of the Kilonovae diffusion.
The time frame for the different physics programs is shown in Fig. 3. The detailed timeline is presented in Table 6.
1.4 Nuclear physics applications
Nuclear physics applications span a very broad range of topics. In Sect. 6 we will discuss the perspectives at the LNS for the coming years on this subject. We can identify three major scientific areas (medical, laser and plasma traps applications) also in relation to the main LNS facilities, the new laser system and the plasma trap PANDORA. Activities related to medical applications (Sect. 6.1) are well consolidated, starting from the 2000s with the construction of the CATANA facility for hadron therapy. Future study programs in this area are still focused on the availability of stable LNS beams, covering hot topics such as the flash radiotherapy and flash BNCT (boron–neutron capture therapy). The forthcoming high-intensity beams (HIBs) and radioactive ion beams (RIBs) that will be available at LNS in the near future (Sect. 6.1.2) will open new and interesting perspectives. In particular, RIBs can trigger new approaches for innovation on treatment methods that could be coupled with online contemporary diagnostic tools and will trigger cross section studies for new exotic radioisotopes and radiopharmaceutical drugs.
The near future of LNS research activities also involves the new high-power laser facility (Sect. 6.2) and the almost unique possibility to have, in the same experimental area, intense laser-accelerated and conventional ion beams. All the new acceleration schemes developed in the recent years triggered ideas and proposals for the development of new and compact laser-driven secondary sources (Sect. 6.2.1), for the measurement of stopping power in warm dense matter (Sect. 6.2.2) and for the hydrogen production from water by focused femtosecond laser pulses (Sect. 6.2.3).
In Sect. 6.3, the potential applications deriving from the developments related to the PANDORA facility are highlighted. The section is divided into three main topics: (i) magnetic plasmas and related issues (ions heating, charge breeding, stopping power, etc., Sect. 6.3.1); (ii) physics and technology aspects for fusion plasmas (Sect. 6.3.2); and (iii) innovative plasma chambers and resonators for compact reactors development (Sect. 6.3.3).
The timeline for the different physics programs is shown in Fig. 4. The detailed timeline is presented in Table 7.
2 Introduction
2.1 The LNS accelerator complex
The LNS accelerator complex consists of a K-800 superconducting cyclotron and a 13.5 MV Tandem.
The LNS superconducting cyclotron (SC) is a three-sector compact machine with a wide operating range, able to accelerate heavy ions of q/A from 0.1 to 0.5 at energies from 10 to 80 AMeV [3]. The SC has been in operation for more than 20 years, delivering beams mainly devoted to nuclear and applied physics experiments. The beam extraction efficiency, during its lifetime, has been lower than 60%, and for such a reason, the maximum beam power was limited to about 100 W, constrained by the beam power dissipation on the electrostatic deflectors.
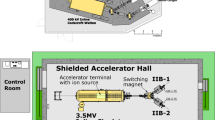
To fulfill the request of users aiming to study rare processes in nuclear physics [4, 5] and provide high-intensity radioactive ion beams, complementary to those delivered by SPES at LNL, a significant upgrade of the entire setup is currently in progress. The upgrade was funded within the POTLNS project, triggered by the NUMEN physics case [4, 5], in the frame of a national program (PON) aimed at strengthening the research infrastructures identified as priorities, according to the European Strategy Forum on Research Infrastructures (ESFRI). The upgrade consists in a new extraction method based on the stripping of the accelerated ions [6,7,8] that will be used alternately with the electrostatic deflectors. Such a method is based on the instantaneous change of the magnetic rigidity of the accelerated ions, when their charge state suddenly increases after crossing a thin stripper foil. The final aim is to increase the beam power up to 2–10 kW for ions with mass A \(\le\) 40 and energy above 15 AMeV. This upper mass limit is connected to the fact that more than 99% of such ions can be fully stripped and therefore extracted from the SC. The reference trajectories for \(^{12}\)C, \(^{18}\)O, \(^{20}\)Ne and \(^{40}\)Ar are shown in Fig. 5. The feasibility of this kind of extraction through an optimized channel with an increased transverse section has been deeply studied in Refs. [9,10,11]. In the meantime, the radio-frequency (RF) system has gone through many improvements for more reliable operation of the SC [12, 13], also increasing to 30 mm the vertical gap between the “dees” of the acceleration chamber, by renewing the existing liners. Other upgrades are under study to further improve the SC performances in terms of intensities and accelerated species.
Figure 6 shows the layout of the new cyclotron, where together with the classical extraction through electrostatic deflection (ED) a second extraction channel has been added, with two further magnetic channels.
Moreover, upgrades of the ion sources and of the axial injection beam line are planned, in order to fully satisfy the requested beam intensity, as well as to optimize the optics and the matching with the SC in the phase space. All these improvements will be performed in the framework of high safety standards for the machine and for the operational staff. The SC recommissioning is foreseen to start in the late 2024 using the electrostatic deflection, while the first extraction by stripping ions is foreseen in the late 2025. Taking profit of the stop for the SC upgrade, also the Tandem is subject to a deep renovation of the hardware, electronics and automation. The power electronics and the diagnostics will be changed, while vacuum and optical element controls will be renewed. An extraordinary maintenance of the Pelletron charge system will be carried out to minimize the ripple and a new Tandem terminal voltage HV stabilizer will be installed. The Tandem has played a crucial role in the framework of nuclear studies as well as cross sections measurements for nuclear astrophysics (see, e.g., Refs. [14, 15]).
2.2 Beams
2.2.1 High-intensity stable beams
A full list of beams produced so far using the extraction by means of electrostatic deflection is shown in Table 1. Such beams will be always available through the ED extraction channel with a maximum power of about 100 W. Table 2 reports a list of the expected beams and intensities obtained through the new stripping extraction. The availability of new sources (aiming to reach higher charged states and injected currents) and further studies triggered by users’ requests will make it possible to significantly extend such list to other ion species over the years.
A list of the ions accelerated by the LNS Tandem in the last 20 years is shown in Table 3. In addition to those beams, the accelerator division is developing a new source able to provide He beams with this accelerator.
2.2.2 FraISe: a new in-flight fragment separator at LNS
In order to exploit the high beam power delivered by the upgraded SC, the POTLNS project has included the construction of a new In-Flight facility for Radioactive Ion Beams (RIBs) production, named Fragment Ion Separator (FraISe) [16,17,18].
The new FraISe facility will be hosted in a shielded area (bunker), as schematically shown in Fig. 7. It will allow to use primary beams of power up to \(\sim\) 2–3 kW. Figure 8 shows a schematic view of FraISe. The new production target is a copy of the CLIM one used in the LISE facility at GANIL [19]. It will be placed in a dedicated chamber and consists of a beryllium (or carbon) rotating disk of appropriate thickness, allowing to distribute the primary beam power on a circular crown of \(\sim\) 10–15 cm mean radius, allowing to keep the target degradation and heating under control. The beam line upstream the target chamber has been designed with a condition of energy achromatism and a very focused spot size of stable beam at target position, in order to optimize the outgoing cocktail beam.
A slit on the symmetry plane can be used to reduce the energetic dispersion of the outgoing beam. The exit slit will be used, when needed, to reduce and possibly remove contaminants from the cocktail beam, thus improving the quality and purity of the produced beams.
The FraISe line will allow to transport beams with a maximum magnetic rigidity of 3.2 Tm. The momentum acceptance is equal to 1.2\(\%\) and the solid angle acceptance to 2.5 msr. The momentum dispersion at symmetry plane is about 5 m, corresponding to an energy resolving power of about 2600 with 1 mm beam spot size. Given the high energy dispersion capability at the symmetry plane, FraISe will be very effective also in reducing the energy spread of the high-intensity primary beam extracted by the SC using the stripping method. These features will allow to use FraISe not only as in-flight facility, but also as a precise energy selector for those experiments requiring stable beams with very small energy dispersion. For example, it will be possible to reach an energy spread of 0.1\(\%\), a value which matches one of the mandatory constraints for the NUMEN experimental program [20].
An aluminum degrader can be placed close to the symmetry plane after the central slit, in order to modify the magnetic rigidity of species with similar A/Z ratio and perform a better rejection of contaminants.
Same as Fig. 9 but using a primary beam of \(^{20}\)Ne at 70 AMeV
Sizeable improvements in the yield production of light and medium mass exotic nuclei in the Fermi energy regime are foreseen due to the higher power of the primary beams following the SC upgrade. In order to present a few examples of the potentialities of the new fragment separator, simulations of RIBs production were carried out using the LISE++ tool [21] for few relevant cases. In these simulations, a 100-\(\upmu \textrm{m}\)-thick aluminum degrader was placed on the symmetry plane, and a 100-\(\upmu\)m-thick SiC detector (presently under test) at the exit of the fragment separator as tagging detector. The results have been obtained assuming 2 kW primary beams for the ions listed in Table 2, but only for a single beam energy. Thus, the same primary beams, but at different energies, can be used while keeping in mind that below E\(_{beam}\) = 25 AMeV the fragmentation becomes less effective in producing RIBs of sufficient intensities.
Simulated spatial distribution at the exit of the fragment separator on the horizontal direction (top panel) and \(\Delta E-ToF\) tagging plot (bottom panel), in the case of \(^{18}\)O\(^{8+}\) at 70 AMeV primary beam and for a tuning of the fragment separator maximizing the \(^{16}\)C production. For the sake of clarity, only the main contaminants are shown in the spatial distribution plot
For each isotope of interest, a \(^{9}\)Be production target was used with optimized thickness and the fragment separator was tuned in order to allow a good separation from the contaminants. To this aim, a \(\Delta\)E-ToF tagging plot was simulated, where the \(\Delta\)E is given by the energy deposited in the SiC detector and the ToF is the time difference between the radio-frequency signal of the SC and the timing signal of the SiC detector (with expected time resolution better than 500 ps). Figure 9 reports the expected intensities and average energies for RIBs produced by \(^{12}\)C\(^{6+}\) at 60 AMeV (left panel) and \(^{18}\)O\(^{8+}\) at 70 AMeV primary beams (right panel). Results indicate that about \(10^{7}\)-\(10^{8}\) pps can be reached for RIBs near the primary beams and the stability valley while yield production for nuclei far from stability valley can reach about \(10^{3}\)–\(10^{4}\) pps. Figure 10 shows the simulated yield production using a primary beam of \(^{20}\)Ne\(^{10+}\) at 70 AMeV.
To evaluate the potentially achievable beam purity, the spatial distribution at the exit of the fragment separator on the horizontal direction and the \(\Delta\)E-ToF tagging plot with \(^{18}\)O\(^{8+}\) at 70 AMeV as primary beam, with the fragment separator optimized for \(^{16}\)C production, were simulated. Results are shown in Fig. 11. The spatial separation with respect to the main contaminants on the plane of the slits is wide enough to ensure a high-purity \(^{16}\)C beam. Moreover, using primary beams of \(\sim\) 30 AMeV will result in a decrease, with respect to the case of \(\sim\) 70 AMeV, of \(\sim\) 1 order of magnitude for the expected intensities and final energies of 20–25 AMeV. Exploiting these light primary beams, it will be possible to efficiently span a relevant part of neutron-poor and neutron-rich unstable nuclei with A\(\le\)20. Figure 12 presents the results obtained using a primary beam of \(^{40}\)Ar\(^{18+}\) at 60 AMeV showing the wide spectrum of exotic isotopes of K, Ar, Cl, S, P, Si and Al that can be produced.
The use of other primary beams is possible, but it requires a special study devoted to investigate the acceleration and extraction trajectories inside the SC and the achievable output power. Further beams would allow to extend the already rich presented offer, and to investigate several physics cases of relevant interest. Possible examples are represented by the \(^{13}\)C primary beam which would allow to increase the yield of neutron-rich B, Be, Li isotopes and by the \(^{16}\)O which would allow to increase the yield of neutron-poor oxygen isotopes, with respect to what shown in Figs. 9 and 10. The \(^{22}\)Ne primary beam could be used to increase the yield of neutron-rich N, O, F isotopes, while the \(^{36}\)Ar beam is suited for a better production of neutron-poor isotopes. In addition, the use of heavier primary beams, such as Ni or Zn, could be also relevant for producing heavier isotopes and will be investigated in a near future, following the detailed characterization of the SC that will take place during the commissioning phase.
Thus, the availability of the RIBs offered by FraISE will be very competitive, in the international scenario, for light and medium mass nuclei at the Fermi energies. This will be complementary to what made available by the SPES facility [22], offering heavier beams at lower beam energies. The operation of both facilities in Italy will be very important for the nuclear physics community.
2.3 Facilities at LNS: present and future scenario
Keeping in with the main scientific mission of the LNS related to the study of fundamental nuclear physics, the LNS hosts several facilities and more are about to come. A brief overview will follow, starting from the existing ones and then moving on to outline the future scenario.
-
Multipurpose scattering chambers: CT2000 and GIRA: the LNS have traditionally provided the users with the CT2000 scattering chamber, placed at the end of the 60 degree beam line, available for experiments with Tandem beams. The chamber, with a diameter of 2 m, is equipped with 2 independently rotating arms to host the detectors and a collimation system with a goniometer that allows to measure precise angular distributions. The interior of CT2000 is shown in Fig. 13. The CICLOPE chamber, devoted to experiments with cyclotron beams, will be soon replaced with a smaller cylindrical chamber, called GIRA, with a diameter of 1.5 m and a length of 2 m, still reliable for complex detection systems with hundreds of detectors.
Multipurpose chambers have been used to perform experiments of nuclear physics and nuclear astrophysics, covering several topics such as the equation of state of nuclear matter and the role of symmetry energy, the influence and role of isospin and clustering, the stellar and primordial nucleosynthesis and energetics by means of the Trojan horse method and the asymptotic normalization coefficient.
-
CHIMERA: it is a 4\(\pi\) multidetector operating at LNS for about 20 years (see, for instance, Ref. [23] and Fig. 14). It is equipped with 1192 detection units, each consisting of a silicon first stage detector, followed by CsI(Tl) crystal coupled to a photodiode as second stage. Different particle identification methods are in operation (\(\Delta\)E–E, time of flight, pulse shape discrimination) for a complete detection of the charged particles emitted in nuclear collisions. Furthermore, the CsI(Tl) crystals can be used to detect and identify neutrons (by shadowing or vetoing the charged particle produced) and \(\gamma\)-rays.
CHIMERA will be coupled with the FARCOS [24] (Femtoscope ARray for COrrelations and Spectroscopy) correlator devoted to high angular and energy resolution particle-particle correlation studies. In its complete configuration, FARCOS will consist of 20 modules, each one made of two stages of double-sided silicon strip detectors (DSSSD) with thickness of 300 and 1500 \(\upmu\)m, respectively, and a third stage with a CsI(Tl) crystal+Si photodiode for a total of 132 detection channels. In future, an ancillary hodoscope for n, \(\gamma\) and charged particles will be also added. Feasibility studies are currently underway on an EJ-276G + SiPM prototype. Future CHIMERA experimental activity will be performed with the new high-intensity stable SC beams (see Sect. 2 and Table 2) as well as FraISe radioactive beams (see Sect. 2.2.2 and Figs. 9 and 10).
-
MAGNEX: it is a large acceptance magnetic spectrometer (see Fig. 15) that combines the advantages of traditional magnetic spectrometry with those of a large angular (50 msr) and momentum (\(-14{\%}\), + 10.3\(\%\)) acceptance detector [25]. The spectrometer consists of two large aperture magnets, i.e., a quadrupole followed by a 55\(^\circ\) dipole and a focal plane detector (FPD) for detecting the ions emitted during a reaction. The quadrupole magnet focuses in the non-dispersive (vertical) direction, while the dipole magnet provides the dispersion and the focusing strength in the dispersive direction (horizontal). Two ancillary surface coils are used to fine-tune and adapt the focusing to the kinematics of the reaction under study (\(\alpha\) coil) and to correct for chromatic aberrations (\(\beta\) coil). The accepted magnetic rigidities, B\(\rho\), range from \(\sim\) 0.2 Tm to \(\sim\) 1.8 Tm, corresponding to energies of the detected ions ranging from E \(\sim\) 0.2 AMeV to E \(\sim\) 40 AMeV, depending on their mass and charge. An intense activity is currently in progress for the upgrade of MAGNEX to withstand the forthcoming high rates (Table 2), while maintaining the current resolution and sensitivity. In particular, this upgrade will include [26]: a new power supply to increase the maximum magnetic rigidity acceptance from 1.8 to 2.2 Tm, resulting in an increase of the energy range of detected particles; a new focal plane detector (FPD), consisting of a gas tracker based on M-THGEM technology and a wall of telescopes of SiC-CsI detectors for ion identification (PID wall); a gamma–array calorimeter of LaBr (G-NUMEN); the development of suitable front-end and readout electronics, for a fast readout of the detector signals, a high signal-to-noise ratio and adequate hardness to radiation; the implementation of a suitable architecture for data acquisition, storage and data handling; the development of the technology for nuclear targets to be used in the future experiments; and a new beam dump in the MAGNEX hall to stop the high power beams.
-
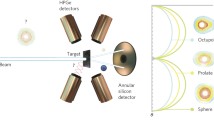
PANDORA: it will be a facility [27] conceived for multidisciplinary studies especially in the nuclear astrophysics framework. The main objective is to perform the first measurements of \(\beta\)-decays of astrophysical relevance in laboratory magnetized plasmas able to mimic some stellar-like conditions. The new experimental approach will allow to check the theoretical predictions about decay rates variation (expected to change dramatically as a function of the ionization state [28]). Only few experimental evidences were, in fact, collected up to now in storage rings (e.g., a lifetime reduction by 9 orders of magnitude was measured for \(^{187}\)Re [29]). Another relevant goal is to measure the opacities of plasmas of astrophysical interest (kilonovae’s ejecta). PANDORA will mainly consist of three subsystems:
-
an innovative superconducting magnetic plasma trap [30], capable to produce and confine plasmas with electron-ion densities up to 10\(^{13}\) cm\(^{-3}\) and electron temperatures of T\(_e \, \sim\) 0.1–30 keV;
-
an advanced plasma multidiagnostic system [31], consisting of a set of noninvasive diagnostic tools capable of operating simultaneously for the non-intrusive monitoring of the thermodynamic plasma properties and the measurement of plasma parameters;
-
an array of 14 HPGe (high-purity germanium) detectors for \(\gamma\)-ray spectroscopy [32], surrounding the plasma trap, to tag the in-plasma nuclear \(\beta\)-decays via the \(\gamma\)-rays emitted from the excited states of the daughter nuclei.
In 2021 the activity of the collaboration was dedicated to the definition of the details of the overall project, reported in the specific Technical Design Report (TDR) [33], as well as to the start of the procurement phase of the main subsystems. As part of a Collaboration Agreement between the PANDORA and GAMMA collaborations, 16 HPGe detectors belonging to the GALILEO setup will be transferred from LNL to LNS in 2023. In the meantime, the phases of know-how transfer and specific skills on the operation, maintenance and management of germanium detectors have been started, including the development of a special laboratory at LNS, already in the design phase. Thanks to the CSN3 financial support, the procurement nowadays includes two RF power supplies (18GHz-Klystrons), a new X-ray-CCD camera, the first part of funding needed to start the so-called Competitive Dialogue (i.e., a negotiated procurement procedure) about the superconducting magnetic trap, that is the most expensive part of the project. Among the ongoing activities it is worth mentioning a preliminary numerical simulation study on the possibility of measuring the opacities of plasmas of astrophysical interest in PANDORA (kilonovae’s ejecta), the study of expected abundances and constraints in AGB stars for some isotopes of interest for PANDORA; the experimental tests and benchmarks, using the normal conductive trap of ATOMKI-Debrecen, of magnetic confinement and turbulence in plasma; and the definition of the analysis algorithm for X imaging and space-resolved spectroscopy.
The first physics cases to investigate are \(^{176}\)Lu (potential cosmo-chronometer), \(^{134}\)Cs (to reproduce adequately the observed abundance ratio of the two s-only isotopes, \(^{134}\)Ba and \(^{136}\)Ba, see Sect. 5.3.1) and \(^{94}\)Nb (solving the puzzle about the exact contribution of s-processing to \(^{94}\)Mo).
-
-
BCT and I-LUCE: the BCT facility (breast cancer therapy with radiosensitizers in proton therapy and conventional radiotherapy) has been recently funded by the Sicilian Region with the main aim to study and define new therapeutic approaches for radiotherapy, drugs development and new treatment modalities of breast carcinoma. The first phase will consist in the installation and commissioning of an ultrashort pulse power laser (50 TW, 25 fs) for the generation of laser-driven ion, proton (maximum energy of 5 MeV), electron (maximum energy of 200 MeV) and gamma beams mainly for radiobiological and preclinical irradiation studies. The second BCT phase will provide an increased laser power up to 250 TW, having a system designed to be upgradable up to 1 PW. From the nuclear physics point of view, the availability of this laser will allow one to carry out studies of reactions directly in plasmas, a topic of interest for nuclear astrophysics.
The I-LUCE (INFN—laser-induced particle acceleration) facility will make the new laser-driven beams available to the community for nuclear and multidisciplinary applications. The acceleration from laser–matter interaction is grafted, moreover, into the new radiotherapy method called “FLASH” in which radiation beams with very intense dose rates are used to irradiate tumors, allowing a huge saving of healthy tissues.
Ion acceleration driven by pulsed laser–plasma sources is an emerging field of research, resulting from recent high-power laser technology achievements in terms of ultrahigh intensities (10\(^{21}\) W/cm\(^2\)) reached on target; as a reference, the first experiments done by LNS researchers in the second half of ‘90 s used laser intensities 10\(^6\) times lower [34]. In addition, studies based on the interaction of high-density plasmas, generated in the interaction of the laser with matter, with the ion beams from the LNS accelerators are foreseen as a future and unique LNS capability, and this will open up a very wide range of perspectives, both in the field of nuclear physics and astrophysics.
-
In-air irradiation with ion beams: LNS is equipped with a multidisciplinary beamline where several international groups perform innovative experiments for different kinds of application, from radiation damage study to irradiation of biological sample and of electronics devices. The new intensities, as well as the new radioactive beams, will open new perspectives for irradiation of samples under extreme conditions: high dose rate measurements and for mimicking of laser-driven accelerated beams or high-power pulsed beam from modern accelerators.
-
X-ray Tube: an X-ray-based high-voltage (up to 320 kVp) facility, capable to deliver a homogeneous and shaped photon beam. It was designed to work with pulsed beams as well as in continuous mode, mainly to perform both 2D imaging and small animal/cells irradiations with doses that can be delivered up to several Gy. After the final commissioning, the X-ray tube will be fully available to nuclear physics users for various activities, such as X-ray beam calibration, radiation hardness studies, and detectors characterization.
3 Nuclear dynamics
Nuclear dynamics is a wide field of nuclear physics, involving a large number of phenomena and effects that allow to explore the relevant properties of the nuclear medium. Heavy-ion collisions (HIC) represent a powerful tool of investigation in this field, spanning a wide range of energies, producing different states of nuclear matter, and providing crucial information on various aspects, ranging from the nuclear equation of state (EOS) to the structure of nuclei and their decay modes, up to the dynamics of the nuclear reactions to produce nuclei in the region of “terra incognita”, far from the stability valley.
In the context of the Mid Term Plan of Nuclear Physics, we present the relevant, current, challenging and key physics cases in nuclear dynamics that we will be able to unravel at LNS thanks to the ongoing upgrade of the accelerator machines and of the available apparatuses, and to the installation of the fragment separator FraISe.
In the framework of nuclear dynamics, we have treated three principal items “Heavy-Ion Collision and Equation of State”, “Clustering” and “Fission Dynamics”.
Contributions and proposals discussed and emerged during the workshop are presented in detail in the devoted paragraphs.
The first item “Heavy-Ion Collision and Equation of State” (Sect. 3.1) explores some new ideas and devices that, by using stable and radioactive beams in the Fermi energy regime at the LNS, will improve our understanding of the symmetry energy constraints at densities below saturation. In this framework, the working group highlighted the \(^{68}\)Ni + \(^{124}\)Sn and \(^{56}\)Ni + \(^{112}\)Sn reactions using FraISe beams (tag LNS-ND-HIC-c0 reported in Table 4 and Sect. 3.1.3) and the \(^{96}\)Zr + \(^{96}\)Zr (N/Z = 1.4) and \(^{96}\)Ru + \(^{96}\)Ru (N/Z = 1.18) reactions using SC stable beams (tag LNS-ND-HIC-b0, reported in Table 4 and Sect. 3.1.3). The symmetry energy can be also investigated through the study of the dynamical dipole, an observable connected to the stiffness parameter, describing the potential term of the symmetry energy (see also Sect. 4.2.2). For these studies, it is proposed to use the new high-intensity SC stable beams of Ar and Ca isotopes on Ca or Ni targets (tag LNS-ND-HIC-b1 in Table 4 and Sect. 3.1.5).
Another interesting point is the study of the caloric curve of nuclear matter and its dependence on the neutron–proton asymmetry and on reaction dynamics. Different theoretical calculations are conflicting and few experimental data are existing. It is proposed to extend this study to the investigation of the reactions \(^{34}\)Ar + \(^{58}\)Ni and \(^{46}\)Ar + \(^{64}\)Ni at energies between 15 and 30 AMeV, taking advantage of the FraISe beams (2.2.2). For these reasons, the development of FraISe beams with A = 30–70 is strongly supported for their relevance in order to further progress in this area of research (tag LNS-ND-HIC-c1 in Table 4 and Sect. 3.1.4).
All the experiments described up to now can be implemented by using the 4\(\pi\) CHIMERA detector [23] and the FARCOS correlator [24].
Still in the domain of nuclear dynamics at Fermi energy and its links to the symmetry term in the EOS, some items are suggested mainly exploiting the enhanced isotopic identification capabilities of the FAZIA array. Among the most relevant beams, we mention neutron-poor Kr (including the stable \(^{78}\)Kr) or Ar beams (including the stable \(^{36}\)Ar) at 35 AMeV on \(^{40}\)Ca, \(^{120}\)Sn, \(^{208}\)Pb targets (tag LNS-ND-HIC-b2 in Table 4 and Sect. 3.1.7). Zero-degree configurations (i.e., modules with specific holding structures mounted at zero degree) can also be envisaged, to perform precise cross section measurements. Relevant reactions might be those induced by FraISe beams, \(^{15}\)C, \(^{14}\)Be and \(^{16,20}\)O, at 40 AMeV on \(^{12}\)C, \(^{197}\)Au targets (tag LNS-ND-HIC-c2 in Table 4 and Sect. 3.1.7).
The second item “Clustering” (Sect. 3.2) proposes some new ideas to carry out fine and very precise measurements of already known cluster states in a number of key nuclei, and to search for new cluster structures and their decays, in previously unstudied nuclei or even new mass regions. Investigations of cluster states other than providing results on clustering effects can also show the presence of neutron halos and skins, or alpha–condensate structures.
Among the highlights for this item, there is the study of the clustering structure of \(^{10}\)Be and \(^{14}\)C both produced in batch mode and accelerated by the TANDEM (tag LNS-ND-CLU-a0 in Table 4 and Sect. 3.2.1).
Besides, the availability of noble gas beams at the Tandem accelerator, for example, \(^4\)He, \(^3\)He or \(^{20}\)Ne, could lead to perform new interesting physics investigation on the structure of light-to-medium mass nuclei (tag LNS-ND-CLU-b0 in Table 4 and Sect. 3.2.3).
Others relevant experiments can be done by using exotic beams produced at FraISe, and benefiting from the high intensity of the beams delivered by the SC. For example, the study of the molecular states predicted for the \(^{13}\)B in breakup reactions (tag LNS-ND-CLU-a1 in Table 4 and Sect. 3.2.4).
An important subject concerning halo nuclei is how the halo can affect the reaction dynamics, and investigation in this field are proposed, by measuring elastic scattering and direct reaction angular distributions in collisions induced by different n-halo and p-halo beams, obtained by FraISe, on a \(^{208}\)Pb target at about 2–3 times the Coulomb barrier (tag LNS-ND-CLU-b1 in Table 4 and Sect. 3.2.4).
The third and last item is “Fission Dynamics” (Sect. 3.3) that presents three lines which can be experimentally addressed with the high-intensity facility under construction at the INFN-LNS: shell effects in fission and quasifission (Sect. 3.3.1), multinucleon transfer reactions to investigate “Terra Incognita” (Sect. 3.3.1), and a possible alternative pathway to produce superheavy elements (Sect. 3.3.5).
Planning experiments to investigate shell effect in supersymmetric fission and quasifission need, other than high beam intensity, the capability of measuring the charge and the mass of fragments in the region of mass about 70–80 a.m.u. This can be achieved with the MAGNEX spectrometer, adding a time-of-flight arm, on the opposite side, to select the reaction mechanism. Main reactions for the superasymmetric channel and for which high-intensity beams will be available are \(^{22}\)Ne + \(^{238}\)U \(\rightarrow\) \(^{260}\)No and \(^{22}\)Ne + \(^{232}\)Th \(\rightarrow\) \(^{254}\)Fm. Reactions that might be a possible channel for \(^{78}\)Ni production are \(^{48}\)Ca induced on \(^{208}\)Pb, \(^{232}\)Th and \(^{238}\)U (tag LNS-ND-FIS-b0 in Table 4 and Sect. 3.3.3).
In this framework, multinucleon transfer (Sect. 3.3.4) is the best mechanism to produce neutron-rich isotopes of the Terra Incognita below \(^{208}\)Pb, with production cross sections ranging from a few mb to a few pb. Interesting case is, for example, the reaction \(^{122}\)Sn + \(^{208}\)Pb (tag LNS-ND-FIS-b1 in Table 4 and Sect. 3.3.4).
Finally, a possible pathway to produce superheavy elements by two-body reactions is suggested (Sect. 3.3.6). A typical reaction could be \(^{32}\)S(193 MeV) + \(^{238}\)U\(\rightarrow\) \(\alpha\) + \(^{266}\)Sg or \(^{66}\)Zn (363 MeV) + \(^{232}\)Th \(\rightarrow \alpha\) + \(^{294}\)Og (tag LNS-ND-FIS-b2 in Table 4 and Sect. 3.3.6).
Figure 16 summarizes the highlights for each item, inserted in a timeline of the upgrades at LNS, called Phase A, B, C.
At the end of this section, we show a table with the list of the selected nuclear reactions proposed for the realization of the highlighted goal and addressing to the experiments described in the text.
3.1 Heavy-ion collisions: EOS
3.1.1 Introduction
A unique aspect in the study of HIC is the production of nuclear matter in different conditions of excitation energy, temperature and density. In this way, it is possible to form, in a short interaction time, large density variations and transient states of nuclear matter: this is the optimal condition to study the nuclear EOS under laboratory controlled conditions as a function of the isospin asymmetry \(\delta = (\rho _n - \rho _p)/\rho\) and barionic densities, where n and p refer to neutron and proton numbers, respectively. In asymmetric nuclear matter, the EOS can be written as a sum of the energy per nucleon for the symmetric nuclear matter \(E(\rho ,\delta =0)\) and the symmetry energy term \(E_{sym}(\rho )\), quadratic with respect to \(\delta\) [35, 36]: \(E(\rho ,\delta ) = E(\rho ,\delta =0) + E_{sym}(\rho ) \delta ^2\).
The symmetry energy term can be expanded around its value at nuclear saturation density (\(\rho _0=0.16 fm^{-3}\)):
where \(E_{sym,0}=S_0\), \(L=3\left( \frac{\partial E_{sym}}{\partial \rho }\right) \bigg |_{\rho _0}\) and \(K_{sym}\) are, respectively, the value of symmetry energy, the slope (related to the neutron pressure in asymmetric nuclear matter) and the curvature at \(\rho _0\). These parameters, and particularly L, have been correlated to several observables in nuclear structure, nuclear dynamics and astrophysics [37, 38]. For example, simulations of neutron-star properties require as main input a model for the EOS as a function of a wide range of densities and isospin asymmetries, from low-density asymmetric matter (neutron-star crust) toward very high densities (outer core). On the other hand, the neutron-skin thickness of neutron-rich nuclei [39, 40] or their electric dipole polarizability, related to the giant dipole resonance (GDR) [41], also depends upon the symmetry energy parametrization. This means that the symmetry term of EOS in asymmetric nuclear matter affects the radius of a given mass neutron star, the neutron skin of a neutron-rich nucleus like \(^{208}\)Pb or \(^{48}\)Ca [42] as well as the dynamic evolution of HICs, because it is related to the fundamental properties of nuclear effective interaction [43]. Moreover, the recent detection of gravitation waves (GW) [44] from the merger of a binary neutron-star system has shown relevant correlations with the EOS and symmetry energy predicting the radius R of a neutron star (the so-called tidal polarizability \(\Lambda\) observable in a GW event is in fact roughly proportional to \(R^5\)) opening the so-called multimessenger astronomy [45, 46] filed. These astrophysical studies can be now compared with those coming from terrestrial experiments, mainly by using HICs.
Adapted and modified from Burgio et al. [47]: correlation between the symmetry energy at saturation S\(_0\) and the slope of the symmetry energy around saturation density. The shaded area corresponds to experimental data. In particular the cyan area (HIC) corresponds to isospin diffusion data on Sn+Sn collisions [48]. Black symbols correspond to results of theoretical microscopic approaches to EOS or (other colors) phenomenological approaches (see text and Ref. [47] for details). Gray area corresponds to AsyEos, Au+Au data from Ref. [49]. The impact of the PREX-II data analysis results [50] is also shown on the right
Figure 17 shows a recent compilation of the constraints in the symmetry energy \(S_0\) versus the slope L obtained from different sources; in particular the shaded bands show experimental data from studies on HICs at the Fermi energies and isospin diffusion [48], neutron-skin thicknesses in Sn [51], electric dipole polarizability in GDR [52], isobaric-analog-state (IAS) analysis and neutron-skin data [53], and from calculations on mass and radius measurements for neutron stars [54] (see ref. [47] for a detailed description). Investigations on the symmetry energy have been also conducted exploiting other collective motions in neutron-rich nuclei such as the pygmy dipole resonances [55] or the giant monopole resonances [56] (see Sect. 4.2.3).
A compilation of 53 experimental results [57] gives the values of 31.7\(\pm 3.20\) MeV and 58.7\(\pm 28.1\) MeV for \(S_0\) and L, respectively. It is interesting to note in Fig. 17 that the neutron-skin thickness for \(^{208}\)Pb, on PREX-II data, based on measurement of the parity-violating asymmetry in the elastic scattering of longitudinally polarized electrons off \(^{208}\)Pb [50, 58], brings to an average slope parameter \(L=106\pm\) 37 MeV, larger than previous values obtained from microscopic theoretical approaches and experimental data. A missing aspect in the plot of Fig. 17 is that it does not show the barionic density domain that is really explored in the experimental data while this information is indeed a fundamental ingredient [59]. Also microscopic “ab-initio” calculations are generally done around the saturation density and the results are extrapolated toward higher densities [60, 61]. In Fig. 17 we have drawn results of the ASYEOS experiment on Au+Au at 400 AMeV at GSI [49] as gray band. This experiment explores the supra-saturation density region in the range 1.5–2 \(\rho _0\) where few experimental data exist [62,63,64], by measuring the elliptic flows of neutrons and light charged particles [49, 65]. Results have shown a noticeable coherence with data coming from astrophysical observations [66, 67].
The consistency of the measurements conducted below and above saturation density is an important challenge also in the context of the “multimessenger” physics and in order to further constrain the coherence of different transport models. In the following, exploring some new ideas or devices, we show how the use of new stable and radioactive beams at LNS could contribute to improve the precision and reliability of symmetry energy constraints at densities below the saturation one.
3.1.2 Plans for midterm advances at LNS with SC beams
In the Fermi energy regime, various reaction mechanisms have been used to probe the symmetry energy at low density from \(\rho _0\) down to 0.1 \(\rho _0\) where clusterization occurs [68,69,70]. From central collisions (multifragmentation and the experimental isoscaling phenomena [71], studies of emitted neutron–proton ratios [72]) to semi-peripheral reactions (isospin diffusion [48, 73, 74] and migration through the “neck” [75,76,77]) many experimental and theoretical contributions have been given to this research line (see the Refs. [78, 79] for some reviews). One of the basic ideas in constraining the symmetry energy at low densities is to look at N/Z of particles and intermediate mass fragments (IMF) emitted from semi-central to semi-peripheral reactions by using projectiles and targets with large isospin asymmetries with stable neutron-rich, neutron-poor or radioactive beams. Isospin transport effects appear as being caused by processes like the isospin diffusion and equilibration or the IMF emission from a transient “neck” region. All these phenomena are related to experimental observables that, in comparison with transport model calculations, can provide information on the density dependence of the symmetry energy. For example, in the neck fragmentation mechanism it is supposed that light IMFs are formed in a dilute n-rich matter in contact with the regions of projectile-like (PLF) and target-like (TLF) fragments at normal densities due to transport of neutrons toward the low-density region [80]. The interplay between experiments and transport model calculations is essential. In the last years, a big effort has been done (and it is in progress) in order to test the robustness of transport model predictions in reaching consistent conclusions with experimental data [81].
Many aspect of this physics case have been independently studied at INFN-LNS by the CHIMERA and INDRA-FAZIA collaborations and by other groups worldwide. All these subjects are related with the density dependence of the isovector part of the nuclear effective interaction and with the in-medium correlation effects; in particular, the latter focus on the microscopic mechanism to form clusters or fragments during the short interaction time when the transient systems explore “exotic” regions of EOS.
New exciting opportunities will be opened by the high-intensity heavy-ion beams and the radioactive beams at Fermi energies delivered by the SC after the upgrade. In fact, a higher sensitivity to the symmetry energy is expected both in experimental observables and theoretical models if we increase the strength of the N/Z dependent observable (by using, for example, more neutron-rich or neutron-poor beams) and at the same time if we improve the experimental device capabilities: (i) better isotopic resolution of fragments, (ii) capability to detect neutrons and charged particles simultaneously, and (iii) high granularity, as it will be presented in the sections below.
3.1.3 Plans with CHIMERA and FARCOS devices in semi-peripheral reactions
The CHIMERA 4\(\pi\) detector [23] has been used both in studies of nuclear EOS in asymmetric nuclear matter at LNS in the Fermi energy regime [82], and in the relativistic energy domain at GSI [49]. The new FARCOS array correlator [24] in its final configuration of 20 telescopes has been recently added. Many experiments have been performed with the CHIMERA detector in the last two decades and more recently by using a portion of the FARCOS array in different configurations [83]. Isospin properties of IMFs were used to constrain the density dependence of the symmetry energy at sub-saturation densities by using observables based on the transport of isospin like the isospin diffusion and N/Z equilibration [73, 84], and the isospin migration of neutrons and protons in the “neck” region [75, 85] causing the neutron enrichment of the light IMFs emitted at mid-rapidity. Values of parameters constraining the symmetry energy at sub-saturation densities were found comparing the experimental data with different transport models.
Adapted from Ref. [86]: ratio of the dynamical component to the total (dynamical+statistical) value in the breakup of the quasi-projectile plotted as a function of the IMF atomic number Z, for the three isobaric systems \(^{124}\)Xe+ \(^{64}\)Zn (empty circles), \(^{124}\)Xe + \(^{64}\)Ni (full triangles) \(^{124}\)Sn + \(^{64}\)Ni (full circles) and for the \(^{112}\)Sn + \(^{58}\)Ni (empty triangles)
Unlike the light IMFs, the dynamical emission of heavier IMFs takes place over longer timescales, mainly due to a non-equilibrated breakup of the PLF (“dynamical fission”) [87, 88] in competition with the statistical emission. A recent study at 35 AMeV of the isobaric systems \(^{124}\)Xe, \(^{124}\)Sn + \(^{64}\)Zn, \(^{64}\)Ni and \(^{112}\)Sn + \(^{58}\)Ni has shown, as highlighted in Fig. 18 from Ref. [86], that the strength of dynamical effects increases with the isospin content of projectile and target, giving evidence of an important dependence of the reaction mechanism evolution on the initial neutron richness of both projectile and target colliding nuclei. This suggests the role of the symmetry energy in the dynamical process.
On the basis of these results, it is suggested to use the capabilities of the new FraISe fragment separator to produce \(^{68}\)Ni and \(^{56}\)Ni beams using primary ones of \(^{70}\)Zn and \(^{58}\)Ni, respectively, at an incident energy of about 25 AMeV. This will increase the N/Z of the initial systems, for example, to study \(^{68}\)Ni+\(^{124}\)Sn (neutron-rich, N/Z = 1.46) and \(^{56}\)Ni+\(^{112}\)Sn (neutron-poor, N/Z = 1.15) (tag LNS-ND-HIC-c0 in Table 4). These asymmetries, wider than those used in the past, enhance the sensitivity to the symmetry energy and put new severe constraints on the different transport codes. Anyway, in order to use FraISe beams to study reaction mechanisms that require high statistics, an intensity beam of at least 10\(^6\) pps is necessary.
Besides radioactive nuclei, great interest in the reaction dynamics community is oriented to the so-called metallic beams that are stable beams but with the possibility to have mixing of isospin in the entrance channel similar to the exotic ones, such as \(^{96}\)Zr and \(^{96}\)Ru. The study of systems like \(^{96}\)Zr + \(^{96}\)Zr (N/Z = 1.4) and \(^{96}\)Ru + \(^{96}\)Ru (N/Z=1.18)(tag LNS-ND-HIC-b0 in Table 4) and the respective projectile–target combinations should permit, in isobaric (no mass-size effects), symmetric (same Coulomb effect for target and projectile) systems, a precise disentangling of isospin diffusion and isospin migration in transport effects exploiting the differential motion of nucleons (protons and neutrons) through the neck. The production of these beams at LNS could be a new challenge due to their high fusion points.
3.1.4 Plans with CHIMERA and FARCOS devices in central collisions
The caloric curve that is the relation between the temperature and the excitation energy per nucleon is of fundamental relevance for many physical systems. The investigation of the dependence of the nuclear caloric curve on the neutron–proton asymmetry is particular interest. In fact, it has been demonstrated a clear mass dependence of the caloric curve for finite nuclei [89], while the dependence on the neutron/proton asymmetry, \((N-Z)/A\), remains uncertain due to conflicting different theoretical calculations and to a relatively small quantity of experimental data on the subject [90]. In addition, the available data show that the dependence of the caloric curve on the neutron–proton asymmetry depends on the reaction mechanism and collision dynamics [79]. These studies were begun by the ISODEC experiment [91] carried out at LNS with the CHIMERA detector. To extend the studies on this subject, it has been proposed to investigate the reactions \(^{34}\)Ar + \(^{58}\)Ni and \(^{46}\)Ar + \(^{64}\)Ni at energies between 15 and 30 AMeV, taking advantage of the FraISe beams and by using the 4\(\pi\) CHIMERA detector and the FARCOS correlator. For these reasons, the development of FraISe beams with A=30–70 is strongly supported for their relevance in order to further progress in this area of research (tag LNS-ND-HIC-c1 in Table 4).
In the past years, the limiting temperature for the formation of compound systems as a function of the isospin has been investigated at LNS. This work was pursued by looking to GDR \(\gamma\) decay measurements [92] and by studying the competition between fusion-like and binary reactions by using the CHIMERA multidetector. It was pointed out that neutron-rich systems, formed for instance through \(^{48}\)Ca + \(^{48}\)Ca reactions, are able to produce a heavy residue (due to an incomplete fusion reaction), having a large temperature (over 5 MeV) and excitation energy (200–300 MeV), more efficiently than a neutron-poor system, such as the \(^{40}\)Ca + \(^{40}\)Ca [93, 94]. Predictions based on Constrained Molecular Dynamics calculations, CoMD-II [95], showed that the competition between fusion-like and binary reactions can constrain the parameterization of the symmetry energy. Thus, it has been proposed to use FraISe beams at energies around 20–30 AMeV. In this way, it will be possible to extend such investigations to further neutron-rich and neutron-poor systems beyond the stable beams used up to now. Secondary beams such as \(^{34}\)Ar (neutron-poor) or \(^{38}\)S (neutron-rich) could be produced from primary beams, respectively, of \(^{36}\)Ar and \(^{40}\)Ar (this last well studied and simulated within the FraISe project [16, 18]). The measurements will be performed with the CHIMERA multidetector. This adds the possibility to study these systems by detecting with the same device both the heavy residues and their GDR \(\gamma\)-decay (see Sect. 4.2.4 on new \(\gamma\) detectors), thus probing that an equilibrated system is really formed.
Adapted and modified from Ref. [96]: for the reaction \(^{48}\)Ca + \(^{27}\)Al the measured average dipolar signal \(<D_a>\) is plotted as a function of charge Z of the detected fragments (red points). Horizontal bars in the data indicate that more than one charge have been added for a given point. Results are compared with the CoMD + GEMINI calculations for different shown values of the \(\gamma\) parameter (lines) characterizing the isovectorial interaction. Grayed area contains the minimum and maximum values in the calculations in order to guide the eyes (see text and Ref. [96] for details)
3.1.5 Dynamical dipole and symmetry energy
In Sect. 4.2.2 an observable \(D_a\) related to the dynamical dipole pre-equilibrium \(\gamma\)-ray emission is defined. The same observable was recently measured in mid-peripheral collisions induced on the system \(^{48}\)Ca + \(^{27}\)Al at 40 AMeV [96] and was constructed by using the charge and velocity of the emitted fragments and particles in quasi-complete events detected with the CHIMERA array.
This observable is closely linked to the charge/mass equilibration process in the reaction dynamics and almost independent of secondary decays. The reconstructed average dipolar signal has been reproduced through molecular dynamics CoMD-II calculations [95, 97]. These calculations show that this global observable is also capable to constrain the symmetry term of the EOS. In fact, a strong correlation was found between the experimental data and the symmetry energy written as \(E_{sym}(\rho ) = 12(\rho /\rho _0)^{2/3}+20(\rho /\rho _0)^\gamma\), being \(\gamma\) the stiffness parameter describing the potential term of the symmetry energy. As shown in Fig. 19, this comparison allowed us to establish a good agreement with experimental data for a stiffness parameter \(\gamma =1.06\pm 0.16\), which corresponds to a E\(_{sym}=32\) MeV and a slope parameter \(L=87.6\pm 14\) MeV.
In order to continue these studies, it has been proposed to use the new high-intensity SC stable beams (of the order of 10–20 nA) of Ar and Ca isotopes beams on Ca or Ni targets measuring \(D_a\) in central or semi-central collisions (tag LNS-ND-HIC-b1 in Table 4). By using the CHIMERA array, we can detect, at the same time, charged particles in complete events and \(\gamma\)-rays (see Sect. 4.2.2 for other details).
3.1.6 Plans for neutron detection and new detection facilities
Neutron-rich high-intensity radioactive beams will allow us to study nuclear matter under extreme conditions, in terms of the isospin equilibration degree of freedom, both for long- and short-lived neutron-rich radioactive nuclei far from the stability valley. For this reason it will be mandatory to detect neutrons as well as the charged particles; therefore, new devices have to be designed for future experiments. In fact, a correlator for neutrons and charged particles, i.e., a device able to detect neutrons with high angular and energy resolution, high granularity and with an acceptable neutron detection efficiency, will allow to study reaction dynamics and carry out nuclear spectroscopy also by using statistical techniques such as the intensity interferometry (HBT). New plastic scintillators materials, where neutron detection is based on the proton recoil technique, are nowadays under study to be used in new advanced compact devices. A starting point was the analysis of the performances of an EJ 299-33 scintillator, in high rate scattering experiments, performed with heavy-ion beams at LNS [98]. Studies for the construction of a prototype for such a device based on EJ-276G (green shifted version) plastic scintillators with SiPM readout are in progress [99, 100].
3.1.7 Plans with the FAZIA detector array
The FAZIA modular array [101] has been used in recent years for experiments in standalone mode at LNS and now at GANIL, coupled with INDRA 4\(\pi\) detector [102]. The telescopes are arranged in blocks of 16 and have as main characteristics the isotopic identification up to Z \(\le\) 25 with \(\Delta\)E–E technique and Z \(\approx\) 20 via pulse shape analysis as shown, for example, in Fig. 4 of Ref. [2].
Besides the natural use of the existing local detectors like CHIMERA and FARCOS, it is proposed to complement the investigation at INFN-LNS also with experiments carried in a multipurpose large chamber substituting the big “CICLOPE” with one which is large enough to host the FAZIA array and new detector systems. These latter could be of composite and modular nature, since they aim at measuring different reaction probes (charge particles and \(\gamma\)-rays). More information can be found in the Sect. 4.2.4 dedicated to future experiments on GDR. The following items are suggested, mainly exploiting the enhanced isotopic identification capabilities of the FAZIA array:
-
(i)
Advanced studies of the dynamical breakup of the projectile-like fragment. The measurement of the momenta of fully identified breakup pairs represents a powerful tool to strictly constrain sophisticated transport models (e.g., [103]), which up to now proved to be able to reproduce many features of the reactions. Detailed study of the (fast) breakup of medium–light excited PLF is important also to explore cluster correlations and their persistence at high energies. Reactions relevant for this point are \(^{56}\)Fe + X at 35 AMeV (X=\(^{40}\)Ca, \(^{120}\)Sn, \(^{208}\)Pb).
-
(ii)
Toward a systematic knowledge of midvelocity emissions. It is proposed further investigation on the isotopic composition of all the ejectiles of dynamical origin, i.e., those related to midvelocity emission. In particular, a limited sensitivity to the symmetry energy parameterization has been observed in the relative yields of the most exotic midvelocity emitted IMFs (e.g., [77, 82, 104]). In future studies the absolute cross section of these emissions should be determined (so far, rare attempts on that exist) as a function of the energy and of the mass asymmetry of the interacting systems. Indeed, the studies of dynamical emission using neutron-deficient systems have been so far rather scarce, impeded by the rarity of energetic beams from in-flight fragmentation facilities and thus FraISe represents a good opportunity in this field. Relevant reaction beams could be neutron-poor Kr (including the stable \(^{78}\)Kr) or Ar beams (including the stable \(^{36}\)Ar) at 35 AMeV on targets \(^{40}\)Ca, \(^{120}\)Sn, \(^{208}\)Pb (tag LNS-ND-HIC-b2 in Table 4).
-
(iii)
Toward a reconstruction of resonances. Useful information can also be gained looking at the excited IMFs reconstructed by means of the particle-fragment correlations and at the relative population of the excited levels. The use of particle correlations is an appealing method to backtrace from the detected fragments toward the primary configurations. It is clear that to fully exploit the isospin degree of freedom an experimental setup able to detect the mass of the ions in the widest possible range of charge is mandatory. At LNS the status-of-the-art for correlation techniques is represented by the FARCOS hodoscope based on Si-strip detectors and characterized by a very high granularity and energy resolution. In their typical operating geometry (100 cm from the target), the FAZIA telescopes, with some modifications, should be also suitable for correlation studies [101, 105] allowing performances comparable to previous studies [106, 107]. Reactions relevant for this point are FraISe beams \(^{15}\)C, \(^{14}\)Be + \(^{12}\)C at 40 AMeV, \(^{32,38}\)S + \(^{28}\)Si at 40 AMeV.
-
(iv)
Zero-degree configurations (i.e., modules with specific holding structure mounted at zero degree) can also be envisaged, provided that the beam currents can be properly reduced to safe values (typically below 1–2 kHz). Precise cross section measurements require a normalization to the known Rutherford cross section (by fast plastic scintillators located below the grazing angle) or a continuous monitoring of the beam current during the experiment. Relevant example reactions might be FraISe beams \(^{15}\)C, \(^{14}\)Be and \(^{16,20}\)O at 40 AMeV on \(^{12}\)C,\(^{197}\)Au targets (tag LNS-ND-HIC-c2 in Table 4).
3.2 Clustering
In light nuclei quantum mechanics plays a major role in creating special nuclear structures such as, nuclear skins and/or nuclear halos, nuclear clusters and molecules or gas condensate (see Fig. 20). The idea of clustering as an important phenomenon in describing structure of light nuclei is almost as old as the nuclear physics itself [108, 109], and the typical cluster is the \(\alpha\) particle. The basic idea of clustering is that the interaction within the cluster is strong, while the clusters weakly interact with each other. Moreover, the threshold rule holds: cluster configurations in nuclei appears at excitation energies at, or above, the decay threshold into the cluster constituents. For this reason, only weakly bound nuclei, as for example \(^{6,7}\)Li and \(^9\)Be, possess cluster structures in their ground state, and for this reason ground state cluster configurations are more common in unstable nuclei. Among the different types of clustering, exotic or molecular clustering, may occur. In the exotic clustering the idea of a stiff particle as cluster is dropped. It can be, in fact, a soft particle easy to excite and to break. These configurations become more and more exotic when moving toward the drip line, e.g., [110].
In molecular clustering, clusters, typically \(\alpha\)s, are bound together by nucleons, which act as the electrons in covalent bonding of ordinary matter. Molecular linear-chain configurations are predicted to exist, as for example in \(^{14}\)C [111], by antisymmetrized molecular dynamics (AMD) (see Fig. 21). Associated to these configurations two bands are predicted [112], having the \(\sigma\)-bond or \(\pi\)-bond valence nucleons.
Molecular clustering could also be the result of the dynamics of the reaction. A molecule made of the two interacting nuclei may be formed during the collision; it rotates and then breaks up without the formation of a compound system. These resonances appear as broad peaks in the elastic channel excitation function having the angular distribution peaked at backward angles [113]. On the other hand, the dynamics of the reaction could be affected by the presence of clustering.
In the last decade, studies of nuclear clustering have reached the precision era. So further studies should follow two paths: (1) fine and very precise measurements of already known cluster states in a number of key nuclei; (2) searches for new cluster structures (and their decays), in previously unstudied nuclei or even new mass regions. New theoretical predictions are being regularly made on cluster structure, often suggesting the existence of states with yet a not observed configuration. Very recent examples are studies of \(^{10}\)Be within the newly developed “real-time evolution method” [114], or \(^{12}\)C within the new “replica exchange Monte Carlo method” [115]. Together with old results (reviewed, e.g., in [116]), obtained within AMD method (e.g., [117]), or molecular orbital model (MOM) [118], there is now a fair amount of theoretical predictions, which awaits for new experimental data. Experimental investigation of cluster states could provide results not only on clustering effects, but also on the radii of the identified states (e.g., [119]) and/or the presence of neutron halos and skins [120]. The high precision data are also needed to identify possible states showing a very special clustering, so-called \(\alpha\)-condensate structure (e.g., [121]).
3.2.1 Studies with the existing Tandem beams
For what discussed above, the LNS Tandem is an ideal accelerator, providing intense beams of \(^6\)Li, \(^7\)Li and \(^9\)Be, which are a standard choice for cluster studies due to their above mentioned ground state cluster structure which can be used, for example, for transfer reaction of the cluster of interest. In the study of clustering in nuclei the first problem that one has to face is to find signatures of clusterization. For example, a large reduced width for \(\alpha\) emission, comparable with the Wigner limit, corresponds to a state where the \(\alpha\) particle is fully preformed. The same argument holds also for clusters different than \(\alpha\)s. Another possible signature is the identification of a sequence of excited states spaced by an energy interval \(\Delta\)E following the J = J + 1 rule, being J the angular momentum of the state. However, the moment of inertia that can be extracted from the slope of a tentative rotational band gives information only on the deformation of states; this can be a hint of clusterization but not a direct evidence. Therefore, the observation of a number of states lying on a rotational sequence is not a clear evidence of clustering. A proper rotational band is defined as a sequence of states corresponding to the same deformed structure, i.e., the wave function describing each state must correspond to the same (clustered) internal structure. Such information can be provided by the measurement of the electromagnetic transition strength, which tests the overlaps of the initial and final states structure. In fact, for states of the same rotational band there should be an enhancement of the E2 transition probability between successive band members. Therefore, the measurement of the B(E2) gives information on the degree of collectivity of the states involved in the transition. The very small \(\gamma\)-decay branches of these states make such measurements very difficult to perform. However, using high-efficiency \(\gamma\)-detector arrays and with the correct choice of the nuclear reaction to populate those states, this is possible. This is shown, for example, in [122] where the B(E2) transition strength from the 4\(^+\) to 2\(^+\) states in \(^8\)Be was measured, providing a description consistent with a rotational picture and GFCM calculation. A preliminary experiment was done at LNS using the CHIMERA multidetector where \(\gamma\)-transitions in \(^{12}\)C were measured [123]; further higher-energy resolution studies are foreseen.
Rotational bands are widely present, especially in light nuclei. Many systems may be studied, but two systems among all are of greater importance: \(^{12}\)C and \(^{16}\)O.
\(^{12}\)C: in \(^{12}\)C two rotational bands are present, one built on the g.s. and one on the second 0\(^+\) state (the so-called Hoyle state). A new rotational band associated to a triangular arrangement of the three \(\alpha\)s have been recently proposed [124, 125] on the basis of an algebraic cluster model calculation [126, 127].
\(^{16}\)O: in \(^{16}\)O several states with a cluster structure have been observed and many attempts have been made to build rotational bands, but without a definitive assignation.
The \(^{18}\)O having two neutrons bound to the \(^{16}\)O core is an excellent tool to study two neutron transfer reactions on various targets as well as to examine clustering in light and medium mass neutron-rich nuclei via (\(^{18}\)O,\(^{16}\)O) and (\(^{18}\)O,\(^{20}\)Ne) reactions.
Regarding studies dedicated to the search for new cluster states, or even new type of clustering, the use of radioactive beams would be essential. As an example, the availability of a \(^{10}\)Be beam allows to investigate the existence of a linear-chain configuration in \(^{14}\)C predicted by AMD calculations [111].
AMD prediction of \(^{10}\)Be-\(\alpha\) linear-chain configuration in \(^{14}\)C [111]
The \(^{10}\)Be beam produced in batch mode, and delivered by the LNS Tandem, has been proven to be of excellent quality and with the highest intensity worldwide (10\(^9\) pps) [128]. The first experimental results concerning the linear chain in \(^{14}\)C are very promising, and further experiments with this beam would be very welcome,(tag LNS-ND-CLU-a0 in Table 4). In addition, preliminary results of the reaction \(^{10}\)Be+\(^{120}\)Sn at 40 MeV measured at LNS have revealed not only the \(^9\)Be particles coming from the breakup of \(^{10}\)Be into \(^9\)Be+n, but also the breakup channel \(^6\)He+\(^4\)He. The latter could be an indication of the \(^6\)He-\(^4\)He configuration of \(^{10}\)Be. Further studies of this reaction, using large solid angle detectors in order to measure the angular and energy distributions of the charged fragments coming from breakup of \(^{10}\)Be, will allow to investigate both the \(^9\)Be+n and the \(^6\)He+\(^4\)He breakup channels of \(^{10}\)Be and to study its cluster structure. The interaction of \(^{10}\)Be with stable target nuclei with excess of neutrons (\(^7\)Li, \(^9\)Be, \(^{11}\)B, \(^{13}\)C, \(^{18}\)O, etc.) makes it possible to study clustering in very neutron-rich systems like \(^{16}\)C, \(^{18}\)N, \(^{20}\)O, \(^{22}\)F etc. Existing data on these nuclei are very limited or completely absent, mainly obtained using low intensity radioactive beams and consequently of poor statistics and resolution. The combination of the large detector arrays and high beam intensity, both available at the LNS Tandem facility, can significantly improve understanding of clustering in the neutron-rich nuclei.
3.2.2 Development of new Tandem radioactive beams
Besides \(^{10}\)Be, an unstable beam of interest for cluster studies is \(^{14}\)C. The development of a \(^{14}\)C beam (also radioactive with a very long half-life \(t_{\frac{1}{2}}= 5700y\)) would, in fact, be rather useful, both for studies of clustering in the A < 20 mass region and for the search of new cluster states in the medium mass nuclei. Radioprotection safety procedures to prevent, for instance, internal and external contamination, have been taken into account by the LNS dedicated service.
The scientific arguments for \(^{14}\)C beam development are very similar to the ones for \(^{10}\)Be, it is the perfect ion beam for studying structure of nuclei with excess of neutrons. In addition to the \(^{10}\)Be case, due to its neutron closed shell, it was proposed that \(^{14}\)C may be a basic building-block for a new form of clustering in medium mass neutron-rich nuclei as for example \(^{14}\)C–\(^{14}\)C configuration in \(^{28}\)Mg or linear-chain configurations of three \(^{14}\)C in \(^{42}\)Ar [118, 129]. These intriguing possibilities can be probed by the measurements on medium mass stable nuclei with N>Z (\(^{18}\)O, \(^{26}\)Mg, etc.).
3.2.3 Development of noble gas beams at the LNS Tandem
The availability of noble gas beams at the Tandem accelerator could lead to perform new interesting physics investigations on the structure of light-to-medium mass nuclei (tag LNS-ND-CLU-b0 in Table 4) The \(^4\)He beam would also be very welcome for resonant elastic and inelastic scattering (RES) studies, since \(\alpha\)-particles are the basic building-blocks of classical cluster structures. The method has already been used at LNS and has given promising preliminary results (e.g., [130]).
For example, with \(^4\)He beams of energies from 9 to 20 MeV, sent to the CT2000 scattering chamber, it will be possible to investigate angular distributions and excitation functions of elastic and inelastic resonant scattering on light nuclei (as \(^9\)Be, \(^{10,11}\)B, \(^{13}\)C etc.) that will populate \(\alpha\)-cluster resonant states in non-self-conjugate compound nuclei (as \(^{13}\)C, \(^{14,15}\)N, \(^{17}\)O etc.). The availability of goniometer systems in the CT2000 chamber will facilitate the measurements of angular distributions in direct kinematics experiments by using high resolution (angular and energy) particle-detection systems [131, 132].
\(^3\)He is one of the key beams for research on the proton-rich nuclei both for reaction dynamics and clustering in nuclei with excess of protons. The two-proton transfer reactions are an adequate tool to explore various possible cluster structures in proton rich light nuclei (\(^8\)B, \(^{12}\)N, \(^{14}\)O, \(^{16}\)F, \(^{18}\)Ne, etc.), which have been poorly investigated, as well as to improve the understanding of the coupling of the proton excess to the \(\alpha\)-core by improving spectroscopic data on the \(n\alpha\)+2p systems (\(^6\)Be, \(^{10}\)C, \(^{14}\)O, \(^{18}\)Ne).
Resonant scattering measurements with the \(^3\)He beam can explore the role of the \(^3\)He cluster in proton-rich environment. This beam enables studies of the \(n\alpha\)-clustering in N = Z nuclei at very high excitation using the moderate ion beam energies accessible by the Tandem. \(^3\)He beams in the bombarding energy domain 10–30 MeV with the geometrical features of the CT2000 chamber could allow to perform new experiments on one-proton transfer reactions on medium mass stable nuclei [133]. (\(^3\)He, d) transfer reactions is in fact a powerful tool to explore single-particle proton strength in ground and excited states of nuclei without having to detect neutrons [134]. It is well known from the literature that several ambiguities in the determination of the spectroscopic factors in medium mass nuclei are still persisting and in some cases prevent the fine-tuning of interactions used in shell model calculations [135, 136]. The use of high-energy-resolution Si detectors able to properly identify the emitted deuterons with low thresholds, coupled with the CT2000 chamber geometrical flexibility, will permit to measure high resolution angular distribution of this transfer reaction. Some interesting examples that have an impact also on nuclear astrophysics can be found in [137, 138].
The neon beams would also be very useful in studying medium/heavy clustering states.
\(^{20}\)Ne: due to its significant \(^{16}\)O+\(^4\)He cluster structure, the \(^{20}\)Ne beam enables the study of clustering in a number of medium mass nuclei. It is particularly suitable to examine possible \(^{16}\)O clustering—as the second double magic nucleus it may have a role of basic cluster in medium mass nuclei like \(\alpha\)s in light nuclei. Reactions of the \(^{20}\)Ne beam with carbon, oxygen and magnesium targets are a good tool to probe this structural mode in medium mass nuclei.
\(^{22}\)Ne: it is a perfect ion beam for studying two-neutron transfer reactions and structure of light and medium mass nuclei with excess of neutrons.
It’s worth mentioning that the number of European facilities providing the mentioned beams is getting smaller every year, therefore LNS is, in that sense, becoming very valuable for the nuclear physics community.
3.2.4 Studies with in-flight radioactive beams from FraISe
The new FraISe fragment separator conceived to operate with the high-intensity primary beams which will be delivered by the LNS Cyclotron by stripping extraction, is expected to produce different light radioactive ion beams. Although maximum intensities for such beams are expected to be achieved at energies around 40–60 AMeV, calculations show that most of such beams can still be produced with interesting intensities between 10\(^2\) and 10\(^5\) pps with lower energies, of the order of 10–15 AMeV. This would open the possibility to perform a variety of investigations.
Study of clustering
\(^6\)He: having two loosely bound neutrons, the \(^6\)He beam is an excellent tool to study clustering in a number of nuclei via the (\(^6\)He,\(^4\)He) and (\(^6\)He,\(^8\)Be) reactions. This beam has been extensively used for clustering studies at many radioactive beam facilities, but its availability in recent times is quite limited. Available results obtained by the \(^6\)He beam are still limited and numerous additional measurements are needed to complete the picture of clustering in the neutron-rich light nuclei, while experimental data on clustering in medium mass neutron-rich are absent which hampers the understanding of the role of clustering in this mass region.
\(^8\)Li: campaign of measurements of the (\(^8\)Li, \(^6\)Li) and (\(^8\)Li, \(^4\)He) reactions on various targets is a promising way to study clustering in neutron-rich nuclei. It is also of significant interest for reaction dynamics studies as it provides insight in the multiparticle transfer reactions. Available experimental data are very limited in both cases, structure and dynamics.
\(^7\)Be: due to its \(^4\)He+\(^3\)He cluster structure, the \(^7\)Be is an excellent beam to study clustering in proton-rich nuclei via \(^3\)He stripping and multinucleon pick-up reactions. The most likely first experiment in a \(^7\)Be campaign would be an even simpler reaction measurement, the use of one proton pick-up reaction to explore clustering in \(^8\)B and consequent astrophysical implications.
\(^{11}\)C: there is significant body of evidence for the \(^7\)Be + \(^4\)He clustering in \(^{11}\)C, so the motivation for the development of this beam is similar to the one for the \(^7\)Be beam; it can be used to explore clustering in the proton-rich light and medium mass nuclei. One example would be to study clustering in \(^{10}\)C by one proton stripping reactions. The \(^{10}\)C structure has attracted particular interest as it is likely the only super-Borromean system, one comprising four (2p + 2\(\alpha\)) bound components in which any subsystem of two and three components is unbound.
\(^{13}\)B: molecular clustering have been predicted to exist in states of \(^{13}\)B, above the \(\alpha\) emission threshold, having the structure \(^9\)Li–\(^4\)He. Breakup reaction of \(^{13}\)B in \(^9\)Li+\(\alpha\) could be used to perform such an investigation. A proposal has been accepted by the LNS-PAC but the experiment could not be performed due to the COVID shut-down. This experiment would highly benefit from the increase in intensity of the future fragmentation beams. (tag LNS-ND-CLU-a1 in Table 4).
\(^{18}\)Ne: having two protons bound to the double magic \(^{16}\)O core, the \(^{18}\)Ne beam is an excellent tool to study the dynamics of two proton transfer reactions and clustering in the proton-rich nuclei by the (\(^{18}\)Ne, \(^{16}\)O) and multinucleon pick-up reactions on various N = Z stable nuclei. Regarding the radioactive beams from FraISe, the ones with the highest intensities (e.g., \(^{18}\)Ne) could be used to selectively populate cluster states using transfer reactions (in this case, on the proton-rich side of the light mass part of the chart of nuclei). Neutron-rich isotopes of beryllium and carbon could also be very useful, if they could be produced with intensities higher than 10\(^4\) pps.
Reaction dynamics with light RIBs
Collisions induced by halo nuclei on various targets at energies from 2 to 3 times the Coulomb barrier down to sub-barrier energies have shown that the presence of the extended low-density halo may deeply affect the reaction dynamics [139,140,141,142,143]. Since halo nuclei are very weakly bound, coupling to continuum may dominate the dynamics generating a suppression of the elastic scattering angular distributions in the region of the Coulomb-nuclear interference peak and an enhancement of the total reaction cross sections. Such an increase in total reaction was usually ascribed to an increased yield for direct processes such as transfer and breakup (e.g., [139, 141, 142]), but effects on fusion were also observed. Most of the available data on the above topic are relative to n-halo-induced reactions. More recently, first experimental studies of collisions induced by p-halo beams seem to suggest the presence of weaker effects when compared to the ones observed with n-halo nuclei, however further investigations are surely necessary (e.g., [143, 144]).
The new FraISe fragment separator is expected to produce different n-halo and p-halo beams such as, for instance: \(^6\)He (2n halo), \(^{11}\)Li (2n halo), \(^{11}\)Be (1n halo), \(^{14}\)Be (2n halo), \(^8\)B (1p halo), \(^{15}\)C (1n halo),\(^{17}\)Ne (2p halo). The availability of such beams at energies of the order 10–15 AMeV opens the possibility to deepen our understanding on the above topic, by measuring elastic scattering and direct reaction angular distributions in collisions induced by different n-halo and p-halo beams on a \(^{208}\)Pb target at about 2–3 times the Coulomb barrier (tag LNS-ND-CLU-b1 in Table 4).
On the n-halo side, an interesting case could be for instance the reaction \(^{15}\)C + \(^{208}\)Pb which could be measured at about two times the Coulomb barrier with an estimated beam intensity of the order of 10\(^5\) pps. A very interesting case could be the more exotic \(^{14}\)Be + \(^{208}\)Pb system; however, here the expected currents for the exotic \(^{14}\)Be projectile are of the order of 10\(^2\) pps making the experiment much more difficult.
Other possibilities on the p-halo side could concern the \(^8\)B + \(^{208}\)Pb and \(^{17}\)Ne + \(^{208}\)Pb systems, which could be measured at energies around 2.5 times the Coulomb barrier with estimated beam currents of the order of 10\(^4\) pps. With p-halo projectiles, the use of a segmented and high-solid-angle detection system would also allow to measure the coincidence between the core and the halo protons gaining further insight on the breakup dynamics (e.g., [143]).
3.3 Fission Dynamics
The known atomic nuclei are arranged in the Chart of Nuclides, a 2D map as function of the neutron (N) and proton (P) numbers. Both stable and radioactive nuclei, for a total of 261, are found on the earth crust. The rest of the so far known nuclei, about 3200, have been artificially made through nuclear reactions. The advent of heavy-ion beam accelerators allowed the generation of new nuclei by exploiting fusion and fission reactions, and paved the way to new reaction types, e.g., fragmentation and transfer.
About 3500 unknown nuclei are predicted to be bounded by accredited nuclear models and are located in the unexplored chart’s region called “Terra Incognita (TI)”. Their properties represent a benchmark for current nuclear structure theories and for a deep understanding of the r-process describing the origin of the elements heavier than Fe [145, 146]. For instance, the neutron shell at N = 126 is the last “waiting point” of the r-process path. Study of the structural properties of nuclei along the N = 126 neutron shell can also contribute to the open question of the quenching of shell effects in nuclei with large neutron excess.
Currently, the properties of unknown nuclei are only predicted by phenomenological models that are built on the systematics of known nuclei. However, the predictions of such models for the unknown regions are problematic because nuclei show diverging properties when moving progressively far from the stability line. Therefore, it is of great interest to investigate nuclear reactions to deal with the production of nuclei in the TI.
The “Island of Stability”, predicted in 1966 in correspondence of a double shell closure at \(Z=114\) and \(N=184\) [147], is another zone of unknown nuclei of noteworthy interest. Superheavy nuclei (SHN, proton number Z greater than 103) belong to this region. A worldwide effort is ongoing since five decades to exactly locate the island [148]. Recently synthesized SHN from Cn (\(Z=112\)) to Og (\(Z=118\)) seem to belong to the border of it [149,150,151,152].
Fusion of projectile and target nuclei is the solely process that has brought to the synthesis of SHN up to Og (\(Z=118\)) [153]. The employment of fusion reactions to synthesize heavier SHN is at risk because fusion between heavier projectiles and targets is more strongly hindered by the competition with another process called Quasifission (QF) whose yield increases with the number of protons involved [154, 155].
Multinucleon transfer (MNT) is the most promising reaction mechanism to access the TI and might also constitute a path to the SHN mass region [156]. Although it is a process identified in the late 70’s, MNT has a general behavior difficult to describe with existing theoretical models due to its complexity as a many-body process and to the lack of accurate and comprehensive experimental data sets [157,158,159,160].
In this framework, we discuss here three items which can be experimentally addressed with the high-intensity facility under construction at LNS: shell effects in fission and quasifission, multinucleon transfer reactions to investigate “Terra Incognita”, and a possible alternative pathway to produce superheavy elements.
3.3.1 Shell effects in fission and quasifission, fission modes and the Island of stability
It is well known that the fission process is strongly affected by shell effects which appear when a nucleus is represented as a set of collective variables, such as elongation and mass asymmetry, linked by a potential energy surface (PES) [161]. Shell effects appear as peaks and valleys in the PES and trajectories in this space can be linked to observables. Within the liquid drop model (LDM) approach, the nucleus is considered as a classical incompressible “macroscopic” liquid drop in which the competition between the repulsive Coulomb force and the attractive surface force creates a smooth PES with a minimum (the ground state). During the fission process, the nucleus elongates along the line of zero mass asymmetry thus initially increasing its potential energy, until at some time the maximum of the potential energy, which is called the saddle point (the top of the fission barrier), is reached. Afterward, at even further elongation, the nucleus reaches the scission point and splits in two equal fission fragments (mass asymmetry = 0). Although the LDM approach was able to qualitatively explain why fission is one of the main decay modes of heavy nuclei, it fails to describe the experimental observation that fission, spontaneous as well as low energy-induced fission, is sometimes symmetric and sometimes asymmetric, namely, multiple humped. However, following the Strutinsky method [162], the PES should be computed as the sum of the macroscopic (LDM) and microscopic (shell effects) energy: V\(_{\textrm{total}}\) = V\(_{\textrm{macro}}\)(LDM) + V\(_{\textrm{micro}}\) (shells). This naturally leads to the appearance of the asymmetric fission valleys which give rise to asymmetric mass distributions. As the microscopic shell effects depend strongly on specific neutron and proton numbers, their influence on the PES is expected to differ among nuclei, often leading to an even more complex PES with several fission valleys and the so-called fission modes [154, 163], each characterized by its unique saddle and scission points and consequently multiple humped mass distributions.
From the discovery of the fission modes, few observations can be put forward: (a) the existence of a complex structure of the PES in term of peaks and valleys induces the appearance of several fission barriers which affect the survival probability of a nucleus against fission; (b) there can be separate thresholds for the onset of the asymmetric or symmetric fission.
In the framework of the research on fission modes, of great interest is the investigation of extreme asymmetric fission modes, or superasymmetric modes because besides giving more insight on the shell effect on the PES, could be a pathway to produce exotic neutron-rich nuclei in the region of mass around 80. The existence of a superasymmetric fission mode (A\(_{H}\)/A\(_{L} > 3\)) can be inferred from the multimodal nature of nuclear fission. An example of such features are given in Fig. 22. In the empirical deconvolution of the mass distributions, the asymmetric and superasymmetric division are determined by the nuclear shells at \(Z = 28\) and \(N = 50\) and by the tail of the second standard asymmetric component and the symmetric component, whose contribution is changing with excitation energy of the fissioning nucleus (see the case of \(^{260}\)No* [166]).
More experimental data for fragment charge and mass distributions for A\(_{L} < 80\) are necessary for determining the parameters describing the superasymmetric mode in models. The fission of heavy nuclei at moderate excitation energies can be used for the production of exotic nuclei, including the very rare \(^{78}\)Ni [167].
Evidence of the involvement of the shell closures at \(Z=28\) \(N=50\) in quasifission. (Top row) Mass-TKE distributions from several reactions leading to superheavy elements. (Bottom row) Mass distribution only for those events located inside the red polygon in the Mass-TKE distributions above. The effect of the shell closure is to enhance the yield of fragments being single or double magic
It is worth noticing that the shell closures at \(Z=28\) and \(N=50\) have also a clear involvement in quasifission of heavy systems (see Fig. 23) and the cross section of fragments with mass around \(^{78}\)Ni is orders of magnitude bigger.
3.3.2 Plan for investigating shell effect in supersymmetric fission and quasifission
To plan experiments for the production and investigation of neutron-rich exotic nuclei at or below Z = 28, it is crucially important to have high beam intensity and the capability of measuring the charge and the mass of the fragments in that mass region. Fragments in the charge region around Z=28 could be produced either in superasymmetric fission or more copiously in quasifission and their charge identification can be achieved with the MAGNEX spectrometer. Additionally, a time-of-flight (TOF) arm on the opposite side of the MAGNEX spectrometer can be used to clean up the two-body reactions from background and to allow the measurements of the primary mass distributions. Reactions of interest for the superasymmetric channel and for which high-intensity beams will be available are \(^{22}\)Ne + \(^{238}\)U \(\rightarrow\) \(^{260}\)No and \(^{22}\)Ne + \(^{232}\)Th \(\rightarrow\) \(^{254}\)Fm. Reactions that might be a possible channel for \(^{78}\)Ni production are \(^{48}\)Ca induced on \(^{208}\)Pb, \(^{232}\)Th and \(^{238}\)U (tag LNS-ND-FIS-b0 in Table 4).
3.3.3 Multinucleon transfer reactions to investigate “Terra Incognita”
It is well known that multinucleon transfer (MNT) is the best candidate mechanism, with stable beams, to produce neutron-rich isotopes of the Terra Incognita below \(^{208}\)Pb. This is shown in Fig. 24. The advantage is that the production cross sections are several orders of magnitude larger than in the case of fragmentation of heavy projectiles, such as \(^{208}\)Pb or \(^{238}\)U.
It has been also recently recognized that MNT might be decisive in the production of new superheavy elements being the measured cross sections for fragments produced with mass antisymmetrization (formation of products lighter and heavier, respectively, than the projectile and target) few orders of magnitude bigger than those expected by the most advanced models [156, 168,169,170,171]. This is an important issue because MNT may solve the many problems connected with the rise of quasifission process in competition with the fusion process in reactions aimed at producing superheavy elements [154, 155].
Multinucleon transfer is however a substantially unknown process. The important degrees of freedom that drive the dynamical evolution of the process are still matter of investigation as the role played by the shell closures or Q values. The mechanism of dissipation, which connects the single particle and collective degrees of freedom, is evidently one of the most important ingredients of any model, but largely unknown.
A deeper understanding of the features of the MNT comes from the observation that Q\(_{gg}\)-values and total kinetic energy loss (TKEL) play a decisive role in determining the rate of the transfer channels and the survival against neutron emission of the primary decay fragments. Indeed, the reaction products (target-like fragments (TLFs) and projectile-like fragments (PLFs)) are excited enough to, even at the barrier energy, evaporate neutrons. Therefore, to preserve the neutron richness of the primary fragments, their excitation energy must be kept as low as possible. However, a larger mass transfer is expected for larger TKEL. As a consequence, the rate of production of neutron-rich fragments is a delicate balance between the Q\(_{gg}\) value of the specific channel and rate of energy loss. This point requires further insights to identify an optimal reaction aimed at producing a specific nuclide. How the excitation energy at the scission point is shared between the two fragments is also a matter of open discussions. In [169] it is shown that TLFs heavier than the target \(^{208}\)Pb are favored by the negative Q\(_{gg}\) values which keep the excitation energy lower, even at larger TKEL.
3.3.4 Plan for a multinucleon transfer study to investigate “Terra Incognita”
Given the order of magnitude of the cross sections involved in the production of nuclides in the Terra Incognita, the availability of high-intensity beams, with an intensity gain of a factor 100, makes their production feasible in a sufficient amount to allow detailed studies.
An interesting case study is shown in Fig. 25. The Mass-TKE distribution and the production cross sections for the reaction \(^{122}\)Sn + \(^{208}\)Pb at the barrier energy were computed with the Langevin type model in Ref. [170, 171]. The benefit of this particular entrance channel is the fact that very exotic W or Os \(N=126\) isotones can be produced with a cross section of the order of few \(\upmu\)b. Such a level of cross section can be reached in a reasonable time with a high-intensity beam. However, much care should be reserved to the experimental method. It is clearly required to measure the mass and charge of the fragments in an environment where other reaction channels are very strong. Therefore, the property of high selectivity of the detectors is mandatory. For such a task, the coupling of the MAGNEX setup, which is also being upgraded to stand high intensity, with a sub-nano-second TOF arm could be sufficient to isolate such rare channels by coincidence measurements.
3.3.5 A possible pathway to produce superheavy elements
In the early 80’s, a campaign of experiments performed at the FLNR-JINR (Dubna) was dedicated to the study of light particle emission in heavy-ion-induced reactions at energies below 10 AMeV [172,173,174]. Measurements were done for different target—projectile combinations and at different angles. The emitted light particles (\(p, d, ^{3,4}\)He) were analyzed in energy and recorded in the focal plane of the stepped pole MSP144 magnetic spectrograph. The most abundant emissions were observed for \(\alpha\) particles.
A unique feature of these reactions is that the measured \(\alpha\)-particle spectra show an exponential decrease that ends to the so-called kinematics upper-limit (KL) for a two-body process. This upper-limit energy value is the maximum energy an \(\alpha\) particle can acquire in a two-body process without excitation of the reaction partners at 0\(^{\circ }\) and is calculated from energy and momentum conservation laws using the mass excess of the reaction partners. Moreover, for an energy interval of more than about 20 MeV below the KL, no other processes but two-body are energetically possible (details are given in the references [172,173,174]) and therefore open.
From these studies, it also resulted that the cross section at the KL for the collinear configuration (measurements at 0\(^{\circ }\)) has a relatively small value, around 6 orders of magnitude below the maximum value of the cross section in the measured spectrum which is located close to the Coulomb barrier in the exit channel. Another observation is that, near the KL, the cross sections are higher for targets that are \(\alpha\) emitters and if the bombarding energies are slightly higher than the Coulomb barrier.
From that series of experiments, the most relevant one is the case of \(\alpha\) emission at 0\(^{\circ }\) in the reaction \(^{40}\)Ar + \(^{232}\)Th at the bombarding energy of 220 MeV. Later on, another experiment performed at the same MSP144 spectrometer [175] studied the reaction \(^{48}\)Ca+\(^{238}\)U at 270 MeV of incident energy and \(\alpha\) emission at 0\(^{\circ }\). The \(\alpha\) spectra at 0\(^{\circ }\) in these experiments are given in Fig. 26.
(Left) Laboratory \(\alpha\)-particle energy spectra measured at 0\(^{\circ }\) in the reaction \(^{22}\)Ne (178 MeV) + \(^{232}\)Th and \(^{40}\)Ar (220 MeV) + \(^{232}\)Th. The \(\alpha\) two-body kinematics upper-limit energies are shown by arrows and are about 125 and 85 MeV for the two reactions, respectively. (right) Laboratory \(\alpha\)-particle energy spectra measured at 0\(^{\circ }\) and 10\(^{\circ }\) in the reaction \(^{48}\)Ca (270 MeV) + \(^{238}\)U with a thin target. The \(\alpha\) two-body kinematics limit energy is around 88 MeV
Given the emission of \(\alpha\) particles at the two-body KL, one may wonder what happens to the heavy residue accompanying the \(\alpha\) particle, which should exist by conservation laws, and emitted also at 0\(^{\circ }\) in the lab reference frame. At the KL, its excitation energy must be zero. For \(\alpha\)-particle energies below the KL, the remaining energy turns into excitation of the heavy residue and the \(\alpha\) particle will be slower (the energy decrease is close to the value of the excitation energy of the residue) while the residue will be slightly faster. If the excitation energy of the residue is higher than the neutron separation energy or fission barrier, a neutron will be promptly evaporated or the heavy residue may undergo fission, respectively. Due to the exponential slope of the \(\alpha\)-particle spectra, for energies lower than the KL the cross section for \(\alpha\) emission increases significantly.
3.3.6 Plan for investigating the production of superheavy elements via two-body reactions
A schematic view of a possible experimental method is showed in Fig. 27. The essential idea is to stop the reaction products onto a thin catcher foil and measure their decay each time a high-energy \(\alpha\) particle is detected in a collinear configuration (zero degree). It is important to remark that in the two-body reaction the \(\alpha\) particles take away an important part of momentum brought by the projectile and the resulting heavy residue will gain an energy smaller than the energy of the compound nucleus, if it occurs in the same reaction. Therefore, the heavy residue can be caught on a thinner catcher foil while the other products, in particular \(\alpha\) particles, will go through. The silicon detectors surrounding the catcher foil serve as detectors of the heavy residue decay products (\(\alpha\) particles or fission fragments). The detection of a high-energy \(\alpha\) particle in the focal plane of MAGNEX could also be accompanied by the stop of the beam (beam-off method) and the wait for the decay of the heavy residue caught on the foil. The spectrometer MAGNEX can also be used to detect the \(\alpha\) particle at 0\(^{\circ }\) regardless of the presence of the heavy residue to check on the occurrence of \(\alpha\) particles at the KL and their cross section. This preliminary step would help in planning the experiment with the catcher foil or even attempt the measurement of the coincidence between the \(\alpha\) particle and the heavy residue. Considering the magnitude of the cross sections (of the order of few \(\mu\)b), this type of study can profit of the high-intensity beam at LNS. A typical reaction could be \(^{32}\)S(193 MeV) + \(^{238}\)U\(\rightarrow\) \(\alpha\) + \(^{266}\)Sg or \(^{66}\)Zn (363 MeV) + \(^{232}\)Th \(\rightarrow \alpha\) + \(^{294}\)Og (tag LNS-ND-FIS-b2 in Table 4).
4 Nuclear structure
The nuclear structure working group focuses on two main topics.
The first topic is the selective study of nuclear structure response to describe the \(0\nu \beta \beta\) NME, both experimentally and theoretically. As it is known, this decay can only exist if neutrinos are Majorana particles. Moreover, its observation would show that the lepton number is not conserved, providing a possible way to understanding the asymmetry between matter and antimatter present in the Universe. In this frame, the NME is a crucial ingredient in the expression of the \(0\nu \beta \beta\) half-life, that expresses the transition probability of a nuclear process. To date, results produced by different models to evaluate NME show a large spread, a factor of about three, that leads to significant uncertainties both on the amount of material required in the experiments and on the neutrino mass, in case \(0\nu \beta \beta\) will be observed. Reducing the uncertainty on the calculations of the NME will be essential if we wish to fully exploit the potential \(0\nu \beta \beta\) measurement. Nuclear structure models must be used for simplifying the computational problem by reducing the number of active degrees of freedom (nuclear many-body problem). In this perspective, SCE and DCE reactions induced by heavy ions as well as double \(\gamma\)-decay process may represent key tools. Within this context, we plan to use the present state-of-the-art nuclear structure models (realistic shell model, Skyrme-QRPA, IBMs) to provide the input for direct and transfer heavy-ion SCE and DCE reactions. Comparison between results from different models will be performed (tag LNS-NS-NMETheo-a0 in Table 5, Sect. 4.1.1). In a second step, calculations with the same models will be carried out for the evaluation of the NME of the double \(\beta\) decay with and without neutrinos (tag LNS-NS-NMETheo-b0 in Table 5, Sect. 4.1.2). Subsequently, results from SM/IBM/QRPA descriptions will be employed to investigate possible correlation between NMEs involved in the weak and strong processes as well as in the double \(\gamma\) decay (tag LNS-NS-NMETheo-c0 in Table 5, Sect. 4.1.6).
To supply experimental information on \(0\nu \beta \beta\) NME, the NUMEN project has proposed the idea to use heavy-ion DCE reactions as a surrogate processes of \(0\nu \beta \beta\), given the similarities with that decay such as, among the others, the same initial and final state. In the experimental approach to DCE reactions a key tool is the MAGNEX magnetic spectrometer, with its upgrade to sustain high rates and, at the same time, to maintain the current resolution and sensitivity. The full understanding of the DCE reaction mechanism implies the study of a wide network of nuclear reactions: the new methodology proposed is the multichannel approach (tag LNS-NS-SelAdSpec-a0 in Table 5, Sect. 4.1.4). Synergies with complementary studies, such as double \(\gamma\) decay, will also be discussed (tag LNS-NS-SelAdSpec-c0 in Table 5, Sect. 4.1.5). Recent experimental results on DCE give significant input to the next phase of the NUMEN project in which deeper investigations of different systems are planned with improved statistics using high-intensity beams (tag LNS-NS-SelAdSpec-a1 in Table 5 Sect. 4.1.3). Indeed, only few systems have been studied in the present conditions, due to the low cross sections (tag LNS-NS-SelAdSpec-b0 in Table 5, Sect. 4.1.5). Second-order isospin excitations of nuclei are key information bridging the gap between nuclear and neutrino physics and heavy-ion DCE reactions are promising tools in this research field, provided that nuclear structure and reaction aspects are accurately and consistently addressed. The goal is the systematic study of all the cases of nuclei candidate to undergo \(0\nu \beta \beta\) using high-intensity beams, at different energies, and advanced spectrometry.
The second topic is the study of collectivity in nuclei and uses the CHIMERA multidetector as main tool, which could be coupled with ancillary detectors depending on the physics case. Some of the proposed items are also related to the dynamics studies, more deeply developed in the WG1 working group. In particular, the search of the Pigmy dipole resonance (PDR) will represent FraISe day-one experiments (tag LNS-NS-COL-a0 in Table 5, Sect. 4.2.1). The aim is to study the link with both the r-process and the nuclear equation of state (EOS) on one hand and on the other to follow the evolution of PDR in small nuclei, studying the possible dependence on neutron number with CHIMERA coupled with FARCOS telescopes and a new neutron detector. In a second step, the study of the dynamical dipole will be addressed in reactions induced by Ar isotopes on Ca or Ni isotopes (tag LNS-NS-COL-b0 in Table 5, Sect. 4.2.2) with the CHIMERA detector and in strong synergy with the nuclear dynamics studies, also studying the density evolution of the system. In this same timescale, we also propose the study of the Isoscalar Giant Monopole Resonance (IGMR) excited in \(^{38}\)S and other nuclei of the cocktail beam (tag LNS-NS-COL-b1 in Table 5, Sect. 4.2.3), using the MAGNEX magnetic spectrometer and the FraISe beams. Measuring the GMR in exotic nuclei will open the possibility to study the isospin dependence of the incompressibility. In a next step, we will also consider some experiments to be performed after important detector upgrade. Those experiments will be dedicated to the solution of some contradicting results about the saturation of the GDR width around a temperature of \(T=2.5\) MeV; to explain the sudden quenching of the GDR \(\gamma\)-ray yield at high excitation energy; to link the GDR disappearance with the liquid–gas phase transition; to study GDR features of light nuclei with cluster structure and the role of collectivity toward the p-drip line (tag LNS-NS-COL-c0 in Table 5, Sect. 4.2.4).
The highlights of all the nuclear structure (NS) topics are summarized in Fig. 28, where at glance it is shown the NS midterm program at LNS, where new physics scenarios will open thanks to the new, high-intensity stable and unstable beams.
4.1 Nuclear matrix elements toward \(0\nu \beta \beta\)
4.1.1 Introduction
The \(0\nu \beta \beta\) decay is a nuclear transition in which two nucleons undergo \(\beta\) decay simultaneously without the emission of neutrinos. The search for evidence of this very rare second-order electroweak process is at present one of the major goal in particle physics since nowadays it represents the most promising way to probe neutrino properties and search for deviations from the Standard Model.
At present, the strongest limits on the \(0\nu \beta \beta\) decay have been set as \(>10^{26}\) yr by the GERDA and KamLAND-ZEN experiments using \(^{76}\)Ge and \(^{136}\)Xe nuclei, respectively, and as \(> 10^{24}\) yr by the CUORE experiment using \(^{130}\)Te. The goal of future experiments, as for instance ton-scale CUPID (CUORE Upgrade with Particle IDentification), is to push the sensitivity to the point at which the decay can be observed if neutrinos are indeed Majorana particles and their masses are arranged in a pattern known as the “inverted hierarchy”. In this context, the NMEs of the \(0\nu \beta \beta\) decay related to the wave functions of the parent and granddaughter nuclei play a fundamental role. In fact, the half-life of this process, when considering only the light neutrino exchange, may be expressed as
where \(G^{0\nu }\) is the so-called phase-space factor which has recently been re-evaluated with improved precision, \(M^{0\nu }\) is the nuclear matrix element, and \(\langle m_{\nu } \rangle\) and \(m_e\) are, respectively, the effective neutrino mass and the electron mass.
NMEs for \(0\nu \beta \beta\) candidates as a function of mass number A. Results are from shell model, interacting boson model, quasi-particle random-phase approximation, and energy density functional theory, and are obtained by using the free value of the axial vector coupling constant \(g_A\). Further explanations can be found in [176], from which the figure was taken
The knowledge of the NMEs when combined with the present limit on \(\langle m_{\nu } \rangle\) is a key point in the choice of the material and the required amount to use in experiments. However, as mentioned above, the calculated matrix elements for nuclei of experimental interest are currently characterized by large uncertainties, predictions from different models differing by a factor of two or three (see Fig. 29). Large efforts have therefore been devoted by the community to better constrain and improve the available nuclear structure models.
It is important to note that, in addition to weak processes, nuclear charge exchange (CE) transitions also include excitations induced by the strong interaction, like the Isobaric Analog (IA) or the Gamow–Teller (GT) Resonances [177,178,179,180,181]. In most cases, these transitions share the same initial and final states of corresponding weak processes and their NMEs can be evaluated within the same nuclear structure models which are usually adopted for the investigation of \(0\nu \beta \beta\) NMEs. A comparison with a more comprehensive set of experimental observables than it has been done so far, including, for instance, M1 polarizability and spin dipole transitions, would be highly desirable to further constrain and improve the nuclear structure models.
The connection between nuclear single CE excitations and \(\beta\) decay has been widely explored in the past. As far as double excitations are concerned, the analogy between strong and weak processes was recently pointed out in Ref. [182], where double Gamow–Teller (DGT) DCE matrix elements are evaluated within the shell - model framework, showing the existence of a linear correlation between DGT DCE and \(0\nu \beta \beta\) NMEs. This linear correlation between the DGT DCE matrix elements and the \(0\nu \beta \beta\) NMEs was also demonstrated in Ref. [183]. In this paper, the explicit form of DGT DCE matrix elements is derived from chiral effective field theory, and it is shown that, under certain approximations, the DCE cross section can be factorized into a reaction and nuclear structure part, showing the possibility to extract DCE matrix elements. These combined analyses of strong and weak processes are expected to lead to a more comprehensive understanding of the spin-isospin phenomenology, including mutual relationships between the NMEs.
Another interesting possibility to extract information about \(0\nu \beta \beta\) NMEs is the study of second-order electromagnetic transitions emitting two photons (\(\gamma \gamma\)), in particular the double-magnetic dipole decays [184]. Shell-model calculations show a good linear correlation between the \(_{Z-2}^{A}X_{N+2} \rightarrow {}^{A}_{Z}Y_{N} +2 e^{-}\) and \(^{A}_{Z}Y^{*}_{N} \rightarrow {}^{A}_{Z}Y_{N} + 2 \gamma\) NMEs, the \(Y^{*}\) referring to the double Isobaric Analog State (DIAS). This means that future \(\gamma \gamma\) measurements, as planned at LNS, can be employed to extract information on the \(0\nu \beta \beta\) NMEs.
Nuclear CE modes can be excited by nuclear reactions, which offer a quite appealing opportunity to explore the physics we have discussed so far. Indeed, already in the past, SCE reactions, mainly induced by light projectiles, have been the major source of information on the isospin and spin–isospin modes of excitation in nuclei. On one hand, these reaction mechanisms provide important clues on the corresponding terms in the effective nucleon–nucleon interaction in the medium; on the other, their study includes the possibility to isolate, out of the reaction cross section, NMEs presenting formal analogies with those of single \(\beta\) decay.
In the case of heavy-ion reactions, an especially interesting aspect is the broad range of projectile-target combinations which, for example, allow to project out selectively specific features, e.g., spin flip and non-spin flip transitions [185]. SCE reactions with heavy ions are expected to also populate states with higher multipolarities, as those corresponding to the intermediate states of the \(0\nu \beta \beta\) decay [181]. Nuclear structure inputs are crucial for the calculation of the associated reaction cross sections, which can be tested against experimental results.
DCE reactions with heavy ions [20, 186], whose investigation is pursued within the NUMEN project, are a new exciting frontier, also because of their possible analogy with double \(\beta\) decay. The key aspects are that the two (weak and strong) processes, beyond involving the same nuclear configurations, are both represented by transition operators that are a superposition of short-range isospin, spin-isospin and rank-two tensor components with a relevant available momentum (100 MeV/c or so) [20]. Thus DCE experimental cross sections can be considered as important benchmarks for theoretical models; tuning the models on experimental data will increase their predictive power for the evaluation of \(0\nu \beta \beta\) NMEs, possibly reducing the undesired spread presently existing among the various calculations [176]. It is also interesting to note that, besides the intimate connection to double-\(\beta\) decay, heavy-ion DCE reactions are of genuine interest for nuclear reaction and structure physics since they give access to the systematic studies of the hitherto unexplored territory of multiple excitations of elementary isovector modes of both GT spin flip and Fermi non-spin flip character. Requests for combined stable ejectiles and high resolution spectroscopy are satisfied only by heavy-ion beams because neither light ion nor (\(\pi ^\pm ,\pi ^{{\mp }}\)) DCE reactions are simultaneously fulfilling these demands, see, e.g., [181].
4.1.2 Heavy-ion-induced direct reactions to access observables correlated to \(0\nu \beta \beta\) decay
Nucleon transfer and charge exchange reactions
The competition of direct and transfer DCE mechanisms is an important issue requiring systematic experimental and accompanying theoretical studies. Experience with heavy-ion SCE reactions shows that the transfer channels in general strongly depend on the kinematic conditions and especially on the spectroscopic properties of the involved ions, so transfer processes can be controlled by an appropriate choice of projectile–target combinations and incident energy, as widely discussed in Ref. [181]. Direct SCE and DCE processes, however, are hard collisional processes on momentum scales defined by the masses of isovector mesons. As such, their yields are only little affected by kinematic conditions or single particle structures. As a rule of thumb, direct SCE and DCE mechanisms dominate provided that the reaction take place at energies well above the mutual Coulomb barrier and projectile–target combinations of incompatible single-particle structures are used, that is easily realized by choosing largely different masses for projectile and target nuclei. This result was confirmed in the recently published study of Ref. [187], where it was demonstrated that the multinucleon transfer contribution to the 116Cd(20Ne,20O)116Sn DCE reaction cross section at 15 AMeV is negligible.
At the start of the NUMEN project, neither reaction nor structure theory had at hand approved methods for second-order processes of this kind. In the last years, significant progresses were made in developing the appropriate theoretical formalism and the numerical methods and computer codes, enabling now the exploration of all reaction channels by using the same experimental conditions and a unique theoretical framework in the so-called multichannel approach described in detail in Sect. 4.1.4. These studies are a selective tool to acquire spectroscopic information and at the same time they allow to pinpoint and constrain the intermediate channels relevant for the population of SCE and DCE channels.
A necessary step forward in the attempt to extract the DCE cross sections and get information on the \(0\nu \beta \beta\) NMEs, is to coherently combine the reaction amplitudes of transfer and direct SCE and DCE processes in order to properly account for the quantal interference effects between these competing reaction mechanisms. A pending problem, yet to be solved, is to describe the transfer states and the configurations reached by direct SCE/DCE transitions through compatible structure models. The task is to make commensurable the shell model results, best suited to describe single-particle and pair structures as discussed in other parts of this report, to the QRPA results used for SCE and DCE transitions.
Reaction mechanism in direct double charge exchange reactions
Heavy-ion direct DCE reactions can be described in terms of a combination of two single direct CE processes, where mechanisms reflecting the presence of short-range correlations can also be included. The treatment of uncorrelated two-step process leads to an expression of projectile and target NMEs close to the ones involved in \(2\nu \beta \beta\) decay of the corresponding nuclei [188, 189]. On the other hand, mechanisms underlying the role of correlations (Majorana-like mechanisms) lead to NMEs exhibiting analogies with the ones involved in the elusive \(0\nu \beta \beta\) decay [186, 190]. However, generally speaking, direct DCE NMEs contain a considerably more complex multipole and spin structure than the corresponding weak counterparts.
Within the sequential (uncorrelated) reaction mechanism, heavy-ion direct DCE reactions are described as a double-SCE process (dSCE), i.e., as a sequence of two independent direct SCE reactions. Second-order DWBA represents the natural framework for developing the theory of the dSCE reaction mechanism. The propagation of the two nuclei generated by the first SCE reaction (the intermediate channel) is accounted for by a Green function. Expanding the latter in the basis of nuclear states and distorted waves associated with the intermediate channel, the dSCE transition matrix element becomes a superposition of two SCE transition matrix elements. Initial and final state interactions (distortion effects) of the two SCE processes constituting the dSCE reaction, are very important and have been studied in detail. Whereas distortion effects of the intermediate channel compensate each other to a large extent, distortion effects related to the entrance and exit channels play a significant role both in the order of magnitude and in the diffraction pattern of the angular distributions, as observed in the case of the single processes.
To single out the information on both projectile and target dSCE NMEs from the analysis of the DCE cross section, some approximations are needed in the treatment of the intermediate channel. In analogy with the weak decays, both the single state dominance hypothesis and the closure approximations were tested. It was found that the order of magnitude of the experimental cross sections can be reproduced only when considering several nuclear states in the intermediate channel, thus supporting the validity of the closure approximation. Within such a scheme and with a proper composition of the nuclear structure elements of the two steps, the structure kernel can be decoupled from the reaction dynamics [188]. Finally, a proper rearrangement of the angular momenta couplings allows to get separate information on projectile and target NMEs [189]. This will give the opportunity to access direct information on NMEs from DCE cross section measurements.
dSCE calculations have been already applied to the study of DCE reactions involving the systems \(^{40}\)Ca \(+^{18}\)O, \(^{76}\)Se \(+^{18}\)O, \(^{76}\)Ge \(+^{20}\)Ne and \(^{116}\)Cd \(+^{20}\)Ne. For the first, the lightest one of these nuclear systems, a good reproduction of the experimental DCE angular distribution was found, while the cross section of the reactions involving heavier systems is presently underestimated, pointing to a possible contribution of other DCE reaction mechanisms. In particular, the Majorana-like reaction mechanism, which is currently under investigation, describes the DCE process as a sequence of two correlated SCE reactions. In each of the two interacting nuclei, the correlation is provided by the exchange of neutral mesons between the two nucleons involved in the DCE process. The exchange of charged (responsible for the CE) and neutral mesons (yielding correlations) can occur in different ways, which contribute coherently to the DCE process [186, 190]. Finally, the total DCE reaction can proceed via sequential as well as Majorana-like mechanisms, so that all possible reaction paths coherently contribute to the whole process. Further investigations of the different DCE reaction mechanisms will allow a more complete analysis of the DCE data and a deeper understanding of the underlying interactions.
4.1.3 The experimental approach to double charge exchange reactions
The DCE reactions induced by heavy ions present some distinctive characteristics which need to be properly taken into account for a successful experimental study. The involved tiny cross sections (\(\sim\) 10 nbarn) call for very precise measurements, maintaining sufficient energy and angular resolution to distinguish among the different possible transitions. Indeed, angular distributions at forward scattering angles, including zero degrees, are necessary to extract meaningful spectroscopic information and provide insight into the reaction mechanism. High performances in terms of medium-/heavy-ion identification is also required. Moreover, a careful control of the signal-to-background ratio is needed due to the large yields generated in the collisions by other reaction channels different from DCE.
In such a context, the magnetic spectrometry presents important advantages compared to other detection techniques. In particular, the MAGNEX magnetic spectrometer [25] plays the central role in the NUMEN experimental campaign. Indeed, its large acceptance in angle (50 msr) and momentum (\(-14\) %, \(+10\) %) allows to explore a wide angular range and a broad momentum transfer window. Moreover, its focal plane detector (FPD) ensures good identification and tracking performances [191]. However, it was not designed to work with high-intensity beams such as those that will be available at the INFN-LNS facility once the accelerator upgrade is completed [192]. Therefore, a new FPD has been designed with the aim of fulfilling specific requirements. The new FPD consists of two sections: a gas tracker allowing the ions to be tracked downstream of the magnetic elements and a particle identification (PID) wall.
The gas tracker is a proportional drift chamber filled with isobutane gas continuously flowing at a pressure that ranges from a few up to tens of mbar. The multiplication stage is based on multiple thick GEM (M-THGEM) technology [193] which is robust and can withstand the high rate expected at the focal plane (about 3 \(\times\) 10\(^4\) pps/cm). When a reaction ejectile crosses the active volume of the gas tracker the primary electrons drift toward the multiplication stage, are multiplied inside the M-THGEM holes and then drift to a segmented anode. From the charges induced on the anodic pads, it is possible to extract the projection of the track on the horizontal plane, while from the drift time of the electrons it is possible to get information on the vertical coordinates, thus obtaining a full 3D reconstruction of the track. The gas tracker was designed to provide a resolution of 5 mrad FWHM on the horizontal and vertical angles \(\theta\) and \(\phi\), and a position resolution better than 0.5 mm FWHM.
The identification of the heavy ions is performed by the PID wall. It is an array of 720 telescopes, each with a surface area of 15 \(\times\) 15 mm\(^2\). The \(\Delta\)E stage is a 100-\(\mu\)m-thick silicon carbide (SiC) detector, while the residual energy \(E_r\) stage is a 5-mm-thick CsI(Tl) coupled to a photodiode. The choice of SiC and CsI(Tl) detectors was motivated by the following requirements:
-
High radiation hardness, since the detectors must withstand a rate of 10\(^{11}\)ions/(cm\(^2 \times\) yr).
-
Good energy resolution (about 2–3 %).
-
Good time resolution (\(\approx\) 2–3 ns).
-
Operation in a low-pressure gas environment.
The degree of segmentation of the PID wall is a compromise between the requirement of a high efficiency and a low number of electronic channels on the one hand and a low double hit probability on the other hand.
In cases where the energy resolution of MAGNEX (\(\Delta E /E \approx\) 1/1000) is not sufficient to separate transitions to the states of interest in the residual nuclei, measurements will be performed in coincidence between MAGNEX and the G-NUMEN \(\gamma\)-ray calorimeter. G-NUMEN will be an array of \(\approx\) 110 cerium-activated lanthanum-bromide (LaBr\(_3\)(Ce)) scintillation detectors [26] that will be positioned around the reaction target to detect the prompt \(\gamma\)-rays from reaction products.
The new detection system is specifically designed to suit the different experimental runs of the NUMEN campaign. Important differences exist in the experimental settings depending on the explored reaction channels, as detailed below. \(\beta ^- \beta ^-\)-like transitions in the target nuclei are probed via the (\(^{20}\)Ne,\(^{20}\)O) and (\(^{12}\)C,\(^{12}\)Be) DCE reactions, induced by \(^{20}\)Ne\(^{10+}\) and \(^{12}\)C\(^{6+}\) beams, respectively, while \(\beta ^+ \beta ^+\)-like transitions are investigated via the (\(^{18}\)O,\(^{18}\)Ne) DCE reaction, induced by \(^{18}\)O\(^{8+}\) beams. In this context it is worth noting that, thanks to the spectrometer large momentum acceptance, many reaction channels can be measured simultaneously, i.e., within a unique magnetic setting. This condition guarantees the optimal exploitation of the beam time as well as stable working conditions.
The DCE channel is characterized by the lowest cross section if compared to competing quasi-elastic reactions. Therefore, specific experimental strategies in terms of beam intensities and FPD acceptances have been defined in order to optimize the data taking.
In measurements focused on the DCE g.s. to g.s. transitions that can be energetically resolved by MAGNEX, the beam intensity will be of the order of 10\(^{13}\) pps, while the FPD momentum acceptance will be reduced to 10%, thus excluding other reaction channels that would produce a prohibitively high count rate. The cases where the MAGNEX inclusive measurements cannot separate the DCE g.s. transition from the low-lying ones will require the coincident detection of the emitted \(\gamma\)-rays with the G-NUMEN array. Then, a reduction of the beam intensity to \(\approx\) \(10^{12}\) pps is foreseen in order to limit the average number of reactions per beam bunch to about 1, thus keeping the best observational limit for the DCE g.s. transitions. Finally, the reaction channels different from the DCE will be explored with a further reduced beam intensity (\(\approx\) 10\(^{11}\) pps) but exploiting the full FPD acceptance. The use of the G-NUMEN array in such runs could also be considered since with such a beam intensity the total reaction rate will be reasonable. These sets of conditions allow to maintain the data throughput from the digital electronics to manageable levels with affordable solutions for transfer and storage.
Stringent constraints are put on the reaction targets by the above experimental conditions. These targets will typically be prepared by evaporation of the isotope of interest, with a high level of enrichment, onto a substrate. The targets should be thin (\(\approx\) 10\(^{18}\) atoms/cm\(^2\)) and uniform to preserve a good energy resolution for the ejectiles detected by MAGNEX FPD. Given the high beam intensities, the power deposited in these fragile targets will be significant (\(\approx\) 1 W), thus requiring an active cooling system. The proposed solution is to use a 2-\(\mu\)m-thick backing of Highly Oriented Pyrolytic Graphite (HOPG), whose high thermal conductivity promotes the heat dissipation in a copper sample holder, in contact with the cold head of a cryocooler. [194, 195]. The HOPG will also serve as a post-stripper, which will shift the charge distribution of the ejectiles closer to a full-stripping condition. This is particularly relevant for reaction studies induced by \(^{20}\)Ne where 8\(^{+}\) and 9\(^{+}\) charge states could enter the active FPD region giving rise to a substantial background, possibly limiting the tolerable beam intensity [196].
A view of the MAGNEX spectrometer after the upgrade is illustrated in Fig. 30.
4.1.4 The multichannel approach
The full understanding of the complete DCE reaction mechanism implies the necessity of studying a wide network of nuclear reactions.
The analysis of each reaction channel allows to access the many features of the dynamical process and the structure of the colliding nuclei involved in the DCE reaction:
-
The initial and final state interactions, such as the ones competing to the intermediate partitions, are responsible for the distortion of the incoming and outgoing wave functions involved in nuclear reactions and play a central role in all the reaction mechanisms. Studies of elastic and inelastic scattering are mandatory to investigate nucleus–nucleus potential and nuclear deformation, respectively.
-
The occupation probabilities of valence orbits active in the decay and reaction dynamics is one of the most relevant features of the nuclear wave functions. In this framework, the study of one-nucleon transfer reactions is an important tool to access the single-particle configurations in nuclear states.
-
Nuclear many-body properties, such as the pairing interaction, play a crucial role in the nuclear structure of the \(\beta \beta\)-candidates nuclei. Two-nucleon transfer reactions are very sensitive to those nuclear features and their study is one the most powerful tool to investigate them.
-
The double-SCE contribution to the total DCE can be estimated considering a folding of two SCE reaction amplitudes [188]. For that reason, it is particularly important to improve the description of the single charge exchange experimental data.
All the studies present in literature on heavy-ion-induced direct reactions are focused on few (often one) reaction channels at the time. In this way the information extracted from data analysis cannot be fully constrained and important parameters need to be taken either from other experimental studies performed in similar conditions, or by model calculations. The comprehensive study of a wide ensemble of reaction channels explored in the same experimental conditions and consistently described by a unique theoretical framework would be desirable to make significant step forward in the field. These limitations can be overcome by means of multichannel approach, recently proposed within the NUMEN project.
Thanks to the large momentum acceptance of the MAGNEX spectrometer, it is possible to detect the ejectiles coming from the mentioned nuclear reaction channels in only few sets of the quadrupole and dipole magnetic fields. This simultaneous measurement of different reaction channels helps to highlight possible systematic uncertainties in the evaluation of the integrated beam charge and target thickness, in the measurement of the scattering ion tracks at the FPD and in the reconstruction of the scattering parameters.
Two examples of these networks are shown in Fig. 31a, b in the case of the 18O and 20Ne-induced reactions on 130Xe and 130Te target nuclei, respectively. The components of the complete DCE reaction mechanism are represented by arrows. In addition to the direct DCE and the two-step double-SCE diagonal paths, many multinucleon transfer routes lead to the same final DCE partition. All the processes shown in Fig. 31a, b coexist during the reaction and compete each other. While the gray arrows in Fig. 31 refer to the transitions not directly measurable in the case of 18O and 20Ne-induced reactions, the other colored arrows refer to measured reaction channels: elastic and inelastic scattering (el. and inel.), one-neutron (n), two-neutron (n–n), one-proton (p), and two-proton (p–p) transfers, SCE and DCE.
The multichannel approach has been recently applied to the 20Ne+116Cd [187, 197, 198], 18O+40Ca [199,200,201], 18O+48Ti [202,203,204] and 18O+12C [205] systems at 15.3 AMeV incident energy.
4.1.5 Recent experimental results on DCE and future plans with the upgraded facility
Two recent experimental studies of DCE reactions have been performed at INFN-LNS, the \(^{40}\)Ca (\(^{18}\)O, \(^{18}\)Ne) \(^{40}\)Ar [4] and the \(^{130}\)Te (\(^{20}\)Ne, \(^{20}\)O) \(^{130}\)Xe reaction [206]. The beams have been delivered by K-800 superconducting cyclotron and the ejectiles produced in the reactions were momentum-analyzed by the MAGNEX spectrometer [25] and detected by its focal plane detector [191]. For both systems, not only the DCE reactions but also the complete net of competing processes (elastic scattering, single charge exchange and transfer reactions) has been measured at very forward angles including zero degrees. Concerning the first reaction, the \(^{18}\)O beam was accelerated with an energy of 270 MeV and impinged on a thin \(^{40}\)C target. In the second experiment, the \(^{20}\)Ne beam was produced with an energy of 306 MeV and impinged on a thin \(^{130}\)Te target. Adopting the identification technique described in [207] the ions of interest were selected. A 10\(^{th}\)-order trajectory reconstruction software was used to determine the excitation energy spectra, shown in Fig. 32.
a Excitation energy spectrum from \(^{40}\)Ca (\(^{18}\)O, \(^{18}\)Ne) \(^{40}\)Ar DCE. The symbols g.s.\(^{\bigtriangleup }\) and 1.46\(^{\bigtriangleup }\) indicate the \(^{40}\)Ca (\(^{18}\)O, \(^{18}\)Ne\(_{1.87\,\textrm{MeV}}\)) \(^{40}\)Ar\(_{\mathrm{g.s.}}\) and \(^{40}\)Ca (\(^{18}\)O, \(^{18}\)Ne\(_{1.87\,\textrm{MeV}}\)) \(^{40}\)Ar\(_{1.47\,\textrm{MeV}}\) transitions, respectively. Figure from Ref. [4]. b Excitation energy spectrum for the \(^{130}\)Te (\(^{20}\)Ne, \(^{20}\)O) \(^{130}\)Xe DCE reaction. Inset: zoomed view for E\(_{x} <\) 10 MeV. Figure from Ref. [206]
In the DCE energy spectrum of Fig. 32a, the \(^{40}\)Ar\(_{\mathrm{g.s.}}\) is clearly separated from the not resolved doublet of states \(^{40}\)Ar 2\(^{+}\) at 1.460 MeV and \(^{18}\)Ne 2\(^{+}\) at 1.887 MeV. At higher excitation energy the measured yield is spread over many overlapping states. The cross section around zero-degree is \(\approx\) 11 \(\upmu\)b/sr for the \(^{40}\)Ca (\(^{18}\)O, \(^{18}\)Ne) \(^{40}\)Ar\(_{g.s.}\). Multistep transfer reactions are expected to be strongly suppressed in the population of the mismatched (L = 0, Q = \(-2.9\) MeV) \(^{40}\)Ar\(_{\mathrm{g.s.}}\). Indeed, the cross section around zero-degree is \(\approx\) 3 \(\upmu\)b/sr for \(^{40}\)Ca (\(^{18}\)O, \(^{20}\)Ne) \(^{38}\)Ar\(_{\mathrm{g.s.}}\) two-proton transfer [200].
Regarding the \(^{130}\)Te (\(^{20}\)Ne, \(^{20}\)O) \(^{130}\)Xe DCE reaction, as it can be seen in Fig. 32b, only a few events were detected for the \(^{130}\)Te\(_{g.s.}\) \(\rightarrow\) \(^{130}\)Xe\(_{g.s.}\) transition, leading to an integrated cross section of 13 nb in the angular range \(0^{\circ }< \theta _{lab} < 9.5^{\circ }\) and in the energy range \(-1\) MeV \(< E_{x}<\) 1 MeV. A contribution due to the first excited state of \(^{130}\)Xe 2\(^{+}\) at 0.536 MeV may be included in the given cross section. The high density of the \(^{130}\)Xe excited states and the finite experimental energy resolution lead to a rather structureless shape of the excitation energy spectrum above the g.s. region.
These results give a significant input to the next phase of the NUMEN project in which a deeper investigation of the system is planned with improved statistics by using high-intensity beams.
With the upgraded facility, it is planned to start the measurements of DCE reactions in both \(\beta ^+\beta ^+\) and \(\beta ^-\beta ^-\) directions on the partner nuclei: 76Ge \(\Longleftrightarrow\) 76Se and 116Cd \(\Longleftrightarrow\)116Sn. These systems were already explored with the low beam intensity at 15 AMeV incident energy during the recent NUMEN experimental activity. The study of such systems at different incident beam energies (from 5 to 60 AMeV) are foreseen at the beginning of time schedule in order to investigate the energy dependence of DCE cross sections. As one of the first systems, the exploration the 100Mo target nucleus, which is candidate for the 0\(\nu \beta \beta\) decay, is also planned, because of the great interest of the scientific community to this isotope nucleus.
4.1.6 Double \(\gamma\) decay
Other measurements that may represent an important tool to acquire information on the \(0\nu \beta \beta\) NMEs are related to the \(\gamma \gamma\) decay. The two-photon decay process is a second-order process in quantum electrodynamics. In the nuclear case, this means that an excited nuclear state simultaneously emits two \(\gamma\)-ray energy-quanta with a continuous \(\gamma\)-energy spectrum, with the sum energy of the two \(\gamma\) rays equaling the energy difference between the initial and the final state. Until very recently, the double \(\gamma\) decay mode was only observed in \(0^+ \rightarrow 0^+\) transitions in nuclei which have ground and first excited 0\(^+\) states so that the decay of the first excited state by a single photon is strictly forbidden [208]. In 2015, Walz et al. published a Nature letter [209] where, for the first time, they observed the competing double-\(\gamma\) nuclear decay (\(\gamma \gamma\)/\(\gamma\)-decay) from a \(11/2^-\) isomeric state in \(^{137}\)Ba to its \(3/2^+\) ground state following the \(\beta\) decay of \(^{137}\)Cs. The branching ratio of this process was measured to be (2.05 ± 0.37) \(10^{-6}\). In that experiment, the authors were able also to determine the important multipolarities involved in the \(\gamma \gamma\)/\(\gamma\) decay. The \(\gamma \gamma\)/\(\gamma\)-decay from the \(11/2^-\) isomeric state in \(^{137}\)Ba has been confirmed in a recent experiment performed at Extreme Light Infrastructure-Nuclear Physics facilities [210]. However, in contrast to the conclusions of [209], the new experiment points to the dominant role of the octupole–dipole term in comparison to the quadrupole–quadrupole term.
The decay rate of the competitive \(\gamma \gamma\)/\(\gamma\)-decay, which is more than five orders of magnitude smaller than that of the allowed \(\gamma\) decay, makes its observation very challenging. However, these measurements may represent an important tool to acquire information on the \(0\nu \beta \beta\) NMEs. In fact, as mentioned in the Introduction, a good linear correlation between the \(\gamma \gamma\) and \(0\nu \beta \beta\) NMEs has been demonstrated in [184] by using large-scale shell model calculations. This work reveals that the correlation holds for \(\gamma \gamma\) transitions driven by the spin or orbital angular momentum due to the dominance of zero-coupled nucleon pairs, a feature common to \(0\nu \beta \beta\) decay. Experimental studies of \(\gamma \gamma\) decay for some selected DIAS relevant for the \(0\nu \beta \beta\) decay are planned.
4.1.7 Nuclear structure input: comparison between different theoretical approaches
The three models mostly employed to describe spectroscopic properties and provide the needed input for reaction studies are: the shell model, the quasi-particle random-phase approximation and the interacting boson model. We shall briefly describe the main features of these models and discuss their present state-of-the-art as well as their future perspectives concerning the calculation of matrix elements involved in \(\gamma \gamma\) decay and CE transitions induced by weak and strong interactions. In order to develop a comprehensive understanding of these phenomena and gain more insight on possible correlations between the corresponding NMEs, it is of great relevance to assess to which extent the results are sensitive to the structure inputs provided by the different approaches.
The shell model
The shell model (SM) is considered as the basic scheme for a microscopic description of the nucleus. Within the SM, the complexity of the many-body system is simplified by considering the nucleus as a closed-shell core with additional valence nucleons that interact in a subspace of the Hilbert space (model space) through an effective Hamiltonian, \(H_{\textrm{eff}}\), accounting for contributions from configurations external to the model space. The SM \(H_{\textrm{eff}}\) can be constructed by following a phenomenological approach, i.e., by adjusting its matrix elements to reproduce a set of experimental data, or can be derived microscopically by means of many-body perturbation theory starting from realistic free nuclear potentials. Non-perturbative methods are recently become available. The use of effective operators for the calculation of observables is also required to account for the missing correlations in the wave functions.
During seventy years of SM calculations, phenomenological interactions have shown to be very successful in reproducing a huge amount of nuclear structure properties. The microscopic approach to both the Hamiltonian and transition/decay operators, we called realistic SM, has largely progressed in the two decades or so, and it is by now also well set [211].
A number of papers have been devoted to the \(0\nu \beta \beta\) NME calculation within the SM framework. However, several problems are still open and further developments are certainly required in the next years [212]. We have learned that (i) SM calculations adopting equally reasonable \(H_{\textrm{eff}}\)s lead to a rather narrow spread among the predictions of the NMEs ranging between 10 and 30%; (ii) the closure approximation usually employed in the calculation of the NMEs is good within 10% [213]; and (iii) the results are slightly sensitive to the variations of correlations induced by the strong short-range two-nucleon interaction. Single-\(\beta\) strengths and \(2\nu \beta \beta\) matrix elements predicted by realistic SM calculations are in good agreement with experiment without resorting to quenching factors of the free value of the axial vector coupling \(g_A\). The quenching is, in fact, provided by the renormalization procedure employed in the derivation of the effective operators. In this connection, it is worth mentioning that renormalization effects, which are found to be relevant in the \(2\nu \beta \beta\) decay, play a minor role in the calculated \(0\nu \beta \beta\) NME [214].
Further investigations will be focused on: (i) the extension of the SM model space with the aim to include spin-orbit partners which may be particularly relevant in \(\beta\) decay processes; (ii) the contribution of the electroweak two-body currents, derived within the framework of the chiral perturbation theory, on the \(0\nu \beta \beta\) operator. Finally, it would be desirable to overcome the limits of the closure approximation in the derivation of the \(0\nu \beta \beta\) operator within many-body perturbative theory.
In order to gain a more comprehensive understanding of spin-isospin phenomenology, including possible mutual relationships between the transition matrix elements involved in the \(\beta\) decays and CE reactions, one needs a consistent description of the nuclear structure input required in both processes. Some work along this line has been performed in [182]. However, a more extensive investigation is needed using state-of-the-art SM calculations, already employed in \(\beta\) decay studies.
Within the NUMEN project, large efforts have been devoted so far, as discussed in Sect. 4.1.2, to the analyses of the nucleon transfer channels. As next step, SM calculations should be employed to provide target and projectile form factors of the SCE reactions which contain the transition matrix elements induced by one-body operators, and then focus will be placed on the same quantities needed in DCE reaction calculations. Studies within the same framework are planned for the \(\gamma \gamma\) decay of some selected DIAS.
The quasi-particle random-phase approximation
The random-phase approximation (RPA) and the quasi-particle RPA (QRPA) are well-known [215] and largely applied microscopic methods to describe nuclear excitations [216, 217], both in the charge conserving and charge exchanging case. Their main advantage, in comparison to other nuclear structure models, is that large single-particle spaces can be used, allowing thus for a full description of the total excitation strength and the corresponding energy weighted sum rules. In the context of CE excitations of relevance in the present contribution, these approximations have been applied in a number of works (see [215] and references therein). Energy density functionals, specially devised for the description of spin-isospin resonances at the RPA/QRPA level are available in the literature [218, 219].
In the RPA and QRPA, excited states are approximated by a linear superposition of one particle-one hole and two-quasi-particle excitations, respectively, neglecting thus high order configurations of the many particle—many hole type. This limit of the RPA and QRPA has been partially overcome by new extensions, such as the particle vibration coupling (PVC) [220, 221], the second RPA (SRPA) [222], the quasi-particle time blocking approximation [223] or the quasi-particle phonon model [224]. These extensions aim at describing the spreading widths of collective excitations and their fragmentation, due to the coupling with more complicated states, like 2p-2h or 4-quasi-particle configurations. In the PVC model, this is achieved in an effective way by taking into account the coupling of single-nucleon states to the collective low-lying nuclear vibrations described by the RPA/QRPA phonons. In the SRPA model, the phonon operators contain explicitly the 2p-2h configurations, besides the 1p-1h ones already introduced in RPA. Some of these extensions have been applied also in the context of CE excitations and single \(\beta\) decay, improving significantly on the RPA/QRPA results [225,226,227].
The task to be accomplished in the near future are in the following. (1) The RPA/QRPA models based on the Skyrme interaction will be used to evaluate: (1.i) the \(2\nu \beta \beta\) and \(0\nu \beta \beta\) NMEs; (1.ii) the form factors needed for the DCE reaction calculations; and (1.iii) the off-diagonal polarizabilities to account for the \(\gamma \gamma\) decay probability. (2) The same quantities described in (1) will be also investigated by using the PVC and SRPA models, in order to study the effect of higher order configurations.
The interacting boson model
The interacting boson model (IBM) is an algebraic model for even–even nuclei that describes the collective excitations in the even–even nuclei in terms of a system of interacting bosons with angular momentum \(L=0\) (s-boson) and 2 (d-boson) [228], and in the proton–neutron version (IBM-2) [228, 229] includes a distinction between proton and neutron bosons. For odd–even nuclei, the interacting boson-fermion model (IBFM-2) [230, 231] is employed, where the bosons are coupled to the single-particle degrees of freedom of the odd nucleon, while odd–odd nuclei are described by coupling the single-particle degrees of freedom of the odd neutron and the odd proton to the bosons (IBFFM) [232,233,234]. All together these models are called the interacting boson models (IBMs).
The formalism to compute the spectroscopic amplitudes from an even–even to an odd–odd nucleus in the IBFFM scheme has been developed for the first time in [234]. In future, one- and two-particle spectroscopic amplitudes of all competing transfer channels will be calculated within the interacting boson schemes, as already done in previous articles within the NUMEN collaboration [197, 235].
Then, calculations of the DCE nuclear matrix elements in closure approximation, useful to put constraints on the \(0\nu \beta \beta\) NMEs [183], will be completed [183]. Finally, developments for other nuclei of interest for the NUMEN project that can be described by means of the IBMs are planned in order to calculate the radial transition densities entering the form factors for the SCE reaction code.
4.2 Collectivity in nuclei
One of the main expressions of collectivity in nuclei are the nuclear GR that were discovered more than 75 years ago [236]. GRs were described as modes of a system having the characteristics of a two component fluid (protons and neutrons) [237, 238] that can move either in phase (isoscalar modes) or out of phase (isovector modes). In particular, GDRs were investigated at LNS with the MEDEA and TRASMA arrays [239, 240]. The experimental work was strongly supported by an excellent theoretical activity [241, 242]. Further investigations at LNS and LNL have been devoted to other pseudo-collective phenomena like the so-called dynamical dipole mode [243,244,245,246] or the PDR (Pygmy dipole resonance) [247]. The research activity in these fields will be pursued in the next future, taking the opportunities given by the LNS upgrades, e.g., using the intense radioactive beams produced with FraISe (see Sect. 2.2.2) [17, 18].
By following the order from the experiments ready for the FraISe day one to those that need further tests and resources, in Sect. 4.2.1 we will shortly describe measurements investigating the excitation and decay of the PDR. In Sect. 4.2.2 we will present new experiments planned on the dynamical dipole mode. In Sect. 4.2.3 we will describe the study on the ISGMR on exotic nuclei, to be performed with MAGNEX spectrometer. Finally in Sect. 4.2.4 we will present the concept of a new detection system replacing the dismissed MEDEA array, coupled to some telescope array of the FAZIA type, for more accurate GDR investigations.
4.2.1 Search for Pygmy resonances
The study of the low-lying E1 strength below and above the neutron emission threshold, known as PDR, is of paramount interest because it has an important link with both r-process and the EOS parameters, as discussed in Sect. 3.1. Some of its features, as the degree of collectivity, are still under debate. Investigations on the possible single-particle nature of PDR are presently carried out at INFN-LNS. The low-lying E1 transitions in \(^{96}\)Mo were populated with (d,p) and (p,d) reactions. The outgoing particles are detected by the MAGNEX spectrometer. The measured angular distributions are compared with DWBA calculations to extract the corresponding spectroscopic factors [248]. Experimental investigations and theoretical predictions show that the PDR is connected to the neutron excess in nuclei and its strength is larger in nuclei far from the stability valley. One of the most important feature of the PDR is the isospin mixing effect [249, 250]. Due to this, as shown in a large number of stable nuclei and in few unstable ones, the PDR excitation can be achieved with both isoscalar and isovector probes [249,250,251]. In stable nuclei and at excitation energies below the neutron separation threshold, the PDR states are separated in two groups: one group, sitting at low energy, refers to states excited by both probes, while the higher energy group is populated only by isovector probes. This effect is known as PDR (or isospin) splitting. The excitation of the PDR at energies above the neutron emission threshold has been observed, until now, only in unstable nuclei [247, 252, 253]. At INFN-LNS the \(\gamma\)-decay of the PDR in the \(^{68}\)Ni above the neutron emission threshold was measured using a \(^{12}\)C target as isoscalar probe [247]. The \(^{68}\)Ni beam was delivered via the FRIBs@LNS facility [16]. The PDR was excited, via inelastic scattering, mostly with nuclear interaction due to the low Coulomb field of the carbon target. The \(\gamma\)-decay channel of the PDR was studied using the CHIMERA multidetector [2, 254], while the FARCOS array provided the full isotopic identification of \(^{68}\)Ni and other reaction products [24]. The shape of the observed resonance, Fig. 33b, is compared with previous relativistic Coulomb excitation measurements [252, 253], Fig. 33a. Even if the strength is different, the similar shape indicates that the isospin splitting does not seem to be present at the energy above the neutron emission threshold.
However, due to statistics limitations and by the modest energy resolution, it is not possible to draw definite conclusions on the absence of isospin splitting.
Aiming at a better understanding of the nature of the PDR, with the help of the new facility FraISe [18] we plan to continue the study of the PDR in \(^{68}\)Ni, using both isoscalar and isovector probes. Moreover we want to extend the study to other systems, in the region of light and medium nuclei such as \(^{20}\)O, \(^{34}\)Si, \(^{38}\)S, \(^{48}\)Ar. The aim is also to measure the neutron shell occupancy dependence of the PDR both below and above the particle emission threshold. A nucleus of particular interest could be the \(^{38}\)S, one of the first nuclei that will be produced by FraISe. Moreover, it will be important also to search for the PDR above the particle emission threshold in stable nuclei, such as \(^{48}\)Ca and \(^{64}\)Ni. The PDR will be excited in Coulex experiments using Pb/Au targets in order to have a strong Coulomb field. A carbon target will be used as an almost pure isoscalar probe due to the low intensity of the Coulomb field. It may be considered the use of a proton target (CH\(_{2}\)) as a further messenger to study the interplay between isoscalar and isovector excitation.
We plan to carry on experiments with a more powerful and efficient setup. Indeed, we will use the CHIMERA multidetector and FARCOS array in its complete configuration. The use of a new prototype of neutron detector (see Sect. 3.1.6) is also envisaged in order to fully characterize the PDR.
4.2.2 Dynamical dipole
Dynamical dipole pre-equilibrium \(\gamma\)-ray emission was observed in fusion and binary reactions around 10–20 MeV/nucleon for different systems in various experiments [243, 245, 246, 255]. It was observed in heavy-ion collisions characterized by strong initial dipole moment connected to the charge/mass asymmetry of the reaction partners. In the framework of a semi-classical approximation, this pre-equilibrium emission is a \(\gamma\)-ray E1 emission. The strength of such \(\gamma\)-emission, as a function of its energy, is determined by the second-order derivative of the total electrical dipole moment (averaged over the selected events) through its Fourier transform. Semi-classical calculations, based on transport models (BNV) [244] and on the CoMD [255], show that the fast variation of the dipole moment, and the consequent \(\gamma\)-ray emission, takes place during the early stage of the interaction below 120fm/c, when the largest changes of the density are produced, as shown in the example of Fig. 34b. Interestingly, according to model predictions (due to conservation rules) statistical decay after the collision does not affect the values of \(\vec {D}\), i.e., the time derivative of the electrical dipole (see also Appendix of Ref. [243]). Therefore, the measured variable, if well reconstructed, should retain the asymptotic D value (see Fig. 34a, dashed line).
CoMD calculations for the collision \(^{48}Ca+^{27}Al\) at 40 MeV/nucleon and impact parameter 4 fm. We plot as a function of time: a \({D_{Z}}\), projection along the beam axis of \(\vec {D}\) and b the density \(\rho\) evaluated in the center of mass. The dashed horizontal line in the a represents the asymptotic value of Dz
In particular, when different charged particles and fragments are produced through the collision, its asymptotic value \(\vec {D_a}\) can be expressed (in units of the elementary charge) as:
In the previous expression \(m_{c}\), \(M_{i}\), \(Z_{i}\) and \(\vec {P_{i}}\) indicate the multiplicity of charged particles, the mass, the charge and the momentum of the generic particle, respectively. \(\vec {P_{i}}\) is evaluated in the center of mass reference frame. Finally the over-line symbol indicates the average on the events.
\(\vec {D_a}\) can therefore furnish a measure of the average degree of isospin or charge/mass equilibration (i.e., redistribution of the neutron excess) in the momentum space as the result of the collision process. According to the definition (3) we can extract the asymptotic value measuring the velocity and charge of all reaction products. Both the pre-equilibrium \(\gamma\)-ray emission and \(\vec {D_a}\) can be considered therefore as signals globally characterizing the charge/mass equilibration process of which the first one can be considered as a heralding messenger. Recently, \(\vec {D_a}\) has been measured in mid-peripheral collisions induced on the system \(^{48}\)Ca + \({}^{27}\)Al at 40 AMeV with the CHIMERA multidetector [96]. The reconstructed average dipolar signal has been reproduced through CoMD calculations [96, 97, 256]. The discussion about the dependence from EOS parameters of the average dipolar signal is reported in Sect. 3.1.5.
In future, we would measure both pre-equilibrium \(\gamma\)-rays emission and the asymptotic value \(\vec {D_a}\) in the same experiment. This will be possible by detecting the \(\gamma\)-rays by means of the CsI crystals of the multidetector CHIMERA in coincidence with the produced particles. These combined measurements could furnish, especially for central/semi-central collisions, a sort of complete time evolution of \(\vec {D}\). Moreover, through the CoMD model, we have also the possibility to evaluate the explored densities during the pre-equilibrium stage in which the \(\gamma\)-rays are emitted [257] (see Fig. 34). The need to perform a complete reconstruction of the event, and the weakness of the pre-equilibrium \(\gamma\)-ray emission ask for high-intensity beams (of the order of 10–20 nA) as for instance of stable Ar, Ca isotopes; the use of Ca, Ni target nuclei will allow to span rather large charge/mass asymmetries.
4.2.3 Exploring the breathing mode in exotic nuclei
Among the nuclear collective modes the ISGMR, also called the breathing mode of nuclei, is of major importance because its properties are related to the nuclear matter incompressibility \(K_\infty\). The latter is a fundamental ingredient in defining the EOS for nuclear matter and it is also a basic parameter in the description of neutron stars and supernovae [258]. The energy of the resonance in the mass A nucleus give the information about \(K_A\) connected to \(K_\infty\) by the following relation:
being Z the charge of the nucleus and \(\delta\) its asymmetry term. The question about the proper value of \(K_\infty\) is still open. Part of the existing uncertainty is due to our poor knowledge of the symmetry energy [259]. The \(K_\tau\) asymmetry term contribution in Eq. (4) has been poorly determined, since it requires accurate studies of the compression modes in an isotopic chain spanning a wide range of \((N-Z)/A\) values. This was recently done for the stable Sn isotopes and a value of \(K_\tau =-550\pm 100\) MeV was obtained [56]. In order to determine \(K_\tau\) with more accuracy and to probe the role of the symmetry energy in the \(K_\infty\), extending the ISGMR measurement to unstable nuclei is mandatory.
Although extremely appealing, the ISGMR measurement in unstable nuclei remains a major experimental challenge due to the low radioactive beam intensities and the unfavorable conditions in inverse kinematics. Indeed, the ISGMR cross section peaks at 0\(^\circ\), resulting in very low recoil velocities for the light isoscalar probes, i.e., deuterons, \(\alpha\) particles and \(^6\)Li [260].
At the LNS the In-Flight FraISe facility will produce radioactive ion beams at Fermi energies with enough intensity to successfully perform challenging nuclear physics experiments. Moreover, we have already demonstrated the capability of the MAGNEX [25] large acceptance spectrometer to perform, with high sensitivity, experiments with beams accelerated by the SC, at 0\(^\circ\) [261].
On the basis of such considerations, we plan to measure the ISGMR in exotic nuclei via deuteron inelastic scattering, detecting the recoiling deuterons emitted at around 0\(^\circ\) by MAGNEX. A challenging aspect of this technique is the detection of deuterons at low kinetic energy. This is possible with the present MAGNEX FPD detector, but it should be specifically proven after the foreseen upgrade. The in-flight production method of FraISe allows to accelerate various isotopes at the same time with rates of hundreds of kHz, which is enough for a statistically significant exploration of ISGMR in few days of data taking, assuming typical differential cross sections of about 80–100 mb/sr at 0\(^\circ\). For instance, by selecting the \(^{38}\)S as main isotope we can get adequate fluxes of \(^{37}\)S, \(^{34,35}\)P, \(^{31,32}\)Si, \(^{29}\)Al. By tagging and tracking the transported fragments on an event-by-event basis, we plan to investigate the ISGMR spectral features in many exotic nuclei in the same experiment.
The target we plan to use is a deuterated polyethylene CD\(_2\) film of about 1 mg/cm\(^2\) thickness. The thickness is chosen in order to ensure a reasonable counting rate without limiting too much the energy resolution in the \(^{38}\)S energy spectrum. This is expected to be about 400 keV, mainly due to the uncertainty associated with the reconstruction of the beam energy.
The energy of the \(^{38}\)S impinging on the target is expected to be in the 1 GeV range. Then to measure its excitation energy spectrum between 10 and 30 MeV, where the ISGMR is expected, it is necessary to detect the recoiling deuterons with energies ranging from about 1 to 10 MeV, in the laboratory angular region between 0\(^\circ\) and 10\(^\circ\). The spectrometer will be set at a fixed position, with the optical axis at 3\(^\circ\), working in full acceptance mode (50 msr solid angle). In this way the whole angular region of interest will be covered. Four magnetic field settings will be used to transport deuterons from 1 to 10 MeV to the focal plane detector (FPD), where they will be tracked and identified, so to have a complete reconstruction of their momentum [262].
In order to disentangle between monopole and quadrupole resonances and to extract the ISGMR strengths, we plan to measure the angular distributions and the excitation energy spectrum selecting different scattering angle ranges.
4.2.4 Study of isovector giant dipole resonance with stable and unstable nuclei
The GDR is the most investigated collective motion both on the ground state and on excited states. It was used to probe basic nuclear properties at finite temperature and angular momentum (e.g., nuclear shapes fluctuations and shape evolution, Jacobi transitions, fission timescales, loss of collectivity and phase transitions). From the experimental side, new experiments will be beneficial at various excitation energies to test model predictions (EDF or RPA approaches) and to solve open issues [263]. In particular, at moderate excitation, recent results showed contrasting evidence concerning the saturation of the GDR width at temperatures \(T \approx\) 2.5 MeV [264,265,266] for nuclei with mass around \(A=100\) and further experiments in this mass region could clarify the specific issue. Future studies can be also envisaged at higher excitation energies where, around \(E^\star\) = 230–250 MeV, a sudden quenching (up to the complete disappearance) of the GDR \(\gamma\)-ray yield was observed [263], at odds with the prediction of the statistical model, possibly due to a competition between the equilibration of collective motion and particle decay [267]. A link between such a disappearance and the liquid–gas phase transition is still an open question, triggered by the similarities between the limiting temperature emerging from the caloric curve and the limiting excitation energy for collective motions. Therefore, dedicated experiments in different mass regions (A \(\approx\) 50–60 and A \(\approx\) 180–190), where data are lacking, are indeed necessary. Moreover, the study of the GDR features of light nuclei with cluster structures [268] and the role of collectivity toward the p-dripline are among the main topics to face with the new facility upgrade at LNS, complemented with the investigation of the heavy-mass zone (accessible via the incomplete fusion channel), which is relatively unexplored. Possible beams could consist of high-intensity Ar, Ni and Zn isotopes (1–10 pnA) at energies 17–30 AMeV.
For such future experiments a composite setup for charged species and \(\gamma\)-rays up to 60–70 MeV is mandatory, in order to identify in charge (and in mass) the emitting sources, generally produced via (complete or incomplete) fusion processes [2]. Also, light charged particles must be detected, to estimate the pre-equilibrium contribution. At Fermi energies also the GDR built on the quasi-projectiles (QP) in semi-peripheral collisions far from the stability valley could be investigated, exploiting the FraISe exotic beams [17, 18]. For the detection of charged species, good candidates are FAZIA-like telescopes [101], capable of isotopic separation up to and beyond Ca isotopes and to resolve the charge of heavier fragments with very low thresholds, thus being a valuable asset to detect both forward emitted QPs and fusion residues. For the latter case, also the TOF method, as exploited by the CHIMERA array [2], might help to put coarse gates on the size of the residues (unit mass resolution from E-TOF is possible only for light nuclei). Concerning hard \(\gamma\)-ray detection, an efficient solution is represented by large BaF\(_2\) scintillators, such as those of MEDEA [239], possibly with new and versatile readout, in order to greatly simplify their use under vacuum. Alternatively, new hard \(\gamma\) sensors can be used such as GAGG crystals, anyhow requiring specific and accurate performance tests. A preliminary rendering of the conceptual detection system is shown in Fig. 35. Finally, whatever the final setup architecture, a well-equipped and large scattering chamber will be mandatory for those experiments. The minimum length for such a chamber, assumed hosting a multidetector of the type reported in the figure, should be about 250 cm in length and 100 cm wide. The target system should be remotely controlled and the complete beam diagnostics should be available.
Rendering of the concept of the new composite setup. The beam enters from left and hits the target (not visible) positioned between the two wheel arrays. The back wheel array could host crystals for hard \(\gamma\) while the forward one contains CsI(Tl) crystals. The four FAZIA blocks cover some forward angles and can be used to trigger the measurement on heavy QP or ER products. Drawing made by Carlo Cialdai, INFN Florence
5 Nuclear astrophysics
Several astrophysics theoretical predictions are strictly dependent on the availability of theoretical/experimental information about reaction cross sections at energies of astrophysical interest.
Nuclear astrophysics studies constitute an interdisciplinary field where knowledge and investigations of different fields of astrophysics (mainly stellar physics and cosmological nucleosynthesis) merge with experimental nuclear physics and theory. Through this synergic effort, in the last twenty years, the overall understanding of many astrophysical phenomena was greatly improved. However, in many practical cases, the still-existing uncertainty affects the predictions of stellar models and element nucleosynthesis. LNS has undoubtedly played a leading role within this framework.
We hereby summarize the possible outcome of this research arising from the upgrading of LNS facilities. In details, it will cover the fundamental topics listed below:
-
Quiescent stellar burning: stellar models are investigated with a balanced focus on both massive and smaller mass stars. Their importance for nucleosynthesis is examined in details with big attention paid to the role of nuclear and atomic inputs in different phases of stellar evolution. In particular, contributions by indirect methods, the asymptotic normalization coefficient (ANC) or Trojan horse method (THM), which may solve puzzles of great importance for stellar structure and evolution as for the \(^{12}\)C + \(^{12}\)C and \(^{12}\)C+\(^{16}\)O reactions (tag LNS-NA-NAI-a1 in Table 6) are discussed in Sect. 5.1.3.
The possibility to accelerate \(^{20}\)Ne in the Tandem thanks to the NESTOR source will allow indirect studies of the \(^{16}\)O + \(^{16}\)O fusion by means of the THM which may uncover important features still unknown for this reaction rate (tag LNS-NA-NAI-c0 in Table 6) as extensively discussed in Sect. 5.1.3. The NESTOR source providing He\(^{-}\) ion beams will be extremely useful to investigate (p, \(\gamma\)) transfer reactions of interest for nuclear astrophysics (tag LNS-NA-NAI-c2 in Table 6) as discussed in Sect. 5.1.4. Another important problem which can be addressed with multimethodical approaches (indirect methods, laser-induced reactions) is the study of light elements depletion which is strongly related to the cosmological lithium problem (tag LNS-NA-NAI-b0 in Table 6) as discussed in Sect. 5.1.1. Advanced experimental techniques, like those provided by PANDORA, which will be present at LNS in the next 5–7 years and will allow the study of \(^7\)Be decay time in plasma conditions, will be presented in Sect. 5.1.2 (tag LNS-NA-NAI-c1 in Table 6). Later stages of stellar evolution give the possibility to investigate reactions involving Ne and Na (tag LNS-NA-NAI-a0 in Table 6) as reported in Sect. 5.1.4;
-
Primordial and explosive nucleosynthesis: the formation of elements in the early universe will be explored at LNS by means of different methods ranging from indirect ones, to studies in laser-induced plasma and PANDORA in Sect. 5.2.1 (tag LNS-NA-EXN-b0 in Table 6). The explosive nucleosynthesis, which is crucial in explaining several dramatic phenomena which take place in the universe–novae (tag LNS-NA-EXN-a1 in Table 6) as discussed in Sect. 5.2.2, X-Ray Bursts, and Core-Collapse SuperNovae (CCSN)–will also be studied at LNS with the possibility of accelerating long-lived isotopes at Tandem (\(^{26}\)Al,\(^{10}\)Be,\(^{44}\)Ti) (tag LNS-NA-EXN-a0 in Table 6–see Sect. 5.2.2) or producing unstable beams from FraISe for studying X-Ray Bursts nucleosynthesis like in the case of the \(^{14}\)O(p,\(\alpha\))\(^{17}\)O and \(^{18}\)Ne(\(\alpha\),p)\(^{21}\)Na reactions (see Sect. 5.2.2 with tag LNS-NA-EXN-c0 in Table 6);
-
Neutron-induced reactions and their consequent importance for s- and r-process will also be examined to the light of multimessenger astronomy achievements of the last years when neutron star mergers in binary systems emerged recently as a fundamental mechanism for nucleosynthesis of heavy elements in the Universe. As regards the s-processes, the PANDORA facility will allow very precise half-life/branching measurements in stellar plasma for elements which are determinant for heavy elements production like Cs, Ba, Hf (see Sect. 5.3.1 tag LNS-NA-NIN-a1 in Table 6). In the same context, the PANDORA facility may allow the measurement of opacities at electron densities and temperatures resembling some ejecta plasma conditions, shedding light on r-process-generated metallic species at specific time stages of the Kilonovae diffusion (tag LNS-NA-NIN-b0 in Table 6) as it is extensively discussed in Sect. 5.3.3. Neutron-induced reactions are also important for understanding the role of neutron-poison reactions in stellar environment (tag LNS-NA-NIN-a0 in Table 6) as discussed in Sect. 5.3. In this framework an important role can be played by lasers for driving continuous and pulsed neutron sources as reported in Sect. 5.3.2 (tag LNS-NA-NIN-c3 in Table 6). Naturally also for n-producing reactions like the \(^{22}\)Ne(\(\alpha\),n)\(^{25}\)Mg, astrophysical studies will benefit from LNS facilities as for Ne-implantation from NESTOR or experiments using MAGNEX (tag LNS-NA-NIN-c0 in Table 6) as explained in details in Sect. 5.3.1. The FraISe facility will also offer relevant possibilities of studying the nucleosynthesis connected to r-process using the POLYFEMO neutron detector as it is reported in Sect. 5.3.4 (see tag LNS-NA-NIN-c1 in Table 6).
We believe that the synergistic efforts of the nuclear and astrophysical or theoretical communities, as well as the building up of a common foundation for new generations of investigators, will lead to a stronger nuclear astrophysical community which may be one of the keys to a better understanding of the physical processes taking place in the Universe. The planned activities have been organized into 3 phases, from phase 1 (experiments which can be performed as soon as machines will be restarted) to phase 3 (experiments where a longer R &D is required). This is synthesized in Fig. 36.
5.1 Nuclear and atomic inputs for quiescent stellar evolution
Most of stellar evolution proceeds via quiescent burnings which produce the largest part of the energy released by a stellar object in its lifetime. Moreover, a large part of nuclides production is strongly related to it, especially in the light elements regime (A \(\le\) 56). In those processes, nuclear and atomic inputs determine many aspects of the overall stellar evolution [269].
5.1.1 Light elements depletion
Important information ranging from the primordial nucleosynthesis to the still-on-going galactic cosmic ray (GCR) and stellar nucleosynthesis are retrieved from the study of lithium, beryllium and boron (hereafter LiBeB) abundances. Those light elements are destroyed during stellar evolution via nuclear processes at temperatures around few 10\(^6\) K (T \(\approx 2 \times 10^6\) K for \(^6\)Li to T\(\approx\)4–5\(\times 10^6\) K for boron isotopes). Therefore, their observed surface abundances are determined by the rates of nuclear burnings as well as by the convective envelope extension [270]. At temperatures around few millions of Kelvin the (p,\(\alpha\)) channel dominates the total proton-capture cross section. Together with direct measurements which at those energies are hindered by the low Coulomb barrier penetration probability, for charged-particle-induced reaction cross section, indirect methods were developed. Several of them have been suggested to access the cross sections relevant for astrophysics without extrapolations. The THM is one of the most powerful and useful and gives the possibility to measure the bare-nucleus cross section of a binary reaction of interest for astrophysics at Gamow energies without the influence of Coulomb suppression or electron screening phenomena [271, 272]. Several of the processes involving LiBeB, as discussed above, were already studied at LNS [273,274,275,276].
The comparison of these indirect methods results with the direct ones may shed light on the electron screening effect that is far from being understood, despite long-standing efforts. Moreover, this phenomenon has been studied in recent years in a series of experiments [277]; such results may be compared with direct and THM measurements in order to better investigate the phenomenon.
Taking advantage of the new noble gases source (NESTOR), reactions involving light elements like \(^7\)Li(p,\(\alpha\))\(^4\)He or \(^6\)Li(p,\(\alpha\))\(^3\)He or \(^{11}\)B(p,\(\alpha\))\(^8\)Be can be studied via THM applied to the \(^3\)He breakup (i.e., using the 3-body reaction \(^7\)Li(\(^3\)He, \(\alpha \alpha\))\(^2\)H for the first process) not only to measure the cross section at Gamow energies but also to further check the “spectator invariance” [278, 279]. The same reactions may be studied in a synergistic effort by using the I-LUCE laser facility which will be soon available at LNS and by applying the Coulomb Explosion technique which has already been successfully applied to \(^2\)H(d,p)\(^3\)H reaction in [280].
5.1.2 \(^{7}\)Be half-life in strongly ionized stellar environments studied with PANDORA
The weak decay of \(^{7}\)Be via electron capture (EC) into \(^{7}\)Li is of relevant interest for both primordial nucleosynthesis models, concerning the cosmological lithium problem, and for the stellar interior structure models which relies on the neutrino flux yields. In particular \(^{7}\)Be leads to one of the several reaction channels for studying the solar neutrino flux [281] and the neutrino oscillations. The EC decay probability of \(^{7}\)Be [282] is a crucial parameter for estimating its abundances in spite of the branching ratio (BR) of other destruction channels (i.e., \(^{7}\)Be(p,\(\gamma\))\(^{8}\)B). Terrestrial decay into \(^{7}\)Li(\(\frac{3}{2}^{-}\)) ground state (BR 89.7 %) or first \(^{7}\)Li excited state (BR 10.3 %) occurs with a half-life of 53 days. This is no longer true for strongly ionized environments [283, 284]. Several theoretical works in the last decade tried to catch the fundamental impact of the atomic environment on the nuclear decay [285]. Models based on single-particle mean-field, with the aim to catch atomic influence—of hot plasma composed of \(^{7}\)Be atoms surrounded by protons/electrons as degenerate quantum Fermi gas—on the weak interaction, have recently shown strong variation of \(^{7}\)Be half-life as a function of plasma density, temperature and charge state distribution (CSD) [284]. The experimental verification of these theoretical predictions would be highly desired. In this context, PANDORA, as a multidisciplinary facility and compact plasma trap, can suit with the experimental requirements [27]. Magneto-plasmas conceived in the facility allow to confine ions of radioisotopes in a microwave-sustained plasma, with electron density up to 10\(^{13}\) cm\(^{-3}\) and energy up to tens of keV. The facility is thought for first-of-its-kind nuclear decay measurements in plasmas resembling stellar conditions, especially in terms of temperature and CSD. The study of the \(^{7}\)Be case decay can be afforded via \(\gamma\)-tagging of 477.6 keV \(\gamma\)-rays emission from first-excited \(^{7}\)Li state using a dedicated high-efficiency and low-resolution hyper-purity germanium (HPGe) detector array [286]. A technological solution for studying such short-living (\(\lesssim\) 60 days) radioisotopes will be provided by the construction of an in-flight injection line of radioactive ion beams (RIBs) into the plasma trap. A feasibility study to produce \(^{7}\)Be nuclei has been performed, considering a SC proton beam hitting a boron nitride compound; fragmentation reaction will produce the isotope from boron. Then, effusing nuclei will be extracted at +1 charge state, and subsequently injected into a radio-frequency quadrupole cooler to optimize the beam envelope properties, longitudinal matching and energy, before entering the plasma potential and penetrate in the plasma core. The line is thought to optimize the capture efficiency in plasma of the RIB and to breed the charge state of nuclei, according to the well-known principles of the charge breeding technique.
5.1.3 Helium, carbon and oxygen burning
Helium, carbon and oxygen burning influences the fate of massive stars (exceeding eight solar masses), especially their late evolutionary stages. The main processes are the triple-\(\alpha\) capture, which involves the so-called Hoyle state, the \(^{12}\)C + \(^{12}\)C fusion reaction, which is efficient at temperatures greater than 0.4 \(\times\) 10\(^9\) K, or the \(^{16}\)O + \(^{16}\)O or \(^{16}\)O + \(^{12}\)C fusion, which determines the fate of SN progenitors and the related nucleosynthesis.
THM has provided in the recent years an important measurement of the \(^{12}\)C + \(^{12}\)C reactions both in the \(\alpha\) as well as in the p emitting channel. The pioneering experiment performed at the LNS Tandem [14], and the measured cross section represent a cornerstone for future application for THM reactions involving heavier nuclei (see Fig. 37). This new reaction rate impacts heavily on the stellar structure and evolution as it was already pointed out by Chieffi et al. [287]. In perspective, the same methodology will be applied to other crucial reactions such as the \(^{16}\)O + \(^{16}\)O (tag LNS-NA-NAI-c0 in Table 6) or \(^{16}\)O + \(^{12}\)C. They will be studied taking advantage of the \(^{20}\)Ne beam which will be produced by NESTOR and accelerated by the Tandem. Indeed, the use of \(^{20}\)Ne as a possible Trojan Horse nucleus was already proved in [288] and reference therein. The possibility to study those three reactions involving C and O can provide ultimate information for stellar evolutionary models for massive stars and help to reduce the huge uncertainties which are present in stellar reaction rates, thus enriching the overall comprehension of several astrophysical problems like the C/O ration in final evolutionary stages, depth of convective zone, and reducing the uncertainties in M\(_{up}\).
Another crucial phase for massive star evolution is the helium burning via the 3-\(\alpha\) interaction. This was recently studied at LNS in two different experiments [289] and in [123]. Using the same methodology as in [123] with an improved energy resolution provided by the use of advanced detector array [2], sounder experimental data on the Hoyle state may be conveyed to the astrophysical community as well as possible experimental evidences of the presence of an Efimov state [290].
\(^{12}\)C + \(^{12}\)C fusion reactions cross section as measured by the THM in [14]
5.1.4 Advanced cycles: NeNaAl cycle
The NeNa and MgAl cycles are typical of high-temperature (T\(_9 (10^{9} \textrm{K})\sim\) 0.05) H-burning reaction networks of evolved stars [269]. Because of the higher Coulomb barriers involved, those cycles are not as relevant as the CNO one for the energy production in stars, but play an important role in the nucleosynthesis of elements heavier than Ne. Recently, the development of \(^{23}\)Na and \(^{27}\)Al beams at LNS has allowed to study such reactions at the Tandem by using the THM. Some studies have already shown the feasibility of such measurements using innovative experimental devices, as reported in [15] for the \(^{27}\)Al(p,\(\alpha\))\(^{24}\)Mg reaction which is the process that drives the destruction of \(^{27}\)Al, the production of \(^{24}\)Mg, and closes the MgAl cycle when its rate exceeds the one of the competing (p,\(\gamma\)) reaction. Asymptotic Giant Branch (AGB) stars have the right values of temperature and density to efficiently host CNO, NeNa and MgAl cycles: all of these play an important role in both Quiescent and Hot Bottom Burning and are relevant for the production of both \(^{20}\)Ne and \(^{27}\)Al via the \(^{23}\)Na(p,\(\alpha\))\(^{20}\)Ne and \(^{23}\)Na(p,\(\gamma\))\(^{24}\)Mg, respectively. Nevertheless, the cross section of both processes is largely unknown at low energies, and extrapolations are affected by large errors (more than one order of magnitude) [291]. On the other side of the NeNa cycle, \(\mathrm{^{20}Ne}\) can be destroyed via the \(^{20}\)Ne(p,\(\gamma\))\(^{21}\)Na: its cross section is also largely unknown [292], leaving many questions regarding the NeNa cycle still opened.
In future, three different experiments may be performed using indirect methods at LNS. The \(^{23}\)Na(p,\(\alpha\))\(^{20}\)Ne will be studied using THM at the Tandem accelerator using the available \(\mathrm{^{23}Na}\) (E\(_{beam}=58\) MeV) on \(\textrm{CD}_2\), using the deuterium as TH nucleus to trigger the \(^{2}\)H(\(^{23}\)Na, \(^{20}\)Ne\(\alpha\))n three-body process. The direct part of the two (p,\(\gamma\)) reactions will be investigated by studying the \(^{23}\)Na(\(^3\)He,d)\(^{24}\)Mg and \(^{20}\)Ne(\(^3\)He,d)\(^{21}\)Na proton transfer reactions: in both cases, the experiments will be performed using the NESTOR source. The latter will also need a gaseous target, while for the former we plan to use a NaF solid one. In the context of the transfer reactions of interest for (p,\(\gamma\)) reactions in p-layer of AGB stars, the possibility to use the OSCAR array (hOdoscope of Silicons for Correlations and Analysis of Reactions) [132, 138] for particle identification, with a good angular coverage/resolution and energy resolution, will allow to perform nuclear spectroscopy of medium mass nuclei. This is relevant both for checking shell models predictions for moderately p-rich and n-rich nuclei, and to determine the resonance strengths of low-energy states involved in transfer reactions. A proposed measurement is about the \(^{34}\)S(p,\(\gamma\))\(^{35}\)Cl via the reaction \(^{34}\)S(\(^{3}\)He,d)\(^{35}\)Cl, using the NESTOR noble gas beam.
5.2 The explosive universe: BBN and explosive nucleosynthesis
Quiescent nuclear burning is characterized by processes such as the pp-chains, the CNO cycles and the He- and C-burning sequences that occur when a star is in Main Sequence or in a most advanced phases as RGB or AGB. Chemical element nucleosynthesis and energy production take place also in explosive conditions. Such conditions can be found in completely different astrophysical scenarios, that is, the Big Bang and final phases of stellar evolution such as Novae, X-Ray Bursts and Supernovae. In particular, in this second explosive environment, where extremes of temperature and density are met, nuclear reactions are often much faster than the timescales for \(\beta\)-decay, consequently nuclear reactions can occur far from \(\beta\)-stability involving unstable nuclei. Several input came from the scientific community about possible experimental studies of nuclear reactions involved in explosive astrophysical environments to be performed at LNS taking advantage of the long-standing expertise in experimental nuclear astrophysics and of the new research facilities which will be available at LNS in the next years.
5.2.1 Big Bang Nucleosynthesis
The Big Bang Nucleosynthesis (BBN) occurred roughly during the first 20 min after the Bang, when the temperature fell down to 10\(^9\) – 10\(^8\) K. Together with the cosmic microwave background radiation (CMB) and the Hubble expansion rate, BBN is one of the three main evidences of the Big Bang Model and allows to probe the universe at the earliest time. In particular, the BBN provides an evaluation of the primordial abundances of light elements, mainly deuterium, \(^{3}\)He, \(^{4}\)He, and lithium as a function of the only free parameter \(\eta = n_{b}/n_{\gamma }\), that is, the baryon-to-photon ratio, once the neutron lifetime, the number of neutrino families, and the nuclear reaction network of 12 reactions are fixed [293, 294]. BBN success relies on the agreement between the predicted primordial abundances and the abundances evaluated from astronomical observations. Moreover, the \(\eta\) parameter inferred considering observations and BBN predictions is in agreement with its independent estimation from CMB measurement [294, 295]. Nevertheless, there is still an unsolved issue referred to as the cosmological lithium problem (CLiP), that is, the discrepancy of about a factor 3 between the predicted \(^7\)Li abundances by BBN [294] and the abundances derived from metal-poor halo-star observations [296].
Nuclear processes involved in the BBN network can be tackled at LNS in the next future from three different sides:
-
with the laser facility I-LUCE, to measure nuclear cross sections under plasma conditions;
-
with “conventional” accelerators, to measure nuclear cross sections via indirect techniques, such as the THM;
-
with the PANDORA plasma trap, to study \(^7\)Be decay under plasma conditions (see Sect. 5.1.2).
The implementation of I-LUCE, a sub-picosecond laser with intensities up to 10\(^{19}\)–10\(^{21}\) W/cm\(^{2}\), will open a new scenario for research in nuclear astrophysics, providing novel experimental approaches. Several physical cases can be studied (see Sect. 5.1.1) such as the nuclear reactions involved in the BBN as d(d,n)\(^3\)He, d(d,p)t, \(^3\)He(d,p)\(^4\)He, t(d,n)\(\alpha\), \(^7\)Li(p,\(\alpha\))\(^4\)He. The main advantage of some of these new experimental paradigms regards the possibility to study nuclear reactions in a controlled laboratory plasma with a thermodynamic status not too different from typical astrophysical scenarios. Moreover, a new evaluation of the electron screening effect will arise from the comparison of the cross section obtained in laboratory plasma conditions with the bare-nucleus cross section obtained from THM measurements, as it has been found for instance in [297].
Different experimental techniques can be used to study nuclear reactions with a high-power, high-intensity laser with decent repetition rate (such as I-LUCE). The Coulomb explosion (CE) of cryogenically cooled gas mixtures allows the generation of a multi-keV plasma with a Maxwell–Boltzmann distribution inducing nuclear reaction at astrophysical energies (Gamow-like window). The CE is based on the interaction of ultrashort high-intensity laser pulse 10\(^{16}\)–10\(^{18}\)W/cm\(^{2}\) with an expanding gas cluster mixture delivered by a nozzle at proper conditions in terms of temperature and pressure, in order to maximize the laser absorption. The laser pulse energy is absorbed by electrons via heating mechanisms such as rapid collisions causing the full strip of the electrons of the gas. The sudden onset of a positive space charge triggers the Coulomb dissociation of the clusters resulting in multi-keV ion acceleration with a nearly isotropic emission. The accelerated ions interact in the surrounding plasma and nuclear reactions take place. By measuring the ion energy distribution and detecting the reaction products, one can infer information to obtain the cross section of the selected nuclear reactions. The first CE experiments that can be performed once that the laser facility will be available will be dedicated to the d-d, d-\(^3\)He, and t+d (as secondary process) using a D\(_2\)-\(^3\)He gas mixture. The feasibility of the proposed measurement is supported by previous experiments performed with the same technique [280]. I-LUCE will allow to extend the explored energy range covering the full range of interest for the BBN. Another possible experimental technique to study nuclear reactions with laser exploits the interaction between an ion beam from standard accelerator (or for an ion source) delivered on a laser-induced plasma target. This will allow in-plasma measurement, with the advantages of a beam from accelerators (low-energy spread and high intensity). The aforementioned technique requires solid feasibility studies, mostly related to the synchronization of the accelerated ion beam with the short plasma lifetimes. Nevertheless, at the present time LNS holds a nearly unique position providing the possibility to perform this kind of research in the next future.
Regarding the study of nuclear reactions of interest for BBN with ”conventional” accelerators, the first physical case is the measurement of the \(^7\)Li(d,n)\(^8\)Be reaction cross section. This process of interest for the CLiP contributes to the \(^7\)Li destruction, affecting the prediction of \(^7\)Li abundance. However, large uncertainties still exist in current \(^7\)Li(d,n)\(^8\)Be reaction rates widely used in BBN models. Existing experimental cross section data for this reaction are very limited and the most majority of them are not in the BBN energy range. Among them, only two sets of data are located in the energy region of BBN interest, but show huge differences [298]. Therefore, new experimental measurements of this reaction in the BBN energy region are needed. This reaction can be studied for the first time with THM applied to the \(^7\)Li(\(^3\)He,n \(^8\)Be)H three-body reaction taking advantage of the \(^3\)He beam (the TH nucleus) that will be provided by the new NESTOR ion source and accelerated by the Tandem.
The opportunity to have a \(^3\)He beam from NESTOR source triggered also the idea to perform a new THM study of the \(^7\)Li(p,\(\alpha\))\(^4\)He reaction of interest for the CLiP as well as for the stellar lithium depletion (see Sect. 5.1.1).
The \(^3\)H(d,n)\(^4\)He reaction is one of the twelve fundamental reactions of the BBN network and it is the most promising for future fusion energy plants. Sensitivity studies underline that a change on \(^3\)H(d,n)\(^4\)He reaction rate has an impact of the \(^7\)Li abundance [299]. The reaction can be studied for the first time with THM applied to the \(^7\)Li(d, n \(\alpha\))\(\alpha\) three-body reaction, where the \(^7\)Li(t+\(\alpha\)) is the TH nucleus. This would be the first THM measurement involving a TH nucleus with inter-cluster motion in p-wave. For this reason preliminary studies dedicated to the experimental measurement of the \(^7\)Li momentum distribution are requires. The same reactions will be studied, in a synergistic effort, also using the I-LUCE laser with the CE technique allowing for a new evaluation of the electron screening effects.
BBN can be tackled also by means of the PANDORA plasma trap. The expected variation (increasing) of the \(^7\)Be half-life could have a relevant impact on the CLiP [281, 284]. The experimental measurement of \(^7\)Be decay in plasma, requires a devoted upgrade of the PANDORA facility (as described in Sec. 5.1.2), but sensitivity studies will be performed soon to evaluate the impact of a change in the \(^7\)Be constant decay on \(^7\)Li abundance.
5.2.2 Nucleosynthesis in Novae, X-Ray Bursts and Supenovae
Classical novae consist in stellar explosions that occur in close binary systems, where H-rich matter is transferred from a low-mass main sequence star (or sometimes a red giant) to the surface of a white dwarf (CO or ONe). On the other hand, X-Ray Bursts are thermonuclear explosions that take place in binary systems where the compact object is a neutron star. Understanding X-Ray bursts is important not only for investigating their properties but also to probe neutron stars. Others dramatic explosive events in galactic history are supernovae, either Thermonuclear (exploding white dwarfs in close binary systems) or Core-Collapse (CCSN whose progenitors are massive stars at the end of their evolution, triggering the birth of neutron stars or black holes).
Nuclear inputs play a crucial role in the physics of the explosion, for all the above mentioned astrophysical scenarios. Many of the reactions involved in these explosive astrophysical scenarios are induced by short-lived unstable nuclei which should be studied by means of RIBs. The expertise obtained at LNS on the production of long-lived RIBS in batch mode and the subsequent availability of FraISe gives us the opportunity to improve the nuclear physics inputs required in the detailed modeling of these stellar events.
\(^{26}\)Al is of outstanding importance in astrophysics. Observations, by space-borne telescopes, of the \(\gamma\)-rays from the decay of \(^{26}\)Al to \(^{26}\)Mg in the interstellar medium confirmed that nucleosynthesis is ongoing in the Galaxy. The distribution of \(^{26}\)Al across the Galaxy confirmed that massive stars dominate the production of this isotope [300]. \(^{26}\)Al abundance inferred from \(\gamma\)-ray astronomy allows to constrain the neutron star formation rate in our Galaxy [300], which is a key parameter in the field of multimessenger astronomy [301]. Moreover, the study of the aluminum isotopic ratio in some meteoritic inclusions (calcium–aluminum-rich inclusions) also provides information about the solar system birth and on the CCSN that maybe triggered its formation [302, 303].
As highlighted by sensitivity studies [304] at temperatures higher than 1 GK, achieved during the pre-supernova stage and the subsequent explosion (CCSN), the \(^{26}\)Al abundances are strongly dependent on the \(^{26}\)Al(n,p)\(^{26}\)Mg and \(^{26}\)Al(n,\(\alpha\))\(^{23}\)Na reactions responsible for the \(^{26}\)Al destruction. Both reaction channels have been recently studied at n-TOF facility [305, 306], reducing the uncertainty on the reaction rates. Nevertheless, the measured energy range did not allow to reach the temperature range of interest for massive stars (pre-supernova and CCSN). This energy region can be however explored by means of a THM measurement. The neutron-induced \(^{26}\)Al\(^{gs}\) destruction channels (n,p) and (n,\(\alpha\)), with \(^{26}\)Al at the ground state, will be investigated applying the THM to the \({}^2\textrm{H}(^{26}\textrm{Al}^{\textrm{gs}},\textrm{p} ^{26}\textrm{Mg})\textrm{p}\) and \({}^2\textrm{H}(^{26}\textrm{Al}^{\textrm{gs}},\alpha ^{23}\textrm{Na})\textrm{p}\) three-body reactions, where the deuteron is the virtual neutron source [307]. THM has been successfully applied to the study of nuclear reactions of astrophysical interest involving unstable nuclei [308,309,310] and induced by neutrons on RIBs [311]
These measurements require the production of the long-lived \(^{26}\)Al\(^{gs}\) RIB in batch mode at the Tandem. The feasibility of these studies relies on: the possibility to have \(^{26}\)Al cathodes, to be used in the LNS Tandem sputter source, provided by Paul Scherrer Institute (PSI); the experience gained in the production of \(^{27}\)Al beam that allowed to understand the proper chemical composition for the \(^{26}\)Al cathode; the successful production of \(^{10}\)Be (\(t_{1/2} = 1.4 \,10^6 y\)) the first RIB beam produced in batch mode at LNS [128] (see Sect. 3.2.1).
In order to perform the THM measurement, the \(^{26}\)Mg and \(^{23}\)Na heavy fragments will be detected in coincidence with the corresponding lighter products, p and \(\alpha\), while the low-energy proton spectator will not be detected. The detection system consisting of several telescopes made up of double-sided silicon strip detectors (DSSSD) will allow to cover a wide angular range since in inverse kinematics the heavy fragments are emitted at very forward angles while the light ones span a very large range of emission angles. A picture of a typical detection setup is shown in Fig. 38.
The availability of a \(^{26}\)Al\(^{gs}\) beam will also allow the study of the \(^{26}\)Al\(^{gs}\)(p,\(\gamma\))\(^{27}\)Si that contributes to the \(^{26}\)Al destruction in Novae and AGB stars having an important impact on \(^{26}\)Al abundance [312]. The reaction will be studied using the ANC indirect method [313] to gain information on the direct capture contribution to the \(^{26}\)Al\(^{gs}\)(p,\(\gamma\))\(^{27}\)Si reaction cross section and to get information on the \(^{27}\)Si resonant states above the proton threshold. The ANC will be extracted from the measurement of a transfer reaction \({}^3\textrm{He}\)(\(^{26}\)Al\(^{\textrm{gs}}\),d)\(^{27}\)Si with a \(^{26}\)Al\(^{\textrm{gs}}\) beam at 3–5 AMeV delivered on a \(^3\)He gas target.
In studying nuclear reactions responsible for the \(^{26}\)Al destruction the ground (gs) and the isomeric (m) state at 228 keV must be taken into account. Indeed, the significant angular momentum difference between ground and isomeric states gives rise to a very small \(\gamma\)-ray decay constant, while \(^{26}\)Al\(^{m}\) \(\beta\)-decays to the ground state of \(^{26}\)Mg with a half-life of T\(_{1/2}\) = 6.35 s. Therefore, at the low temperatures that characterize many astrophysical scenarios, T < 400 MK, the \(^{26}\)Al ground and isomeric states do not reach thermal equilibrium and must be treated as two separate isotopes. While the reactions with \(^{26}\)Al at the ground state will be studied at LNS, reactions with \(^{26}\)Al at the isomeric state will be investigated at LNL where the \(^{26}\)Al\(^{m}\) beam will be provided by SPES in a framework of complementarity between LNS and LNL research activities.
The availability of a \(^{10}\)Be beam at LNS (see Sect. 3.2.1) allows the possibility to study the \(^{10}\)Be(\(\alpha\),n)\(^{13}\)C reaction. The \(^{10}\)Be abundance in early solar system, inferred from \(^{10}\)B excesses in a range of meteoritic samples, can provide a constraint on the mass value of the CCSN responsible for the formation of our solar system [303]. \(^{10}\)Be(\(\alpha\),n)\(^{13}\)C is the main destruction channel of \(^{10}\)Be, but the adopted reaction rate is obtained from theoretical calculations since no experimental measurements are available in the literature [303]. The \(^{10}\)Be(\(\alpha\),n)\(^{13}\)C reaction cross section can be measured via THM with a \(^{10}\)Be beam delivered to the TH nucleus (a possible candidate being \(^{6}\)Li) to transfer the \(\alpha\) particle.
Another very important long-lived nucleus for CCSN is \(^{44}\)Ti, since it allows a direct diagnostic of the CCSN explosion energy and timescale [314]. The \(^{44}\)Ti abundance is strongly affected by the \(^{44}\)Ti(\(\alpha\),p)\(^{47}\)V reaction, the main \(^{44}\)Ti destruction channel. Very few direct data are available in the literature, in particular, only an upper limit has been provided at energies of astrophysical interest [315]. A possible experimental approach to measure the \(^{44}\)Ti(\(\alpha\),p)\(^{47}\)V cross section at the energies typical of the CCSN environment could be by means of the THM with a \(^{44}\)Ti beam produced in batch mode at the Tandem accelerator. Given the technical difficulties related to \(^{44}\)Ti beam production, in particular due to radio safety issues, preliminary feasibility studies must be performed.
Regarding X-Ray Bursts nucleosynthesis, \(^{14}\)O(\(\alpha\),p)\(^{44}\)F and \(^{18}\)Ne(\(\alpha\),p)\(^{21}\)Na have been proposed as possible physical cases that have an influence on the X-Ray Bursts light curve [299]. Moreover, \(^{18}\)Ne(\(\alpha\),p)\(^{21}\)Na reaction leads to CNO breakout while powering a strong rp-process, responsible for the synthesis of A \(\sim\) 60 nuclei. These reactions can be studied applying the THM and taking advantage of the short-lived RIBs \(^{14}\)O and \(^{18}\)Ne provided by FraISe and of the new scattering chamber GIRA (see Sect. 2.3) with a degrading and focusing system to produce RIBs at energies useful for the THM application. Another possible solution might be the coupling between the Tandem accelerator and the FraISe separator. It is clear that important feasibility tests as well as improvements in the experimental setup are required, thus increasing experimental opportunities at LNS over a longer time range.
Nova nucleosynthesis includes the production of some intermediate-mass nuclei. The \(^{31}\)P(p,\(\alpha\))\(^{28}\)Si and \(^{35}\)Cl(p,\(\alpha\))\(^{32}\)S reactions are of particular interest in the synthesis of elements in the SiCl mass region. Variation of their reaction rates may affect production of several elements from Si to Ar [316]. The availability of few experimental data reinforces the need to study such reactions via THM with \(^{31}\)P and \(^{35}\)Cl provided by the Tandem accelerator.
5.3 s- and r-process
Neutron-capture nucleosynthesis allows for the production of elements with masses beyond A\(\approx\)60 through two different processes, namely the s(slow)-process and the r(rapid)-process, during which \(\beta\)-unstable nuclei can be also produced [269]. The slow neutron-capture process (s-process) produces heavy elements via a series of neutron captures occurring at timescales \(\tau _{n \gamma }\) much longer than the \(\beta\)-decay lifetimes \(\tau _{\beta }\) of radioactive species (\(\tau _{n \gamma }\gg \tau _{\beta }\)). This will allow for the production of stable nuclei close to the stability valley. On the contrary, the rapid neutron-capture process (r-process) defines those series of neutron-capture reactions occurring at shorter timescales, if compared to typical \(\beta\)-decay lifetimes (\(\tau _n \ll \tau _{\beta }\)), thus allowing for the production of neutron-rich (radioactive) species, far from the stability valley [269].
5.3.1 The s-process nucleosynthesis
The s-process nucleosynthesis is responsible for most of the elements between iron and strontium (60 \(\le\) A \(\le\) 90) through the so-called weak component of the s-process occurring in massive stars, being the needed neutrons mainly produced by the neutron reaction source \(^{22}\)Ne(\(\alpha\),n)\(^{25}\)Mg [317, 318]. Furthermore, the so-called main component of the s-process, allowing for the production of A\(\ge\)90 nuclei is mostly related to asymptotic giant branch (AGB) stars where the \(^{13}\)C(\(\alpha\),n)\(^{16}\)O reaction acts as the main neutron source [319, 320].
Besides the role played by stellar models and mixing phenomena [318, 320], several experimental nuclear physics investigations have been made in the recent years for studying either the two main neutron sources [321, 322], as well as the processes removing neutrons for the next stages of nucleosynthesis (the so-called neutron-poison reactions) and recycling processes [307, 323, 324].
Thanks to the new or freshly upgraded facilities at LNS, some of the most important studies can be performed for reducing the still present experimental uncertainties on s-process nucleosynthesis. In particular, the reactions which plays the role of a major stellar neutron source, i.e., \(^{22}\)Ne(\(\alpha\),n)\(^{25}\)Mg, can be investigated by applying the THM [325] on Ne-implanted solid targets thanks to the NESTOR ECR ion source which can allow accelerating noble gas, as neon and helium. A possible complementary study involves the implantation of \(^{22}\)Ne in a heavy metal (e.g., tungsten or tantalum) using the NESTOR source, followed by measurements of the \(^{22}\)Ne(\(^6\)Li,d)\(^{26}\)Mg or \(^{22}\)Ne(\(^7\)Li,t)\(^{26}\)Mg reactions in order to extract \(\alpha\) particle widths of \(^{22}\)Ne+\(\alpha\) resonances. In fact, there is a significant disagreement about the energy and the character of these resonances, thus measurements to clarify if these resonances exist are vital. The MAGNEX large acceptance magnetic spectrometer is the ideal device for these types of measurements, since it offers a large angular range combined with a high resolution.
The corresponding neutron-poison reactions, i.e., \(^{25}\)Mg(n,\(\gamma\))\(^{26}\)Mg and \(^{22}\)Ne(n,\(\gamma\))\(^{23}\)Ne, can be also investigated via the ANC method where the \(^{22}\)Ne+n process could benefit from the new NESTOR noble gas coupled with the Tandem accelerator.
With particular attention to the main component, the neutron-poison reaction \(^{16}\)O(n,\(\gamma\))\(^{17}\)O can be investigated by applying the ANC method [313], while the recycling \(^{17}\)O(\(\alpha\),n)\(^{20}\)Ne can be studied by coupling THM with nuclei having strong \(\alpha\)-cluster structure or by investigating the reverse \(^{20}\)Ne(n,\(\alpha\))\(^{17}\)O process by using the foreseen \(^{20}\)Ne Tandem beam provided by the NESTOR source. Moreover, the measurement of the \(^{21}\)Ne(p,p’)\(^{21}\)Ne inelastic scattering cross section can be decisive to constrain the resonance information in \(^{21}\)Ne. At present, there is a lack of clarity about the number and location of levels in the \(^{21}\)Ne compound nucleus and the \(^{21}\)Ne(p,p’)\(^{21}\)Ne measurement will help to clarify this information as it has been done in a number of previous experimental studies [326].
The nucleosynthesis of the elements heavier than Fe is the tarnish of neutron processes. Among these, the s-process is considered the best known, although its understanding is still affected by a lack of data. In particular, those about \(\beta\)-decay and electron capture rates in stellar conditions, which could be soon investigated experimentally for the first time at LNS thanks to the PANDORA experiment [27, 286]. Measuring lifetimes of unstable isotopes in plasma conditions, along with measuring with high accuracy the cross sections for their (n,\(\gamma\)) reactions as the up to date RIBS facilities are allowing, will shed light on the branching of the s-nucleosynthesis path. The recent sensitivity study of the s-process to \(\beta\)-decay and neutron-capture rates reported in [320] has shown how using different nuclear data set (e.g., cross sections, from the online compilation KADONIS 0.3 and 1.0 [327]) the predicted abundances (from nucleosynthesis computations in AGB stars of different mass and metallicity) for the solar system and meteorite grains can be very different, addressing or not the observational constraints. In particular, the authors focused their attention on the branching points around \(N=50\) and \(N=82\) affecting the Kr–Rb nucleosynthesis and the production of Ba isotopes. However, a further inspection of the branching and related nuclear physics inputs is needed also at higher atomic mass, where several complexities are induced by the presence of short-lived isomeric states of otherwise stable isotopes. Those make the s-process network poorly defined around key nuclei such as the pairs of cosmochronometers: \(^{176}\)Lu–\(^{176}\)Hf and \(^{187}\)Os–\(^{187}\)Re processes.
5.3.2 Continuous and pulsed neutron sources driven by laser and ion beams for nuclear astrophysics
The availability of intense and pulsed neutron sources driven by ion beams, could open new perspectives for research at LNS thus allowing for the investigation of neutron-capture processes of astrophysical relevance. Well-established techniques are currently being adopted in several laboratories to produce neutron beams, that meet the specific requirements of many scientific fields [328,329,330,331,332]. The LNS accelerators could exploit conversion reactions such as (p,n), (d,n), and (\(\alpha\),n) to produce neutron beams. The flux, angular, and the energy distribution of the neutrons depend on the adopted conversion reaction and on properties of the ion beam, which can be varied within the operational limits of the accelerators and of any radiation protection constraints. As an example of practical application, an accurate setup including, if necessary, a neutron moderator, may allow to produce neutrons with energy distributions well approximated by the Maxwell–Boltzmann distributions at energies of astrophysical interest [329]. These neutrons may be suitable for measurements of Maxwellian Averaged Cross Sections (MACS) for nuclear reactions involved in nucleosynthesis processes, exploiting the well-established technique of neutron activation [330]. Depending on the measurement to be performed and the available neutron fluxes, the driver beams can be either continuous or pulsed, the latter to provide neutron bunches with adjustable duty cycle and repetition rate. In those cases where it is necessary to measure the neutrons time of flight, a flight path of about 5 m should be sufficient to discriminate the neutron energy up to a few tens of MeV. A further important opportunity is represented by the 250 TW laser I-LUCE, that will be available in the next few years at LNS. The production of huge quantities of light particles (such as protons and deuterons) with energy up to a few tens of MeV, in combination with suitable conversion targets, can lead to provide very short (<1ns) neutron bunches with flux around 105–106 neutron/sr/shot, with angular distribution strongly peaked in the forward angles [331]. A careful selection of the targets, respectively, for the laser beam and for the neutron conversion, combined with a well-designed setup (based for example on the so-called pitcher–catcher setup), can represent a valid solution to produce neutron bunches with high fluxes and high time resolution. The flexibility of a laser-based approach may allow for the irradiation of relatively short-lived elements, which can be produced by the fragmentation of the projectile using Tandem and cyclotron beams, by implanting into a target placed close to the laser-driven neutron source. This technique allows for the measurement of radioactive isotopes that typically need to be rapidly transported from the production site to the experimental site. With respect to the s-process nucleosynthesis, two possible applications of the described technique are 1) the measurement of the \(^{140}\)Ce(n,\(\gamma\))\(^{141}\)Ce (\(^{141}\)Ce T\(_{1/2}\) = 32.5 days) that represents a bottleneck for the s-process nucleosynthesis and determines to a large extent the cerium abundance in stars, and 2) the measurement of \(^{94}\)Zr(n,\(\gamma\))\(^{95}\)Zr (\(^{95}\)Zr \(t_{1/2}\)= 64 days) that is crucial in the modeling of s-process nucleosynthesis in AGB stars because Zr is situated at a crucial point, where the two s-components (weak and main) match. These measurements will be two complementary studies to activation and TOF measurements already existing in the literature [333, 334].
5.3.3 The r-process nucleosynthesis
The r-process nucleosynthesis is called for to explain the production of the stable (and some long-lived radioactive) neutron-rich nuclides heavier than iron that are observed in stars of various metallicities (i.e., in the solar system), as it extensively discussed in [335]. Nowadays, several sites for r-process have been suggested, such as CCSN, neutrino-induced processes in the outer shells of massive stars, ejecta from compact binary mergers, and the so-called magnetohydrodynamic MHD-jet supernovae (having fast rotation, high magnetic fields and neutron eject along the poles) [335]. Recently, the discovery of neutron star mergers (NSM) [336] events strongly confirms the occurrence of such processes responsible for the production the elements beyond lead and bismuth. Besides the production of gravitational waves and \(\gamma\)-ray Bursts, NSM produces also transient optical–near-infrared source powered by the synthesis of large amounts of very heavy elements via the r-process. Such brilliant electromagnetic signals are known as kilonovae (KN) [336] from which, in principle, the r-process element abundances could be derived via the inspection of the transient light curves. Because of the composition complexity, relying on both freshly synthesized light and heavy r-process elements, the matter opacity (\(\kappa\)) is an intricate feature, varying from relatively low to high values depending on the ejecta dynamics, thermodynamic parameters, and r-process nucleosynthesis yield [337,338,339,340].
A complete understanding of such phenomena, i.e., the reproduction of the r-elements abundances in the cosmos via devoted nucleosynthesis codes, passes through focused studies in astrophysics, nuclear physics, atomic physics, and plasma physics. The EoS of hot and dense nuclear matter is of highest importance for modeling the astrophysical environments expected to be the sites for rapid neutron-capture process, providing the pressure response during the dynamic phases and the particle composition [341]. Simulations of core-collapse supernova and neutron-star mergers are, therefore, very sensitive to the adopted EoS and in particular to its stiffness and its isovector part (i.e., symmetry energy).
An important uncertainty factor, which complicates the theoretical interpretations, arises from the limited knowledge about KN ejecta opacity data in typical conditions. However, the new possibilities given by radioactive beam facilities will allow the production of several neutron-rich nuclei, improving the present understanding of the r-process. Experiments, in particular, will allow to predict the elemental abundance of such elements and to link the observed abundances with the KN features as well as with the astrophysical conditions and constraints on the nucleosynthesis sites.
Experimental measurements of opacities at electron densities and temperatures typical of astrophysical sites will be boosted by trapped magneto-plasmas conceived in PANDORA [27], thus paving the way to further developments such as shedding light on r-process generated metallic species at specific time stages of KN diffusion [342]. To this aim, a feasibility study has been recently performed.
In particular, astrophysical models for KN ejecta in the post-merging phase bound plasma conditions, typical of ECR plasma, to a time stage between few hours and few days after the merging, which corresponds to the blue-KN stage (low opacity, light r element component, KN light curve peak in the optical range) has been considered. The numerical calculations of expected opacities for the most relevant physics cases (in terms of nucleosynthesis abundances at that stage) have been performed, reporting on mean opacities for some relevant r-process elements as expected at different electron fractions \(Y_{e}\). The design of experimental setup and measurements have been started using the operative Flexible Plasma Trap (FPT) available at the LNS, characterizing on a smaller scale, with respect to the under-construction PANDORA trap, plasma parameters to provide sounder experimental conditions to resemble astrophysical conditions of the blue-KN stage ( \(\sim\)eV, \(\sim\)10\(^{11}\) cm\(^{-3}\)) [343]. First experimental results have been recently collected on gaseous plasmas (Ar, H) to closely reproduce Kilonovae conditions, posing the bases for the envisaged future plasma opacity measurements on light r-process elements to be performed in the PANDORA trap. Preliminary numerical results on mean opacity for r-process elements abundances and plasma experimental conditions that can be reached in the plasma trap are shown in Fig. 39.
a Weighted mean opacity (\(\alpha\)) for r-process element abundances (elements vs. neutron richness) at \(k_{B}T\) = 0.65 eV and density \(10^{18}\) m\(^{-3}\). The weighting was performed [342] by using relative abundances of species as resulting from SKYNET [344] nuclear network calculations of r-process nucleosynthesis yields as a function of \(Y_{e}\). b Grid of experimental values for electron density \(\rho\) [m\(^{-3}\)]—temperature (in terms of \(k_{B}T\) [eV]) from optical emission spectroscopy measurements on the Flexible Plasma Trap, with the experimental uncertainties range (\(\delta \rho\), \(\delta k_{B}T\))
5.3.4 \(\beta\)-delayed neutron emission probability P\(_n\) measurements at LNS
Since the r-process occurs far from the nuclear stability valley, it leads to very neutron-rich nuclei that then decay toward the line of stability. Most of these nuclei are \(\beta _n\) emitters. The initial abundance distribution is shaped by the decay half-life \(t_{1/2}\), but the neutron emission affects the final abundances in two ways: on the one hand it shifts the decay path to lower masses, and on the other hand it provides a source of neutrons for late captures that will shift it in the opposite way. Thus, a good knowledge of the \(\beta\)-delayed neutron emission probability P\(_n\) and \(t_{1/2}\) values of the nuclei between the line of stability and the r-process path is needed for a correct understanding of the observed abundances [146]. In this sense, at the LNS, P\(_n\) measurements for many neutron emitters such as \(^{66}\)Co (\(t_{1/2}\sim\) 0.2 s) or \(^{72}\)Ni (\(t_{1/2}\sim\)0.2 s) could be performed by using the FraISe facility for RIBs production coupled with the high-efficiency neutron counter (polycube) POLYFEMO successfully used in the past for \(^8\)Li(\(\alpha\),n)\(^{11}\)B cross section measurements [345].
5.3.5 Low-mass r-process nucleosynthesis
In neutrino-driven winds above nascent neutron stars or after the merging of two neutron stars low-mass r-process elements may be formed at high temperatures in a very short timescale of the order of milliseconds. After the explosion, the abundances are in nuclear statistical equilibrium due to the high temperature, but as matter expands, the temperature and the density decrease and protons and \(\alpha\) particles start to build up heavier nuclei by, e.g., (\(\alpha\),xn), and (p,xn) reactions. In this so-called weak r-process nucleosynthesis scenario, isotopes between Sr and Ag may be formed [346,347,348,349].
The study of the synthesis of these low-mass r-isotopes requires the use of a large reaction network involving a few thousand, mostly unstable nuclei. The necessary reaction rates are calculated from the cross sections computed with the Hauser-Feshbach statistical model which relies on different nuclear physics parameter sets. Recently, a series of sensitivity calculations were performed to evaluate the theoretical uncertainty of these cross section calculations [350,351,352]. These works identified the \(\alpha\)+nucleus optical potential parameter sets (\(\alpha\)OMP’s) as the main source of uncertainty.
The difference between the cross section based on various \(\alpha\)OMP’s can exceed even an order of magnitude [350, 352]. Therefore, experiments are critical to determine the parameters of the \(\alpha\)OMP, to reduce the uncertainties of the (\(\alpha\),n) rates and to increase the reliability of the astrophysical calculations. The direct measurement of the \(\alpha\)-induced reaction cross sections on unstable isotopes are extraordinarily challenging. However, the parameters of the \(\alpha\)OMP can be derived experimentally from the analysis of the angular distributions and excitation functions of elastically scattered \(\alpha\) particles. In the last decade several elastic \(\alpha\) scattering experiments were performed worldwide to constrain the parameters of the \(\alpha\)OMP [353, 354] (and references therein). However, the systematic measurement of \(\alpha\) elastic scattering angular distributions along isotopic and isotopic chains showed that there is no parametric solution able to describe the variation of the scattering cross sections as a function of the neutron/proton numbers [355, 356]. Thus, the extrapolation of the potential parameters toward the region of unstable nuclei is questionable. Furthermore, there are no experimental elastic \(\alpha\) scattering data on unstable nuclei, and accordingly the parametric system used in the astrophysical calculations remained untested to this day.
According to the above discussed arguments, the neutron-rich RIBs available at LNS can be useful to study the \(\alpha\)OMP parameterizations by inverse elastic scattering experiments, for example \(^{63}\)Co(\(\alpha\),\(\alpha\))\(^{63}\)Co, \(^{67}\)Cu(\(\alpha\),\(\alpha\))\(^{67}\)Cu or \(^{59}\)Fe(\(\alpha\),\(\alpha\))\(^{59}\)Fe.
It’s worth mentioning that inverse elastic \(\alpha\) scattering experiments were already performed at LNS—using stable Sn beams—thus the experimental approach is certainly feasible.
6 Nuclear physics applications
Nuclear physics applications span a very broad range of topics. In this section, the perspectives at the LNS-INFN for the coming years on this subject will be discussed. Three major scientific topics can be identified: (i) medical, (ii) laser and (iii) plasma traps applications.
-
(i)
Activities related to Medical applications (Sect. 6.1) are well consolidated, starting from the 2000s with the construction of the CATANA facility for hadrontherapy. Future study programs in this area are still focused on the availability of stable LNS beams, covering hot topics such as the Flash radiotherapy (LNS-A-MA-a0) and Flash BNCT (boron–neutron-capture therapy, LNS-A-MA-b0) or the more recent perspective of the possible use of multiple beams to perform more efficient treatment plans. The huge variety of ion beams available at LNS opens up study perspectives also in the field of space science; in particular the investigation of not well-known cross sections useful for the radiation risk model evaluation applied to cosmonauts during space missions (LNS-A-MA-b1). All these topics will be explored in details in Sect. 6.1.1. A new and interesting outlook will be raised from the future availability of radioactive ion beams (RIBs) and high-intensity beams (HIBs) (Sect. 6.1.2). In particular, RIBs opportunity can trigger new approach for innovation on treatment methods that could be coupled with online contemporary diagnostic tools, to perform innovative treatment plans (LNS-A-MA-c0) while HIBs (HIBs) open to investigation on cross sections studies for new exotic radioisotopes and radiopharmaceutical (LNS-A-MA-c1).
-
(ii)
The near future of LNS research activities also involves the new high-power laser facility and the almost unique possibility to have, in the same experimental area, intense laser-accelerated and conventional ion beams. This will open unprecedented possibilities of investigations of nuclear and plasma physics. All the new acceleration schemes developed in the recent years even by LNS users, triggered ideas and proposals for the development of new and compact laser-driven secondary sources (Sect. 6.2.1) useful for several applications (electrons and ions LNS-A-LA-a0, neutrons LNS-A-LA-b1, positrons and photons LNS-A-LA-c1). High-intensity lasers interacting with solids produce non-equilibrium plasma having high equivalent temperatures and high ion energies. Under these conditions, different nuclear reactions can be induced (LNS-A-LA-a1). New and interesting perspectives for applications in the field of health LNS-A-LA-c0 and energy can come out from these studies (Sect. 6.2.1). Fundamental aspects like ion energy loss and the stopping power in plasmas (LNS-A-LA-b0) should be mentioned because they have strong impact on energy production from fusion power. A novel approach to the direct production of pure H2 (LNS-A-LA-c2) from liquid water using femtosecond laser-induced plasma has been also proposed in Sect. 6.2.2. This topic provides the basis for exploring further concepts of hydrogen production.
-
(iii)
Magnetic confinement is one of major topics of fusion energy research. The plasma trap PANDORA will be the new LNS facility designed for multidisciplinary studies in the fields of nuclear and plasma physics, astrophysics, etc., including applicative issues like fusion power. In the section dedicated to plasma traps, Sect. 6.3, most of the potential applications deriving from the developments related to the PANDORA facility are highlighted. The section is divided essentially into three main topics: (i) magnetic Plasmas and related issues (ions heating, charge breeding, stopping power, etc.; (ii) physics and technology aspects for fusion plasmas; (iii) innovative plasma chambers and resonators for compact reactors development. Ion beam plasma interaction is a relevant topic in several fields of plasma physics, from fusion devices to modern ion source and Sect. 6.3.1 is dedicated to the several R &D studies proposed on this subject (LNS-A-PT-a0). Section 6.3.2 deals with the R &D on plasma diagnostics and wave propagation/absorption; detection, collimation and active shuttering methods for soft X and hard X spectroscopy and tomography or innovative heating and energy transport mechanisms for increasing confinement and reaction rates (LNS-A-PT-b0). In Sect. 6.3.3, new plasma chambers and resonators ensuring better radiation–plasma coupling, stability, control and confinement are proposed (LNS-A-PT-b1).
The midterm timescale has been divided into three phases, from the phase A (which includes the activities which can be performed as soon as the facilities will be ready) to phase C (where a more longer R &D work will be requested). Time schedules and priority codes of the previous discussed research topics are synthetically reported in Fig. 40 and in Table 7.
6.1 Medical applications
The possibility to have, in the next future, proton and ion beams of high intensity (up to hundreds or even thousands of Grays per second) and in a wide energy range (30–100 AMeV) will pave the way toward new applications and investigations in the field of Medical Physics. Stable and, if needed, intense ion beams can be used to study the projectile and target fragmentation with higher accuracy, to investigate the frontier of the multiple-ion approach also in the ’FLASH’ regime, to better quantify the effects of the cosmic radiation on humans, especially for space radioprotection applications and, finally, to explore the possibility of production of exotic radioisotopes. The concurrent opportunity of radioactive beams will moreover give the chance to perform and study advanced imaging techniques as the case of the in-beam positron emission tomography (in-beam PET) that is, nowadays, a new and almost non-explored functional imaging technique.
6.1.1 Stable proton and ions beams
The quality and variety (in terms of ion species, energy and dose rate) of the ion beams available at INFN-LNS will open the possibility to investigate many advanced and pioneering research topics connected to the Medical physics applications. Among these, we can certainly consider advanced studies for a better quantification of the projectile and target fragmentation in hadrontherapy, the possibility to study the multi-ion approach in radiotherapy and the chance to investigate the “FLASH” effects also with charged particles heavier than protons.
Projectile and target fragmentation
Protons and heavier ions entering in the tissues when used for radiotherapy purposes generate target and projectile fragmentation in a way depending on the incident energy, material constitution and projectile type. In particle therapy, proton or \(^{12}\)C ion beams are used to treat deep-seated solid tumors exploiting the advantageous characteristics of charged particles energy deposition in matter and a larger relative biological effectiveness (RBE). He ions are currently not exploited in clinics and would provide a reduced lateral scattering and an improved RBE with respect to proton, while decreasing the fragmentation tail with respect to C ions. For \(Z>1\) ions, fragmentation of projectiles needs to be carefully taken into account when planning a treatment. The fragmentation cross section for He, C and O ions at energy of interest for particle therapy (roughly between 60 and 250 MeV/u) is not known with sufficient accuracy and Monte Carlo models are scarcely reliable. For all these reasons the FOOT experiment [357] has been designed to measure the fragmentation cross section relevant for particle therapy applications with a movable setup, capable to fit the experimental rooms of different facilities. We propose to exploit He, C and O beams, available at INFN-LNS, whose energy is compliant for particle therapy application, to study the fragmentation with the FOOT apparatus Fig. 41.
FOOT is a table-top setup, with a lever arm of about 2 m. It includes a ToF system, composed of two detectors made of plastic scintillator for ToF and dE/dx measurement, a drift chamber as a beam monitor, a magnetic spectrometer formed of three different silicon detectors for the momentum measurements and a BGO calorimeter to obtain the kinetic energy, thus the mass of the fragment. FOOT is able to evaluate cross section value with errors within the 10\(\%\).
The full FOOT apparatus was completed in 2022 and experimental campaign at GSI (D) and (CNAO hadrontherapy facility, I) have been already performed with the aim of characterize the ion beams and measure the relevant cross section of Oxygen (200 AMeV - 400 AMeV) and Carbon (at 200 AMeV). The FOOT group is proposing to perform a set of experimental data taking campaign at INFN-LNS, in order to measure the \(^4\)He, \(^{12}\)C and \(^{16}\)O fragmentation cross sections at energy below 80 AMeV.
The new multi-ion radiotherapy (MIRT) approach theoretically provides an higher optimization in terms of LET (Linear Energy Transfer) distributions. In such scenario, \(^4\)He offers a decreased lateral scatter effect versus proton with less fragmentation tail dose versus carbon. The energy available at LNS (80 AMeV) is compliant for possible particle therapy application. Moreover, the knowledge of fragmentation cross sections of \(^{12}\)C and \(^{16}\)O ion beams at such energies allow for the investigation the fragmentation reactions in the entrance channel, where the phenomenon is clinically important for the presence of the health tissues.
Multiple-ion radiotherapy
Treatment design and delivery techniques for particle radiotherapy are becoming more sophisticated: from passive scattering (broad beam), that was the first implemented transport approach, to active scanning (spot/raster-scanning) widely used today in almost any new facility. On the other side, the treatment approach always make use of a single ion species: protons, helium, carbon, oxygen or neon ions are employed in patient treatment in an exclusively way. Conversely, a new approach known as multi-ion therapy (MIT) is emerging as potential new treatment concept that involves mixing ion species into a single treatment fraction. By mixing low (p, He) and high (C, O, Ne) LET particles, MIT offers additional degrees of freedom in treatment design, planning and optimization otherwise not attainable with the use of a single radiation quality. MIT dedicated treatment planning and optimization systems must handle the mixed radiation field of multiple primary particle beams to accurately predict effective dose. Accuracy of these systems relies on precise and detailed measurement and modeling of nuclear interactions of ion beams. MIT approach is nowadays studied at the Hidelberg Ion Therapy center or HIT (D), at the National Institute of Radiological Sciences or NIRS (J) and at GSI Helmholtzzentrum für Schwerionenforschung (D) where different aspects of this new modality are studied. Figure 42 [358, 359] shows the study conducted at GSI, where MIT is used to overcome the hypoxia related tumor radio-resistance using a combination of \(^{16}\)O and \(^{4}\)He ions that is also called multi-ion kill painting.
INFN-LNS beams (that include all the aforementioned beams) will be an ideal candidate to study either from a physics (fragmentation cross sections) and from a radiobiology point of view, the capability of a multi-ion approach. Even if, in fact, the maximum available energies per nucleon cannot be used for clinical treatments, they are ideal for studying the most basic effects of ions being the low-energy region (below 100 AMeV), in fact the most critical and unknown region from a radiotherapy point of view.
Heavy-ion cross section measurements for therapy and space applications
The reliability of particle transport codes, widely used for medical and space radiation applications, strongly depends on nuclear cross section models. A recent cross section data base [360] pointed out that for several important systems either no or only limited total reaction cross section data can be found in literature and sometimes not consistent values are reported. The same is true for single and double differential cross section systems and neutron production cross sections [361]. Future measurements at the LNS cyclotron facility could help to close some of these gaps, in particular for the intermediate to low energy range. Interesting systems to study are combinations of elements largely present in the space radiation environment (e.g., helium, carbon, nitrogen, oxygen, silicon, iron) with the constituents of relevant shielding materials (e.g., lithium, carbon, aluminum, silicon, oxygen). In the cases where either the projectile is not available or the target material is of difficult production or handling, inverse kinematic approaches could be very efficient to overcome these difficulties.
The research infrastructure for the proposed cross section measurements is the LNS Cyclotron Facility where total reaction and double differential cross sections for neutron and light ion fragments cane be measured exploiting the power of the CHIMERA facility. Here the following nuclear reactions, in the energy range of the incident particle of 40–80 MeV/u, can be considered: \(^4\)He, \(^{14}\)Ne, \(^{28}\)Si, \(^{56}\)Fe + \(^{7}\)Li, \(^{12}\)C, \(^{27}\)Al \(\rightarrow\) n, \(^{1,2,3}\)H, \(^{3,4}\)He + X
6.1.2 Radioactive ions beams (RIBs) and high-intensity beams (HIBs)
RIBs-Advanced imaging techniques: in-beam PET “In-beam PET” is a PET (positron emission tomography) where \(\beta ^+\) are produced from unstable (\(^{15}O\), \(^{11}C\), \(^{10}C\) mainly) isotopes generated by the interaction of the irradiation beam with human tissues beam and the generated gamma pairs are measured online during the irradiation. Figure 43 shows the dose (dashed lines) profile of a \(^{12}\)C beam (left) and proton (right) beam. The corresponding activity profiles, of the induced radionuclides, are reported with the continuous black lines. Data are reproduced, with permission, from Parodi [362].
In case of stable ion beams with a sufficient energy to generate an appreciable PET signal, the possibility to have high beam currents might be beneficial not only for tests in relation to radiation hardness and suppression/exploitation of radiation background, but also for generating special delivery regimes like FLASH or mini-beams, as well as secondary radioactive beams.
Activity and dose profiles generated by some of the most abundant radioisotopes produced in the interaction of \(^{12}\)C (left) and proton (right) beams in a PMMA target. The most common radioisotopes generated are reported in the cyan rectangle. Figure from Parodi [362]
HIBs-FLASH radiotherapy Delivery of current particle radiotherapy treatments lasts order of a few minutes using conventional dose rates (\(\approx\) 0.1 Gy/s). However, recent experimental evidences suggest that sub-second treatment at ultrahigh dose rates (uHDR, > 40 Gy/s for a delivered dose > 10 Gy) may provide several clinical advantages. Aside from increasing clinical efficiency and reducing uncertainties of intra-fraction organ-motion, the so-called FLASH effect has been observed experimentally, which elicits a potential differential sparing between surrounding healthy tissue and the tumor. To understand clinical potential of several ion species (proton [p], helium [He], carbon [C], oxygen [O] or neon [Ne] ions), dose rate dependencies on biological effect (in vitro and in vivo) must be measured across a broad range of dose and linear energy transfer (LET) levels in various tissue types. Subsequently, these data will guide future clinical practice via treatment design and modeling during planning to predict biological effect as a function of the major endpoints for FLASH (dose, LET and dose rate) for the mixed radiation spectra produced by therapeutic ion beams. A major limitation of performing such experiments at existing clinical facilities (e.g., clinical cyclotron- or synchrotron-based) is the inability to achieve “FLASH” conditions (\(\gg\) 40 Gy/s at 10 Gy) for experimentally and clinically relevant volumes (> 1 cm\(^2\)), as shown in previous work for proton and helium ions [363, 364] for high dose levels in both low and high LET regions. In this work, comprehensive radiobiological investigations will be made possible via delivery using the high-intensity cyclotron present at the facility. All these studies will be potentially possible at the INFN-LNS thanks to the high-intense ions beams that will be available.
HIBs-innovative radioisotopes
The new frontier of nuclear medicine is the “theranostic approach”, where radionuclides that combine imaging and radiotherapy properties (e.g., local tumors treatment) are employed by using a single radiopharmaceutical product as described in Fig. 44. The most important theranostic radionuclides nowadays known, i.e., having a nuclear decay pattern suitable for both applications, are \(^{67}\)Cu, \(^{64}\)Cu, \(^{47}\)Sc and \(^{67}\)Ga.
The theranostic approach may be also obtained with “theranostic pair,” i.e., isotopic radionuclides, one specific for imaging, while the other one for therapy. The most known pairs belonging to this group are \(^{61-64}\)Cu/\(^{67}\)Cu, \(^{43-44}\)Sc/\(^{47}\)Sc, \(^{68}\)Ga/\(^{67}\)Ga, \(^{149-152}\)Tb/\(^{155-161}\)Tb.
Most of the radionuclides nowadays used in nuclear medicine are massively produced by using nuclear reactors (e.g., \(^{99}\)Mo/\(^{99m}\)Tc generators, the most used radionuclide worldwide). On the other side, particles accelerators (accelerating p, d, alpha, etc.) as cyclotrons/linacs (or e-linacs producing a \(\gamma\)-source) are becoming the alternative supplying route of choice (in some cases, the only way), not only for the already established radionuclides, but also for the new emerging ones. Of course, to select the optimal radionuclides’ production pathway, it is mandatory to investigate all the possible nuclear reaction routes (cross sections measurements) and determine the full map of isotopic contaminants. For most of them, optimal production routes still needs to be clarified and investigated and exploring reaction routes by using heavier (\(Z>2\)) ions hitting particles may be certainly of interest.
While the most accelerator-based radionuclides are nowadays, produced by public/private facilities using large network of low-energy medical cyclotrons ( Ep < 20 MeV), some mid-energy p,d,\(\alpha\) cyclotrons (i.e., Ep 20–35 MeV), a few high-energy p,d,\(\alpha\) cyclotrons (i.e., Ep > 35 MeV) as the machine installed at ARRONAX (F), ZEVACOR (US), LARAMED (I), see Fig. 45.
With the planned upgrade of the acceleration machines, currently underway, the INFN-LNS will have:
-
A K-800 superconducting cyclotron with an improved beam intensities which will be available for low-mid Z ion species with respect to the past.
-
A Tandem accelerator with the availability of noble gasses.
Considering this, a dedicated (and very-well characterized) beamline for high quality nuclear cross sections measurements may be envisaged. On the other hand, new p, d, \(\alpha\) and heavier ion-driven nuclear reaction routes may be explored in order to produce specific and emerging radionuclides for imaging/therapy/theranostic applications.
It would be desirable that this the proposed facility (and the related research activities) shall be coordinated between LNS and LNL laboratories, where the LARAMED facility is under construction, in order to avoid overlaps. The LARAMED facility will have a dedicated beamline to carry out nuclear cross sections measurements but based upon the SPES cyclotron that will accelerate (at least in the initial years) only protons.
6.2 Laser applications
The perspective to install an high-power (TW-PW scale), ultrashort (fs order) laser system to generate extremely dense plasmas by its interaction with matter and the almost unique possibility to have, in the same environment, the availability of accelerated (4–80 AMeV energy range) and intense ion beams from conventional accelerators will open unprecedented possibilities to study the physics of the plasma acceleration and of the Warm Dense Matter at the INFN-LNS laboratory (Catania, I). The perspectives of the use and applications (in medical, energetic and multidisciplinary fields) of radiation generated in laser–matter interaction processes are analyzed and briefly discussed in this Section.
6.2.1 Laser-driven secondary sources
In the past few decades, researchers have continued to explore the extent to which extreme laser–plasma environments, abruptly created at a target site by pulsed laser irradiation of very high intensity, can generate energetic particle and associated radiation emission. In the case of proton/ion acceleration, this has been especially true since 2000 [365].
For electrons, laser systems with peak powers of hundreds of terawatts (TW) can accelerate bunches to GeV energy levels with charges of 0.1 nano-Coulombs or more and for an intrinsically ultrashort ‘at-source’ duration. Higher laser powers are typically needed for laser-driven ion acceleration, but the highest kinetic energies remain sub-relativistic to date. For example, hundreds of terawatts of peak laser power can accelerate proton bunches to tens of MeV energies (the recently published maximum energies approach 100 MeV [366] with nano-Coulomb charge levels and with an intrinsically ultrashort ‘at-source’ duration.
These proton energies are therefore adequate also for generating energetic neutrons in nuclear reactions. In general, we may look to laser-driven particle acceleration as an innovative optical component of accelerator science advancement.
Laser-driven particle sources offer a unique set of parameters in a relatively compact and versatile setup. Their intrinsic short duration (as short as a few femtoseconds) opens up novel applications and allows to study the response of materials and biological samples in unprecedented regimes.
Protons and electrons acceleration Laser–matter interaction mechanisms represent one of the most innovative and promising approaches for particle acceleration and radiation generation. Among the different radiations, the generation, optimization and use of laser-driven electrons and protons are, nowadays, the most investigated; the production and use of neutrons, positrons and electromagnetic radiation are also considered by many research groups and it represents a frontier in radiation generation, as it will be discussed in Sect. 6.2.1.
The most established laser-based ion acceleration mechanism is Target Normal Sheath Acceleration [367], where energized electrons create a strong sheath field at the rear surface of a laser-irradiated foil (see Fig. 46), accelerating contaminant protons in a diverging, broadband beam (with cutoff energies up to 60–85 MeV depending on laser pulse duration).
Target Normal Sheath Acceleration-TNSA. A thin target foil is irradiated by an intense laser pulse. The laser pre-pulse creates a pre-plasma on the target’s front side. The main pulse interacts with the plasma and accelerates MeV energy electrons mainly in the forward direction. The electrons propagate through the target, where collisions with the background material can increase the divergence of the electron current. The electrons leave the rear side, resulting in a dense sheath. An electric field due to charge separation is created. The field is on the order of the laser electric field (TV/m), which ionizes atoms at the surface. The ions are then accelerated in this sheath field, pointing in the target normal direction
Acceleration of heavier ions (e.g., carbon) from the bulk of a foil is possible through a different mechanism, Radiation Pressure Acceleration (or RPA), which leads to a spectral peak, so far in the 20–30 MeV/nucleon range.
Current work involves the use of miniature structures for collimating TNSA protons, as well as techniques for optimizing and upscaling carbon acceleration. Researchers are also working on more efficient schemes where sheath acceleration is driven by a different electron population accelerated from laser-excited surface plasma waves (see Fig. 47 [368]), as well as coupling collimation technique to RPA for delivery of high-flux carbon ion beamlets. These techniques promise proton and ion acceleration at energies higher than those today reached with the TNSA approach.
Schematics of the peeler scheme. A femtosecond laser (red and blue) is incident on the edge of a microscale tape (gray). The micron-thick tape is infinitely long across the laser focus and is a few tens of microns wide along the laser propagation direction. Abundant electrons are continuously dragged out and accelerated forward by the intense laser. When these energetic electrons arrive at the rear edge of the tape, a longitudinal bunching field is established (yellow). Protons (green dots) are simultaneously accelerated and bunched by this field, leading to a highly mono-energetic proton beam. From [368]
Electron acceleration by laser is based on the so-called laser wake field acceleration (LWFA) process in a plasma [369] allowing the generation of electron bunches with typical energy up to hundreds of MeV level to be produced, using 100-TW-scale, ultrashort laser systems. The typical electron charge per laser shot is up to 100 pC this opening the possibility to use high-energy electron beams for future radiotherapy protocols including the FLASH and the very high-energy electron approaches [370].
Positrons and photons generation High-power lasers also offer a unique degree of versatility, where not only the particle parameters can be seamlessly tuned to suit the desired application, but even the type of generated particle (e.g., electrons, positrons, and \(\gamma\)) can be selected with minor adjustments in the setup. Some of these generation mechanisms have been pioneered and developed by the plasma Group of the Queen’s University in Belfast (UK) and by the INO-CNR laboratory in Pisa (I), where the production of high-flux \(\gamma\)-rays from Compton scattering [371], high energy positron beams [372, 373], low-energy positron populations for material characterization [374] and the production of X and \(\gamma\)-ray beams, up to the multi-MeV level, for imaging and nuclear studies [375, 376] is investigated. MeV- and GeV-scale positron beams can be generated with the 45 and 250 TW laser systems that will be installed at the I-LUCE facility of LNS. These beams will allow for volumetric material inspection at unprecedented spatial resolution, with the so-called positron annihilation lifetime spectroscopy or PALS, and a typical production setup is shown in Fig. 48.
Setup for the high-brilliance \(\gamma\) production via inverse Compton-scattering (from Sarri et al. [371])
To optimize the exploitation of all these sources, systematic studies of the generation mechanisms and their application must be carried out: the laser system that will be installed at INFN-LNS will be a natural candidate.
Neutrons generation In recent years, laser-driven neutron sources have attracted significant attention as they offer the compactness and affordability required for a university-scale facility to promote multidisciplinary applications. While the MeV neutrons are relevant for some specific applications, such as testing materials for fusion reactors and homeland security, most neutron science deals with thermal and epithermal neutrons. For instance, boron–neutron-capture therapy is one of the major drivers for the development of ultracompact neutron sources, mainly using conventional technologies to accelerate protons and electrons. High repetition rate lasers of moderate power (10 s–100 TW) can be highly useful in developing a compact source based on p-Li reaction. Near the reaction threshold of 1.88 MeV, the p-Li reaction yields neutrons of 10 s of keV energies in a narrow cone along the beam forward direction, which can in principle be deployed for the BNCT application without any moderation. Since moderate power lasers can efficiently accelerate the modest proton energies of 2 MeV, this route may prove to be more effective than using other higher yield neutron converters such as Be, which would require high proton energies and incurs significant losses in neutron flux due to moderation.
6.2.2 Fusion, fission and nuclear scheme for applications
High-intensity lasers interacting with solids in vacuum produce non-equilibrium plasma having high equivalent temperatures and high ion energies. Under these conditions, depending on the laser parameters, irradiation characteristics and target composition and geometry, different nuclear reactions can be induced due to both the high plasma temperature and the wide ion energy distribution of the accelerated species. By focusing the laser spot of very high laser intensities above 10\(^{15}\) W cm\(^2\) on solid targets it is possible to accelerate electrons and ions at relativistic energies above 1–10 MeV/nucleon, sufficient to penetrate into the nucleus of many light atoms. Thus laser–plasma may induce activation, transmutation, fission (to produce and study neutron-rich nuclei toward the \(N = 126\) waiting point of the r-process for astrophysical investigations Fig. 49 [377]) and fusion processes (i.e., material of Sect. 6.2.2). The high plasma density and the non-isotropic plasma distribution enhance the number of nuclear events during the laser–plasma interaction along special directions. X and \(\gamma\) rays, electrons, different ion species and neutrons can be produced mono-energetically or in wide energy distribution.
Many nuclear reactions as the \(^2\)H(d,n)\(^3\)He, \(^2\)H(d,p)\(^3\)H, \(^7\)Li(d,n)\(^8\)Be and \(^{11}\)B(p,a)\(^8\)Be can be so triggered opening the route to a new physics (reactions in plasma are affected by phenomena like the electron screening, stopping power changes, still unknown) and application as the use of this system for energy production (inertial confinement fusion), table-top source realization and radioisotopes production.
Proton–boron nuclear reaction in plasma The proton–boron fusion reaction channel is of interest to many different research groups as a potential candidate for future advanced fusion ignition schemes and for the development of laser-driven \(\alpha\) particles sources and their possible use, among others, in the production of short half-life radioisotopes for medical applications.
In the last 15 years, proton-\(^{11}\)B fusion reaction has effectively been induced by means of high-power lasers, showing an impressive progression in the reaction yield. Recent experimental findings and theoretical predictions, along with the advent of dramatically enhanced laser capabilities, call for an urgent, systematic investigation of laser-driven proton-boron fusion. Such study would also include the generation of intense sources of \(\alpha\) particles (pulsed beams) at high repetition rate (1 Hz–1 kHz) and in compact geometries for multidisciplinary applications, including radioisotope production.
In order to produce laser-driven \(\alpha\)-particle sources that can be competitive with today’s dedicated cyclotrons (e.g., Arronax produces 70\(\,\upmu\)A of \(\alpha\) particles or about 10\(^4\) \(\alpha\)/s), we would need high-intensity lasers working at 100 Hz that are becoming a reality, indeed.
One of the goals of the present research consists of how to optimize the \(\alpha\) production per laser shot. This implies several research lines: (i) comparing pitcher–catcher and in-target configurations, (ii) optimizing the proton beam (generated by TNSA or hole boring) and (iii) testing different kinds of targets enriched in hydrogen and/or with different geometrical configurations.
Such experimental investigation can be carried out in two different laser intensity regimes that will be also present at the INFN I-LUCE facility:
-
1.
100-TW-class laser (femtosecond) systems operating at 1–10 Hz (intensity \(\ge\) 1E\(^{19}\) W/cm\(^2\)).
-
2.
1-TW class laser (femtosecond) systems operating at 0.1–1 kHz (intensity \(\ge\) 1E\(^{17}\) W/cm\(^2\)).
A dedicated target system, able to operate at the required rates and the associated plasma and radiation diagnostics is also required.
Radioisotopes production There are hundreds of radioisotopes that can be produced with charged particle accelerators, i.e., that are accessible through proton or deuteron collisions (or, less frequently, with \(^3\)He or \(\alpha\)-particles). The cyclotron is the most commonly used accelerator for the isotopes accessible via reactions with projectiles at 10 MeV energies or less. Linacs (linear accelerators) are also frequently used. A few isotopes are obtained using nuclear reactors. An interesting comparison between different kinds of conventional accelerators can be found in [378].
Lasers, in turn, are a very promising alternative for this application [379, 380]. Laser technology is, in fact, quickly evolving in performance and cost reduction and, even if laser technology is still not mature enough to match or exceed the capabilities of the cyclotron, many perspectives are opening in this way. Laser-driven particles are very intense and, while often showing a wide energy spread, this could not be a limitation in the case of isotope generation but an added value covering wider cross section intervals, therefore, what could be the future role of a laser-driven accelerator? It is clear that to accelerate protons, deuterons or other ions at the energies relevant to radioisotope production, one needs [367] multi-TW laser systems, probably beyond 50 TW. On the other hand, the laser power itself is not sufficient: we also need lasers generating particle bunches at a repetition rate sufficient to ensure adequate average current. In this perspective, while high-power high repetition rate systems are at the horizon of technology, the relevant breakthroughs appear in target development [381]. Such systems, in fact, now typically operate at repetition rates of 10 shots per second (10 Hz) but the required major increase in laser repetition rate and power must be investigated developing advanced and faster target schemes.
On the other side, laser-based systems also present challenges and issues to be exceeded. One important difference, already discussed above, between conventionally accelerated and laser-accelerated protons, is the energy spectrum (or energy spread). With a conventional accelerator, the energy spectrum corresponds to a relatively narrow Gaussian velocity distribution. For a laser-driven proton accelerator, the energy spectrum is much broader. (This can be influenced greatly by the chosen acceleration mechanisms.) In certain cases, it opens the possibility of having competing reactions. For example, the foreseen \(^{15}\)N(p,n)\(^{15}\)O reaction channel might not be the only one favored by the incoming proton energies; \(^{15}\)N(p,2p)\(^{14}\)C could be also possible. In the last twenty years, tens of proof-of-principles experiments have been performed demonstrating the potentiality of a future laser-based approach in radioisotope production [382]. Different medical radioisotopes have been produced (from \(^{18}\)F, to \(^{11}\)C and \(^{13}\)N) and activities of the order of fractions of GBq have been obtained in many cases for 1/10 Hz repetition rate systems. Such activity levels even not yet sufficient for use in human diagnostics can be already adopted for preclinical studies with small animals.
A lot of work remains to be done in laser acceleration optimization, with the goal to optimize the proton velocity distributions and to better control the acceleration mechanisms. Furthermore, the development of optimized high repetition targets is critically needed; particularly for high repetition rate applications. Moreover, target structures can affect the final energy spectrum of accelerated electrons that drive ion acceleration [383] and can significantly enhance it in certain cases.
An optimized laser target system, with basic metrology, can be designed to be much more compact with respect to the currently used, representing a strong potential advantage of the laser approach. In this case, the radioactive shielding is just for the small volume around the focal spot (including the primary target, accelerated ion yield and secondary target, as shown in Fig. 50) and this will certainly dramatically reduce the costs of radioprotection in such approaches.
Schematic representation of the radionuclide generation process using laser acceleration of protons. The laser pulse hits the primary target and generates by TNSA (target normal sheath acceleration) a proton bunch. Protons subsequently hit a secondary target where the nuclear reaction occurs. The distance between the primary and the secondary target can be reduced and also the geometry (not necessarily flat as seen in the figure) to use the complete not collimated proton beam
In conclusion, laser-driven ions and photons could represent an innovative and effective way to generate future radioisotopes also in new exotic schemes and to exploit the extreme intensity and the new physics underlying the nuclear reaction processes in extreme dens plasmas.
Stopping power in warm dense matter (WDM) and applications Ion stopping in warm dense matter (a matter state well described in Fig. 51 in terms of electron temperature and mass density) is a process of fundamental importance for the understanding of the properties of dense plasmas. The realization and the interpretation of experiments involving ion beam heated warm dense matter samples, astrophysics and inertial confinement fusion research and, in general, nuclear reaction processes in plasma that could produce interesting applications like the realization of table-top sources of neutrons (Sect. 6.2.1) or \(\alpha\) particles (Sect. 6.2.2) or the radioisotope generation in advanced irradiation schemes (Sect. 6.2.2).
The theoretical description of the ion stopping power in warm dense matter is a challenge due to electron coupling and degeneracy, and measurements are still largely missing. In particular, the low velocity stopping range, which features the largest modeling uncertainties, remains virtually unexplored. Recently, the Group of the CPLU (Centre de Laseres Pulsados) in Salamanca (S)) reported proton energy loss measurements in warm dense plasma at unprecedented low projectile velocities by using the 200 TW system there available. They demonstrated a significant reduction (about 18\(\%\)) of the stopping power from classical models in this regime (Fig. 52) in agreement with recent first principles simulations based on time-dependent density functional theory.
Hundreds of TW-class laser systems are an ideal environment to perform “ultrafast pump and probe” experiments in WDM and in general for high energy density physics. Pump and probe experiments for WDM and HED physics require a <30 fs 10–200 TW laser systems. The I-LUCE facility of INFN-LNS will represent the second world-facility [with the PHELIX laser at the GSI (Darmstradt, D)] where, in the same experimental room, plasmas from high-power lasers and conventional medium energy (4–100 AMeV) protons and ions beams, produced by the already operating Tandem and cyclotron accelerators already operating, will coexist. This configuration will allow for the realization of WDM experiments with an unprecedented novelty (due to the wide ranges of ions and energies available), precision and accuracy.
6.2.3 Novel approach to hydrogen production from water by focused femtosecond laser pulses
In recent years, femtosecond laser-driven water splitting has also attracted increasing attention, offering a novel approach to the direct production of pure hydrogen [384]. Although the interactions between ultrashort laser pulses and liquid water have been studied in the past, trying to explain the mechanism of non-equilibrium plasma formation in the focal spot [385, 386], the dynamics of associated bubble nucleation [387], as well as providing preliminary signals about the possibility of obtaining hydrogen gas in this way [388, 389], the production of hydrogen by focused pulses of a femtosecond laser is a completely new concept that attracts considerable interest from researchers [390]. In the pioneering research developed by the Lodz University of Technology (Poland), the decomposition of water using femtosecond laser pulses (100 fs, \(\lambda\) = 800 nm) focused into a rectangular quartz cell containing ultrapurified water was thoroughly investigated and quantified [384]. The scheme of the measuring setup is shown in Fig. 53a. As a result of numerous radical reactions induced by plasma, the formation of stable products including molecular hydrogen (H\(_2\)) and hydrogen peroxide (H2O2) was identified and analyzed as a function of irradiation time, repetition rate (0.1–1 kHz), and pulse energies up to 1 mJ. Most importantly, the experiments demonstrated that decreasing the pulse energy and repetition rate boosted the energy efficiency of H2 generation (expressed in nmol H\(_2\) per Joule of incident energy in Fig. 53b). Interestingly, under specific irradiation conditions at 1 kHz, only hydrogen and hydrogen peroxide were generated (without O\(_2\), which corresponds to the ratio of H\(_2\)/H\(_2\)O\(_2\) equal 1) as the products of water decomposition (see Fig. 53b). This finding is advantageous from the practical point of view because no gas separation step is required and the molecular hydrogen can be easily collected as the sole gaseous product, as opposed to the typical stoichiometric decomposition of water into H\(_2\) and O\(_2\).
a Setup for hydrogen production from water by focused femtosecond laser; b H\(_2\) production. Adopted from Kierzkowska-Pawlak et al. [384]
In the discussed study [384], to optimize the energy yield of H2 production in a particular regime, in which the only gaseous product of water decomposition is hydrogen, the authors proposed a concept of process intensification involving a series of split low-energy laser beams generating plasma in different zones with a sufficiently fast flow of water. For the suggested solution, the predicted energy efficiency of hydrogen production of 0.4 g H2/kWh was found to be comparable to other methods for H2 generation using plasma discharges in water. This research put a step forward in understanding the chemical mechanism of femtosecond laser-water interactions and it provided the basis for exploring other concepts of hydrogen generation from aqueous solutions, such as seawater. This has been explored at Shizuoka University (Japan) [391] using a previously developed approach [384]. The reported yield of hydrogen generation from seawater was approximately 30\(\%\) higher than the ultrapure water case. What is more, using a cylindrical cell rather than a rectangular one, as expected, further improved the production rate of hydrogen under certain irradiation conditions. These results suggest that the use of femtosecond lasers to generate hydrogen from aqueous solutions is a method with a promising future, for both research and application.
6.3 Plasma traps
The activities related to the plasma trap topic have been subdivided into three different sub-units.
-
Magnetic plasma stopping power and charge breeding: numerical simulation studies of the capture processes of multicharged ions in magneto-plasmas at different densities and temperatures, relevant for ISOL facilities and for inertial fusion purposes (both heating and diagnostics). These activities are ongoing even by looking experimental perspectives in PANDORA-Phase 2 (5–7 years) with charge breeding techniques adopted for in-flight capture isotopes at \(\tau <60 d\).
-
Physics and technology for fusion plasmas: R &D on diagnostics: detection, collimation and active shuttering methods for soft X-ray and hard X-ray spectroscopy and tomography useful for the study of magnetized plasmas for fusion in compact traps and reactors (TOKAMAK). Innovative diagnostic systems such as reflectometers and interferometers for the control of plasma density and its spatial profile. Wave propagation/absorption in fusion plasmas: theoretical study of electromagnetic propagation and related absorption mechanisms in magnetized plasmas for fusion and compact traps; study of innovative heating and energy transport mechanisms for increasing confinement and reaction rates; development of antennas and systems for the excitation and control of thermonuclear fusion plasmas and/or for ion propulsion; ion cyclotron heating with innovative compact antennas; ICH in case of polarized ions.
-
New generation plasma chambers and resonators for compact reactors: design, numerical investigation and experimental tests of advanced plasma chambers ensuring better radiation–plasma coupling, stability, control and confinement.
As far as compact trap and related setups are concerned, we refer to the existing testbench facility now operating at LNS, such as the flexible plasma trap (FPT) for the development of diagnostics, heating systems, etc. (see Fig. 54) or the new PANDORA scenario that has been described in Sect. 2.3.
The flexible plasma trap at INFN-LNS is made of three solenoids allowing different magnetic field profile, it has three microwave inputs (one axial and two radials) and operates in the microwave frequency range 4–7 GHz. Different noninvasive diagnostic tools can be installed simultaneously in the flanges of FPT in order to characterize plasma parameters
6.3.1 Magnetic plasma
The ion beam–plasma interaction is a relevant topic in several fields of plasma physics, from fusion devices to modern ion sources. The numerical modeling of the whole beam-plus-plasma-target system in case of singly or multiply charged ions entering an electron–cyclotron–resonance (ECR) trap (e.g., an ECR-based charge breeder, ECR-CB) has been started since 5 years in a collaboration between LNS and LNL [392,393,394]. Possible non-linear interactions and the role played by the eventual onset of instabilities have also been addressed. A code aiming at modeling ECR-CB has to be particularly suitable to reproduce the elastic Coulomb collisions between injected and plasma ions (see Fig. 55); this issue is relevant also in other fields such as astrophysics or inertial confinement fusion [391, 395,396,397]. Electron dynamics in high-density processing plasmas also require advanced Coulomb collisions simulations, even in those cases where 90\(^{\circ }\) scattering is dominated by e-neutral collisions: e–e collisions determine in fact the electron energy distribution function, populating the high-energy tail by energy up-scattering.
6.3.2 Fusion plasma
In the context of the laboratory plasmas (including fusion plasmas in toroidal devices, plasma traps, plasma thruster), as well as astrophysical tenuous plasmas, the role of the RF plasma interaction both for heating or instability studies remains a crucial point. Solution of the Maxwell–Vlasov system and Fokker–Planck equations (in collisional regime) is mandatory to understand the physics of interaction. Numerical codes based on the theoretical analysis of the model equations have been developed [398, 399]. The exploitation of the numerical codes for some specific experimental or technological goals enables to study the features of the RF wave propagation, absorption or wave instability in plasma including technological as well as astrophysical applications. In particular, the above numerical codes could be applied and used in planned and under-construction devices as DTT (for fusion applications), plasma traps, plasma thruster, electromagnetic instabilities in galactic plasmas, in the polarization or depolarization of the nuclear ions in order to increase the ion cross section. This activity could be easily executed in a midterm time range (5 years), and it can produce some interesting results making it possible some cross-over among different physical context as, for example, thermonuclear fusion vs plasma propulsion, thermonuclear fusion vs polarized ions, plasma traps vs acceleration of neutral beam for fusion application, and lab plasma physics vs astrophysical plasma in growing electromagnetic instabilities.
Another topic of research in the field of wave-plasma interaction are the non-linear phenomena taking place at the plasma edge, e.g., due to ponderomotive force and RF sheaths. Their effects span from harmless modification of the edge plasma density via convective cells to deleterious impurity generation via sputtering yields. If equipped with a suitable RF system, the PANDORA facility at LNS may provide a noteworthy contribution to the improvement of physics models for such phenomena and/or their experimental benchmark. The LNS is involved in several activities involving the Laboratory plasmas both via collaboration with some partners like ENEA for the design and construction of a high-power ion cyclotron resonance heating (ICRH) antenna for DTT plasma heating and by planning the construction of devices like Plasma Traps or studying the feasibility of a plasma thruster for propulsion application. In this context of already started mutual scientific interests, this kind of activity could be extremely profitable. Efforts are now focused in particular on the design of compact ion cyclotron heating antennas for compact traps (ICH-CT) (see Fig. 56) resulting in different ion density and energy distributions such as the one shown in Fig. 57 [400, 401].
Ion density and energy distribution for two antenna types. In particular, projection maps along the cavity z-axis of particle numerical density (top) and energy (bottom) in [eV], resulting from kinetics simulation of ions \(^{16}\)O\({4+}\) under the presence of cavity coupled EM field as computed for simple loop (left) and helical (right) antennas. Dashed-lines indicate the ICR surface in the simulation domain
Fusion from polarized fuel An important breakthrough in the future of fusion energy may come from the use of polarized nuclear fuel. From the point of view of the nuclear physics, the use of polarized fuel seems the viable way in order to increase nuclear fusion rates for energy production, thanks to:
-
enhancement of fusion cross sections,
-
control of angular distribution of reaction products,
-
possible neutron lean reactors.
It was known that fusion reactions take place only when the nuclear spins of the reacting nuclei are aligned, relative to each other, in well-defined ways; therefore, at least in theory, \(D-T\), \(D-D\), or \(D-^3\)He plasmas could have higher fusion yields by factors of 1.5–2 with suitable polarization of the ion nuclear spins (see for more details the book-proceedings and papers therein: [402]).
This field of research is still challenging but, on the other side, really promising. One major issue still relies to the procurement of the polarized fuel to be used in fusion suitable environments. This holds also from the point of view of testbench characterizations and cross section measurements in laboratory: for instance, only few ion sources for polarized beams of D or T are available at the present time [403]. For this reason, fusion of DD-double polarized cross sections data are still missing. In a midterm perspective, laboratory measurements and development of suitable theory in the 10–100 keV range and beyond would be of paramount relevance and impact. Of extremely relevant impact is also the issue of mastering polarized fuel in nuclear fusion reactors. Powerful RF sources could be used for plasma heating in Tokamaks aiming at selective heating that could polarize and/or prevent depolarization of the nuclear fuel, or be used for plasma diagnostic purposes as with a sort of MRI technique [404]. The possibility of including spin-wave interaction effects into the ion cyclotron resonant heating (ICRH) models has been evaluated and included in the ICRH wave propagation/absorption codes [405].
6.3.3 Compact reactors
A reshaping of both plasma chamber and launching system is proposed here. Looking at the fusion reactors (e.g., Stellarators)—where the vessels have been fashioned in a way that closely imitates the magnetic field structure—herein we propose for ECRISs a new development mostly in terms of: (i) novel cavity resonator shapes fashioned to the twisting magnetic structure, and, therefore, to the shape of an electron isodensity surface; (ii) new RF launching schemes based on “Slotted Waveguides”, allowing diffractive, high-efficiency irradiation inside the plasma chamber [406].
A reshaping of both the plasma chamber and related RF launching system (see Fig. 58) is considered as a possible solution for a better wave-to-plasma coupling in ECRIS, maximizing the absorption of the RF power into the plasma core, and avoiding “hollow” plasma (where most of the electrons are concentrated in the near resonance region, as well as plasma ions, leaving a “hole” in the near axis zone [407]) in order to obtain the most desirable configurations maximizing the ion beam brilliance where the power is deposited in the plasma core.
Moreover, it will be possible to online evaluate in noninvasive mode the plasma structure change in the new shape of the plasma chamber and directly compare it with the conventional cylindrical one, through high resolution spectrally-resolved X-ray imaging. This technique, by means of a X-ray pin-hole camera setup, represents a powerful method for obtaining structural information on the plasma and for investigating the deep plasma dynamics [408, 409]. Recently, both the X-ray imaging setup [410] and the algorithm of analysis [411] have been updated and improved to remarkably increase signal-to-noise ratio at relatively high pumping RF power mode (up to 200 W in compact traps). In addition, this system, with new collimation and active shuttering methods for soft X and hard X spectroscopy/tomography, which could be executed in a midterm time range (5 years), is a very useful for the study of magnetized plasmas for fusion in compact traps and reactors (TOKAMAK).
Break of cylindrical symmetry for plasma chamber-resonator in compact traps, allowing innovative microwave launching schemes: on the left, the geometry of a classical cylindrical cavity; on the right, the unconventional chamber implemented in COMSOL Multiphysics where the shape consists of two “three-brunches” stars rotated of 60\(^\circ\) one with respect to the other, that overlap in the middle of the plasma chamber
Data Availability Statement
No data associated in the manuscript.
Abbreviations
- ANC:
-
Asymptotic normalization coefficient
- BNCT:
-
Boron–neutron capture therapy
- BNV:
-
Boltzmann–Nordheim–Vlasov
- CoMD:
-
Constrained molecular dynamics
- CPLU:
-
Centre de Laseres Pulsados
- DWBA:
-
Distorted-wave Born approximation
- ECR:
-
Electron cyclotron resonance
- ECR-CB:
-
Electron cyclotron resonance-based charge breeder
- ED:
-
Electrostatic deflector
- EOS:
-
Equation of state
- FPT:
-
Flexible plasma trap
- GDR:
-
Giant dipole resonances
- GR:
-
Giant resonances
- HIBs:
-
High-intensity beams
- HIT:
-
Hidelberg ion therapy
- ICH:
-
Ion cyclotron heating
- ICRH:
-
Ion cyclotron resonance heating
- ICH-CT:
-
Ion cyclotron heating antennas for compact traps
- ISGMR:
-
Isoscalar giant monopole resonance
- LET:
-
Linear energy transfer
- LWFA:
-
Laser wakefield acceleration
- MIRT:
-
Multi-ion radiotherapy
- MIT:
-
Multi-ion therapy
- NIRS:
-
National Institute of Radiological Sciences
- PALS:
-
Positron annihilation lifetime spectroscopy
- PDR:
-
Pygmy dipole resonances
- PET:
-
Positron emission tomography
- RBE:
-
Relative biological effectiveness
- RF:
-
Radio-frequency
- RIBs:
-
Radioactive ion beams
- RPA:
-
Radiation pressure acceleration
- SC:
-
Superconductive cyclotron
- THM:
-
Trojan horse method
- uHDR:
-
Ultrahigh dose rates
- WDM:
-
Warm dense matter
References
C. Broggini, O. Straniero, M.G.F. Taiuti, G. de Angelis, G. Benzoni, G.E. Bruno, S. Bufalino, G. Cardella, N. Colonna, M. Contalbrigo, G. Cosentino, S. Cristallo, C. Curceanu, E. De Filippo, R. Depalo, A. Di Leva, A. Feliciello, S. Gammino, A. Galatà, M. La Cognata, R. Lea, S. Leoni, I. Lombardo, V. Manzari, D. Mascali, C. Massimi, A. Mengoni, D. Mengoni, D.R. Napoli, S. Palmerini, S. Piano, S. Pirrone, R.G. Pizzone, G. Politi, P. Prati, G. Prete, P. Russotto, G. Tagliente, G.M. Urciuoli, Experimental nuclear astrophysics in Italy. Nuovo Cim. Riv. Ser. 42, 103 (2019). https://doi.org/10.1393/ncr/i2019-10157-1. arXiv:1902.05262 [nucl-ex]
A. Badalà, M. La Cognata, R. Nania, M. Osipenko, S. Piantelli, R. Turrisi, L. Barion, S. Capra, D. Carbone, F. Carnesecchi, E.A.R. Casula, C. Chatterjee, G.F. Ciani, R. Depalo, A. Di Nitto, A. Fantini, A. Goasduff, G.L. Guardo, A.C. Kraan, A. Manna, L. Marsicano, N.S. Martorana, L. Morales-Gallegos, E. Naselli, A. Scordo, S. Valdré, G. Volpe, Trends in particle and nuclei identification techniques in nuclear physics experiments. Nuovo Cim. Riv. Ser. 45(3), 189–277 (2022). https://doi.org/10.1007/s40766-021-00028-5
L. Calabretta et al., Commissioning of the K800 INFN Cyclotron, in 14th International Conference on Cyclotrons and Their Applications (1996), p. 02
F. Cappuzzello, M. Cavallaro, C. Agodi, M. Bondì, D. Carbone, A. Cunsolo, A. Foti, Heavy-ion double charge exchange reactions: a tool toward 0 \({{\nu }}{{\beta }}{{\beta }}\) nuclear matrix elements. Eur. Phys. J. A 51, 145 (2015). https://doi.org/10.1140/epja/i2015-15145-5. arXiv:1511.03858 [nucl-ex]
F. Cappuzzello et al., The numen project: nuclear matrix elements for neutrino-less double beta decay. Eur. Phys. J. A 54(5), 72 (2018). https://doi.org/10.1140/epja/i2018-12509-3
A. Calanna, L. Calabretta, G. Cuttone, G. Dagostino, A. Radovinsky, D. Rifuggiato, A.D. Russo, Proposal to increase the extracted beam power from the LNS-INFN superconducting cyclotron, in 13th International Conference on Heavy Ion Accelerator Technology (2016), pp. 1–03. https://doi.org/10.18429/JACoW-HIAT2015-MOA1C03
L. Calabretta, A. Calanna, G. Cuttone, G. D’Agostino, D. Rifuggiato, A.D. Russo, Upgrade of the LNS superconducting cyclotron for beam power higher than 2–5 kW (21), 7–10 (2017). https://doi.org/10.18429/JACoW-Cyclotrons2016-MOA02. Proc. of International Conference on Cyclotrons and Their Applications (Cyclotrons’16), Zurich, Switzerland, September 11–16, 2016
A. Calanna, High-intensity extraction from the superconducting cyclotron at LNS-INFN. Nuovo Cim. C 40(2), 101 (2017). https://doi.org/10.1393/ncc/i2017-17101-y
G. D’Agostino, L. Calabretta, W. Kleeven, D. Rifuggiato, A central region upgrade of the k800 superconducting cyclotron at INFN-LNS, in Proceeding of the 10th International Particle Accelerator Conference (IPAC2019) (2019), p. 023. https://doi.org/10.18429/JACoW-IPAC2019-TUPTS023
L. Neri, L. Allegra, L. Calabretta, G. Costa, G. D’Agostino, G. Gallo, D. Rifuggiato, A.D. Russo, G. Torrisi, 3D magnetic optimization of the new extraction channel for the LNS superconducting cyclotron, in 22nd International Conference on Cyclotrons and Their Applications (CYC2019) (2020), p. 014. https://doi.org/10.18429/JACoW-Cyclotrons2019-MOP014
G. Gallo, L. Allegra, L. Calabretta, A. Caruso, G. Costa, E. Messina, M. Musumeci, D. Rifuggiato, E. Zappalà, Mechanical Modifications of the median plane for the superconducting cyclotron upgrade, in 22nd International Conference on Cyclotrons and Their Applications (CYC2019) (2020), p. 013. https://doi.org/10.18429/JACoW-Cyclotrons2019-MOP013
A. Caruso, The RF system of the K-800 superconducting cyclotron at INFN-LNS, 1–5, in Proc. of Indian Particle Accelerator Conference, Nov 19–22, 2013, VECC, Kolkata (2013)
A.C. Caruso, F. Caruso, A. Longhitano, A. Spartà, G. Primadei, J. Sura, Hybrid configuration, solid state-tube, revamps an obsolete tube amplifier for the INFB K-800 superconducting cyclotron, in Proc. of International Conference on Cyclotrons and Their Applications (Cyclotrons’16), Zurich, Switzerland, September 11–16, 2016 (21) (2017), pp. 263–266. https://doi.org/10.18429/JACoW-Cyclotrons2016-WEB02
A. Tumino, C. Spitaleri, M. La Cognata et al., Publisher correction: an increase in the \(^{12}\)C + \(^{12}\)C fusion rate from resonances at astrophysical energies. Nature 561(7721), 3 (2018). https://doi.org/10.1038/s41586-018-0269-x
M. La Cognata, S. Palmerini, P. Adsley, F. Hammache, A. Di Pietro, P. Figuera, R. Alba, S. Cherubini, F. Dell’Agli, G.L. Guardo, M. Gulino, L. Lamia, D. Lattuada, C. Maiolino, A. Oliva, R.G. Pizzone, P.M. Prajapati, S. Romano, D. Santonocito, R. Spartá, M.L. Sergi, A. Tumino, Exploring the astrophysical energy range of the \(^{27}\)Al(p,\({{\alpha }}\))\(^{24}\)Mg reaction: a new recommended reaction rate. Phys. Lett. B 826, 136917 (2022). https://doi.org/10.1016/j.physletb.2022.136917
P. Russotto et al., Status and perspectives of the INFN-LNS in-flight fragment separator. J. Phys.: Confer. Ser. 1014(1), 012016 (2018). https://doi.org/10.1088/1742-6596/1014/1/012016
A.D. Russo, L. Calabretta, G. Cardella, P. Russotto, Preliminary design of the new FRAgment In-flight SEparator (FRAISE). Nucl. Inst. Methods Phys. Res. B 463, 418–420 (2020). https://doi.org/10.1016/j.nimb.2019.04.037
N.S. Martorana, Status of the FraISe facility and diagnostics system. Il Nuovo Cim. C 44, 1–10 (2021). https://doi.org/10.1393/ncc/i2021-21001-2
R. Anne, D. Bazin, A.C. Mueller, J.C. Jacmart, M. Langevin, The achromatic spectrometer LISE at GANIL. Nucl. Instrum. Methods A 257, 215–232 (1987). https://doi.org/10.1016/0168-9002(87)90741-8
F. Cappuzzello, C. Agodi, M. Cavallaro, D. Carbone et al., The numen project: nuclear matrix elements for neutrinoless double beta decay. Eur. Phys. J. A 54(5), 72 (2018). https://doi.org/10.1140/epja/i2018-12509-3
O.B. Tarasov, D. Bazin, Lise++: Radioactive beam production with in-flight separators. Nucl. Instr. Methods Phys. Res. Sect. B: Beam Interact. Mater. Atoms 266(19), 4657–4664 (2008). https://doi.org/10.1016/j.nimb.2008.05.110. Proceedings of the XVth International Conference on Electromagnetic Isotope Separators and Techniques Related to their Applications
G. Prete, The LNL radioactive beam facility. Scholarpedia 5(5), 9751 (2010). https://doi.org/10.4249/scholarpedia.9751. Revision #143504
A. Pagano, Studies of nuclear reactions and time scale with the 4\(\pi\) detector CHIMERA. Nucl. Phys. News 22(1), 28 (2012). http://www.nupecc.org/npn/npn221.pdf
E.V. Pagano et al., Status and perspective of FARCOS: a new correlator array for nuclear reaction studies. EPJ Web Confer. 117, 10008 (2016). https://doi.org/10.1051/epjconf/201611710008
F. Cappuzzello, C. Agodi, D. Carbone, M. Cavallaro, The \({\rm MAGNEX}\) spectrometer: results and perspectives. Eur. Phys. J. A 52, 167 (2016). https://doi.org/10.1140/epja/i2016-16167-1
F. Cappuzzello, C. Agodi, L. Calabretta, D. Calvo, D. Carbone et al., The NUMEN technical design report. Int. J. Mod. Phys. A 36(30), 2130018–290 (2021). https://doi.org/10.1142/S0217751X21300180
D. Mascali, D. Santonocito et al., A novel approach to beta-decay: Pandora, a new experimental setup for future in-plasma measurements. Universe 8, 80 (2022). https://doi.org/10.3390/universe8020080
Y. Litvinov et al., Beta decay of highly charged ions. Rep. Progr. Phys. (2011). https://doi.org/10.1088/0034-4885/74/1/016301
F. Bosch et al., Observation of bound-state beta\(^{-}\) decay of fully ionized \(^{187}\)Re: \(^{187}\)Re–\(^{187}\)Os cosmochronometry. Phys. Rev. Lett. (1996). https://doi.org/10.1103/PhysRevLett.77.5190
G. Mauro et al., An innovative superconducting magnetic trap for probing \(\beta\)-decay in plasmas. Front. Phys. (2022). https://doi.org/10.3389/fphy.2022.931953
E. Naselli et al., Multidiagnostics setups for magnetoplasmas devoted to astrophysics and nuclear astrophysics research in compact traps. J. Instrum. (2019). https://doi.org/10.3389/fphy.2022.935728
E. Naselli et al., Design study of a HPGe detector array for \(\beta\)-decay investigation in laboratory ECR plasmas. Front. Phys. (2022). https://doi.org/10.3389/fphy.2022.935728
D. Mascali, D. Santonocito, M. Busso, A. Galatà, F. Odorici, G. Torrisi, others, TDR PANDORA_Gr3 plasma for astrophysics. Nucl. Decays Observ. Radiat. Archaeom (2021). https://pandora.infn.it/public/pandora-tdr
L. Torrisi, Tantalum ions produced by 1064 nm pulsed laser irradiation. J. Appl. Phys. 91, 4685 (2002). https://doi.org/10.1063/1.1446660
I. Bombaci, U. Lombardo, Asymmetric nuclear matter equation of state. Phys. Rev. C 44, 1892–1900 (1991). https://doi.org/10.1103/PhysRevC.44.1892
B.-A. Li, L.-W. Chen, C.M. Ko, Recent progress and new challenges in isospin physics with heavy-ion reactions. Phys. Rep. 464(4), 113–281 (2008). https://doi.org/10.1016/j.physrep.2008.04.005
B.-A. Li, À. Ramos, G. Verde, I. Vidaña, Topical issue on nuclear symmetry energy. Eur. Phys. J. A 50, 9 (2014). https://doi.org/10.1140/epja/i2014-14009-x
M. Baldo, G.F. Burgio, The nuclear symmetry energy. Prog. Part. Nucl. Phys. 91, 203–258 (2016). https://doi.org/10.1016/j.ppnp.2016.06.006
C. Mondal, B.K. Agrawal, M. Centelles, G. Colò, X. Roca-Maza, N. Paar, X. Viñas, S.K. Singh, S.K. Patra, Model dependence of the neutron-skin thickness on the symmetry energy. Phys. Rev. C 93, 064303 (2016). https://doi.org/10.1103/PhysRevC.93.064303
X. Viñas, M. Centelles, X. Roca-Maza, M. Warda, Density dependence of the symmetry energy from neutron skin thickness in finite nuclei. Eur. Phys. J. A 50(2), 27 (2014). https://doi.org/10.1140/epja/i2014-14027-8
A. Tamii et al., Complete electric dipole response and the neutron skin in \(^{208}{\rm Pb}\). Phys. Rev. Lett. 107, 062502 (2011). https://doi.org/10.1103/PhysRevLett.107.062502
D. Adhikari et al., Precision determination of the neutral weak form factor of \(^{48}{\rm Ca}\). Phys. Rev. Lett. 129, 042501 (2022). https://doi.org/10.1103/PhysRevLett.129.042501
V. Baran, M. Colonna, V. Greco, M. Di Toro, Reaction dynamics with exotic nuclei. Phys. Rep. 410(5), 335–466 (2005). https://doi.org/10.1016/j.physrep.2004.12.004
B.P. Abbott et al., Properties of the binary neutron star merger GW 170817. Phys. Rev. X 9, 011001 (2019). https://doi.org/10.1103/PhysRevX.9.011001
B.P. Abbott, GW170817: measurements of neutron star radii and equation of state. Phys. Rev. Lett. 121, 161101 (2018). https://doi.org/10.1103/PhysRevLett.121.161101
J. Piekarewicz, F.J. Fattoyev, Impact of the neutron star crust on the tidal polarizability. Phys. Rev. C 99, 045802 (2019). https://doi.org/10.1103/PhysRevC.99.045802
G.F. Burgio, H.-J. Schulze, I. Vidaña, J.-B. Wei, Neutron stars and the nuclear equation of state. Prog. Part. Nucl. Phys. 120, 103879 (2021). https://doi.org/10.1016/j.ppnp.2021.103879
M.B. Tsang, Y. Zhang, P. Danielewicz, M. Famiano, Z. Li, W.G. Lynch, A.W. Steiner, Constraints on the density dependence of the symmetry energy. Phys. Rev. Lett. 102, 122701 (2009). https://doi.org/10.1103/PhysRevLett.102.122701
P. Russotto, S. Gannon, S. Kupny, P. Lasko et al., Results of the ASY-EOS experiment at GSI: the symmetry energy at suprasaturation density. Phys. Rev. C 94, 034608 (2016). https://doi.org/10.1103/PhysRevC.94.034608
B.T. Reed, F.J. Fattoyev, C.J. Horowitz, J. Piekarewicz, Implications of PREX-2 on the equation of state of neutron-rich matter. Phys. Rev. Lett. 126, 172503 (2021). https://doi.org/10.1103/PhysRevLett.126.172503
L.-W. Chen, C.M. Ko, B.-A. Li, J. Xu, Density slope of the nuclear symmetry energy from the neutron skin thickness of heavy nuclei. Phys. Rev. C 82, 024321 (2010). https://doi.org/10.1103/PhysRevC.82.024321
X. Roca-Maza, X. Viñas, M. Centelles, B.K. Agrawal, G. Colò, N. Paar, J. Piekarewicz, D. Vretenar, Neutron skin thickness from the measured electric dipole polarizability in \(^{68}\text{ Ni }\), \(^{120}\text{ Sn }\), and \(^{208}\text{ Pb }\). Phys. Rev. C 92, 064304 (2015). https://doi.org/10.1103/PhysRevC.92.064304
P. Danielewicz, J. Lee, Symmetry energy II: Isobaric analog states. Nucl. Phys. A 922, 1–70 (2014). https://doi.org/10.1016/j.nuclphysa.2013.11.005
A.W. Steiner, J.M. Lattimer, E.F. Brown, The neutron star mass-radius relation and the equation of state of dense matter. Astrophys J 765(1), 5 (2013). https://doi.org/10.1088/2041-8205/765/1/l5
A. Carbone, G. Colò, A. Bracco, L.-G. Cao, P.F. Bortignon, F. Camera, O. Wieland, Constraints on the symmetry energy and neutron skins from pygmy resonances in \(^{68}{\rm Ni}\) and \(^{132}{\rm Sn}\). Phys. Rev. C 81, 041301 (2010). https://doi.org/10.1103/PhysRevC.81.041301
T. Li, U. Garg et al., Isotopic dependence of the giant monopole resonance in the even-\(A\)\(^{112-124}{\rm Sn}\) isotopes and the asymmetry term in nuclear incompressibility. Phys. Rev. Lett. 99, 162503 (2007). https://doi.org/10.1103/PhysRevLett.99.162503
M. Oertel, M. Hempel, T. Klähn, S. Typel, Equations of state for supernovae and compact stars. Rev. Mod. Phys. 89, 015007 (2017). https://doi.org/10.1103/RevModPhys.89.015007
D. Adhikari et al., Accurate determination of the neutron skin thickness of \(^{208}{\rm Pb}\) through parity-violation in electron scattering. Phys. Rev. Lett. 126, 172502 (2021). https://doi.org/10.1103/PhysRevLett.126.172502
W.G. Lynch, M.B. Tsang, Decoding the density dependence of the nuclear symmetry energy. Phys. Lett. B 830, 137098 (2022). https://doi.org/10.1016/j.physletb.2022.137098. arXiv:2106.10119
G.F. Burgio, H.-J. Schulze, I. Vidaña, J.-B. Wei, A modern view of the equation of state in nuclear and neutron star matter. Symmetry (2021). https://doi.org/10.3390/sym13030400
C. Fuchs, H.H. Wolter, Modelization of the EOS. Eur. Phys. J. A (2006). https://doi.org/10.1140/epja/i2005-10313-x
W. Trautmann, High density with elliptic flows. AIP Confer. Proc. 2127, 020003 (2019). https://doi.org/10.1063/1.5117793
B.-A. Li, B.-J. Cai, W.-J. Xie, N.-B. Zhang, Progress in constraining nuclear symmetry energy using neutron star observables since GW170817. Universe 7(6), 182 (2021). https://doi.org/10.3390/universe7060182
J. Estee, W.G. Lynch, C.Y. Tsang, J. Barney, G. Jhang, M.B. Tsang, R. Wang, M. Kaneko, J.W. Lee, T. Isobe, M. Kurata-Nishimura, T. Murakami et al., Probing the symmetry energy with the spectral pion ratio. Phys. Rev. Lett. 126, 162701 (2021). https://doi.org/10.1103/PhysRevLett.126.162701
M.D. Cozma, Y. Leifels, W. Trautmann, Q. Li, P. Russotto, Toward a model-independent constraint of the high-density dependence of the symmetry energy. Phys. Rev. C 88, 044912 (2013). https://doi.org/10.1103/PhysRevC.88.044912
S. Huth, P.T.H. Pang, I. Tews, T. Dietrich, A. Le Fèvre, A. Schwenk, W. Trautmann, K. Agarwal, M. Bulla, M.W. Coughlin, C. Van Den Broeck, Constraining neutron-star matter with microscopic and macroscopic collisions. Nature 606(7913), 276–280 (2022). https://doi.org/10.1038/s41586-022-04750-w
P. Russotto, M.D. Cozma, E. De Filippo, A. Le Fèvre, Y. Leifels, J. Łukasik, Studies of the equation of state of nuclear matter by heavy-ion collisions at intermediate energy in the multi-messenger era. La Riv. del Nuovo Cim. 46, 1 (2023). https://doi.org/10.1007/s40766-023-00039-4
C.J. Horowitz, E.F. Brown, Y. Kim, W.G. Lynch, R. Michaels, A. Ono, J. Piekarewicz, M.B. Tsang, H.H. Wolter, A way forward in the study of the symmetry energy: experiment, theory, and observation. J. Phys. G: Nucl. Part. Phys. 41(9), 093001 (2014). https://doi.org/10.1088/0954-3899/41/9/093001
M.B. Tsang, J.R. Stone, F. Camera, P. Danielewicz, S. Gandolfi, K. Hebeler, C.J. Horowitz, J. Lee, W.G. Lynch, Z. Kohley, R. Lemmon, P. Möller, T. Murakami, S. Riordan, X. Roca-Maza, F. Sammarruca, A.W. Steiner, I. Vidaña, S.J. Yennello, Constraints on the symmetry energy and neutron skins from experiments and theory. Phys. Rev. C 86, 015803 (2012). https://doi.org/10.1103/PhysRevC.86.015803
J.B. Natowitz, G. Röpke, S. Typel, D. Blaschke, A. Bonasera, K. Hagel, T. Klähn, S. Kowalski, L. Qin, S. Shlomo, R. Wada, H.H. Wolter, Symmetry energy of dilute warm nuclear matter. Phys. Rev. Lett. 104, 202501 (2010). https://doi.org/10.1103/PhysRevLett.104.202501
D.V. Shetty, S.J. Yennello, G.A. Souliotis, Density dependence of the symmetry energy and the nuclear equation of state: a dynamical and statistical model perspective. Phys. Rev. C 76, 024606 (2007). https://doi.org/10.1103/PhysRevC.76.024606
D.D.S. Coupland, M. Youngs, Z. Chajecki, W.G. Lynch, M.B. Tsang, Y.X. Zhang et al., Probing effective nucleon masses with heavy-ion collisions. Phys. Rev. C 94, 011601 (2016). https://doi.org/10.1103/PhysRevC.94.011601
Z.Y. Sun, M.B. Tsang, W.G. Lynch, G. Verde, F. Amorini, L. Andronenko, M. Andronenko, G. Cardella, M. Chatterje, P. Danielewicz, E. De Filippo, P. Dinh, E. Galichet, E. Geraci, H. Hua, E. La Guidara, G. Lanzalone, H. Liu, F. Lu, S. Lukyanov, C. Maiolino, A. Pagano, S. Piantelli, M. Papa, S. Pirrone, G. Politi, F. Porto, F. Rizzo, P. Russotto, D. Santonocito, Y.X. Zhang, Isospin diffusion and equilibration for \({\rm Sn}+{\rm Sn}\) collisions at \(E/A=35\) MeV. Phys. Rev. C 82, 051603 (2010). https://doi.org/10.1103/PhysRevC.82.051603
A. Camaiani, G. Casini, S. Piantelli, A. Ono, E. Bonnet et al., Isospin diffusion measurement from the direct detection of a quasiprojectile remnant. Phys. Rev. C 103, 014605 (2021). https://doi.org/10.1103/PhysRevC.103.014605
E. De Filippo, A. Pagano, P. Russotto et al., Correlations between emission timescale of fragments and isospin dynamics in \({}^{124}\)Sn+\({}^{64}\)Ni and \({}^{112}\)Sn+\({}^{58}\)Ni reactions at 35\(A\) MeV. Phys. Rev. C 86, 014610 (2012). https://doi.org/10.1103/PhysRevC.86.014610
S. Hudan, A.B. McIntosh, R.T. de Souza et al., Tracking saddle-to-scission dynamics using \(N/Z\) in projectile breakup reactions. Phys. Rev. C 86, 021603 (2012). https://doi.org/10.1103/PhysRevC.86.021603
S. Piantelli, G. Casini, A. Ono, G. Poggi, G. Pastore et al., Isospin transport phenomena for the systems \(^{80}{\rm Kr}+^{40,48}\!{\rm Ca}\) at 35 MeV/nucleon. Phys. Rev. C 103, 014603 (2021). https://doi.org/10.1103/PhysRevC.103.014603
M. Colonna, Collision dynamics at medium and relativistic energies. Prog. Part. Nucl. Phys. 113, 103775 (2020). https://doi.org/10.1016/j.ppnp.2020.103775
A.B. McIntosh, S.J. Yennello, Interplay of neutron-proton equilibration and nuclear dynamics. Prog. Part. Nucl. Phys. 108, 103707 (2019). https://doi.org/10.1016/j.ppnp.2019.06.001
J. Rizzo, M. Colonna, V. Baran, M. Di Toro, H.H. Wolter, M. Zielinska-Pfabe, Isospin dynamics in peripheral heavy ion collisions at Fermi energies. Nucl. Phys. A 806(1), 79–104 (2008). https://doi.org/10.1016/j.nuclphysa.2008.02.307
H. Wolter, M. Colonna, D. Cozma, P. Danielewicz, C.M. Ko, R. Kumar, A. Ono, M.B. Tsang, J. Xu, Y.-X. Zhang et al., Transport model comparison studies of intermediate-energy heavy-ion collisions. Prog. Part. Nucl. Phys. 125, 103962 (2022). https://doi.org/10.1016/j.ppnp.2022.103962
E. De Filippo, A. Pagano, Experimental effects of dynamics and thermodynamics in nuclear reactions on the symmetry energy as seen by the CHIMERA 4\(\pi\) detector. Eur. Phys. J. A 50(2), 32 (2014). https://doi.org/10.1140/epja/i2014-14032-y
E. Geraci et al., Highlights from CHIMERA Collaboration. Nuovo Cim. C 45, 44 (2022). https://doi.org/10.1393/ncc/i2022-22044-5. Proceedings of the IWM-EC conference, GANIL Nov. 23–26 2021
I. Lombardo et al., Isospin transport effects in nuclear reactions at 25 MeV/nucleon. Phys. Rev. C 82, 014608 (2010). https://doi.org/10.1103/PhysRevC.82.014608
A. Pagano, E. De Filippo, E. Geraci, E.V. Pagano, P. Russotto, K. Siwek-Wilczyńska et al., Nuclear neck-density determination at Fermi energy with CHIMERA detector. Eur. Phys. J. A 56(4), 102 (2020). https://doi.org/10.1140/epja/s10050-020-00105-z
P. Russotto, E. De Filippo, E.V. Pagano et al., Dynamical versus statistical production of intermediate mass fragments at Fermi energies. Eur. Phys. J. A 56(1), 12 (2020). https://doi.org/10.1140/epja/s10050-019-00011-z
P. Russotto, E. De Filippo, A. Pagano et al., Production cross sections for intermediate mass fragments from dynamical and statistical decay of projectile-like fragments in \(^{124}{\rm Sn}+^{64}\!{\rm Ni}\) and \(^{112}{\rm Sn}+^{58}\!{\rm Ni}\) collisions at \(35\, A\) MeV. Phys. Rev. C 91, 014610 (2015). https://doi.org/10.1103/PhysRevC.91.014610
A. Jedele, A.B. McIntosh, K. Hagel, M. Huang, L. Heilborn, Z. Kohley, L.W. May, E. McCleskey, M. Youngs, A. Zarrella, S.J. Yennello, Characterizing neutron-proton equilibration in nuclear reactions with subzeptosecond resolution. Phys. Rev. Lett. 118, 062501 (2017). https://doi.org/10.1103/PhysRevLett.118.062501
J.B. Natowitz, R. Wada, K. Hagel, T. Keutgen, M. Murray, A. Makeev, L. Qin, P. Smith, C. Hamilton, Caloric curves and critical behavior in nuclei. Phys. Rev. C 65, 034618 (2002). https://doi.org/10.1103/PhysRevC.65.034618
A.B. McIntosh, A. Bonasera, P. Cammarata, K. Hagel, L. Heilborn, Z. Kohley, J. Mabiala, L.W. May, P. Marini, A. Raphelt, G.A. Souliotis, S. Wuenschel, A. Zarrella, S.J. Yennello, Asymmetry dependence of the nuclear caloric curve. Phys. Lett. B 719(4), 337–340 (2013). https://doi.org/10.1016/j.physletb.2012.12.073
S. Pirrone, G. Politi, B. Gnoffo, M. La Commara, E. De Filippo, P. Russotto, M. Trimarchi, M. Vigilante, M. Colonna, Sh.A. Kalandarov et al., Isospin influence on fragments production in \(^{78}\)Kr + \(^{40}\)Ca and \(^{86}\)Kr + \(^{48}\)Ca collisions at 10 MeV/nucleon. Eur. Phys. J. A 55(2), 22 (2019). https://doi.org/10.1140/epja/i2019-12695-4
F. Amorini, G. Cardella, A. Di Pietro, P. Figuera, G. Lanzalone, L. Jun, A. Musumarra, M. Papa, S. Pirrone, F. Rizzo, W. Tian, S. Tudisco, Statistical and preequilibrium \(\gamma\)-ray emission in heavy ion reactions at 25 MeV/nucleon. Phys. Rev. C 69, 014608 (2004). https://doi.org/10.1103/PhysRevC.69.014608
F. Amorini, G. Cardella, G. Giuliani, M. Papa et al., Isospin dependence of incomplete fusion reactions at 25 MeV/nucleon. Phys. Rev. Lett. 102, 112701 (2009). https://doi.org/10.1103/PhysRevLett.102.112701
G. Cardella, G. Giuliani, I. Lombardo, M. Papa et al., Effects of neutron richness on the behavior of nuclear systems at intermediate energies. Phys. Rev. C 85, 064609 (2012). https://doi.org/10.1103/PhysRevC.85.064609
M. Papa, T. Maruyama, A. Bonasera, Constrained molecular dynamics approach to fermionic systems. Phys. Rev. C 64, 024612 (2001). https://doi.org/10.1103/PhysRevC.64.024612
M. Papa, I. Berceanu et al., Dipolar degrees of freedom and isospin equilibration processes in heavy ion collisions. Phys. Rev. C 91, 041601 (2015). https://doi.org/10.1103/PhysRevC.91.041601
M. Papa, Many-body correlations in semiclassical molecular dynamics and Skyrme interaction. Phys. Rev. C 87, 014001 (2013). https://doi.org/10.1103/PhysRevC.87.014001
E.V. Pagano et al., Measurements of pulse shape discrimination with EJ 299-33 plastic scintillator using heavy ion reaction. Nucl. Instr. Methods A 905, 47–52 (2018). https://doi.org/10.1016/j.nima.2018.07.034
E.V. Pagano, L. Auditore, G. Cardella, E. De Filippo, E. Geraci, B. Gnoffo, G. Lanzalone, C. Maiolino, N.S. Martorana, A. Pagano, M. Papa, S. Pirrone, G. Politi, F. Rizzo, P. Russotto, M. Trimarchi, The NArCoS project: efficiency estimation and the cross talk problem studied through Monte Carlo simulations. J. Phys: Confer. Ser. 1643(1), 012037 (2020). https://doi.org/10.1088/1742-6596/1643/1/012037
Project ANCHISE (Array for Neutron and Charged particle detection with High Linear momentum Selection) funded (PRIN2020, grant. no. 2020H8YFRE) by MUR (Ministry for Universities and Research, Italy)
R. Bougault, G. Poggi, S. Barlini et al., The FAZIA project in Europe: R &D phase. Eur. Phys. J. A 50, 47 (2014). https://doi.org/10.1140/epja/i2014-14047-4
C. Ciampi, S. Piantelli, G. Casini, G. Pasquali, J. Quicray et al., First results from the INDRA-FAZIA apparatus on isospin diffusion in \(^{58,64}{\rm Ni}+^{58,64}{\rm Ni}\) systems at Fermi energies. Phys. Rev. C 106, 024603 (2022). https://doi.org/10.1103/PhysRevC.106.024603
A. Ono, Dynamics of clusters and fragments in heavy-ion collisions. Prog. Part. Nucl. Phys. 105, 139–179 (2019). https://doi.org/10.1016/j.ppnp.2018.11.001
E. Plagnol, J. Łukasik et al., Onset of midvelocity emissions in symmetric heavy ion reactions. Phys. Rev. C 61, 014606 (1999). https://doi.org/10.1103/PhysRevC.61.014606
A. Rebillard-Soulié, D. Gruyer, G. Verde et al., Study of the Hoyle state in \(^{12}\)C produced by \(^{20}\)Ne+\(^{12}\)C reactions. Nuovo Cim. C 45, 57 (2022). https://doi.org/10.1393/ncc/i2022-22057-0. Proceedings of the IWM-EC conference, GANIL Nov. 23–26 2021
B. Borderie, A.R. Raduta, G. Ademard, M.F. Rivet, E. De Filippo, E. Geraci, N. Le Neindre et al., Probing clustering in excited alpha-conjugate nuclei. Phys. Lett. B 755, 475–480 (2016). https://doi.org/10.1016/j.physletb.2016.02.061
G. Cardella, A. Bonasera, N.S. Martorana et al., Search for rare 3-\(\alpha\) decays in the region of the Hoyle state of \(^{12}\)C. Nucl. Phys. A 1020, 122395 (2022). https://doi.org/10.1016/j.nuclphysa.2022.122395
J.A. Wheeler, Molecular viewpoints in nuclear structure. Phys. Rev. 52, 1083–1106 (1937). https://doi.org/10.1103/PhysRev.52.1083
E. Wigner, On the structure of nuclei beyond oxygen. Phys. Rev. 51, 947–958 (1937). https://doi.org/10.1103/PhysRev.51.947
Y. Kanada-En’yo, Y. Kawanami, Y. Taniguchi, M. Kimura, Cluster states in 13B. Progr. Theoret. Phys. 120(5), 917–935 (2008). https://doi.org/10.1143/PTP.120.917
T. Suhara, Y. Kanada-En’yo, Cluster structures of excited states in \(^{14}\)C. Phys. Rev. C 82(4), 044301 (2010). https://doi.org/10.1103/PhysRevC.82.044301
T. Baba, M. Kimura, Three-body decay of linear-chain states in \(^{14}\)C. Phys. Rev. C 95(6), 064318 (2017). https://doi.org/10.1103/PhysRevC.95.064318
K.W. McVoy, Regge Poles and strong absorption in heavy-ion and \({\alpha }\)-nucleus scattering. Phys. Rev. C 3, 1104–1117 (1971). https://doi.org/10.1103/PhysRevC.3.1104
B. Zhou, M. Kimura, Q. Zhao, S.-h Shin, Microscopic calculations for Be isotopes within real-time evolution method. Eur. Phys. J. A 56(11), 298 (2020). https://doi.org/10.1140/epja/s10050-020-00306-6
T. Ichikawa, N. Itagaki, Optimization of basis functions for multiconfiguration mixing using the replica exchange Monte Carlo method and its application to \(^{12}{\rm C}\). Phys. Rev. C 105, 024314 (2022). https://doi.org/10.1103/PhysRevC.105.024314
M. Freer, H. Horiuchi, Y. Kanada-En’yo, D. Lee, U.-G. Meißner, Microscopic clustering in light nuclei. Rev. Mod. Phys. 90, 035004 (2018). https://doi.org/10.1103/RevModPhys.90.035004
Y. Kanada-En’yo, H. Horiuchi, Structure of light unstable nuclei studied with antisymmetrized molecular dynamics. Prog. Theor. Phys. Suppl. 142, 205 (2001). https://doi.org/10.1143/PTPS.142.205. arXiv:nucl-th/0107044
N. Itagaki, A.V. Afanasjev, D. Ray, Possibility of \(^{14}{\rm C}\) cluster as a building block of medium-mass nuclei. Phys. Rev. C 101, 034304 (2020). https://doi.org/10.1103/PhysRevC.101.034304
A.S. Demyanova, V.I. Starastsin, A.N. Danilov, A.A. Ogloblin, S.V. Dmitriev, S.A. Goncharov, T.L. Belyaeva, V.A. Maslov, Y.G. Sobolev, W. Trzaska, P. Heikkinen, G.P. Gurov, N. Burtebaev, D. Janseitov, Possible neutron and proton halo structure in the isobaric analog states of \(A=12\) nuclei. Phys. Rev. C 102, 054612 (2020). https://doi.org/10.1103/PhysRevC.102.054612
Q. Zhao, Y. Suzuki, J. He, B. Zhou, M. Kimura, \(\alpha\) clustering and neutron-skin thickness of carbon isotopes. Eur. Phys. J. A 57(5), 157 (2021). https://doi.org/10.1140/epja/s10050-021-00465-0
R. Smith, J. Bishop, J. Hirst, T. Kokalova, C. Wheldon, The Hoyle Family: the search for alpha-condensate states in light nuclei. Few-Body Syst. 61(2), 14 (2020). https://doi.org/10.1007/s00601-020-1545-5
V.M. Datar, S. Kumar, D.R. Chakrabarty, V. Nanal, E.T. Mirgule, A. Mitra, H.H. Oza, Direct observation of \({4}^{+}\)-to-\({2}^{+}\) gamma transition in \(^8\)Be. Phys. Rev. Lett. 94(12), 122502 (2005). https://doi.org/10.1103/PhysRevLett.94.122502
G. Cardella, F. Favela, N.S. Martorana, L. Acosta, A. Camaiani, E. De Filippo, N. Gelli, E. Geraci, B. Gnoffo, C. Guazzoni et al., Investigating \(\gamma\)-ray decay of excited \(^{12}\)C levels with a multifold coincidence analysis. Phys. Rev. C 104, 064315 (2021). https://doi.org/10.1103/PhysRevC.104.064315
D.J. Marín-Lámbarri, R. Bijker, M. Freer, M. Gai, T. Kokalova, D.J. Parker, C. Wheldon, Evidence for triangular \({\cal{D} }_{3h}\) symmetry in \(^{12}\)C. Phys. Rev. Lett. 113(1), 012502 (2014). https://doi.org/10.1103/PhysRevLett.113.012502
M. Freer, The clustered nucleus-cluster structures in stable and unstable nuclei. Rep. Prog. Phys. 70(12), 2149 (2007). https://doi.org/10.1088/0034-4885/70/12/r03
R. Bijker, F. Iachello, The algebraic cluster model: three-body clusters. Ann. Phys. 298(2), 334–360 (2002). https://doi.org/10.1006/aphy.2002.6255
R. Bijker, F. Iachello, Evidence for tetrahedral symmetry in \(^{16}\)O. Phys. Rev. Lett. 112(15), 152501 (2014). https://doi.org/10.1103/PhysRevLett.112.152501
P. Figuera, E.A. Maugeri et al., Development of an intense \(^{10}\)Be radioactive beam in ‘off-line mode’ at the Catania Tandem accelerator. Nucl. Inst. Methods Phys. Res. A 972, 164120 (2020). https://doi.org/10.1016/j.nima.2020.164120
W. von Oertzen, M. Freer, Y. Kanada-En’yo, Nuclear clusters and nuclear molecules. Phys. Rep. 432(2), 43–113 (2006). https://doi.org/10.1016/j.physrep.2006.07.001
A. Di Pietro, J. Fernández-García, P. Figuera, M. Fisichella, S. Heinitz, M. Lattuada, D. Torresi, M. Alcorta, M.J. García Borge, T. Davinson et al., Exotic clustering investigation in \(^{13}\)B and \(^{14}\)C using RIBs. Nuovo Cim. Soc. Ital. Fis., C 41, 186 (2019). https://doi.org/10.1393/ncc/i2018-18186-4
I. Lombardo, D. Dell’Aquila, G. Spadaccini, G. Verde, M. Vigilante, Spectroscopy of \(^{13}\)C above the \(\alpha\) threshold with \(\alpha\)+ \(^9\)Be reactions at low energies. Phys. Rev. C 97(3), 034320 (2018). https://doi.org/10.1103/PhysRevC.97.034320
D. Dell’Aquila, I. Lombardo, G. Verde, M. Vigilante, G. Ausanio, A. Ordine, M. Miranda, M. De Luca, R. Alba, L. Augey et al., OSCAR: A new modular device for the identification and correlation of low energy particles. Nucl. Instrum. Methods Phys. Res., Sect. A 877, 227–237 (2018). https://doi.org/10.1016/j.nima.2017.09.046
D. Bardayan, Transfer reactions in nuclear astrophysics. J. Phys. G: Nucl. Part. Phys. 43(4), 043001 (2016). https://doi.org/10.1088/0954-3899/43/4/043001
R.L. Kozub, D.H. Youngblood, Single-particle strengths for quasibound levels in \(^{33}\)Cl. Phys. Rev. C 5(2), 413 (1972). https://doi.org/10.1103/PhysRevC.5.413
P. Endt, Spectroscopic factors for single-nucleon transfer in the \(A\) = 21–44 region. At. Data Nucl. Data Tables 19(1), 23–61 (1977). https://doi.org/10.1016/0092-640X(77)90008-0
M.B. Tsang, J. Lee, W.G. Lynch, Survey of ground state neutron spectroscopic factors from Li to Cr isotopes. Phys. Rev. Lett. 95(22), 222501 (2005). https://doi.org/10.1103/PhysRevLett.95.222501
S. Gillespie, A. Parikh, C.J. Barton, T. Faestermann, J. José, R. Hertenberger, H.-F. Wirth, N. De Séréville, J.E. Riley, M. Williams, First measurement of the \(^{34}{\rm S}(p,{\gamma })^{35}{\rm Cl}\) reaction rate through indirect methods for presolar nova grains. Phys. Rev. C 96(2), 025801 (2017). https://doi.org/10.1103/PhysRevC.96.025801
I. Lombardo, D. Dell’Aquila, M. Cinausero, L.R. Gasques, M. Vigilante, V.A.B. Zagatto, S. Barlini, R. Bolzonella, M. Bruno, A. Buccola et al., Study of the \(^{33}\)Cl spectroscopic factors via the \(^{32}\)S(\(^3\)He, d)\(^{33}\)Cl one-proton transfer reaction. J. Phys. G: Nucl. Part. Phys. 48(6), 065101 (2021). https://doi.org/10.1088/1361-6471/abdee4
A. Di Pietro, P. Figuera, F. Amorini, C. Angulo, G. Cardella, S. Cherubini, T. Davinson, D. Leanza, J. Lu, H. Mahmud et al., Reactions induced by the halo nucleus \(^6\)He at energies around the Coulomb barrier. Phys. Rev. C 69(4), 044613 (2004). https://doi.org/10.1103/PhysRevC.69.044613
M. Cubero, J. Fernández-García, M. Rodríguez-Gallardo, L. Acosta, M. Alcorta, M. Alvarez, M. Borge, L. Buchmann, C. Diget, H. Al Falou et al., Do halo nuclei follow Rutherford elastic scattering at energies below the barrier? The case of \(^{11}{\rm Li}\). Phys. Rev. Lett. 109(26), 262701 (2012). https://doi.org/10.1103/PhysRevLett.109.262701
A. Di Pietro, G. Randisi, V. Scuderi, L. Acosta, F. Amorini, M.J.G. Borge, P. Figuera, M. Fisichella, L.M. Fraile, J. Gomez-Camacho et al., Elastic scattering and reaction mechanisms of the halo nucleus \(^{11}\)Be around the Coulomb barrier. Phys. Rev. Lett. 105(2), 022701 (2010). https://doi.org/10.1103/PhysRevLett.105.022701
A. Di Pietro, V. Scuderi, A.M. Moro, L. Acosta, F. Amorini, M.J.G. Borge, P. Figuera, M. Fisichella, L.M. Fraile, J. Gomez-Camacho et al., Experimental study of the collision \(^{11}\)Be+ \(^{64}\)Zn around the Coulomb barrier. Phys. Rev. C 85(5), 054607 (2012). https://doi.org/10.1103/PhysRevC.85.054607
R. Spartà, A. Di Pietro, P. Figuera, O. Tengblad, A.M. Moro, I. Martel, J.P. Fernández-García, J. Lei, L. Acosta, M.J.G. Borge et al., Probing proton halo effects in the \(^8\)B+ \(^{64}\)Zn collision around the Coulomb barrier. Phys. Lett. B 820, 136477 (2021). https://doi.org/10.1016/j.physletb.2021.136477
Y.Y. Yang, X. Liu, D.Y. Pang, D. Patel, R.F. Chen, J.S. Wang, P. Ma, J.B. Ma, S.L. Jin, Z. Bai et al., Elastic scattering of the proton drip line nuclei \(^7\)Be, \(^8\)B, and \(^9\)C on a lead target at energies around three times the Coulomb barriers. Phys. Rev. C 98(4), 044608 (2018). https://doi.org/10.1103/PhysRevC.98.044608
F. Käppeler, F.-K. Thielemann, M. Wiescher, Current quests in nuclear astrophysics and experimental approaches. Annu. Rev. Nucl. Part. Sci. 48, 175–251 (1998). https://doi.org/10.1146/annurev.nucl.48.1.175
M.R. Mumpower, R. Surman, G.C. McLaughlin, A. Aprahamian, The impact of individual nuclear properties on r-process nucleosynthesis. Prog. Part. Nucl. Phys. 86, 86–126 (2016). https://doi.org/10.1016/j.ppnp.2015.09.001. arXiv:1508.07352 [nucl-th]
A. Sobiczewski, F.A. Gareev, B.N. Kalinkin, Closed shells for Z \(>\) 82 and N \(>\) 126 in a diffuse potential well. Phys. Lett. 22, 500 (1966). https://doi.org/10.1016/0031-9163(66)91243-1
Y.T. Oganessian, V.K. Utyonkov, Super-heavy element research. Rep. Prog. Phys. 78, 036301 (2015). https://doi.org/10.1088/0034-4885/78/3/036301
Y.T. Oganessian et al., Synthesis of the isotopes of elements 118 and 116 in the \(^{249}{\rm Cf}\) and \(^{245}{\rm Cm}+^{48}\!{\rm Ca}\) fusion reactions. Phys. Rev. C 74, 044602 (2006). https://doi.org/10.1103/PhysRevC.74.044602
K. Morita et al., New result in the production and decay of an isotope, \(^{278}\)113, of the 113th element. J. Phys. Soc. Jpn. 81, 103201 (2012). https://doi.org/10.1143/JPSJ.81.103201
P.J. Karol, R.C. Barber, B.M. Sherrill, E. Vardaci, T. Yamazaki, Discovery of the elements with atomic number \(Z\) = 113, 115 and 117 (IUPAC technical report). Pure Appl. Chem. 88, 139 (2016). https://doi.org/10.1515/pac-2015-0502
P.J. Karol, R.C. Barber, B.M. Sherrill, E. Vardaci, T. Yamazaki, Discovery of the element with atomic number \(Z\) = 118 completing the 7th row of the periodic table (IUPAC technical report). Pure Appl. Chem. 88, 155 (2016). https://doi.org/10.1515/pac-2015-0501
Y.T. Oganessian, Heaviest nuclei from \(^{48}\)Ca-induced reactions. J. Phys. G: Nucl. Part. Phys. 34, 165 (2007). https://doi.org/10.1088/0954-3899/34/4/r01
M.G. Itkis, E. Vardaci, I.M. Itkis, G.N. Knyazheva, E.M. Kozulin, Fusion and fission of heavy and superheavy nuclei (experiment). Nucl. Phys. A 944, 204–237 (2015). https://doi.org/10.1016/j.nuclphysa.2015.09.007
E. Vardaci, M.G. Itkis, I.M. Itkis, G.N. Knyazheva, E.M. Kozulin, Fission and quasifission toward the superheavy mass region. J. Phys. G: Nucl. Part. Phys. 46, 103002 (2019). https://doi.org/10.1088/1361-6471/ab3118
V.I. Zagrebaev, W. Greiner, Production of heavy trans-target nuclei in multinucleon transfer reactions. Phys. Rev. C 87, 034608 (2013). https://doi.org/10.1103/PhysRevC.87.034608
M. Schädel et al., Isotope distributions in the reaction of \(^{238}\)U with \(^{238}\)U. Phys. Rev. Lett. 41, 469 (1978). https://doi.org/10.1103/PhysRevLett.41.469
M. Schädel et al., Actinide production in collisions of \(^{238}\)U with \(^{248}\)Cm. Phys. Rev. Lett. 48, 852 (1982). https://doi.org/10.1103/PhysRevLett.48.852
J. Töke et al., Quasi-fission—the mass-drift mode in heavy-ion reactions. Nucl. Phys. A 440, 327 (1985). https://doi.org/10.1016/0375-9474(85)90344-6
J.V. Kratz, W. Loveland, K.J. Moody, Syntheses of transuranium isotopes with atomic numbers Z \(\le\) 103 in multi-nucleon transfer reactions. Nucl. Phys. A 944, 117 (2015). https://doi.org/10.1016/j.nuclphysa.2015.06.004
A.V. Karpov, A. Kelic, K.H. Schmidt, On the topographical properties of fission barriers. J. Phys. G: Nucl. Part. Phys. 35, 035104 (2008). https://doi.org/10.1088/0954-3899/35/3/035104
V.M. Strutinsky, “Shells’’ in deformed nuclei. Nucl. Phys. A 122, 1 (1968). https://doi.org/10.1016/0375-9474(68)90699-4
U. Brosa, S. Grossmann, A. Muller, Nuclear scission. Phys. Rep. 197, 167–262 (1990). https://doi.org/10.1016/0370-1573(90)90114-H
M.G. Itkis, V.N. Okolovich, A.Y. Rusanov, G.N. Smirenkin, Asymmetric fission of the pre-actinide nuclei. Z. Phys. A 320, 433 (1985). https://doi.org/10.1007/BF01415720
D. Rochman, I. Tsekhanovich, F. Gönnenwein, V. Sokolov, F. Storrer, G. Simpson, O. Serot, Super-asymmetric fission in the \(^{245}\)Cm(n\(_{th}\), f) reaction at the Lohengrin fission-fragment mass separator. Nucl. Phys. A 735, 3 (2004). https://doi.org/10.1016/j.nuclphysa.2004.01.121
I.M. Itkis, M.G. Itkis, G.N. Knyazheva, E.M. Kozulin, T.A. Loktev, K.V. Novikov, F. Hanappe, E. Vardaci, Bimodal fission of Hs\(^{*}\). J. Phys. Confer. Ser. 515, 012008 (2014). https://doi.org/10.1088/1742-6596/515/1/012008
C. Engelmann et al., Production and identification of heavy Ni isotopes: evidence for the doubly magic nucleus \(^{78}\)Ni. Z. Phys. A 352, 351 (1995). https://doi.org/10.1007/BF01299748
V.I. Zagrebaev, W. Greiner, Production of heavy and superheavy neutron-rich nuclei in transfer reactions. Phys. Rev. C 83, 044618 (2011). https://doi.org/10.1103/PhysRevC.83.044618
E.M. Kozulin, E. Vardaci et al., Mass distributions of the system \(^{136}\)Xe + \(^{208}\)Pb at laboratory energies around the Coulomb barrier: a candidate reaction for the production of neutron-rich nuclei at \(N\) = 126. Phys. Rev. C 86, 044611 (2012). https://doi.org/10.1103/PhysRevC.86.044611
A.V. Karpov, V.V. Saiko, Modeling near-barrier collisions of heavy ions based on a Langevin-type approach. Phys. Rev. C 96, 024618 (2017). https://doi.org/10.1103/PhysRevC.96.024618
V.V. Saiko, A.V. Karpov, Analysis of multinucleon transfer reactions with spherical and statically deformed nuclei using a Langevin-type approach. Phys. Rev. C 99, 014613 (2019). https://doi.org/10.1103/PhysRevC.99.014613
C. Borcea et al., Alpha-particle energy spectra measured at forward angles in heavy-ion induced reactions. Nucl. Phys. A 351, 312 (1981). https://doi.org/10.1016/0375-9474(81)90447-4
C. Borcea et al., Emission of high-energy charged particles at zero degrees in Ne-induced reactions. Nucl. Phys. A 391, 520 (1982). https://doi.org/10.1016/0375-9474(82)90623-6
C. Borcea et al., Angular and energy dependences of emission probability for light particles in \(^{22}\)Ne-induced reactions at 8 MeV/nucleon. Nucl. Phys. A 415, 169 (1984). https://doi.org/10.1016/0375-9474(84)90605-5
C. Borcea et al., Superheavy elements: a new Paradigm, inProceedings of the International Symposium On Exotic Nuclei 2016 Kazan, Russia (World Scientific, 2016), p. 132. https://doi.org/10.1142/9789813226548_0021. ISBN 978-9813226531
J. Engel, J. Menéndez, Status and future of nuclear matrix elements for neutrinoless double-beta decay: a review. Rep. Prog. Phys. 80(4), 046301 (2017). https://doi.org/10.1088/1361-6633/aa5bc5
F. Osterfeld, Nuclear spin and isospin excitations. Rev. Mod. Phys. 64, 491–557 (1992). https://doi.org/10.1103/RevModPhys.64.491
M.N. Harakeh, A. van der Woude, Giant Resonances. Fundamental High-Frequency Modes of Nuclear Excitations (Clarendon Press, Oxford, 1992)
M. Ichimura, H. Sakai, T. Wakasa, Spin-isospin responses via (p, n) and (n, p) reactions. Prog. Part. Nucl. Phys. 56(2), 446–531 (2006). https://doi.org/10.1016/j.ppnp.2005.09.001
Y. Fujita, B. Rubio, W. Gelletly, Spin-isospin excitations probed by strong, weak and electro-magnetic interactions. Prog. Part. Nucl. Phys. 66(3), 549–606 (2011). https://doi.org/10.1016/j.ppnp.2011.01.056
H. Lenske, F. Cappuzzello, M. Cavallaro, M. Colonna, Heavy ion charge exchange reactions as probes for nuclear \(\beta\)-decays. Prog. Part. Nucl. Phys. 109, 103716 (2019). https://doi.org/10.1016/j.ppnp.2019.103716
N. Shimizu, J. Menéndez, K. Yako, Double gamow-teller transitions and its relation to neutrinoless \({\beta }{\beta }\) decay. Phys. Rev. Lett. 120, 142502 (2018). https://doi.org/10.1103/PhysRevLett.120.142502
E. Santopinto, H. García-Tecocoatzi, R.I. Magaña Vsevolodovna, J. Ferretti, Heavy-ion double-charge-exchange and its relation to neutrinoless double-\({\beta }\) decay. Phys. Rev. C 98, 061601 (2018). https://doi.org/10.1103/PhysRevC.98.061601
B. Romeo, J. Menéndez, C.P.N.: \({\gamma }{\gamma }\) decay as a probe of neutrinoless \({\beta }{\beta }\) decay nuclear matrix elements. Phys. Lett. B 827, 136965 (2022). https://doi.org/10.1016/j.physletb.2022.136965
H. Lenske, H.H. Wolter, H.G. Bohlen, Reaction mechanism of heavy-ion charge-exchange scattering at intermediate energies. Phys. Rev. Lett. 62, 1457–1460 (1989). https://doi.org/10.1103/PhysRevLett.62.1457
F. Cappuzzello, H. Lenske, M. Cavallaro, C. Agodi, N. Auerbach, J.I. Bellone, R. Bijker, S. Burrello, S. Calabrese, D. Carbone, M. Colonna, G. De Gregorio, J.L. Ferreira, D. Gambacurta, H. García-Tecocoatzi, A. Gargano, J.A. Lay, R. Linares, J. Lubian, E. Santopinto, O. Sgouros, V. Soukeras, A. Spatafora, Shedding light on nuclear aspects of neutrinoless double beta decay by heavy-ion double charge exchange reactions. Prog. Part. Nucl. Phys. 128, 103999 (2023). https://doi.org/10.1016/j.ppnp.2022.103999
J.L. Ferreira, J. Lubian, F. Cappuzzello, M. Cavallaro, D. Carbone, Multinucleon transfer in the \(^{116}{\rm Cd}(^{20}{\rm Ne},^{20}{\rm O})^{116}{\rm Sn}\) double charge exchange reaction at 306 \({\rm MeV}\) incident energy. Phys. Rev. C 105, 014630 (2022). https://doi.org/10.1103/PhysRevC.105.014630
J.I. Bellone, S. Burrello, M. Colonna, J.A. Lay, H. Lenske, Two-step description of heavy ion double charge exchange reactions. Phys. Lett. B 807, 135528 (2020). https://doi.org/10.1016/j.physletb.2020.135528
H. Lenske, J. Bellone, M. Colonna, D. Gambacurta, Nuclear matrix elements for heavy ion sequential double charge exchange reactions. Universe 7(4), 98 (2021). https://doi.org/10.3390/universe7040098. arXiv:2104.05472 [nucl-th]
H. Lenske, Probing double beta-decay by heavy ion charge exchange reactions. J. Phys: Confer. Ser. 1056, 012030 (2018). https://doi.org/10.1088/1742-6596/1056/1/012030
D. Torresi, O. Sgouros, V. Soukeras, M. Cavallaro, F. Cappuzzello, D. Carbone, C. Agodi, G.A. Brischetto, S. Calabrese, I. Ciraldo, N. Deshmukh, A. Hacisalihoglu, L.L. Fauci, A. Spatafora, Numen collaboration: an upgraded focal plane detector for the MAGNEX spectrometer. Nucl. Inst. and Methods A 989, 164918 (2021). https://doi.org/10.1016/j.nima.2020.164918
C. Agodi et al., The numen project: Toward new experiments with high-intensity beams. Universe (2021). https://doi.org/10.3390/universe7030072
M. Cortesi, S. Rost, W. Mittig, Y. Ayyad-Limonge, D. Bazin, J. Yurkon, A. Stolz, Multi-layer thick gas electron multiplier \({\rm (M-THGEM)}\): a new \({\rm MPGD}\) structure for high-gain operation at low-pressure. Rev. Sci. Instrum. 88(1), 013303 (2017). https://doi.org/10.1063/1.4974333
F. Iazzi, S. Ferrero, R. Introzzi, F. Pinna, L. Scaltrito, D. Calvo, M. Fisichella, C. Agodi, F. Cappuzzello, D. Carbone, M. Cavallaro, A new cooling technique for targets operating under very intense beams. WIT Trans. Eng. Sci. 116, 61–70 (2017). https://doi.org/10.2495/MC170071
F. Pinna, V. Capirossi, F. Delaunay, F. Iazzi, O. Brunasso, D. Calvo, M. Fisichella, Tests of a cooling system for thin targets submitted to intense ion beams for the NUMEN experiment. Acta Phys. Pol., B 51(3), 655 (2020). https://doi.org/10.5506/APhysPolB.51.655
M. Cavallaro, G. Santagati, F. Cappuzzello, D. Carbone, R. Linares et al., Charge-state distributions of \(^{20}\)Ne ions emerging from thin foils. Results Phys. 13, 102191 (2019). https://doi.org/10.1016/j.rinp.2019.102191
D. Carbone, J.L. Ferreira, S. Calabrese, F. Cappuzzello, M. Cavallaro et al., Analysis of two-nucleon transfer reactions in the \(^{20}{\rm Ne}+^{116}{\rm Cd}\) system at 306 MeV. Phys. Rev. C 102, 044606 (2020). https://doi.org/10.1103/PhysRevC.102.044606
S. Burrello, S. Calabrese, F. Cappuzzello, D. Carbone, M. Cavallaro et al., Multichannel experimental and theoretical constraints for the \(^{116}{\rm Cd}(^{20}{\rm Ne},^{20}{\rm F})^{116}{\rm In}\) charge exchange reaction at 306 mev. Phys. Rev. C 105, 024616 (2022). https://doi.org/10.1103/PhysRevC.105.024616
M. Cavallaro, J.I. Bellone, S. Calabrese, C. Agodi, S. Burrello et al., A constrained analysis of the \(^{40}\)Ca(\(^{18}\)O, \(^{18}\)F)\(^{40}\)K direct charge exchange reaction mechanism at 275 \({\rm MeV}\). Front. Astron. Sp. Sci. 8, 61 (2021). https://doi.org/10.3389/fspas.2021.659815
J.L. Ferreira, D. Carbone, M. Cavallaro, N.N. Deshmukh, C. Agodi et al., Analysis of two-proton transfer in the \(^{40}{\rm Ca}(^{18}{\rm O},^{20}{\rm Ne})^{38}{\rm Ar}\) reaction at 270 mev incident energy. Phys. Rev. C 103, 054604 (2021). https://doi.org/10.1103/PhysRevC.103.054604
S. Calabrese, M. Cavallaro, D. Carbone, F. Cappuzzello, C. Agodi et al., \(^{18}{\rm O}\)-induced single-nucleon transfer reactions on \(^{40}{\rm Ca}\) at \(15.3A\) MeV within a multichannel analysis. Phys. Rev. C 104, 064609 (2021). https://doi.org/10.1103/PhysRevC.104.064609
O. Sgouros, M. Cavallaro, F. Cappuzzello, D. Carbone, C. Agodi et al., One-proton transfer reaction for the \(^{18}{\rm O}+^{48}{\rm Ti}\) system at 275 MeV. Phys. Rev. C 104, 034617 (2021). https://doi.org/10.1103/PhysRevC.104.034617
O. Sgouros, A multi-channel approach in the study of the \({}^{18}\)O+ \({}^{18}\)Ti reaction within the NUMEN project. Nuovo Cim. Soc. Ital. Fis. 45(4), 70 (2022). https://doi.org/10.1393/ncc/i2022-22070-3
G. Brischetto, Data reduction of the \({}^{18}\)O + \({}^{48}\)Ti elastic and inelastic scattering at 275 MeV in the context of the NUMEN project. Nuovo Cim. Soc. Ital. Fis. 45(5), 96 (2022). https://doi.org/10.1393/ncc/i2022-22096-5
A. Spatafora et al., A full-comprehensive experimental and theoretical approach applied to the \({}^{12}\)C(\({}^{18}\)O,\({}^{18}\)F)\({}^{12}\)B single charge-exchange reaction at 15.3 AMeV. Nuovo Cim. Soc. Ital. Fis. 45(5), 131 (2022). https://doi.org/10.1393/ncc/i2022-22131-7
V. Soukeras, F. Cappuzzello, D. Carbone, M. Cavallaro, C. Agodi, L. Acosta, I. Boztosun, G.A. Brischetto, S. Calabrese, D. Calvo, E.R. Chávez Lomelí, I. Ciraldo, M. Cutuli, F. Delaunay, P. Finocchiaro, M. Fisichella, A. Foti, A. Hacisalihoglu, F. Iazzi, L.L. Fauci, G. Lanzalone, R. Linares, J.R.B. Oliveira, A. Pakou, L. Pandola, H. Petrascu, F. Pinna, G. Russo, O. Sgouros, S.O. Solakci, G. Souliotis, A. Spatafora, D. Torresi, S. Tudisco, A. Yildirim, V.A.B. Zagatto, Numen collaboration: measurement of the double charge exchange reaction for the \(^{20}\)Ne + \(^{130}\)Te system at 306 MeV. Results Phys. 28, 104691 (2021). https://doi.org/10.1016/j.rinp.2021.104691
S. Calabrese, F. Cappuzzello, D. Carbone, M. Cavallaro, C. Agodi, L. Acosta, D. Bonanno, D. Bongiovanni, T. Borello-Lewin, I. Boztosun, D. Calvo, E.R. Chàvez Lomeli, N. Deshmukh, P.N. de Faria, P. Finocchiaro, M. Fisichella, A. Foti, G. Gallo, A. Hacisalihoglu, F. Iazzi, R. Introzzi, G. Lanzalone, R. Linares, F. Longhitano, D. Lo Presti, N. Medina, A. Muoio, J.R.B. Oliveira, A. Pakou, L. Pandola, F. Pinna, S. Reito, G. Russo, G. Santagati, O. Sgouros, S.O. Solakci, V. Soukeras, G. Souliotis, A. Spatafora, D. Torresi, S. Tudisco, A. Yildirim, V.A.B. Zagatto, First measurement of the (116) Cd((20) Ne, (20) O)(116) Sn reaction at 15 A MeV. Acta Phys. Pol., B 49(3), 275 (2018). https://doi.org/10.5506/APhysPolB.49.275
J. Kramp, D. Habs, R. Kroth, M. Music, J. Schirmer, D. Schwalm, C. Broude, Nuclear two-photon decay in 0 \(^{+}{\rightarrow }0 ^{+}\) transitions. Nucl. Phys. A 474(2), 412–450 (1987). https://doi.org/10.1016/0375-9474(87)90625-7
C. Walz, H. Scheit, N. Pietralla, T. Aumann, R. Lefol, V.Y. Ponomarev, Observation of the competitive double-gamma nuclear decay. Nature 526, 406. https://doi.org/10.1038/nature15543
P.A. Söderström et al., Electromagnetic character of the competitive \(\gamma \gamma /\gamma\)-decay from \(^{137m}\)Ba. Nat. Commun. 11(1), 3242 (2020). https://doi.org/10.1038/s41467-020-16787-4. arXiv:2001.00554 [nucl-ex]
L. Coraggio, N. Itaco, Perturbative approach to effective shell-model Hamiltonians and operators. Front. Phys. 8, 325 (2020). https://doi.org/10.3389/fphy.2020.00345
L. Coraggio, N. Itaco, G. De Gregorio, A. Gargano et al., Present status of nuclear shell-model calculations of \({0\nu \beta \beta }\) decay matrix elements. Universe 6(12), 233 (2020). https://doi.org/10.3390/universe6120233
R.A. Sen’kov, M. Horoi, Neutrinoless double-\({\beta }\) decay of \({}^{48}\)ca in the shell model: closure versus nonclosure approximation. Phys. Rev. C 88, 064312 (2013). https://doi.org/10.1103/PhysRevC.88.064312
L. Coraggio, A. Gargano, N. Itaco, R. Mancino, F. Nowacki, Calculation of the neutrinoless double-\({\beta }\) decay matrix element within the realistic shell model. Phys. Rev. C 101, 044315 (2020). https://doi.org/10.1103/PhysRevC.101.044315
P. Ring, P. Schuck, The Nuclear Many-body Problem (Springer, New York, 1980)
X. Roca-Maza, N. Paar, Nuclear equation of state from ground and collective excited state properties of nuclei. Prog. Part. Nucl. Phys. 101, 96–176 (2018). https://doi.org/10.1016/j.ppnp.2018.04.001
N. Paar, D. Vretenar, E. Khan, G. Colò, Exotic modes of excitation in atomic nuclei far from stability. Rep. Prog. Phys. 70, 02 (2007). https://doi.org/10.1088/0034-4885/70/5/r02
X. Roca-Maza, G. Colò, H. Sagawa, New skyrme interaction with improved spin-isospin properties. Phys. Rev. C 86, 031306 (2012). https://doi.org/10.1103/PhysRevC.86.031306
S. Shen, G. Colò, X. Roca-Maza, Skyrme functional with tensor terms from ab initio calculations of neutron-proton drops. Phys. Rev. C 99, 034322 (2019). https://doi.org/10.1103/PhysRevC.99.034322
G. Colò, N. Van Giai, P.F. Bortignon, R.A. Broglia, Escape and spreading properties of charge-exchange resonances in \(^{208}{\rm Bi}\). Phys. Rev. C 50, 1496–1508 (1994). https://doi.org/10.1103/PhysRevC.50.1496
G.C.P.F. Bortignon, Qrpa plus phonon coupling model and the photoabsorption cross section for 18,20,22O. Nucl. Phys. A 696(3), 427–441 (2001). https://doi.org/10.1016/S0375-9474(01)01217-9
D. Gambacurta, M. Grasso, J. Engel, Subtraction method in the second random-phase approximation: first applications with a skyrme energy functional. Phys. Rev. C 92, 034303 (2015). https://doi.org/10.1103/PhysRevC.92.034303
E. Litvinova, P. Ring, V. Tselyaev, Relativistic quasiparticle time blocking approximation: dipole response of open-shell nuclei. Phys. Rev. C 78, 014312 (2008). https://doi.org/10.1103/PhysRevC.78.014312
V.G. Soloviev, Theory of Atomic Nuclei: Quasiparticles and Phonons (Institute of Physics, Bristol, 1992)
Y.F. Niu, Z.M. Niu, G. Colò, E. Vigezzi, Particle-vibration coupling effect on the \({\beta }\) decay of magic nuclei. Phys. Rev. Lett. 114, 142501 (2015). https://doi.org/10.1103/PhysRevLett.114.142501
D. Gambacurta, M. Grasso, J. Engel, Gamow-teller strength in \(^{48}{\rm Ca}\) and \(^{78}{\rm Ni}\) with the charge-exchange subtracted second random-phase approximation. Phys. Rev. Lett. 125, 212501 (2020). https://doi.org/10.1103/PhysRevLett.125.212501
C. Robin, E. Litvinova, Nuclear response theory for spin-isospin excitations in a relativistic quasiparticle-phonon coupling framework. Phys. Rev. C 52, 205 (2016). https://doi.org/10.1140/epja/i2016-16205-0
F. Iachello, A. Arima, The Interacting Boson Model. Cambridge Monographs on Mathematical Physics (Cambridge University Press, 2006). https://doi.org/10.1017/CBO9780511895517
T. Otsuka, A. Arima, F. Iachello, Nuclear shell model and interacting bosons. Nucl. Phys. A 309, 1–33 (1978). https://doi.org/10.1016/0375-9474(78)90532-8
C.E. Alonso et al., A calculation of low-lying collective states in odd-even nuclei. Phys. Lett. B 144, 141–144 (1984). https://doi.org/10.1016/0370-2693(84)91790-8
J.M. Arias, C.E. Alonso, R. Bijker, Description of the odd-even xenon and cesium isotopes in the proton-neutron interacting boson-fermion model. Nucl. Phys. A 445, 333–349 (1985). https://doi.org/10.1016/0375-9474(85)90073-9
S. Brant, V. Paar, Zeit. Phys. A 329, 151 (1988)
N. Yoshida, F. Iachello, Two neutrino double-\(\beta\) decay in the interacting boson-fermion model. PTEP 2013, 043–01 (2013). https://doi.org/10.1093/ptep/ptt007. arXiv:1301.7172 [nucl-th]
R. Magaña Vsevolodovna, E. Santopinto, R. Bijker, Transfer reactions between odd-odd and even-even nuclei by using IBFFM. arXiv:2101.05659, accepted by Phys. Rev. C
B. Paes, G. Santagati, R.M. Vsevolodovna, F. Cappuzzello et al., Long-range versus short-range correlations in the two-neutron transfer reaction \(^{64}{\rm Ni}(^{18}{\rm O},^{16}{\rm O})^{66}{\rm Ni}\). Phys. Rev. C 96, 044612 (2017). https://doi.org/10.1103/PhysRevC.96.044612
G.C. Baldwin, G.S. Klaiber, Photo-fission in heavy elements. Phys. Rev. 71, 3–10 (1947). https://doi.org/10.1103/PhysRev.71.3
M. Goldhaber, E. Teller, On nuclear dipole vibrations. Phys. Rev. 74, 1046–1049 (1948). https://doi.org/10.1103/PhysRev.74.1046
H. Steinwedel, J.J.H. Jensen, Hydrodynamik von kerndipolschwingungen. Z. Naturforsch. 5a, 413–420 (1950)
E. Migneco et al., MEDEA: a multi element detector array for gamma ray and light charged particle detection at the LNS-Catania. Nucl. Inst. Methods Phys. Res. A 314(1), 31–55 (1992). https://doi.org/10.1016/0168-9002(92)90497-R
A. Musumarra et al., Trasma, a detector for \(\gamma\)-charged particle coincidences. Nucl. Instrum. Methods Phys. Res., Sect. A 370(2), 558–562 (1996). https://doi.org/10.1016/0168-9002(95)00819-5
D.M. Brink, A. Dellafiore, M. Di Toro, Nucl. Phys. A 456, 205–234 (1986). https://doi.org/10.1016/0375-9474(86)90390-8
G.F. Burgio, M. Di Toro, Nuclear collective motions in a self-consistent Landau–Vlasov approach. Nucl. Phys. A 476, 189–212 (1988). https://doi.org/10.1016/0375-9474(88)90480-0
M. Papa, W. Tian, G. Giuliani et al., Pre-equilibrium \({\gamma }\)-ray emission induced in the \(^{40}{\rm Ca}+^{48}\!{\rm Ca}\) system at 10 MeV/nucleon and isospin equilibration processes. Phys. Rev. C 72, 064608 (2005). https://doi.org/10.1103/PhysRevC.72.064608
D. Pierroutsakou, B. Martin et al., Evolution of the prompt dipole \({\gamma }\)-ray emission with incident energy in fusion reactions. Phys. Rev. C 71, 054605 (2005). https://doi.org/10.1103/PhysRevC.71.054605
D. Pierroutsakou, B. Martin et al., Dynamical dipole mode in fusion reactions at 16 MeV/nucleon and beam energy dependence. Phys. Rev. C 80, 024612 (2009). https://doi.org/10.1103/PhysRevC.80.024612
A. Corsi, O. Wieland, V.L. Kravchuk et al., Excitation of the dynamical dipole in the charge asymmetric reaction \(^{16}\)O+\(^{116}\)Sn. Phys. Lett. B 679(3), 197–202 (2009). https://doi.org/10.1016/j.physletb.2009.07.045
N.S. Martorana, G. Cardella, E.G. Lanza et al., First measurement of the isoscalar excitation above the neutron emission threshold of the Pygmy Dipole Resonance in \(^{68}\)Ni. Phys. Lett. B 782, 112–116 (2018). https://doi.org/10.1016/j.physletb.2018.05.019
L. Pellegri et al., private communication
A. Bracco, F.C.L. Crespi, E.G. Lanza, Gamma decay of pygmy states from inelastic scattering of ions. Eur. Phys. J. A 51(8), 99 (2015). https://doi.org/10.1140/epja/i2015-15099-6
A. Bracco, E.G. Lanza, A. Tamii, Isoscalar and isovector dipole excitations: nuclear properties from low-lying states and from the isovector giant dipole resonance. Prog. Part. Nucl. Phys. 106, 360–433 (2019). https://doi.org/10.1016/j.ppnp.2019.02.001
D. Savran, T. Aumann, A. Zilges, Experimental studies of the pygmy dipole resonance. Prog. Part. Nucl. Phys. 70, 210–245 (2013). https://doi.org/10.1016/j.ppnp.2013.02.003
O. Wieland, A. Bracco, F. Camera et al., Search for the pygmy dipole resonance in \(^{68}\)Ni at \(600\) MeV nucleon. Phys. Rev. Lett. 102, 092502 (2009). https://doi.org/10.1103/PhysRevLett.102.092502
D.M. Rossi et al., Measurement of the dipole polarizability of the unstable neutron-rich nucleus \(^{68}{\rm Ni}\). Phys. Rev. Lett. 111, 242503 (2013). https://doi.org/10.1103/PhysRevLett.111.242503
A. Pagano et al., Fragmentation studies with the CHIMERA detector at LNS in Catania: recent progress. Nucl. Phys. A 734, 504–511 (2004). https://doi.org/10.1016/j.nuclphysa.2004.01.093
M. Papa, A. Bonanno et al., Coherent and incoherent giant dipole resonance \({\gamma }\)-ray emission induced by heavy ion collisions: study of the \({}^{40}{\rm Ca}{+}^{48}{\rm Ca}\) system by means of the constrained molecular dynamics model. Phys. Rev. C 68, 034606 (2003). https://doi.org/10.1103/PhysRevC.68.034606
M. Papa, Cluster production and nuclear dynamics. J. Phys: Confer. Ser. 863, 012056 (2017). https://doi.org/10.1088/1742-6596/863/1/012056
G. Giuliani, M. Papa, Nucleon-nucleon symmetry potential term and giant dipole resonance \({\gamma }\)-ray emission. Phys. Rev. C 73, 031601 (2006). https://doi.org/10.1103/PhysRevC.73.031601
N.K. Glendenning, Equation of state from nuclear and astrophysical evidence. Phys. Rev. C 37, 2733–2743 (1988). https://doi.org/10.1103/PhysRevC.37.2733
G. Colò, N. Van Giai, J. Meyer, K. Bennaceur, P. Bonche, Microscopic determination of the nuclear incompressibility within the nonrelativistic framework. Phys. Rev. C 70, 024307 (2004). https://doi.org/10.1103/PhysRevC.70.024307
X. Chen, Y.-W. Lui, H.L. Clark, Y. Tokimoto, D.H. Youngblood, Giant resonances in \(^{116}{\rm Sn}\) from 240 MeV \(^{6}{\rm Li}\) scattering. Phys. Rev. C 79, 024320 (2009). https://doi.org/10.1103/PhysRevC.79.024320
M. Cavallaro, C. Agodi et al., The magnex magnetic spectrometer for double charge exchange reactions. Nucl. Inst. Methods Phys. Res. B 463, 334–338 (2020). https://doi.org/10.1016/j.nimb.2019.04.069
F. Cappuzzello, D. Carbone, M. Cavallaro, Measuring the ions momentum vector with a large acceptance magnetic spectrometer. Nucl. Instr. Methods A 638(1), 74–82 (2011). https://doi.org/10.1016/j.nima.2011.02.045
D. Santonocito, Y. Blumenfeld, The hot GDR revisited. Eur. Phys. J. A 56(11), 279 (2020). https://doi.org/10.1140/epja/s10050-020-00279-6
A. Bracco, J.J. Gaardhøje et al., Saturation of the width of the giant dipole resonance at high temperature. Phys. Rev. Lett. 62(18), 2080–2083 (1989). https://doi.org/10.1103/PhysRevLett.62.2080
O. Wieland, A. Bracco, F. Camera et al., Giant dipole resonance in the hot and thermalized Ce132 nucleus: damping of collective modes at finite temperature. Phys. Rev. Lett. 97(1), 012501 (2006). https://doi.org/10.1103/PhysRevLett.97.012501
M. Ciemała, M. Kmiecik, A. Maj, K. Mazurek, A. Bracco, V.L. Kravchuk et al., Giant dipole resonance built on hot rotating nuclei produced during evaporation of light particles from the \(^{88}\)Mo compound nucleus. Phys. Rev. C 91(5), 054313 (2015). https://doi.org/10.1103/PhysRevC.91.054313
D. Santonocito, Y. Blumenfeld, C. Maiolino et al., Mapping the demise of collective motion in nuclei at high excitation energy. Phys. Lett. B 782, 427–432 (2018). https://doi.org/10.1016/j.physletb.2018.05.052
B. Dey, S.-S. Wang, D. Pandit et al., Exotic nuclear shape due to cluster formation at high angular momentum. Phys. Rev. C 102(3), 031301 (2020). https://doi.org/10.1103/PhysRevC.102.031301
C.E. Rolfs, W.S. Rodney, D.D. Clayton, Cauldrons in the Cosmos. Am. J. Phys. 57(2), 188–189 (1989). https://doi.org/10.1119/1.16074
L. Lamia, C. Spitaleri, E. Tognelli et al., Astrophysical impact of the updated \(^{9}\)Be(p,\({{\alpha }}\))\(^{6}\)Li and \(^{10}\)B(p,\({\alpha }\))\(^{7}\)Be reaction rates as deduced by THM. Astrophys. J. 811(2), 99 (2015). https://doi.org/10.1088/0004-637X/811/2/99
C. Spitaleri et al., Nuclear astrophysics and the Trojan Horse Method. Eur. Phys. J. A 52(4), 77 (2016). https://doi.org/10.1140/epja/i2016-16077-2
C. Spitaleri et al., Astrophysics studies with the Trojan Horse Method. Eur. Phys. J. A 55(9), 161 (2019). https://doi.org/10.1140/epja/i2019-12833-0
M. Aliotta, C. Spitaleri et al., Improved information on electron screening in \(^{7}\)Li (p,\({\alpha }\))\({{\alpha }}\) using the Trojan-horse method. Eur. Phys. J. A 9(4), 435–437 (2000). https://doi.org/10.1007/s100500070001
S. Romano, L. Lamia, C. Spitaleri, C. Li et al., Study of the \(^{9}\)Be(p,\({{\alpha }}\))\(^{6}\)Li reaction via the Trojan Horse Method. Eur. Phys. J. A 27(1), 221–225 (2006). https://doi.org/10.1140/epja/i2006-08-034-5
C. Spitaleri, S.M.R. Puglia, M. La Cognata, L. Lamia, S. Cherubini, A. Cvetinović, G. D’Agata, M. Gulino, G.L. Guardo, I. Indelicato, R.G. Pizzone, G.G. Rapisarda, S. Romano, M.L. Sergi, R. Spartá, S. Tudisco, A. Tumino, M.G. Del Santo, N. Carlin, M.G. Munhoz, F.A. Souza, A.S. de Toledo, A. Mukhamedzhanov, C. Broggini, A. Caciolli, R. Depalo, R. Menegazzo, V. Rigato, I. Lombardo, D. Dell’Aquila, Measurement of the \(^{10}\)B(p,\({{\alpha }}\)\(_{0}\))\(^{7}\)Be cross section from 5 keV to 1.5 MeV in a single experiment using the Trojan horse method. Phys. Rev. C 95(3), 035801 (2017). https://doi.org/10.1103/PhysRevC.95.035801
G.G. Rapisarda, C. Spitaleri, A. Cvetinović, R. Spartà et al., Study of the \(^{10}\)B(p,\({{\alpha }}_{1}\))\(^{7}\)Be reaction by means of the Trojan Horse Method. Eur. Phys. J. A 54(11), 189 (2018). https://doi.org/10.1140/epja/i2018-12622-3
A. Cvetinovic et al., Molecular screening in nuclear reactions. Phys. Rev. C 92, 065801 (2015). https://doi.org/10.1103/PhysRevC.92.065801
R.G. Pizzone, C. Spitaleri, L. Lamia, C. Bertulani, Mukhamedzhanov et al., Trojan horse particle invariance studied with the Li6(d,\({{\alpha }}\))He4 and Li7(p,\({{\alpha }}\))He4 reactions. Phys. Rev. C 83(4), 045801 (2011). https://doi.org/10.1103/PhysRevC.83.045801
R.G. Pizzone, C. Spitaleri, C.A. Bertulani, A.M. Mukhamedzhanov, Blokhintsev et al., Updated evidence of the Trojan horse particle invariance for the \(^{2}\)H(d,p)\(^{3}\)H reaction. Phys. Rev. C 87(2), 025805 (2013). https://doi.org/10.1103/PhysRevC.87.025805. arXiv:1211.0940 [nucl-ex]
D. Lattuada et al., Model-independent determination of the astrophysical s factor in laser-induced fusion plasmas. Phys. Rev. C 93, 045808 (2016). https://doi.org/10.1103/PhysRevC.93.045808
D. Vescovi, L. Piersanti, S. Cristallo, M. Busso, F. Vissani et al., Effects of a revised \(^{7}\)Be e\(^{-}\)-capture rate on solar neutrino fluxes. A &A 623, 126 (2019). https://doi.org/10.1051/0004-6361/201834993
J.N. Bahcall, C.P. Moeller, The 7Be electron-capture rate. Astrophys. J. 155, 511 (1969). https://doi.org/10.1086/149887
J.N.A.V. Gruzinov, Bahcall: screening in thermonuclear reaction rates in the sun. Astrophys. J. 504(2), 996–1001 (1998). https://doi.org/10.1086/306116
S. Simonucci, S. Taioli, S. Palmerini, M. Busso, Theoretical estimates of stellar e\(^{-}\) captures. I. The half-life of 7Be in evolved stars. Astrophys. J. 764(2), 118 (2013). https://doi.org/10.1088/0004-637x/764/2/118
T. Morresi, S. Taioli, S. Simonucci, Nuclear beta decay: relativistic theory and ab initio simulations of electroweak decay spectra in medium-heavy nuclei and of atomic and molecular electronic structure (adv. theory simul. 11/2018). Adv. Theory Simul. 1(11), 1870030 (2018)
D. Mascali, A. Musumarra, F. Leone, F.P. Romano et al., PANDORA, a new facility for interdisciplinary in-plasma physics. Eur. Phys. J. A 53(7), 145 (2017). https://doi.org/10.1140/epja/i2017-12335-1. arXiv:1703.00479 [physics.ins-det]
A. Chieffi, L. Roberti et al., Impact of the new measurement of the \(^{12}\)C + \(^{12}\)C fusion cross section on the final compactness of massive stars. Astrophys. J. 916(2), 79 (2021). https://doi.org/10.3847/1538-4357/ac06ca. arXiv:2106.00013 [astro-ph.SR]
R.G. Pizzone et al., Clusters and their fundamental role for Trojan Horse Method. Eur. Phys. J. A 56(11), 283 (2020). https://doi.org/10.1140/epja/s10050-020-00285-8
D. Dell’Aquila, I. Lombardo, G. Verde, M. Vigilante et al., High-precision probe of the fully sequential decay width of the Hoyle State in \(^{12}\)C. Phys. Rev. Lett. 119(13), 132501 (2017). https://doi.org/10.1103/PhysRevLett.119.132501. arXiv:1705.09196 [nucl-ex]
H. Zheng, A. Bonasera, The Thomas theorem and the EFIMOV states within a generalized Bohr model. J. Phys. Commun. 4(8), 085011 (2020). https://doi.org/10.1088/2399-6528/abaca4
S.E. Hale, A.E. Champagne, C. Iliadis, V.Y. Hansper, D.C. Powell, J.C. Blackmon, Investigation of the \(^{23}\)Na (p,\({{\gamma }}\)) \(^{24}\)Mg and \(^{23}\)Na (p,\({{\alpha }}\)) \(^{20}\)Ne reactions via ( \(^{3}\)He, d) spectroscopy. Phys. Rev. C 70(4), 045802 (2004). https://doi.org/10.1103/PhysRevC.70.045802
G. Christian, D. Hutcheon et al., Strength of the E\(_{{\rm c.m.}}\)=1113 keV resonance in \(^{20}\)Ne(p,\({{\gamma }}\))\(^{21}\)Na. Phys. Rev. C 88(3), 038801 (2013). https://doi.org/10.1103/PhysRevC.88.038801. arXiv:1309.1503 [nucl-ex]
C.A. Bertulani, T. Kajino, Frontiers in nuclear astrophysics. Prog. Part. Nucl. Phys. 89, 56–100 (2016). https://doi.org/10.1016/j.ppnp.2016.04.001. arXiv:1604.03197 [nucl-th]
C. Pitrou et al., Precision big bang nucleosynthesis with improved Helium-4 predictions. Phys. Rep. 754, 1–66 (2018). https://doi.org/10.1016/j.physrep.2018.04.005. arXiv:1801.08023 [astro-ph.CO]
R.J. Cooke, Big bang nucleosynthesis and the helium isotope ratio. Astrophys. J. Lett. 812(1), 12 (2015). https://doi.org/10.1088/2041-8205/812/1/L12. arXiv:1510.02801 [astro-ph.CO]
L. Sbordone et al., The metal-poor end of the Spite plateau. I. Stellar parameters, metallicities, and lithium abundances. Astron. Astrophys. 522, 26 (2010). https://doi.org/10.1051/0004-6361/200913282. arXiv:1003.4510 [astro-ph.GA]
A. Tumino, R. Spartà, C. Spitaleri, A.M. Mukhamedzhanov, S. Typel, R.G. Pizzone, E. Tognelli, S. Degl’Innocenti et al., New determination of the \(^{2}\)H(d, p)\(^{3}\)H and \(^{2}\)H(d, n)\(^{3}\)He reaction rates at astrophysical energies. Astrophys. J. 785(2), 96 (2014). https://doi.org/10.1088/0004-637X/785/2/96
S.Q. Hou, T. Kajino, T.C.L. Trueman, M. Pignatari, Y.D. Luo, C.A. Bertulani, New thermonuclear rate of \(^{7}\)Li(d, n)2\(^{4}\)He relevant to the cosmological lithium problem. Astrophys. J. 920(2), 145 (2021). https://doi.org/10.3847/1538-4357/ac1a11. arXiv:2105.05470 [astro-ph.CO]
R.H. Cyburt et al., Big bang nucleosynthesis: present status. Rev. Mod. Phys. 88(1), 015004 (2016). https://doi.org/10.1103/RevModPhys.88.015004. arXiv:1505.01076 [astro-ph.CO]
R. Diehl et al., Radioactive \(^{26}\)Al from massive stars in the Galaxy. Nature 439(7072), 45–47 (2006). https://doi.org/10.1038/nature04364. arXiv:astro-ph/0601015 [astro-ph]
E.F. Keane, M. Kramer, On the birthrates of Galactic neutron stars. Mon. Not. RAS 391(4), 2009–2016 (2008). https://doi.org/10.1111/j.1365-2966.2008.14045.x. arXiv:0810.1512 [astro-ph]
J. Baker, M. Bizzarro, N. Wittig, J. Connelly, H. Haack, Early planetesimal melting from an age of 4.5662Gyr for differentiated meteorites. Nature 436(7054), 1127–1131 (2005). https://doi.org/10.1038/nature03882
P. Banerjee et al., Evidence from stable isotopes and \(^{10}\)Be for solar system formation triggered by a low-mass supernova. Nat. Commun. 7, 13639 (2016). https://doi.org/10.1038/ncomms13639. arXiv:1611.07162 [astro-ph.SR]
C. Iliadis et al., The Effects of Thermonuclear Reaction Rate Variations on \(^{26}\)Al Production in Massive Stars: A Sensitivity Study. Astrophys. J. Suppl. Ser. 193(1), 16 (2011). https://doi.org/10.1088/0067-0049/193/1/16. arXiv:1101.5553 [astro-ph.SR]
C. Lederer-Woods, P.J. Woods, T. Davinson, D. Kahl, S.J. Lonsdale et al., Destruction of the cosmic gamma-ray emitter \(^{26}\)Al in massive stars: Study of the key \(^{26}\)Al(n, p) reaction. Phys. Rev. C 104(2), 022803 (2021). https://doi.org/10.1103/PhysRevC.104.L022803
C. Lederer-Woods, P.J. Woods, T. Davinson, A. Estrade, J. Heyse, D. Kahl, S.J. Lonsdale, C. Paradela, P. Schillebeeckx et al., Destruction of the cosmic \({{\gamma }}\) -ray emitter \(^{26}\)Al in massive stars: study of the key \(^{26}\)Al(n,\({{\alpha }}\)) reaction. Phys. Rev. C 104(3), 032803 (2021). https://doi.org/10.1103/PhysRevC.104.L032803
G.L. Guardo, C. Spitaleri, L. Lamia et al., Assessing the near threshold cross section of the \(^{17}\)O(n,\({{\alpha }}\))\(^{14}\)C reaction by means of the Trojan horse method. Phys. Rev. C 95(2), 025807 (2017). https://doi.org/10.1103/PhysRevC.95.025807
S. Cherubini, M. Gulino, C. Spitaleri, G.G. Rapisarda et al., First application of the Trojan horse method with a radioactive ion beam: study of the \(^{18}\)F(p, \({{\alpha }}\))\(^{15}\)O reaction at astrophysical energies. Phys. Rev. C 92(1), 015805 (2015). https://doi.org/10.1103/PhysRevC.92.015805. arXiv:1505.00593 [nucl-ex]
R.G. Pizzone, B.T. Roeder, M. McCleskey, L. Trache, R.E. Tribble, C. Spitaleri et al., Trojan Horse measurement of the \(^{18}\)F(p, \({{\alpha }}\))\(^{15}\)O astrophysical S(E)-factor. Eur. Phys. J. A 52, 24 (2016). https://doi.org/10.1140/epja/i2016-16024-3
M. La Cognata, R.G. Pizzone, J. José, M. Hernanz et al., A Trojan Horse approach to the production of \(^{18}\)F in Novae. Astrophys. J. 846(1), 65 (2017). https://doi.org/10.3847/1538-4357/aa845f
L. Lamia, M. Mazzocco, R.G. Pizzone, S. Hayakawa, M. La Cognata, C. Spitaleri et al., Cross-section measurement of the cosmologically relevant \(^{7}\)Be(n, \({{\alpha }}\))\(^{4}\)He reaction over a broad energy range in a single experiment. Astrophys. J. 879(1), 23 (2019). https://doi.org/10.3847/1538-4357/ab2234
C. Iliadis et al., The effects of thermonuclear reaction-rate variations on nova nucleosynthesis: a sensitivity study. Astrophys. J. Suppl. Ser. 142(1), 105–137 (2002). https://doi.org/10.1086/341400. arXiv:astro-ph/0206020 [astro-ph]
G. D’Agata, A.I. Kilic, V. Burjan, J. Mrazek et al., \(^{26}\)Si(p,\({{\gamma }}\))\(^{27}\)P direct proton capture by means of the asymptotic normalization coefficients method for mirror nuclei. Phys. Rev. C 103(1), 015806 (2021). https://doi.org/10.1103/PhysRevC.103.015806
R. Sawada, K. Maeda, Nucleosynthesis constraints on the energy growth timescale of a core-collapse supernova explosion. Astrophys. J. 886(1), 47 (2019). https://doi.org/10.3847/1538-4357/ab4da3. arXiv:1910.06972 [astro-ph.HE]
V. Margerin, A.S.J. Murphy et al., Study of the 44Ti(\({{\alpha }}\), p)47V reaction and implications for core collapse supernovae. Phys. Lett. B 731, 358–361 (2014). https://doi.org/10.1016/j.physletb.2014.03.003
B.H. Moazen, C. Matei et al., Direct studies of low-energy resonances in \(^{31}\)P(p, \({{\alpha }}\))\(^{28}\)Si and \(^{35}\)Cl(p, \({{\alpha }}\))\(^{32}\)S. Eur. Phys. J. A 47, 66 (2011). https://doi.org/10.1140/epja/i2011-11066-7
M. Pignatari, R. Gallino, M. Heil, M. Wiescher et al., The weak s-process in massive stars and its dependence on the neutron capture cross sections. Astrophys. J. 710(2), 1557–1577 (2010). https://doi.org/10.1088/0004-637X/710/2/1557
N. Nishimura et al., Uncertainties in s-process nucleosynthesis in massive stars determined by Monte Carlo variations. Mon. Not. RAS 469(2), 1752–1767 (2017). https://doi.org/10.1093/mnras/stx696. arXiv:1701.00489 [astro-ph.SR]
F. Käppeler, R. Gallino, S. Bisterzo et al., The s process: nuclear physics, stellar models, and observations. Rev. Mod. Phys. 83(1), 157–194 (2011). https://doi.org/10.1103/RevModPhys.83.157. arXiv:1012.5218 [astro-ph.SR]
S. Palmerini, M. Busso, D. Vescovi, E. Naselli, A. Pidatella, R. Mucciola et al., Presolar grain isotopic ratios as constraints to nuclear and stellar parameters of asymptotic giant branch star nucleosynthesis. Astrophys. J. 921(1), 7 (2021). https://doi.org/10.3847/1538-4357/ac1786. arXiv:2107.12037 [astro-ph.SR]
M. La Cognata, C. Spitaleri, O. Trippella, G.G. Kiss, G.V. Rogachev, A.M. Mukhamedzhanov et al., On the measurement of the \(^{13}\)C(\({{\alpha }}\), n)\(^{16}\)O S-factor at negative energies and its influence on the s-process. Astrophys. J. 777(2), 143 (2013). https://doi.org/10.1088/0004-637X/777/2/143
P. Adsley et al., Reevaluation of the \(^{22}\)Ne(\({{\alpha }}\),\({{\gamma }}\) )\(^{26}\)Mg and \(^{22}\)Ne(\({{\alpha }}\), n )\(^{25}\)Mg reaction rates. Phys. Rev. C 103(1), 015805 (2021). https://doi.org/10.1103/PhysRevC.103.015805. arXiv:2005.14482 [nucl-ex]
A. Best, M. Beard, J. Görres et al., Measurement of the reaction \(^{17}\)O(\({{\alpha }}\), n)\(^{20}\)Ne and its impact on the s process in massive stars. Phys. Rev. C 87(4), 045805 (2013). https://doi.org/10.1103/PhysRevC.87.045805. arXiv:1304.6443 [nucl-ex]
M.L. Sergi, G. D’Agata, G.L. Guardo, G.G. Rapisarda et al., Trojan Horse investigation for AGB stellar nucleosynthesis. Universe 8(2), 128 (2022). https://doi.org/10.3390/universe8020128
A. Tumino et al., The Trojan Horse method: a nuclear physics tool for astrophysics. Annu. Rev. Nucl. Part. Sci. 71(1), 345–376 (2021). https://doi.org/10.1146/annurev-nucl-102419-033642
P. Adsley et al., High-resolution study of levels in the astrophysically important nucleus \(^{26}\)Mg and resulting updated level assignments. Phys. Rev. C 97, 045807 (2018). https://doi.org/10.1103/PhysRevC.97.045807
I. Dillmann, T. Szücs, R. Plag et al., The Karlsruhe astrophysical database of nucleosynthesis in stars project—status and prospects. Nucl. Data Sheets 120, 171–174 (2014). https://doi.org/10.1016/j.nds.2014.07.038
I.S. Anderson et al., Research opportunities with compact accelerator-driven neutron sources. Phys. Rep. 654, 1–58 (2016). https://doi.org/10.1016/j.physrep.2016.07.007. Research opportunities with compact accelerator-driven neutron sources
J. Praena, P.F. Mastinu, G.M. Hernández, A method to obtain a Maxwell–Boltzmann neutron spectrum at \(kT = 30\) keV for nuclear astrophysics studies. Public. Astron. Soc. Aust. 26(3), 225–231 (2009). https://doi.org/10.1071/AS08043
G. Gyürky et al., The activation method for cross section measurements in nuclear astrophysics. Eur. Phys. J. A 55(3), 41 (2019). https://doi.org/10.1140/epja/i2019-12708-4. arXiv:1903.03339 [nucl-ex]
A. Alejo, H. Ahmed, A. Green, S.R. Mirfayzi et al., Recent advances in laser-driven neutron sources. Nuovo Cim. C Geophys. Sp. Phys. C 38, 188 (2016). https://doi.org/10.1393/ncc/i2015-15188-8
T.J. Renk, P.F. Ottinger, R.E. Durrer, Production of pulsed high-energy neutron bursts from beam-target interaction using a 15 MeV HERMES III ion beam. AIP Adv. 10(12), 125106 (2020). https://doi.org/10.1063/5.0023480
S. Amaducci et al., Results of the \(^{140}\)Ce(n,\(\gamma\))\(^{141}\)Ce cross-section measurement at n_TOF. Universe (2021). https://doi.org/10.3390/universe7060200
G. Tagliente, P.M. Milazzo, K. Fujii et al., Neutron capture on \(^{94}{\rm Zr}\): resonance parameters and Maxwellian-averaged cross sections. Phys. Rev. C 84, 015801 (2011). https://doi.org/10.1103/PhysRevC.84.015801
F.-K. Thielemann et al., Neutron star mergers and nucleosynthesis of heavy elements. Annu. Rev. Nucl. Part. Sci. 67, 253–274 (2017). https://doi.org/10.1146/annurev-nucl-101916-123246. arXiv:1710.02142 [astro-ph.HE]
E. Pian, P. D’Avanzo et al., Spectroscopic identification of r-process nucleosynthesis in a double neutron-star merger. Nature 551(7678), 67–70 (2017). https://doi.org/10.1038/nature24298. arXiv:1710.05858 [astro-ph.HE]
B.D. Metzger, G. Martínez-Pinedo, S. Darbha, E. Quataert et al., Electromagnetic counterparts of compact object mergers powered by the radioactive decay of r-process nuclei. Mon. Not. R. Astron. Soc. 406(4), 2650–2662 (2010). https://doi.org/10.1111/j.1365-2966.2010.16864.x
B.D. Metzger, Kilonovae. Living Rev. Relat. 23(1), 1 (2019). https://doi.org/10.1007/s41114-019-0024-0
S. Rosswog, The multi-messenger picture of compact binary mergers. Int. J. Mod. Phys. D 24(05), 1530012 (2015). https://doi.org/10.1142/S0218271815300128
M. Tanaka, D. Kato et al., Systematic opacity calculations for kilonovae. Mon. Not. R. Astron. Soc. 496(2), 1369–1392 (2020). https://doi.org/10.1093/mnras/staa1576. arXiv:1906.08914 [astro-ph.HE]
J.J. Cowan, C. Sneden, J.E. Lawler, A. Aprahamian, M. Wiescher, K. Langanke, G. Martínez-Pinedo, F.-K. Thielemann, Origin of the heaviest elements: the rapid neutron-capture process. Rev. Mod. Phys. 93, 015002 (2021). https://doi.org/10.1103/RevModPhys.93.015002
A. Pidatella, et al., In-plasma study of opacity relevant for compact binary ejecta. Nuovo Cimento C (2021). https://doi.org/10.1393/ncc/i2021-21065-x
A. Pidatella et al., Experimental and numerical investigation of magneto-plasma optical properties toward measurements of opacity relevant for compact binary objects. Front. Astron. Sp. Sci. 9, 18 (2022). https://doi.org/10.3389/fspas.2022.931744
J. Lippuner, L.F. Roberts, SkyNet: a modular nuclear reaction network library. Astrophys. J. Suppl. Ser. 233(2), 18 (2017). https://doi.org/10.3847/1538-4365/aa94cb
M. La Cognata, A. Del Zoppo et al., Solving the large discrepancy between inclusive and exclusive measurements of the \(^{8}\)Li + \(^{4}\)He \({\rightarrow }\)\(^{11}\)B + n reaction cross section at astrophysical energies. Astrophys. J. Lett. 706(2), 251–255 (2009). https://doi.org/10.1088/0004-637X/706/2/L251. arXiv:0911.2585 [astro-ph.SR]
B.S. Meyer, G.J. Mathews, W.M. Howard, S.E. Woosley, R.D. Hoffman, R-process nucleosynthesis in the high-entropy supernova bubble. Astrophys. J. 399, 656 (1992). https://doi.org/10.1086/171957
Y.-Z. Qian, G. Wasserburg, Where, oh where has the r-process gone? Phis. Rep. 442, 237–268 (2007). https://doi.org/10.1016/j.physrep.2007.02.006
A. Arcones, F. Montes, Production of light-element primary process nuclei in neutrino-driven winds. Astrophys. J. 731(1), 5 (2011). https://doi.org/10.1088/0004-637X/731/1/5. arXiv:1007.1275 [astro-ph.GA]
A. Arcones, J. Bliss, Nucleosynthesis of elements between sr and ag in neutron- and proton-rich neutrino-driven winds. J. Phys. G: Nucl. Part. Phys. 41(4), 044005 (2014). https://doi.org/10.1088/0954-3899/41/4/044005
J. Pereira, F. Montes, Theoretical uncertainty of \(({\alpha }, n)\) reactions relevant for the nucleosynthesis of light \(r\text{-process }\) nuclei in neutrino-driven winds. Phys. Rev. C 93, 034611 (2016). https://doi.org/10.1103/PhysRevC.93.034611
J. Bliss et al., Impact of (\({{\alpha }}\), n) reactions on weak r-process in neutrino-driven winds. J. Phys. G: Nucl. Phys. 44(5), 054003 (2017). https://doi.org/10.1088/1361-6471/aa63bd. arXiv:1612.02435 [astro-ph.SR]
P. Mohr, Role of \(({\alpha },\, n)\) reactions under \(r\)-process conditions in neutrino-driven winds reexamined. Phys. Rev. C 94, 035801 (2016). https://doi.org/10.1103/PhysRevC.94.035801
G.G. Kiss, P. Mohr, Z. Fülöp, T. Rauscher, G. Gyürky, T. Szücs, Z. Halász, E. Somorjai, A. Ornelas, C. Yalçın, R.T. Güray, N. Özkan, High precision \({}^{113}\)In(\({\alpha },{\alpha }\))\({}^{113}\)In elastic scattering at energies near the coulomb barrier for the astrophysical \({\gamma }\) process. Phys. Rev. C 88, 045804 (2013). https://doi.org/10.1103/PhysRevC.88.045804
A. Palumbo, W.P. Tan, J. Görres et al., Systematic study of the \({\alpha }\)-optical potential via elastic scattering near the \(z=50\) region for \(p\)-process nuclei. Phys. Rev. C 85, 035808 (2012). https://doi.org/10.1103/PhysRevC.85.035808
D. Galaviz, Z. Fülöp et al., Elastic \({\alpha }\) scattering on \(^{112}{\rm Sn}\) and \(^{124}{\rm Sn}\) at astrophysically relevant energies. Phys. Rev. C 71, 065802 (2005). https://doi.org/10.1103/PhysRevC.71.065802
G.G. Kiss, P. Mohr, Z. Fülöp, G. Gyürky, Z. Elekes et al., Phys. Rev. C 83, 065807 (2011). https://doi.org/10.1103/PhysRevC.83.065807
S.M. Valle, A. Alexandrov, G. Ambrosi, S. Argir, G. Battistoni, N. Belcari, S. Biondi, M.G. Bisogni, G. Bruni, S. Brambilla, N. Camarlinghi, P. Cerello, E. Ciarrocchi, A. Clozza, G. De Lellis, A. Di Crescenzo, M. Durante, M. Emde, R. Faccini, V. Ferrero, F. Ferroni, C. Finck, M. Francesconi, M. Franchini, L. Galli, M. Garbini, G. Giraudo, R. Hetzel, E. Iarocci, M. Ionica, K. Kanxheri, A. Lauria, C. La Tessa, M. Marafini, I. Mattei, R. Mirabelli, M.C. Montesi, M.C. Morone, M. Morrocchi, S. Muraro, L. Narici, A. Pastore, N. Pastrone, V. Patera, M. Pullia, L. Ramello, V. Rosso, M. Rovituso, C. Sanelli, A. Sarti, G. Sartorelli, O. Sato, A. Schiavi, C. Schuy, E. Scifoni, A. Sciubba, M. Selvi, L. Servoli, M. Sitta, R. Spighi, E. Spiriti, G. Sportelli, A. Stahl, F. Tommasino, G. Traini, M. Vanstalle, M. Villa, U. Weber, A. Zoccoli, Foot: a new experiment to measure nuclear fragmentation at intermediate energies. Perspect. Sci. 12, 100415 (2019). https://doi.org/10.1016/j.pisc.2019.100415
O. Sokol et al., Kill painting of hypoxic tumors with multiple ion beams. Phys. Med. Biol. 64, 045008 (2019). https://doi.org/10.1088/1361-6560/aafe40
W. Tinganelli et al., Kill-painting of hypoxic tumours in charged particle therapy. Sci. Rep. 5, 17016 (2015). https://doi.org/10.1038/srep17016
F. Luoni et al., Total nuclear reaction cross-section database for radiation protection in space and heavy-ion therapy applications. New J. Phys. 23, 101201 (2021). https://doi.org/10.1088/1367-2630/ac27e1
J.W. Norbury et al., Are further cross section measurements necessary for space radiation protection or ion therapy applications? Helium projectiles. Front. Phys. 8, 565954 (2020). https://doi.org/10.3389/fphy.2020.565954
K. Parodi, Experimental study on the feasibility of in-beam PET for accurate monitoring of proton therapy. EEE Trans. Nucl. Sci. 52(3), 778–786 (2005). https://doi.org/10.1109/TNS.2005.850950
E.S. Diffenderfer et al., Design, implementation, and in vivo validation of a novel proton flash radiation therapy system. Int. J. Radiat. Oncol. Biol. Phys. 106, 440–448 (2020). https://doi.org/10.1016/j.ijrobp.2019.10.049
T. Tessonnier et al., Flash dose-rate helium ion beams: first in vitro investigations. Int. J. Radiat. Oncol. Biol. Phys. 111, 1011–1022 (2021). https://doi.org/10.1016/j.ijrobp.2021.07.1703
R.A. Snavely, Intense high-energy proton beams from petawatt-laser irradiation of solids. Phys. Rev. Lett. 85, 2945 (2000). https://doi.org/10.1103/PhysRevLett.85.2945
A. Higginson, Near-100 MeV protons via a laser-driven transparency-enhanced hybrid acceleration scheme. Nat. Commun. 9(724), 2945 (2018). https://doi.org/10.1038/s41467-018-03063-9
A. Macchi, M. Borghesi, M. Passoni, Ion acceleration by superintense laser-plasma interaction. Rev. Mod. Phys. 85(751), 751–793 (2013). https://doi.org/10.1103/RevModPhys.85.751
X.F. Shen, A. Pukhov, B. Qiao, Monoenergetic high-energy ion source via femtosecond laser interacting with a microtape. Phys. Rev. X 11, 041002 (2021). https://doi.org/10.1103/PhysRevX.11.041002
E. Esarey, C.B. Schroeder, W.P. Leemans, Physics of laser-driven plasma-based electron accelerators. Rev. Mod. Phys. 81, 1229 (2009). https://doi.org/10.1103/RevModPhys.81.1229
L. Labate, D. Palla, D. Panetta, A. Gizzi et al., Toward an effective use of laser-driven very high energy electrons for radiotherapy: feasibility assessment of multi-field and intensity modulation irradiation schemes. Sci. Rep. 10, 17307 (2020). https://doi.org/10.1038/s41598-020-74256-w
G. Sarri, D.J. Corvan, W. Schumaker, J.M. Cole, A. Di Piazza et al., Ultrahigh brilliance multi-MeV \(\gamma\)-ray beams from nonlinear relativistic Thomson scattering. Phys. Rev. Lett. 113, 224801 (2014). https://doi.org/10.1103/PhysRevLett.113.224801
A. Alejo, G.M. Samarin, W. Warwick, C. McCluskey et al., Non-invasive characterisation of a laser-driven positron beam. Plasma Phys. Control. Fus. 62, 055013 (2020). https://doi.org/10.1088/1361-6587/ab7e81
J. Warwick, T. Dzelzainis, M.E. Dieckmann, W. Schumaker, D. Doria, L. Romagnani, K. Poder, J.M. Cole et al., Experimental observation of a current-driven instability in a neutral electron-positron beam. Phys. Rev. Lett. 119, 185002 (2017). https://doi.org/10.1103/PhysRevLett.119.185002
T.L. Audet et al., Ultrashort, MeV-scale laser-plasma positron source for positron annihilation lifetime spectroscopy. Phys. Rev. Accel. Beams 24, 073402 (2021). https://doi.org/10.1103/PhysRevAccelBeams.24.073402
D. Panetta, L. Labate, A. Gizzi, P. Russo et al., Numerical simulation of novel concept 4d cardiac microtomography for small rodents based on all-optical Thomson scattering X-Ray sources. Sci. Rep. 9, 8439 (2019). https://doi.org/10.1038/s41598-019-44779-y
A. Giulietti, P. Martin et al., Intense \(\gamma\)-ray source in the giant-dipole-resonance range driven by 10-tw laser pulses. Phys. Rev. Lett. 101, 105002 (2008). https://doi.org/10.1103/PhysRevLett.101.105002
D. Habs, P.G. Thirolf, M. Gross, Introducing the fission-fusion reaction process: using a laser-accelerated th beam to produce neutron-rich nuclei towards the n=126 waiting point of the r-process. Appl. Phys. B 103, 471–484 (2011). https://doi.org/10.1007/s00340-010-4261-x
E. Conard, High intensity accelerator for a wide range of applications. Nucl. Instrum. Methods Phys. Res., Sect. A 353, 1–5 (1994). https://doi.org/10.1016/0168-9002(94)91589-X
E. Lefebvre, Numerical simulation of isotope production for positron emission tomography with laser-accelerated ions. J. Appl. Phys. 100, 113308 (2006). https://doi.org/10.1063/1.2362908
C.-M.C. Ma, T. Lomax, Proton and Carbon Ion Therapy. Med. Phys. 40, 057301 (2013). https://doi.org/10.1118/1.4802213
E. d’Humières, A. Brantov, V.Y. Bychenkov, V.T. Tikhonchuk, Optimization of laser-target interaction for proton acceleration. Phys. Plasmas 20, 023103 (2013). https://doi.org/10.1063/1.4791655
Z. Sun, Review: production of nuclear medicine radioisotopes with ultra-intense lasers. AIP Adv. 11, 040701 (2021). https://doi.org/10.1063/5.0042796
A. Zigler, S. Eisenman, M. Botton, E. Nahum, E. Schleifer, A. Baspaly, I. Pomerantz, K.W.D. Ledingham et al., Enhanced proton acceleration by an ultrashort laser interaction with structured dynamic plasma targets. Phys. Rev. Lett. 110, 215004 (2013). https://doi.org/10.1103/PhysRevLett.110.215004
H. Kierzkowska-Pawlak, J. Tyczkowski, A. Jarota, H. Abramczyk, Hydrogen production in liquid water by femtosecond laser-induced plasma. Appl. Energy 247, 24–31 (2019). https://doi.org/10.1016/j.apenergy.2019.04.010
P.K. Kennedy, D.X. Hammer, B.A. Rockwell, Laser-induced breakdown in aqueous media. Prog. Quantum Electron. 21, 155–248 (1997). https://doi.org/10.1016/S0079-6727(97)00002-5
A. De Giacomo, M. Dell’Aglio, R. Gaudiuso, S. Amoruso, O. De Pascale, Effects of the background environment on formation, evolution and emission spectra of laser-induced plasmas. Spectrochim. Acta, Part B 78, 1–19 (2012). https://doi.org/10.1016/j.sab.2012.10.003
F. Liu, S. Yuan, Z. Zuo, W. Li, L.E. Ding, H. Zeng, Laser filamentation induced bubbles and their motion in water. Opt. Express 24, 13258–13263 (2016). https://doi.org/10.1364/OE.24.013258
S.L. Chin, S. Lagacé, Generation of H2, O2, and H2O2 from water by the use of intense femtosecond laser pulses and the possibility of laser sterilization. Appl. Opt. 35, 907–911 (1996). https://doi.org/10.1364/AO.35.000907
G. Maatz, A. Heisterkamp, H. Lubatschowski, S. Barcikowski, C. Fallnich, H. Welling, W. Ertmer, Chemical and physical side effects at application of ultrashort laser pulses for intrastromal refractive surgery. J. Opt. A: Pure Appl. Opt. 2, 59 (1996). https://doi.org/10.1088/1464-4258/2/1/311
A. Kuwahara, Y. Mizushima, M. Matsui, T. Kozuka, N. Mase, Electrodeless hydrogen production from seawater using femtosecond laser pulses. RSC Adv. 12, 9304–9309 (2022). https://doi.org/10.1039/D2RA01337A
S. Manservisi, V.G. Molinari, Charged-particle distribution in velocity, angle and time by Fokker–Planck equation. Il Nuovo Cim. D 14, 9–25 (1992). https://doi.org/10.1007/BF02455340
A. Galatà, D. Mascali, L. Neri, L. Celona, A new numerical description of the interaction of an ion beam with a magnetized plasma in an ECR-based charge breeding device. Plasma Sour. Sci. Technol. 25, 045007 (2016). https://doi.org/10.1088/0963-0252/25/4/045007
A. Galatà, D. Mascali, G. Torrisi, L. Neri, L. Celona, J. Angot, Influence of the injected beam parameters on the capture efficiency of an electron cyclotron resonance based charge breeder. Phys. Rev. Accel. Beams 20, 063401 (2017). https://doi.org/10.1103/PhysRevAccelBeams.20.063401
A. Galatà, D. Mascali, C.S. Gallo, G. Torrisi, Self-consistent modeling of beam-plasma interaction in the charge breeding optimization process. Rev. Sci. Instrum. 91(1), 013506 (2020). https://doi.org/10.1063/1.5130704
S. Manservisi, V.G. Molinari, Slowing-down time of fast electrons in plasmas via the Fokker–Planck equation. Nucl. Sci. Eng. 112, 296–300 (1992). https://doi.org/10.13182/NSE92-A23979
M.E. Jones, J.M. Lemons, R.J. Mason, V.A. Thomas, D. Winske, A grid-based Coulomb collision model for PIC codes. J. Comput. Phys. 123, 169–181 (1996). https://doi.org/10.1006/jcph.1996.0014
C.K. Birdsall, J.M. Lemons, R.J. Mason, V.A. Thomas, D. Winske, Particle-in-cell charged-particle simulations, plus Monte Carlo collisions with neutral atoms, pic-mcc. IEEE Trans. Plasma Sci. 19, 65–85 (1991). https://doi.org/10.1109/27.106800
D. Mascali, G. Torrisi, L. Neri, G. Sorbello, G. Castro, L. Celona, S. Gammino, 3D-full wave and kinetics numerical modelling of electron cyclotron resonance ion sources plasma: steps towards self-consistency. Eur. Phys. J. D 69(1), 27 (2015). https://doi.org/10.1140/epjd/e2014-50168-5
G. Torrisi, D. Mascali, G. Sorbello, L. Neri, L. Celona, G. Castro, T. Isernia, S. Gammino, Full-wave FEM simulations of electromagnetic waves in strongly magnetized non-homogeneous plasma. J. Electromagn. Waves Appl. 28(9), 1085–1099 (2014). https://doi.org/10.1080/09205071.2014.905245
G. Torrisi, D. Mascali, A. Galatà, L. Celona, G. Mauro, E. Naselli, G. Sorbello, S. Gammino, Investigation of radiofrequency ion heating in the magnetoplasma of an ECR ion trap, in 2019 International Conference on Electromagnetics in Advanced Applications (ICEAA) (2019), pp. 1203–1207. https://doi.org/10.1109/ICEAA.2019.8879288
G.S. Mauro, G. Torrisi, A. Pidatella, A. Galatà, D. Mascali, Numerical Design of RF Antennas for Ion Cyclotron Resonance Heating in ECRIS Environment, in 2021 19th International Conference on Ion Sources (ICIS2021) (2022), J. Phys.: Conf. Ser. 2244, 012023. https://doi.org/10.1088/1742-6596/2244/1/012023
G. Ciullo, R. Engels, M. Buescher, A. Vasilyev, Nuclear Fusion with Polarized Fuel. Springer Proceedings in Physics, vol. 187 (2016). https://doi.org/10.1007/978-3-319-39471-8
A. Solovev, A. Andreyanov, L. Barion, G. Ciullo, R. Engels, V. Fotyev, K. Ivshin, L. Kochenda, P. Kravchenko, P. Kravtsov, V. Larionov, A. Rozhdestvensky, S. Sherman, I. Solovyev, V. Trofimov, A. Vasilyev, M. Vznuzdaev, Optimization and first tests of the experimental setup to investigate the double-polarized DD-fusion reactions. J. Instrum. 15(8), 08003 (2020). https://doi.org/10.1088/1748-0221/15/08/C08003. arXiv:2006.09816 [physics.ins-det]
S.J. Zweben, T.W. Kornack, D. Majeski, G. Schilling, C.H. Skinner, R. Wilson, N. Kuzma, Evaluation of possible nuclear magnetic resonance diagnostic techniques for tokamak experiments. Rev. Sci. Instrum. 74(3), 1460–1464 (2003). https://doi.org/10.1063/1.1530388
F. Bombarda, A. Cardinali, C. Castaldo, Relevant spatial and time scales in tokamaks. Springer Proc. Phys. (2016). https://doi.org/10.1007/978-3-319-39471-8_6
D. Mascali, A. Galatà, S. Gallo, O. Leonardi, G.S. Mauro, E. Naselli, A. Pidatella, F. Russo, G. Sorbello, G. Torrisi, Redefining plasma chambers for ECR ion sources: the IRIS structure. J. Phys: Confer. Ser. 2244(1), 012003 (2022). https://doi.org/10.1088/1742-6596/2244/1/012003
L. Celona et al., Observations of the frequency tuning effect in the 14 GHz CAPRICE ion source. Rev. Sci. Instrum. 79, 023305 (2008). https://doi.org/10.1063/1.2841694
D. Mascali, E. Naselli, R. Racz et al., Experimental study of single- vs two-close-frequency heating impact on confinement and loss dynamics in ECR ion source plasmas by means of X-ray spectroscopy and imaging. Plasma Phys. Control. Fus. 64, 035020 (2022). https://doi.org/10.1088/1361-6587/ac4349
E. Naselli, R. Racz, S. Biri, M. Mazzaglia, A. Galatà, D. Mascali et al., Quantitative analysis of an ECR Ar plasma structure by X-ray spectroscopy at high spatial resolution. JINST 17, 01009 (2022). https://doi.org/10.1088/1748-0221/17/01/C01009
S. Biri et al., Innovative experimental setup for X-ray imaging to study energetic magnetized plasmas. J. Instrum. 16, 03003 (2021). https://doi.org/10.1088/1748-0221/16/03/P03003
E. Naselli, R. Racz, S. Biri, M. Mazzaglia, A. Galatà, D. Mascali et al., Innovative analytical method for X-ray imaging and space-resolved spectroscopy of ECR plasmas. Condens. Matter 7(1), 5 (2022). https://doi.org/10.3390/condmat7010005
Acknowledgements
We thank S. Piantelli and G. Verde for carefully reading this manuscript.
Funding
Open access funding provided by Università degli Studi di Catania within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Agodi, C., Cappuzzello, F., Cardella, G. et al. Nuclear physics midterm plan at LNS. Eur. Phys. J. Plus 138, 1038 (2023). https://doi.org/10.1140/epjp/s13360-023-04358-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjp/s13360-023-04358-7