1 Introduction

1.1 Neutron dosimetry

Exposure to neutron fields occurs in several working scenarios, such as the nuclear fuel cycle, radiation therapy, and material testing. Moreover, aircraft crews are subjected to an intense cosmic neutron radiation fields at flight altitudes. It is also worth considering that, near photon and hadron accelerators with energies above some MeV, a stray neutron field is always generated by photonuclear reactions and intra-nuclear cascades.

This means that in several occasions it is necessary to assess the dose to which workers are exposed. The operational dosimetric quantity used for environmental monitoring is the ambient dose equivalent. If the neutron spectrum \(\Phi (E)\) is known, this quantity can be calculated as

$$\begin{aligned} H^{*}(10)(E)= \int h^{*}_{10}(E) \Phi (E) \,{\mathrm{d}}E \end{aligned}$$
(1)

The factor \(h^{*}_{10}(E)\) indicates the neutron fluence-to-dose conversion factors, which are tabulated in the ICRP74 [1] and shown in Fig. 1.

Fig. 1
figure 1

Neutron fluence to ambient dose equivalent conversion factors, as tabulated in ICRP74

Full size image

Therefore, one way of assessing the ambient dose equivalent is measuring the neutron spectral fluence (using for instance a Bonner Sphere Spectrometer [2]) and folding it with the fluence-to-dose conversion factors. However, neutron spectrum measurements are difficult and time-consuming, because several irradiations (up to 10–12) are usually needed to unfold a single neutron spectrum. For this reason, estimating the operational dosimetric quantity from Eq. (1) is not feasible for an environmental monitoring system and a different approach is generally adopted. Rem counters are a category of neutron area monitors whose characteristic is to have a response function R(E) proportional to the \(h^{*}_{10}(E)\) coefficients, meaning that they are more sensitive to neutrons with greater biological importance [3]. They usually consist of a thermal neutron detector which is placed inside a moderator sphere mainly made of polyethylene. The sphere can also host some inserts of cadmium, that are used to decrease the instrument sensitivity to thermal neutrons (which have low biological importance), and some layers of lead or other high-Z material, that allow the detection of high energy neutrons (in fact, polyethylene can effectively moderate neutrons only up to 20 MeV). The term ’extended range’ Rem Counters is conventionally used for the ambient monitors that can be used also above 20 MeV [4]. The reading of a Rem Counter is given by:

$$\begin{aligned} C=\int R(E) \cdot \Phi (E) \,{\mathrm{d}}E = \int k \cdot h^{*}_{10}(E) \cdot \Phi (E) \,{\mathrm{d}}E = k \cdot H^{*}_{10} \end{aligned}$$
(2)

Equation (2) shows that the counts measured by a Rem Counter are proportional to the ambient dose equivalent. The proportionality factor k is the instrument calibration parameter, which can be assessed with a single irradiation in a reference neutron field.

1.2 Pulsed radiation fields

A radiation field is defined as pulsed when its intensity changes significantly over short timescales with respect to the characteristic time of the used detector. Pulsed fields are associated with much greater dose rates than stationary fields, which often lead active detection systems to saturation, making them unusable in these situations [5, 6]. This effect is shown in Fig. 2, which shows the different time structures of a pulsed and stationary field that have the same average dose rate over the considered time interval. In the stationary case, the instantaneous dose rate is always lower than the limit of operation of the active detector, which can be correctly used as a monitor. However, in a pulsed field, the instantaneous dose rate overcomes the instrument limit and leads to the saturation of the detector, whose reading becomes unreliable in this way.

Fig. 2
figure 2

Examples of the time structure of stationary and pulsed radiation fields. The two fields deliver the same dose in the observed time interval but with very different rates. Because of this, an active instrument that can be used in stationary conditions is not adequate for a pulsed field

Full size image

When considering a Rem Counter (which can be assumed as a neutron detector encapsulated in a moderating sphere), the time required for detecting an incoming neutron is the sum of three contributions:

  1. 1.

    The time needed to thermalize the incident neutron in the moderating sphere.

  2. 2.

    The time needed by the thermalized neutron to diffuse toward the inner detector.

  3. 3.

    The time needed for the neutron capture in the detector sensitive volume.

Summing these contributions, the time needed for a spherical Rem Counter to detect an incident neutron has an exponential distribution, with a characteristic time of 10–100 \(\upmu \)s, depending on the moderating sphere size and the neutron energy. Figure 3 shows the mechanism of detection of an incident neutron, and Fig. 4 shows the density probability of the neutron detection times for a 25.4 cm diameter moderating sphere in which a 3 cm diameter neutron detector is encapsulated, assuming an incident neutron energy of 1 MeV. The data were obtained by simulating the irradiation of the sphere with the Monte Carlo code MCNP6, assuming a spherical source of monoenergetic neutrons impinging on the surface of the sphere at time \(t = 0\).

Fig. 3
figure 3

Process of neutron detection in a Rem Counter: the incoming neutron is thermalized in the moderating sphere, reaches the inner detector and is captured. Each neutron has a unique story before being captured, hence the time needed for detection is not fixed, but has a statistical distribution

Full size image
Fig. 4
figure 4

Time distribution of neutron captures in the inner detector for a spherical rem counter with a diameter of 25.4 cm and an incident neutron energy of 1 MeV. The probability density function is fitted by an exponential curve with a characteristic time of approximately 100 \(\upmu \)s

Full size image

Therefore, it can be assumed that the characteristic time of a Rem Counter is around 100 \(\upmu \)s, which means that any neutron fields significantly varying on a timescale of some \(\upmu \)s can be considered a pulsed field for a neutron monitor. These types of fields are especially common close to particle accelerators. For example, a medical LINAC generates bursts of photons with a duration of around 10 \(\upmu \)s, and the secondary neutron field arising from photonuclear reactions has essentially the same structure.

1.3 The LUPIN

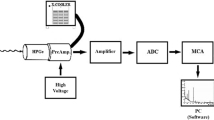
The LUPIN (Long interval, Ultra-wide dynamic Pile-up free Neutron rem counter) is a Rem Counter especially developed for pulsed neutron fields [7]. It is based on a BF\(_{3}\) thermal neutron detector at a pressure of 2664 Pa inserted in a 25-cm-diameter cylinder made of polyethylene with some cadmium and lead inserts. The innovative electronics of the LUPIN is the feature that allows its use in pulsed fields. The signal generated by the detector is directly amplified by a LOG114 logarithmic amplifier, which can work over a dynamic range of several decades and withstand high currents without suffering from saturation. The LOG114 replaces the conventional preamplifier and shaping amplifier, making the amplification stages considerably faster. The amplified signal is digitalized by a Float Programmable Gate Array (FPGA), which samples the current value every 100 ns. The derivative of the acquired current is then calculated as:

$$\begin{aligned} \frac{{\mathrm{d}}I_{n}}{{\mathrm{d}}t}=\frac{I_{n+1}-I_{n-1}}{2\delta t} \end{aligned}$$
(3)

where \(I_{n}\) is the nth current sample and \(\delta t\) is the time distance between two samples (100 ns). When the derivative calculated in this way exceeds an amplitude threshold for a user settable number of samples, a neutron interaction is recorded. In this way, the neutron interactions can easily be discriminated from a steady photon background, in which the current derivative is always close to zero.

The LUPIN calibration factor [i.e., the parameter k in Eq. (2)] was assessed in the reference field generated by a PuBe source, and this Rem Counter has been successfully used in several intercomparisons of radiation protection instruments to test its performance in pulsed neutron fields [8,9,10,11]. These irradiations allowed an accurate evaluation of the linearity of the LUPIN response, whereas a characterization of its energy dependence is still missing. The aim of this paper is to fill this gap, comparing the simulated response function with experimental data.

2 Materials and methods

2.1 Monte Carlo simulations

Monte Carlo simulations aimed to evaluate the response of the instrument as a function of the incident neutron energy were performed via the MCNP ver 6.2 code. MCNP is a general-purpose Monte Carlo N-Particle code that can be used for neutron, photon, electron, or coupled neutron/photon/electron transport [12].

The computational model of the detector shown in Fig. 5 represents the inner part of the detector, the surrounding cylinder of polyethylene, and the inserts of lead and cadmium. The detector handling hosting the electronics is represented as well.

Fig. 5
figure 5

Representation of the LUPIN geometry in the Monte Carlo model

Full size image

The irradiation in an expanded and aligned field of monoenergetic neutrons impinging on the detector in a radial direction was simulated. MCNP estimated the capture reaction rate occurring in the detector active volume scoring the spectral neutron fluence \(\Phi (E)\) in the volume, and then folding it with the 10B(n,\(\alpha \))7Li reaction cross section, as shown in Eq. (4).

$$\begin{aligned} RR\; [{\text{cm}}^{-3}] = \int N \Phi (E) \sigma (E) \,{\mathrm{d}}E \end{aligned}$$
(4)

The term N in Eq. (4) is the 10B atomic density in the volume, expressed in \(\frac{{\mathrm{atoms}}}{{\mathrm{barn}} \cdot {\mathrm{cm}}}\) and can be assessed being the BF\(_{3}\) pressure and the 10B enrichment known. The capture reactions occurring in the detector were then calculated multiplying the reaction rate for the active volume. A second simulation was performed with the same source without the LUPIN to assess the neutron fluence at position of the centre of the detector. The instrument response was then calculated as:

$$\begin{aligned} R (E)\; [{\text{cm}}^{2}] = \frac{{\text{Capture reactions}}}{{\text{Neutron fluence}}} \end{aligned}$$
(5)

Both the capture reactions and the neutron fluence estimated by the code are normalized on the number of simulated primaries, whereas the response, which is the ratio of these quantities, is independent on the number of simulated stories (which only affects the precision of the simulation). The response was calculated varying the incident neutron energy from 10 meV to 1 GeV.

2.2 Neutron monoenergetic fields

The measurements were performed in the low-scatter facility at the National Physical Laboratory (NPL). The facility generates monoenergetic neutron fields with accurately known fluence values exploiting the nuclear reactions occurring between charged particles (protons or deuterons) and a target containing lithium, deuterium, or tritium. The charged particles are accelerated by a Van de Graaf accelerator with a maximum accelerating voltage of 3.5 MV. The energy of the neutron field generated by the nuclear reactions depends on the accelerated particle energy and the measuring angle. The LUPIN was irradiated in the fields reported in Table 1, which are advised for instrument calibrations (with the exception of 16.5 MeV) by ISO8529 [13]. For all these energies, the neutron emission was measured a \(0^{\circ }\), i.e., in the same direction of the impinging charged particles beam, with the exception of the 71 keV field, which was measured at \(50^{\circ }\).

Table 1 Neutron reactions and associated energies used for the LUPIN calibration at NPL
Full size table

Neutron fluences are measured by the NPL standard long counter [14, 15]. It is placed at a fixed distance from the neutron emitting target, and at the same angles as the LUPIN according to the neutron energy, as shown in Table 1. The experimental area of the accelerator facility is a free scattering room, and the shadow cone technique is employed for further reducing the counts induced by the air and room in-scattered component of the neutron flux [13]. The technique consists of making two consecutive measurements for each energy: in the first one, the detector is irradiated by the target emission as it is, while in the second one a cone made of iron and polyethylene is placed between the target and the detector. In the first measurement, the direct emission from the reaction and the scattered component are measured, whereas in the second measurement the direct emission is shielded by the cone and only the scattered component is measured. The response to the direct component is then assessed by performing the difference between the two measurements. The contribution of air out-scattering was calculated using the well-known oxygen and nitrogen cross sections. The long counter reading was corrected for dead time effects and the fluence at the centre of the instrument was assessed being the instrument response at neutrons of the energy of interest known [16,17,18]. The LUPIN was irradiated at a different distance to the long counter, and the fluence value at the LUPIN centre position was assessed using the law of the inverse of the square of the distance. The shadow cone technique was used to correct also the reading of the LUPIN, which means that four different measurements were necessary to establish the LUPIN response at one energy:

  1. 1.

    Irradiation of the long counter;

  2. 2.

    Irradiation of the long counter with the shadow cone;

  3. 3.

    Irradiation of the LUPIN;

  4. 4.

    Irradiation of the LUPIN with the shadow cone.

Irradiations 1 and 2 were necessary for establishing the neutron fluence, whereas irradiations 3 and 4 were necessary for establishing the LUPIN counts.

3 Results

Figure 6 shows the comparison between the response calculated with MCNP6 and the experimental points measured at NPL. The error bars shown in the figure correspond to a confidence interval of 95%. The combined uncertainty considers the statistical uncertainty of the counts measured by the LUPIN in each irradiation (which follow a Poisson distribution), the uncertainty on the flux value (which is provided by the NPL), and the uncertainty related to the instrument position. This one was assessed assuming that the exact position of the LUPIN was known with an accuracy of 1 cm, which means that the instrument distance from the neutron-producing target was considered textcolor uniformly distributed between the nominal value (180 cm) \(\pm \,1\) cm. Among these three contributions, the uncertainty on the neutron flux value has the greatest importance on the overall response. Conversely, the positioning of the instrument has a negligible effect on the total uncertainty, since the LUPIN was so far from the target, that the neutron flux did not significantly vary on a distance of 1 cm. The maximum discrepancy between the calculated and measured textcolor data is 5%, which roughly corresponds to the uncertainty of the measured response. For this reason, the agreement between the simulation and the experiments can be considered very satisfactory for calibration purposes.

Fig. 6
figure 6

Comparison between the calculated response and the experimental points measured at NPL

Full size image

Equation (2) shows that, for a Rem Counter, the response should be proportional to the neutron fluence to dose conversion factors. Figure 7 shows the comparison between these two curves. In this case, the instrument response was multiplied by the LUPIN calibration factor to overlap it with the conversion coefficients.

Fig. 7
figure 7

Comparison between the calculated response and the neutron fluence to dose conversion

Full size image

Figure 8 shows the ratio between the \(H^{*}(10)\) measured by the LUPIN and the real value as a function of the neutron energy, i.e., it shows the ratio between the two curves represented in Fig. 7. In an ideal case, these two curves should be perfectly overlapped and the ratio should be equal to 1 for any neutron energy. This is approximately true between 1 and 10 MeV, which is the emission energy range of the PuBe with which the instrument calibration factor was assessed. Conversely, at low energies, the LUPIN can overestimate the dose of a factor bigger than 5, while for energies above 10 MeV, it tends to underestimate the dose.

Fig. 8
figure 8

Ratio between the expected reading of the LUPIN and the real value of the ambient dose equivalent as a function of the incident neutron energy

Full size image

However, in most cases, the neutron spectrum in a workplace ranges over several orders of magnitude of energies. The LUPIN is mainly sensitive to neutrons above 1 MeV and, at these energies, the measured dose is generally quite accurate. On the other hand, a severe overestimation of the dose occurs for 10 eV–10 keV neutrons, but it has little effect on the overall instrument reading due to the low value of the response at these energies. In the energy range 100 keV–1 MeV, the instrument reading tends to underestimate the dose, but, as shown in Fig. 7 the slope of the response function is fairly similar to the conversion coefficients. This means that the two curves overlap if a specific calibration factor k is chosen. If neutrons in this energy range have to be measured, re-calculating the calibration factor from Eq. 2 significantly improves the instrument accuracy.

This behavior is quite common in REM counters, since in most cases the shape of the response function is dictated by the size and shape of the moderator surrounding the detector, and it is generally not possible to keep a perfect agreement with the fluence-to-dose conversion coefficient over several orders of magnitude. The response of the LUPIN is compared to the ones of other cylindrical rem counters (WENDI [19] and LINUS [20]) in Fig. 9. In all cases, the response to a side irradiation (i.e., in radial direction) was considered. Like the LUPIN, the two other rem counters are based on a central thermal neutron detector encapsulated in a moderator made of polyethylene, borated rubber and lead (for the LINUS), or of polyethylene and tungsten powder (for the WENDI-II). A detailed description of the instruments is provided in the cited references. It is clear that the instruments are quite similar in terms of response functions. What makes the LUPIN unique is its electronics, which allows its use in very intense pulsed fields where active detectors are often unreliable due to saturation effects.

Fig. 9
figure 9

Comparison between the responses of three rem counters

Full size image

4 Conclusions

This paper describes the calibration of the LUPIN Rem Counter in the monoenergetic fields of the National Physical Laboratory. A Monte Carlo model of the instrument was developed to calculate its response to neutrons between 10 meV and 1 GeV. The LUPIN was tested at five different energies between 71 keV and 16.5 MeV, which allowed the validation of the model with a maximum deviation of 5%. The main limitation of this calibration is that it validates the model only in the energy range 100 keV–20 MeV. In fact, this is the energy region in which monoenergetic neutrons can be obtained with nuclear reactions. An exact validation at lower energies is of little interest, considering that the detector is quite insensitive to thermal and epithermal neutrons. This is not the case for neutrons above 20 MeV, which have significant biological weight and must be measured in some cases (e.g., in fields close to accelerator facilities or for cosmic neutron measurements). Moreover, the lead layer plays a crucial role in the detection of these neutrons, whereas its relevance is almost negligible when compared to polyethylene for lower energies. This means that imperfect modeling of the lead layer (in terms of exact thickness and positioning, material density, and physical models employed for the simulations of high-energy neutron interactions...) might still be present in the simulation without having been shown by these measurements. Quasi monoenergetic neutron fields up to 200 MeV can be obtained in specifically designed facilities, and it is advisable to calibrate the instrument response also in these conditions for its use in high-energy neutron measurements.