Abstract
In this review, starting with the essence of phase singularities (Sect. 1) and continuing with the methods for the generation of singular beams of different kind (Sect. 2), we concentrate on optical vortices (OVs), which are the only known purely two-dimensional dark beams carrying point phase singularities. We describe some methods to determine their topological charges (Sect. 3) and how to convert them, e.g., in the linear process of diffraction from a hologram with an encoded OV, as well as after nonlinear processes of cascaded four-wave mixing and of the non-perturbative process of high harmonic generation (Sect. 5). In Sect. 6, we describe a method based on singular optics for the generation of long-range Bessel-Gaussian beams. Particular attention is paid to the suppression of the interaction of pairs of OVs and to the generation of large arrays of hundreds of OVs on a common background beam in square-shaped and hexagonal OV lattices (Sect. 7). The rich possibilities for the controllable generation of ordered focal structures of bright peaks and the possible additional structuring of each peak with other singular beams are illustrated, as well as the mixing of such OV arrays. New experimental results, devoted to novel possibilities for generating rich structures composed by bright peaks in the artificial far field from OV lattices with high TCs, are also presented for the first time in this paper and discussed in detail in (Sect. 8). In the last section, we describe a new method for the generation of arrays of long-range Bessel–Gaussian beams (Sects. 9). Without any claim for completeness or comprehensiveness, we believe that this overview will present to reader at least some of the beauty of experimental singular optics in space and could serve as a valuable initial step in order to dig deeper into the field.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let us recall the meaning of the terms “dislocation” and “singularity” using an illustrative example: The North and South Poles of the earth globe lie at points where all meridians intersect. Hence, they are not in any unique time zone. In a certain sense, there is a time singularity at the poles. For this trivial example, the indeterminacy is resolved by convention: The Greenwich Mean Time is taken as standard at the poles. The vortex and the tornado are two other familiar examples. Dislocations of a screw and edge type, in the form of abrupt changes in the arrangement of atoms, are also well known. More precisely, singularities (dislocations) are places where mathematical or physical quantities become infinite, or change abruptly [1]. The early history of wave singularities is related to the names of W. Hamilton, Whewel and Airy [1] and to their works devoted to conical refraction (1832), tides in the oceans (1833, 1836), and the rainbow phenomenon (1838). The simplest function with a phase singularity is the map from Cartesian space to the complex plane [2]
which is zero at the origin of the coordinate system (\(x=y=0\), i.e., at \(R=0\)). The phase can be interpreted (see Fig. 1) as the polar angle \(\varphi\), which is defined everywhere except at the origin. In each diametral cross section of \(\varphi\), there is a phase jump of \(\pi\) at the origin.
The usual optical beams can be described as localized (e.g., bell-shaped) waves in space with rapidly decreasing intensity at increasing distances from the beam axis. Examples of such beams are Gaussian beam and hyperbolic-secant beam (see Fig. 2a), which we often denote as “bright beams” in the following. Characteristics for their phase profiles are their flat phases. The presence of phase dislocations (singularities) in the wavefront of a light beam (see Fig. 2b) determines its intensity structure. In the case of a \(\pi\)-phase dislocation, the phase is indeterminate at the singularity point, both the real and the imaginary parts of the field amplitude vanish, and the field intensity decreases to zero [3]. Such beams, nested on a bright background of finite extend, will be referred to as “dark beams.” Since both dark and bright beams are localized in space, they become broadened by diffraction in the course of their free-space propagation. The formulas shown above the graphs in Fig. 2 refer to the specific case when the diffraction in one spatial dimension is exactly compensated by a third-order local nonlinearity (positive—for bright beams, negative—for dark beams) such that bright and, respectively, dark one-dimensional Schrödinger solitons are formed.
The focus of this paper is on optical vortices (OVs)—the only known singular optical beams carrying truly two-dimensional phase dislocations. OVs have spiral phase wavefronts (Fig. 3a) and characteristic toroidal (doughnut-shaped) intensity profiles (Fig. 3b) [3,4,5]. An essential parameter of an OV is its topological charge (TC)—a positive or negative integer number \(\ell\) corresponding to the total phase change 2\(\pi \ell\) over the azimuthal coordinate
Sometimes the TC is also called winding number of the loop or dislocation strength. The sign of the TC is depending on the sign of the azimuthal phase gradient[6,7,8]. We will restrict this presentation to canonical vortices, i.e., vortices for which the spiral phase varies uniformly with the azimuthal angle \(\varphi\) (see Fig. 3a and, e.g., Fig. 2 in [9]). Also, we will not discuss the other broad class of OVs, namely OVs carrying polarization singularities [10, 11].
The first experimental observations of dark pulses in the form of dark solitons were reported in the publications of Emplit ([12] in 1987) and Weiner ([13] in 1988) and their co-workers. It is interesting to note that the more complex experiments in the time domain preceded the first experiments on dark beams and dark solitons in space ([14] in 1990 and [15] in 1991). In these experiments, amplitude masks are used to ensure the desired even initial conditions, i.e., pure amplitude modulation without phase jumps. In self-defocusing nonlinear media input even dark beams split into a pair (or pairs) of diverging grey beams with abrupt opposite phase changes located at their dark cores. Because the abrupt phase changes are smaller than \(\pi\), the modulation depth is less than unity, thus the adopted beam notation is “grey beams”. Odd initial conditions are created by using glass plates with two levels of thickness as phase masks. When properly aligned, they imprint \(\pi\) phase jumps along two crossed lines on the input continuous wave beam. The simplicity of these experiments, firmly supported by physical intuition, is remarkable. It was also shown that there is no intensity threshold for the splitting and repulsion between such grey beams [16]; however, their transverse velocity is intensity-dependent [17].
The theoretical analyses on the existence of stable two-dimensional self-supported beams [18, 19] were followed by the experimental generation of optical vortex solitons [20]. In Swartzlander and Law [20], a simple three-level phase plate was used. Interest in OVs began to grow rapidly. Some of the first follow-up analyses are worth being mentioned [21, 22]. Around this time, the interest in singular optics was also born in the Department of Quantum Electronics of the Sofia University (Sofia, Bulgaria). Numerical results on the dynamics of optical vortices and the first experimental results on the existence and evolution of ring dark solitary waves were published [23, 24].
2 Methods for generation and characterization of optical vortices
In this section, without any claim for completeness, we will briefly introduce some known ways for the generation of optical fields with vortex singularities. We can distinguish methods applicable outside of the laser cavity from intracavity methods, where the laser directly generates higher-order modes with the corresponding singularity.
2.1 Spiral phase plates
Figure 1 shows the probably most obvious approach for the generation of OVs: A plate of optical material whose thickness increases in azimuthal direction (see e.g., [25,26,27]). It is necessary to adjust the difference between the maximal and minimal optical thickness to be equal to the wavelength \(\lambda\) for which the phase plate is designed. Then, a flat phase front of a beam passing through it will change azimuthally from 0 to 2\(\pi\) and an OV with a unit TC will be generated. The sign of TC can easily be inverted by reversing (flipping) the phase plate. The great advantage of this method is that its efficiency is of the order of 80% [25] including the Fresnel reflections of the air-glass interfaces. It can be enhanced by a suitable anti-reflection coating. To our knowledge, the first such commercially available phase plates were fabricated for relatively low TCs. For e.g. \(|\)TC\(|= 1\), the necessary spiral growth of their thicknesses was discretized into 16 sub-levels (see e.g., Figs. 1 and 2 in [27]). Currently, such phase plates can be obtained with relatively high TCs (e.g., \(\sim\)32), with a thickness discretization at 64 sub-levels. Liquid-crystal spiral phase plates with cell thicknesses suitably chosen to generate OVs with TCs of 1–4, as well as stacking such plates to obtain OVs with higher TCs are also known [28].
The great disadvantage of phase plates is that they are applicable almost exclusively for the wavelength for which they are designed. By “almost” we mean that a phase plate designed for a wavelength \(\lambda\) but illuminated with, e.g., the second harmonic (\(\lambda /2\)) will approximately reproduce an OV with twice the topological charge. Figure 4 clarifies the meaning of “approximately.” When the used wavelength deviates from the design wavelength, the phase plates generate OVs with fractional TCs (TCs whose value is not an integer number). In the intensity distribution of the beam, this fractional TC appears as a radial dark stripe (see Fig. 4). The larger the deviation of the used wavelength from the design wavelength, the larger is the modulation depth. As the phase plates are usually (to the best of our knowledge) produced with a sawtooth azimuthal thickness profile (i.e., the phase is encoded modulo 2\(\pi\)), the number of radial dark stripes is equal to the design TC. This outlines one possible simple method for determining the unknown TC encoded in such a phase plate. We will dwell on the problem of determining the TCs of the OVs later in this review. Last but not least, phase plates that provide linear phase retardations on one half of a laser beam only are also able to produce optical vortices [29].
Intensity distributions of optical vortex beams generated by spiral phase plates designed for nominal topological charges \(|\)TC\(|=2\) at 570 nm (upper row of frames) and \(|\)TC\(|=3\) at 530 nm (lower row of frames), when illuminated also with wavelength which deviates from the design wavelength of the phase plates. The corresponding wavelengths are denoted on top of each column of frames. The larger the deviation of the used wavelength from the design wavelength, the larger is the modulation depth (see the radial dark stripes)
2.2 Computer-generated holograms
The use of computer-generated holograms (CGHs) is another powerful method for generating beams with a desired singular phase distribution. In Fig. 5, we illustrate the computation of a CGH reproducing OVs with topological charges TC \(=1\) and TC \(=-3\). The first step is to calculate the two-dimensional intensity distribution, which would be observed as a result of the interference of a reference wave with intensity \(I_R(x,y) \propto |E_R(x,y) |^2\) propagating at an angle \(\theta\) with respect to the object (dark) wave \(I_D(x,y) \propto |E_D(x,y) |^2\). In the simplest approach, the reference wave is a plane wave and is overlapping with an object wave with the desired phase profile \(\Phi (x,y)\). One can even assume that the amplitude modulation of the object wave is a result of the diffraction from the CGH, thus neglecting its initial amplitude modulation. The interference signal \(I_{\text{interf}} (x,y)\) can then be calculated by considering only the interference term \(I_{\text{interf}} (x,y) \propto \cos [\Phi (x,y)+\alpha x]\). In the particular case of an OV with a TC = \(\ell\), the interference signal \(I_{\text{interf}} (x,y) \propto \cos [\ell \arctan (y/x) + \alpha x]\). Here \(\alpha\) is the spatial frequency of the interference lines and is inversely proportional to their spatial period. Physically, \(\alpha\) is related to the angle between the interfering reference and object beams. In Fig. 5a1, b1, grayscale plots of the phases of OVs with TCs \(=1\) and \(-3\) are shown. Black and white denote phases 0 and 2\(\pi\), respectively. The positions of the phase jumps are easily identified in the phase plots. They correspond to the points of fork-like splitting of one interference line into \((1+\ell )\) lines (see frames (a2) and (b2) in Fig. 5), where \(\ell\) is the TC. The orientation of the fork-like splitting depends on the sign of the encoded TC.
Grayscale plots of the phase distributions of an OV with TC \(=+1\) (a1) and of an OV with TC \(=-3\) (b1) and the corresponding grayscale ((a2) and (b2)) and binary computer-generated holograms (a3 and b3, respectively). The orientation of the fork-like splitting depends on the sign of the encoded TC
In order to create practically applicable and cheaper CGHs, the calculated pattern is discretized in a finite number of gray levels. When using discretization in two levels, the CGH consists only of transmitting and reflecting zones and can be manufactured by a standard photolithographic technology. The typical grating period is of the order of 20 µm, the size of the CGH on the order of (10\(\times\)10) mm\(^2\). In frames (a3) and (b3) we show the binary versions of the CGHs shown in panels (a2) and (b2), respectively. When binary CGHs are reproduced, the diffraction efficiency in the even diffracted order beams is negligible. This feature, as well as the maximum achievable diffraction efficiency of only \(\sim\)10% in the 1-st diffraction order and the unavoidable quantization error of \(\pi\)/24 (mean square root) are discussed in the classical work of Lee [30].
Another limitation stems from the fact that once produced by photolithographic technology, the CGH cannot be reconfigured (which, however, is possible if it is displayed on an, e.g., liquid-crystal spatial light modulator). This limitation is slightly mitigated by the fact that the TC of the OV in the m-th diffraction order is m times higher than the one reproduced in the first diffraction order. It was shown by the authors in [31] that when a Gaussian laser beam diffracts by a fork-shaped grating with encoded phase singularity of order \(\ell\), the diffracted beam in the positive and negative m-th diffraction order has TC equal to \(+m\ell\) and \(-m\ell\), respectively.
When working with CGHs, proper attention must be paid to the shielding of the diffraction orders that are not used. However, we would not like to be understood that CGHs do not have specific advantages. They can operate with continuous laser beams at any wavelength for which the binary structure is of high transmission/reflection contrast. Their applicability to few-cycle femtosecond laser pulses with broad spectra is also possible and will be discussed later in this review.
2.3 Generation of OVs with spatial light modulators
In terms of reconfiguration flexibility, spatial light modulators (SLMs) are, in our opinion, unrivaled. The principle of their operation is based on the voltage-controlled optical and electrical anisotropy of the liquid crystal molecules with which each individual pixel of the array is filled. When the desired and preliminary calculated phase distribution (see Fig. 5a1, b1) is sent to the SLM, the phase of each pixel is converted to a voltage across the liquid crystal cell corresponding to this pixel. The modulation of the phase of the laser beam leads to a modulation of its amplitude/intensity. Some researchers prefer to project computer-synthesized holograms onto the modulators. It is a matter of choice and experimental demands which option to choose. However, one should take into account that the efficiency of the modulated signal is reduced when using computer-synthesized holograms. Also blocking beams of unwanted diffraction order is required. When adequately calibrated, grey levels of the calculated phase vary from 0 to 255 corresponding to a linear increase of the introduced phase from 0 to 2\(\pi\). When switched off, the reflective SLM is acting as a flat mirror.
One of the main advantages of the SLMs over the above-mentioned methods for OV generation is their flexibility and reconfiguration options. SLMs support a wide spectral range covering the VIS and NIR region. A fine calibration of the device can be performed by projecting an OV and tuning the voltages sent to the SLM such that the radial amplitude modulations similar to those seen on Fig. 4 are minimized. The angle of incidence of the laser beam on the SLMs with respect to the normal incidence should be kept relatively low, in order to avoid possible birefringence (\(<4^{\circ }\)).
We would like to point out that a SLM is particularly useful for, e.g., interferometric measurements. For instance, when aligned in an interferometer, even if it encodes a particular complicated phase distribution, the necessary constant (over the entire area of the SLM) phase distributions can be added to the complicated distribution. In this way, without any readjustment, one can implement some of the known techniques for quantitative reconstruction of the phase profiles of the generated beams [32].
2.4 Generation of optical vortices directly from a laser cavity
Without any claim for completeness, we briefly review some of the most well-known techniques for constructing laser cavities emitting vortex beams. Respective methods include pumping with doughnut-shaped beams [33, 34], using spot-defect cavity mirrors [35], side-pumped design [36], and off-axis pumping [37, 38]. In Zhao et al. [33], the discrimination between the pure Laguerre–Gaussian LG\(_{0,+1}\) and LG\(_{0,-1}\) modes is obtained with the help of an uncoated YAG crystal plate and a proper thermal gradient on the ceramic. In Wang et al. [34], a single-frequency OV beam is generated from an Er:YAG non-planar ring oscillator pumped by an annular beam created with an axicon. The spot-defect cavity mirror used in Qiao et al. [35] is produced by laser inscribing round patterns on the surface of the cavity mirror. Based on this design, OVs with TCs up to 288 are generated [35]. In [36], a diode-side-pumped laser is described, producing a high-power TEM\(_{00}\) mode. Minor modification of the design to exploit the spherical aberration of the thermal lens is shown to allow for the generation of a doughnut-shaped high-power vortex mode with low astigmatism [36]. In Nam et al. [37], the slightly off-axis pumping geometry, achieved by a minor shift of the pump beam, supported the HG\(_{10}\) mode in the femtosecond regime. This HG\(_{10}\) laser beam of the mode-locked laser is externally converted into LG\(_{0,\pm 1}\) modes by a single-cylindrical-lens mode converter [37]. In Ma et al. [38], direct generation of red and orange optical vortex beams from an off-axis diode-pumped Pr\(^{3+}\):YLF laser is demonstrated. Vortex fiber lasers use additional elements for either mode selection or conversion of the LP\(_{01}\) mode. Optical metasurfaces (compact planar components which can manipulate light with high efficiency in a broad wavelength range) provide a suitable alternative. In Wang et al.[39], the authors demonstrate a plasmon metasurface-assisted vortex fiber laser generating OVs with reconfigurable TCs around 1030 nm.
2.5 Laser mode converters to optical vortices
In Allen et al. [40], the authors present a mode converter consisting of two cylindrical lenses which is able to transform Hermite–Gaussian (HG) modes to Laguerre–Gaussian (LG) modes and vice versa. Its operation is based on the dexterous use of the Gouy phase. The underlying analytical result is that a LG mode can be decomposed into a set of HG modes (see Fig. 3 in [41] and Fig. 1 in [40]). The beam to be converted should be made astigmatic in a confined region only, but remains isotropic outside this region. When passing through this confined region, the necessary phase difference will be introduced between the HG components which are oriented along the axes of astigmatism. Two cylindrical lenses with focal lengths f aligned at a distance \(2d = \sqrt{2}f\) form the so-called “\(\pi /2\)-converter” are able to transform a diagonal HG mode to a LG mode. The authors introduce also a “\(\pi\)-converter” which exchanges the indices of the incoming LG mode, thus converting it into one with opposite azimuthal dependence (TC).
In the figure below, we show test results based on a \(\pi /2\)-converter built at Sofia University. The input HG\(_{01}\) mode (Fig. 6a1) was generated directly by a He-Ne laser by carefully aligning its cavity. The cylindrical lenses were rotated such that they were at an angle of 45\(^\circ\) to the principal axes of the HG\(_{01}\) mode. The obtained LG\(_{10}\) mode (OV with a \(|\)TC\(|= 1\)) is shown in Fig. 6b1. When this beam is partially cut with a sharp blade, the diffraction from the edge partially overlaps with the dark vortex beam and a fork-like splitting of one interference line becomes visible, see Fig. 6c1. As mentioned, this is indicative for a single topological charge. In panels (a2, b2, c2) in Fig. 6, we show results obtained with the same convertor when aligning the laser cavity to emit HG\(_{02}\) mode. It was converted to a doubly charged OV beam. As seen in panel (b2) of Fig. 6, the OV with \(|\)TC\(|= 2\) has decayed into two OVs with identical topological charges (see also panel (c2)). Note that no special efforts were made in this test to prevent the decay.
Using the described cylindrical-lens converter, mode-locked HG beams (TEM\(_{0m}\) modes with \(m=\) 0–9) from a Nd:GdVO\(_4\) laser are converted into picosecond optical vortex pulses with TCs from 0 to 9 and with an excellent spatial beam quality [42]. In Chen et al. [43], symmetric and asymmetric HG modes are generated from an off-axis pumped solid-state laser and are thereafter converted into elliptic vortex beams with different spatial asymmetries by using an astigmatic mode converter.
Since cylindrical-lens mode converters are incompatible with fiber optic components, we will also briefly mention mode conversion in optical fibers. Perhaps, the most simple converter can be realized by using a helical long-period fiber grating [44]. It ensures high mode conversion efficiency and low loss. In Zhou et al. [45], a broadband tunable optical vortex based on such grating inscribed in a single-mode fiber is experimentally demonstrated. In this case, core-cladding mode dual resonance near the dispersion turning point is used. Ultra-broadband operation based on the same principle is reported in [46]. In Zhang et al. [47], high-order OVs are generated in a few-mode fiber via cascaded acoustically driven mode conversion by means of an acoustically induced fiber grating. Two such gratings were simultaneously induced in the same segment of the fiber by a radio frequency source containing two different frequency components. One of the gratings converted the left- and right-handed circular polarization fundamental modes to OVs with TCs \(\pm 1\), which were further converted to OVs with TCs \(\pm 2\) by the second grating.
2.6 Generation based on modulational instability
It is possible to create pairs of OVs based on the instability of singular beams. In the following we will distinguish between modulational instability of highly-charged OVs and instability of one-dimensional dark beams.
OV solitons were first generated by using discrete “spiral”-type phase masks [20, 29, 48] and by taking advantage of the modulational instability of one-dimensional dark beams [21]. In the case of an \(\ell\)-fold charged screw dislocation, the addition of a small coherent background at the reproduction of, e.g., computer-generated holograms gives rise to its splitting in \(\ell\) dislocations of charge 1 [49]. A theoretical and experimental study on the propagation and decay of highly charged optical vortices in a medium with an anisotropic nonlocal nonlinearity can be found in [49]. Even for an isotropic nonlinearity, the vortex dynamics of the nonlinear wave equation shows that OV beams of charge \(|\ell |\ge 2\) are topologically unstable [50]. The suppression of the transverse instability by saturating the nonlinearity [51] allowed us to generate stable OV solitons with TCs up to \(|\ell |=4\) [52]. In Dreischuh et al. [53], we present a linear analysis and numerical simulations of the instability of optical vortex solitons of arbitrary topological charge. The numerical results show a rich variety of instability scenarios depending on the type of perturbation. The saturation of the nonlinearity is shown to slow down the decay of multiple charged dark beams at an intermediate evolution stage and to prevent their ultimate decay into singly charged OV solitons. This concept is experimentally verified by the observation of a partial decay of a triple-charged OV beam [52]. A rare case in which such decay is useful will be described later in this paper, when introducing a method developed for generating long-range Bessel-Gaussian beams.
As already mentioned, soon after their discovery, OV solitons were generated by modulational instability of one-dimensional dark beams [54]. In Fig. 5 in Dreischuh et al. [55], we showed the characteristic snake-like bending of the one-dimensional dark spatial soliton (see also [56]). In the final stage of the instability, pairs of interacting OV solitons with opposite topological charges should appear even with saturated self-defocusing nonlinearity [54]. In Dreischuh et al. [57], we showed by numerical simulations (see e.g., Fig. 6 in [57]) that optical vortex dipoles with fractional topological charges carrying mixed edge-screw phase dislocations are prone to such instabilities provided that the length-to-width ratio of the dipole is 4 or more. A semi-infinite vortex dipole can be viewed as a one-dimensional phase dislocation of \(\pi\) spanning from far outside the background beam to, e.g., its center and ending with a phase semi-helix from 0 to \(\pi\). Equivalently, the semi-infinite vortex dipole can also be viewed as a fractional vortex dipole shifted asymmetrically with respect to the axis of the background beam. In Fig. 2 in Dreischuh et al. [58] is shown that in a self-defocusing Kerr nonlinear medium such dipole develops snake instability. Vortices with alternating TCs separate from the dark stripe near the center of the background.
In our opinion, snake instability is difficult to control, which limits the approach of generating vortex beam based on modulational instability.
2.7 Generation with metasurfaces
The generation of OV is also possible by using metasurfaces. Producing them requires precision both in design and fabrication, but it seems that the resulting vortices can be well-controlled. In turn, with structured beam interferometry (e.g., with OV beams), such metamaterials can be precisely characterized.
In very general terms [59], a metamaterial (MM) is any material engineered to have a property that is not found in naturally occurring materials. Metasurfaces (MS) consist of a single or a few layers of nanoscale building blocks called meta-atoms, arranged in a two-dimensional structure [60]. By engineering the meta-atoms, the (optical) properties of the MSs can be controlled, which is especially important when used with ultrashort or shaped laser pulses [60]. An overview of the mechanisms that enable control over the local linear and nonlinear interactions on such MSs is published in [61]. Here we will provide some references regarding the generation of OVs carrying phase dislocations by means of metasurfaces, although MSs are capable to shape the polarization state of the beam as well (see e.g., [62,63,64]).
In Jiang et al. [64], an azimuthally symmetric MS for the GHz range is demonstrated to convert, e.g., a left-handed circularly polarized incident plane wave to a right-handed circularly polarized vortex with \(|\)TC\(|=2\). In Cheng et al. [65], a kind of THz vortex beam generator based on square split-ring MSs is analyzed. In Liu et al. [66], a MS with unit-cell structure comprising three resonators is designed. It is shown to generate vortex beams at three distinct THz frequencies with up to \(|\)TC\(|=3\). The performance of a reflective MS generating OV beams with \(|\)TC\(|=1\) and 2 between 0.3 THz and 0.45 THz is reported in [67]. A thermally tunable MS composed of cylindrical dielectric micropillars is also proposed to generate OVs in the region from 0.69 to 1.65 THz [68]. A MS that can simultaneously generate two vortices with TC \(=1\) and four vortices with TC \(=-1\) at 1 THz is described in [69]. At the same time, it generates two vortices with TC \(= -2\) and one with TC \(= 2\) at 1.3 THz. A MS combined with a material changing between amorphous and crystalline state is shown to operate as a switchable vortex beam generator from TC \(= 2\) to TC \(= -2\) and vice versa for the \(\sim\)80 GHz range [70]. An inverted action, namely a mode converter based on anisotropic MSs converting a waveguide TE\(_{01}\) mode into a circularly polarized Gaussian beam, is reported in [71], again for the range 35–38 GHz.
The intense research in the THz domain is at least partially provoked by the application prospects of MMs in future THz communication [69]. For the optical domain, we will mention only two new results. In the wavelength range from 820 to 900 nm, a plasmonic MS with rectangular nanoapertures is capable of generating beams with arbitrary spatial variation of phase and linear polarization, as well as radially and azimuthally polarized vector beams and double mode vector beams [72]. Metasurfaces that generate OVs with \(|\)TC\(|=1\) at 532 nm are produced in a crystalline silicon 100-nm-thin film [73].
Let us also give some examples in which MMs are objects of the study with optical vortices. In conventional interferometry, displacements of linear fringes are measured. In vortex-based interferometry, the interference patterns resulting from overlapped focused Gaussian and vortex beams can have spiral structure (see Fig. 7, row (b)). The phase shift due to the MS results in a rotation of a spiral interference pattern. In this way, small and spatially inhomogeneous samples of MMs and MSs can be measured directly, thus visualizing the phase changes introduced by subwavelength-thick nanostructures [74]. Measured phase shifts in transmission and reflection along with the measured transmittance and reflectance spectra allow for retrieving the real and imaginary parts of effective permittivity and permeability, as well as the refractive index for metamaterials having positive, zero and negative refractive indices [75]. A pure OV with a \(|\)TC\(|= \ell\) becomes deformed when transmitted through a thin slab, and decomposes in to OVs with \(|\)TC\(|=(\ell +1)\) and \((\ell -1)\) [76]. This deformation is accompanied with a TC-dependent Goos-Hänchen shift. In [76], the authors show that epsilon-near-zero metamaterial is suitable to achieve the TC-dependent Goos-Hänchen shift.
2.8 Generation of OVs in femtosecond laser fields
The above-mentioned methods for the generation of OVs in the cw and the quasi-cw regimes are not suitable for few-cycle femtosecond lasers. The shorter the femtosecond pulse, the broader its spectrum. Hence, the magnitude of the phase jump in the different spectral components will deviate from \(\pi\), even when the vortex phase plate is designed for the central wavelength of the emission spectrum. The use of liquid crystal spatial phase modulators is also not always possible, since they cannot withstand high powers and high peak intensities. Astigmatic transverse-mode converters cannot be used directly, since mode locking is achieved if the cavity is aligned to emit the fundamental TEM\(_{00}\) mode.
One possible solution [77] of the problem is a computer-generated hologram aligned as a part of a dispersionless 4-f system [78]. Assuming that a singly charged OV is encoded in the CGH serving as one diffraction grating of the setup, an iris diaphragm located in the Fourier plane should not affect the propagation of the first-order diffracted beam but has to remove all other beams. When correctly aligned, with a second diffraction grating of the same period as this of the CGH, the 4-f system cancels for the spatial dispersion introduced by the CGH. Vortices generated by the CGH in each individual spectral component are recombined spatially and temporally to overlap at the exit of the 4-f system without spatial chirp (see Eq. 5 in [77]). Using a binary CGH, produced photolithographically with a stripe period of 30 µm, we successfully generated optical vortices in the output beam of a 20-fs Ti:Sapphire laser [77] by using a 4-f setup. In this case, the two gratings were arranged in a double-pass configuration.
Alternatively, in Mariyenko et al. [79] the authors demonstrated the applicability of a 2f-2f setup for the generation of femtosecond OVs. The incoming optical beam/pulse first passes through the first ordinary diffraction grating. An off-axis aperture transmits the beam diffracted in first-order only. A lens then focuses the optical beam into the exit grating, which is a CGH. This lens having a focal length f is positioned at a distance 2f from both gratings. A second lens, identical to the first one, is placed immediately behind the CGH in order to ensure a linear magnification of \(-1\). However, it should be kept in mind, that the 2f-2f system is acting as pulse stretcher. In Bezuhanov et al. [80], we demonstrated that OVs and other dark beams carrying phase dislocations can be generated in double-pass grating compressors without introducing additional spatial dispersion. One of the gratings has to be replaced by a CGH of a period equal to that of the other grating. In a proof of principle experiment with a double-pass compressor, the broad bandwidth of femtosecond laser pulses is imitated by sets of measurements conducted with a cw laser tuned between 780 nm and 805 nm. The OV is embedded in the beam by the first grating (CGH). It passed through the entire system and was used as a spatial marker. It was shown that the OV preserved its output position in space for all wavelengths.
An alternative approach based on vortex phase plates is analyzed by Swartzlander [81]. A suitably designed stack of two materials whose interface resembles a helicoid could serve as an achromatic vortex phase plate. However, to the best of our knowledge, only theoretical data for the visible spectral range have been published [81] and no experiments were performed with such elements. Even if proper pairs of optical glasses are available for the typical spectral widths of few-cycle laser pulses, the flexibility in changing the TCs will be lost with this approach. On the other hand, much higher pulse energies will be afforded.
3 Methods for measuring the topological charges of OVs
Bearing in mind that computer-generated holograms are one possible method for generating OVs, the idea of determining TCs of OVs from interference patterns arises naturally. If a Mach–Zehnder interferometer is used, the laser beam is divided into two parts, conventionally denoted as reference and object beams. Let us assume that an optical vortex is shaped in the object arm in one of the already described ways. After re-combining the beams at the second beam splitter of the interferometer, the resulting interference pattern is recorded by a CCD camera for subsequent analysis.
a1 Near-field intensity distribution of an elementary cell, portion of a bigger hexagonal OV lattice (see dashed yellow triangle). a2 Related interference pattern of the marked elementary cell with an inclined plane wave, indicative for the value and the sign of the TC of every single OV forming the cell. Frames b1 to b4 show interference patterns obtained by overlapping OVs with TCs \(=1,2,3\) and 4 with spherical waves
In panel (a2) of Fig. 7, we show a result, obtained when in the object arm of the interferometer a hexagonal OV lattice is created. We will describe the idea of the vortex lattices in details later in Sect. 4 of this paper. Briefly it is a large “lattice” (array) composed by OVs with alternating TCs. The elementary cell of the particular lattice shown in Fig. 7, consists of three OVs located in the apices of an imaginary equilateral triangle, having equal in value and sign TCs, and a fourth OV in its center with opposite TC. All OVs carry unit topological charges (with the mentioned different signs). The dashed yellow triangle in panel (a1) of Fig. 7 is intended to mark one such elementary cell. The picture was taken in the near field after a liquid crystal spatial phase modulator, which explains the wide dark cores of the OVs. Outside the triangle, a hexagonal structure of OV dark cores is visible, which motivates the name of this OV lattice. In the related interferogram in panel (a2) of Fig. 7, the dashed triangle encloses the same cell. As with the computer-generated holograms (see panel (a2) in Fig. 5) an OV with \(|\)TC\(|=1\) is identified by the splitting of one interference line into two. The orientation of the fork-like splitting (up or down) indicates the sign of the TC. The splittings of the interference lines in panel (a2) of Fig. 7 at the apices of the imaginary triangle are downwards. For the central OV, they point upwards. In all cases, one interference line splits into two lines. Therefore, the OVs have unit topological charges, whereby the central OV has an opposite TC as compared to the other three OVs.
To the best of our knowledge, one of the simplest ways to determine the TC of an OV by an interference pattern is by using a single-lens interferometer [82, 83]. Briefly, when an uncoated focusing lens is used, two weak Fresnel reflections from its surfaces occur. In this way, a low intensity “ghost” beam is formed. Its focal plane is at a distance much shorter than the focal length of the lens. This “ghost” beam is co-axial with respect to the main “background” beam which is serving as a reference beam in this short single-lens interferometer. A detailed description of single-lens interferometers can be found in [82, 83]. In the present geometry, the “ghost” beam is focused and, therefore, it has a spherical wavefront. The main (reference) beam is also converging, but more weakly, which implies a larger radius of curvature of its wavefront. Therefore, for spherical wavefronts with significantly different radii of curvature, the interference pattern of an optical vortex does not consist of interference lines, but of interference spirals, which seem to emerge from the dark core of the OV beam. It should be noted that with a perfectly aligned single-lens interferometer, the two dark vortex cores overlap and interference spirals cannot be observed because there is no light in the cores of the OVs.
In Fig. 7 (lower row of frames), experimental frames taken with such setup are shown. They are slightly perturbed such that the dark core of the focused OV overlaps with the bright ring arc of the reference OV. In frames (b1)–(b4) of Fig. 7, it can readily be seen that the measured OVs have topological charges 1 for frame (b1), 2 for frame (b2), 3 for frame (b3), and 4 for frame (b4), all of them with the same sign. Specifically, these measurements are made with OVs generated by directly projecting the respective helical phase distributions (see e.g., frames (a1) and (b1) in Fig. 5) onto a liquid crystal phase modulator. According to our experience, a single-lens interferometer is applicable only for a small number of OVs with relatively small TCs (up to e.g., \(|\)TC\(|=5\)). Unfortunately such interferometer is not applicable for femtosecond pulses.
Another simple, yet efficient method, applicable only to individual vortices (not to arrays of OVs), is to focus the vortex beam with a cylindrical lens [84,85,86,87]. Near the focus of the lens, the beam becomes highly elliptical and the vortex becomes strongly perturbed. Multiply charged OVs break up into singly charged vortices, each one with a highly elliptical core. The focused background beam appears to be cut by inclined dark lines, which are actually the distinct cores of the optical vortices. This feature is shown in Fig. 8 for different values of topological charges. The change in the sign of the TCs is reflected in a change in the direction of the slope of the dark stripes on the focused elliptical background beam.
Intensity distributions of OV beams with different TCs when focused by a cylindrical lens. The TCs denoted to the left of each frame are identified by the number of dark inclined lines (actually the highly-elliptical cores of the decayed OVs). The different directions of the inclined lines indicate different signs of the measured TCs
The value of the OV’s TC can also be determined by the number of dark fringes after diffraction from an annular grating, where its sign is identified by the orientation of the diffraction pattern [88]. Topological charges can also be measured by analyzing the far-field diffraction pattern when such beams pass through pairs of slits [89], through triangular [90,91,92,93], square [94, 95], annular [96], or sectorial apertures [97].
Yet another method is using an inverted field interferometer—either as Michelson or Mach–Zehnder type. The peculiarity of an inverted field interferometer is that the number of reflections in one of its arms differs from the number of reflections in the other arm by one (or by an odd number). As a result, the beam in one of the arms is flipped with respect to the beam in the other arm. Originally, such interferometers were used in autocorrelators for detecting the pulse front tilt of femtosecond laser pulses [98, 99], which, in fact, was also our initial motivation to analyze and use an inverted-field autocorrelator/interferometer [100,101,102]. When an optical vortex beam enters the device, two OVs with the same absolute value, but with opposite signs overlap on the second beam-splitter of the device (provided that Mach–Zehnder-type interferometer is used) and interfere thereafter. The result is an interference pattern similar to a cosine-LG beam with a radial mode index equal to zero. Neglecting a possible pulse front tilt, the result (see Eq. 7 in [103]) shows that the power density P of the interference signal is proportional to
Here \(r,\varphi\) are the polar coordinates, \(r_0\) is the background beam width, \(\omega _0\) is the carrier frequency, \(\tau _{d}\) is the delay between the interfering waves, and \(\ell\) is the topological charge of the input OV. Because of the \(\cos ^2\)-function, the number of azimuthal peaks is twice as large as the actual TC (see Fig. 9). From the argument of the \(\cos ^2\)-function, one also can deduce that the increase/decrease of the time delay will result in a change of the direction of rotation of the interference pattern. Calibration of the rotation direction with an OV with a known TC can be used to subsequently unambiguously determine the signs of tested OVs.
The potential broader use of such a device is discussed in [103]. Obviously, the technique is well-suited for calibrating delay lines without any realignment by self-reference. In addition, by blocking one of the arms of the interferometer, one can use OV beams/pulses with opposite TCs, which are well located in the plane of a desired target and have precisely known time delays. In Dimitrov et al. [104], we reported a novel technique that allows realignment-free switching between the interferometric and the background-free mode of autocorrelation of ultrashort laser pulses. It is based on a collinearly aligned inverted-field interferometer and an optical vortex phase plate that is added/removed in front of the device in order to switch between these two modes. The applicability down to the 10-fs range of the technique is also shown in [104].
4 Interactions between optical vortices and generation of vortex lattices
The generation of complex periodic structures (lattices) and the interaction of waves with complex wavefronts with such lattices are of undoubted interest since they offer new possibilities to engineer the diffraction properties of light (see e.g., the review paper [105] and references therein). The reader may be interested to refer also to the classical paper describing the formation of periodic refractive index structures in photorefractive materials [106]. Here we will briefly review our results on the suppression of the interaction between optical vortices leading to the generation of stable OV lattices.
Analogously to point vortices in fluid dynamics [107, 108], OVs of the same unit TC repel and orbit each other at a rate that is inversely proportional to the square of the vortex separation distance [109,110,111]. OVs with opposite TCs translate with respect to the background beam [111], attract each other and eventually annihilate. From a fundamental point of view, the type of OV interaction, both in linear and nonlinear media, is dictated by the combined phase structure of the vortices on the broad background beam. In Hansinger et al. [112] is shown that in the initial stage of nonlinear evolution, regardless of the sign of the Kerr nonlinearity, the behavior of a pair of vortices is the same as in the linear regime—rotation for equal TCs and translation on the background beam for opposite TCs. In a self-focusing medium, at a later stage of propagation, this evolution is strongly affected by the change of the background beam structure.
The possibility to control and stabilize ensembles of OV solitons against rotation and translation by a proper choice of the topological charge of a “control” OV nested in the center of the ensemble is confirmed numerically in [110]. In the context of this work, ensemble means a symmetrically ordered structure of equally-charged OVs. Positioning in the ensemble center (namely on the axis of rotation) an OV with an appropriate sign and value of the TC, one can cancel or even reverse its rotation. Moreover, the mutual OV solitons’ position remains unchanged. An extension of vortex ensembles to large regular lattices is also analyzed in this work. Stable large hexagonal OV lattices composed of a simple elementary cell–three equally-charged OV solitons situated in the apices of an equilateral triangle and a “control” OV with the opposite TC located in the center of the triangle is also found [110]. In the subsequent theoretical analyses followed by an experiment, we successfully generated a rigid square-shaped OV lattice as well [113]. The elementary cell of this lattice was composed of four OVs of the same TCs and a central “control” OV with opposite TC.
Both hexagonal and square-shaped OV lattices were reconstructed experimentally using computer-generated holograms. The +\(1\textrm{st}\) or \(-1\textrm{st}\) order of the diffraction was weakly focused on the input face of a glass cell containing a thermal nonlinear medium (slightly absorbing ethylene glycol). The generated OV lattices were stable in space (see Fig. 5 in [113]). In the nonlinear regime, the periodic intensity modulation created a periodic modulation of the refractive index of the medium, i.e., an effective phase grating was formed in it. Diffraction of a perpendicularly propagating probe beam from this grating was observed. The formation of stable OV lattices deserves some attention indeed. In the further course of this review, some intriguing results and some new data on the transformation of such lattices in the (artificial) far field will be provided.
5 Arithmetics with topological charges of optical vortices
Here we will consider some possibilities to controllably change the TCs of OVs. Different scenarios in both, linear and nonlinear regime will be discussed.
5.1 Conversion of the topological charge of an optical vortex in a linear process
The transformation of incident OV beam through different types of diffractive optical elements with encoded phase singularities is studied in [114,115,116]. In Topuzoski et al. [114], the authors have shown analytically that in the process of diffraction of Laguerre–Gaussian beams with zero radial mode number and arbitrary azimuthal mode number \(\ell\), by a fork-shaped grating with encoded integer TC p, the diffracted beam carries a topological charge of \(s=\ell \pm mp\) in the positive and negative m-th diffraction order. The experimental data presented in [117] confirm the predicted transformation of the TC of an incident OV beam after diffraction by a fork-shaped computer-generated hologram: The final TC of the vortex is equal to the TC of the incident beam plus the diffraction order (including its sign) times the TC encoded in the binary grating. In this experiment, the incident vortex beam was also obtained by diffraction of a Gaussian laser beam by another fork-shaped hologram. In Fig. 10, we schematically present the interaction process and its result. The presented data refer to an incident OV beam with a TC \(\ell =2\) and a hologram with an encoded singly charged OV (i.e., \(p=1\)).
For the \(-2\textrm{nd}\) diffraction order (\(m=-2\)), the TC transformation rule predicts a resultant TC equal to zero. The upper row of frames of Fig. 10 shows experimentally recorded intensity distributions in the focus of a lens (i.e., in the artificial far field). The lower row of frames presents the corresponding interferograms in the far-field obtained with a Mach-Zehnder interferometer. As seen in the panel corresponding to diffraction in \(-2\textrm{nd}\) order, a well-formed single bright peak is obtained at the former position of the OV dark core in the focal plane of a lens. Within the central part of the corresponding interferogram, parallel interference lines without any fork-like splittings are seen. This confirms the erasure (annihilation) of the TC. Because of its absence, there is indeed no reason for the existence of a dark core on the bright background anymore. The theoretical results in [31, 114] for the algebraic transformation of the TCs of the OVs, as well as for the change of the vortex ring radii of the transformed beams vs. final TC are found in perfect agreement with the experimental data [117].
A detailed examination of the interferograms obtained in the other diffraction orders shows that the analytically derived rule for the TC transformation is followed exactly. As expected and evident from Fig. 10, the bright OV ring radii increase with increasing of the resulting TC. In the full extent of this experiment [117], we generated incident OVs with TCs equal to 2, 3 and 4 and let them, subsequently, diffract to the far field by other forked gratings encoded with TCs equal to 1 and 2 (see Fig. 10). The normalized OV ring radii retrieved from the experiment were also found to be in excellent agreement with the theoretical prediction (see Table 2 in [117]).
Transformation of an input OV beam with a TC \(=2\) after diffraction from a computer-generated hologram with an encoded singly-charged OV. In the different diffraction orders m, both the far-field intensities and interference patterns obtained with an inclined plane wave are shown. Notation for the final TC of the OV is shown below. See the text for details
The results described in this section raise at least two important questions: (1) Is it possible to erase high topological charges of OVs in the (artificial) far field and if yes what are the consequences? (2) Is it possible to annihilate a stable optical vortex lattice consisting of many (for example, several hundred) OVs of alternating topological charges and arranged in different symmetries? What a pure OV lattice looks like in the artificial far field is another though-provoking question. Answers and additional details will be given later in this paper.
In Topuzoski et al. [118], another interesting situation is demonstrated both theoretically and experimentally. A background beam, whose amplitude profile is X-modulated in azimuthal direction (consisting of four bright petals, separated by crossed one-dimensional dark beams with \(\pi\) phase jumps) is diffracted at a fork-shaped grating encoded with an OV with integer topological charge p. The X-modulated beam was generated in the first (and higher odd) diffraction orders when a Gaussian laser beam diffracts in the far field by the so-called four-sector binary grating [119]. As a result of Fraunhofer diffraction of the X-modulated beam by the fork-shaped grating, it transforms into an ordered array of five vortices. More precisely, it consists of a central vortex (whose value and sign of its TC depends on the diffraction order m) and four “satellite” vortices situated in the apices of a rotated square. A particularly interesting case is when \(|m |= 1\) and \(p=1\) (see Figs. 9 and 10 in [118]). In both, the positive and negative first diffraction orders, all generated vortices (one central and four “satellite”) have TCs with unit value. The difference is the following: in the \(+1^{\textrm{st}}\) diffraction order the “satellite” vortices have TC \(=1\) and the central vortex has TC \(=-1\), while in the \(-1^{\textrm{st}}\) diffraction order the “satellite” vortices have TC \(=-1\) and the central vortex has TC \(=1\). A special case is when the product of the diffraction order and the TC encoded in the fork-shaped grating is equal to two. Then a central vortex is absent, but the four “satellite” vortices (again with TCs of the same value and sign) are present.
We have intentionally drawn the reader’s attention to this experimentally confirmed theoretical model, because the resulting vortex structure is a rotationally stable elementary cell—the constituent part of a square OV lattice. Similar OV lattices were described in Sect. 4.
5.2 Nonlinear methods for converting the TCs of OVs
Moving on to the nonlinear methods for converting TCs to OVs, it is natural to start by considering the generation of their second harmonic. Second-harmonic generation (SHG) is a parametric process in which the orbital angular momentum of a vortex beam is doubled. When OVs with TCs \(\ell _1\) and \(\ell _2\) are frequency mixed in a second-order nonlinear process, the generated vortex has a TC of \(\ell _3 = \ell _1 +\ell _2\) [120]. Therefore, as a result of the SHG, the topological charge of an optical vortex should double its value [121,122,123,124,125]. However, since vortices with \(|\)TC\(|>1\) are unstable, weak perturbation can initiate a decay of the second-harmonic vortices into pairs of singly-charged vortices [53].
In Dreischuh et al. [126], we reported a systematic study of the vortex dynamics in the process of non-phase matched SHG in an iron-doped lithium niobate crystal. There, SHG is accompanied by different nonlinear processes such as thermal defocusing, the photorefractive effect, and self- or induced phase modulation. The OVs are generated by passing the laser beam through a computer generated hologram and selecting the \(\pm 1^{\textrm{st}}\) diffraction order. We employed three different laser sources which enabled us to distinguish between different nonlinear phenomena induced in the same SHG crystal: a Ti:Sapphire femtosecond oscillator emitting 140-fs pulses at a wavelength of 845 nm (Case 1), a mode-locked laser emitting 18-ps pulses at 1064 nm (Case 2), and a Ti:Sapphire amplified system involving a parametric amplifier emitting 150-fs pulses at 1464 nm (Case 3). When the SHG crystal is photosensitive (in the sense of photorefraction) at both the fundamental and second-harmonic wavelengths (Case 1), the combined action of the thermal and photovoltaic nonlinearities lead to an alignment of the OVs at the fundamental and the second harmonic in the near field and to the generation of complex spatial patterns in the far field (see Fig. 4 in [126]). When photorefraction is initiated in the SHG crystal by the generated second-harmonic beam only (Case 2), the nonlinear self-phase matching is accompanied by a rotation of a two-color vortex by 90\(^{\circ }\) (see Fig. 7 in [126]). In contrast to the previous two cases, in Case 3, under the influence of positive nonlinearity, we achieved nonlinearly accelerated vortex rotation, as well as spectral broadening of the femtosecond vortices due to the pump-induced phase modulation. In summary, in the process of SHG of OV beams, their topological charge is doubled, which, under certain conditions of perturbations, leads to their decay into OVs with unit topological charges.
In [127], the first experimental generation of high harmonics with femtosecond OV beams reaching the extreme ultraviolet is reported. Despite the fact that this process is non-perturbative, it was expected that the TC of the \(n-\)th harmonic is n times the TC of the OV at the fundamental frequency. The experiment was done with singly-charged OVs. It was found that the two-dimensional point phase singularity imprinted on the fundamental beam survived the highly nonlinear process. The physical expectation (see e.g., [128]) that the TC is multiplied by the harmonic order was definitely confirmed in a subsequent experiment [129].
In Hansinger et al. [130], we reported for the first time cascaded nonlinear four-wave frequency mixing with femtosecond OVs and coherent transfer of their helical point phase singularities over multiple orders. Whereas, the generation of white-light supercontinuum by vortex beams in CaF\(_2\) [131] led to the breakup of the vortex ring into single filaments and destroyed the spatial coherence of the beam completely, in [130] special attention was paid to the control of the nonlinearity strength to reduce the effect of filamentation and improve the coherent transfer of the phase throughout the nonlinear cascade. Under the combined action of non-phasematched four-wave mixing as well as self- and cross-phase modulation, we succeeded to generate complex singular beams within a spectral bandwidth larger than 200 nm [130]. The topological charge conservation during the nonlinear wave mixing process was found to be fulfilled. In other words (see Fig. 11), the rule for the transformation of the TCs (\(\ell _s=2\ell _1-\ell _2\)) follows the rule for the conversion of the photon energies \(\hbar \omega _s = \hbar (2\omega _1-\omega _2)\). The experimental results are in good agreement with frequency-domain numerical calculations based on a set of four [132] and ten [130] coupled nonlinear Schrödinger-type equations for the newly generated spectral satellites. Numerical results from the model with 10 equations are shown in Fig. 11. The particular data correspond to a singly-charged OV beam/pulse in one of the pump components (\(m_0\)) and to a Gaussian beam/pulse without any TC in the other one (\(m_1\)). Please note that the authors in [130] denoted the TC with m, instead of \(\ell\) as adopted so far in this paper.
Algebra of vortex TCs due to cascaded four-wave mixing. The experimental double-peak input spectrum is shown in red, together with simulated intensity (top) and phase (bottom) profiles after nonlinear propagation for the mixing of a Gaussian beam with a vortex of unit TC. The magnitude of the TC denoted here with \(m_i\) changes by 1 with the order of the cascading process, which can be seen in the steeper phase spirals further away from the pump beams. The intensity profile in 3rd order already shows distortion due to strong intensity dependence. Reprinted with permission from [130]. ©The Optical Society
The above-mentioned experiment deserves a more detailed description. In order to generate pump beams with sufficient spectral separation, the 38-fs amplified Ti:Sapphire laser beam is split with a dichroic beam-splitter (see the spectrum in Fig. 11). This beam-splitter (BS) was the first BS of a Mach–Zehnder interferometer. In each of its arms, vortex phase plates were added/removed. After additional spectral filtering and recombination with a low-dispersion broadband BS, the vortex beams were then focused with a spherical mirror into an evacuated gas cell. Nonlinear wave mixing is observed only in the 3-mm-thick fused silica glass entrance window. The evacuated cell was used to terminate the nonlinear process. The peak intensity inside the entrance window was estimated to be \(\sim\)1.1\(\times 10^{10}\,\)W/cm\(^2\). After the gas cell, the beam was recollimated and interfered with a broadband reference beam from a gas-filled hollow-core fiber. For the synchronization in time of the laser pulses, a delay line with a length of some 17 m was aligned. Combination of long- and short-pass filters was used to study the TCs of the vortices in the particular spectral windows (see Fig. 3 in [130]). In Fig. 12, we show a small part of this published figure based on experimental data, that confirms the formulated rule for conversion of the TCs.
Experimental interferograms (upper row) and beam profiles (lower row) for vortex pump beams with TCs \(+1\) and 0 and for the components generated by the nonlinear four-wave mixing (enclosed frames). The experimental data correspond to the numerical results as shown in Fig. 11. The numbers in the small boxes indicate the TCs of the vortices. Adapted with permission from [130]. ©The Optical Society
6 Generation of long-range Bessel–Gaussian beams
In this section, we will first discuss the question posed above, namely is it possible to annihilate (erase) highly charged OVs? This will lead to a, perhaps, surprising application, specifically the generation of Bessel-Gaussian beams (BGBs) of impressive quality.
The intuitive answer concerning the feasibility of the annihilation of highly charged OVs would be yes. However, one should keep in mind that highly charged OVs are very unstable and they decay into singly charged OVs. By the “high topological charge” or highly charged OV, we will understand TCs with a value of 10 or more. The experiments we are reporting are done with TCs up to 50. At these high TCs, the modulation instability is very strong and the decay of these multiply charged states is complete—they decay into individual OVs with TC of one. Since all TCs have the same sign, their mutual repulsion is strong. As a result, the OVs tend to arrange in a circle and to broaden the dark core of the bright ring-shaped beam. Interferograms have shown that the vortices are distributed along the inner arc of the bright ring. There are no phase singularities in its central part. Therefore there is no reason for the central part of the beam to be “black”. Light can penetrate into the central area and the beam becomes slightly “gray.” However, the contrast between the bright ring and the dark core remains very high. Moreover, the bright ring-shaped beam originating from an OV with high topological charge has a large ratio of ring radius \(r_0\) to ring width \(\omega _0\).
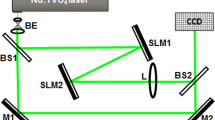
If such a highly charge OV is created by, e.g., programming the first half of an SLM, the erasure of the TCs of the individual vortices arranged in a ring can be done on the second half of the same SLM as shown in Fig. 13. The effort to do so is minimal; cw beam coming from a Ti:Sapphire laser oscillator (central wavelength of 805 nm), reaches the first half of a SLM encoded with a phase distribution of multiply charge OV. The beam is then redirected by a flat mirror (M) to the second half of the same SLM. This half is programmed with phase distribution with inverted sign of the TCs. It should be kept in mind that the TC of an OV reverses upon every refection. Therefore, when a setup with two SLMs is preferred (and there is no intermediate reflection from a mirror), the second SLM has in fact to be programmed with the same OV phase distribution as the first one. Independent of which experimental setup is used, the result is an annular bright beam with a large radius-to-ring width ratio and without phase singularities in it.
Experimental setup: Ti:Sapphire laser oscillator emitting in cw regime at a central wavelength of 805 nm. BE – beam expander (magnification factor of 3); SLM—computer-controlled liquid-crystal spatial light modulator; M—flat silver mirror; L—converging lens with \(f = 75\) cm; CCD camera placed in the focal plane of the lens L, with the option for following the beam up to 200 cm after the focal plane of the lens. Distance from SLM to M – 10 cm
An intriguing change of the beam shape occurs, when this ring-shaped beam is focused by a thin lens (L). As is well known, this is equivalent to a Fourier transformation in space, and thus the focal plane is the (artificial) far field. As the Fourier transform of a narrow ring is a Bessel beam, a Bessel–Gaussian beam is formed from the ring-shaped beam in and after the focus of the lens. If the TCs of all OVs were erased, a zero-order Bessel–Gaussian beam is formed, if all but one were erased, a first-order Bessel–Gaussian beam will be formed [133,134,135]. The method allows for the generation of higher-order Bessel–Gaussian beams as well.
Let us briefly present the corresponding analytical model. In polar coordinates (\(r,\theta\)), the amplitude of the electric field E of the ring-shaped beam where all but \(\ell\) optical vortices are already annihilated can be represented as
Applying the Fourier transformation, we obtain for the electric field amplitude \(E'\) of the optical beam in the far field
provided \(r_0\) \(\gg\) \(\omega _0\) is fulfilled. Not surprisingly, the residual TC\(=\ell\) determines the order of the Bessel multiplier \(J_\ell\)(\(r_0\rho\)). This term is multiplied by a Gaussian function. Hence, a Bessel–Gaussian beam is formed. In the particular case of \(\ell =1\), this is a first-order BGB carrying an on-axis OV.
In Fig. 14, a comparison of theoretical results (green curve) and experimental data (red circles) is shown for zeroth- (Fig. 14(a)) and first-order (b) BGBs. The experimental data were recorded after annihilating OVs with a \(|\)TC\(|=21\), 15 cm behind the focus of a thin lens. The intensity distribution of the BGBs is shown in the upper insets. The lower insets show the respective interferograms. One can clearly see that for the zeroth-order BGB there is a continuous interference fringe in the central peak, indicating flat phase front. One can also see that in the dark rings the interference fringes are offset by a half period, which indicates radial phase jumps of \(\pi\) between the adjacent rings.
Radial profiles of zeroth- and first-order Bessel–Gaussian beams (graphs (a) and (b), respectively) measured experimentally (red hollow circles) in comparison with theoretical profiles of zeroth- and first-order Bessel beams (solid green curves). Insets—the corresponding intensity profiles and interferograms visualizing the absence/presence of an on-axis OV and of radial phase jumps. See the text for details
In Fig. 15, we show results, for the creation and annihilation of OVs with TCs \(+25\) and \(-25\) and followed by Fourier transformation of the ring-shaped beam. Again the experimental setup with single phase modulator and two reflections from it was used (Fig. 13). Each half of the SLM is programmed with the corresponding phase distribution. The measured divergence half-angle of the BGBs shown in Fig. 15 was 45 µrad.
The analysis presented here and in [133,134,135] shows that the generated BGBs have negligible transverse evolution up to several meters due to a divergence on the microradian scale and thus can be regarded as quasi-non-diffracting. The method is much more efficient as compared to those using annular slits in the back-focal plane of lenses [136,137,138]. Moreover, at large propagation distances the quality of the generated BGBs significantly surpasses the quality of BGBs created by low angle axicons as demonstrated in, e.g., the supplementary material to [133], as well as Fig. 7 of [134]. The increase of the ring radius to ring width ratio of the beam in the plane of the focusing lens, obtained by increasing the TCs prior to their subsequent annihilation, leads to a radial shrinking of the central peak and of the bright rings surrounding it [133]. Also, the shorter the focal length of the lens, the narrower the central peak of the BGB; however, at the expense of its propagation range [134].
In Stoyanov et al. [139], we generated zeroth- and first-order BGBs using a single reflective spatial light modulator in the sub-8-fs range (see Fig. 1 in [139]). No noticeable consequences for the pulse duration were measured. The only observed effect was a weak “coloring” of the outer-lying satellite rings of the beams due to the spectrum spanning over more than 300 nm (Fig. 5 in [139]). The self-healing property of the generated few-cycle BGBs was also confirmed. The obtained beams had diffraction half-angles below 45 µrad and reached propagation distances in excess of 1.5 m. On the other hand, the use of SLMs limits the applicable maximum average powers and peak intensities. However, this limitation is, to a certain extent, compensated by their great flexibility: By using SLMs one can vary the TC of the annihilated OVs with ease, thus controlling the order of the generated BGBs but also the size of the central peak (or ring for higher-order BGBs). If high powers are needed, commercially available phase plates for generating OVs with high TCs are a possible solution.
7 Formation of arrays of bright beams in the focus of a lens
7.1 Creation and erasure of vortex lattices
In the context of the arithmetics with TCs of OVs, our attention was also attracted by the following set of questions: What is the spatial profile of an OV lattice in the artificial the far field? Is it possible to erase the alternatively varying topological charges of many, even hundreds of OVs arranged in such stable optical vortex lattices? And again: what will be the result of that in far field?
Throughout this and the following sections, we will use the terms period of the array, array (lattice) node spacing, and lattice constant as equivalent, denoting the distance between two neighboring vortices in any vortex lattice. Furthermore, terms OV lattice, OV array or array of OVs have the same meaning and are interchangeable.
Figure 16 provides some answers to the above questions. In its upper part, we present results of numerical simulations based on the linear paraxial equation for the slowly-varying optical beam envelope amplitude E
Here, the transverse part of the Laplace operator, accounting for diffraction, is denoted by \(\Delta _T\), the diffraction length of an individual OV by \(L_d = ka^2\), where k is the wave number and a is the width of an individual optical vortex.
The scenario is the following: A Gaussian laser beam (leftmost panel) enters the optical setup and illuminates the first spatial light modulator SLM1, programmed with the phase distribution corresponding to a square (upper frame) or hexagonal array (lower frame) of optical vortices. By convention, the zero coordinate, from which the propagation distance is measured, is at the position of SLM1 and z is measured in units of diffraction lengths \(L_d\) of an isolated OV. Once the corresponding vortex array was created by SLM1, diffraction is computed until \(z=1L_d\), where the second suitably programmed modulator SLM2 is reached. After the reflection at it, all OVs are erased. The subsequent propagation of \(2.5L_d\) up to the converging lens again is governed by diffraction only. Focusing then is accounted for by adding the thin-lens phase \(T(x,y) = \exp \{-ik(x^2 + y^2)/(2f) \}\) to the phase of the beam.
From the calculated data on the distributions of the beam intensities at the focal plane, it can be seen that after the erasure of both optical vortex arrays, well-localized bright beams are restored in the artificial far field. After the focus, they diffract similar to focused Gaussian beams. The respective calculated phase distributions clearly show the absence of phase dislocations in the bright peaks. For better visibility, the computed intensity distributions in the simulated focus at \(z=40\,L_d\) and \(7.5\,L_d\) behind it are magnified by a factor of 4. The same has been done with the computed phase distributions presented in the most right panels of the upper part of Fig. 16.
Upper part—numerical results. Erasure of all OVs of large square-shaped (upper row) and hexagonal OV lattices (lower row). Panels denoted with SLM1 show the phase distributions sent to the first SLM. SLM2 and L denote the intensity distributions just after the annihilation of all TCs at the (suitably programmed) second modulator and the resulting beam in the plane of the focusing lens. The intensities of the recovered bright beams in and after its focus and the calculated phase portraits are magnified for better visibility. The simulated propagation distance z is measured in units of Rayleigh diffraction lengths of a single OV. Lower set of frames—experimentally recorded intensity distributions of the recovered bright beams ((a) from a square-shaped OV lattice, (c) from a hexagonal lattice) and their corresponding interferograms ((b) and (d)). For better visibility all frames are magnified by a factor of 4
In the lower row of frames in Fig. 16, we provide experimental confirmations for the recovery of a more or less Gaussian beams after the erasure of square-shaped (SQ-SQ) and hexagonal OV arrays (HEX-HEX). Frames (a) and (c) present experimentally recorded intensity distributions in the beam’s foci. In the case of erasing the square OV array, faint satellite beams are seen which could be weak higher diffraction orders from the array itself. Around the focal peak obtained by annihilating the hexagonal array, no such satellites are visible. Frames (b) and (d) in the same figure present interferograms of the respective beams in the focus. Close examination of the interferograms shows continuous interference fringes across the peaks and confirms that there are no phase dislocations in these focal peaks.
7.2 Vortex lattices in the far field
Toward the end of this section, we will try to answer the question how an OV lattice looks like in the artificial far field [140, 141]? Let us start with the relatively simple case of square lattice of OVs with alternating unit TCs. This case is illustrated in Fig. 17. In its left part (a), results of numerical simulations based on Eq. 6 for lattice constants 41 pix. and 21 pix. are presented.
The two leftmost frames labeled with “L” show the simulated intensity distributions of the OV arrays in the plane of the focusing lens. Again, the simulated free-space propagation from the (virtual) SLM modulating the Gaussian beam to the lens is \(z=1L_{d}\). Throughout the propagation, the dark beams remain modulated down to zero intensity. When a square array of OVs is present in the plane of the lens, four axisymmetric bright peaks are observed in its focal plane in the simulations. They are located at the apices of a quadrangle. It is also seen that the OV lattice with the smaller period (the distance between two neighboring vortices in the OV array) leads to a focal array with more distant peaks, as compared to the one with a larger period, where more closely spaced peaks can be observed. This is easy to understand by recalling that the thin focusing lens performs a Fourier transformation in space, and for the Fourier transformation the scaling theorem holds (“wide” functions in the space domain correspond to “narrow” functions in the spatial frequency domain). The rightmost distributions present the calculated phase distributions of the beams in the focal plane of the lens. A closer look reveals that the phases of the bright beams are flat, and the optical vortices are located in the dark area between them. The two frames shown in panel (b) of Fig. 17 are the corresponding experimental data using a square-shaped OV array with a period of 21 pix. The quadrangle structure of well-formed bright peaks is clearly visible (b1), although there is a residual weak signal in the center, presumably it is zero-order diffraction from the vortex array. The corresponding interferogram (b2) shows straight interference lines at the positions of the peaks, thus confirming their flat phase fronts.
Transformation of square-shaped OV lattices in the artificial far field. Left set of frames (a) numerically calculated intensity distributions of the OV lattices of different periods in the plane of the lens, followed by the respective intensity and phase distributions in its focus. (b) Experimentally recorded focal structure (b1) and interference pattern (b2) of a square-shaped OV array with a period of 21 pix
Analogous to the preceding discussion, Fig. 18 is devoted to the transformation of a hexagonal OV lattices in the artificial far field. The simulations (left panels) show that three bright beams situated in the apices of a triangle are formed when such an OV array is present in the plane of the lens. This is confirmed by the experiment (right panels). However, three weak satellites are present as well, see panel (b1). The OV-to-OV separation in the experiment was 41 pix. The numerical data for the intensity distribution in the artificial far field again show a nice manifestation of the scaling theorem. Also, the prediction that the phase fronts of the bright peaks are flat is confirmed by the straight interference lines at the positions of the three beams in Fig. 18b2. When the signs of all topological charges are inverted, the same triangular structure of beams will be observed in the focal plane, however rotated by 180\(^\circ\). Such rotation is not possible in case of square OV array, since it is due to the characteristic symmetry of the hexagonal OV matrix.
Transformation of hexagonal OV lattices in the artificial far field. Left set of frames (a) numerically calculated intensity distributions of the OV lattices of different periods in the plane of the lens, followed by the respective intensity and phase distributions in its focus. (b) Experimentally recorded focal structure and interference pattern of a hexagonal OV array with a period of 41 pix
7.3 Mixing of vortex lattices
It is natural to expect that OV arrays of different types can also be mixed. This has been worked out in [139, 142, 143]. Similar to the previous subsections, phase distributions encoded on the two halves of the SLM (see Fig. 13) are superimposed. However, now the goal is not to erase all vortices; rather two OV arrays with different lattice constants and/or symmetries will be superimposed. Of course, this mixing takes place before the beam is focused by the lens.
We will start with the simplest case of mixing two square OV arrays, then we will proceed with mixing two hexagonal arrays, and finally a square array will be mixed with a hexagonal one. Figure 19 displays the results of two series of experiments for the first case. The same experimental setup as shown in Fig. 13 is used. In each series, the square OV array on the first half of the SLM (for simplicity we will refer to it as SLM1) was kept constant with an OV spacing of 41 and 61 pixels, respectively. On the second half of the SLM (SLM2), a square array with varying OV node spacings was programmed. The first thing to notice is that we reproduce the result of Sect. 7.1 in case both arrays have the same lattice constant: Then the OVs from the first half of the SLM are annihilated by those from the second half and a single Gaussian beam similar to the input beam emerges (first panel in the first row and second panel in the second row). Another observation is that it is irrelevant for a given pair of OV arrays which of both is programmed on SLM1 or SLM2. Accordingly, the second panel in row 1 shows the same far-field pattern as the first panel in row 2.
The cases of interest are two square OV lattices with different lattice constants. In order to reveal their behavior, the lattice constant on the second half of the SLM is changed between 41 and 151 pixels. As expected, having the convolution theorem in mind, one gets two square patterns of different dimensions nested into each other. We can distinguish large-scale square array of peaks, composed by four identical small-scale patterns (see the yellow dashed squares in Fig. 19). The quickest way to recognize what is going on in detail is to start watching the series with the largest lattice constant (151 pix.) on SLM2, i.e., to follow the row of panels from right to left. According to the scaling theorem, the largest lattice constant on SLM2 produces the smallest features (small-scale structures) in the far-field. These are the yellow dashed squares in the apices of a large (imaginary) square. As the lattice constant on the SLM2 shrinks, the size of the yellow squares grows. In contrast, the size of green dashed square (see Fig. 19) does not change within each row, corresponding to the fact that the OV lattice node spacing on SLM1 remains the same. However, their size in both rows is different, in fact in the ratio 41/61—once again a manifestation of the scaling theorem. The apices of the green squares are actually pointing to the “center of the masses” of the small-scale structures. The shrinking of the small-scale pattern leads to an seemingly overall shrinking of the large scale.
Let us compare two frames from one column of frames in Fig. 19 (for example these for a distance of 101 pix. on SLM2). It can be seen that the vortex array with the larger period on SLM1 gives more transversely concentrated peaks in the focus. In both frames, the size of the small-scale structure is unchanged, but the overall size of the large-scale structure is different. To sum up, one can control both the small-scale pattern and the large-scale pattern by a proper choice of the constants of the used lattices.
Experimental results showing the far-field pattern formation for two mixed square OV lattices. The two rows of the figure show two series of experiments. For each series, the lattice created by the first half of the SLM is kept constant with lattice constants of 41 and 61 pix (green letters). The lattice constant of the second lattice is varied between 41 and 151 pix (yellow letters). The yellow dashed squares are intended to guide the eye, showing the shrinking of the small-scale structures with the increase of the lattice node spacings on the second half of the SLM. The apices of the green squares points to the “center of the masses” of the small-scale structures
In Fig. 20, we present experimental data obtained when two hexagonal vortex arrays, again with different periods, are programmed on the two halves of the SLM. For the upper row of frames, Fig. 20a, the observed large-scale structure in the focal plane is triangular. At the apices of the (imaginary) triangle, the small-scale structure of beams is triangular as well. Again, the observed behavior is well explained by the similarity and convolution theorems. The data in the second row of frames in Fig. 20b are obtained by changing the signs of all TCs of all OVs of the hexagonal lattices with larger periods (61–151 pix.). As a result, all small-scale structures are rotated by 180\(^\circ\), while the large-scale structure keeps its orientation. Already at this point, the reader quite likely is convinced that the variety of structures in the focal plane can be controllably generated using an appropriate type of array, array node spacing, as well as the signs of the TCs of the OVs forming the array as control parameters.
a Experimental results showing different focal arrays of bright beams observed by mixing hexagonal OV lattices of node spacings denoted to the left of the row and in the left corner of every single frame. b Same as case (a), however the data are obtained by changing the signs of all TCs of all OVs of the hexagonal arrays with larger periods. As a result, all small-scale structures are rotated at 180\(^\circ\). See text for details
An even greater variety of far-field structures can be obtained by the mixing OV lattices of different symmetry and period, here demonstrated with square-shaped and hexagonal OV lattices. Figure 21 shows experimentally recorded far-field bright beam intensity distributions obtained by varying the node spacing of the square-shaped OV lattice and keeping the period of the hexagonal OV lattice constant (row (a)). The opposite case, where we vary the period of the hexagonal OV lattice while the period of the square OV array is kept unchanged is presented in row (b).
In case (a), the hexagonal lattice period is 41 pix. One can clearly see, that for OV-to-OV spacing of 21 pix. for the square OV lattice (row (a), left frame) the far-field beam profile has a triangular small-scale structure. This means that the small-scale structure is a result of the hexagonal OV lattice, which has larger node spacing of 41 pix. The large-scale focal structure is diamond-shaped with four of the mentioned triangular small-scale structures in its apices. Thus, the large-scale structure is formed by the square OV lattice with the smaller node spacing of 21 pix. Very intriguing is the other limiting case, shown in the most right frame of Fig. 21a: The OV-to-OV spacing of the square-shaped lattice is increased to 151 pix. The change in the symmetry of the structure is impressive. The small-scale structure becomes diamond-shaped. Three such structures are ordered in a triangle-like large-scale structure.
The experimentally recorded frames shown in row (b) in Fig. 21 provide yet another beautiful manifestation of the by now frequently cited similarity theorem: For a lattice node spacing of the hexagonal OV array larger than the one for the square array (hexagonal lattice from 41 to 121 pix. and square lattice node spacing fixed to 21 pix.) the result is shrinking of the small-scale (triangular) structures in the far-field. It is important to note, that a reversal of the phase distributions of the square-shaped and hexagonal OV lattice encoded on the two halves of the SLM will only change the orientation of the triangular small-scale structures but it will not affect the overall composition of the focal array [143].
Experimentally-recorded far-field beam reshaping by varying the node spacing of the square-shaped (row (a)) or of the hexagonal OV lattice (row (b)). In case a the hexagonal lattice node spacing is \(\Delta _{hex}=41\) pix. and \(\Delta =\Delta _{sq}/\Delta _{hex}\) varies between 0.5 and 3.7. In case b \(\Delta _{sq}=21\) pix. and \(\Delta\) varies between 0.5 and 0.17. This figure is first published in [143] as Fig. 7 and is reproduced here under a CC BY license
Without overloading this review with too much detailed information, we would like to briefly further mention that the results presented in [135] for triple mixing of square-shaped and/or hexagonal OV lattices substantially expand the results described up to this point. They are clear manifestations for the possibility to create a rich variety of focal arrays composed of bright beams. The OV lattice node spacing, independently of the type of the used OV lattices and independently of its orientation (rotation), can serve as a control parameter [135]. In the same work, besides the already commented large-scale and small-scale structures resulting correspondingly from the OV lattices with smaller period and from the OV lattice with the larger period, there is also a third intermediate-scale focal structure determined by the medial OV lattice period (independent of the OV lattice type—square or hexagonal.) This is in agreement with the similarity theorem of Fourier transformation. The possibility for an additional beam structuring of each of the peaks of the focal arrays by hosting one-dimensional and quasi-two-dimensional phase dislocations or even a singly-charged OV was also proven and demonstrated in the Supplementary material to [135], as well as in Fig. 6 in [142] and in Figs. 4 and 6 in [143]).
8 Focal beam sculpting using OV lattices with higher TCs
So far we have demonstrated the rich possibilities for the controllable generation of ordered focal structures by using square and/or hexagonal OV lattices. As shown, such lattices could be mixed, which in turn leads to a whole new sets of ordered focal arrays. We commented on two reliable control parameters: the type of the used OV lattices and its node spacing. In this section, we will present results showing that an additional third degree of freedom is available, namely the increase of the absolute value of the TC of every single OV in the lattice. The possibility for additional structuring of every single peak will also be presented and discussed. As in the previous, relatively simpler cases, such OV lattices can be mixed with other OV lattices with (unit or higher) TCs.
We already introduced in Fig. 13 the experimental setup which we also used to generate the ordered focal structures coming from optical vortex lattices with TCs higher than 1. We will briefly remind its basic concept. The cw beam from a Ti:Sapphire laser oscillator emitting at a central wavelength of 805 nm is expanded by a beam expander (BE) with a magnification factor of 3. Then, the beam reaches the first half of the computer-controlled liquid-crystal SLM, encoded with the phase profile of an OV lattices with \(|\)TC\(|= 1\) or higher. The beam then is redirected by a flat mirror (M) to the second half of the appropriately programmed SLM. On the second half of the SLM, again depending on the desired focal structure, different phase distributions can be used (or it can be used as a flat mirror). The point of interest is in the focal plane of the lens L (\(f = 75\) cm), where a CCD camera is placed. As already mentioned, when using square-shaped OV lattices, the order of projecting (encoding) the phase distribution on the SLM is not playing an important role in forming the desired focal arrays.
The projected OV lattices on the SLM are synthesized numerically by arranging OVs in periodic square-shaped arrays with alternating signs of their TCs, where the absolute value of the TCs varies from 1 to 5. The resulting far-field structures composed by ordered bright peaks are presented in Fig. 22. The clearly visible result of increasing the TCs of the initial vortices is the change in the number of peaks and the size of the focal structure. The explanation, with a high degree of credibility, may be the following. Each OV with a high TC decays into OVs with single TCs and they interact in a symmetric potential, causing a complex but symmetric change of the initial array of OVs. The yellow dashed square is intended to mark one small-scale pattern. Its size remains unchanged since the OV lattices constants does not change. The much richer pattern of bright peaks is only due to the increase of the absolute value of the TCs forming the OV lattices. Interestingly, at higher TCs there is a regular modulation of the intensity of the individual peaks.
Similar to the simple arrays of focal beams (see e.g., Fig. 8 in [140] and Fig. 4 in [143]), here in the right panel is presented the case of additional structuring of each focal peak with a single-charged OV. This was done by programming a second half of the SLM with the phase of an OV with \(|\)TC\(|=1\). The result is the sculpting of each focal peak with a singly charged OV evident by the splittings in the interference lines over the OV core. The fork-like splitting of the interference lines, always downwards, shows that each peak carries a singly charged OV and the signs of all OVs are the same.
Far-field intensity distribution of square-shaped OV lattice with \(|\)TC\(|=1\), 2, 3, 4, and 5, and node-spacing 41 pix., Fourier-transformed by a thin lens with a focal length \(f=75\) cm. Yellow dashed square denotes the small-scale structure in each case. Rightmost frame—demonstration of the possibility for additional sculpting of the focal beams. The interference pattern confirms the existence of singly-charged OV with the same sign in each focal beam
Analogous to the already commented cases of mixing different types of OV lattices, here we show that OV lattices with (unit or higher) TCs can also be mixed. In Fig. 23, this is demonstrated by an experimental example of mixing square-shaped OV lattices with node spacings 41 pix. and 81 pix. but with an increase of the TCs of the individual vortices in one of the lattices. We programmed the first OV lattice denoted as Sq.81 on the first half of the SLM, and the second OV lattice denoted with Sq.41 on the second half. These notations are used in Fig. 23 presenting the observed focal peak structures in the artificial far-field. All vortices constituting the lattice Sq.81 are with unit TCs. The Sq.41 is the same lattice used to obtain the data shown in Fig. 22. We varied the TCs from 1 to 5. As mentioned, in recording the results shown in Fig. 23 the OV lattice of larger period (81 pix.) remains unchanged. This explains the observation that the size of the small-scale focal structure remains constant. The convolution theorem is reflected in the size and form of the large-scale structure with increasing the TCs of the OVs in the array with a period of 41 pix. This large-scale structure is becoming richer with increasing the TCs. Denoting it “richer,” we also mean that in some parts of the multi-peak distributions the intensities of groups of peaks are lower; however, not chaotic, but in regular structures.
In the sense of the new results shown in Fig. 22 and 23, we could formulate the following partial conclusion. The structures composed of bright focal peaks in the artificial far field can be shaped by using OV arrays with different symmetries (square, hexagonal, inverted hexagonal), changing the node spacings of each array individually, mixing twice (or even three times [139]) OV lattices, or by changing the absolute values of the TCs of the OV, of which the lattices are arranged. Last but not least, by fine structuring every focal peak with a desired singular beam (one-dimensional, quasi-two-dimensional or two-dimensional (OV)).
9 Generation of arrays of Bessel-Gaussian beams in and behind the focal plane of a lens
Let us briefly recall the approach used for generating Bessel-Gaussian beams (BGBs). As described in Sect. 6, first an OV with a high TC is generated. This OV breaks up into many singly charged OVs, arranged such that a ring-shaped beam with a large radius-to-ring width ratio develops. All the vortices are then annihilated and the ring-shaped beam is Fourier-transformed in space by focusing it with a thin lens. In this way, long-range BGBs of very low divergence are obtained in and after the focal plane of the lens. Let us also recall how a relatively simple focal structure of bright beams is generated (see, e.g., Fig. 17 in Sect. 7). As a first step, a square-shaped (or hexagonal) array of OVs with alternating TCs has to be generated. Thereafter, it is Fourier-transformed in space by a thin converging lens.
Upper row of frames—typical phase distributions encoded on the first half of the SLM. Left to right—pure square-shaped OV lattice with node spacings 21 pix., same OV lattice with one (central) OV calculated to be with \(|\)TC\(|=20\), or with \(|\)TC\(|=30\) (last frame on the row). Captions below—the corresponding phase distributions encoded on the second half of the SLM in order to annihilate the central highly charged OV from the OV lattice. Below the line—Generation of arrays of zeroth-order long-range Bessel-Gaussian beams followed up to 40 cm behind the lens’s focus and comparison of their longitudinal evolution with the evolution of a pure square-shaped OV lattices of the same period (leftmost column of frames)
With both in mind, an interesting question arises: Is it possible to combine these two simple recipes in order to generate arrays of long-range Bessel-Gaussian beams? This is the essence of the new results to be presented in this section.
To show this, we use again the experimental setup introduced in Fig. 13. As a first step, we generate a simple square-shaped OV lattice with OVs of unit TC but alternating signs. The corresponding phase distribution is shown on the upper left frame of Fig. 24. A relatively small node spacing (21 pix.) was chosen in order to ensure a clear separation of the expected BGBs (small node spacing of the OV lattice in the near field results in large focal peak separation in the far field and vice versa).
Next, one of the OVs in the OV lattice’s phase distribution, preferentially one in the center of the lattice/beam, is replaced by a highly charged OV. The respective quite complex phase distributions for \(|\)TC\(|=20\) or 30 are shown in Fig. 24. According to the recipe for the generation of BGBs, we need to erase the highly charged OV on the second half of the SLM (or on the second SLM, if two SLMs are available) by programming it with an oppositely highly charged OV. However, the OV lattice must be kept. Therefore, for the above examples, only 19 or 29 TCs should be erased, such that nominally the phase distribution of simple square lattice is restored (although the intensity distribution has been disturbed quite heavily).
The final step of the beam shaping is to focus the beam with a thin lens. The result is shown in the second and third column of frames in the lower part of Fig. 24: Four BGBs arranged in the characteristic diamond-shaped pattern. They are recorded at distances of 20 cm, 30 cm, and 40 cm behind the focal plane of the lens. For comparison and as a proof of the low divergence of these BGBs the evolution of the four beams generated by the “pure” square-shaped OV array are displayed at the same distances after the focus of the lens (Fig. 24, left column of frames). The comparison of the BGBs at equal distances from the focal plane shows another familiar trend: The higher the encoded (and subsequently erased) TC, the narrower the central peak of the zeroth-order BGBs.
Generation of zeroth- and first-order long-range arrays of Bessel–Gaussian beams by annihilating one central OV with \(|\)TC\(|=30\) of square-shaped OV lattices with node spacings 21 pix. (left column of frames) and 41 pix. right column of frames. The labels to the left of each column of frames indicate the TCs of the OVs encoded on the second SLM, which partially or fully erase the highly charged OV in the center of the OV lattice array encoded on the first SLM
In Sect. 6, in the discussion on BGBs, eventually also first-order BGBs were discussed, i.e., hollow BGBs with an embedded OV. Therefore, it is natural to ask, which phase distribution one should use in order to produce an array of first-order BGBs. Probably, the answer is as natural as the question: In the end, we need to have the phase distribution of, e.g., square lattice, where one OV is missing in the center. This can be realized by starting with on the first half of the SLM as before, i.e., with a square OV array, where a central OV is replaced by a highly charged OV, for instance \(|\)TC\(|=30\). On the second half of the SLM, the highly charged OV is removed completely, such that no vortex remains in its former position in the lattice. Indeed, after focusing, an array of first-order BGBs appears as shown in Fig. 25.
So far, we took care that the BGBs of our BGB array were spatially well separated in order to avoid that the rings enclosing the individual Bessel beams would overlap. This was achieved by using a small lattice constant (21 pix.). Of course, the opposite case is interesting, too (Fig. 25, right column). By using a lattice constant of 41 pix, the separation of the BGBs can be halved. As a consequence, the rings surrounding the BGBs start to overlap and produce a rich interference pattern. Interestingly, the central beams remain stable.
The results shown in this section are strong confirmation in favor of the idea that the developed method for generating zeroth- and first-order long-range Bessel–Gaussian beams behind the lens’ focus can be successfully combined with the formation of ordered structure of focal peaks in the artificial far-field, resulting in arrays of low divergent long-ranged Bessel–Gaussian beams in and behind the focal plane of a lens.
10 Conclusion
In this review, we have tried to give an impression of the vast opportunities to manipulate and shape the propagation of light by vortices. The presentation has been made from the perspective of the experimentalist and kept at an largely elementary level. Likewise, the necessary optical elements and equipment (e.g., spatial phase modulators, phase plates, beam profilers) are not particularly complex, but are available in many laboratories. Future experiments and potential applications thus are only limited by the imagination of the researchers.
One possible direction of research we are planning to explore is controllable beam splitting and reversed beam recombination after a nonlinear process in the vicinity of the focal plane. Another interesting problem is related to the possible reshaping of low even and odd harmonics of Bessel–Gaussian beams in space. The optimization of long-range Bessel–Gaussian beams and of arrays of such beams may appear interesting for future free-space communications. Some of the mentioned approaches may appear suitable for new mode division multiplexing/demultiplexing schemes.
Data availability
The datasets generated and analyzed during the current study are available from the corresponding author on reasonable request.
References
M. Berry, Making waves in physics. Nature 403(6765), 21–21 (2000). https://doi.org/10.1038/47364
M.R. Dennis, H.H. Wills, Topological singularities in wave fields, (2001). https://api.semanticscholar.org/CorpusID:116621753
J.F. Nye, M.V. Berry, Dislocations in wave trains. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 336(1605), 165–190 (1974). https://doi.org/10.1098/rspa.1974.0012
S.M. Baumann, D.M. Kalb, L.H. MacMillan, E.J. Galvez, Propagation dynamics of optical vortices due to Gouy phase. Opt. Express 17(12), 9818–9827 (2009). https://doi.org/10.1364/OE.17.009818
A.S. Desyatnikov, Y.S. Kivshar, L. Torner, Optical vortices and vortex solitons, in Progress in Optics. ed. by E. Wolf (Elsevier, Amsterdam, 2005), pp.291–391. https://doi.org/10.1016/S0079-6638(05)47006-7
N.R. Heckenberg, R. McDuff, C.P. Smith, A.G. White, Generation of optical phase singularities by computer-generated holograms. Opt. Lett. 17(3), 221–223 (1992). https://doi.org/10.1364/OL.17.000221
M. Harris, C.A. Hill, J.M. Vaughan, Optical helices and spiral interference fringes. Opt. Commun. 106(4), 161–166 (1994). https://doi.org/10.1016/0030-4018(94)90314-X
J. Vickers, M. Burch, R. Vyas, S. Singh, Phase and interference properties of optical vortex beams. J. Opt. Soc. Am. A 25(3), 823–827 (2008). https://doi.org/10.1364/JOSAA.25.000823
G. Lao, Z. Zhang, D. Zhao, Propagation of the power-exponent-phase vortex beam in paraxial ABCD system. Opt. Express 24(16), 18082–18094 (2016). https://doi.org/10.1364/OE.24.018082
E. Otte, C. Denz, Sculpting complex polarization singularity networks. Opt. Lett. 43(23), 5821–5824 (2018). https://doi.org/10.1364/OL.43.005821
R. Liu, L.-J. Kong, W.-R. Qi, S.-Y. Huang, Z.-X. Wang, C. Tu, Y. Li, H.-T. Wang, Compact, robust, and high-efficiency generator of vector optical fields. Opt. Lett. 44(9), 2382–2385 (2019). https://doi.org/10.1364/OL.44.002382
P. Emplit, J.P. Hamaide, F. Reynaud, C. Froehly, A. Barthelemy, Picosecond steps and dark pulses through nonlinear single mode fibers. Opt. Commun. 62(6), 374–379 (1987). https://doi.org/10.1016/0030-4018(87)90003-4
A.M. Weiner, J.P. Heritage, R.J. Hawkins, R.N. Thurston, E.M. Kirschner, D.E. Leaird, W.J. Tomlinson, Experimental observation of the fundamental dark soliton in optical fibers. Phys. Rev. Lett. 61, 2445–2448 (1988). https://doi.org/10.1103/PhysRevLett.61.2445
D.R. Andersen, D.E. Hooton, G.A. Swartzlander, A.E. Kaplan, Direct measurement of the transverse velocity of dark spatial solitons. Opt. Lett. 15(14), 783–785 (1990). https://doi.org/10.1364/OL.15.000783
G.A. Swartzlander, D.R. Andersen, J.J. Regan, H. Yin, A.E. Kaplan, Spatial dark-soliton stripes and grids in self-defocusing materials. Phys. Rev. Lett. 66, 1583–1586 (1991). https://doi.org/10.1103/PhysRevLett.66.1583
S.A. Gredeskul, Y.S. Kivshar, M.V. Yanovskaya, Dark-pulse solitons in nonlinear-optical fibers. Phys. Rev. A 41, 3994–4008 (1990). https://doi.org/10.1103/PhysRevA.41.3994
Y.S. Kivshar, X. Yang, Dark solitons on backgrounds of finite extent. Opt. Commun. 107(1), 93–98 (1994). https://doi.org/10.1016/0030-4018(94)90109-0
A.W. Snyder, L. Poladian, D.J. Mitchell, Self-tapered beams. Opt. Lett. 17(4), 267–269 (1992). https://doi.org/10.1364/OL.17.000267
A.W. Snyder, L. Poladian, D.J. Mitchell, Stable black self-guided beams of circular symmetry in a bulk Kerr medium. Opt. Lett. 17(11), 789–791 (1992). https://doi.org/10.1364/OL.17.000789
G.A. Swartzlander, C.T. Law, Optical vortex solitons observed in Kerr nonlinear media. Phys. Rev. Lett. 69, 2503–2506 (1992). https://doi.org/10.1103/PhysRevLett.69.2503
C.T. Law, G.A. Swartzlander, Optical vortex solitons and the stability of dark soliton stripes. Opt. Lett. 18(8), 586–588 (1993). https://doi.org/10.1364/OL.18.000586
B. Luther-Davies, R. Powles, V. Tikhonenko, Nonlinear rotation of three-dimensional dark spatial solitons in a Gaussian laser beam. Opt. Lett. 19(22), 1816–1818 (1994). https://doi.org/10.1364/OL.19.001816
S. Baluschev, A. Dreischuh, I. Velchev, S. Dinev, O. Marazov, Generation and evolution of two-dimensional dark spatial solitons. Phys. Rev. E 52, 5517–5523 (1995). https://doi.org/10.1103/PhysRevE.52.5517
S. Baluschev, A. Dreischuh, I. Velchev, S. Dinev, O. Marazov, Odd and even two-dimensional dark spatial solitons. Appl. Phys. B 61(1), 121–124 (1995). https://doi.org/10.1007/BF01090982
M.W. Beijersbergen, R.P.C. Coerwinkel, M. Kristensen, J.P. Woerdman, Helical-wavefront laser beams produced with a spiral phaseplate. Opt. Commun. 112(5), 321–327 (1994). https://doi.org/10.1016/0030-4018(94)90638-6
V.V. Kotlyar, A.A. Almazov, S.N. Khonina, V.A. Soifer, H. Elfstrom, J. Turunen, Generation of phase singularity through diffracting a plane or Gaussian beam by a spiral phase plate. J. Opt. Soc. Am. A 22(5), 849–861 (2005). https://doi.org/10.1364/JOSAA.22.000849
C. Jun, K. Deng-Feng, G. Min, F. Zhi-Liang, Generation of optical vortex using a spiral phase plate fabricated in quartz by direct laser writing and inductively coupled plasma etching. Chin. Phys. Let. 26(1), 014202 (2009). https://doi.org/10.1088/0256-307X/26/1/014202
Q. Wang, X.W. Sun, P. Shum, Generating doughnut-shaped beams with large charge numbers by use of liquid-crystal spiral phase plates. Appl. Opt. 43(11), 2292–2297 (2004). https://doi.org/10.1364/AO.43.002292
G.-H. Kim, J.-H. Jeon, K.-H. Ko, H.-J. Moon, J.-H. Lee, J.-S. Chang, Optical vortices produced with a nonspiral phase plate. Appl. Opt. 36(33), 8614–8621 (1997). https://doi.org/10.1364/AO.36.008614
W.-H. Lee, III computer-generated holograms: Techniques and applications, in Progress in optics. ed. by E. Wolf (Elsevier, Amsterdam, 1978), pp.119–232. https://doi.org/10.1016/S0079-6638(08)70072-6
L. Janicijevic, S. Topuzoski, Fresnel and Fraunhofer diffraction of a Gaussian laser beam by fork-shaped gratings. J. Opt. Soc. Am. A 25(11), 2659–2669 (2008). https://doi.org/10.1364/JOSAA.25.002659
K. Creath, Temporal phase measurement methods. Interferogram. Analysis 96, 94–140 (1993)
Y. Zhao, Q. Liu, W. Zhou, D. Shen, \(\sim\)1 mJ pulsed vortex laser at 1645 nm with well-defined helicity. Opt. Express 24(14), 15596–15602 (2016). https://doi.org/10.1364/OE.24.015596
K. Wang, X. Zhang, S. Fu, C. Gao, 1645-nm single-frequency vortex laser from an Er:YAG nonplanar ring oscillator. Opt. Lett. 48(2), 331–334 (2023). https://doi.org/10.1364/OL.478505
Z. Qiao, G. Xie, Y. Wu, P. Yuan, J. Ma, L. Qian, D. Fan, Generating high-charge optical vortices directly from laser up to 288th order. Laser Photon. Rev. 12(8), 1800019 (2018). https://doi.org/10.1002/lpor.201800019
S.P. Chard, P.C. Shardlow, M.J. Damzen, High-power non-astigmatic TEM\(_{00}\) and vortex mode generation in a compact bounce laser design. Appl. Phys. B 97(2), 275–280 (2009). https://doi.org/10.1007/s00340-009-3642-5
H.A. Nam, M.G. Cohen, J.W. Noé, A simple method for creating a robust optical vortex beam with a single cylinder lens. J. Opt. 13(6), 064026 (2011). https://doi.org/10.1088/2040-8978/13/6/064026
Y. Ma, A. Vallés, J.-C. Tung, Y.-F. Chen, K. Miyamoto, T. Omatsu, Direct generation of red and orange optical vortex beams from an off-axis diode-pumped Pr\(^{3+}\):YLF laser. Opt. Express 27(13), 18190–18200 (2019). https://doi.org/10.1364/OE.27.018190
C. Wang, L. Gui, T. Zhang, F. Ding, S.I. Bozhevolnyi, K. Xu, Vortex beam generation directly from a fiber laser incorporating plasmon metasurface. in 2022 Conference on lasers and electro-optics (CLEO), pp. 1–2 (2022)
L. Allen, M.W. Beijersbergen, R.J.C. Spreeuw, J.P. Woerdman, Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 45, 8185–8189 (1992). https://doi.org/10.1103/PhysRevA.45.8185
M.W. Beijersbergen, L. Allen, H.E.L.O. van der Veen, J.P. Woerdman, Astigmatic laser mode converters and transfer of orbital angular momentum. Opt. Commun. 96(1), 123–132 (1993). https://doi.org/10.1016/0030-4018(93)90535-D
H.C. Liang, Y.J. Huang, Y.C. Lin, T.H. Lu, Y.F. Chen, K.F. Huang, Picosecond optical vortex converted from multigigahertz self-mode-locked high-order Hermite-Gaussian Nd:GdVO\(_4\) lasers. Opt. Lett. 34(24), 3842–3844 (2009). https://doi.org/10.1364/OL.34.003842
Y.F. Chen, Y.H. Lai, M.X. Hsieh, Y.H. Hsieh, C.W. Tu, H.C. Liang, K.F. Huang, Wave representation for asymmetric elliptic vortex beams generated from the astigmatic mode converter. Opt. Lett. 44(8), 2028–2031 (2019). https://doi.org/10.1364/OL.44.002028
S. Oh, K.R. Lee, U.-C. Paek, Y. Chung, Fabrication of helical long-period fiber gratings by use of a CO\(_2\) laser. Opt. Lett. 29(13), 1464–1466 (2004). https://doi.org/10.1364/OL.29.001464
M. Zhou, Z. Zhang, L. Shao, S. Liu, Y. Liu, Y. Pang, Z. Bai, C. Fu, W. Cui, L. Qi, Y. Wang, Broadband tunable orbital angular momentum mode converter based on a conventional single-mode all-fiber configuration. Opt. Express 29(10), 15595–15603 (2021). https://doi.org/10.1364/OE.421967
K. Ren, M. Cheng, L. Ren, Y. Jiang, D. Han, Y. Wang, J. Dong, J. Liu, L. Yang, Z. Xi, Ultra-broadband conversion of OAM mode near the dispersion turning point in helical fiber gratings. OSA Continuum 3(1), 77–87 (2020). https://doi.org/10.1364/OSAC.381877
W. Zhang, L. Huang, K. Wei, P. Li, B. Jiang, D. Mao, F. Gao, T. Mei, G. Zhang, J. Zhao, High-order optical vortex generation in a few-mode fiber via cascaded acoustically driven vector mode conversion. Opt. Lett. 41(21), 5082–5085 (2016). https://doi.org/10.1364/OL.41.005082
G.-H. Kim, J.-H. Jeon, Y.-C. Noh, K.-H. Ko, H.-J. Moon, J.-H. Lee, J.-S. Chang, An array of phase singularities in a self-defocusing medium. Opt. Commun. 147(1), 131–137 (1998). https://doi.org/10.1016/S0030-4018(97)00605-6
I.V. Basistiy, V.Y. Bazhenov, M.S. Soskin, M.V. Vasnetsov, Optics of light beams with screw dislocations. Opt. Commun. 103(5), 422–428 (1993). https://doi.org/10.1016/0030-4018(93)90168-5
J.C. Neu, Vortices in complex scalar fields. Phys. D Nonlinear Phenom. 43(2), 385–406 (1990). https://doi.org/10.1016/0167-2789(90)90143-D
B. Luther-Davies, J. Christou, V. Tikhonenko, Y.S. Kivshar, Optical vortex solitons: experiment versus theory. J. Opt. Soc. Am. B 14(11), 3045–3053 (1997). https://doi.org/10.1364/JOSAB.14.003045
A. Dreischuh, G.G. Paulus, F. Zacher, F. Grasbon, H. Walther, Generation of multiple-charged optical vortex solitons in a saturable nonlinear medium. Phys. Rev. E 60, 6111–6117 (1999). https://doi.org/10.1103/PhysRevE.60.6111
A. Dreischuh, G.G. Paulus, F. Zacher, F. Grasbon, D. Neshev, H. Walther, Modulational instability of multiple-charged optical vortex solitons under saturation of the nonlinearity. Phys. Rev. E 60, 7518–7524 (1999). https://doi.org/10.1103/PhysRevE.60.7518
A.V. Mamaev, M. Saffman, A.A. Zozulya, Propagation of dark stripe beams in nonlinear media: Snake instability and creation of optical vortices. Phys. Rev. Lett. 76, 2262–2265 (1996). https://doi.org/10.1103/PhysRevLett.76.2262
A. Dreischuh, G.G. Paulus, F. Zacher, I. Velchev, Steering one-dimensional odd dark beams of finite length. Appl. Phys. B 69(2), 113–117 (1999). https://doi.org/10.1007/s003400050781
A.A. Dreischuh, T. Arabadjiev, D. Neshev, G.G. Paulus, F. Zacher, H. Walther, Stability of one-dimensional dark spatial solitons of finite second transverse extent, in Tenth International School on Quantum Electronics: Laser Physics and Applications. ed. by P.A. Atanasov, D.V. Stoyanov vol. 3571 (1999), pp.169–173. https://doi.org/10.1117/12.347611
A. Dreischuh, G.G. Paulus, F. Zacher, Quasi-two-dimensional dark spatial solitons and generation of mixed phase dislocations. Appl. Phys. B 69(2), 107–111 (1999). https://doi.org/10.1007/s003400050780
P. Hansinger, G. Maleshkov, N. Gorunski, N. Dimitrov, A. Dreischuh, G.G. Paulus, Interaction between one-dimensional dark spatial solitons and semi-infinite dark stripes. Opt. Commun. 313, 106–112 (2014). https://doi.org/10.1016/j.optcom.2013.08.085
Wikipedia: Metamaterial. https://en.wikipedia.org/wiki/Metamaterial
M.R. Shcherbakov, F. Eilenberger, I. Staude, Interaction of semiconductor metasurfaces with short laser pulses: From nonlinear-optical response toward spatiotemporal shaping. J. Appl. Phys. 126(8), 085705 (2019). https://doi.org/10.1063/1.5108630
S. Keren-Zur, L. Michaeli, H. Suchowski, T. Ellenbogen, Shaping light with nonlinear metasurfaces. Adv. Opt. Photon. 10(1), 309–353 (2018). https://doi.org/10.1364/AOP.10.000309
X.-Y. Zeng, Y.-Q. Zhang, R.-R. Zhang, X.-R. Ren, Z.-J. Zhan, M.-N. Gu, R. Sun, C.-X. Liu, C.-F. Cheng, Generation of vector beams of Bell-like states by manipulating vector vortex modes with plasmonic metasurfaces. Opt. Lett. 46(3), 528–531 (2021). https://doi.org/10.1364/OL.415981
Y. Zhang, J. Gao, X. Yang, Spatial variation of vector vortex beams with plasmonic metasurfaces. Sci. Rep. 9(1), 9969 (2019). https://doi.org/10.1038/s41598-019-46433-z
S. Jiang, C. Chen, H. Zhang, W. Chen, Achromatic electromagnetic metasurface for generating a vortex wave with orbital angular momentum (OAM). Opt. Express 26(5), 6466–6477 (2018). https://doi.org/10.1364/OE.26.006466
K. Cheng, Z. Hu, Y. Wang, J. Ma, J. Wang, High-performance terahertz vortex beam generator based on square-split-ring metasurfaces. Opt. Lett. 45(21), 6054–6057 (2020). https://doi.org/10.1364/OL.401231
J. Liu, Y. Cheng, F. Chen, H. Luo, X. Li, High-efficiency reflective metasurfaces for terahertz vortex wave generation based on completely independent geometric phase modulations at three frequencies. J. Opt. Soc. Am. B 39(7), 1752–1761 (2022). https://doi.org/10.1364/JOSAB.460153
J.-S. Li, L.-N. Zhang, Simple terahertz vortex beam generator based on reflective metasurfaces. Opt. Express 28(24), 36403–36412 (2020). https://doi.org/10.1364/OE.410681
B. He, J. Fan, Y. Cheng, F. Chen, H. Luo, R. Gong, Thermally tunable terahertz vortex beam generator based on an InSb metasurface. J. Opt. Soc. Am. B 38(5), 1518–1524 (2021). https://doi.org/10.1364/JOSAB.420928
J.-S. Li, J.-Z. Chen, Multi-beam and multi-mode orbital angular momentum by utilizing a single metasurface. Opt. Express 29(17), 27332–27339 (2021). https://doi.org/10.1364/OE.434206
Y. Ha, Y. Guo, M. Pu, X. Li, X. Ma, X. Luo, Tunable beam manipulation based on phase-change metasurfaces. Appl. Opt. 58(29), 7996–8001 (2019). https://doi.org/10.1364/AO.58.007996
W. Fu, S. Hu, C. Zhang, X. Guan, Y. Yan, Compact quasi-optical mode converter based on anisotropic metasurfaces. Opt. Express 29(11), 16205–16213 (2021). https://doi.org/10.1364/OE.426525
P. Yu, S. Chen, J. Li, H. Cheng, Z. Li, W. Liu, B. Xie, Z. Liu, J. Tian, Generation of vector beams with arbitrary spatial variation of phase and linear polarization using plasmonic metasurfaces. Opt. Lett. 40(14), 3229–3232 (2015). https://doi.org/10.1364/OL.40.003229
H. Li, D.P. Stellinga, Y. Qiu, Q. Sun, B. Chen, H. Liang, T.F. Krauss, J. Li, Ultra-thin transmissive crystalline silicon high-contrast grating metasurfaces. Opt. Express 27(21), 30931–30940 (2019). https://doi.org/10.1364/OE.27.030931
Y. Xu, J. Sun, W. Walasik, N.M. Litchinitser, Probing metamaterials with structured light. Opt. Express 24(23), 26249–26254 (2016). https://doi.org/10.1364/OE.24.026249
W. Cao, J. Gao, X. Yang, Determination of effective parameters of fishnet metamaterials with vortex based interferometry. Opt. Express 28(14), 20051–20061 (2020). https://doi.org/10.1364/OE.391873
W. Zhu, H. Guan, H. Lu, J. Tang, Z. Li, J. Yu, Z. Chen, Orbital angular momentum sidebands of vortex beams transmitted through a thin metamaterial slab. Opt. Express 26(13), 17378–17387 (2018). https://doi.org/10.1364/OE.26.017378
K. Bezuhanov, A. Dreischuh, G.G. Paulus, M.G. Schätzel, H. Walther, Vortices in femtosecond laser fields. Opt. Lett. 29(16), 1942–1944 (2004). https://doi.org/10.1364/OL.29.001942
A.M. Weiner, J.P. Heritage, E.M. Kirschner, High-resolution femtosecond pulse shaping. J. Opt. Soc. Am. B 5(8), 1563–1572 (1988). https://doi.org/10.1364/JOSAB.5.001563
I.G. Mariyenko, J. Strohaber, C.J.G.J. Uiterwaal, Creation of optical vortices in femtosecond pulses. Opt. Express 13(19), 7599–7608 (2005). https://doi.org/10.1364/OPEX.13.007599
K. Bezuhanov, A. Dreischuh, G.G. Paulus, M.G. Schätzel, H. Walther, D. Neshev, W. Królikowski, Y. Kivshar, Spatial phase dislocations in femtosecond laser pulses. J. Opt. Soc. Am. B 23(1), 26–35 (2006). https://doi.org/10.1364/JOSAB.23.000026
A. Grover, J. Swartzlander, Achromatic optical vortex lens. Opt. Lett. 31(13), 2042–2044 (2006). https://doi.org/10.1364/OL.31.002042
P. Munjal, K.P. Singh, A single-lens universal interferometer: Towards a class of frugal optical devices. Appl. Phys. Lett. 115(11), 111102 (2019). https://doi.org/10.1063/1.5108587
J. Peatross, M.V. Pack, Visual introduction to Gaussian beams using a single lens as an interferometer. Am. J. Phys. 69(11), 1169–1172 (2001). https://doi.org/10.1119/1.1397461
A.Y. Bekshaev, M.S. Soskin, M.V. Vasnetsov, Transformation of higher-order optical vortices upon focusing by an astigmatic lens. Opt. Commun. 241(4), 237–247 (2004). https://doi.org/10.1016/j.optcom.2004.07.023
A.Y. Bekshaev, M.V. Vasnetsov, V.G. Denisenko, M.S. Soskin, Transformation of the orbital angular momentum of a beam with optical vortex in an astigmatic optical system. J. Exp. Theor. Phys. Lett. 75(3), 127–130 (2002). https://doi.org/10.1134/1.1469497
S.N. Alperin, R.D. Niederriter, J.T. Gopinath, M.E. Siemens, Quantitative measurement of the orbital angular momentum of light with a single, stationary lens. Opt. Lett. 41(21), 5019–5022 (2016). https://doi.org/10.1364/OL.41.005019
V.V. Kotlyar, A.A. Kovalev, A.P. Porfirev, Astigmatic transforms of an optical vortex for measurement of its topological charge. Appl. Opt. 56(14), 4095–4104 (2017). https://doi.org/10.1364/AO.56.004095
S. Zheng, J. Wang, Measuring orbital angular momentum (OAM) states of vortex beams with annular gratings. Sci. Rep. 7(1), 40781 (2017). https://doi.org/10.1038/srep40781
H.I. Sztul, R.R. Alfano, Double-slit interference with Laguerre-Gaussian beams. Opt. Lett. 31(7), 999–1001 (2006). https://doi.org/10.1364/OL.31.000999
H. Zhou, S. Yan, J. Dong, X. Zhang, Double metal subwavelength slit arrays interference to measure the orbital angular momentum and the polarization of light. Opt. Lett. 39(11), 3173–3176 (2014). https://doi.org/10.1364/OL.39.003173
J.M. Hickmann, E.J.S. Fonseca, W.C. Soares, S. Chávez-Cerda, Unveiling a truncated optical lattice associated with a triangular aperture using light’s orbital angular momentum. Phys. Rev. Lett. 105, 053904 (2010). https://doi.org/10.1103/PhysRevLett.105.053904
C. Stahl, G. Gbur, Analytic calculation of vortex diffraction by a triangular aperture. J. Opt. Soc. Am. A 33(6), 1175–1180 (2016). https://doi.org/10.1364/JOSAA.33.001175
L.A. Melo, A.J. Jesus-Silva, S. Chávez-Cerda, P.H.S. Ribeiro, W.C. Soares, Direct measurement of the topological charge in elliptical beams using diffraction by a triangular aperture. Sci. Rep. 8(1), 6370 (2018). https://doi.org/10.1038/s41598-018-24928-5
M.E. Anderson, H. Bigman, L.E.E. de Araujo, J.L. Chaloupka, Measuring the topological charge of ultrabroadband, optical-vortex beams with a triangular aperture. J. Opt. Soc. Am. B 29(8), 1968–1976 (2012). https://doi.org/10.1364/JOSAB.29.001968
J.G. Silva, A.J. Jesus-Silva, M.A.R.C. Alencar, J.M. Hickmann, E.J.S. Fonseca, Unveiling square and triangular optical lattices: a comparative study. Opt. Lett. 39(4), 949–952 (2014). https://doi.org/10.1364/OL.39.000949
P.H.F. Mesquita, A.J. Jesus-Silva, E.J.S. Fonseca, J.M. Hickmann, Engineering a square truncated lattice with light’s orbital angular momentum. Opt. Express 19(21), 20616–20621 (2011). https://doi.org/10.1364/OE.19.020616
C.-S. Guo, L.-L. Lu, H.-T. Wang, Characterizing topological charge of optical vortices by using an annular aperture. Opt. Lett. 34(23), 3686–3688 (2009). https://doi.org/10.1364/OL.34.003686
F. Grasbon, A.A. Dreischuh, G.G. Paulus, F. Zacher, H. Walther, Femtosecond interferometric autocorrelations in the presence of pulse-front distortions, in Tenth International School on Quantum Electronics: Laser Physics and Applications. ed. by P.A. Atanasov, D.V. Stoyanov vol. 3571 (1999), pp. 164–168. https://doi.org/10.1117/12.347610
G. Pretzler, A. Kasper, K.J. Witte, Angular chirp and tilted light pulses in CPA lasers. Appl. Phys. B 70(1), 1–9 (2000). https://doi.org/10.1007/s003400050001
N. Dimitrov, L. Stoyanov, I. Stefanov, A. Dreischuh, P. Hansinger, G.G. Paulus, Pulse front tilt measurement of femtosecond laser pulses. Opt. Commun. 371, 51–58 (2016). https://doi.org/10.1016/j.optcom.2016.03.054
N. Dimitrov, L. Stoyanov, I. Stefanov, A. Dreischuh, P. Hansinger, G.G. Paulus, Measuring the relation between pulse-front-tilt angle and beam size for ultrashort laser pulses. Bulg. J. Phys. (Print) 43(1), 021–029 (2016)
N. Gorunski, N. Dimitrov, A. Dreischuh, G.G. Paulus, Pulse-front tilt created in misaligned dispersionless optical systems and correct interferometric autocorrelation. Opt. Commun. 283(24), 5192–5198 (2010). https://doi.org/10.1016/j.optcom.2010.07.032
N. Dimitrov, M. Zhekova, G.G. Paulus, A. Dreischuh, Inverted field interferometer for measuring the topological charges of optical vortices carried by short pulses. Opt. Commun. 456, 124530 (2020). https://doi.org/10.1016/j.optcom.2019.124530
N. Dimitrov, M. Zhekova, Y. Zhang, G.G. Paulus, A. Dreischuh, Background-free femtosecond autocorrelation in collinearly-aligned inverted field geometry using optical vortices. Opt. Commun. 504, 127493 (2022). https://doi.org/10.1016/j.optcom.2021.127493
C. Denz, B. Terhalle, D. Göries, P. Rose, J. Xavier, T. Richter, A.S. Desyatnikov, J. Imbrock, T.J. Alexander, D.N. Neshev, J. Joseph, F. Kaiser, W. Krolikowski, Y.S. Kivshar, Nonlinear photonics in multi-dimensional and complex photonic lattices, in Nonlinear Optics and Applications. ed. by M. Bertolotti Vol. 7354 (2009), p.73402. https://doi.org/10.1117/12.823758
J.W. Fleischer, M. Segev, N.K. Efremidis, D.N. Christodoulides, Observation of two-dimensional discrete solitons in optically-induced nonlinear photonic lattices. in: Conference on lasers and electro-optics/quantum electronics and laser science conference (2003). https://opg.optica.org/abstract.cfm?URI=QELS-2003-QThK1
D. Rozas, Z.S. Sacks, G.A. Swartzlander, Experimental observation of fluidlike motion of optical vortices. Phys. Rev. Lett. 79, 3399–3402 (1997). https://doi.org/10.1103/PhysRevLett.79.3399
E.B. Sonin, Vortex oscillations and hydrodynamics of rotating superfluids. Rev. Mod. Phys. 59, 87–155 (1987). https://doi.org/10.1103/RevModPhys.59.87
D. Rozas, C.T. Law, G.A. Swartzlander, Propagation dynamics of optical vortices. J. Opt. Soc. Am. B 14(11), 3054–3065 (1997). https://doi.org/10.1364/JOSAB.14.003054
D. Neshev, A. Dreischuh, M. Assa, S. Dinev, Motion control of ensembles of ordered optical vortices generated on finite extent background. Opt. Commun. 151(4), 413–421 (1998). https://doi.org/10.1016/S0030-4018(98)00075-3
L. Stoyanov, N. Gorunski, M. Zhekova, I. Stefanov, A. Dreischuh, Vortex interactions revisited: Formation of stable elementary cells for creation of rigid vortex lattices, in 20th international conference and school on quantum electronics: laser physics and applications. ed. by T.N. Dreischuh, L.A. Avramov vol. 11047 (2019), p.110471. https://doi.org/10.1117/12.2516531
P. Hansinger, A. Dreischuh, G.G. Paulus, Optical vortices in self-focusing Kerr nonlinear media. Opt. Commun. 282(16), 3349–3355 (2009). https://doi.org/10.1016/j.optcom.2009.05.037
A. Dreischuh, S. Chervenkov, D. Neshev, G.G. Paulus, H. Walther, Generation of lattice structures of optical vortices. J. Opt. Soc. Am. B 19(3), 550–556 (2002). https://doi.org/10.1364/JOSAB.19.000550
S. Topuzoski, L. Janicijevic, Fraunhofer diffraction of a Laguerre-Gaussian laser beam by fork-shaped grating. J. Mod. Opt. 58(2), 138–145 (2011). https://doi.org/10.1080/09500340.2010.543292
S. Topuzoski, L. Janicijevic, Conversion of high-order Laguerre-Gaussian beams into Bessel beams of increased, reduced or zeroth order by use of a helical axicon. Opt. Commun. 282(17), 3426–3432 (2009). https://doi.org/10.1016/j.optcom.2009.05.052
S. Topuzoski, Fresnel and Fraunhofer diffraction of (l, n)th-mode Laguerre-Gaussian laser beam by a fork-shaped grating. J. Mod. Opt. 66(14), 1514–1527 (2019). https://doi.org/10.1080/09500340.2019.1637549
L. Stoyanov, S. Topuzoski, I. Stefanov, L. Janicijevic, A. Dreischuh, Far field diffraction of an optical vortex beam by a fork-shaped grating. Opt. Commun. 350, 301–308 (2015). https://doi.org/10.1016/j.optcom.2015.04.020
S. Topuzoski, L. Janicijevic, L. Stoyanov, I. Stefanov, A. Dreischuh, Five-vortex spot patterns generated by diffraction of azimuthally X-shaped beam from a fork-shaped grating. Opt. Commun. 428, 206–215 (2018). https://doi.org/10.1016/j.optcom.2018.07.059
L. Janicijevic, S. Topuzoski, L. Stoyanov, A. Dreischuh, Diffraction of a Gaussian beam by a four-sector binary grating with a shift between adjacent sectors. Opt. Commun. 389, 203–211 (2017). https://doi.org/10.1016/j.optcom.2016.12.041
A. Beržanskis, A. Matijošius, A. Piskarskas, V. Smilgevičius, A. Stabinis, Conversion of topological charge of optical vortices in a parametric frequency converter. Opt. Commun. 140(4), 273–276 (1997). https://doi.org/10.1016/S0030-4018(97)00178-8
L. Allen, M.J. Padgett, M. Babiker, IV The orbital angular momentum of light, in Progress in optics, vol. 39, ed. by E. Wolf (Elsevier, Amsterdam, 1999), pp.291–372. https://doi.org/10.1016/S0079-6638(08)70391-3
A.S. Desyatnikov, Y.S. Kivshar, L. Torner, Chapter 5 optical vortices and vortex solitons, in Progress in optics, vol. 47, ed. by E. Wolf (Elsevier, Amsterdam, 2005), pp.291–391. https://doi.org/10.1016/S0079-6638(05)47006-7
I.V. Basistiy, V.Y. Bazhenov, M.S. Soskin, M.V. Vasnetsov, Optics of light beams with screw dislocations. Opt. Commun. 103(5), 422–428 (1993). https://doi.org/10.1016/0030-4018(93)90168-5
K. Dholakia, N.B. Simpson, M.J. Padgett, L. Allen, Second-harmonic generation and the orbital angular momentum of light. Phys. Rev. A 54, 3742–3745 (1996). https://doi.org/10.1103/PhysRevA.54.R3742
M.S. Soskin, M.V. Vasnetsov, Nonlinear singular optics. Pure Appl. Opt. J. Euro. Opt. Soc. Part A 7(2), 301 (1998). https://doi.org/10.1088/0963-9659/7/2/019
A. Dreischuh, D.N. Neshev, V.Z. Kolev, S. Saltiel, M. Samoc, W. Krolikowski, Y.S. Kivshar, Nonlinear dynamics of two-color optical vortices in lithium niobate crystals. Opt. Express 16(8), 5406–5420 (2008). https://doi.org/10.1364/OE.16.005406
M. Zürch, C. Kern, P. Hansinger, A. Dreischuh, C. Spielmann, Strong-field physics with singular light beams. Nat. Phys. 8(10), 743–746 (2012). https://doi.org/10.1038/nphys2397
Y. Toda, S. Honda, R. Morita, Dynamics of a paired optical vortex generated by second-harmonic generation. Opt. Express 18(17), 17796–17804 (2010). https://doi.org/10.1364/OE.18.017796
G. Gariepy, J. Leach, K.T. Kim, T.J. Hammond, E. Frumker, R.W. Boyd, P.B. Corkum, Creating high-harmonic beams with controlled orbital angular momentum. Phys. Rev. Lett. 113, 153901 (2014). https://doi.org/10.1103/PhysRevLett.113.153901
P. Hansinger, G. Maleshkov, I.L. Garanovich, D.V. Skryabin, D.N. Neshev, A. Dreischuh, G.G. Paulus, Vortex algebra by multiply cascaded four-wave mixing of femtosecond optical beams. Opt. Express 22(9), 11079–11089 (2014). https://doi.org/10.1364/OE.22.011079
D.N. Neshev, A. Dreischuh, G. Maleshkov, M. Samoc, Y.S. Kivshar, Supercontinuum generation with optical vortices. Opt. Express 18(17), 18368–18373 (2010). https://doi.org/10.1364/OE.18.018368
G. Maleshkov, P. Hansinger, I.L. Garanovich, D. Skryabin, D.N. Neshev, A. Dreischuh, G.G. Paulus, Degenerate four-wave mixing of optical vortices assisted by self-phase and cross-phase modulation, in 16th international school on quantum electronics: laser physics and applications, vol. 7747, ed. by T. Dreischuh, D. Slavov (2011), p.77471
L. Stoyanov, M. Zhekova, A. Stefanov, I. Stefanov, G.G. Paulus, A. Dreischuh, Zeroth- and first-order long range non-diffracting Gauss-Bessel beams generated by annihilating multiple-charged optical vortices. Sci. Rep. 10(1), 21981 (2020). https://doi.org/10.1038/s41598-020-78613-7
L. Stoyanov, M. Zhekova, A. Stefanov, B. Ivanov, I. Stefanov, G.G. Paulus, A. Dreischuh, Generation of long range low-divergent Gauss-Bessel beams by annihilating optical vortices. Opt. Commun. 480, 126510 (2021). https://doi.org/10.1016/j.optcom.2020.126510
L. Stoyanov, Y. Zhang, A. Dreischuh, G.G. Paulus, Long-range quasi-non-diffracting Gauss-Bessel beams in a few-cycle laser field. Opt. Express 29(7), 10997–11008 (2021). https://doi.org/10.1364/OE.419486
D. McGloin, K. Dholakia, Bessel beams: Diffraction in a new light. Contemp. Phys. 46(1), 15–28 (2005). https://doi.org/10.1080/0010751042000275259
J. Durnin, J.J. Miceli, J.H. Eberly, Diffraction-free beams. Phys. Rev. Lett. 58, 1499–1501 (1987). https://doi.org/10.1103/PhysRevLett.58.1499
G. Indebetouw, Nondiffracting optical fields: some remarks on their analysis and synthesis. J. Opt. Soc. Am. A 6(1), 150–152 (1989). https://doi.org/10.1364/JOSAA.6.000150
L. Stoyanov, G. Maleshkov, I. Stefanov, G.G. Paulus, A. Dreischuh, Focal beam structuring by triple mixing of optical vortex lattices. Opt. Quantum Electron. 54(1), 34 (2021). https://doi.org/10.1007/s11082-021-03399-5
L. Stoyanov, G. Maleshkov, M. Zhekova, I. Stefanov, D.N. Neshev, G.G. Paulus, A. Dreischuh, Far-field pattern formation by manipulating the topological charges of square-shaped optical vortex lattices. J. Opt. Soc. Am. B 35(2), 402–409 (2018). https://doi.org/10.1364/JOSAB.35.000402
L. Stoyanov, G. Maleshkov, M. Zhekova, I. Stefanov, G.G. Paulus, A. Dreischuh, Far-field beam reshaping by manipulating the topological charges of hexagonal optical vortex lattices. J. Opt. 20(9), 095601 (2018). https://doi.org/10.1088/2040-8986/aad30e
M. Zhekova, G. Maleshkov, L. Stoyanov, I. Stefanov, G.G. Paulus, A. Dreischuh, Formation of multi-spot focal arrays by square-shaped optical vortex lattices. Opt. Commun. 449, 110–116 (2019). https://doi.org/10.1016/j.optcom.2019.05.051
L. Stoyanov, G. Maleshkov, M. Zhekova, I. Stefanov, G.G. Paulus, A. Dreischuh, Controllable beam reshaping by mixing square-shaped and hexagonal optical vortex lattices. Sci. Rep. 9(1), 2128 (2019). https://doi.org/10.1038/s41598-019-38608-5
Acknowledgements
With gratitude for the fruitful collaborations over the years, the authors would like to thank D. N. Neshev, Y. Kivshar from the Australian National University (Canberra, Australia), P. Hansinger, Th. Weber, Y. Zhang, F. Wiesner and Ch. Spielmann from the Friedrich Schiller University (Jena, Germany), Lj. Janicijevic from the University “Ss. Cyril and Methodius” (Skopje, Republic of North Macedonia), F. Grasbon and the late H. Walther from Max Planck Institute for Quantum Optics (Garching, Germany), I. Stefanov, G. Maleshkov, K. Besuchanov, N. Dimitrov, M. Zhekova, N. Gorunski, A. Stefanov from Sofia University “St. Kliment Ohridski” (Sofia, Bulgaria) and all other collaborators over the years. We acknowledge funding of the Deutsche Forschungsgemeinschaft (project PA 730/13). This work was also supported by the European Regional Development Fund within the Operational Programme “Science and Education for Smart Growth 2014–2020” under the Project CoE “National center of mechatronics and clean technologies” BG05M2OP001\(-\)1.001-0008-C01 and by the Bulgarian Ministry of Education and Science as a part of National Roadmap for Research Infrastructure, grant number D01-401/18.12.2020 (ELI ERIC BG). L.S. would like to gratefully acknowledge the funding from the Alexander von Humboldt Foundation.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stoyanov, L., Topuzoski, S., Paulus, G.G. et al. Optical vortices in brief: introduction for experimentalists. Eur. Phys. J. Plus 138, 702 (2023). https://doi.org/10.1140/epjp/s13360-023-04227-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjp/s13360-023-04227-3