Novel prediction of fluid forces on obstacle in a periodic flow regime using hybrid FEM-ANN simulations

Abstract

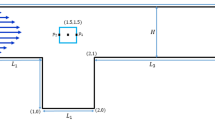
A lot of computational resources are required for time-dependent CFD simulations for the accurate prediction of the quantities of interest. To circumvent such difficulties, an artificial neural network (ANN) has been coupled with CFD simulations. Training and validation datasets have been generated by CFD and then are fed through ANN with optimal number of neurons and inner layers. A well-known benchmark problem for incompressible flows, namely, the flow around cylinder has been considered for the hybrid CFD network. The mathematical formulations are based on nonstationary Navier–Stokes equations incorporating the viscosity through power-law fluid constitutive model. The underlying ANN model consists of 3 input layers, 2 output layers, and 10 hidden layers. The network has been trained through one of the most efficient backpropagation algorithms, namely, Levenberg–Marquardt (LM) algorithm that provides second-order training speed. The obtained finite element results for drag and lift coefficients have been validated with the ANN predicted values through statistical measures represented by mean square error (MSE) and the coefficient of determination (R). For all cases, we have obtained a higher predictivity for drag coefficient $C_{D}$ and lift coefficient $C_{L}$ as MSE values approached zero and R values found to be close to unity. The agreement between the CFD results and the data predicted from ANN determined via the correlations is within less than ± 5% errors. It is concluded that ANNs may help to reduce the computing time and other resources required for time-dependent simulations.