Application of machine learning to model the pressure poisson equation for fluid flow on generic geometries

Abstract

This study addresses the importance of enhancing traditional fluid-flow solvers by introducing a Machine Learning procedure to model pressure fields computed by standard fluid-flow solvers. The conventional approach involves enforcing pressure–velocity coupling through a Poisson equation, combining the Navier–Stokes and continuity equations. The solution to this Poisson equation constitutes a substantial percentage of the overall computational cost in fluid flow simulations, therefore improving its efficiency can yield significant gains in computational speed. The study aims to create a versatile method applicable to any geometry, ultimately providing a more efficient alternative to the conventional pressure solver. Machine Learning models were trained with flow fields generated by a Computational Fluid Dynamics solver applied to the confined flow over multiple geometries, namely wall-bounded cylinders with circular, rectangular, triangular, and plate cross-sections. To achieve applicability to any geometry, a method was developed to estimate pressure fields in fixed-shape blocks sampled from the flow domain and subsequently assemble them to reconstruct the entire physical domain. The model relies on multilayer perceptron neural networks combined with Principal Component Analysis transformations. The developed Machine Learning models achieved acceptable accuracy with errors of around 3%. Furthermore, the model demonstrated enhanced computational efficiency, outperforming the classical PISO algorithm by up to 30 times.

1 Introduction

Artificial Intelligence (AI) algorithms have been expanding toward scientific computation [1], predicting protein structures in biology [2], optimizing drug discovery [3, 4], accelerating material discovery [5], aiding climate modeling [6,7,8] and enhancing Computational Fluid Dynamics (CFD) solvers [9,10,11]. Broadly, there are three groups of models: (i) purely data-driven models working blindly to physical laws and requiring large amounts of data; (ii) physics-informed models that respect governing equations and boundary conditions [12]; and (iii) hybrid approaches of those two groups. Commonly the application of AI to physical problems aims to create an ambitious model that outputs a solution to the problem. Alternatively, the aim may focus on a surrogate model replacing a component of the physical solver to accelerate computations, e.g. turbulence closures in CFD models [13], or enhance the solution [10].

Fluid flow is a highly complex phenomenon for which analytical solutions are frequently unattainable in many engineering applications. Instead, numerical simulation alongside experimental studies plays an essential role in modeling. CFD is the process of employing numerical methods to solve mathematical models that describe fluid flow. Generally, these are based on the discretization of the Navier–Stokes (NS) equations over a computational grid that characterizes the volume occupied by the fluid. The computation of a pressure field that is consistent with the flow velocity is governed by a Poisson equation whose solution comprehends a significant percentage of the computational cost.

Deep learning (DL) is a subset of Machine Learning (ML) based on artificial neural networks (ANN), typically claimed to mimic the human brain allowing it to learn from a large dataset. It is inspired by information processing of biological systems and has been successfully applied to problems such as computer vision [14], speech recognition [15], drug design [16], medical image analysis [17], material inspection [18], board and video game [19] and in some of these even surpassing the human expert performance [20]. Algorithms and DL networks can be of immense complexity to tackle a specific problem. Some examples of supervised learning algorithms are generally distinguished as i) Multilayer perceptrons (MLP): Consisting of a collection of connected units (neurons) which act together as a network to map an input to an output; ii) Convolutional neural networks (CNNs): Commonly used to analyze visual imagery and are a regularized version of MLP. CNNs take advantage of hierarchical patterns in data, and are a specialized type of neural networks that uses the convolution mathematical operation instead of matrix multiplication [21]; iii) Recurrent neural networks (RNNs): Typically used for sequential data or time series analysis, commonly used in natural language processing and speech recognition. iv) Graphical neural networks (GNNs): Incorporating graphical models to capture intricate relationships between variables, particularly useful when complex dependencies exist among data elements organized in a graph structure. One application of ML models in CFD is in assisting flow solvers by replacing computations with surrogate models that improve execution time whilst decreasing resource consumption. One candidate is the Poisson equation used to compute the pressure field as it requires significant computational effort. Additionally, the ability to find solutions to the Poisson equation is not merely useful for fluid dynamics problems, but can be applied to other physics problems such as heat transfer, electromagnetism, and astronomy. Recent studies solved Poisson equations with ML techniques employing CNNs [22, 23] or even GNNs [24]. Examples of applications to CFD include Özbay et al [25] where a CNN architecture was used to compute the pressure field for 2D cartesian meshes, Illarramendi et al [26] which coupled a CNN model with a traditional interactive solver to ensure user-defined accuracy and Weymouth [27] where a technique to accelerate classic Multi-Grid methods was proposed. Nonetheless, there are open challenges such as the generalization to different geometries and the ability of ML-based surrogate models to cope with laminar and turbulent flow regimes.

In this work, several fluid flow simulations were computed using the open-source CFD software OpenFOAM v6 [28] to construct multiple datasets. An algorithm capable of dealing with any geometry was designed and used to construct ML surrogate models capable of solving the pressure Poisson equation in CFD solvers. The novelty of the proposed approach is in its flexibility to tackle any kind of geometry by ensuring the neural network (NN) is decoupled from the CFD mesh. This enables the application of a trained surrogate model to any flow domain. Furthermore, application to different flow regimes was attempted by taking advantage of the the structure of the Poisson system of equations, as it was independent of assuming laminar or turbulent regime when solving the flow, the latter employing eddy-viscosity turbulence models.

Section 2 introduces the methodology, and Sect. 3 describes the numerical setup. The attained results are displayed in Sect. 4. Section 5 finishes by presenting the Conclusions.

2 Methodology | mathematical models

2.1 Fluid-flow solver

The fluid-flow simulation was performed with the OpenFOAM v6 [28] CFD toolbox, whose computer model is based on the NS equations discretized over a numerical grid using the Finite Volume Method (FVM) [29]. Both laminar and turbulent flow regimes were encompassed in a general set of equations with further changes associated with the respective regime: while for laminar flow the stress tensor is the Stokes law of friction [30], for turbulent flow a Boussinesq eddy-viscosity is employed together with further equations to model turbulence quantities.

All flow simulations were performed in a time-dependent approach by integrating the equations with the backward Euler scheme. The Pressure Implicit with Split Operator (PISO) algorithm [31] was used to ensure consistency between the velocity and pressure fields. The following text addresses a minimal description of the flow model sufficient to depict how ML methods can be integrated. Further details on CFD modeling may be found in OpenFOAM [28] and Moukalled et al. [29], namely the treatment of boundary conditions and discretization for unstructured grids.

2.1.1 Laminar flow regime

Following Schlichting and Gersten [30] the conservation of momentum for a Newtonian fluid undergoing incompressible flow is governed by:

$$\begin{aligned} \dfrac{\partial \textbf{u}}{\partial t} + (\textbf{u}\cdot \nabla )\,\textbf{u} = -\nabla p + \nabla \cdot \varvec{\tau } + \textbf{a}_b, \end{aligned}$$

(1)

where $\textbf{u}$ is the flow velocity vector with each component describing the velocity along each spatial coordinate, p corresponds to the kinematic pressure,¹$\varvec{\tau }$ is the deviatoric stress tensor and the ${{\textbf {a}}}_b$ term is the net acceleration of all body forces acting on the fluid. Tensor $\varvec{\tau }$ is related to the rate-of-strain tensor, ${{\textbf {S}}} = \tfrac{1}{2}\,[\nabla \textbf{u} + (\nabla \textbf{u})^{\textsc {t}}]$, by

$$\begin{aligned} \varvec{\tau } = \nu \,\left[ 2\,{{\textbf {S}}} - \textbf{I}\,\tfrac{2}{3}\,\nabla \cdot \textbf{u}\right] , \end{aligned}$$

(2)

where $\textbf{I}$ is the identity tensor. Incompressible flow is characterized by negligible changes in density during fluid flow and can be assumed in a wide range of applications. This is not exclusive of liquids, rather, it applies to any fluid under specific flow conditions, highlighting its broad applicability. Considering incompressibility, the velocity field becomes solenoidal, and a continuity equation governing the conservation of mass is given by:

$$\begin{aligned} \nabla \cdot \textbf{u} = 0. \end{aligned}$$

(3)

In addition to eqs. (1–3), initial and spatial boundary conditions must be specified to fully solve the system.

2.1.2 Turbulent flow regime

Many engineering applications focus on flows under turbulent regimes. The main characteristic of this flow regime is the presence of eddies and vortices, which promote better mixing and more fluid momentum transfer in contrast to laminar flow [32]. According to Wang et al [33], turbulent flow is characterized by chaotic and irregular fluid motion.

Turbulent flows of Newtonian fluids are associated with high Reynolds number (Re) defined as $\text {Re} = UL/\nu$ with U and L being representative scales of velocity and length, while $\nu$ is the fluid kinematic viscosity [30].

Under turbulent regime, generally it is not feasible to simulate the instantaneous flow field as the required computer resources would be prohibitive. Instead, the flow may be described in terms of the statistics of its fields. To tackle this the NS equations are averaged to establish a mean field, with any deviation from it being modeled as a fluctuation field, in a procedure known as Reynolds decomposition. Following an unsteady Reynolds-averaged Navier–Stokes (uRaNS) approach [30], the $\textbf{u}$ field becomes representative of the average fluid velocity. This allows to use the same formulation as in eqs. (1) and (3), with changes to the deviatoric stress tensor $\varvec{\tau }$ to accommodate for extra terms, i.e. Reynolds stresses, together with further changes to the boundary conditions near walls.

The stress terms for flow under turbulent regime were modeled via a Boussinesq eddy-viscosity and the k-$\omega$ SST turbulence model, with resolved laminar sub-layer to better cope with adverse pressure gradients. A detailed description is given in Appendix A.

2.1.3 Pressure-momentum coupling

Analytical solutions for most flows are currently unattainable due to the mathematical properties of eq. (1), namely the non-linearity of the advection term and the need to simultaneously solve the continuity eq. (3), i.e. the coupling between $\textbf{u}$ and p. The PISO algorithm [31] was proposed to address this problem as it provides stable results and reduces computational effort when compared to iterative methods [34]. Rather than solving all the coupled equations iteratively, PISO splits the operator into an implicit momentum predictor and multiple explicit correction steps.

An algebraic system of equations was obtained by employing the FVM to discretize eq. (1) in a computational grid [29], resulting in:

$$\begin{aligned} \textbf{M}\cdot \textbf{U} = -\nabla p + \textbf{a}_b, \end{aligned}$$

(4)

where $\textbf{M}$ is a matrix of coefficients, and $\textbf{U}$ the velocity field. Note that eq. (4) is the same for both laminar and turbulent flow regime formulations, as these merely imply changes to values in $\textbf{M}$.

A Poisson equation for pressure is derived by coupling eq. (4) with eq. (3):

$$\begin{aligned} \nabla \cdot (\textbf{A}^{-1} \nabla p) = \nabla \cdot (\textbf{A}^{-1}\,\textbf{H} + \textbf{A}^{-1}\,\textbf{a}_b), \end{aligned}$$

(5)

where ${{\textbf {A}}}$ is the matrix with the diagonal components of $\textbf{M}$, and $\textbf{H}$ arises from the $\textbf{MU} - \textbf{a}_b = \textbf{AU} -\textbf{H}$ decomposition. Equation (5) can be solved to yield a pressure field that can be used to correct the velocity field to satisfy mass conservation.

Considering constant viscosity a similar procedure may be used to derive an analytical form of the pressure Poisson equation by taking the divergence of eq. (1), resulting in:

$$\begin{aligned} \frac{\partial }{\partial x_i} \left( \frac{\partial p}{\partial x_i}\right) = - \frac{\partial }{\partial x_i} \left[ \frac{\partial \left( u_i u_j \right) }{\partial x_j}\right] , \end{aligned}$$

(6)

as shown by Ferziger and Perić [35] in index notation which is valid for laminar flow after subtracting the hydrostatic pressure from the p field, i.e. equivalent to removing the gravity acceleration from the $\textbf{a}_b$ term. Once again considering incompressibility, in vector form eq. (6) can be shown to be equivalent to

$$\begin{aligned} \nabla ^2 p = - \nabla \textbf{u}\!:\! (\nabla \textbf{u})^{\textsc {t}} \,. \end{aligned}$$

(7)

2.2 Surrogate model

2.2.1 Fundamentals of Deep Learning

The basic unit of the ANN is an artificial neuron and its output follows the equation

$$\begin{aligned} y = f \left( \sum _{i=1}^{N} x_i w_i + b_i \right) , \end{aligned}$$

(8)

where f represents the activation function, $w_i$ the weight of the neuron i, and $b_i$ the bias of the present neuron. A neural network consists of multiple connected layers which consist of multiple neurons. The output of a node i from layer l is calculated as:

$$\begin{aligned} a_i^{l} = f \left( z_i^{l} \right) = f \left( \sum _{j=1}^{N} x_{j}^{l} w_{ji}^{l} + b_i^{l} \right) , \end{aligned}$$

(9)

where f can be any chosen activation function, and $w_{ji}^{l}$ the weight of the neuron j, where j represents nodes at layer $l-1$, in neuron i from layer l. The bias $b_i^{l}$ represents a zero-order coefficient associated with node i from layer l. The training process consists of sequentially computing each node output $a_i^{l}$ from the input layer through all the hidden layers until the last as in eq. (9). This process is called forward propagation which ends in a computed prediction. The predicted output $Y_{pred}$ can be compared to the known label Y, and the discrepancy between these values is evaluated through a chosen loss function as in

$$\begin{aligned} J = L(Y_{pred},Y). \end{aligned}$$

(10)

The derivatives of the loss in relation to the weights $w_{ji}$ and bias $b_i^{l}$ at every node i and layer l are also computed and used to update the weights in a process called backward propagation.

2.2.2 Model input

The surrogate model aims to match a set of input fields to the pressure field p, such that the latter can be predicted from such inputs. The inputs consist of flow-field data and an extra argument that represents the geometry. A signed-distance function (SDF) was established so to provide information on the distance to the nearest wall at each position ${{\textbf {x}}}$ of the computational domain, defined as:

$${\text{SDF}}({\mathbf{x}}) = \left\{ {\begin{array}{*{20}l} {\min \left( {\delta ({\mathbf{x}},{\mkern 1mu} \partial \Omega _{b} ),{\mkern 1mu} \delta ({\mathbf{x}},{\mkern 1mu} \partial \Omega _{o} )} \right)} \hfill & {{\text{if}}{\mkern 1mu} {\mathbf{x}} \in \Omega ,} \hfill \\ 0 \hfill & {{\text{if}}{\mkern 1mu} {\mathbf{x}} \in \Omega _{o} ,} \hfill \\ \end{array} } \right.{\text{ }}$$

(11)

where $\Omega$ represents the computational domain where fluid exists and $\Omega _o$ the domain encompassed by the obstacle. The $\partial \Omega _b$ and $\partial \Omega _o$ represent the boundaries of $\Omega$ and $\Omega _o$, respectively.

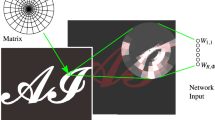
Two model families were established based on how the flow field is input into the model: $\mathbf {M_u}$ and $\textbf{M}_{f(\textbf{u})}$. An overview of the model families is illustrated in Fig. 1. In $\mathbf {M_u}$ models the input flow field corresponds to the components of the velocity field $\textbf{u}$. An alternative family of models, $\textbf{M}_{f(\textbf{u})}$, is established by using the r.h.s. of eq. (7) as input, hence $f(\textbf{u}) = - \nabla \textbf{u}\!:\! (\nabla \textbf{u})^{\textsc {t}}$.

Fig. 1

Model families classified based on the input fields

2.2.3 Data sampling and normalization

The CFD model was run to provide data fields to train the ML model, and to serve as a reference to assess the error of the ML model predictions. To ensure the flow fields are referred to consistently, a characteristic time-scale was defined as $t^* = \phi / U_{\infty ,c}$ where $\phi$ is the characteristic length and $U_{\infty ,c}$ is the centerline velocity at the inlet. The CFD model was run for a total time of $300\,t^*$ to fully capture the dynamic behavior of the flow. The sampling was performed with a time step of $\Delta t = 3\,t^*$, resulting in 100 fields extracted from each simulation run.

The flow fields were normalized as $\textbf{u}^{*} = \textbf{u}/\max (|\textbf{u}|)$ or $f(\textbf{u})^{*} = f({{\textbf {u}}})/\max (|\textbf{u}|^2)$, depending on the model family $\mathbf {M_u}$ or $\textbf{M}_{f(\textbf{u})}$, respectively. The kinematic pressure field was normalized as $p^{*} = p/\max (|\textbf{u}|^2)$.

Instead of training the ML model with a monolithic dataset (as done in most applications of NN models) each temporal frame of a CFD simulation was decomposed into hundreds of thousands of different blocks, as illustrated in Fig. 2. This allowed generalization to different geometries. Using Latin Hyper-cube Sampling (LHS) [36] N blocks were sampled from the CFD domain.

Fig. 2

Representation of the sampling method from the original domain

Training with the real values of pressure after pre-processing and sampling would consist of an ill-posed optimization problem as the random pressure offsets in the solution are not correlated with the inputs, i.e. the same input value can have multiple different outputs depending on the boundary conditions. To tackle this, the pressure spatial mean, $\overline{p^*}$, was removed from each output block, e.g. $p' = p^* - \overline{p^*}$. The normalization of a field quantity $\phi$ was $\phi ^* = \phi /\max (|\phi |)$, hence bounding $\phi ^*$ to $[-1,\,1]$.

The loss function for eq. (10) was defined as the mean squared error (MSE),

$$\begin{aligned} \text {MSE} = \frac{1}{N_{\text {points}}}\,\sum _{i=1}^{N_{\text {points}}} \left[ \hat{\theta } - \theta \right] ^2 , \end{aligned}$$

(12)

where $N_{points}$ was the number of grid points where an estimation was computed, $\theta$ corresponds to the reference values, i.e. the CFD results, and $\hat{\theta }$ the values computed with the surrogate model on this set of points.

The error metrics considered for evaluating the models accuracy consisted of BIAS,

$$\begin{aligned} \text {BIAS} = \frac{1}{N_{\text {points}}}\sum _{i=1}^{N_{\text {points}}} \left( \hat{\theta } - \theta \right) , \end{aligned}$$

(13)

standard-deviation error (STDE),

$$\begin{aligned} \text {STDE} = \left[ \frac{1}{N_{\text {points}-1}} \sum _{i=1}^{N_{\text {points}}} \left( \hat{\theta } - \overline{\hat{\theta }} \right) ^2 \right] ^{\frac{1}{2}}, \end{aligned}$$

(14)

where $\overline{\hat{\theta }}$ is the mean of the predicted values, and root mean squared error (RMSE)

$$\begin{aligned} \text {RMSE} = \left[ \frac{1}{N_{\text {points}}} \sum _{i=1}^{N_{\text {points}}} \left( \hat{\theta } - \theta \right) ^2 \right] ^{\frac{1}{2}}, \end{aligned}$$

(15)

and afterward normalizing each of those by dividing them by $\left( max(\theta ) - min(\theta ) \right)$.

The set of CFD results consisted of simulations characterized by different Re numbers defined as $\text {Re} = \overline{U_\infty }\,D/\nu$, where D is the cylinder diameter and $\overline{U_\infty }$ the mean longitudinal inlet velocity.

2.3 Blocks assembly into the flow domain

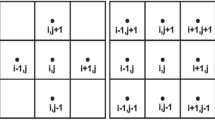
Once the solution field for each block is predicted by the ML surrogate model, an assembly algorithm was developed to reconstruct the full pressure field, as illustrated in Fig. 3a. The pressure value at location (0) is taken as the reference pressure to ensure the fulfillment of the outlet fixed value boundary condition and was set to 0 for simplicity. The assembly process begins by placing the predicted field of the first block into the domain and applying its initial correction at (0) to meet the boundary condition. Subsequently, the predicted field of the second block from the same row is placed, and a correction is applied at (1) to ensure consistency in the intersection zone, facilitating coherence between the two blocks. This incremental placement and correction process is repeated until reaching the left end of the domain for the first row. Similar reconstructions and corresponding corrections are done incrementally up to the left end of the domain. Once the first row is completed, corrections are made at the upper end of the new block in the intersection zone indicated by (n+1). This iterative process continues until the entire domain is fully defined.

Having considered the fixed value boundary condition at the furthest downstream centroid (and not in the cell face where the boundary condition is defined) a correction must be applied to the whole domain. Considering the schematic representation from Fig. 3b, enforcing the gradient in the nearby upstream cell to be equal to the gradient at the outlet boundary, i.e. $(p_{(1,0)} - p_{(0,0)})/(\Delta x/2) = (p_{(2,0)} - p_{(1,0)})/\Delta x$, one can estimate the deviation caused by the incorrect assumption reaching

$$\begin{aligned} p_{\text {deviation}} = \overline{p_{(1,:)} - \tfrac{1}{3}\,p_{(2,:)}}\,. \end{aligned}$$

(16)

The corrected pressure field is computed by removing the deviation, $p_{\text {corr}} = p - p_{\text {deviation}}$, leading to consistent results with respect to the reference fields.

Fig. 3

Assembly algorithm methods

The model architecture, size of the blocks, and NN training-related hyper-parameters such as batch size, learning ratio, and moving average parameters were properly optimized. Since some of these (such as the model architecture and the size of the blocks) are not easily decoupled from the assembly algorithm, all of the above were optimized considering the surrogate model as a whole, i.e. using the RMSE normalized of the surrogate model results as the target. The alternative would be to consider the parameters that better optimize the NN individually but not in the way it interacts with the assembly process. The only parameter whose influence could be partially decoupled from the NN training was the overlap ratio, i.e. the ratio between the overlap region size and the block size, but it was also optimized considering the whole surrogate model accuracy. Refer to Appendix B to follow the parameters selection process.

2.4 Neural Network architecture

The NN model developed can be classified as an MLP with 3 hidden layers, whose purpose is to act as a transfer function between velocity and pressure values. Following Sousa [37] a Principle Component Analysis (PCA) was applied to the input and output layers of the NN model, hence acting as encoder and decoder stages as shown in Fig. 4. Rectified Linear Unit (RELU) and Linear activation functions were used in the hidden and output layers, respectively.

The application of PCA and its subsequent truncation to a few Principal Components (PC) that explain most of the variance found on the input data saves large amounts of computational resources since it helps the model training by reducing the dimensionality of the input/output data, and only yield the most relevant information.

In the current setup, the PCs were attained from the normalized values directly (cf. Sect. 2.2.3) without applying further operations such as standardization.

Fig. 4

Schematic representation of the multilayer perceptron (MLP) neural network. Adapted from Liang et al [38]

3 Numerical setup

3.1 Training and evaluation method

After proper hyperparameter tuning, the training was done with the different families of geometries listed in Table 1 and the same Re number, but its performance was also accessed for different flow conditions to study the generalization capability. The training convergence criteria consisted of stopping whenever the decrease in the loss value, computed from eq. (10), considering the test dataset (i.e. the group of blocks sampled according to Sect. 2.2.3) was lower than 0.1$\%$ over 250 epochs. Each of the following evaluations was performed based on 100 temporal frames from 4 different simulations with different obstacles (from the same family of geometries) providing a representative evaluation of the model performance over the whole family of geometries as well as predicting the dynamical behavior of each one. The notation to identify the models is defined in Table 2.

Table 1 Dataset symbology and kind of obstacle

Table 2 Description of the models and their symbology based on the training datasets

Regarding the number of blocks to be extracted from each temporal frame, N, it was necessary to arrive at a good compromise between accuracy and training cost. Using all available blocks would be infeasible in terms of computational cost and would bring mostly redundant information, therefore two distinct N were tested: $N_1 = 500$ and $N_2 = 2500$ (resulting in a total number of blocks per simulation of $N_{total,1} = 5\times 10^4$ and $N_{total,2} = 2.5\times 10^5$ for $N_1$ and $N_2$, respectively). Further details on the size of the datasets used are provided in Appendix C for models ${{{\textbf {M}}}}_{{{\textbf {u}}}}$ and ${{\textbf {M}}}_{\text{f}({{\textbf {u}}})}$. It is shown that the application of PCA achieves dimensionality reduction (i.e. reduction of the total number of points attained by multiplying the input and output sizes by the number of samples) of up to 3 orders of magnitude. The convergence curves from the training of each model can also be found in Appendix C.

3.2 Data generation - CFD setup

The training and test cases consisted of flow around a bi-dimensional obstacle in confined flow as represented in Fig. 5 for the $\circ$ obstacle, where H is the distance between plates, and $\hat{n}$ the unit vector perpendicular to the domain boundary at any point. The boundaries and corresponding boundary conditions are defined in Table 3 according to Fig. 5 following OpenFOAM [28] nomenclature. The flow was induced by the inlet velocity where it to was specified to follow the analytical solution for fully developed laminar flow between parallel plates given by $u(y) = 3\overline{U_\infty }/2\left[ 1-\left( y/h\right) ^2\right]$ where y is the distance from the centerline, h half of the distance between plates and $\overline{U_\infty }$ the mean longitudinal velocity.

Fig. 5

Simulation case representation with domain dimensions and boundary conditions

Table 3 Boundary conditions for laminar flow

The generated meshes had finer refinement near every wall as illustrated in Fig. 6.

Fig. 6

Mesh illustration for each obstacle: a $\circ$, b $\Box$, c  /, d $\triangleleft$. For illustration purposes, the mesh density is $\frac{1}{100}$ of the original

The simulations performed at high Re numbers had a different numerical setup. Since for pressure and velocity the boundary conditions were maintained, only the boundary conditions for the additional variables: the turbulent kinetic energy, k, and specific turbulent dissipation rate, $\omega$, are defined in Table 4 following OpenFOAM [28] nomenclature. The free-stream values, i.e. at the inlet, had to be estimated, hence the following relations were taken

$$\begin{aligned} k_\infty = \frac{3}{2}\left( U_\infty I\right) ^2, \end{aligned}$$

(17)

$U_\infty$ is the free stream velocity, here defined as the mean inlet velocity and I the turbulence intensity which was set to $10\%$ and

$$\begin{aligned} \omega _\infty = C_\mu ^{-\frac{1}{4}} \frac{\sqrt{k}}{\ell }, \end{aligned}$$

(18)

where l is the turbulent length scale which was defined based on the characteristic inlet length scale, L, as $\ell = 0.07L$ [39], $C_\mu$ is a turbulence model constant which was set to $C_\mu =0.09$. These free stream conditions were taken following OpenCFD [40] guidelines in agreement with the broader recommendation on Menter [41]. The estimations used for the turbulent quantities are not precise, hence the region of interest, i.e. the obstacle, was distanced $10\,L$ and $25\,L$ from the inlet and outlet, respectively, with L as the characteristic length. The boundary conditions are defined using the nomenclature from OpenFOAM, further information can be found either in the documentation or in the source code.

Table 4 Boundary conditions for turbulent flow quantities

The mesh was refined to guarantee that the elements adjacent to the wall were within the viscous sub-layer, hence at $y^+ < 5$ [42, c.f.]. This practice avoids the use of logarithmic boundary layer wall functions, as that implies constant-stress conditions for those near-wall grid cells.

4 Results

4.1 Model ${{{\textbf {M}}}}_{{{\textbf {u}}}}$

The first results obtained consisted in the testing of M$_{\circ }$, M$_{{\circ },\, \Box}$, M$_{{\circ },\, {\Box},\, {\triangleleft}}$, and M$_{{\circ },\, {\Box},\, {\triangleleft}}$, _/ to predict within all the families of geometries in flows characterized by the training Re number, $\text {Re} = 100$, as presented in Table 5.

Table 5 ${{{\textbf {M}}}}_{{{\textbf {u}}}}$ results from training with multiple datasets and tested in $\text {Re} = 100$ flows. Every error metric, $Error(\phi )$ was normalized according to $Error(\phi )_{norm} = Error(\phi )/(\phi _{max} - \phi _{min})$

From Table 5 an increase in training data diversity allows the model to improve its generalization to multiple geometries. Incrementation in training datasets resulted in a tendency to increase overall performance, but also impaired results for a particular dataset, i.e. a model trained with multiple datasets (including the test data) had lower performance in a particular obstacle than the model trained only with the test dataset. This effect came from the difficulty of overfitting to a particular case. Regarding the number of samples from each time frame, N, it is already possible to conclude the inadequacy of using $N_2$ datasets since the improvements seen do not compensate for the training increased computational cost. This amount of samples from each flow field introduced redundant data leading to overfit. To visually illustrate predictions from Table 5, in Fig. 7 a single flow field is shown for each geometry.

Fig. 7

${{\textbf {M}}}_{{{\textbf {u}}}}$ prediction examples for each geometry at $\text {Re} = 100$

Table 6 ${{{\textbf {M}}}}_{{{\textbf {u}}}}$ results trained with each dataset and tested in $\text {Re} = 100$ flows. Every error metric, $Error(\phi )$ was normalized according to $Error(\phi )_{norm} = Error(\phi )/(\phi _{max} - \phi _{min})$

Table 6 shows the contribution of each dataset to the training to inspect the influence of each training set on the surrogate model accuracy. The results from M $_{\triangleleft }$ showed to be promising since, by learning from only the $\triangleleft$ dataset, the model could make accurate predictions across all the other flows. The overall accuracy across different datasets was accompanied by the difficulty in predicting the training datasets, i.e., the higher complexity of these flows dynamical structures. This allowed the NN to learn different flow patterns with only one family of geometries, indicating a richer learning process. Therefore, an increase in the number of simulations or further obtaining larger flow diversity, by producing additional simulations with the same obstacles tilted in the $\triangleleft$ and / datasets, could be very beneficial to the training.

The uncertainty in the results may be decomposed into two parts: the uncertainty of the trained NN to accurately output the pressure in each block regardless of the rest of the flow domain geometry; and the uncertainty in the assembly procedure.

As mentioned in Sect. 2.3 the assembly procedure ensures the consistency between neighbor blocks by removing bias estimated based on the overlapping regions. The discussion of the results was focused on the first part of uncertainty, but the assembly algorithm may be responsible for most of the remaining error seen in the easier-to-predict cases (such as the $\circ$ and $\Box$ datasets), and by increasing error in the cases where the NN performs the worst. Small errors in the blocks may be heavily weighted by this algorithm. The uncertainty here arises both from how the domain is integrated, i.e. whether it is integrated over the longitudinal direction and afterward spanwise or the reverse order, and the way the agreement between the pressure field of neighbor blocks is ensured.

Tested each surrogate model at $\text {Re} = 100$, its performance in extrapolation was inspected on flow conditions corresponding to $\text {Re} =$ 10, 50, 500 and 1000 flows over the $\circ$ obstacle in Table 7. $N_2$ datasets did not bring important improvements in the tests at the training Re number, therefore N₂ results were removed from the following tables. The reference data to evaluate the predictions within turbulent regime consisted of simulations at $\text {Re} = 3\times 10^5$ and $4\times 10^5$. The results from these evaluations were also appended to Table 7.

Table 7 ${{{\textbf {M}}}}_{{{\textbf {u}}}}$ extrapolation test in the laminar regime. Prediction case: $\circ$ dataset. Every error metric, $Error(\phi )$ was normalized according to $Error(\phi )_{norm} = Error(\phi )/(\phi _{max} - \phi _{min})$

Table 7 results showed the difficulty of generalization to other flow conditions, particularly at low-Re numbers where the flow becomes stationary with no dynamical structures, and at Re numbers orders of magnitude higher than the training Re number. As the test simulations were at different flow regimes, the NN failed to predict the pressure upstream of the obstacle and the overall pressure gradient, resulting in large errors. At $\text {Re} = 10$, friction losses introduced by the obstacle resulted in an increase of the pressure upstream and steeper pressure gradients in the downstream region (cf. Fig. 8a). On the opposite side, at turbulent regime, $\text {Re}=3\times 10^5$, friction losses were overpredicted (cf. Fig. 8b). Both were not accurately predicted. The error was mainly due to BIAS.

Fig. 8

${{{\textbf {M}}}}_{{{\textbf {u}}}}$ accuracy in extrapolation

In the laminar regime, friction losses are known to increase with the viscosity (or decrease with the Re number), i.e. with the decrease of the Re, therefore it is clear that in different Re number flows estimating these quantities must correctly account for the viscosity. The surrogate models lacked information to correctly find the relation between velocity and pressure fields consistently for different Re without the explicit inclusion of the viscosity, thus the problem may be ill-posed for training with different Re numbers.

Despite the mentioned limitation, it was still possible to see an improvement trend within the tests at $\text {Re} =$ 50, 500, and 1000, as long as the flow conditions are similar. Training with more complicated geometries (cf. M $_{\circ }$, $\Box$, $\triangleleft$, / results on Table 7), introduced different flow characteristics that could be similar to other Re flows in the $\circ$ cases, considerably improving the estimations. This trend could steadily go into lower errors, however, the ill-posed optimization problem may eventually set a lower limit impossible of being surpassed. This limit would go up in concordance with the increase in the Re test range.

The difficulties in extrapolation tests allowed us to understand the inadequacy of extending a model trained with only one Re number flows to general usage, however, an improving trend was visible as long as new training examples were added, hereby represented by the increment of simulation data with different obstacles to the training dataset, showing an increase in performance up until M $_{\circ }$, $\Box$, $\triangleleft$, / - ${\textbf {u}}$ in moderate Re-number flows. For both high and low Re numbers the results were completely inadequate (cf. Table 7). The results showed the model difficulty in estimating the upstream pressure, directly related to an inadequate prediction of the head pressure losses caused by the obstacle, and pressure gradient downstream of the object resulting in high BIAS. Further improving the surrogate model and allowing training/extrapolation to different Re numbers, it could be required to either pre-process the data differently, allowing to disconnect the pressure values from the viscous effects, or change the inputs and outputs given in training. More details about the training can be found in Appendix B.

4.2 Model ${{\textbf {M}}}_{\text{f}({{\textbf {u}}})}$

The relevance of this approach comes from leveraging the knowledge of the differential equation governing the phenomenon. Results from M$_{\text{f}({{\textbf {u}}})}$ were captured for each geometry in Table 8 enabling direct comparison with the ${{{\textbf {M}}}}_{{{\textbf {u}}}}$ results from Table 6.

The current approach proved challenging as the immense amount of variance present in the $f({{\textbf {u}}})$ field severely crippled the model learning process. However, with the proper pre-processing, given by the PCA transformation, it could potentially be used to generalize to any problem represented by the Poisson differential equation as in equation (7) provided the potential field here represented by $f({{\textbf {u}}})$ applied in its general form. Several PCs were necessary to represent a sufficient amount of the input variance, therefore an upper limit was defined: the number of PCs had to jointly represent up to $95 \%$ of the total variance without surpassing the upper limit defined by the hidden layers width (512 neurons). Since this was an additional test, hyperparameter tuning was not performed prior to the application of this NN.

Table 8 ${{\textbf {M}}}_{\text{f}({{\textbf {u}}})}$ results trained with each dataset and tested in $\text {Re} = 100$ flows. Every error metric, $Error(\phi )$ was normalized according to $Error(\phi )_{norm} = Error(\phi )/(\phi _{max} - \phi _{min})$

From Table 8, ${{\textbf {M}}}_{\text{f}({{\textbf {u}}})}$ had far lower performance when compared to results from models ${{{\textbf {M}}}}_{{{\textbf {u}}}}$, but with the appropriate hyperparameter tuning these results have a large margin of improvement. However, some information was in agreement with the results from Table 6 with complex flow conditions providing richer training.

Table 9 M$_{\text{f}({{\textbf {u}}})}$ extrapolation test. Prediction case: $\circ$ dataset in laminar regime.Every error metric, $Error(\phi )$ was normalized according to $Error(\phi )_{norm} = Error(\phi )/(\phi _{max} - \phi _{min})$

M$_{\text{f}({{\textbf {u}}})}$ models were also tested in extrapolation and the results are shown in Table 9. Every model failed in predicting low Re number flows exactly as ${{{\textbf {M}}}}_{{{\textbf {u}}}}$ models due to the same reason. However, in medium to high-Re numbers, models M $_{\circ }$ - $f({{\textbf {u}}})$ and M $_{/}$ - $f({{\textbf {u}}})$ achieved better results.

Fig. 9

M$_{\text{f}({{\textbf {u}}})}$ accuracy in extrapolation at $\text {Re}=3\times 10^5$

M$_{\text{f}({{\textbf {u}}})}$ in moderate Re numbers was able to achieve relatively good predictions when compared to its prediction at the training Re number, which suggests that the $f({{\textbf {u}}})$ input field could be more sensible to changes in Re number by heavily weighting variations in the velocity field.

At $\text {Re} = 10$, M$_{\text{f}({{\textbf {u}}})}$ also provided unacceptable predictions. Lastly, in extrapolation into turbulent regime, the results from M$_{\text{f}({{\textbf {u}}})}$ were far superior to results of models ${{{\textbf {M}}}}_{{{\textbf {u}}}}$, reaching an overall superior accuracy with every single model as illustrated in Fig. 9 for a single example. These results at $3000-4000\times$ the training Re number may be an indication of the superior adequacy of using $f({{\textbf {u}}})$ as input to predict in such different flow conditions, or just an indication of the incomplete adjust to the training set providing moderate errors in a large range of flow conditions. Regarding the evaluation tests at turbulent regime, given that the simulation set was generated based on a uRaNS turbulence model simulation approach, the corresponding $f({{\textbf {u}}})$ field formulation should account for Reynolds stress terms. However, the DNS formulation, eq. (7), was taken to use the NNs previously trained with the laminar cases directly.

4.3 Performance evaluation

To assess the usefulness of the developed surrogate model, its computational performance was benchmarked against the conventional PISO algorithm as implemented in OpenFOAM pisoFoam solver. Model M $_{\circ }$, $\Box$, $\triangleleft$, / was selected for the benchmarking.

The overlap ratio, i.e. the ratio between the overlap region size and the block size is used to assemble the full flow domain based on multiple blocks (cf. Section 2.3 and Fig. 3), determines the number of calls to the NN and the number of calls to the reconstruction loop, hence it has high impact on the model performance. Therefore it is taken as a parameter on the following evaluations.

The evaluation procedure consisted of comparing the execution time taken in 1000 calls to the PISO method and the surrogate model using a single core from an Intel$\circledR$ Xeon$\circledR$ Processor E5-2650.

Figure 10 shows the speedup factor attained when using the surrogate model, with the PISO algorithm implementation as is in OpenFOAM as a reference. As detailed in Appendix B the results shown in the Results Section used an overlap ratio $= 0.75$ since it seemed to show the best possible results. However, the current results show that lower overlap ratios can be used to decrease computational cost with a very low loss of accuracy as shown in Fig. 11 which displays the average RMSE normalized as a function of the overlap ratio for all simulation types.

Fig. 10

Average speedup obtained by using the ML surrogate model to solve the pressure Poisson equation in a CFD simulation. The average speedup is defined as the ratio between the execution time of the PISO algorithm as implemented in OpenFOAM and the execution time of the surrogate model

Fig. 11

Average RMSE normalized when using the ML surrogate model to solve the pressure Poisson equation in a CFD simulation. The results from the PISO algorithm, as implemented in OpenFOAM, were used as a reference

The simulation cases showed very little influence on the time of a surrogate model call (c.f. Tables 14,  15 and  16). The performance of the surrogate model was agnostic to the case geometric complexity since it predicts each block and reconstructs the full domain with the same set of steps independently of the simulation geometry. The number of cells in the CFD mesh had a low impact on the surrogate model, since it only impacted the interpolation operations, i.e. interpolating from a grid defined from the CFD mesh cell centers converted to a uniform grid of points from where the blocks were extracted. For a complete view of these results the reader may refer to Appendix D. In these detailed results, some uncertainty can be detected. This came from the variability in the high-performance computing node performance as a function of the load it was submitted to. This variability could not be removed.

The surrogate model yielded higher advantages in terms of computation expenses for complex cases (where the PISO would perform many iterations until reaching convergence) and cases with meshes with a high number of cells.

For the sake of visualization, only the average speedups attained in each type of flow case were shown. Tables with the time-dependent results are provided in Appendix D.

These results both in terms of performance and accuracy show that a combination of PCA and a simple MLP was found to be efficient and capable of being adequately trained with low computational resources. Using PCA to replace whether the encoding or decoding layers provided training efficiency as demonstrated in Sousa [37] and Appendix B.

5 Conclusions

An algorithm capable of dealing with any geometry was proposed and used to construct ML surrogate models capable of solving the pressure Poisson equation in CFD solvers with low to moderate errors by ensuring the neural network (NN) is decoupled from the CFD mesh. This enables the application of a trained surrogate model to generic flow geometries.

Two types of ML surrogate models were established based on the selected set of inputs: models that took the velocity field as input were referred to as ${{{\textbf {M}}}}_{{{\textbf {u}}}}$, and the ones receiving the source term of the pressure Poisson equation as input were called M$_{\text{f}({{\textbf {u}}})}$.

• ${{{\textbf {M}}}}_{{{\textbf {u}}}}$ models revealed to be good interpolators, managing to predict with very low error in every test case within training flow conditions (cf. Tables 5 and 6).

• ${{{\textbf {M}}}}_{{{\textbf {u}}}}$ models trained with every dataset (M $_{\circ }$, $\Box$, $\triangleleft$, / - ${{\textbf {u}}}$) had a maximum amount of RMSE normalized of  3$\%$ and performed with RMSE normalized lower than  2$\%$ in the remaining datasets while enabling speedups of up to 30 times when compared to the classical PISO algorithm.

• The effect of a fivefold increase in the number of training samples from each CFD simulation (i.e. from $N_1$ to $N_2$) was depicted by Tables 6 and 7 and was shown not to be beneficial.

• Increased diversity in the training dataset improved the overall performance of each model in the training flow conditions and even in extrapolation (cf. Tables 5 and 7).

• The surrogate models failed at extrapolation into very different flow conditions, as those failed to learn the correct mapping between friction losses and the Re number. However, the improvement trend with the increase in training data diversity suggested the possibility of this model having practical application near the training conditions given that it is trained with larger diversified datasets.

• M$_{\text{f}({{\textbf {u}}})}$ models showed to be able to learn how to solve the Poisson equation with medium errors and had some capacity for generalization. The moderate accuracy in some extrapolation tests accompanied by medium errors in the training tests also indicated that the NN could not properly fit the training examples. This may have come from the non-optimization of the NN hyperparameters and the amount of variance from its input flow field.

• A combination of PCA and a simple MLP was found to be efficient and capable of being adequately trained with low computational resources, without losing accuracy. Using PCA to replace whether the encoding or decoding layers provided training efficiency.

Future works will focus on:

• Improving the training formulation of ${{{\textbf {M}}}}_{{{\textbf {u}}}}$ to enable a well-formulated optimization problem for learning flow characteristics over a wide range of Re numbers. It was hypothesized that having the pressure gradient (instead of the pressure) as the output of the NN and integrating it over the domain could lead to obtaining a pressure field with more consistent gradients over a wide range of flow conditions;

• Better tuning the M$_{\text{f}({{\textbf {u}}})}$ parameters and adding additional pre-processing to the input field to access if this model can be capable of accurate extrapolation;

• Optimizing the assembly algorithm and reducing the uncertainty associated with it. This requires an uncertainty analysis of the assembly algorithm and NN separately, as individual components.

Appendices

Appendix A The k-$\omega$ SST turbulence model

Following eq. (1) the Newtonian deviatoric stress tensor, $\tau$, was defined for laminar flows in eq. (2). For turbulent flows, it is given by the combination of both viscous and turbulent stresses, the latter modeled with a Boussinesq eddy-viscosity hypothesis [43]:

$$\begin{aligned} \varvec{\tau } = \varvec{\tau }_v - \rho \overline{\textbf{u}'\textbf{u}'} = (\mu + \mu _t)\,[2\,{{\textbf {S}}} - \tfrac{2}{3}\,\textbf{I}\,\nabla \cdot \textbf{U}] - \tfrac{2}{3}\,\textbf{I}\,\rho \,k, \end{aligned}$$

(A1)

where $\mu$ and $\mu _t$ are the molecular and eddy viscosities, ${{\textbf {S}}} = \tfrac{1}{2}\,[\nabla \textbf{U} + (\nabla \textbf{U})^{\textsc {t}}]$ is the rate-of-strain tensor, $\textbf{I}$ the identity tensor, and $\rho$ the fluid density. $\textbf{u}'$ is the velocity fluctuations coming from the decomposition of the velocity vector, $\textbf{u}$, in its average, $\textbf{U}$, and fluctuation components:

$$\begin{aligned} \textbf{u}' = \textbf{u} - \textbf{U}, \end{aligned}$$

(A2)

and k is the turbulent kinetic energy defined as $k=\frac{1}{2}\overline{\textbf{u}'\cdot \textbf{u}'}$.

To close the system of equations, it is necessary to estimate a value for the eddy viscosity, $\mu _t$. To this end, among the two-equation models, the k-$\epsilon$ and k-$\omega$ could be used. These have their respective advantages, but the k-$\omega$ SST (Shear Stress Transport) turbulence model [41] connected both by the use of blending functions, $F_1$ and $F_2$ (below defined in equations (A6) and (A10)). It is well known that the k-$\epsilon$ is not accurate in near-wall regions and k-$\omega$ is inaccurate when dealing with high-pressure gradients and too sensitive to the free stream values of $\omega$ [44]. To overcome the previous challenges, the blending functions retain the k-$\omega$ model characteristics in the near-wall flow, and k-$\epsilon$ is used away from the walls. The k-$\omega$ SST is often characterized by its good behavior in adverse pressure gradients and separating flow [45]. The transport equations for k and $\omega$ are:

$$\begin{aligned}{} & {} \rho \frac{\text{D} k}{\text{D} t} = \nabla \cdot \left( \left[ \mu + \eta _k\,\mu _t \right] \nabla k \right) + P -\rho \,C_{\mu }\omega \,k, \end{aligned}$$

(A3)

$$\begin{aligned}{} & {} \rho \frac{\text{D} \omega }{\text{D} t} = \nabla \cdot \left( \left[ \mu + \eta _{\omega }\,\mu _t \right] \nabla \omega \right) + \frac{\rho \,\gamma }{ \mu _t} P -\rho \,\beta \,\omega ^2 + (1-F_1) \frac{2\,\rho \,\eta _{\omega 2}}{\omega }\nabla k \cdot \nabla \omega , \end{aligned}$$

(A4)

respectively, with the mechanical turbulence production defined as

$$\begin{aligned} P= & {} - \rho \overline{\textbf{u}'\textbf{u}'}: \nabla \varvec{U} = \mu _t \left[ \,2 \varvec{S}:\varvec{S} - \frac{2}{3} \left( \nabla \cdot \varvec{U} \right) ^2 \right] - \frac{2}{3}\,\rho \,k\,\nabla \cdot \varvec{U}, \end{aligned}$$

(A5)

which is limited by $\min \left( P,\,10\,\rho \,C_{\mu }\,\omega \,k \right)$ to prevent excessive turbulence in stagnant regions [46].

The constants $\gamma$, $\beta$ and the turbulent Prandtl inverse numbers, $\eta _k$ and $\eta _{\omega }$, are blended by a function $F_1$, such that $\phi = F_1 \phi _1 + \left( 1-F_1\right) \phi _2$, where $\phi$ is any of $\gamma$, $\beta$, $\eta _k$ or $\eta _\omega$.

The blending function $F_1$ is given by

$$\begin{aligned} F_1 = \tanh (\Gamma )^4, \end{aligned}$$

(A6)

where $\Gamma$ is defined as

$$\begin{aligned} \Gamma = \min \left( \max \left( \frac{\sqrt{k}}{\beta ^*\,\omega \,\delta _w}, \frac{500\mu }{\rho \,\omega \,\delta _w^2} \right) , \frac{4 \,\rho \,\eta _{\omega 2}\, k}{CD_{k\omega }\,\delta _w^2} \right) , \end{aligned}$$

(A7)

with $\delta _w$ as the distance to the nearest wall, and $CD_{k\omega }$

$$\begin{aligned} CD_{k\omega } = \max \left( \frac{2\,\rho \,\eta _{\omega 2}}{\omega }\nabla k \cdot \nabla \omega , 10^{-10} \right) , \end{aligned}$$

(A8)

$\mu _t$ is defined as

$$\begin{aligned} \mu _t = \frac{\rho \,\alpha _1\,k}{\max \left( \alpha _1 \omega , \sqrt{2 \varvec{S}:\varvec{S}} F_2 F_3 \right) } \end{aligned}$$

(A9)

using two additional blending functions: $F_2$ and $F_3$ defined as

$$\begin{aligned} F_2= & {} \tanh \left( \left[ \max \left( \frac{2\,\sqrt{k}}{C_{\mu }\,\omega \,\delta _w}, \frac{500\,\mu }{\rho \,\omega \,\delta ^2_w} \right) \right] ^2 \right) \end{aligned}$$

(A10)

$$\begin{aligned} F_3= & {} 1- \tanh \left( \left[ \frac{150\,\mu }{\rho \,\omega \,\delta ^2_w} \right] ^4 \right) \end{aligned}$$

(A11)

$F_3$ is activated for rough-wall flows. The coefficients are based on Menter et al [44] and defined as $C_{\mu } = 0.09$, $\eta _{k1} = 0.85$, $\eta _{k2} = 1$, $\eta _{\omega 1} = 0.5$, $\eta _{\omega 2} = 0.856$, $\beta _1 = 0.075$, $\beta _2 = 0.0828$, $\gamma _1 = 5/9$, $\gamma _2 = 0.44$ and $\alpha _1 = 0.31$. More information about different versions of the k-$\omega$ SST turbulence model can be found at NASA [47].

Appendix B Model parameters selection

This section holds the selection process of the ML surrogate model parameters. For this purpose, the training process was employed for 1000 epochs without early stopping. The error metrics used consisted of the RMSE normalized, BIAS normalized, and STDE normalized from the ML surrogate model predictions at multiple temporal frames with the results from CFD simulations taken as the reference. The training set here consisted of bi-dimensional cylinders (N1 dataset) using the ${{{\textbf {M}}}}_{{{\textbf {u}}}}$ model. The best-behaving parameters here were selected for all the models.

The first and most impactful choice was the architecture of the model. Alongside the MLP architecture shown in the body of the article, multiple CNN architectures, represented in Fig. 12, were tested. The inspiration for the proposed CNN architectures was the U-Net [48] since it has been previously applied to fluid dynamics in the form of standard U-Net’s [49, 50] or even a combination of those [51].

Fig. 12

U-net-based modified architectures

In Fig. 12, Models 1 (M1), 2 (M2), and 3 (M3) were schematically illustrated. Model 4 (M4) refers to the MLP architecture from Fig. 4.

To synthesize the results, in the error chart from Fig. 13 only the best performances of each architecture and block size combination are presented. The results from M1 were not shown in Fig. 13 due to its inferior performance, which would deteriorate the plot. Considering the low computational effort required by Model 4 and its overall superior accuracy (c.f. Fig. 13), it was selected.

Fig. 13

Error chart for performance comparison. Mx &By represents the error for model x predictions with a block size of y

To select the block size and overlap ratio, the influence of those was depicted in Fig. 14. From this representation, a block size of 64 seemed to work significantly worse than the other options. The best combination found was a block size of 128 and an overlap ratio of 0.75, thus these were taken as the default values.

Fig. 14

Error chart of Model 4 results, where x &y represents the error for a block size of x and overlap ratio y

Selected the most relevant surrogate model parameters, it was still necessary to optimize the training hyper-parameters. These included:

• Loss formulation.

• Batch size.

• Learning rate, $\alpha$, and moving average parameter, $\beta$. These are parameters required by the Adam optimization algorithm [52].

The most elementary loss function would be the MSE of the model prediction as defined in eq. 12, therefore it constituted $L_1$. To force the NN to better predict the most important parameters, a modification was applied to the loss function to weight each component’s importance in the loss computation, being the weight defined by each PC contribution to the total variance, $L_2$ and $L_3$, respectively represented in equations

$$\begin{aligned} L_2 = \frac{1}{N_{points}}\sum _{i=1}^{N_{points}} \left( \hat{\theta } - \theta \right) ^2 Explained_{var} \end{aligned}$$

(B12)

and

$$\begin{aligned} L_3 = \frac{1}{N_{points}}\sum _{i=1}^{N_{points}} \left( \hat{\theta } - \theta \right) ^2 Explained_{var}^2 , \end{aligned}$$

(B13)

where $Explained_{var}$ is a vector with the total variance explained by each PC. The influence of this parameter was analyzed in conjunction with the batch size as shown in Fig. 15. Since it behaved reasonably well and is conceptually simpler, $L_1$ was selected.

Fig. 15

Batch size and loss function selection study

The influence of the number of PCs used (or the total variance explained) by these was also studied resulting in the results presented in Fig. 16. A total of 32 principal components were selected which represented $95\%$ of the total variance on the output dataset.

Fig. 16

The number of truncated principal components from pressure/output principal component analysis (PCA)

To select the most appropriate learning rate range, the evolution of the loss is plotted for a range of learning rates as in Fig. 17 allowing to first pick an optimal learning rate range to further study.

Fig. 17

Learning rate (lr) tuning

From Fig. 17 the range from $10^{-5}$ to $10^{-4}$ seemed optimal, and values in that range were tested resulting in selecting the learning rate as $lr = 10^{-4}$ and $\beta = 0.99$ accordingly to results from Fig. 18.

Fig. 18

Learning rate (lr) and moving average parameter ($\beta _1$) study

The last parameter optimized consisted of the model depth, defined by the number of hidden layers with a constant width of 512 neurons as represented in Fig. 4. Since increased model complexity typically allows for a better fit of the data, namely in the BIAS of each block field prediction (note that after assembling this effect can no longer be analyzed), increasing it could be beneficial only up to a point. The optimal point was selected from the results shown in Fig. 19 and the number of hidden layers was fixed at 3.

Fig. 19

Accuracy of the surrogate model at multiple MLP depths

Appendix C Datasets description and Training convergence curves

In Tables 10 and 11 the original and pre-processed datasets used for training models ${{{\textbf {M}}}}_{{{\textbf {u}}}}$ and M$_{\text{f}({{\textbf {u}}})}$ are described. PCA reduced the dimensionality of the data by considering only the PCs necessary to represent $99.5\%$ and $95\%$ of the input variance for ${{{\textbf {M}}}}_{{{\textbf {u}}}}$ and M$_{\text{f}({{\textbf {u}}})}$ respectively, and $95\%$ of the total variance of the output.

After pre-processing, the data is split as 90$\%$ for training and 10$\%$ for validation.

Table 10 Description of dataset sizes before and after pre-processing for ${{{\textbf {M}}}}_{{{\textbf {u}}}}$ datasets. The input and output size refers to the size of each input and output sample, while the No. of points refers to the total of points across all the samples

Table 11 Description of dataset sizes before and after pre-processing for M$_{\text{f}({{\textbf {u}}})}$ datasets. The input and output size refers to the size of each input and output sample, while the No. of points refers to the total of points across all the samples

The training of both ${{{\textbf {M}}}}_{{{\textbf {u}}}}$ and ${{\textbf {M}}}_{\text{f}({{\textbf {{\textbf {u}}}}})}$ NNs was performed using 16 CPUs in parallel. The training execution times are shown in Tables 12 and 13 for ${{{\textbf {M}}}}_{{{\textbf {u}}}}$ and ${{\textbf {M}}}_{\text{f}({{\textbf {{\textbf {u}}}}})}$, respectively.

Table 12 ${{{\textbf {M}}}}_{{{\textbf {u}}}}$ training specifications

Table 13 ${{\textbf {M}}}_f({{\textbf {u}}})$ training specifications

The training of each NN was characterized by the convergence curves, i.e. the evolution of the training and validation losses along the epochs, from Figs. 20, 21, 22 and 23 for the NNs used in Models ${{{\textbf {M}}}}_{{{\textbf {u}}}}$ and Fig. 24 for the NNs of Models ${{\textbf {M}}}_f({{\textbf {u}}})$.

Fig. 20

Convergence curves from the training of Model ${{{\textbf {M}}}}_{{{\textbf {u}}}}$ with ${\text{N}}_1$ datasets

Fig. 21

Convergence curves from the training of Model ${{{\textbf {M}}}}_{{{\textbf {u}}}}$ with ${\text{N}}_2$ datasets

Fig. 22

Convergence curves from the training of Model ${{{\textbf {M}}}}_{{{\textbf {u}}}}$ with ${\text{N}}_1$ datasets

Fig. 23

Convergence curves from the training of Model ${{{\textbf {M}}}}_{{{\textbf {u}}}}$ with ${\text{N}}_2$ datasets

Fig. 24

Convergence curves from the training of Model ${{\textbf {M}}}_f({{\textbf {u}}})$

Appendix D Surrogate model performance evaluation

Tables 14, 15, and 16 contain the elapsed time taken to run the surrogate model for each family of obstacle geometries at a timestamp, t, as a function of the characteristic time scale, $t^*$.

Tables 17, 18, and 19 contain the speedup attained by benchmarking the surrogate model against the OpenFOAM PISO implementation.

Table 14 Execution time (in [ms]) when using M $_{\circ }$, $\Box$, $\triangleleft$, / to solve the pressure Poisson Equation for multiple times defined as a function of the characteristic time, $t*$. The characteristic time is defined as $t^* = \phi / U_{\infty ,c}$ where $\phi$ is the characteristic length and $U_{\infty ,c}$ is the centerline velocity at the inlet. Overlap ratio = 0.25

Table 15 Execution time (in [ms]) when using M $_{\circ }$, $\Box$, $\triangleleft$, / to solve the pressure Poisson Equation for multiple times defined as a function of the characteristic time, $t*$. The characteristic time is defined as $t^* = \phi / U_{\infty ,c}$ where $\phi$ is the characteristic length and $U_{\infty ,c}$ is the centerline velocity at the inlet. Overlap ratio = 0.50

Table 16 Execution time (in [ms]) when using M $_{\circ }$, $\Box$, $\triangleleft$, / to solve the pressure Poisson Equation for multiple times defined as a function of the characteristic time, $t*$. The characteristic time is defined as $t^* = \phi / U_{\infty ,c}$ where $\phi$ is the characteristic length and $U_{\infty ,c}$ is the centerline velocity at the inlet. Overlap ratio = 0.75

Table 17 Acceleration factor obtained by using M $_{\circ }$, $\Box$, $\triangleleft$, / to solve the pressure Poisson Equation for multiple times defined as a function of the characteristic time, $t*$. The characteristic time is defined as $t^* = \phi / U_{\infty ,c}$ where $\phi$ is the characteristic length and $U_{\infty ,c}$ is the centerline velocity at the inlet. Overlap ratio = 0.25

Table 18 Acceleration factor obtained by using M $_{\circ }$, $\Box$, $\triangleleft$, / to solve the pressure Poisson Equation for multiple times defined as a function of the characteristic time, $t*$. The characteristic time is defined as $t^* = \phi / U_{\infty ,c}$ where $\phi$ is the characteristic length and $U_{\infty ,c}$ is the centerline velocity at the inlet. Overlap ratio = 0.50

Table 19 Acceleration factor obtained by using M$_{\circ }$, $\Box$, $\triangleleft$, / to solve the pressure Poisson Equation for multiple times defined as a function of the characteristic time, $t*$. The characteristic time is defined as $t^* = \phi / U_{\infty ,c}$ where $\phi$ is the characteristic length and $U_{\infty ,c}$ is the centerline velocity at the inlet. Overlap ratio = 0.7