Ensemble reservoir computing for dynamical systems: prediction of phase-space stable region for hadron storage rings

Abstract

We investigate the ability of an ensemble reservoir computing approach to predict the long-term behaviour of the phase-space region in which the motion of charged particles in hadron storage rings is bounded, the so-called dynamic aperture. Currently, the calculation of the phase-space stability region of hadron storage rings is performed through direct computer simulations, which are resource- and time-intensive processes. Echo State Networks (ESN) are a class of recurrent neural networks that are computationally effective, since they avoid backpropagation and require only cross-validation. Furthermore, they have been proven to be universal approximants of dynamical systems. In this paper, we present the performance reached by ESN based on an ensemble approach for the prediction of the phase-space stability region and compare it with analytical scaling laws based on the stability-time estimate of the Nekhoroshev theorem for Hamiltonian systems. We observe that the proposed ESN approach is capable of effectively predicting the time evolution of the extent of the dynamic aperture, improving the predictions by analytical scaling laws, thus providing an efficient surrogate model.

1 Introduction

The advent of superconducting, high-energy hadron storage rings and colliders elevated nonlinear beam dynamics to the forefront of accelerator design and operation. When studying phenomena in the field of single-particle beam dynamics, the concept of dynamic aperture (DA), that is, the extent of the phase-space region where bounded motion occurs, has been a key observable to guide the design of several past (see, e.g. [1,2,3,4,5,6]), present, e.g. the CERN Large Hadron Collider (LHC) [7], and future hadron machines (see e.g.  [8,9,10,11,12,13,14,15]).

DA prediction involves many challenging aspects, including understanding the mechanisms that determine its behaviour and addressing several computational problems. An important issue is the possibility of modelling the evolution of DA as a function of the number of turns, which has been studied since the end of the 90s [16, 17]. Indeed, determining how to describe and efficiently predict the value of the DA might solve some fundamental problems in accelerator physics, linked to performance optimisation of storage rings and colliders. The high computational cost of direct numerical simulations would be significantly reduced if a reliable model for the time evolution of the DA were available. In fact, the numerical simulations required to assess the performance of a circular accelerator cannot cover a time span comparable with operational intervals. For the LHC case, simulations up to $10^6$ turns are at the limit of the CPU-time capabilities, although this represents only about 89 s of storage time, knowing that a typical fill time is of the order of several hours. Eventually, a model for the evolution of DA over time would also open the possibility of studying observables that are more directly related to machine performance, such as beam losses and lifetime [18] and luminosity evolution in colliders [19, 20].

A successful solution to this problem has been found by building models for DA scaling with time based on fundamental results of the dynamical system theory, such as the Nekhoroshev theorem [21,22,23]. In fact, models with two or three parameters can be derived that can be fitted to numerical data that represent the evolution of the DA and used to predict the DA value for times beyond the current computational capabilities [24].

In the last decade, the use of neural networks has increased significantly in a large number of diverse research areas, and this observation has suggested their application to the prediction of the evolution of DA. For example, neural networks are used for speech recognition [25] or to forecast wind power [26]. Some examples of the application of neural networks to particle accelerator modelling are reported in [27, 28], and the use of Uncertainty Quantification techniques to build surrogate models for accelerator systems is discussed in [29]. Among neural network techniques, the most common architectures are feedforward [30], convolutional [31], and recurrent [32] neural networks. Feedforward neural networks are made up of neurons connected to other neurons, only. They provide only input–output relationships and can approximate very large classes of functions. On the other hand, recurrent neural networks are made up of neurons connected to themselves and other neurons. They preserve an internal state that is a nonlinear transformation of the input signal and can therefore be considered as dynamical systems.

Echo State Networks (ESN) are one of the classes of recurrent neural networks that use the reservoir computing approach [33]. This approach has the main advantage of significantly reducing the computational time required by the training process, which is performed to find the optimal parameters (called weights) of a neural network. In fact, the peculiarity of the ESN is that training is performed, usually using linear regression [34], to calculate the weights used to project the reservoir state onto the output state. Therefore, no backpropagation is needed. Backpropagation [35] refers to the numerical procedure, usually based on the stochastic gradient method, used for the training of feedforward networks, which is responsible for a large share of its computational cost. ESN have also been proven to be universal approximants of dynamical systems [36].

Note that in this work we only focus on the prediction of DA evolution with time, which can be interpreted as a functional of the underlying dynamical system, for which ESN represent an appropriate tool. A first attempt to apply ESN to the prediction of DA evolution with time was presented in [37]. The present paper presents an improved model for the ESN applied to the same data presented in [37] and to new data generated on purpose to test the robustness of the improved ESN model. This paper is organised as follows: In Sect. 2, we introduce the concept of DA and the approach used to provide numerical estimates of its value. Analytical scaling laws, based on the Nekhoroshev theorem and used to predict the time evolution of DA, are also presented. Section 3 introduces the continuous-time leaky ESN framework that is used for the prediction of DA. The Echo State Property (ESP), and a sufficient condition that can be applied in practice to satisfy it, are discussed in the Appendix 1. Section 4 describes the ensemble procedure used in the cross-validation of the ESN and in the prediction of DA. The results are presented and discussed in Sect. 5, while conclusions are drawn in Sect. 6.

2 Dynamic aperture

2.1 Generalities

We consider a Hamiltonian system in $\mathbb {R}^{2n}$, with a stable fixed point at the origin, whose dynamics is generated by a polynomial map $\mathcal {M}$, and such that the linear part of $\mathcal {M}$ is described by the direct product of rotations. Under these conditions, the DA of the system under consideration is the extent of the region of phase space in which bounded motion occurs.

Following [38] and restricting the analysis to the case of Hamiltonian systems in $\mathbb {R}^4$, which are relevant for accelerator physics, we consider the phase-space volume of the initial conditions that are bounded after N iterations, namely

$$\begin{aligned} \int \int \int \int \chi (x_1,p_{x_1},x_2,p_{x_2}) \; {\rm d}x_1 \, {\rm d}p_{x_1} \, {\rm d}x_2 \, {\rm d}p_{x_2} , \end{aligned}$$

(1)

where $\chi (x_1,p_{x_1},x_2,p_{x_2})$ is the characteristic function defined as equal to one if the orbit starting at $(x_1,p_{x_1},x_2,p_{x_2})$ is bounded and zero if it is not.

The disconnected part of the stability domain that is involved in the computation of the integral (1) should be removed [39], and to this end a suitable coordinate transformation should be selected. As linear motion is given by the direct product of constant rotations, the natural choice is to use the polar variables $(r_i,\vartheta _i)$, where $r_1$ and $r_2$ are the linear invariants of dynamics. The nonlinear part of the equations of motion adds a coupling between the two planes, the perturbative parameter being the distance from the origin. It is customary to use the polar variables $r \cos \alpha$ and $r \sin \alpha$ instead of $r_1$ and $r_2$, thus obtaining

$$\begin{aligned} \left\{ \begin{array}{lcll} x_1 &=& r \cos \alpha \cos \vartheta _1 & \\ p_{x_1} &=& r \cos \alpha \sin \vartheta _1 & \qquad \qquad r \in [0,+\infty [ \\ & & & \qquad \qquad \alpha \in [0,\pi /2] \\ x_2 &=& r \sin \alpha \cos \vartheta _2 & \qquad \qquad \theta _i \in [0,2\pi [ \qquad i=1,2 \\ p_{x_2} &=& r \sin \alpha \sin \vartheta _2 , & \end{array} \right. \end{aligned}$$

(2)

which replaced in Eq. (1) gives

$$\begin{aligned} \int _0^{2\pi } \int _0^{2\pi } \int _0^{\pi /2}\int _0^\infty \; \chi (r, \alpha , \vartheta _1, \vartheta _2) \, r^3 \sin \alpha \cos \alpha \; d \Omega _4 , \end{aligned}$$

(3)

where ${\rm d}\Omega _4$ represents the volume element

$$\begin{aligned} {\rm d}\Omega _4 = {\rm d}r \, {\rm d}\alpha \, {\rm d}\vartheta _1 \, {\rm d}\vartheta _2 . \end{aligned}$$

(4)

If $r(\alpha , \varvec{\vartheta },N)$ is the largest value r whose orbit is bounded after N iterations in the direction given by $\alpha$ and $\varvec{\vartheta }=(\vartheta _1,\vartheta _2)$, the volume of a connected domain where the bounded motion occurs is obtained by

$$\begin{aligned} A_{\alpha ,\varvec{\vartheta },N} = \frac{1}{8} \, \int _0^{2\pi } \int _0^{2\pi } \int _0^{\pi /2} [r(\alpha ,\varvec{\vartheta },N)]^4 \sin 2 \alpha \; {\rm d}\Omega _3 , \end{aligned}$$

(5)

where

$$\begin{aligned} {\rm d}\Omega _3 = {\rm d}\alpha \, {\rm d}\vartheta _1 \, {\rm d}\vartheta _2 . \end{aligned}$$

(6)

In this way, we exclude stable islands that are not connected to the main stable domain. Note that, in principle, this method might also lead to excluding connected parts. The DA corresponds to the radius of the hypersphere with a volume equivalent to that of the stability domain

$$\begin{aligned} r_{\alpha ,\varvec{\vartheta },N} = \left( \frac{2 A_{\alpha ,\varvec{\vartheta },N} }{\pi ^2} \right) ^{1/4} . \end{aligned}$$

(7)

When Eq. (5) is implemented in a computer code, one considers K steps in the angle $\alpha$ and L steps in the angles $\vartheta _i$, and the dynamic aperture reads

$$\begin{aligned} r_{\alpha ,\varvec{\vartheta },N} = \left[ \frac{\pi }{2 \,K L^2} \sum _{k=1}^{K} \sum _{l_1,l_2=1}^L [r(\alpha _k,\varvec{\vartheta }_{\mathbf {\ell }},N)]^4 \sin 2 \alpha _k \right] ^{1/4} \,, \end{aligned}$$

where $\mathbf {\ell }=(l_1,l_2)$.

The numerical error is given by the discretization in angles $\vartheta _i$, $\alpha$, and radius r, which gives a relative error proportional to $L^{-1}$, $K^{-1}$, and $J^{-1}$, respectively. This numerical error can be optimised by choosing integration steps that produce comparable errors, i.e. $J \propto K \propto L$. To achieve a relative error of 1/(4J), $J^4$ orbits should be computed, corresponding to $N J^4$ iterations. The fourth power of the number of orbits originates from the phase-space dimension, and this makes an accurate DA estimate very time-consuming.

It is possible to reduce the size of the scanning procedure, and hence the CPU time needed, by setting the angles $\varvec{\theta }$ to a constant value, e.g. zero, thus performing only a 2D scan over r and $\alpha$. This is what is generally done in SixTrack simulations [40, 41]. In this case, the transformation (2) reads

$$\begin{aligned} \left\{ \begin{array}{lcll} x_1 &=& r \cos \alpha & \\ p_{x_1} &=& 0 & \qquad \qquad r \in [0,+\infty [ \\ x_2 &=& r \sin \alpha & \qquad \qquad \alpha \in [0,\pi /2] \\ p_{x_2} &=& 0 ,& \end{array} \right. \end{aligned}$$

(8)

and the original integral is transformed to

$$\begin{aligned} \int _0^{\pi /2}\int _0^\infty \; r \; {\rm d} r \, {\rm d}\alpha . \end{aligned}$$

(9)

Having fixed $\alpha$, let $r(\alpha ,N)$ be the last value of r whose orbit is bounded after N iterations. Then, the volume of a connected stability domain is given by

$$\begin{aligned} A_{\alpha ,N} = \frac{1}{2} \int _0^{\pi /2} [r(\alpha ,N)]^2 \; {\rm d}\alpha . \end{aligned}$$

(10)

We define the dynamic aperture as the radius of the sphere that has the same volume as the stability domain¹

$$\begin{aligned} r_{\alpha ,N} = \left( \frac{4 A_{\alpha ,N} }{\pi } \right) ^{1/2} . \end{aligned}$$

(11)

When Eq. (10) is implemented in a computer code, one considers K steps in the angle $\alpha$, and the dynamic aperture reads

$$\begin{aligned} r_{\alpha ,N} = \left[ \frac{1}{K} \sum _{k=1}^{K} [r(\alpha _k,N)]^2 \right] ^{1/2} , \end{aligned}$$

(12)

so that the numerical error is given by discretising the angle $\alpha$ and the radius r, which yields a relative error proportional to $K^{-1}$ and $J^{-1}$, respectively. In this case, the integration steps should also be selected to produce comparable errors, i.e. $J \propto K$. To achieve a relative error of 1/(2J), $J^2$ orbits should be computed, corresponding to $N J^2$ iterations. Note that Eq. (10) can be evaluated using higher-order numerical integration rules as implemented in the post-processing tools linked with SixTrack [41].

It is worth noting that in some applications, the simplified formula

$$\begin{aligned} r_{\alpha ,N} = \frac{1}{K} \sum _{k=1}^{K} [r(\alpha _k,N)] , \end{aligned}$$

(13)

which corresponds to computing the average of $r(\alpha _k,N)$ over the angle $\alpha _k$, was used [17].

2.2 DA scaling law

All the definitions of DA estimates presented in the previous section are functions of N, the turn number used to estimate the orbit stability from the results of numerical simulations. It is evident that the definition of DA itself implies that it is a non-increasing function of N. The key point is whether it is possible to find the functional form of this time dependence, and several studies have shown that this is indeed the case [17, 24]. In fact, such a functional form can be built by considering the estimate of the stability time provided by the Nekhoroshev theorem [21,22,23], which is a key and very general theorem in the theory of Hamiltonian dynamical systems. The first models were described in [17] and then reviewed in depth in [24].

An estimate of N(r), i.e. the turn number such that the orbit of an initial condition corresponding to an amplitude r remains bounded, is the subject of the Nekhoroshev theorem [21,22,23]

$$\begin{aligned} \frac{N(r)}{N_0} = \sqrt{\frac{r}{r_*}}\exp {\left( \frac{r_*}{r}\right) ^{\frac{1}{\kappa }}} , \end{aligned}$$

(14)

where $r_*$ and $\kappa$ are positive quantities that describe the key characteristics of the system being considered. Note that this estimate implies exponentially long stability times for orbits starting close to the origin of phase space.

The properties of the parameter $\kappa$ are worth mentioning. In the original formulation [21], $\kappa$ depends on the number d of degrees of freedom of the system considered, although this estimate may not be optimal. For a symplectic map in the neighbourhood of an elliptic fixed point [22, 23], $\kappa \propto (d+1)/2$, is a simpler expression, once again without the guarantee of being an optimal estimate. Equation (14) can be inverted to determine the value of r as a function of N(r), which corresponds to the value of the amplitude that is stable up to N turns. This is exactly the meaning of the dynamic aperture, as discussed in the previous section. The inversion of Eq. (14) can be carried out by making the approximation consisting of dropping the square root term that multiplies the exponential or considering the full expression. This leads to two models for the scaling law of the dynamic aperture, namely

$$\begin{aligned} \begin{aligned} {\textbf {Model 2}} \qquad \Rightarrow \qquad D(N) =\rho _*\left( \frac{\kappa }{2 \text {e}} \right) ^\kappa \, \frac{1}{ \ln ^\kappa \frac{N}{N_0}} ,\end{aligned} \end{aligned}$$

(15)

where the free parameters are $\rho _*, \kappa , N_0$, but it is customary to set $N_0=1$, and

$$\begin{aligned} \begin{aligned} \;\, {\textbf {Model 4}} &\Rightarrow D(N) = \rho _*\\ &\qquad \times \displaystyle {\frac{1}{\left[ -2 \, \text {e} \, \lambda \,\mathcal {W}_{-1}\!\!\,\!\left( -\frac{1}{2 \, \text {e} \, \lambda }\left( \frac{\rho _*}{6} \right) ^{1/\kappa } \, \left( \frac{8}{7} N \right) ^{-1/(\lambda \, \kappa )} \right) \right] ^{\kappa }}} ,\end{aligned} \end{aligned}$$

(16)

where the free parameters are $\rho _*$, $\kappa$, and possibly $\lambda$, unless it is fixed to the value of 1/2 according to the analytic Nekhoroshev estimate.

$\mathcal {W}_{-1}$ stands for the negative branch of the Lambert-$\mathcal {W}$ function, a multi-valued special function (see, e.g. [42] for a review of the properties and applications of the Lambert function). Note that D(N) stands for $r_{\alpha ,\varvec{\vartheta },N}$ or $r_{\alpha ,N}$, depending on the numerical approach used to estimate the DA. The nomenclature of the models presented in Eqs. (15) and (16) reflects the historical development of these models and the nomenclature used in [24]. The derivation of the two models indicates that the general one is Model 4, but Model 2, which is simpler in form and numerical implementation, is in most cases enough. In this study, we have also chosen Model 2 to describe the dynamic aperture behaviour.

An example of the numerical calculation of the DA for a realistic model of the luminosity upgrade of the CERN LHC, HL-LHC [13], and the corresponding fitted scaling law using all available DA data are shown in Fig. 1, where the excellent agreement between the numerical data and the fit model is clearly visible. In the following, we refer to SL as the scaling law given by Model 2 and to SL-ALL as the fitting of Model 2 using all available DA data.

Fig. 1

Example of DA numerical computation for a realistic model of the HL-LHC with the corresponding fitted scaling law. The excellent agreement between the numerical data and the fit model is clearly visible

2.3 DA data organisation

In this section, we present the data sets used to test the predictive model introduced in Sect. 4. The first data set is obtained from a realistic model of the HL-LHC, whereas the second one is obtained from the 4D Hénon map.

2.3.1 The HL-LHC case

The HL-LHC data set, presented in Fig. 2, is composed of 60 realisations (also called seeds due to the underlying random generator used for the generation of the realisations) of the magnetic field errors of the magnetic lattice of the HL-LHC, for the collision optics with $\beta ^{*}$=15 cm and proton energy of 7 TeV. The 60 realisations are supposed to accurately represent the actual lattice of the HL-LHC; for this reason, the DA computation is customarily performed using the complete set of realisations to provide an accurate estimate of the DA of the actual accelerator. Magnetic field errors are assigned to all magnets that make up the ring. Initial conditions (also called particles) are distributed in physical space to probe the orbit stability and thus determine the DA. Different amplitudes and angles in the x–y plane are used to sample the phase space. In the cases considered here, 11 angles, uniformly distributed in the interval $]0, \pi /2[$, are used, while the amplitudes are uniformly distributed in the interval $]0,28 \sigma [$, with 30 initial conditions defined in each 2$\sigma$ interval. Note that 30 particles are evenly distributed in each amplitude interval of $2\sigma$, and $\sigma$ represents the root mean square (rms) beam size, which is used as a natural unit in these studies. All initial conditions are tracked for $10^5$ turns. The numerical estimates of DA as a function of N are calculated according to Eq. (10) and are shown in Fig. 2 (left).

Fig. 2

Left: Evolution of DA as a function of time for the 60 realisations of the HL-LHC magnetic lattice. Right: Splitting of the HL-LHC data set into training, validation, and test sets

We build piecewise constant functions so that each DA estimate now contains $10^3$ data points, with the aim of obtaining DA estimates in constant time steps. These $10^3$ data points are then divided into training set, validation set, and test set. The first $k_{\rm train} = 450$ data are used for training, the next $k_{\rm val} = 50$ data for validation, and the remaining $k_{\rm test} = 500$ data for testing. Note that the end of the training and validation sets corresponds to $N = 5.10^4$, and the end of the testing to $N = 10^5$ turns. A graph of the 60 piecewise constant functions split into training set, validation set and test set is shown in Fig. 2 (right). Note that each of the 60 realisations corresponds to a different DA on which we will train, validate, and test our ESN model.

2.3.2 The 4D Hénon map case

The 4D Hénon map is a well-known dynamical system that displays a rich dynamical behaviour as presented in, e.g. [43]. The model used to generate DA estimates is defined as:

$$\begin{aligned} \begin{pmatrix} x_{n+1} \\ p_{x, n+1} \\ y_{n+1}\\ p_{y, n+1}\\ \end{pmatrix} = \widetilde{R} \begin{pmatrix} x_{n} \\ p_{x, n} + x_{n}^2 - y_{n}^2 + \mu \left( x_{n}^3 - 3 y_{n}^2 x_{n} \right) \\ y_{n}\\ p_{y, n} - 2 x_{n} y_{n} + \mu \left( y_{n}^3 - 3 x_{n}^2 y_{n} \right) \ \end{pmatrix} \end{aligned}$$

(17)

where the subscript n denotes the discrete time and $\widetilde{R}$ is a $4\times 4$ matrix given by the direct product of two $2\times 2$ rotation matrices R:

$$\begin{aligned} \widetilde{R} = \begin{pmatrix} R(\omega _{x, n}) & 0\\ 0 & R(\omega _{y, n}) \end{pmatrix} , \end{aligned}$$

(18)

where the linear frequencies vary with the discrete time n according to

$$\begin{aligned} \omega _{x, n}&= \omega _{x, 0} \left( 1+\varepsilon \sum _{k=1}^{m} \varepsilon _k {\rm cos}(\Omega _k n) \right) \end{aligned}$$

(19)

$$\begin{aligned} \omega _{y, n}&= \omega _{y, 0} \left( 1+\varepsilon \sum _{k=1}^{m} \varepsilon _k {\rm cos}(\Omega _k n) \right) , \end{aligned}$$

(20)

where $\varepsilon$ denotes the amplitude of the frequency modulation, m the number of components in the modulation and $\varepsilon _k$ and $\Omega _k$ are fixed parameters, which are taken from previous studies [24].²

The 4D Hénon map is a simplified model of a circular accelerator. In particular, it describes the effects of a sextupole and octupole magnet on the transverse particle motion through the quadratic, due to the sextupole, and cubic, due to the octupole, nonlinear terms. Being a simplified accelerator model, it allows one to track particles up to a much larger number of turns, and for more amplitudes and angles, namely 100 amplitudes and angles uniformly distributed in the interval ]0, 0.25[ and $]0, \pi /2[$, respectively. The 4D Hénon map data set is composed of 60 cases, for 20 different values of $\varepsilon$ uniformly distributed in the interval [0, 20[ and $\mu \in \{-0.2, 0, 0.2\}$, covering up to $10^8$ turns. Similarly to the HL-LHC data set, we build piecewise constant functions so that each case yields 1000 data points. The first $k_{\rm train} = 450$ data are used for training, the next $k_{\rm val} = 50$ data for validation, and the last $k_{\rm test} = 500$ data for testing. Note that we used the same number of training, validation, and test data for the HL-LHC case. The 60 piecewise constant functions divided into training set, validation set, and test set are shown in Fig. 3.

Fig. 3

Splitting of the 4D Hénon map data set into training, validation, and test sets. The sudden drop in DA visible for $N \approx 10^3$ occurs when $\varepsilon > 15$

Note that because of the larger number of amplitudes and angles considered, the DA data are smoother than those of the HL-LHC case. Furthermore, each of the 60 cases generated in this data set corresponds to a different dynamics for which we will train, validate, and test our ESN model.

3 Echo state networks

In this section, we present some general concepts about ESN. More specifically, we introduce the mathematical framework of continuous-time leaky ESN applied to supervised learning tasks.

3.1 Shallow ESN

Shallow ESN are a class of Recurrent Neural Networks using the Reservoir Computing approach [33]. In this type of neural network, the data input is fed into a single, random, and non-trainable network, called the reservoir. The reservoir is eventually connected by trainable weights to the ESN output. The use of ESN for time series prediction has become widespread due to its inexpensive training process and its remarkable performance in the modelling of dynamical systems [44].

Contrary to feedforward neural networks, ESN do not suffer from vanishing or divergent gradients (caused by the fact that the parameters of neural networks remain almost constant or lead to numerical instabilities), which induces poor performance of the training algorithm [45].

ESN can be defined for discrete- or continuous-time systems. The reservoir dynamics can be defined with or without the leaking rate parameter, which can be considered as the speed of the reservoir update dynamics. We introduce the definition of a shallow leaky ESN in continuous time as in [46]. We consider the case of networks with continuous-time t, K inputs, $N_{\rm r}$ reservoir neurons, and M outputs. Note that we will use small letters to indicate vectors and capital letters to indicate matrices. We define by $u = u(t) \in \mathbb {R}^K$ the input data and $x^{{\rm train}}$ = $x^{{\rm train}}(t) \in \mathbb {R}^M$ the training data that we want to learn with the ESN model. The ESN output is denoted by $x^{{\rm out}} =x^{{\rm out}}(t) \in \mathbb {R}^M$, while the internal reservoir activation state is given by $x = x(t) \in \mathbb {R}^{N_{\rm r}}$. Furthermore, we define the input weight matrix $W^{\text {in}} \in \mathcal{M}_{N_{\rm r}\times K}(\mathbb {R})$, the reservoir weight matrix $W \in \mathcal{M}_{N_{\rm r}\times N_{\rm r}}(\mathbb {R})$, and the output weight matrix $W^{\text {out}} \in \mathcal{M}_{M\times (N_{\rm r}+K)}(\mathbb {R})$. The continuous-time dynamics of a leaky ESN is given by:

$$\begin{aligned}&\frac{{\rm d}x}{\text{d}t} = \frac{1}{c} (-ax + f(W^{\text {in}}u + Wx)) \end{aligned}$$

(21)

$$\begin{aligned}&x^{\text {out}} = g(W^{\text {out}}[x;u]) \end{aligned}$$

(22)

where c is a global time constant, a the leaking rate, f a sigmoid function, g the output activation function and [.;.] denotes vector concatenation. Equation (21) can be discretised in time, in our case by the explicit Euler method, so as to obtain the discretised time dynamics of a leaky ESN:

$$\begin{aligned} x_{k}&= F(x_{k-1},u_{k}) = \left( 1-a\Delta t\right) x_{k-1} + \Delta t f(W^{\text{in}}u_{k} + Wx_{k-1}) \end{aligned}$$

(23)

$$\begin{aligned} x_{k}^{\text{out}}&= g(W^{\text{out}}[x_{k};u_k]) . \end{aligned}$$

(24)

Here $\Delta t$ = $\delta /c,$ where $\delta$ denotes the size of the time discretization step, $x_{k}$ the update of the reservoir activation state at discrete time k and $x^{\text{out}}_{k}$ the ESN output at the same time k. In the case of a linear readout, i.e. when g is the identity function, we can rewrite Eq. (24) in matrix notation as:

$$\begin{aligned} X^{\text{out}} = W^{\text{out}}X \end{aligned}$$

(25)

where $X^{\text{out}} \in \mathcal{M}_{M\times (k_{\text{train}}-BI)}(\mathbb {R})$ contains the M ESN outputs $x^{\text{out}}$ at every time step $k=BI,\ldots ,k_{\text{train}}$ and where $X \in \mathcal{M}_{(N_{\rm r}+K)\times (k_{\text{train}}-BI)}(\mathbb {R})$ contains the concatenation of the input u and the internal activation state x of the reservoir at every discrete time $k=BI+1,\ldots ,k_{\text{train}}$, namely

$$\begin{aligned}&X = \begin{pmatrix} u_{BI+1} & \ldots & u_{k_{\text{train}}}\\ x_{BI+1} & \ldots & x_{k_{\text{train}}} \end{pmatrix} , \end{aligned}$$

(26)

where BI denotes the amount of Burn-In data, i.e. the number of input data we want to discard at the beginning of the training phase.

The optimal output weight matrix $W^{\text{out}}$ can be found by solving the following minimisation problem:

$$\begin{aligned} \begin{aligned} W^{\text {out}}&= {\mathop {\text{argmin}}\limits _{w_{i,j}^{\text{out}}}} J(W^{\text{out}}) \\&= {\mathop {\text{argmin}}\limits _{w_{i,j}^{\text{out}}}} \frac{1}{M} \sum _{i=1}^{M}\Big (\sum _{k=BI}^{T}(x_{ik}^{\text{out}} - x_{ik}^{\text{train}})^2 + \beta \Vert w_i^{\text{out}}\Vert ^2\Big ) , \end{aligned} \end{aligned}$$

(27)

where J denotes the cost function we want to minimise and $\Vert w_i^{\text{out}}\Vert$ is the Euclidean norm of the ith row of $W^{\text{out}}$.

The solution of the minimisation problem stated in Eq. (27) can be found efficiently using linear regression with Tikhonov (Ridge) regularisation [47]:

$$\begin{aligned} W^{\text{out}} = X^{\text{train}}X^{T}(XX^{T}+\beta I)^{-1} \end{aligned}$$

(28)

where the superscript T denotes the transpose, $I \in \mathcal{M}_{(N_{\rm r}+K)\times (N_{\rm r}+K)}(\mathbb {R})$ is the identity matrix, and $X^{\text {train}} \in \mathcal{M}_{M\times (k_{\text {train}}-BI)}(\mathbb {R})$ is the training data matrix, which contains the M training data $x^{\text {train}}$ at time step $k = BI, \ldots , k_{\text{train}}$.

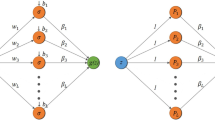
The learning phase is carried out on the so-called training set, which contains the $k_{\text{train}}$ training data $x^{\text{train}}$. A sketch of the training phase of the ESN is provided in Fig. 4. In this sketch, the only trainable weights are contained in $W^{\text{out}}$ and coloured in red, whereas the randomly generated reservoir weight matrices $W^{\text{in}}$ and W are coloured in blue.

Fig. 4

Sketch of the training procedure for a shallow leaky ESN. The size of the matrices has been arbitrarily selected. E denotes the square of the Euclidean norm error between the ESN output $x_{k}^{\text{out}}$ and the training data $x_{k}^{\text{train}}$, $k = BI,\ldots , k_{\text{train}}$

After training, the ESN hyperparameters, defined in Sect. 4, are tuned using $k_{\text{val}}$ validation data. Finally, the ESN is tested using the $k_{\text{test}}$ data to check the ability of the ESN to predict new data. The validation and test procedures are detailed in Sect. 4. As stated in Eq. (27), only the output weight matrix $W^{\text{out}}$ is trained, while the input and reservoir matrices $W^{\text{in}}$ and W are randomly generated, as explained in detail in Sect. 4.

3.2 Deep ESN

A deep ESN is an ESN composed of L stacked reservoirs, as shown in the sketch of the deep ESN training phase in Fig. 5. In this sketch, the additional stacked randomly generated reservoirs are coloured in green. The only trainable weights are still contained in $W^{\text{out}}$, coloured in red.

Fig. 5

Sketch of the training procedure for deep ESN with L reservoirs

In this case, $W^{(l)}$ denotes the lth reservoir weight matrix, $W^{\text{in}(l)}$ the lth input weight matrix, $x_k^{(l)}$ the local internal reservoir state vector, and $x_k$ the global internal reservoir state vector. Equations (23) and (24) for a shallow ESN read now

$$\begin{aligned} x_{k}^{(l)}&= \left( 1-a \Delta t \right) x_{k-1}^{(l)} + \Delta t f(W^{(l-1)}x_{k}^{(l-1)} + W^{(l)}x{^{(l)}}_{k-1}) \qquad l>1 \nonumber \\ x_{k}^{\text{out}}&= g(W^{\text{out}}[x_{k};u_k]) , \end{aligned}$$

(29)

where $x_k$ is the concatenation of all $x_k^{(l)}$.

4 ESN predictive model for DA evolution

In the previous section, we have introduced the definition of a shallow leaky ESN and its extension as a deep ESN. In Eqs. (23) and (29), we can already identify some parameters (called hyperparameters) of the ESN predictive model. These are the leaking rate a, the number of stacked reservoirs L, the dimension $N_{\rm r}$ of the reservoir matrix W and the activation function f usually set as the hyperbolic tangent function $\tanh$. In Appendix 1, we give a sufficient condition on the spectral radius $\rho$ of the reservoir matrix W, which can also be considered as a hyperparameter, that guarantees the Echo State Property (ESP).

Other hyperparameters are often introduced in the implementation of ESN equations, specifically the sparsity ratio s of the reservoir matrix W, i.e. the fraction of 0 elements in the reservoir matrix W and BI (as in [48]), which corresponds to the number of time steps of the input data that are discarded. Furthermore, the regularisation parameter $\beta$ in Eq. (28) also needs to be optimised and is also considered a hyperparameter of the ESN model. Setting large values for $\beta$ is generally used to avoid overfitting and may improve prediction in the test set. To complete the definition of the predictive model of the ESN, we must assign a value to all hyperparameters, knowing that the performance of the model strongly depends on the choice of their values.

It is a common procedure in ESN training to perform an optimisation of these hyperparameters, which is usually done by grid search methods [49], in the validation set. The validation procedure considered here is based on an ensemble approach to deal with the randomness of the reservoirs. Eventually, once the predictive model has been trained and validated, we can test it in the test set with unseen data.

4.1 ESN ensemble validation approach

The ensemble validation approach used in our studies is based on the principle of minimising the average of the Relative Root Mean Square Error (RRMSE) of $N_{\text{d}}$ dynamics predicted (i.e, 60 seeds for the HL-LHC dataset and 60 cases for the 4D Henon map) for $N_{\text{W}}$ different randomly generated reservoirs and various hyperparameters values on the validation set. Note that for each of the $N_{\text{d}}$ dynamics, we predict a mean over the $N_{\text{W}}$ reservoirs. Additionally, each of the $N_{\text{d}}$ dynamics contains different input/training/validation/test data, so that each prediction is performed independently of the others. We define this RRMSE on the validation set $\mathrm {RRMSE^{val}}$ as:

$$\begin{aligned} \mathrm {RRMSE^{val}} = \frac{1}{N_{\text{d}}}\sum _{i=1}^{N_{\text{d}}} \left( 100 \sqrt{\frac{\sum _{k=1}^{k_{\text{val}}} (x_{\text{mean},k}^{\text{out}-i} - x_k^{\text{val}-i})^2}{\sum _{k=1}^{k_{\text{val}}} (x_k^{\text{val}-i})^2}} \right) \end{aligned}$$

(30)

where $k_{\text{val}}$ is the number of validation data, $x_{\text{mean}}^{\text{out}-i}$ is the mean over the $N_{\text{W}}$ reservoirs for the ith dynamics at time k, and $x_{k}^{\text{val}-i}$ is the validation data at the same time k for the same ith dynamics.

This procedure aims to build a robust predictive model in which all hyperparameters are fixed. The search of the hyperparameters values minimising the $\mathrm {RRMSE^{val}}$ is done over a domain $S_h$. Each of the hyperparameters is updated one by one using the value in $S_h$, which minimises $\mathrm {RRMSE^{val}}$. Furthermore, as mentioned above, this ensemble validation method requires the generation of different random matrices W and $W^{\text{in}}$. This is done by sampling their elements from a uniform pseudorandom distribution in (0, 1) and scaling them to the interval ($-$0.5, 0.5) so that they also have negative elements. The procedure for generating $W^{\text{in}}$ and W is detailed in Algorithm 1, while a pseudocode of the general ensemble validation procedure is presented in Algorithm 2.

Note that the functions Training() and Prediction() implement the equations presented in Sect. 3.

4.2 ESN ensemble test approach

Once the parameters and hyperparameters of the ESN predictive model have been tuned using training set and validation set, we can test our ESN model for the prediction of not previously used data, i.e. DA values at a larger time. We denote by $k_{\text{test}}$ the number of data in the test set we try to predict.

The Algorithm 3 describes the test procedure for a single dynamics, i.e. a single realisation of the HL-LHC magnetic lattice or a single case for the 4D Hénon map data set. We can loop the procedure to perform the prediction in the test set for the $N_{\text{d}}$ dynamics. Note that, contrary to the validation, here the prediction is performed in the test set for data not previously used.

5 Results and discussion

In this section, we present the DA predictions obtained with our ESN-based predictive model. In particular, we compare these predictions with those of the fitted scaling law presented in Eq. (15) and used in [24]. We recall that the ESN output $x_{\text{mean}}^{\text{out}}$ is the mean prediction over $N_{\text{W}} = 100$ random reservoirs. The validation and testing methods are those introduced in Sect. 4. We tested the proposed approaches with the HL-LHC data sets and the 4D Hénon map presented in Sect. 2.

5.1 DA predictions for the HL-LHC data set

5.1.1 Validation of the ESN

In this stage, we search for the set of hyperparameters H that minimises, on average over the $N_{\text{d}}=60$ seeds and $N_{\text{W}}=100$ randomly generated reservoirs, the RRMSE in the validation set. Here, the number of predicted dynamics is equal to the number of seeds. We also recall that the number of validation data is $k_{\text{val}}= 50$ and the definition of $\text{RRMSE}^{\text{val}}$ is presented in Algorithm 2. The optimal hyperparameters are determined one by one by a grid search over a wide range of possible parameter values, and the search domains $S_h$ of the hyperparameters are listed in Table 1.

Table 1 Search domains $S_h$ of the various hyperparameters h

Figure 6 shows $\mathrm {RRMSE^{val}}$ as a function of the various hyperparameters in $S_h$. The values of the hyperparamters are updated one-by-one with those that minimise RRMSE$^{val}$.

Fig. 6

$\mathrm {RRMSE^{val}}$ as a function of the various hyperparameters in $S_h$

As we can see, a shallow ESN with a small number of neurons $N_{\rm r}$ provides the best results. Stacking more reservoirs does not improve the predictions. In fact, adding reservoirs or increasing the number of neurons makes the model overfit, so it cannot predict correctly in the validation set. This can be explained by the small number of features that the ESN must learn and by the characteristics of the DA data, which are not enough.

Regarding the other hyperparameters, the optimum spectral radius value initially set to 0.1 is updated to 0.99 and satisfies the ESP. Furthermore, since the optimal value of $N_{\rm r}$ is smaller than 100, it can be considered small, which justifies setting the sparsity ratio s = 0 so that all elements of W are non-zero. Then, we decided to choose the activation function $f = \tanh$, since it is the most used in ESN, and the leaking rate $a = 1$ to simplify the equations described in (29). Eventually, the values of $\beta$ and $\Delta t$ initially set to $2\times 10^{-1}$ and $9\times 10^{-2}$ have been updated to $2\times 10^{-2}$ and $9\times 10^{-3},$ respectively. The values of the hyperparameters updated after validation and used for the prediction stage in the test set are summarised in Table 2.

Table 2 Set H of the hyperparameters tuned after validation using HL-LHC DA data

5.1.2 The ESN model

Once the ESN has been trained and validated, we can test it with the $\textit{test set}$ for data not previously used using the hyperparameters reported in Table 2. We recall that the number of test data is $k_{\text{test}} = 500$, i.e. half of the total number of data used. In Fig. 7, we show the mean prediction $x_{\text{mean}}^{\text{out}}$ in the test set together with the envelope (i.e. minimum and maximum) of the predictions $x^{\text{out}}$ that are associated with the $N_{\text{W}} = 100$ randomly generated reservoirs for an arbitrary seed (number 1). We also plot the distribution of the prediction of DA at $N = 10^5$ turns (end of the $\textit{test set}$).

Fig. 7

Left: Numerical DA data, prediction of DA $x_{\text{mean}}^{\text{out}}$, average, minimum, and maximum over the $N_{\text{W}} = 100$ randomly generated reservoirs as a function of time. Right: distribution for the $N_{\text{W}} = 100$ randomly generated reservoirs at $N=10^5$. The seed used for both plots is number 1

As mentioned above, we will denote by $x_{\text{mean}}^{\text{out}}$ the ESN mean prediction and only plot this mean value to avoid overloading the graphs with the values generated by $N_{\text{W}}$ random reservoirs. To have a complete view, Fig. 8 shows the predictions of $N_{\text{d}} = 60$ seeds in the train set, validation set and test set. Vertical dashed lines indicate the end of the train set and validation set for ESN (left graph) and SL (right graph). The scaling law fit is performed using the first $k_{\text{fit}} = k_{\text{train}}+k_{\text{val}}=500$ DA data. Note that ESN and SL share the same test set. Figure 9 shows the distribution of the $\mathrm {RRMSE^{test}}$ values defined in Algorithm 3, for both the ESN model and SL.

Fig. 8

DA predictions for ESN (left) and SL (right) for $N_{\text{d}}$ = 60 seeds

Fig. 9

Distribution of $\mathrm {RRMSE^{test}}$ for $N_{\text{d}}$=60 seeds for ESN and SL

We report in Table 3 the mean, maximum, minimum, and standard deviation of $\text{RRMSE}^{test}$ for the predictions of ESN and SL over $N_{\text{d}}$ = 60 seeds.

Table 3 Mean, maximum, minimum, and standard deviation of the $\mathrm {RRMSE^{test}}$ distribution

The ESN model and SL generate predictions whose distributions have essentially the same mean and minimum values. However, some outliers appear in the SL distribution, which affect the maximum and standard deviation values. This contributes to the generation of more stable predictions by ESN, i.e. without outliers, and significantly lower values of the standard deviation and maxima.

5.1.3 The SL-ESN model

In this section, we consider whether ESN predictions can possibly be used to replace the tracking simulations that generated the data in the test set. In this sense, we fit the SL to the $k_{\text{fit}}$ data plus the ESN predictions in the test set. We denote this fit procedure by SL-ESN and compare it with the results of SL-ALL, which represents the best results that can be achieved with the SL approach.³ The idea is to check the quality of the approximation of SL-ESN in the test set, in view of further prediction beyond this set. The predictions provided by SL-ESN and SL-ALL for the $N_{\text{d}}$ = 60 seeds can be seen in Fig. 10 and the distribution of $\mathrm {RRMSE^{test}}$ is shown in Fig. 11, while the mean, maximum, minimum, and standard deviation of $\mathrm {RRMSE^{test}}$ in Table 4.

Fig. 10

Predictions for SL-ESN (left) and SL-ALL (right) for $N_{\text{d}}$ = 60 seeds

Fig. 11

Distribution of $\mathrm {RRMSE^{test}}$ for $N_{\text{d}} = 60$ seeds for SL-ESN and SL-ALL

As it might be expected, all indicators of the distribution of $\mathrm {RRMSE^{test}}$ for SL-ESN are significantly larger than those for SL-ALL, as the first approach fits the prediction of ESN, not the real DA data. In fact, SL-ESN is essentially equivalent to ESN alone and hence more stable than SL alone as far as outliers are concerned. In other words, the SL-ESN seems to be an effective surrogate model that improves the predictions given by the SL only.

Table 4 Mean, maximum, minimum, and standard deviation of the $\mathrm {RRMSE^{test}}$ distribution

After having evaluated the accuracy of the SL-ESN model in the test set, we can check if it can replace the tracking simulations in this set. To do so, we compute predictions beyond the test set and up to $N = 10^8$ turns. Since we do not have real DA data in this time interval, we cannot compute any metrics, and we use the envelope, i.e. minimum and maximum, of the predictions given by SL-ESN and SL-ALL to check whether SL-ESN approximates well the predictions given by SL-ALL beyond the test set. We plot the envelope of the predictions given by SL-ESN and SL-ALL beyond the test set in Fig. 12 (left), and we also show the relative error $\epsilon _{\rm r}$ defined as $\epsilon _{\text{r}}^{i}$ = $( DA_{\mathrm {SL-ALL}}^{i}-DA_{\mathrm {SL-ESN}}^{i})/DA_{\mathrm {SL-ALL}}^{i}$, where i is $\text{max}$ or $\text{min}$ of the DA values(right).

Fig. 12

Left: Envelope, i.e. minimum and maximum values of the SL-ESN and SL-ALL predictions extrapolated beyond the test set. Right: Relative error $\epsilon _{\text{r}}$ of the minimum and maximum DA predictions up to $N = 10^{8}$ turns

The two envelopes almost overlap until $N = 10^8$ turns, with $\epsilon _{\text{r}}^{\text{max}}$ and $\epsilon _{\text{r}}^{\text{min}}$ that are below $1\%$. From this observation, we conclude that we may only need to perform the tracking simulation until the end of the validation so that the tracking in the test set could be spared. In fact, the predictions provided by SL-ESN are very similar to those of SL-ALL. In this way, we could use the ESN predictions to replace the tracking in the test set. This result is in line with what was found in [50], i.e. that the addition of synthetic points obtained by using Gaussian Processes improved the quality of the fitted SL model.

Running the SixTrack code [40, 41] and the ESN model on the same CPU architecture, we have a speed-up of a factor 20 by replacing the tracking simulations on $5\times 10^4$ turns, representing the test set, with the prediction of the DA values by ESN. This evaluation of CPU-time reduction can be easily improved by a trivial parallelisation of the ESN over the 100 reservoirs. Of course, the actual gain depends on several details, such as the model under consideration and the definition of the times that define the validation and test sets. It is worth stressing that whenever an actual accelerator lattice is used for the numerical DA computations, the CPU time needed depends not only on the number of turns used for the tracking, but also on the size of the accelerator, which corresponds approximately to the number of magnets comprised in the lattice, and on the characteristics of the magnetic field errors included in the accelerator model. In this respect, the computational gain implied by the proposed approach is even more relevant for the case of large future colliders, such as the Future Circular Hadron Collider (FCC-hh) under study at CERN [51, 52].

5.2 DA predictions for the Hénon map data set

To check the robustness of the current strategy, we apply it to a new system, which is the 4D Hénon map introduced in Sect. 2.

5.2.1 The ESN model

Hyperparameters have been determined using the same approach as for the HL-LHC data and are reported in Table 5. In this case, we also use $N_{\text{d}} = 60$, but we have to stress that the various dynamics differ between them much more than the dynamics of the HL-LHC case. In fact, changes in the values of $\varepsilon$ and $\mu$ lead to radically different dynamical behaviours, whereas the HL-LHC realisations are much closer to each other, representing minor variations of the same dynamical behaviour.

Only the values of $\Delta t$ and $\beta$ are different from those of the HL-LHC case. Note that the value of $\beta$ found is much lower than that of HL-LHC. This means that the model is less overfitting than with the HL-LHC data, especially because the Hénon DA data are much smoother.

Table 5 Set H of the hyperparameters tuned after validation using Hénon map DA data

In Fig. 13, we plot the $N_{\text{d}} = 60$ DA predictions given by ESN and SL. For ESN, we recall that we used $k_{\text{train}}=450$ and $k_{\text{val}}=50$ data, and for SL we used the $k_{\text{fit}}=500$ data. Furthermore, test set is the same for both ESN and SL. As we can see, the SL predictions in the test set do not perform well, whereas those provided by the ESN fit the training/validation/test data much better.

Fig. 13

DA predictions for ESN (left) and SL (right) for $N_{\text{d}}$ = 60 seeds

In Fig. 14, we compare the distributions of $\mathrm {RRMSE^{test}}$ for ESN and SL, and the first is clearly much narrower and closer to zero than the latter. This behaviour is easily explained by considering the fact that the scaling law is an asymptotic law that aims to describe the long-term behaviour of the DA (using very few model parameters). Therefore, it is not effective in reproducing the detailed behaviour of the DA for low numbers of turns. Our ESN model is able to fit both the short-term and long-term behaviour simultaneously, thus explaining the observed better performance.

Fig. 14

Distribution of $\mathrm {RRMSE^{test}}$ for $N_{\text{d}}$=60 seeds for ESN and SL

The mean, maximum, minimum, and standard deviation of $\mathrm {RRMSE^{test}}$ for the two approaches are reported in Table 6.

Table 6 Mean, maximum, minimum, and standard deviation of the $\mathrm {RRMSE^{test}}$ distribution

The table shows, in a quantitative way, the differences observed in the histogram of the distributions. In fact, the RRMSE of the ESN is on average about 3 times lower than that of the SL, which is a significant improvement compared to the case of HL-LHC. Several reasons can explain this behaviour. First, the DA data for the Hénon map are much smoother than those of the HL-LHC data set, which improves training and limits overfitting of the ESN. Second, as already mentioned, the behaviour of the $N_{\text{d}}$ dynamics is very diverse, and the SL, with only two free parameters, is clearly disadvantaged with respect to the ESN. Moreover, since the SL is an asymptotic law, its performance has been downgraded by including low-turn DA data.

5.2.2 The SL-ESN model

We repeat the procedure to check if the ESN predictions can replace the tracking simulation in the test set. As previously, we compare SL-ESN with SL-ALL. The predictions given by SL-ESN and SL-ALL for the 60 cases can be seen in Fig. 15, the distribution of $\mathrm {RRMSE^{test}}$ is shown in Fig. 16, and the mean, maximum, minimum, and standard deviation of $\mathrm {RRMSE^{test}}$ are reported in Table 7.

Fig. 15

Predictions for SL-ESN (left) and SL-ALL (right) for $N_{\text{d}}$ = 60 seeds

Fig. 16

Distribution of $\mathrm {RRMSE^{test}}$ for $N_{\text{d}} = 60$ seeds for SL-ESN and SL-ALL

Table 7 Mean, maximum, minimum, and standard deviation of the $\mathrm {RRMSE^{test}}$ distribution

In this case, the SL-ESN performs equally well as the SL-ALL. In fact, the mean of $\mathrm {RRMSE^{test}}$ is the same. Furthermore, fitting the SL to the predictions of the ESN allows us to improve the accuracy of the ESN and the SL. Taking into account the average, SL-ESN is almost 2 times and 4 times more accurate than ESN and SL, respectively. Similarly to the HL-LHC case, the standard deviation and maximum $\mathrm {RRMSE^{test}}$ of SL-ESN are much lower than those of SL, which shows a certain robustness of the conclusions that SL-ESN helps improve SL.

To further check whether the ESN predictions can replace the tracking simulation in the test set, we perform the prediction beyond the test set up to $N = 10^{11}$ turns. As previously, we do not have the real DA data in this range, so we cannot compute any metrics. We plot the envelope of the predictions given by SL-ESN and SL-ALL in Fig. 17.

Fig. 17

Left: Envelope, i.e. minimum and maximum values of the SL-ESN and SL-ALL predictions extrapolated beyond the test set. Right: Relative error $\epsilon _{\text{r}}$ of the minimum and maximum DA predictions up to $N = 10^{11}$ turns

The two envelopes of the predictions almost overlap until $N = 10^{11}$, and the relative errors $\epsilon _{\text{r}}^{\text{max}}$ and $\epsilon _{\text{r}}^{\text{min}}$ are below $1.5\%$, as for the case HL-LHC. This indicates, once again, that the tracking simulation in the test set could be replaced by the ESN predictions. The computational cost of the ESN emulation is the same as for the HL-LHC case, but here we do not compute speed-up because it is not relevant due to low computational cost of the dynamics of the Hénon map.

6 Conclusions

In this article, we have presented the results obtained with an ensemble approach to ESN reservoir computing for the prediction of the dynamic aperture of a circular hadron accelerator. In particular, we have compared the performance of ESN with that of a scaling law based on the Nekhoroshev theorem to predict the evolution of the dynamic aperture over time. This analysis has been carried out on two data sets that have been generated using numerical simulations performed on realistic models of the transverse beam dynamics in the HL-LHC and on a modulated 4D Hénon map with quadratic and cubic nonlinearities.

We have shown that the average accuracy in the test set of the scaling law used to fit the ESN predictions was better than that of the scaling law alone. In particular, we have observed that the standard deviation of the RRMSE of the scaling law combined with the ESN is much lower than that of the scaling law alone. This leads to more reliable predictions. The fact that this observation is confirmed for both data sets gives us confidence that the combination of the scaling law and the ESN is the best approach.

A consequence of this result is that the tracking performed in the test set can be avoided by replacing it with the predictions of the ESN. In fact, for both the HL-LHC and Hénon map data sets, the predictions of the scaling law combined with the ESN and of the scaling law fitted to the entire data set are close to the percent level, even for numbers of turns three orders of magnitude beyond that of the test set. The gain in CPU time depends on the size of the accelerator and the complexity of its model. For the HL-LHC simulations used in this study we obtain a speed-up of a factor 20. However, it is clear that the proposed approach is particularly appealing for hadron colliders of the post-LHC era that are currently being studied.

The study presented here represents only the beginning of a research area that could be further developed in the future given the promising results obtained. The partition of available data into training, validation, and test data sets should be studied in more detail to assess whether such a partition could be obtained using an appropriate algorithm. The established link between dynamic aperture and models for the evolution of intensity in hadron rings and the evolution of luminosity in hadron colliders could be further developed by using the promising results discussed in this paper. Investigations on the possibility of using ESN to improve the modelling of beam lifetime and luminosity evolution should be seriously considered and pursued. Finally, the predictive power of ESN could be applied to indicators of chaos, which are dynamical observables computed over the orbit of an initial condition to establish whether the motion is regular or chaotic, to improve their performance. This would be another important topic that could bring important insight to the field of nonlinear beam dynamics.

Appendix A: The echo state property

An important prerequisite for the output-only training is the so-called Echo State Property (ESP), which guarantees that initial conditions have an effect that vanishes over time. In fact, satisfying the ESP allows us to guarantee that the reservoir activation state $x_{k-1}$ is uniquely determined by any left-infinite input sequence $\ldots , u_{k-2},u_{k-1}$. We summarise here some of the results presented in [53], so as to recall a precise definition of ESP and a sufficient condition for ESP that can be used in practice for the kind of ESN employed in this paper.

To define ESP, we require the compactness condition, that is, we assume that the states and inputs belong to compact sets $\mathcal {X} \subset \mathbb {R}^{N_{\rm r}}, \mathcal {U} \subset \mathbb {R}^{K}$ and that $F(x_{k-1},u_k) \in \mathcal {X}$ and $u_{k-1} \in \mathcal {U}, \, \forall k \in \mathbb {Z}$. In practice, the ESN inputs will always be bounded, so the compactness of $\mathcal {U}$ is guaranteed. Furthermore, for bounded sigmoid functions f, such as $\tanh$, the state space $\mathcal {X}$ is also compact. We define $\mathcal {U}^{-\infty } = \{ u^{-\infty } = (\ldots , u_{-1},u_0), \, u_{k} \in \mathcal {U} \, \forall k \in \mathbb {Z} \}$ and $\mathcal {X}^{-\infty } = \{x^{-\infty } = (\ldots , x_{-1},x_0), \, x_k \in X \, \forall k \in \mathbb {Z}\}$, which are the sets of infinite left input and reservoir activation state sequences.

Definition 1

(Echo State Property (ESP)). A network $F: \mathcal {X} \times \mathcal {U} \rightarrow \mathcal {X}$ with the compactness condition has the ESP with respect to $\mathcal {U}$ if for any left input sequence $u^{-\infty } \in \mathcal {U}^{-\infty }$ and any two state sequences $x^{-\infty }, y^{-\infty } \in \mathcal {X}^{-\infty }$ compatible with $u^{-\infty }$ (i.e. $x_k = F(x_{k-1},u_k), \forall k \le 0$), then for all $k \ge 0, \Vert x_k - y_k\Vert \le \delta _k$, where $\delta _k$ denotes a small value.

Definition 1 cannot be easily checked in practice. Thus, we introduce the following Theorem 1, that should be used in practice as it provides a sufficient condition to satisfy the ESP in the case of a leaky ESN:

Theorem 1

(Sufficient condition for the ESP). If the spectral radius of the matrix

$$\begin{aligned} \tilde{W} = \frac{\Delta t}{c}W+\left( 1 -a\frac{\Delta t}{c}\right) I \end{aligned}$$

is smaller than 1, then the leaky ESN with f = $\tanh$ satisfies the ESP for all inputs. However, this condition is only sufficient, but not necessary. In other words, setting $\rho (\tilde{W}) \ge 1$ does not necessarily lead to poor performance of leaky ESN.