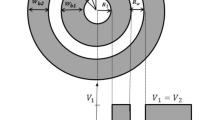
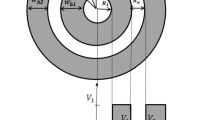
Abstract
The ground state energy of a helium atom inside a spherical multilayer quantum dot as a function of the atomic impurity location inside the quantum dot has been calculated. The multilayer quantum dot is modeled by a core/shell/well/shell structure using a parabolic confinement. The Configuration Interaction method and the Diffusion Monte Carlo have been used to solve the Schrödinger equation. Results obtained showed that the lowest energy configuration depends on the size of the different layers of the quantum dot and agreement between Configuration Interaction and Diffusion Monte Carlo results indicates that the Configuration Interaction approach used here would be suitable to compute excited states of this system.
Graphical abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Quantum effects in low-dimensional structures are broadly employed in new electronic devices, therefore these structures have been extensively studied for many years and nowadays they still attract great attention, see [1,2,3,4,5,6,7] and references therein. One of such electronic structures are the quantum dots (QDs), which have gained importance owing to their unique properties that are used in several fields as medical imaging [8], biosensing applications [9], quantum computing [10, 11], solar cells [12,13,14] or lasers [15, 16].
Electronic properties of an electron in a QD are similar to those of an atom because the electron is confined in all dimensions. The study of a hydrogenic impurity inside a QD, considering both on- and off-center configurations, has been the focus of extensive research [17,18,19,20,21,22]. This problem constitutes a useful means to understand the electronic and optical properties of low-dimensional quantum structures and to determine the influence of the physical properties of the QD on those properties. In particular, it has been deeply analyzed the way that the binding energy is governed by the shape of the QD or by an external field [23,24,25,26,27,28,29]. Recently, there has been an increasing interest in two-electron QDs [30,31,32,33,34,35]. Thus, different properties of confined two-electron atoms like Helium have been studied extensively [36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51].
Another field of research interest has been the study of other structures more complex than QD such as the multilayer quantum dots (MLQDs), because they give rise to higher values of the absorption cross section [52]. Many theoretical studies have been devoted to the characterization of optical and electronic properties of hydrogenic impurities located at the center of these structures [53,54,55,56,57,58]. However, much less information is available in the literature for the case where the atomic impurity is not at the center of the structure. A recent work [59] has investigated the influence of the position of the impurity in MLQDs as well as the effect of electric and magnetic fields.
In this work, we address the problem of a Helium atom in a spherical MLQD with parabolic confinement and study the variations in its ground state and binding energy by tuning some parameters of the MLQD structure. This system can be representative of a two-electron MLQD with an attractive Coulomb impurity. On- and off-center configurations have been considered to study the importance of the position of the impurity. Different reference systems can be considered for the latter, being more suitable the partial wave expansion with the origin at the nucleus. A Configuration-Interaction approach with generalized Sturmian functions [60] with an efficient scheme for the partial wave expansion of the non-central potential [61] has been implemented to obtain ground state energies and wave functions. The accuracy of the multi configuration expansion has been tested by comparing with Diffusion Monte Carlo calculations for different representative configurations.
The paper is organized as follows: in Sect. 2, we present the theoretical approach used to describe the confined Helium atom in a spherical MLQD; in Sect. 3, we give the numerical results of the study; finally, in Sect. 4 some conclusions are shown. Atomic units are used throughout this work.
2 Methodology
The MLQD considered in this work consists of two quantum dots, one inside the other and separated by a shell, with the whole system coated by another spherical layer. The multilayer spherical quantum dot can therefore be described by a core/shell/well/shell type structure. Here we use the following parabolic confinement [55, 59]
where \(r_1\) is the core radius, \(T_s=r_2-r_1\) and \(T_w=r_3-r_2\) are the shell thickness and well width, respectively, see Fig. 1, and \(a=(r_2+r_3)/2\).
When the atomic impurity is not at the center of the MLQD, i.e. an off-center configuration, the potential acting on each electron is not spherically symmetric. Different partial-wave expansions can be conceived for the non-spherical part of the total potential. A convenient choice due to its good convergence performance [61] is to place the atomic nucleus at the origin of coordinates in such a way that the center of the confinement potential is located at a point of spherical coordinates \(\{R_{OC},\theta _c,\phi _c\}\). Within this scheme, the single electron Hamiltonian can be expressed as
where Z is the nuclear charge, \(f_{l}(r,R_{OC})\) are the radial partial wave terms of the multipole expansion of off-centered confinement potential [61], and \(P_l\) are the Legendre polynomials [62]. Due to the symmetry of the confinement of the MLQDs, we can take without loss of generality \(\theta _c=\phi _c=0\). Thus, the time independent Schrödinger equation for a two-electron atom inside a MLQD is
where \(\alpha\) stands for the quantum numbers of the stationary state and \(1/r_{12}\) is the Coulomb potential between the electrons.
Here, the following Configuration-Interaction (CI) expansion of the wave function is employed
where
with S as the total spin of the state and \(\nu\) represents the orbital quantum numbers \(\left\{ n_{i},l_{i},m_{i}\right\}\) (\(i=1,~2\)), with \(0\le l_{1},~l_{2} \le L_{max}\) and the usual conditions for the magnetic quantum numbers. The value of \(L_{max}\) sets the size of the multipole expansion of the non-spherically symmetric part. The analysis done in previous work [61], shows that \(L_{max}=5\) provides accurate results.
The single particle wave functions of Eq. (5) can be written as
where \(Y_{lm}\) are the spherical harmonics, while the radial part is given by the Sturminan functions, obtained by solving an eigenvalue equation of the form[63]
where \(E_s\) is a parameter, \(\beta\) is the eigenvalue and U(r) and V(r) are the auxiliary and generating potentials, respectively, which can be used to incorporate some features of the problem leading to improved convergence [63, 64]. For the He atom we have used \(U(r)=-2/r\). We could also introduce, for example, the s-wave term \(f_{0}(r,R_{OC})\) in the right-hand side of Eq. (7) which would give us better energies for a given fixed value of \(R_{OC}\). Since this value is going to be changed in the calculations, that would be computationally demanding. Using \(V(r)=1/r\), Eq. (7) gives rise to the Coulomb Sturmian Functions which are a suitable choice [65] for bound state calculations.
Once the energies of the system are known, the one-electron binding energy of the He atom inside the MLQD is computed as [66]
where \(E_0,~E(\text {He}^+)\) and \(E(\text {He})\) are the ground state energy of one electron, the He\(^+\) ion and the He atom inside the MLQD, respectively. If \(E_B>0\), the electron is bound.
The accuracy of the CI expansion of this work has been studied by comparing the ground state energy with the results of a Diffusion Monte Carlo (DMC) calculation for some selected configurations. Here, we briefly outline the basic ideas of the method; for further details see, for example, ref. [67]. The starting point of the DMC method is the time-dependent Schrödinger equation in imaginary time. This is a diffusion equation, solved by using random walks. In the DMC method a short time approximation is invoked to compute the Green’s function. A guiding function, which is an approximate wave function for the ground state of the system, is employed to bias the random walk towards those regions where the probability is larger. A large number of configurations, called walkers, are employed in the simulation. Each step of the random walk consists of an anisotropic diffusion and branching of the walkers. After a very large number of time steps, the excited state contributions are projected out and the ground state energy can be obtained from the simulation. The time step error can be eliminated by extrapolating the results to zero time steps. If the nodes of the exact wave function are known, as it is the case of the nodeless ground state here, the method provides the exact energy within the numerical error. The role of the guiding function here is only to improve the convergence of the algorithm, therefore we employ a guiding function written as the product of two single electron wave functions. These orbitals are obtained by solving the radial equation of the He\(^+\) confined either by a square-well or by a finite barrier, depending on the position of the He atom in the MLQD. The analytic continuation method (ACM) is used here to solve the corresponding radial Schödinger equation [68,69,70].
3 Results and discussion
We study the effect of the size of the core, \(r_1\), and the effect of the position of the atom inside the MLQD, \(R_{OC}\), on the ground state energy of the system and its corresponding binding energy. For this purpose, we consider different values for the parameters of the MLQD structure which are of the same order as those used in other two-electron QDs studies [50].
In order to assess the accuracy of the CI expansion employed in this work, the energies for some representative configurations are compared with the results of a DMC calculation. We have considered a MLQD modeled with parameters \(V_0=0{.}5,~r_1=1{.}0,~r_2=5{.}0,~r_3=6{.}0\) and two different positions of the atom, \(R_{OC}=2{.}6\) and \(R_{OC}=5{.}5\). The energy provided by the CI wave function of Eq. (4) is \(E_1=-1{.}9079\) for \(R_{OC}=2{.}6\) and \(E_2=-2{.}3983\) for \(R_{OC}=5{.}5\). The DMC values are \(E_1=-1{.}906\pm 0{.}002\) and \(E_2=-2{.}397\pm 0{.}002\), respectively, both in excellent agreement. In the DMC we use a guiding function for the importance sampling built in terms of atomic orbitals. The atomic orbitals are obtained by solving the single electron radial Schrödinger equation using the ACM method for the He\(^+\) confined by a finite barrier of width \(\Delta =T_s=4{.}0\) and height \(V_0=0{.}5\) for the case of \(R_{OC}=2{.}6\), while for \(R_{OC}=5{.}5\) the orbitals are those of He\(^+\) confined by a well of width \(\Delta =T_w=1{.}0\) and height \(V_0=0{.}5\).
In Fig. 2 we show the ground state energy of the He atom as a function of the radius of the spherical core, \(r_1\), for constant depth of the barrier, \(V_0=0{.}5\), and widths of the shell and the well, \(T_s=T_w=1{.}0\). We have considered three different nuclear positions: on-center atom, \(R_{OC}=0{.}0\), and \(R_{OC}=2{.}5,~5{.}0\). It is seen that the energy presents a number of maxima and minima as a function of \(r_1\) which depends on the position of the nucleus inside the MLQD. The energy decreases as the core radius increases, approaching the free atom energy in the case of the on-center configuration.
For the on-center atom, the behavior of the energy with the core size is similar to that found for a MLQD with a hydrogenic impurity [55]. The energy increases for small \(r_1\) values and a maximum at \(r_1=0{.}3\) is found. Then the energy decreases reaching the free atom value for very large cage sizes. For very small core sizes, as \(r_1\) increases, the electronic charge approaches the nucleus leading to lower values of potential energy but larger values of the kinetic energy in such a way that the effect on the total energy depends on the balance between both effects. For core radii smaller than 0.3 the energy rises, while the opposite holds for larger sizes of the core. As \(r_1\) increases, both the potential energy and kinetic energy are reduced because the charge is less confined. For very large core sizes, the effect of the MLQD becomes less important and the energy approaches that of the free atom. For the two off-center situations considered, \(R_{OC}=2{.}5,~5{.}0\), we find a local minimum of the energy as a function of the core size, one local maximum and one absolute maximum for \(r_1=0\). The value of the minimum energy is very similar in both cases and it corresponds to a configuration where the atomic nucleus is located in the center of the well of the MLQD. The energy is minimum in this configuration because of the contribution of the potential energy; the MLQD favors the charge to be close to the nucleus. This configuration is not possible when the nucleus is at the center of the MLQD, and this is the reason why no local minimum is found for that case. The value of the local maxima is also very similar and also very close to the maximum obtained for the on-center atom. In the off-center cases, this corresponds to a configuration where the nucleus is located in the first shell, so the center of the Coulomb force is in the barrier leading to two opposite contributions to the potential energy and the total energy is \(\approx -2{.}1\) with the electron cloud distributed between the core and the shell. The global maximum corresponds to a configuration where the nucleus lies within the second shell, so the Coulomb attraction with the electrons is shielded by the shell. For larger core sizes, the electronic charge is almost completely inside the core, so that contributions from the shells become less important and the energy of the system decreases. Finally, it is worth to stress here that the lowest energy configuration does not necessarily correspond to an impurity located at the center of the MLQD.
In Fig. 3 we study the ground state energy as a function of the position of the atomic impurity for different sizes of the MLQD. The energy presents a similar structure in all the cases: there is a first minimum for the on-center atom and a second one for an off-center position which corresponds to the atom inside the well. For the lowest core size here considered, \((r_1=1{.}0, r_2=2{.}0, r_3=3{.}0)\) and \((r_1=1{.}0, r_2=5{.}0, r_3=6{.}0)\), the global minimum corresponds to an off-center configuration with the electron density located in the well; while for wider core values, \((r_1=10{.}0, r_2=11{.}0, r_3=12{.}0)\), the lowest energy configuration is with the atom in the center of the MLQD. In this case, the energy and the electronic charge distribution are close to that of the free atom. The plateau regions correspond to the nucleus inside the shells: in first region the nucleus is in the first shell while in the second region the nucleus lies in the second shell. The size of the \(R_{OC}\) domain where the energy is maximum and constant depends on the width of the shells.
In order to assess the influence of the height of the shells on the energy we have considered a fixed MLQD structure with three different \(V_0\) values. In Fig. 4 we plot the ground state energy of the He atom as a function of the distance from the nucleus to the center of the MLQD for \(r_1=1{.}0,~r_2=5{.}0\) and \(r_3=6{.}0\) and three different values of \(V_0\). These results show that the structure of the energy curve is very similar. The quantitative differences in the energy values are due to the different \(V_0\) values: the higher the shell barrier height, the larger the energy.
In Fig. 5a we show the ground state energy of He\(^+\) and in Fig. 5b we plot \(E_B\), the binding energy of one electron calculated according to Eq. (8), for a MLQD with \(V_0=0{.}5,~r_1=1{.}0,~r_2=2{.}0\) and \(r_3=3{.}0\) for different atomic positions. An important dependence of the binding energy with the location of the atom inside the MLQD is found. This shows that larger binding energies are obtained for configurations with lower atomic energies. The energy profile of the cation, He\(^+\), inside the MLQD is the same as that of the neutral atom, but the minima and maxima are more pronounced for He, see Fig. 5a. Thus, the lowering in the energy when the atom is inside the well with respect to the energy of the atom in the second shell is more important for the He atom than for He\(^+\), and the same happens for the rise in the first shell, in such a way that the lower the energy of the atom, the larger the binding energy of the electron, as it is shown in Fig. 3. For \(R_{OC}\gtrsim r_3\), the atom and the cation are located at the second shell and an approximately constant contribution to the energy per electron of \(V_0\) is obtained for both He and He\(^+\), and the energy of the single electron is also equal to \(V_0\), in such a way that \(E_B\) tends to 0.9, i.e. the ionization energy of the free atom as \(R_{OC}\) increases.
In Fig. 6 we plot: the ground state energy of one electron, \(E_0\) (Fig. 6a), the ground state energy of the cation, \(E(\textrm{He}^+)\) (Fig. 6b), and the binding energy, \(E_B\) (Fig. 6c), as a function of the core radius for three different atomic positions. An important dependence of the binding energy with the position of the atom within the MLQD and with the core size is found. The binding energy presents an oscillatory behavior, with a series of maxima and minima, as a function of the core radius. Again, the lower the energy of the atom, the larger the binding energy. For greater values of \(r_1\), confinement effects are less important for He and He\(^+\) and their energies tend to the free values, while in the case of the single electron, it is still bound to the MLQD, so larger values of \(r_1\) are needed to obtain that the binding energy also tends to the ionization energy of the free atom.
a Ground state energy of one electron, \(E_0\), as a function of the core radius, \(r_1\), for \(V_0=0{.}5\), \(T_s=T_w=1{.}0\); b same for the ground state energy of the He\(^+\) ion, E(He\(^+\)), for different atom locations, \(R_{OC}=0{.}0,~2{.}5,~5{.}0\); c same for the ground state binding energy, \(E_B\)
4 Conclusions
In this work, the ground state energy of one atomic impurity of one He atom within a spherical multilayer quantum dot is studied. A core/shell/well/shell structure with parabolic confinement is considered to model the MLQD. Different sizes of this structure have been analyzed and different atomic positions within the quantum dot have been considered. A Configuration-Interaction approach has been employed with the atomic radial orbitals built in terms of Sturmian functions. The accuracy of the CI approximation has been addressed by comparing with Diffusion Monte Carlo calculations for some representative configurations.
In the cases where the position of the atomic nucleus is off-centered from the spherical layers of the material, the spherical symmetry of the two electron Hamiltonian is broken. In this contribution we have exploited a technique, proposed in a recent contribution for H\(_2\) [61], which to the best of our knowledge has not been previously employed for the He atom. Off-center configurations are studied by placing the center of the coordinate system at the atomic nucleus and performing a multipole expansion of the confining potential. This approach presents the conceptual advantage that the exact treatment is maintained for the Coulomb potential, whereas the approximate treatment induced by the loss of spherical symmetry is applied to the confining potential, which is a model of the MLQD. Furthermore, it presents faster convergence than expanding the Coulomb potential.
An important dependence of the energy and the binding energy of the impurity with the atomic position has been found. The energy as a function of the distance from the nucleus to the center of the MLQD increases as the atom is separated from the center and presents a series of maxima and minima that corresponds to configurations with the atom located in the shells and in the well, respectively. These maxima and minima depend on \(V_0\) and the size of the core. We have found that, depending on the MLQD parameters, the lowest energy configuration does not necessarily correspond to the atom located at the center, but for large core sizes such that confinement effects are small, the global minimum of the energy corresponds to an on-center impurity. The binding energy also presents an oscillatory behavior and a strong dependence on the nuclear position and increases when the atomic energy decreases.
Data Availibility Statement
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
E. Tangarife, C.A. Duque, Appl. Surf. Sci. (2010). https://doi.org/10.1016/j.apsusc.2010.05.057
B. Liang, P.S. Wong, T. Tran, V.G. Dorogan, Y.I. Mazur, M.E. Ware, G.J. Salamo, C.K. Shih, D.L. Huffaker, Nano Res. (2013). https://doi.org/10.1007/s12274-013-0299-5
Y. Huang, Y. Puttisong, I.A. Buyanova, W.M. Chen, Nano Res. (2016). https://doi.org/10.1007/s12274-015-0940-6
W. Zhou, J.J. Coleman, Curr. Opin. Solid State Mater. Sci. (2016). https://doi.org/10.1016/j.cossms.2016.06.006
M.T. Hasan, R. González-Rodríguez, C. Ryan, K. Pota, K. Green, J.L. Coffer, A.V. Naumov, Nano Res. (2019). https://doi.org/10.1007/s12274-019-2337-4
N. Pramjorn, A. Amthong, Appl. Surf. Sci. (2020). https://doi.org/10.1016/j.apsusc.2019.145195
Z. Chen, Z. Qin, S. Su, S. Chen, Nano Res. (2021). https://doi.org/10.1007/s12274-021-3354-7
E. Petryayeva, W.R. Algar, I.L. Medintz, Appl. Spectrosc. (2013). https://doi.org/10.1366/12-06948
N. Hildebrandt, C.M. Spillmann, W.R. Algar, T. Pons, M.H. Stewart, E. Oh, K. Susumu, S.A. Díaz, J.B. Delehanty, I.L. Medintz, Chem. Rev. (2017). https://doi.org/10.1021/acs.chemrev.6b00030
L.M.K. Vandersypen, H. Bluhm, J.S. Clarke, A.S. Dzurak, R. Ishihara, A. Morello, D.J. Reilly, L.R. Schreiber, M. Veldhorst, npj Quantum Inf. (2017). https://doi.org/10.1038/s41534-017-0038-y
P. Huang, Adv. Quantum Technol. (2021). https://doi.org/10.1002/qute.202100018
J. Chen, D. Jia, E.M.J. Johansson, A. Hagfeldt, X. Zhang, Energy Environ. Sci. (2021). https://doi.org/10.1039/D0EE02900A
M. Albaladejo-Siguan, E.C. Baird, D. Becker-Koch, Y. Li, A.L. Rogach, Y. Vaynzof, Adv. Energy Mater. (2021). https://doi.org/10.1002/aenm.202003457
G. Shi, H. Wang, Y. Zhang, C. Cheng, T. Zhai, B. Chen, X. Liu, R. Jono, X. Mao, Y. Liu, X. Zhang, X. Ling, Y. Zhang, X. Meng, Y. Chen, S. Duhm, L. Zhang, T. Li, L. Wang, S. Xiong, T. Sagawa, T. Kubo, H. Segawa, Q. Shen, Z. Liu, W. Ma, Nat. Commun. (2021). https://doi.org/10.1038/s41467-021-24614-7
Y.S. Park, J. Roh, B.T. Diroll, R.D. Schaller, V.I. Klimov, Nat. Rev. Mat. (2021). https://doi.org/10.1038/s41578-020-00274-9
Y. Wan, C. Xiang, J. Guo, R. Koscica, M.J. Kennedy, J. Selvidge, Z. Zhang, L. Chang, W. Xie, D. Huang, A.C. Gossard, J.E. Bowers, Laser Photonics Rev. (2021). https://doi.org/10.1002/lpor.202100057
A. Özmen, B. Çakır, Y. Yakar, J. Lumin. (2013). https://doi.org/10.1016/j.jlumin.2013.01.005
T. Chen, W. Xie, S. Liang, J. Lumin. (2013). https://doi.org/10.1016/j.jlumin.2013.02.030
A.S. Baimuratov, I.D. Rukhlenko, V.K. Turkov, I.O. Ponomareva, M.Y. Leonov, T.S. Perova, K. Berwick, A.V. Baranov, A.V. Fedorov, Sci. Rep. (2014). https://doi.org/10.1140/epjp/s13360-020-00321-y
M.F. Morcillo-Arencibia, J.M. Alcaraz-Pelegrina, A.J. Sarsa, Eur. Phys. J D (2021). https://doi.org/10.1140/epjd/s10053-021-00096-6
F.S. Nammas, Phys. Scr. (2020). https://doi.org/10.1088/1402-4896/ab3d5d
C. Heyn, C.A. Duque, Sci. Rep. (2020). https://doi.org/10.1038/s41598-020-65862-9
A. Corella-Madueño, R. Rosas, J.L. Marín, R. Riera, J. Appl. Phys. (2001). https://doi.org/10.1063/1.1329143
L. Jiang, H. Wang, H. Wu, Q. Gong, S. Feng, J. Appl. Phys. (2009). https://doi.org/10.1063/1.3080175
A. Fatemidokht, H.R. Askari, Opt. Laser Technol. (2013). https://doi.org/10.1016/j.optlastec.2012.05.011
D.B. Hayrapetyan, G.L. Ohanyan, D.A. Baghdasaryan, H.A. Sarkisyan, S. Baskoutas, E.M. Kazaryan, Physica E (2018). https://doi.org/10.1016/j.physe.2017.09.006
M. Solaimani, Mater. Sci. Eng. C (2020). https://doi.org/10.1016/j.mseb.2020.114694
L. Belamkadem, O. Mommadi, J.A. Vinasco, D. Laroze, A. El Moussaouy, M. Chnafi, C.A. Duque, Physica E (2021). https://doi.org/10.1016/j.physe.2021.114642
C.O. Edet, E.B. Al, F. Ungan, N. Ali, N. Rusli, S.A. Aljunid, R. Endut, M. Asjad, Nanomaterials (2022). https://doi.org/10.3390/nano12162741
T. Meunier, I.T. Vink, L.H. Willems van Beveren, K.J. Tielrooij, R. Hanson, F.H.L. Koppens, H.P. Tranitz, W. Wegscheider, L.P. Kouwenhoven, L.M.K. Vandersypen, Phys. Rev. Lett. (2007). https://doi.org/10.1103/PhysRevLett.98.126601
L. Lu, W. Xie, H. Hassanabadi, J. Appl. Phys. (2011). https://doi.org/10.1063/1.3560541
Y. Yakar, B. Çakır, A. Özmen, Comput. Phys. Commun. (2015). https://doi.org/10.1016/j.cpc.2014.11.011
W. Luo, A. Naseri, J. Sirker, T. Chakraborty, Sci. Rep. (2019). https://doi.org/10.1038/s41598-018-35837-y
S. Chaudhuri, Physica E (2021). https://doi.org/10.1016/j.physe.2020.114571
K. Hai, Y. Wang, Q. Chen, W. Hai, Sci. Rep. (2021). https://doi.org/10.1038/s41598-021-98152-z
T. Sako, G.H.F. Diercksen, J. Phys. B (2003). https://doi.org/10.1088/0953-4075/36/18/304
X. Wen-Fang, Commun. Theor. Phys. (2007). https://doi.org/10.1088/0253-6102/48/2/025
D.M. Mitnik, J. Randazzo, G. Gasaneo, Phys. Rev. A (2008). https://doi.org/10.1103/PhysRevA.78.062501
C. Laughlin, S.I. Chu, J. Phys. A (2009). https://doi.org/10.1088/1751-8113/42/26/265004
H.E. Montgomery, N. Aquino, A. Flores-Riveros, Phys. Lett. A (2010). https://doi.org/10.1016/j.physleta.2010.02.074
H.E. Montgomery, V.I. Pupyshev, Phys. Lett. A (2013). https://doi.org/10.1016/j.physleta.2013.08.043
L.G. Jiao, Y.K. Ho, in Electronic Structure of Quantum Confined Atoms and Molecules, ed. by K.D. Sen (Springer International Publishing, Cham, 2014), pp. 145–168. https://doi.org/10.1007/978-3-319-09982-8_6
J.K. Saha, S. Bhattacharyya, T.K. Mukherjee, Commun. Theor. Phys. (2016). https://doi.org/10.1088/0253-6102/65/3/347
A. Luzón, E. Buendía, F.J. Gálvez, Int. J. Quantum Chem. (2020). https://doi.org/10.1002/qua.26048
D. Chakraborty, P.K. Chattaraj, J. Phys. Chem. A (2019). https://doi.org/10.1021/acs.jpca.9b00830
H.E. Montgomery, V.I. Pupyshev, Phys. Scr. (2019). https://doi.org/10.1088/1402-4896/ab45a1
C. Martínez-Flores, Int. J. Quantum Chem. (2021). https://doi.org/10.1002/qua.26529
C. Martínez-Flores, Phys. Lett. A (2021). https://doi.org/10.1016/j.physleta.2020.126988
Y. Yakar, C. Çakır, B. Demir, A. Özmen, J. Lumin. (2021). https://doi.org/10.1016/j.jlumin.2021.118346
S. Mondal, K. Sen, J.K. Saha, Phys. Rev. A (2022). https://doi.org/10.1103/PhysRevA.105.032821
Y. Yakar, C. Çakır, B. Demir, A. Özmen, Phys. Lett. A (2023). https://doi.org/10.1016/j.physleta.2023.128724
J. Nanda, S.A. Ivanov, H. Htoon, I. Bezel, A. Piryatinski, S. Tretiak, V.I. Klimov, J. Appl. Phys. (2006). https://doi.org/10.1063/1.2168032
F.K. Boz, S. Aktas, A. Bilekkaya, S.E. Okan, Appl. Surf. Sci. (2009). https://doi.org/10.1016/j.apsusc.2009.02.040
F. Boz, S. Aktas, A. Bilekkaya, S. Okan, Appl. Surf. Sci. (2010). https://doi.org/10.1016/j.apsusc.2010.01.036
S. Akgül, M. Şahin, K. Köksal, J. Lumin. (2012). https://doi.org/10.1016/j.jlumin.2012.02.012
M. Karimi, G. Rezaei, M. Nazari, J. Lumin. (2014). https://doi.org/10.1016/j.jlumin.2013.07.046
F.K. Boz, B. Nisanci, S. Aktas, S.E. Okan, Appl. Surf. Sci. (2016). https://doi.org/10.1016/j.apsusc.2016.06.035
F. Rahimi, T. Ghaffary, Y. Naimi, H. Khajehazad, Eur. Phys. J. Plus (2022). https://doi.org/10.1140/epjp/s13360-021-02188-z
K. Kirak, Eur. Phys. J. Plus (2021). https://doi.org/10.1140/epjp/s13360-021-01644-0
G. Gasaneo, L.U. Ancarani, D.M. Mitnik, J.M. Randazzo, A.L. Frapiccini, F.D. Colavecchia, in Proceedings of MEST 2012: Exponential Type Orbitals for Molecular Electronic Structure Theory, Advances in Quantum Chemistry, vol. 67, ed. by P.E. Hoggan (Academic Press, 2013), p. 153. https://doi.org/10.1016/B978-0-12-411544-6.00007-8
M.F. Morcillo-Arencibia, J.M. Alcaraz-Pelegrina, A.J. Sarsa, J.M. Randazzo, Phys. Chem. Chem. Phys. (2022). https://doi.org/10.1039/D2CP03456E
NIST Digital Library of Mathematical Functions. F. W. J. Olver, A. B. Olde Daalhuis, D. W. Lozier, B. I. Schneider, R. F. Boisvert, C. W. Clark, B. R. Miller, B. V. Saunders, H. S. Cohl, and M. A. McClain, eds. http://dlmf.nist.gov/, Release 1.1.6 of 2022-06-30http://dlmf.nist.gov/18
J.M. Randazzo, L.U. Ancarani, G. Gasaneo, A.L. Frapiccini, F.D. Colavecchia, Phys. Rev. A (2010). https://doi.org/10.1103/PhysRevA.81.042520
J.M. Randazzo, A. Aguilar-Navarro, Int. J. Quantum Chem. (2018). https://doi.org/10.1002/qua.25611
J. Avery, J. Avery, J. Math. Chem. (2003). https://doi.org/10.1023/A:1023204016217
X. Du, W. Sheng, J. Appl. Phys. (2008). https://doi.org/10.1063/1.2981205
B.L. Hammond, W.A. Lester Jr., P.J. Reynolds, Monte Carlo Methods Ab Initio Quantum Chem. (World Scientific, Singapore, 1994)
A. Holubec, A.D. Stauffer, J. Phys. A (1985). https://doi.org/10.1088/0305-4470/18/12/011
A. Holubec, A.D. Stauffer, P. Acacia, J.A. Stauffer, J. Phys. A (1990). https://doi.org/10.1088/0305-4470/23/18/014
M.F. Morcillo, J.M. Alcaraz-Pelegrina, A. Sarsa, Int. J. Quantum Chem. (2018). https://doi.org/10.1002/qua.25563
Acknowledgements
This work was partially supported under Grant PID2020-114807GB-I00 by the Spanish MCIN/ AEI /10.13039/501100011033. M.F. M.-A. acknowledges partial support through a Ph.D fellowship from the Spanish Ministerio de Universidades, Grant FPU16/05950, and through a mobility grant from the Asociación Universitaria Iberoamericana de Posgrado.
Funding
Funding for open access publishing: Universidad de Córdoba/CBUA.
Author information
Authors and Affiliations
Contributions
JMR and AJS conceived the idea and the model, JMR and AJS designed the computational framework; JMR and MFMA carried out the implementation; MFMA performed the calculations; MFMA and JMAP contributed to the analysis of results; MFMA, JMAP and JMR wrote the initial version of the manuscript; all the authors contributed to the final version of the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
There are no conflicts of interest to declare.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Morcillo-Arencibia, M.F., Alcaraz-Pelegrina, J.M., Sarsa, A.J. et al. On- and off-center helium atom in a spherical multilayer quantum dot with parabolic confinement. Eur. Phys. J. Plus 138, 456 (2023). https://doi.org/10.1140/epjp/s13360-023-04064-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjp/s13360-023-04064-4