1 Introduction

The Covid-19 pandemic is an emerging infectious disease, which causes high mortality and affects the economy and health system [1, 2]. This virus presents as a severe acute respiratory syndrome [3]. Infection with this virus appears in initial symptoms, such as fever, cough, muscle aches, or feeling very tired, and some cases may progress to pneumonia and acute respiratory illnesses, especially in the older and people with chronic diseases [4]. To achieve an effective solution than inventing a new vaccine, the rapid detection of this virus seems to be a faster and less expensive solution [5]. For this purpose, the study of a biosensor has attracted attention, recently to control the pandemic situation [6]. Among these biosensors are microfluidic devices that can be adopted to quantify antibodies and protein biomarkers with accuracy and relative ease compared to traditional methods. Microfluidic biosensors are devices that can detect the presence or activity of biological molecules in samples, such as blood [7], urine[8], saliva [9] or water [10]. They are increasingly used in the fields of biology [11], the environment [12], food safety [13] and medicine [11, 14]. Microfluidic biosensors are increasingly used for the detection of infectious diseases, including COVID-19 [15, 16]. Antibodies to SARS-CoV-2 can be detected with ease, reliability, and cost-effectiveness using these devices. Seo et al. [17] have developed a biosensor device based on a field effect transistor for the detection of SARS-CoV-2 in clinical samples. The device has successfully detected the virus in a culture medium for a specific concentration. In another report, Layqah et al. [18] have developed an electrochemical immunosensor for the detection of MERS-CoV. The detection is performed on a gold nanoparticle-modified carbon electrode with square wave voltammetry. Using bioactivated microchannels and antibody-functionalized microspheres, Javanmard [19] developed a label-free impedance-based protein biomarker sensor. As low as 1 ng/ml concentration of anti-hCG antibodies could be detected with the researchers’ system after one hour of assaying. An IgG antibody quantification device developed by Dong et al. [20] uses a screen-printed microfluidic device. With this device, the detection limit is approximately 10 ng/mL, and the dynamic range is 100 ng/ml to 10 ug/ml. Chin et al. [21] developed a miniaturized ELISA microfluidic chip named mChip (Mobile Microfluidic Chip for Protein Biomarker Immunoassay) using a small amount (< 1 μL) of untreated whole blood. An immunoassay-based multiplexed microfluidic device by Lafleur et al. [22] detected disease-specific antigens or IgM antibodies in blood via a disposable microfluidic device. An ELISA test at benchtop level can detect 20 ng/ml in 30 min. Lee et al. [23] developed an integrated microfluidic sensor for the detection of dengue virus IgG and IgM antibodies in human serum. The detection limit is 21 pg and the total assay time is approximately 30 min. Surface plasmon resonance (SPR) sensor, impedance-based sensor and immunoassays are the main methods used in most cases for the detection of biomolecules. These sensors involve the same specific binding kinetics of analytes and immobilized ligands. They mix a small concentration of a biological analyte with the fluid in a microchannel. When the analyte takes longer to be transported by convection and diffusion to the sensitive surface than the chemical reaction, the entire reaction is retained by the mass transport process usually causing the formation of a diffusion boundary layer [24]. This leads to the limitation of the response time and performance of the microfluidic biosensor. In order to improve the reaction rate, several experimental and numerical approaches have been developed [25,26,27,28,29,30,31,32,33,34,35]. Selmi et al. [28, 36] have analyzed the electrothermal effect on the immunoassay of a biosensor. They studied the binding reaction efficiency in the microchannel of a biosensor with asymmetrical interdigitated electrodes. In another study, Selmi et al. [28] have analyzed the effect of the cylindrical obstacle on the microfluidic biosensor efficiency. On the other hand, Selmi et al. [29] studied the effect of confinement by the secondary flow on the chemical kinetics but they did not optimize the confinement parameters. Echouchene et al. [30] have improved the analyte transport of microfluidic immunosensors using a new sensing area shape. In a recent study, Kaziz et al. [31] optimized the design parameters of an electrothermal flow biosensor for SARS-CoV-2 protein S immunoassay. Recently, Kaziz et al. [31, 32] have developed numerical methods for optimizing the performance of microfluidic biosensors for the detection of COVID-19. Based on the Taguchi method, they determined the degree of influence of different optimization parameters [32]. In a very recent work, Kaziz et al. [33] and Ben mariem et al. [34] used the Taguchi approach and artificial intelligence based on artificial neural networks for the optimization of the performance of a microfluidic biosensor under electrothermal force for the detection of COVID-19. Excellent results were obtained in this work.

In this work, we propose the optimization of a two-dimensional configuration to confine an analyte flow to the surface of the microfluidic biosensor. Two-dimensional Navier–Stokes equations coupled with the analyte transport and binding reaction equations are used for this simulation. The effects of confinement flow parameters such as the confinement flow coefficient, the position of the confinement channel and its angle with respect to the main channel are analyzed by calculating the response time via the time evolution of the average concentration of the complex analyte-ligand. This paper follows the following plan: In Sect. 2, we describe the mathematical model describing our physical problem as well as the geometric configuration studied. The numerical method has been described in this section. Section 3 is devoted to the presentation of the results of the numerical calculation of the effect of the optimization parameters. In this section, we have presented the different configurations to be analyzed. An experimental design approach based on the Taguchi method was used in this section to give the best combination of the studied factors as well as their contribution percentages in the response time of the microfluidic biosensor with confinement. Finally, two models, one based on multiple linear regression (MLR) and the other on artificial neural network (ANN), were developed to predict the biosensor response time.

2 Physical model and boundary conditions

2.1 Geometric structure

The modeled system involves mixing a small concentration of a biological analyte with the water in a microchannel where a reaction surface is located on the bottom wall of the microchannel. A secondary water flow (inlet 2) without an analyte located on the top with an angle of inclination α to the primary flow (inlet 1). The analyte flows through a microfluidic channel of dimensions 40 µm × 40 µm × 250 µm. Figure 1 shows the three-dimensional structure of a microfluidic biosensor suitable for the detection of COVID-19.

Fig. 1
figure 1

Tridimensionnel configuration of the microfluidic biosensor with confinement flow

Full size image

2.2 Physical model

The proposed work is based on the two-dimensional Navier–Stokes equations for the numerical simulation of the fluid flow inside the microchannel. For this purpose, the fluid is assumed to be incompressible so that [37]:

$$\nabla .\overrightarrow {U} = 0$$
(1)
$$\rho \nabla \left( {\overrightarrow {U} \otimes \overrightarrow {U} } \right) - \mu \nabla^{2} \overrightarrow {U} + \nabla p = 0$$
(2)

where \(\overrightarrow{U}\) is the velocity vector, \(\rho\) is the density, \(\mu\) is dynamic viscosity, and p is the pressure.

The detection of these sensors is based on the immobilized analytes and ligands. The immunosensors are the necessary tools for the detection of analytes in antibody-antigen interactions [38,39,40,41]. The reaction surface of a biosensor is a liquid–solid surface in which specific recognition of immobilized analytes and ligands occurs. The kinetics of the reaction takes place in two steps [42] (Fig. 2):

  • Step 1: diffusion of analyte from bulk to the reaction surface.

  • Step 2: binding reaction between the analyte and the ligands.

where [A]bulk and [A]surface are the analyte concentration in the bulk and at the reaction surface, respectively. [B] stands for the ligand concentration and [AB] is the complex concentration, ka and kd are respectively the association and dissociation rates.

Fig. 2
figure 2

Kinetic reaction process

Full size image

The transient analyte transport of biological species is described by Fick’s second law:

$$\frac{\partial [C]}{{\partial t}} + \overrightarrow {U} .\nabla [C] = D\nabla^{2} [C]$$
(3)

where [C] is the analyte concentration and D is the diffusion coefficient of the analyte.

Using the first-order Langmuir adsorption model, the reaction rate at the reaction surface between ligand and analyte is:

$$\frac{\partial [AB]}{{\partial t}} = k_{a} \left[ A \right]_{surface} \Big\{ {\left[ {B_{0} } \right] - \left[ {AB} \right]} \Big\} - k_{d} \left[ {AB} \right]$$
(4)

where [B0] is the ligand density.

2.3 Boundary conditions

In order to solve the previous system of equations, boundary conditions must be applied. Table 1 summarizes the boundary conditions used for this simulation.

Table 1 Boundary conditions used for the simulation
Full size table

2.4 Numerical method

The finite element method was used to solve the mathematical model of this problem [28]. The equations from 1 to 4 are solved by the finite element method [28], which consists in seeking an approximate solution after discretization of the domain into triangular elements refined in the vicinity of the reaction surface whose concentration gradient is significant. By applying the weak formulation, Eqs. (1)–(4) are transformed into a non-dependent and time-dependent system of ordinary equations. The temporal discretization of the ordinary differential equations was carried out via the explicit Euler method. Newton’s method was adopted for solving the problem. After the spatial discretization of the field of study, we adopted the following approach to solve the differential problem: In the first case, we solve the Navier–Stokes equations to determine the velocity field then we simultaneously solve the analyte transport equation coupled with the equation of transient chemical kinetics to determine the concentrations of the target analytes, [C] in the microchannel and the concentration of the analyte/ligand complex [AB] on the sensitive surface.

3 Results and discussion

3.1 Validation

First, the physical model is validated against results taken from the literature [25]. The data used for validation is shown in the following Table 2 for a 3D configuration of dimension 25 mm × 5 mm × 0.02 mm.

Table 2 Input parameters used for model validation
Full size table

Figure 3 shows that obtained results with the current numerical study are in good agreement with the experimental data of Hofmann et al. [25].

Fig. 3
figure 3

Validation of numerical results of the normalized complex concentration with the experimental data of Hofmann et al. [25] for flow rate Qv = 66 µL/min

Full size image

3.2 3D to 2D approximation

Assuming that the variation in analyte concentration is small along the y-axis, the 3D geometry can be reduced to a 2D approximation [25]. Figure 4 shows that a good agreement is obtained for 2D results compared to 3D simulation. Thus, the two-dimensional microfluidic biosensor will be considered, hereafter, in order to study the effect of several physical and geometrical parameters on the performance of microfluidic biosensors.

Fig. 4
figure 4

Validation of 3D/2D approximation

Full size image

3.3 Design of microfluidic biosensor

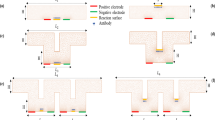
Three microfluidic biosensors with different angles α = 30°, 60°, and 90° were used to improve the time detection of the COVID-19 virus. Each inlet was set to 40 µm high, and 100 µm length. The sensor, 20 μm wide, is placed on the bottom wall, 90 μm from inlet 1. The detailed diagram of the four configurations of microfluidic biosensors is shown in Fig. 5.

Fig. 5
figure 5

Schematic diagram of four microfluidic biosensors for different angles between inlets A α = 30°, B α = 60° and C α = 90°. All proposed configurations are 250 µm in length and have a cross section of 40 µm width and 40 µm height

Full size image

For an electrochemical problem, the convective diffusion equation was solved by Levich et al. [43, 44] and given as:

$$k_{m} = 0.98D^{\frac{2}{3}} \left( {\frac{u}{h \times l}} \right)^{1/3 }$$
(5)

where D is the analyte diffusion coefficient, u is the average inlet velocity, h is the channel height and l is the position along the sensing zone. The thickness of the diffusion layer, for [A] < [A0], can be calculated as:

$$d_{{{\text{diff}}}} = \frac{D}{{k_{m} }} = \frac{1}{0.98}\left( {\frac{D \times h \times l}{u}} \right)^{1/3 }$$
(6)

The affinity of the antibodies used for the detection of SARS-COV is 106 Mol/m3 [45] and the absorption and dissociation rates are 103 m3/Mol s and 10−3 s−1 respectively. In the numerical simulation, sample analyte concentration flows a 250 µm microchannel length. A reaction surface of 20 µm in length with a ligand concentration of 1.668 × 10−8 mol/m2 is used. The diffusion coefficient of the analyte is 3 × 10−11 m2/s. The association and the dissociation rates are 7.5 m3/mol s and 6.6 × 10−4 s−1, respectively.

3.4 Optimization with the Taguchi method

3.4.1 Taguchi method

The Taguchi method is a robust technique for the optimization of multivariate systems, including mass transport in microfluidic biosensors, where response time is controlled by several key factors with an optimization goal. The Taguchi method involves optimizing key factors to achieve the desired goal with the application of mathematical and statistical concepts. This method is used in this study to minimize the microfluidic biosensor response time. Taguchi method uses the orthogonal array (OA) networks that form the matrix of numerical experiments and the signal-to-noise ratio (S/N) to study a large number of variable processes with a small number of numerical experiments.

3.4.2 Factors and levels

For the optimization of two-dimensional microfluidic confinement for microfluidic biosensors for the detection of COVID-19, the Taguchi method was used in order to evaluate the influence of the chosen independent variables which are the inclination angle \(\alpha\), the confinement coefficient \(\beta\), and confinement position X. The factors and levels used in the present study are summarized in Table 3. These factors are selected based on the above numerical database. In this study, the response time TR is taken as the signal factor.

Table 3 Levels of each factor in this study
Full size table

3.4.3 Taguchi approach

Taguchi’s method is an approach for modeling difficult multivariate systems where the response is pretentious from several key factors with an optimization goal. This approach involves optimizing key parameters to achieve the desired goal with applications of mathematical and statistical concepts. This method is used in this work to minimize the microfluidic biosensor response time with confinement. Rather than using a large number of numerical experiments to study a large number of variables, Taguchi used orthogonal (OA) matrices to study a large number of variables [33].

Through OA, maximum information can be obtained in a minimum number of numerical experiments and optimal levels can be determined for each parameter.

In the present study, the L9 orthogonal matrix is chosen based on the number of key factors and their levels. With Taguchi fractional factorial design, there are only nine experiments required instead of 27 for three factors at three levels in a factorial design. In the Taguchi method, the least number of executions possible can be estimated as follows [46]:

$$N_{{{\text{Taguchi}}}} = 1 + {\text{NF}}\left( {L - 1} \right)$$
(7)

where \(N_{{{\text{Taguchi}}}}\) is the minimum number of experiments to perform, \({\text{NF}}\) is the number of control factors and L is the number of levels used. In the present study, three parameters (\({\text{NF}} = 3\)) and three levels (L = 3) were considered as shown in Table 3. Using this equation, a minimum of 7 numerical experiments are required. However, for three level factors, only the L9 orthogonal array is available. Table 4 shows the three parameter levels for each run using the orthogonal array closest to L9 for the present experimental runs.

Table 4 Experimental configurations for the response time according to the \(L_{9} \left( {3^{3} } \right)\) factorial design
Full size table

Figure 6 shows the analyte diffusion boundary layers during the association phase for all the assays in Table 5 at t = 150 s compared with that without confinement. The boundary layer gradually disappears in the association phase because the confinement coefficient is so important when the confinement channel is in front of the reaction surface.

Fig. 6
figure 6

The development of the diffusion boundary layer of the binding reaction. (1) without confinement and (2–9) for configurations of Table 4 at time of 150 s

Full size image
Table 5 Results of the \(L_{9}\) experimental configurations
Full size table

Figure 7 illustrates the response of microfluidic biosensor for all experiment configurations that are enumerated in Table 4. The curves are plotted as the average surface concentration of complexes versus time.

Fig. 7
figure 7

Complex concentration in association phase for all tests illustrated in Table 4

Full size image

3.4.4 Signal-to-noise analysis

The signal-to-noise ratio, introduced by Taguchi, is used in quality engineering and experimental design. It can help engineers determine the effectiveness of control factor levels. The S/N ratio makes it possible to obtain the optimal parameters of these responses. Since the lowest value of the response time is a desirable condition to achieve a higher performance of the microfluidic biosensor, the best S/N ratio approach has been adopted to schematize the S/N ratio. The characteristic “smaller is better” means that the smaller the value of an objective function f, the closer the systematic optimization of the control factors is [32]:

$${\text{S/N}} = - 10\log \left( {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} y_{i}^{2} } \right)$$
(8)

where n is the total number of simulation tests and yi is the calculated response time value at a given factor combination.

3.4.5 Evaluation of numerical results

Table 5 shows the L9 orthogonal array of the three control factors, detection times, and signal-to-noise ratios (SNRs) calculated for each experimental configuration. The detection time is the time during which the average concentration is equal to 95% of its saturation value [32].

The factorial effect and contribution ratio of every factor are presented in Table 6 and Fig. 8a and b, respectively. To assess the effect of each key parameter, the mean values of the responses time and S/N ratio obtained for each level must be calculated. To do this, the sum of the results associated with each level of the orthogonal table divided by the number of tests for this level provides the appropriate averages which is equal to 5.22 min for TR and− 14.22 dB for S/N ratio. The S/N ratio response table for TR is shown in Table 5. Using Tables 4 and 5, it is straightwordward to obtain the results summarized in Table 6. This table indicates the optimal levels of the simulation variables responsible for the minimum TR which are also graphically represented in Fig. 8a and b.

Table 6 Average peak-to-peak value of response time and S/N ratio for all levels of all factors
Full size table
Fig. 8
figure 8

mean of a response time TR and b S/N ratio for the three key parameters at different levels

Full size image

The optimal combination of control factors for minimum response time TR of microfluidic biosensor for COVID-19 can be easily detected either from Table 6 or from Fig. 8a and b. The optimization factor levels giving the minimum response time TR have been specified by bold numbers in Table 6 and surrounded with a circle in Fig. 8a and b. The horizontal magenta line indicates the average value over all the configurations. For the inclination angle \(\alpha\), the optimal level is level 3 (mean = 5.017 and S/N ratio = − 13.78 dB). In regards to the confinement coefficient \(\beta\), the optimal level is level 3 (mean = 4.69 and S/N ratio = − 13.21 dB). Finally, the optimal level of the confnement channel position X is obtained for level 2 (mean = 4.637 and S/N ratio = − 13.23 dB). Especially, the minimum response time was achieved with the folowing papameters:\(\alpha_{3} \beta_{3} X_{2}\) that corresponds to \(\alpha = 90^\circ\), \(\beta = 25\) and X = 40 µm.

The factor with the strongest influence was determined by the difference values, Delta, between the maximum value and the minimum value of the average values obtained (Table 6). The greater the difference, the more influential the control factor. Figure 8a and b and Table 6 indicate that the value of Delta related to the parameter X is greater that the two other values of delta related to the angle \(\alpha\) and the confinement coefficient. Therefore, the confinemnt channel position X has the strongest influence.

In order to determine the magnitude and significance of the effects of three optimization factors, the Pareto chart is used (Fig. 9). Figure 9 shows the absolute values of the standardized effects from largest effect to smallest effect. Only the X factor intersects the reference line at 2.571 which shows that it is statistically significant at the 0.05 level.

Fig. 9
figure 9

Pareto chart of the standardized effects of response time for confidence level 95%

Full size image

3.4.6 Analysis of Variance

The Analysis of Variance (ANOVA) is used to investigate which parameters significantly affected the quality characteristics and to estimate the percentage of key factors on the response time of the biosensor. In ANOVA many quantities as the degree of freedom (DoF), the sums of squares (SS), the F-ratio (F), and the percentage contribution are determined. Table 7 illustrates the ANOVA results for response time.

Table 7 ANOVA results for response time
Full size table

It is clear from Table 7 and Fig. 10 that the main contributions is related to the confinement coefficient β (~ 27%) and the confinement position X (~ 62%) while the angle of inclination (α) has the minimum contribution (~ 7%) to reduce response time among the key factors.

Fig. 10
figure 10

Contributions of key parameters (X, α, β, Error) on biosensor detection time

Full size image

3.4.7 Prediction and verification

Under the optimal setting conditions, the optimal value of the microfluidic biosensor response time is estimated as follows:

$$\hat{T}_{{\text{R}}} = \overline{\beta }_{3} + \overline{X}_{2} - \overline{T}_{{\text{R}}} = 4.69 + 4.64 - 5.22 = 4.11 \;{\text{min}}$$
(9)

where \(\overline{\beta }_{3}\) is the average \(T_{{\text{R}}}\) for \(\beta\) at level 3 obtained from Table 6, \(\overline{X}_{2}\) is the average \(T_{{\text{R}}}\) for \(X\) at level 2 obtained from Table 5, \(\overline{T}_{{\text{R}}}\) is the mean of \(T_{{\text{R}}}\). By running the FEM simulation under the optimal tuning conditions, we can get \(T_{{\text{R}}} = 3.71\; {\text{min}}\), relative error: \(\left| {\frac{{T_{{\text{R}}} - \hat{T}_{{\text{R}}} }}{{T_{{\text{R}}} }}} \right| \times 100 = 10.66\%\), which is acceptable in engineering.

3.4.8 Comparison with experimental data

In Fig. 11, we plotted the completion time related to the work of Hofmann et al. [25] against that of our study to verify the validity of the confinement effect on the binding reaction in the biosensor. Our simulation appears to respond faster than Hofmann et al. [25], probably because the kon and koff values used in our study are higher than those of Cy5-labeled anti-rabbit IgG used by Hofmann et al. [25]. The response time found by Hofmann et al. [25] is higher than that obtained in our present work because the affinity of the Cy5-labeled rabbit anti-IgG molecule is higher than that used in our study.

Fig. 11
figure 11

Comparison of the response time obtained by our work with that reported by Hofmann et al. [25]

Full size image

4 Predictive models

4.1 Modeling using Multiple linear regression analysis

Multiple linear regression (MLR) technique is employed to ascertain the relationship prevailing among the variables. In the multiple linear regression, the response \(Y\) takes the following form [15].

$$Y = a_{0} + \mathop \sum \limits_{i = 1}^{N} a_{i} X_{i}$$
(10)

where \(Y \equiv T_{{\text{R}}}\) is the response (the unit is minutes), \(a_{0}\) is the average of response, \(X_{i}\) are the known variables on which predictions are to be made and \(a_{i}\) are the coefficients which are determined by the least squares method using the MATLAB software. In our case the multiple regression model gives:

$$T_{{\text{R}}} = 5.609 - 0.00789{\varvec{\alpha}} - 0.0486{\varvec{\beta}} + 0.01833{\varvec{X}}$$
(11)

The relationship between the numerical simulation values and those predicted by the multiple linear regression model for response time is shown in Fig. 12. Based on this figure, it can be seen that MLR data points are moderately dispersed around the regression line. The error in these two sets of values is due to the MLR model which does not take into account the interactions between the control factors: \(\alpha \beta ,\alpha X,\beta X, \;{\text{and}}\; \alpha \beta X\).

Fig. 12
figure 12

Cross-correlation of predicted by MLR model and actual values of TR

Full size image

The previous models are valid for \(30^\circ \le \alpha \le 90^\circ\), \(5 \le \beta \le 25 \;{\text{and}}\; 0 \le X \le 80 \;{\mu m}\). A positive value in the models of Eq. 10 indicates a synergistic effect and a negative value indicates an opposite effect, and the absolute values of the coefficients indicate their significance for the response time.

Figure 13 illustrates the isosurfaces of response time as a function of principal key factors: Inclination angle α, confinement coefficient β and confinement position X. The revelant results prove that the model obtained with the multiple linear regression gives similar results as previous approaches.

Fig. 13
figure 13

Surface plot for response time versus α, β and X. a TR = f(α, β), b TR = f(α, X), and c TR = f(β, X)

Full size image

The design of experiment method shows that it is possible to optimize an efficient, inexpensive and reliable microfluidic biosensor in a very short period of time aimed at fighting against pandemics. These results prove the accuracy of this method compared to other previous numerical studies [29, 47]. The above numerical analysis by the design of experiment method shows the effects of optimization factors on analyte transport by concevtion-diffusion and binding kinetics. It allows us to determine the optimal position and inclination as well as the optimal confinement factor in a microfluidic biosensor for a better approach of the target molecules to the reaction surface by reducing or eliminating the diffusive boundary layer. Improving microfluidic biosensor performance by confining analytes with secondary flow is efficient and economical. The optimal detection time found by experimental design method shows that it is very small compared to other methods that use the electrothermal force [31, 48,49,50]. Based on this multiple linear regression model and using a genetic algorithm (GA) included in MATLAB software [51], the best combination giving the minimum response time in the studied intervals of these factors is the following: \(\alpha = 90^\circ\), \(\beta = 25\), and \(X = 40\;{\mu m}\).

According this combination, the response time obtained with the GA is TR = 3.6839 min. In comparison with that obtained by the optimal combination obtained by the ANOVA analysis (TR = 3.71 min) a reduction of 0.7% is achieved.

4.2 Modeling using artificial neural network (ANN)

An artificial neural network (ANN) is a system inspired by the functioning of biological neurons. It is then related to statistical methods and are generally optimized by probabilistic-type learning methods. The computed data, based on the OA design, is used to develop and train the ANN. The input and output parameters used to model the ANN are shown in Fig. 14.

Fig. 14
figure 14

ANN structure

Full size image

The optimization of a number of hidden layer neurons is important in artificial intelligence. For this, several networks with different hidden layer neurons were trained and tested using the simulation data in Table 9. Figure 15 illustrates the mean absolute percentage error as a function of the number of neurons in the hidden layer. The network with the minimum error percentage (15 neurons in the hidden layer) was chosen as the optimal network (Fig. 15).

Fig. 15
figure 15

Mean percent error versus the hidden layer neuron number

Full size image

The model configuration used in this study is displayed in Table 8.

Table 8 Model configuration
Full size table

After learning the network, a test is assigned to predict the response time of the microfluidic biosensor to affirm the consistency of this model. The input data used to training the ANN are generated based on the ANOVA analysis using full factorial design. Table 9 and Fig. 16a present a comparison of the numerical simulation, the fitted data (ANOVA analysis), and the results predicted by the ANN. From these results, it can be observed that the response time of the biosensor predicted by the ANN model exhibits excellent consistency with the simulation data with an average percentage error lower to 1.5%.

Table 9 Response time obtained by numerical simulation and predicted by ANN model
Full size table
Fig. 16
figure 16

Cross-correlation of predicted and actual values of TR for ANN model

Full size image

A comparison of the results predicted by ANN model and simulation results of TR is shown in Fig. 16. A regression coefficient very close to unity (R2:0.98) is obtained (Fig. 16). From this figure, it can be seen that the points predicted by the ANN model are close to the regression line. The values of RMSE, VAF, and R2 shown in Table 10 indicated that the ANN model showed the best prediction performance compared to MLR model.

Table 10 Performance indices (RMSE, VAF, MAPE, R2, and \(R_{{{\text{adj}}}}^{2}\)) for models
Full size table

According to Fig. 17, MSE gradients for the response time are shown as a function of the number of epochs during the training of the selected network. According to Fig. 17, the MSE gradients for the response time are plotted as a function of the number of epochs during the training of the selected network. From this figure, the best validation performance is obtained at epoch 20 where the gradient is 6.4353 × 10−5.

Fig. 17
figure 17

Learning behavior of the ANN model

Full size image

Figure 18 illustrates the regression between the network outputs and the corresponding targets during the training, the validation, and the testing process. The ideal model and the best match are respectively represented by a dotted line and a solid line. The output and the target are related by the value of R.

Fig. 18
figure 18

Linear regression analysis between the values calculated numerically with the finite element method and the predicted values ANN of the response time TR for the training, the validation, the tests and the assembly

Full size image

The efficient neural network chosen is one that regresses through training, validation, and testing with an R value very close to 1 (Fig. 18). The correlation coefficients (R) are 0.89 for training, 0.97 for validation, 0.999 for testing and 0.998 for the set in the simulation TR. Therefore, this trained network can be used to predict responses for datasets used in microfluidic biosensor simulation.

4.3 Comparison between MLR and ANN predictive models

In order to evaluate the performance of the prediction capacity of the different model, the following coefficients are used [52, 53]:

  • Value adjustment factor

    $${\text{VAF}} = \left[ {1 - \frac{{{\text{var}} \left( {y - \hat{y}} \right)}}{{{\text{var}} \left( {y_{i} } \right)}}} \right] \times 100$$
    (12)

  • Root-mean-square error

    $${\text{RMSE}} = \sqrt {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {y_{i} - \hat{y}_{i} } \right)^{2} }$$
    (13)

  • Mean absolute percentage error

    $${\text{MAPE}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left| {\frac{{y_{i} - \hat{y}_{i} }}{{y_{i} }}} \right|$$
    (14)

  • Correlation coefficient

    $$R^{2} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {y_{i} - \hat{y}_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{N} \left( {\overline{y} - y_{i} } \right)^{2} }}$$
    (15)

  • Adjusted R squared

    $$R_{{{\text{adj}}}}^{2} = 1 - \left( {1 - R^{2} } \right) \times \frac{N - 1}{{N - k - 1}}$$
    (16)

where VAF is value adjustment factor, RMSE is root-mean-square error, MAPE is mean absolute percentage error, \(R^{2}\) is the coefficient of determination, and \(R_{{{\text{adj}}}}^{2}\) is the adjusted R2. \(y_{i}\) is the actual value, \(\hat{y}_{i}\) is the predicted value, \(\overline{y}\) is average value of y, and k is number of input variables. When the value of VAF is 100 and RMSE is 0, then the model will be excellent. A large R2 value (around 1) proves that the regression model fits the data well.

In this section, the results calculated by multiple linear regression (MLR) model, and ANN model in order to predict the response time of microfluidic biosensor were compared to the results calculated by finite element method. In order to evaluate the performance of the prediction capacity of these models, we calculate the quantities defined above, namely the value adjustment factor VAF, the root-mean-square error \({\text{RMSE}}\), the mean absolute percentage error \({\text{MAPE}}\), the correlation coefficient \(R^{2}\), and adjusted value of \(R^{2}\).

The comparative study of these models is illustrated in Fig. 19a and b. The MAPE, VAF, RMSE, R2, and \(R_{{{\text{adj}}}}^{{2}}\) and the Taylor Diagram are used to show the most efficient and simple model to predict the response time of the microfluidic biosensor.

Fig. 19
figure 19

a Simulation data and ANN data compared, and b the variation of the values predicted by ANN model from the CFD values

Full size image

In Fig. 19b, the distances of the predicted values of the models built from the simulation values are shown to illustrate how far they depart from the observed values of TR. This graph indicates that the deviation intervals (− 0.72 min to + 0.55 min) of the predicted values from ANN are smaller than the deviation intervals of MLR (− 0.14 to + 0.23 min).

The capabilities of the MLR and ANN models to predict the response time of microfluidic biosensor were examined by equating the responses of each approach to observed data, thereby calculating MAPE, VAF, RMSE, R2, and \(R_{{{\text{adj}}}}^{{2}}\) using Eqs. (11)–(15), as shown in the Taylor diagram (Fig. 20) and Table 10. Developed by Karl E. Taylor [34], Taylor diagrams show which model is most realistic for a specific phenomenon. Three statistics are used here to measure the model’s suitability—Pearson’s correlation coefficient, root-mean-square error (RMSE), and standard deviation. It is demonstrated in Fig. 20 that only the predicted by the ANN model and the observed values of R2, the standard deviation and the RMSE for the response time are statistically significant, whereas the MLR model is not statistically significant since R2 < 0.9. Only the ANN model is taken into account for data prediction and optimization. The ANN model, indicated by point C, is closest to point A in terms of correlation coefficient R2 and standard deviation. This indicates that the ANN model is the most realistic for prediction of microfluidic biosensor response time with confinement. Nevertheless, the values of R2, \(R_{{{\text{adj}}}}^{2}\), RMSE, MAE and VAF are much better for ANN than the MLR method (Table 10). The results illustrated in Figs. 12 and 16 show that the fluctuation distribution for ANN is much smaller and regular than that obtained by the MLR model. From Table 10; Figs. 12, 16 and 20, it can be concluded that ANN is superior to MLR.

Fig. 20
figure 20

Taylor diagrams of the developed LMR and ANN models

Full size image

5 Conclusion

The time detection of the virus plays a key role in fighting against the COVID-19 pandemic. Thus, the study of the response time of a biosensor seems to be crucial to saving lives and the economy. In this study, the best combination of microfluidic biosensor confinement parameters, namely confinement coefficient β, position of the confinement flow X and its inclination relative α to the main channel to minimize detection time was determined. Taguchi’s approach, ANOVA analysis, multiple linear regression (MLR) model and predictive ANN model were used. Based on the results and analysis, the following conclusions can be drawn:

  • An optimal combination of control parameters to minimize the detection time was obtained by using the S/N ratio. The optimal control factor settings obtained are shown as \(\alpha = 90^\circ\)(level 3), \(\beta = 25\) (level 3) and X = 40 µm (level 2) for minimum detection time.

  • From the ANOVA analysis, X was found to be the most dominant parameter for response time with a percentage contribution of 62%.

  • The R2 values were calculated as 0.73 for the MLR model and 0.99 for the ANN model to predict the response time of this microfluidic biosensor.

  • The VAF values were calculated as 73.23% for the MLR model and 98.64% for the ANN model to predict the response time of this microfluidic biosensor.

  • Based on R2, and VAF the ANN model performed better than the MLR model in terms of prediction accuracy.

The design and optimization of an effective detection system, aiming to fight against the COVID-19 pandemics can be possible with an accurate numerical simulation which can be inexpensive and reliable in a short period of time.