Squeezed coherent states for a free particle with time-varying mass

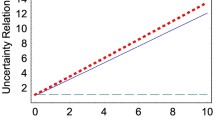
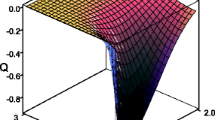
Abstract

We obtain the squeezed coherent states (SCS) for a free particle with exponentially time-varying mass. We write these states in terms of the squeeze and displacement parameters on the time-independent Fock states. Thus, we find a condition on the displacement parameter such that the SCS can be considered semiclassical states. We show that it is possible to obtain the coherent states (CS) for a free particle with minimal uncertainty as long as the mass increases with the time. We analyze the transition probability of a system initially prepared in the time-independent Fock states to the free particle SCS.

Appendices

Appendix A: Determination of $\Phi$–function

We aim to get the $\Phi$–function present in the states (18). For this, we must substitute the states $\left| \xi ,\zeta \right\rangle$ in the Schrödinger equation, and multiply it by $\left\langle \zeta ,\xi \right|$, to have the following differential equation for $\Phi$,

$$\begin{aligned} \frac{{\dot{\Phi }}}{\Phi }=\frac{1}{i\hbar }\frac{\left\langle \xi ,\zeta \left| {\hat{H}}\right| \xi ,\zeta \right\rangle }{\left\langle \xi ,\zeta |\xi ,\zeta \right\rangle }+{\dot{\xi }}\frac{\left\langle \xi ,\zeta \left| {\hat{a}}^{\dagger }\right| \xi ,\zeta \right\rangle }{\left\langle \xi ,\zeta |\xi ,\zeta \right\rangle }+\frac{1}{2}{\dot{\zeta }}\frac{\left\langle \xi ,\zeta \left| {\hat{a}}^{\dagger 2}\right| \xi ,\zeta \right\rangle }{\left\langle \xi ,\zeta |\xi ,\zeta \right\rangle }. \end{aligned}$$

(A1)

The derivative of parameters $\zeta$ and $\xi$ is found by assuming the definitions (13) and (14) together with Eqs. (11), as follows

$$\begin{aligned} {\dot{\zeta }}=\frac{d}{dt}\left( \frac{g}{f}\right) =-\frac{i\hbar }{2l^{2}m}\left( 1+\zeta \right) ^{2},\quad {\dot{\xi }}=\frac{d}{dt}\left( \frac{\varphi }{f}\right) =-\frac{i\hbar }{2l^{2}m}\left( 1+\zeta \right) \xi . \end{aligned}$$

(A2)

The mean value of the operators ${\hat{H}}\left( t\right)$, ${\hat{a}}^{\dagger }$ and ${\hat{a}}^{\dagger 2}$ can be easily obtained by considering these operators in terms of the integrals of motion (6), in the form

$$\begin{aligned} {\hat{a}}^{\dagger }&=\frac{{\hat{B}}^{\dagger }-\zeta ^{*}{\hat{B}}}{1-\left| \zeta \right| ^{2}}+\frac{\zeta ^{*}\xi -\xi ^{*}}{1-\left| \zeta \right| ^{2}},\quad {\hat{B}}\equiv \frac{1}{f}{\hat{A}},\nonumber \\ {\hat{a}}^{\dagger 2}&=\frac{{\hat{B}}^{\dagger 2}+\zeta ^{*2}{\hat{B}}^{2}-2\zeta ^{*}{\hat{B}}^{\dagger }{\hat{B}}+2\left( \zeta ^{*}\xi -\xi ^{*}\right) {\hat{B}}^{\dagger }-2\left( \zeta ^{*}\xi -\xi ^{*}\right) \zeta ^{*}{\hat{B}}}{\left( 1-\left| \zeta \right| ^{2}\right) ^{2}}+\frac{\left( \zeta ^{*}\xi -\xi ^{*}\right) ^{2}}{\left( 1-\left| \zeta \right| ^{2}\right) ^{2}}-\frac{\zeta ^{*}}{1-\left| \zeta \right| ^{2}},\nonumber \\ {\hat{H}}\left( t\right)&=\frac{\hbar ^{2}}{4l^{2}m}\frac{2\left[ 1+\left| \zeta \right| ^{2}+2{\text {Re}}\left( \zeta \right) \right] {\hat{B}}^{\dagger }{\hat{B}}-\left( 1+\zeta ^{*}\right) ^{2}{\hat{B}}^{2}-\left( 1+\zeta \right) ^{2}{\hat{B}}^{\dagger 2}}{\left( 1-\left| \zeta \right| ^{2}\right) ^{2}}\nonumber \\&\quad +\,\frac{\hbar ^{2}}{4l^{2}m}\frac{4i{\text {Im}}\left( \zeta \xi ^{*}-\xi \right) \left[ \left( 1+\zeta \right) {\hat{B}}^{\dagger }-\left( 1+\zeta ^{*}\right) {\hat{B}}\right] }{\left( 1-\left| \zeta \right| ^{2}\right) ^{2}}+\frac{\hbar ^{2}}{2l^{2}m}\frac{\left| \zeta \xi ^{*}-\xi \right| ^{2}}{\left( 1-\left| \zeta \right| ^{2}\right) ^{2}}+\frac{\hbar ^{2}}{4l^{2}m}\nonumber \\&\quad +\,\frac{\hbar ^{2}}{2l^{2}m}\frac{{\text {Re}}\left[ \left( \zeta +\left| \zeta \right| ^{2}\right) \left( 1-\left| \zeta \right| ^{2}\right) -\left( \zeta \xi ^{*}-\xi \right) ^{2}\right] }{\left( 1-\left| \zeta \right| ^{2}\right) ^{2}}. \end{aligned}$$

(A3)

Substituting the relations (A3) together with the condition (17), we can rewrite Eq. (A1) as follows

$$\begin{aligned} \frac{{\dot{\Phi }}}{\Phi }=\frac{i\hbar }{4l^{2}m}\left( \xi ^{2}-\zeta -1\right) =\frac{1}{2}\frac{d}{dt}\left( \frac{\zeta ^{*}\xi ^{2}}{1-\left| \zeta \right| ^{2}}-\frac{i\hbar }{2l^{2}}\int _{0}^{t}\frac{\zeta +1}{m}d\tau \right) . \end{aligned}$$

(A4)

Therefore, the general solution of (A1) is given by

$$\begin{aligned} \Phi =C\exp \left( \frac{1}{2}\frac{\zeta ^{*}\xi ^{2}}{1-\left| \zeta \right| ^{2}}-\frac{i\hbar }{4l^{2}}\int _{0}^{t}\frac{\zeta +1}{m}d\tau \right) , \end{aligned}$$

(A5)

where C is an arbitrary real constant that will be fixed by imposing the normalization condition on the state $\left| \xi ,\zeta \right\rangle$.

Appendix B: Normalization condition

We will determine the constant C by imposing the normalization of the states $\left| \xi ,\zeta \right\rangle$. First, consider the generating function of the Hermite polynomials, see the formula $\left( 10.13.19\right)$ in [29],

$$\begin{aligned}&\exp \left( 2yz-z^{2}\right) = {\displaystyle \sum \limits _{n=0}^{\infty }} \frac{H_{n}\left( y\right) }{n!}z^{n},\nonumber \\&z=-\sqrt{\frac{\zeta }{2}}{\hat{a}}^{\dagger },\quad y=\frac{\xi }{\sqrt{2\zeta }}. \end{aligned}$$

(B1)

Thus, we can write (18), in the form

$$\begin{aligned} \left| \xi ,\zeta \right\rangle =C\exp \left( \frac{1}{2}\frac{\zeta ^{*}\xi ^{2}}{1-\left| \zeta \right| ^{2}}-\frac{i\hbar }{4l^{2}}\int _{0}^{t}\frac{\zeta +1}{m}d\tau \right) {\displaystyle \sum \limits _{n=0}^{\infty }} \frac{\left( -1\right) ^{n}}{\sqrt{n!}}\left( \frac{\zeta }{2}\right) ^{\frac{n}{2}}H_{n}\left( \frac{\xi }{\sqrt{2\zeta }}\right) \left| n\right\rangle . \end{aligned}$$

(B2)

In what follows, let us calculate $\left\langle \zeta ,\xi |\xi ,\zeta \right\rangle$, which will be given by

$$\begin{aligned} \left\langle \zeta ,\xi |\xi ,\zeta \right\rangle =\left| C\right| ^{2}\exp \left[ \frac{{\text {Re}}\left( \zeta ^{*}\xi ^{2}\right) }{1-\left| \zeta \right| ^{2}}+\frac{\hbar }{2l^{2}}\int _{0}^{t}\frac{{\text {Im}}\left( \zeta \right) }{m}d\tau \right] {\displaystyle \sum \limits _{n=0}^{\infty }} \frac{\left| \zeta \right| ^{n}}{2^{n}n!}H_{n}\left( \frac{\xi }{\sqrt{2\zeta }}\right) H_{n}\left( \frac{\xi ^{*}}{\sqrt{2\zeta ^{*}}}\right) . \end{aligned}$$

(B3)

From the formula (10.13.22) in [29],

$$\begin{aligned}&{\displaystyle \sum \limits _{n=0}^{\infty }} H_{n}\left( x\right) H_{n}\left( y\right) \frac{z^{n}}{2^{n}n!}=\frac{1}{\sqrt{1-z^{2}}}\exp \left[ \frac{2xyz-\left( x^{2}+y^{2}\right) z^{2}}{1-z^{2}}\right] ,\nonumber \\&x=\frac{\xi }{\sqrt{2\zeta }},\quad y=\frac{\xi ^{*}}{\sqrt{2\zeta ^{*}}},\quad z=\left| \zeta \right| , \end{aligned}$$

(B4)

and imposing the normalization of the states $\left| \xi ,\zeta \right\rangle$, i.e., $\left\langle \zeta ,\xi |\xi ,\zeta \right\rangle =1$, we have C in the form

$$\begin{aligned} C=\left( 1-\left| \zeta _{0}\right| ^{2}\right) ^{1/4}\exp \left( -\frac{1}{2}\frac{\left| \xi \right| ^{2}}{1-\left| \zeta \right| ^{2}}\right) . \end{aligned}$$

(B5)

Appendix C: Completeness relation

Let us get the completeness relation for the states $\left| \xi ,\zeta \right\rangle$. As we can see from Eqs. (13) and (14), the displacement and squeeze parameters are related to each other. Thus, we will obtain the completeness relation for the SCS by sweeping the entire complex plane of the constant $\varphi =\varphi _{0}$. Therefore, we must have

$$\begin{aligned}&\int \left| \varphi ,\zeta \right\rangle \left\langle \zeta ,\varphi \right| d^{2}\varphi =1,\nonumber \\&d^{2}\varphi =\eta \left( u_{1},u_{2}\right) du_{1}du_{2},\quad u_{1}={\text {Re}}\left( \varphi \right) ,\quad u_{2}={\text {Im}}\left( \varphi \right) . \end{aligned}$$

(C1)

where $\eta \left( u_{1},u_{2}\right)$ is a weight function, which will be fixed in order to ensure the completeness relation (C1).

Consider the real functions $z_{1}$ and $z_{2}$, in the following form

$$\begin{aligned} z_{1}=\frac{\cos \left( \theta _{f}+\frac{1}{2}\theta _{\zeta }\right) u_{1}+\sin \left( \theta _{f}+\frac{1}{2}\theta _{\zeta }\right) u_{2}}{\sqrt{2\left| \zeta \right| }\left| f\right| },\quad z_{2}=\frac{\cos \left( \theta _{f}+\frac{1}{2}\theta _{\zeta }\right) u_{2}-\sin \left( \theta _{f}+\frac{1}{2}\theta _{\zeta }\right) u_{1}}{\sqrt{2\left| \zeta \right| }\left| f\right| }, \end{aligned}$$

(C2)

where we made the substitutions $\zeta =\left| \zeta \right| e^{i\theta _{\zeta }}$ and $f=\left| f\right| e^{i\theta _{f}}$. From here, we can write

$$\begin{aligned} \left( \begin{array}{c} z_{1}\\ z_{2} \end{array}\right) =Z\left( \begin{array}{c} u_{1}\\ u_{2} \end{array}\right) ,\quad Z=\frac{1}{\sqrt{2\left| \zeta \right| }\left| f\right| }\left( \begin{array}{ll} \cos \left( \theta _{f}+\frac{1}{2}\theta _{\zeta }\right) &{} \sin \left( \theta _{f}+\frac{1}{2}\theta _{\zeta }\right) \\ -\sin \left( \theta _{f}+\frac{1}{2}\theta _{\zeta }\right) &{} \cos \left( \theta _{f}+\frac{1}{2}\theta _{\zeta }\right) \end{array}\right) . \end{aligned}$$

(C3)

Thus, the element of integration $d^{2}\varphi$ in the new variables $z_{1}$ and $z_{2}$ takes the form

$$\begin{aligned} d^{2}\varphi =\eta \left( z_{1},z_{2}\right) \det \left( Z^{-1}\right) dz_{1}dz_{2}=2\left| f\right| ^{2}\left| \zeta \right| \eta \left( z_{1},z_{2}\right) dz_{1}dz_{2}. \end{aligned}$$

(C4)

Therefore, we can rewrite (C1), as follows

$$\begin{aligned}&\int \left| \varphi ,\zeta \right\rangle \left\langle \zeta ,\varphi \right| d^{2}\varphi =2\left| f\right| ^{2}\left| \zeta \right| \sqrt{1-\left| \zeta \right| ^{2}} {\displaystyle \sum \limits _{n,n^{\prime }=0}^{\infty }} \frac{\left( -1\right) ^{n+n^{\prime }}\zeta ^{\frac{n}{2}}\left( \zeta ^{*}\right) ^{\frac{n^{\prime }}{2}}}{\sqrt{2^{n+n^{\prime }}n!n^{\prime }!}}\left| n\right\rangle \left\langle n^{\prime }\right| \times \nonumber \\&\int \int \exp \left( -\frac{2\left| \zeta \right| }{1+\left| \zeta \right| }z_{1}^{2}-\frac{2\left| \zeta \right| }{1-\left| \zeta \right| }z_{2}^{2}\right) H_{n}\left( z_{1}+iz_{2}\right) H_{n^{\prime }}\left( z_{1}-iz_{2}\right) \eta \left( z_{1},z_{2}\right) dz_{1}dz_{2}. \end{aligned}$$

(C5)

Now $\left( i\right)$ making the following identification

$$\begin{aligned} a=\frac{2\left| \zeta \right| }{1+\left| \zeta \right| },\quad b=\frac{2\left| \zeta \right| }{1-\left| \zeta \right| }, \end{aligned}$$

(C6)

(ii) considering the orthogonality of the Hermite polynomials [34, 35],

$$\begin{aligned} \int \int dxdyH_{n}\left( x+iy\right) H_{n^{\prime }}\left( x-iy\right) e^{-ax^{2}-by^{2}}=\frac{\pi }{\sqrt{ab}}2^{n}n!\left( \frac{a+b}{ab}\right) ^{n}\delta _{n,n^{\prime }}, \end{aligned}$$

(C7)

and $\left( iii\right)$ choosing the weight function $\eta \left( z_{1},z_{2}\right) =\left( \pi \mu \right) ^{-1}$, we will have

$$\begin{aligned} \int \left| \varphi ,\zeta \right\rangle \left\langle \zeta ,\varphi \right| d^{2}\varphi = {\displaystyle \sum \limits _{n=0}^{\infty }} \left| n\right\rangle \left\langle n\right| =1. \end{aligned}$$

(C8)

Thus, we show that the resolution of the identity for the SCS of a free particle is satisfied in the complex plane of the constant $\varphi$.