On the expected performance of the SORGENTINA-RF fusion neutron source

Abstract

A study devoted to assessing the neutronic performance of the SORGENTINA-RF fusion neutron source is here presented. The calculation is performed considering the characteristics of the accelerated mixed deuterium/tritium ion beam from the ion source, the transport of ions into the titanium layer that constitutes the ion beam target, their implantation and the fusion reaction cross section. An investigation has been done by varying the ion composition of the beam in order to assess if and to what extent diatomic and triatomic ion species affect the neutron emission rate of the plant. This calculation is also instrumental to evaluate the cost-effectiveness of equipping the ion source with a filtering system to remove secondary ions from the beam.

1 Introduction

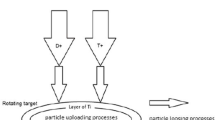
The main scope of the SORGENTINA-RF project is the production of medical radioisotopes using 14 MeV fusion neutrons, with a special focus on $^{99}$Mo as precursor of the $^{99m}$Tc. The SORGENTINA-RF plant will be an accelerator-driven facility where deuterium-tritium fusion reactions will produce the source neutrons that in turn will trigger the $^{100}$Mo(n,2n)$^{99}$Mo reaction. The reader is referred to Ref. [1] for a more detailed description of the plant. The engine of the plant will be an ion source that will operate to: i) produce positive ions of deuterium (D$^{+}$) and tritium (T$^{+}$), ii) extract and accelerate them up to a given energy and iii) transport them toward a suitable target. The latter is designed to be a rotating wheel covered with a titanium layer where ion beam will get implanted, in turn making it to fuse with the incoming ion beam particles. In a previous study [2], an investigation was carried out to assess the optimal ion beam parameters that the SORGENTINA-RF ion source must have. In particular, the use of a 300 keV mixed D$^{+}$/T$^{+}$ ion beam (in the proportion of 50:50 in terms of ion current) providing a total current of 833 mA guarantees to realize a testing plant where a quasi-industrial $^{99}$Mo production can be achieved. A 2 $\upmu$m thick layer of titanium was considered in that assessment and after some design activity it was found convenient to increase it to 3 $\upmu$m. Starting from the results obtained in the study discussed in Ref. [2], a more refined analysis is here presented and devoted to assess the neutronic performance of the ion source-target system of the SORGENTINA-RF plant with a more accurate model. The calculation is performed considering the characteristics of the accelerated D/T beam, the transport of ions into the titanium layer that constitutes the ion beam target, their implantation and the fusion cross section. Moreover, an investigation is carried out by varying the ion composition of the beam to check if and to what extent diatomic and triatomic ion species affect the emission rate of the neutron source. This allowed to assess the cost-effectiveness of a filtering system to remove secondary ions from the beam.

2 Model description

The neutron emission rate of SORGENTINA-RF was assessed in [2] as a function of the operation time of the machine with the purpose of making a comparative assessment of the achievable neutron yield in different beam configurations (e.g., as the fraction of D$^{+}$ and T$^{+}$ in the ion beam varies) according to:

$$\begin{aligned} Y_{n}(t)=\frac{I_{D}(t) }{e} \cdot \epsilon _{\mathrm{impl}}^{D}\cdot n_{T}(t) \cdot \sigma _{DT}\cdot R_{D}+\frac{I_{T}(t) }{e} \cdot \epsilon _{\mathrm{impl}}^{T}\cdot n_{D}(t) \cdot \sigma _{TD}\cdot R_{T} \end{aligned}$$

(1)

where $I_{H}(t)$ is H-component (H = D,T) of the ion beam current, e the electric charge unit, $\epsilon _{\mathrm{impl}}^{H}$ the ion implantation efficiency in Ti, $n_{H}(t)$ average density along the titanium layer, $\sigma _{\mathrm{DT}}$ and $\sigma _{\mathrm{TD}}$ are the average value of fusion cross section and $R_{H}$ the ion range in Ti. There are two aspects, in particular, which have to be modeled to provide a more realistic calculation of the expected $Y_{n}(t)$, namely: (1) the ion population of the impinging beam; (2) the density profile of deuterium and tritium implanted in the titanium layer. With this additional information, the neutron yield rate achievable in steady state can be written as:

$$\begin{aligned} Y_{n}=\sum _{j=1}^{3}\int _{0}^{R_{\max }}j\cdot \frac{I_{D}\left( \frac{E_{0}}{j}\right) \cdot f_{D}(j)}{e} \cdot n_{T}(y) \cdot \sigma _{DT}\left( \frac{E_{0}}{j},y\right) \cdot {\mathrm{d}}y + \sum _{j=1}^{3}\int _{0}^{R_{max}}j\cdot \frac{I_{T}\left( \frac{E_{0}}{j}\right) \cdot f_{T}(j)}{e}\cdot n_{D}(y)\cdot \sigma _{TD}\left( \frac{E_{0}}{j},y\right) \cdot {\mathrm{d}}y \end{aligned}$$

(2)

Ion implantation efficiency is here assumed equal to 1 as not precise measurements are available and some recent experimental evidence reported that is a realistic assumption [3]. The contributions to the total neutron emission rate are divided in two main components, i.e., deuterium and tritium beams. The sum over the j-index ($j=1,2,3$) is used to take into consideration that the ion population for both D and T is formed by monoatomic ($j=1$), diatomic ($j=2$) and triatomic ($j=3$) species, while the upper integration limit is the maximum value of the range among those relative to the different species at their given energy, as explained in the following. In fact, the diatomic and triatomic ions are supposed to split upon interaction with the Ti layer before penetrating into that as monoatomic units, in turn giving rise to two or three $H^{+}$ ions which feature one half and one third of the initial beam energy $E_{0}$, respectively. The quantities $f_{D}(j)$ and $f_{T}(j)$ are the ion fractions of the j-th group with respect to the total deuterium and tritium ions, respectively. A further assumption is that mixed diatomic and triatomic ions, e.g., DT$^{+}$ or D$_{2}$T$^{+}$ are discarded in the calculation. Also, the decrease in the number of ions in the target due to fusion reactions is neglected, since the fusion rate is several orders of magnitude lower the ion implantation rate. The cross section $\sigma _{{\mathrm{DT}}}$, that refers to a deuteron impacting on a triton according to the fusion reaction $T(D,n)^{4}$He, is taken from TENDL 2017 library [4] and shown in Fig 1. This cross section is supposed equal to that of the $D(T,n)^{4}$He reaction, i.e., $\sigma _{DT}$ = $\sigma _{TD}$. This assumption at the level of detail of the present calculation, does not introduce any significant approximation.

Fig. 1

Cross section of the fusion reaction $T(D,n)^{4}$He [4]

2.1 Ion beam composition

The ion population of the beam depends on the ion source characteristics. The majority of the ion beam is made of positive monoatomic ions $H^{+}$, but there is also a non-negligible fraction of $H_{2}^{+}$ and $H_{3}^{+}$. As a matter of fact, the plasma chamber of the ion source (where the gas get ionized) can be optimized to limit the production and extraction of the secondary species, by means of properly designed filtering systems. However, before taking into consideration ion filtering (which would make the machine more complex), it is important to estimate to what extent these secondary species might affect the neutron emission rate. In the following, some realistic beam compositions are considered, namely from the ideal case of a pure D$^{+}$ and T$^{+}$ beam to one made of 50% of single ions, 30% of diatomic ions and 20% of triatomic ions.

2.2 Ion implantation in the titanium layer

By modeling the transport of ions in the metal lattice of titanium, it is important to determine: (1) the maximum range of the ions, (2) the H$^{+}$ energy profile in the titanium layer and (3) the density profiles of deuterium and tritium implanted, namely $n_{H}(y)$. The $H^{+}$ stopping power in titanium, i.e., the energy released in titanium per unit length (as a function of energy per atomic mass unit), can be used to cover the first two points. The stopping power is extracted from the database of the SRIM code suite [5] (see Fig. 2), and it was found coherent with the stopping power and range tables for protons provided by the NIST database [6]. Given the $H_{j}^{+}$ composition of the beam at the initial energy $E_{0}=300$ keV and the equal distribution of the energy among the monatomic units after mass splitting upon interaction with the Ti surface, the energy profiles needed are at initial energy of 300 ($H^{+}$), 150 ($2H^{+}$ from $H_{2}^{+}$), 100 keV ($3H^{+}$ from $H_{3}^{+}$), as shown in Fig. 3. From the plot it is evident that the maximum range is smaller than 3 $\upmu$m. From the stopping power, the range of D$^{+}$ and T$^{+}$ units coming from all the atomic species can be calculated as follows:

$$\begin{aligned} R_{H} = \int _{0}^{E_{\mathrm{ion}}}\frac{{\mathrm{d}}E}{S_{H}(E)} \end{aligned}$$

(3)

where E is in unit of eV and S$_{H}$(E) is the stopping power for the given H ion as a function of its energy in units of eV/$\upmu$m. The upper limit R$_{max}$ in the integrals of Eq. (2) can be set as the maximum among the ones calculated above. From Eq. (3) one obtaines: $R_{D}=2.2\,\upmu$m, $R_{D_{2}}=1.3\,\upmu$m, $R_{D_{3}}= 1.0\,\upmu$m, $R_{T}= 2.4\,\upmu$m, $R_{T_{2}}= 1.5\,\upmu$m and $R_{T_{3}}= 1.2\,\upmu$m.

The energy profiles are then used to determine the local value of the fusion cross section along the titanium layer.

Fig. 2

Stopping power of H$^{+}$ in titanium from SRIM [5]. Contributions due to the interaction with electrons and nuclei of titanium are also plotted

Fig. 3

Energy profile of deuterium and tritium ions within the titanium layer

Fig. 4

Deuterium and tritium deposition profile per unit fluence of incident deuterons and tritons, respectively. Beam composition is H:H2:H3 = 70%:20%:10%. The $\sigma _{DT}(y)$ for the impinging deuterons is also plotted

To model the density profile, a number of simulations were done by means of the TRIM tool, a code from the SRIM suite [5]. TRIM calculates the interaction of energetic ions with targets and their spatial distribution along the target layer via a Monte Carlo approach. The incident ions are supposed to impinge perpendicularly to the Ti surface and 10$^{5}$ particles are simulated to have adequate statistics. As TRIM treats only mono-energetic ions, simulations are repeated for each initial ion energy of interest, i.e., 300, 150 and 100 keV. Each output is given per unit fluence (i.e., flux integrated over time) and they are then combined to make all the combinations studied, i.e., they are renormalized to the total ion fluence of deuterons and tritons, respectively. As an example, Fig. 4 shows the profile of the implanted deuterium and tritium for the case of two deuteron and tritons beams, made by 70% of single, 20% of diatomic and 10% of triatomic ions each. The distributions of H$^{+}$ (H=D, T) are multiplied by 0.7, the ones due to H$_{2}^{+}$ by 2 $\times$ 0.2 (as they made 2H$^{+}$ and the fraction of H$_{2}^{+}$ is 0.2) and the ones due to H$_{3}^{+}$ by 3 $\times$ 0.1. The three peaks of D and T are due to the three energy components, the more penetrating being of course at the highest energy. The fact that tritium is more penetrating than deuterium can be explained by considering the stopping power plot in Fig. 2. At the initial energy of 300 keV, which means 150  keV/amu for D$^{+}$ and 100 keV/amu for T$^{+}$, the stopping power is slightly higher for tritium but as the energy decreases, this is reversed and D$^{+}$ ions start losing more energy than T$^{+}$ ions. This is even more valid for the beam components at initial energy of 150 and 100 keV.

2.3 Neutron yield calculation

The deposition profiles obtained by combining the mono-energetic ion simulations, as described in the previous section, are valid per unit of deuteron and triton fluence, respectively. As the aim is the calculation of the neutron yield at steady state, i.e., the nominal working condition of the neutron source, it is important to model properly the implantation mechanism. It is reasonable to assume that the hydrogen saturation is reached first in correspondence of the peaks shown in Fig. 4 and afterward, upon further implantation, in the other regions up to the maximum ion range. This gives rise to a flat density profile of deuterium and tritium implanted at the maximum loading factor taken from ref. [7], that is 1.8 times the titanium atomic density. Three representative times of what is considered (in lack of some experimental evidence) the evolution of the density profile of deuterium and tritium in the titanium layer are chosen to show the neutron production evolution, i.e., (1) after 1 second of operation, (2) when the hydrogen saturation is reached in correspondence of the highest peaks in Figs. 3 and 4) when full hydrogen saturation is reached (flat profile at maximum hydrogen concentration in titanium). Six beam compositions, identical both for deuterons and tritons, are considered to assess how the fraction of secondary ions affect the neutron production. These are H:H$_{2}$:H$_{3}=100$:0:0; 90:8:2; 80:15:5; 70:20:10; 60:25:15; 50:30:20. For the sake of completeness, to see also the effect of the initial energy of the beam, the study done at the nominal beam energy of 300 keV, is repeated also for a 100 keV (energy components are at 100, 50, 33.3 keV) and 200 keV (energy components are at 200, 100, 66.7 keV) beams. The results are plotted in Figs. 5, 6 and 7, for the three times mentioned before, respectively. From these plots, it can be pointed out that during the transient phase (and until steady state is reached) the presence of secondary ions enhances the neutron production. In order to provide a possible explanation, the $\sigma _{DT}(y)$ cross section of the impinging deuterons is superimposed to the density profile of deuterium and tritium in the example reported in Fig. 4. It is evident that the probability to get fusion reactions for D$^{+}$ at 300 keV is maximum in the region where tritium implantation is due to T$_{2}^{+}$ and T$_{3}^{+}$. As a matter of fact, the combined effect of impinging single ions D$^{+}$ (T$^{+}$) and the deposition due to diatomic and triatomic ions, gives a strong contribution to the neutron production.

Fig. 5

Neutron yield rate after 1 second of operation for ion beam at initial energy of 100, 200, 300 keV. Beam composition for each case is written as H:H$_{2}$:H$_{3}$

Fig. 6

Neutron yield rate when density peaks reach saturation for ion beam at initial energy of 100, 200, 300 keV. Beam composition for each case is written as H:H$_{2}$:H$_{3}$

Fig. 7

Neutron yield rate in steady state (i.e., full hydrogen saturation within the titanium layer) for ion beam at initial energy of 100, 200, 300 keV. Beam composition for each case is written as H:H$_{2}$:H$_{3}$

Apparently, at steady state, the presence of secondary ions in the 300 keV beam does not affect the neutron yield production. Secondary species, on the contrary, sligthly improve the neutron production of the source. This is not true at lower beam energy. For the cases at 100 and 200 keV, reported only for the sake of completeness, the pure single ion beam achieves the best performance and the difference increases as the initial beam energy is reduced. According to these results, secondary ions seem to degrade the neutron yield in case of a beam less energetic than the one that SORGENTINA-RF has to produce and they should not represent a concern for the ion source. A composition H:H$_{2}$:H$_{3}$ = 70:20:10 both for deuterium and tritium, which should not be hardly achievable without any filtering system, seems acceptable at 300 keV. The expected neutron emission rate in that case is $1.32\times \,10^{14}$  s$^{-1}$. To conclude this section, the neutron production along the titanium layer is plotted in Fig. 8, where the contributions of deuterons and tritons due to H (H$^{+}$ at 300 keV), H$_{2}$ (H$^{+}$ at 150 keV) and H$_{3}$ (H$^{+}$ at 100 keV) are plotted in panel (a), while the total is in panel (b). Neutron yield rate profile is strongly dependent from the beam composition H:H2:H3 and in the present case the maximum neutron production occurs in the first 500 nm, where the fusion cross sections of ions coming from H$_{2}^{+}$ (i.e., H$^{+}$ at 150 keV) and H$_{3}^{+}$ (i.e., H$^{+}$ at 100 keV) have maximum values. A relevant contribution in that region comes also from H$^{+}$, which are also responsible to produce a second peak at about 1.1–1.2 $\upmu$m. In Fig. 8b, the cases of single ion beams where 90% of total D ions and 90% of total T ions are monoatomic are reported. In this case, as expected, the region where the 300 keV monoatomic ions are implanted is more effective in neutron production. It also seems that the secondary ions are not a concern for SORGENTINA-RF (for a fixed ion energy) and a filtering system can be avoided. Depending on the ion population, the neutron emission profile within the titanium layer can vary significantly.

Fig. 8

Neutron yield rate profile along the titanium layer for the nominal ion beam and with H:H$_{2}$:H$_{3}$ = 70:20:10. Contributions due D and T impinging ions for each energy group (E$_{0}$, $\frac{E_{0}}{2}$, $\frac{E_{0}}{3}$) are plotted in (a) and the total in (b). A comparison with the case H:H$_{2}$:H$_{3}$ = 90:8:2 is also reported in (b)

3 Conclusions and future works

An accurate evaluation of the neutronic performance of the SORGENTINA-RF fusion neutron source was presented in this work and the main outcomes can be summarized as follows. First, the effect of secondary ions on the neutron source yield depends on the beam energy and at 300 keV (i.e., the nominal beam energy of SORGENTINA-RF) the presence of secondary ions as in typical ion beam population does not degrade the neutron performance of the machine. At lower beam energy the presence of secondary ions can have an important negative effect on the neutron performance of the source. So, secondary ions are not a concern for SORGENTINA-RF at 300 keV and a filtering system can be avoided. Considering a beam composition H:H2:H3 = 70:20:10 both for deuterium and tritium, which should not be hardly achievable without any filtering system and full hydrogen saturation within the titanium layer, the expected neutron yield rate is 1.32 $\times$ 10$^{14}$ s$^{-1}$. The maximum neutron production in this case occurs in the first 500 nm, where the fusion cross sections of ions coming from H$_{2}^{+}$ (i.e., H$^{+}$ at 150 keV) and H$_{3}^{+}$ (i.e., H$^{+}$ at 100 keV) have maximum values. The neutron yield rate profile along the titanium layer depends on the beam composition H:H$_{2}$:H$_{3}$. The neutron performance of SORGENTINA-RF is strongly dependent from the density profile of deuterium and tritium implanted along the titanium layer and an experimental validation of the hypothesis of full saturation of the layer is part of the future work. Such experimental activity could be done at the Frascati Neutron Generator (FNG) of ENEA [8] by implanting deuterons at about 300 keV into a titanium layer and then performing measurements on the retained deuterium with proper techniques.