Neutron waveguides with finite repulsive potential in clad

Abstract

The interaction of an incoming slow neutron with a straight semi-infinite material waveguide (physically, a very lengthy one) located in vacuum (clad) in the infinite three-dimensional (3D) space is studied. The waveguide creates an attractive potential on the neutron. The physical quantum-mechanical wave phenomena are: (i) reflection and scattering of the neutron by the waveguide and (ii) its confined propagation along the latter, in specific propagation modes. The direct application of standard scattering integral equations meets several difficulties, arising mainly from the infinite length of the waveguide and (ii). New and more convenient 3D scattering integral equations are proposed and discussed, using suitable Green functions, adequate for the semi-infinite waveguide and accounting for (i) and the above difficulties. Approximate formulae for the probability amplitudes and fluxes for (i) and (ii) are given: in particular, the formulas for slow neutron confined propagation extend the ones given previously for optical waveguides. Some detailed applications and numerical computations for two-dimensional media and waveguides are presented.

1 Introduction

1.1 Neutron optics

Neutron optics is the branch of neutron physics that describes propagation and scattering of slow neutron beams in media [1,2,3,4,5,6]. Throughout this work, we shall deal only with material media having properties which do not vary with time. The neutron behaviour (i.e. reflection, refraction, confined propagation, scattering and diffraction) may be well characterized by exploiting the similarities with electromagnetic wave phenomena in classical physical optics [5]. In the general analysis below, the three-dimensional (3D) case will be analysed, while applications and numerical applications will be restricted to two-dimensional (2D) situations.

The interaction of a slow neutron (say, thermal, in this paper) at the position $\mathbf {x}$ (used here as a generically 3D vector, unless otherwise stated) with the nuclei in the medium can be described by a time-independent effective potential $V=V\left( \mathbf {x}\right)$. Accordingly, the propagation of the slow neutron is described by a stationary wave function $\psi =\psi \left( \mathbf {x}\right)$ (time-independent formulation). The latter satisfies the stationary Schrödinger wave equation:

$$\begin{aligned} \left[ \frac{-\hbar ^2}{2m}\varDelta _{\mathbf {x}}+V\left( \mathbf {x}\right) -E\right] \psi \left( \mathbf {x}\right) =0 \end{aligned}$$

(1)

where $\hbar$ is Planck’s constant, m is the neutron mass, and $\varDelta _{\mathbf {x}}$ is the 3D Laplacian. Equation (1) is an eigenvalue equation, $\psi =\psi \left( \mathbf {x}\right)$ being the eigenfunction with eigenvalue $E=\frac{2\pi ^{2}\hbar ^2}{m\lambda _{db}^2}$. E is the total energy of the neutron and $\lambda _{db}$ is its de Broglie wavelength. Equation (1) is the quantum-mechanical counterpart to scalar wave equations describing propagation of classical electromagnetic fields. In neutron optics, these analogies are exploited for characterizing the behaviour of a neutron beam.

In general, $V\left( \mathbf {x}\right)$ relates to the neutron interaction (via strong nuclear forces) with the isotopes in the media, where it propagates. Since the slow neutron wavelength (1.8 Å  for thermal neutrons) is orders of magnitude larger than the radius of the atomic nucleus in the media (in the order of fm), that interaction is usually described by using the well-known Fermi pseudopotential [1, 2, 5]:

$$\begin{aligned} V=\frac{2\pi \hbar ^2}{m}b\rho \end{aligned}$$

(2)

where $\rho$ is the density of nuclei per unit volume (of order $10^{22}$ nuclei/$cm^{3}$) and b is the (bound) scattering amplitude for a slow neutron by one nucleus. In general, b is a complex value that depends only on the isotopes present in the media and the nucleus spin. In the most general case, b takes into consideration the coherent and incoherent scattering cross sections as well as the absorption cross section by atomic nuclei (for more details see Sears [1]).

In the present case, nucleus spin is assumed to vanish and neutron absorption will be disregarded, so that b and, thus, the potential V in Eq. (2) are real. b is of the order of $10^{-13}$ cm and, so yields $V\approx 10^{-8}$ eV. Notice that $V=0$ in vacuum. Although, in principle, the potential V depends on $\mathbf {x}$, in practice it is allowed to regard the former as constant in various 3D spatial regions of interest, in which the slow neutron is propagating. In principle, different spatial regions have different values for the product $b\rho$.

The main motivation of this work is the analysis of the confined propagation of a slow neutron along a straight semiinfinite material waveguide (see Fig. 1), in specific propagation modes. Then, it will be adequate to remind here briefly various proposals and experiments. Proposals for exciting propagation modes for slow neutrons were made for thin planar films (basically, a 2D phenomenon) in 1973 [7] and for thin 3D fibres in 1984 [8] and 1986 [9]. Experiments establishing slow neutrons 3D waveguiding, using polycapillary glass fibres, were conducted in 1992 [10] and [11]. The experiments in Kumakhov and Sharov [10] and [11] were analysed in Calvo [12], in the framework of [8] and [9]. On the other hand, the theoretical prediction [7] was confirmed experimentally in 1994 [13] for slow neutrons in 2D thin titanium films. Later, further experiments were conducted with confined polarized slow neutrons in thin films: for instance, the one in 1996 [14], achieving birefringency behaviour. See also [15]. Nowadays, slow neutron 2D waveguiding stands as an active field of research: see, for instance, [16].

This interest on neutron waveguiding and its possible applications implies an interest in the precise characterization of those possible waveguides. In this case, while physical basis are well established, obtaining numerical results from them is not trivial. Waveguides are typically of the order of 1000 Å  aperture and a length of the order a few cm (see, for example [13]), while thermal neutrons have a short wavelength (1.8 Å) in comparison. For larger transverse sizes of the waveguide, one may use the geometrical optics approximation by defining a refraction index, $n^2\left( \mathbf {x}\right) =1-V\left( \mathbf {x}\right) /E$, at the cost of loosing the description of any wave-related effect. For smaller transverse sizes of the waveguide, Finite Differences Methods (FDM) may yield accurate results at low computational effort. In the actual cases, waveguides characterization requires the use of a formulation that preserves the wave-related effects, such as diffraction, reflection, evanescence, etc., but this leads to a challenging computational problem. Typical FDMs fail since the correct numerical representation of the wave requires an enormous amount of computer memory and processor time. In Molina de la Peña et al. [17], the limitations of these computational methods, with computations of a simple scheme close to 80 hours are exposed. It is indeed proved that the characterization of neutron waveguides with sizes of actual interest must be addressed from a different formulation.

Let a slow neutron propagate confined inside and along the inner part of a waveguide (core) with Fermi pseudo-potential $V_{core}$, surrounded by a medium (clad) corresponding to another Fermi pseudo-potential $V_{clad}<+\infty$. Confined (trapped) propagation occurs if $V_{core}<V_{clad}$ (the clad providing a repulsive $V_{clad}$, relative to that of the core, $V_{core}$), but there still remains a non-vanishing (exponentially decreasing) probability for the neutron to penetrate into the clad.

The interaction of an incoming slow neutron beam with a 2D straight semi-infinite waveguide, surrounded by an infinitely extended clad with an infinitely repulsive potential (forbidding completely penetration into the clad, as a zeroth approximation), has been analysed in Molina de la Peña et al. [18]. That characterization was performed by using a Green function formalism analogous to that for classical optics description and Dirichlet boundary conditions. For such a waveguide, an efficient algorithm has been developed and, based upon it, detailed numerical simulations for several thermal neutron beam diffraction cases, due to the waveguide aperture, and for propagation have been carried out and presented in [19]. The algorithm yields interesting results on reflection and confined propagation, with the subsequent extinction of the incoming wave, along the waveguide.

The extension of the results in Molina de la Peña et al. [18, 19] to the more general case including neutron penetration into the clad, in search for a more accurate description of the neutron wave, is an interesting, open and non-trivial problem. Specifically, the physical difficulties involved in it are: (i) the infinite length of the straight semi-infinite waveguide (see the comment in Sect. 1.2 ), (ii) a clad with finitely repulsive potential relative to that of the core (finite $V_{clad}-V_{core}>0$) (allowing penetration into the former), iii) explicit treatment of the propagation modes along the semi-infinite waveguide. A proper analysis of those issues constitutes the aim of the present work.

A direct study to the latter problem, based upon the standard Lippmann–Schwinger equation for quantum-mechanical scattering [20] meets the difficulties (i) and (iii). Rather, a more adequate approach to deal with (i), (ii) and (iii) must be addressed by using a suitable combination of two Lippmann-Schwinger equations (namely, the standard one and a second, less familiar but crucial, one). The latter approach appears to be new (to the best of the present authors’ knowledge). A general analysis will be developed for a 3D waveguide, while its simplification for a 2D one will be adequate later in order to carry out numerical studies.

This work is organized as follows. In Sect. 1.2, the system to be studied is characterized (i.e. a Ti waveguide with a finitely extended Si clad, located in an infinitely extended vacuum clad). In Sect. 2, the Hamiltonians, Green operators and equivalent Green functions, to be used throughout the work, are given, rather succinctly: total Hamiltonian and Green operators (Sect. 2.1), partial Hamiltonians and Green operators (Sect. 2.2), standard Green function (Sect. 2.3 ), interlude devoted to 2D scattering and bound states (Sect. 2.4) and (less familiar) complementary Green function (Sect. 2.5). In Sect. 3: (a) the standard Lippmann-Schwinger $LS_{1}$ equation (with the standard Green function) is discussed (Sect. 3.1), and the complementary and essential $LS_{2}$ one (with the complementary Green function), is studied (Sect. 3.2), and b) the overall system description by combining the previous equations $LS_{1}$ and $LS_{2}$ into new equations are given: the new $LS_{1} \rightarrow LS_{2}$ equation (Sect. 3.3) and $LS_{2} \rightarrow LS_{1}$ one (Sect. 3.4). In Sect. 4, Sect. 3.3 and Sect. 3.4 are devoted to obtaining the amplitudes for reflection (Sect. 4.1), propagation modes and scattering (Sect. 4.2), as well as the lowest order approximations for all of them. In Sect. 5, the probability fluxes for the incoming wave and for the propagation modes are given. In Sect. 6, the precedent 3D analysis is simplified to an analogous 2D waveguide: detailed numerical results are presented for a low order approximation in a Ti-Si waveguide, for propagation modes and scattering (Sects. 6.1 and 6.2) and for reflection (Sect. 6.3). Finally, Sect. 7 is devoted to summarizing results and discussions.

In Appendix A, the derivation of the complementary Lippmann-Schwinger equation in 3.2, is outlined. Appendix B is devoted to the total probability fluxes. The conservation of the total probability fluxes and the cancellation of certain divergent terms are outlined in Appendix C.

1.2 System description

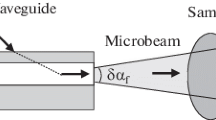
In the infinite 3D space, let $\mathbf {x}=\left( {\bar{x}},z\right)$ denote a 3D vector, ${\bar{x}}$ being a 2D one, $\bar{x}=(x,y)$. Let a straight semi-infinite waveguide, located in and surrounded by a medium (clad) with negligible Fermi pseudo-potential on neutrons (i.e. vacuum or, approximately, air), have its axis parallel to the z-axis, from $z=0$ up to $z=+\infty$. See Fig. 1.

Fig. 1

Schematic representation of a Si-Ti neutron waveguide. Both clad and core have transverse dimensions of the order of 100 $\mu$m. The finite 2D domain $\varOmega$ contains a subdomain with $V\left( \bar{x}\right) \left( =V_{core}\right) <0$ (the core, strictly speaking) and another one (finite clad) with $V\left( \bar{x}\right) (=V_{clad})>0$. Outside $\varOmega$, there is an infinitely extended clad, with $V\left( \bar{x}\right) =0$

Let one incoming slow neutron with energy E (say, thermal, but not necessarily) propagate freely from $z\rightarrow -\infty$, in the above medium with negligible Fermi potential in 3D space, and approach the waveguide. That neutron is represented by an incoming plane wave with wavevector $\left( {\bar{k}}, k_{z}\right)$ and energy E ($k_{z}>0$):

$$\begin{aligned}&\psi _{in}\left( \mathbf {x}\right) =\exp i\left( \bar{k}\bar{x}+k_{z}z\right) \end{aligned}$$

(3)

$$\begin{aligned}&E=\hbar ^{2} \frac{\bar{k}^{2}+k_{z}^{2}}{2m} \end{aligned}$$

(4)

Physically, the length of the waveguide is assumed to be much larger than the neutron de Broglie wavelength ($2\pi \hbar /\left( 2mE\right) ^{1/2}$). One approximates such a very lengthy waveguide by a semi-infinite one. While in $z<0$ and outside the waveguide in $z>0$ there is no potential acting on the neutron, in $z>0$ inside the semi-infinite waveguide the neutron will be subject to interactions with the material medium.

The waveguide is composed by appropriate materials and its interactions with the neutron are characterized for $z>0$, by assumption, by the z-independent potential $V\left( \bar{x}\right) =V\left( {\bar{x}},z\right)$. See Fig. 1. By assumption, $V\left( {\bar{x}}\right)$: (i) is real (vanishing absorption in the material) and finite , (ii) vanishes ($V\left( \bar{x}\right) =0$) for $\bar{x}$ outside some finite 2D domain $\varOmega$ (the projection of the waveguide on the ${\bar{x}}$-plane), (iii) is strictly attractive (the core, strictly speaking) with $V\left( \bar{x}\right) <0$, either in the whole $\varOmega$ or, at least, in a subdomain of it. In case that $V\left( \bar{x}\right) > 0$ in a (necessarily finite) subdomain of $\varOmega$, the generic notation $V_{clad}(>0)$ will also denote such values of $V\left( \bar{x}\right)$. The treatment here will allow for $V_{clad}(>0)$ to be either $\bar{x}$-dependent or to take on several different constant values ($>0$). Figure 1 displays the case of only one $V_{clad}(>0)$.

The physical quantum-mechanical wave phenomena to be studied here are: reflection and scattering of the incoming neutron by and its confined propagation along the waveguide (giving rise to propagation modes).

The present study could be extended readily to the case in which $V\left( \bar{x}\right)$ does not vanish outside any finite domain but, instead, tends to zero quickly as $\mid \bar{x}\mid \rightarrow +\infty$, along any direction. In the present (3D) work, there are neither infinitely repulsive potentials in an infinitely extended clad nor Dirichlet boundary conditions nor extinction of the incoming wave in the whole half-plane $z>0$ .

2 Hamiltonians and Green operators and functions

2.1 Total Hamiltonian and Green operator

Use will be made of (time-independent) Green operators in order to have compact notations and formulas, as it is customary in general studies devoted to quantum scattering. Notice that Green operators and potentials do not commute among themselves in the various equations below. This noncommutativity poses no problem whatsoever, provided that the orderings of operators, as they stand, be respected. Upon proceeding to specific analysis later, Green operators will no longer be used but, instead, their equivalent representations by means of Green functions will be employed. The total Hamiltonian operator of the slow neutron in the whole 3D space ($-\infty<z<+\infty$), and any $\mathbf {x}$ is:

$$\begin{aligned}&H=\frac{-\hbar ^{2}}{2m}\varDelta _{\mathbf {x}}+V\left( \mathbf {x}\right) \end{aligned}$$

(5)

$$\begin{aligned}&\varDelta _{\mathbf {x}}=\varDelta _{{\bar{x}}}+\frac{\partial ^{2}}{\partial z^{2}} \end{aligned}$$

(6)

$$\begin{aligned}&V\left( \mathbf {x}\right) =0, \ z<0 \end{aligned}$$

(7)

$$\begin{aligned}&V\left( \mathbf {x}\right) =V\left( {\bar{x}} \right) , \ z>0 \end{aligned}$$

(8)

$\varDelta _{\mathbf {x}}$ and $\varDelta _{{\bar{x}}}$ are the 3D and 2D Laplacians, respectively. The total Green operator determined by H (see Messiah [21], Chapter XIX) is:

$$\begin{aligned}&G \left( E\right) =\frac{1}{E+i\epsilon -H} \end{aligned}$$

(9)

with energy E (to be identified to the incoming neutron energy), $\epsilon >0$ is small and $\rightarrow 0$ at the end of a calculation. Equations (5–8) and (9) are general and independent on initial conditions (like the one in Sect. 1.2). In order to analyse properly the physical phenomena listed in Sect. 1.1, partial Hamiltonians and Green operators and functions will be defined in the following subsections. Those definitions, when the initial condition in Sect. 1.2 be included, will lead to the formulations in Sect. 3.

2.2 Partial Hamiltonians and Green operators

Consider a slow neutron propagating freely in the whole 3D space. In the absence of interaction from $z=-\infty$ to $z=+\infty$, the slow free neutron propagation is described by the partial free Hamiltonian $H_{1}$ (see Eq. 10 below) and its eigenfunctions are plane waves. The interaction with the waveguide from $z=0$ to $z\rightarrow +\infty$ leads to adding $V_{1}$ (Eq. 11) to $H_{1}$, which yields Eq. (12). Moreover, one may define the partial Green operator $G_{1}\left( E\right)$ by making use of $H_{1}$ and, so, obtain the total Green operator $G\left( E\right)$ (Eq. 9) in terms of $G_{1}\left( E\right)$. Then, the set of Eqs. (5–9), describing the slow neutron propagation from left ($z=-\infty$) to right($z=+\infty$), is also recast as follows:

$$\begin{aligned}&H_{1}=-\frac{\hbar ^{2}}{2m}\varDelta _{\mathbf {x}} \end{aligned}$$

(10)

$$\begin{aligned}&V_{1}\left( \mathbf {x}\right) = V\left( \mathbf {x}\right) \end{aligned}$$

(11)

$$\begin{aligned}&H=H_{1}+V_{1}\left( \mathbf {x}\right) \end{aligned}$$

(12)

$$\begin{aligned}&G_{1} \left( E\right) =\frac{1}{E+i\epsilon -H_{1} } \end{aligned}$$

(13)

$$\begin{aligned}&G\left( E\right) = G_{1} \left( E\right) +G_{1} \left( E\right) V_{1}G \left( E\right) \end{aligned}$$

(14)

Equation (14) is an exact relationship, which follows formally by expanding and resumming geometric series: $\frac{1}{A-B}=\frac{1}{A}+\frac{1}{A}B\frac{1}{A}+\frac{1}{A}B\frac{1}{A}B\frac{1}{A}+...=\frac{1}{A}+\frac{1}{A}B\frac{1}{A-B}$ (with $\frac{1}{A-B}=G\left( E\right)$, $\frac{1}{A}=G_{1}\left( E\right)$ and $B=V_{1}\left( \mathbf {x}\right)$ respectively). For more details, see Messiah [21], Chapter XIX.

On the other hand, one may deal with the same physical situation by formulating it in an alternative and equivalent, but less familiar, way. In this case, one introduces the partial Hamiltonian $H_{2}$ (see Eq. 15). This Hamiltonian describes an infinite waveguide (from $z=-\infty$ to $z=+\infty$) by the presence of a potential extended in the whole space, $V_{ext}\left( \mathbf {x}\right)$ that accounts for the interaction (and will match $V\left( \bar{x}\right)$). Its eigenfunctions are propagation modes and scattering states (respectively associated to $\phi _{\alpha }\left( \bar{x}\right)$ and $\phi _{{\bar{q}}}\left( \bar{x}\right)$ in the forthcoming Sect. 2.4). Then, one may recast the same total Hamiltonian in Eq. (5) for $z=-\infty$ to $z=+\infty$ as in Eq. (17). This approach leads a new partial Green operator $G_{2}\left( E\right)$ and, so, a new representation for the total Green operator $G\left( E\right)$ in terms of $G_{2}\left( E\right)$. Then, the set of Eqs. (5–9), describing the slow neutron propagation from left ($z=-\infty$) to right($z=+\infty$), is also given as:

$$\begin{aligned}&H_{2}=-\frac{\hbar ^{2}}{2m}\varDelta _{\mathbf {x}}+V_{ext}\left( \mathbf {x}\right) \end{aligned}$$

(15)

$$\begin{aligned}&V_{ext}\left( \mathbf {x}\right) = V\left( {\bar{x}}\right) , \ -\infty<z<+\infty \end{aligned}$$

(16)

$$\begin{aligned}&H=H_{2}+V_{2}\left( \mathbf {x}\right) \end{aligned}$$

(17)

$$\begin{aligned}&V_{2}\left( \mathbf {x}\right) =0, 0<z<+\infty \end{aligned}$$

(18)

$$\begin{aligned}&V_{2}\left( \mathbf {x}\right) =-V\left( \bar{x}\right) , -\infty<z<0 \end{aligned}$$

(19)

$$\begin{aligned}&G_{2} \left( E\right) =\frac{1}{E+i\epsilon -H_{2} } \end{aligned}$$

(20)

$$\begin{aligned}&G \left( E\right) = G_{2} \left( E\right) +G_{2} \left( E\right) V_{2} G \left( E\right) \end{aligned}$$

(21)

Equation (21) is another exact relationship, which follows formally by handling geometric series in similar way: $\frac{1}{A-B}=\frac{1}{A}+\frac{1}{A}B\frac{1}{A}+\frac{1}{A}B\frac{1}{A}B\frac{1}{A}+...=\frac{1}{A}+\frac{1}{A}B\frac{1}{A-B}$ (now with $\frac{1}{A-B}=G\left( E\right)$, $\frac{1}{A}= G_{2}\left( E\right)$ and $B=V_{2}\left( \mathbf {x}\right)$, respectively): [21], Chapter XIX.

Equations (10–21) are general and independent from initial conditions (like the one in Sect. 1.2). Equations (14) and (21) play a key role in our development of the Lippmann-Schwinger equations, named $LS_{1}$ and $LS_{2}$ in Sects. 3.1 and 3.2 , respectively, by using the quantum scattering theory recipe $\psi \left( \bar{x},z\right) =\lim _{\epsilon \rightarrow 0}+i\epsilon G \left( E\right) \psi _{in}$ stated in Appendix A, where $\psi \left( \bar{x},z\right)$ is the total wavefunction that solves the problem and $\psi _{in}$ is the incoming wavefunction (the neutron plane wave that impinges the waveguide from $z=-\infty$, in our case).

2.3 $G_{1} \left( E\right)$: equivalent Green function

$G_{1} \left( E\right)$ is the standard Green operator for the infinite 3D space. The standard Green function equivalent to it is [21]:

$$\begin{aligned}&G_{1}\left( \mathbf {x}-\mathbf {x}_{1}\right) =G_{1}\left( {\bar{x}}-{\bar{x_{1}}},z-z_{1}\right) = -\frac{m}{2\pi \hbar ^{2}} \frac{\exp \left( i\left( 2mE/\hbar ^{2}\right) ^{1/2}\mid {\mathbf {x}}-{\mathbf {x}_{1}\mid }\right) }{\mid \mathbf { x}-\mathbf { x}_{1}\mid }=\nonumber \\&\int \frac{d^{2}{\bar{l}}}{\left( 2\pi \right) ^{2}}\int \frac{d l_{z}}{2\pi } \frac{\exp \left[ i\left( \bar{l}\left( \bar{x}-\bar{x_{1}}\right) + l_{z}\left( z-z_{1}\right) \right) \right] }{{E+i\epsilon -\left( \hbar ^{2}/2m\right) \left( \bar{l}^{2}+l_{z}^{2}\right) }} \end{aligned}$$

(22)

One also has, by integrating over $l_{z}$ by residues:

$$\begin{aligned}&G_{1} \left( {\bar{x}}-\bar{x}_{1},z-z_{1}\right) = \nonumber \\&\int \frac{d^{2}{\bar{l}}}{\left( 2\pi \right) ^{2}}\exp \left( i{\bar{l}}\left( {\bar{x}}-\bar{x}_{1}\right) \right) \exp \left( i\left( 2m\left( E+i\epsilon \right) /\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}\mid z-z_{1}\mid \right) \frac{\left( -2mi\right) }{\left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}} \end{aligned}$$

(23)

Notice in the compact Eq. (23) the presence of the absolute value $\mid z-z_{1}\mid$. This comes from the $l_{z}$ integration by residues. In fact, in Eq. (22) consider: $\exp \left[ il_{z}\left( z-z_{1}\right) \right] =\exp \left[ i Re \left( l_{z}\right) \left( z-z_{1}\right) \right] \cdot \exp \left[ - Im\left( l_{z}\right) \left( z-z_{1}\right) \right]$, with $l_{z}=Re \left( l_{z}\right) +iIm\left( l_{z} \right)$, Re and Im denoting real and imaginary parts of $l_{z}$. $\exp \left[ -Im \left( l_{z}\right) \left( z-z_{1}\right) \right]$ is exponentially decreasing in $Im \left( l_{z}\right) >0$ for $\left( z-z_{1}\right) >0$ and, so, forces to integrate in Eq. (22) by residues in the half-plane $Im \left( l_{z}\right) >0$. And conversely, $\left( z-z_{1}\right) <0$ forces to integrate in Eq. (22) by residues in the half-plane $Im \left( l_{z}\right) <0$.

Physically, that absolute value guarantees that the Green function obeys the Sommerfeld radiation condition for the actual sign choice of $+i\epsilon$ (i.e. outgoing waves).

Notice, as well, that the representation Eq. (23) includes both propagating waves and evanescent waves depending on $\left( 2m\left( E+i\epsilon \right) /\hbar ^{2}-{\bar{l}}^{2}\right)$ being $\ge 0$ or $\le 0$, respectively.

2.4 Hamiltonian analysis: 2D scattering and bound states

Let us consider the 2D Hamiltonian $\left[ -\frac{\hbar ^{2}}{2m}\varDelta _{{\bar{x}}}+ V\left( {\bar{x}}\right) \right]$. It has the following continuum eigenfunctions $\phi _{{\bar{ q}}}\left( {\bar{x} }\right)$ with real eigenvalues $\hbar ^{2}{\bar{q}}^{2}/2m \left( \ge 0\right)$

$$\begin{aligned}&\left[ -\frac{\hbar ^{2}}{2m}\varDelta _{{\bar{x}}}+V\left( {\bar{x}}\right) \right] \phi _{{\bar{q}}}\left( {\bar{x}}\right) = \frac{\hbar ^{2}{\bar{q}}^{2}}{2m}\phi _{{\bar{q}}}\left( {\bar{x}}\right) \end{aligned}$$

(24)

${\bar{q}}$ being a real 2D wavevector, varying continuously. $\phi _{{\bar{q}}}\left( {\bar{x}}\right)$ describes 2D scattering of a neutron by the same (short-range) potential $V\left( {\bar{x}}\right)$ as in Sect. 1.2. More specifically, $\phi _{{\bar{q}}}\left( {\bar{x}}\right)$ is the total 2D wavefunction determined by the incoming 2D plane wave $\exp \left( i{\bar{k}}{\bar{x}}\right)$. Then, $\phi _{{\bar{q}}}\left( {\bar{x}}\right)$ fulfils the 2D inhomogeneous scattering integral equation [20]

$$\begin{aligned}&\phi _{{\bar{q}}}\left( {\bar{x}}\right) = \exp \left( i{\bar{q}}{\bar{x}}\right) +\int d^{2}{\bar{x}}_{1}g\left( {\bar{x} }-{\bar{x}}_{1}\right) V\left( {\bar{x}}_{1}\right) \phi _{{\bar{q}}}\left( {\bar{x}}_{1}\right) \end{aligned}$$

(25)

$$\begin{aligned}&g\left( {\bar{x}}-{\bar{x}}_{1}\right) =\int \frac{d^{2}{\bar{l}}}{\left( 2\pi \right) ^{2}} \frac{\exp \left[ i{\bar{l}}\left( {\bar{x}}-{\bar{x}}_{1}\right) \right] }{\left( \hbar ^{2}/2m\right) {\bar{q}}^{2} +i\epsilon -\left( \hbar ^{2}/2m\right) {\bar{l}}^{2}} \end{aligned}$$

(26)

$g\left( {\bar{x}}-{\bar{x}}_{1}\right)$ is the standard 2D Green function (employed, for instance, in Molina de la Peña et al. [18] and [19]). The above 2D Lippmann–Schwinger equation is the direct 2D counterpart of the standard 3D one [21], to be used in Sect. 3. The integration in Eq. (25) is extended over the whole domain ($\varOmega$) in which $V\left( {\bar{x}}_{1}\right) \ne 0$. On the other hand, since $V\left( {\bar{x}}\right)$ is attractive (at least in some subdomain of $\varOmega$), the 2D Hamiltonian also has a finite number of bound states $\phi _{\alpha }\left( {\bar{x}}\right)$ with eigenvalues $- \frac{\hbar ^{2}\chi _{\alpha }^{2}}{2m}<0$:

$$\begin{aligned}&\left[ -\frac{\hbar ^{2}}{2m}\varDelta _{{\bar{x}}}+V\left( {\bar{x}}\right) \right] \phi _{\alpha }\left( {\bar{x}}\right) =- \frac{\hbar ^{2}\chi _{\alpha }^{2}}{2m}\phi _{\alpha }\left( {\bar{x}}\right) \end{aligned}$$

(27)

where $i\chi _{\alpha }$ ( $\chi _{\alpha }$, real) could be regarded as the (pure imaginary) wavenumber associated with the bound state, $\phi _{\alpha }\left( \bar{x}\right)$. This state, $\phi _{\alpha }\left( {\bar{x}}\right)$, vanishes quickly as $\mid {\bar{x}}\mid \rightarrow +\infty$ and $\alpha$ is a set of indices, characterizing the finite number of bound states. All those states fulfil the following normalization and orthogonality relationships:

$$\begin{aligned}&\int d^{2}{\bar{x}} \phi _{{\bar{q}}}\left( {\bar{x}}\right) ^{*}\phi _{{\bar{q}}_{1}}\left( {\bar{x}}\right) =\delta ^{\left( 2\right) }\left( {\bar{q}}-{\bar{q}}_{1}\right) \end{aligned}$$

(28)

$$\begin{aligned}&\int d^{2}{\bar{x}} \phi _{\alpha }\left( {\bar{x}}\right) ^{*}\phi _{{\bar{q}}}\left( {\bar{x}}\right) =0 \end{aligned}$$

(29)

$$\begin{aligned}&\int d^{2}{\bar{x}} \phi _{\alpha }\left( {\bar{x}}\right) ^{*}\phi _{\alpha _{1}}\left( {\bar{x}}\right) =\delta _{\alpha , \alpha _{1}} \end{aligned}$$

(30)

where $*$ denotes complex conjugate. $\delta ^{\left( 2\right) }$ is the 2D Dirac delta function. $\delta _{\alpha , \alpha _{1}}$ is the Kronecker symbol $\delta _{\alpha , \alpha _{1}}$=0, 1 for $\alpha \ne \alpha _{1}$, $\alpha = \alpha _{1}$, respectively). Completeness of all those 2D wavefunctions reads:

$$\begin{aligned}&\sum _{\alpha } \phi _{\alpha }\left( {\bar{x}}\right) \phi _{\alpha }\left( {\bar{x}}_{1}\right) ^{*} +\int \frac{d^{2}{\bar{l}}}{\left( 2\pi \right) ^{2}} \phi _{{\bar{l}}}\left( {\bar{x}}\right) \phi _{{\bar{l}}}\left( {\bar{x}}_{1}\right) ^{*} =\delta ^{\left( 2\right) }\left( {\bar{x}}-{\bar{x}}_{1}\right) \end{aligned}$$

(31)

According to those possible values for $V\left( \bar{x}\right)$ (i.e. negative or zero values in the core and positive or zero values in the clad, being, in any case, $V_{clad}>V_{core}$), let there be several possible values $V_{clad}$ of such $V(\bar{x})$ ( recall Sect. 1.2) and let $V_{clad,max}$ be the maximum value among all those $V_{clad}$. Then, the following class of 2D eigenfunctions will be met: a) a finite set with $\hbar ^{2}{\bar{q}}^{2}/2m= - \frac{\hbar ^{2}\chi _{\alpha }^{2}}{2m}< 0$, b) a continuous set with $0<\hbar ^{2}{\bar{q}}^{2}/2m \le V_{clad,max}$, c) a continuous set with $0<V_{clad,max}< \hbar ^{2}{\bar{q}}^{2}/2m$ . The set b) may contain a discrete subset of wavefunctions representing resonant states of positive energy. Section 6 will deal with (a) and (b) in somewhat simpler cases with the actual 2D space replaced straightforwardly by the one-dimensional (1D) one: in such a case, compare with Figs. 3 and 4.

Combining these results with the propagation along the z-axis by multiplying those 2D wavefunctions by $\exp \left( ik_{z}z\right)$, a 3D wavefunction, $\psi \left( \mathbf {x}\right)$, is obtained. Then, the 2D set (a) will be associated to propagation modes for neutrons in the 3D waveguide. The 2D set (b) has a unique and physically appealing feature: it may contain a discrete subset determined by those resonances and corresponding to 3D quasipropagation modes (travelling trapped along the 3D waveguide along certain finite length and, then, escaping from it by tunnelling effect). The 2D set (c) will be associated to neutrons experiencing reflection or scattering by the 3D waveguide. See further discussion in Sect. 6.1.

Notice that, for an arbitrary $q^{2}$ and some fixed $E(>0)$ (not necessarily the energy of the incoming neutron) and by imposing $k_{z}^2=2mE/\hbar ^{2}-q^2$, the possible combinations would yield both propagating modes (i.e. those such that $2mE/\hbar ^{2}-q^2\ge 0$) and evanescent waves (in the case that $2mE/\hbar ^{2}-q^2\le 0$). Compare with the last comments in Sects. 2.3 and 2.5.

2.5 $G_{2}\left( E\right)$: equivalent Green function

Let the 2D Hamiltonian in Sect. 2.4 be compared to the 3D $H_{2}$ in Eq. (15). Then, the 3D Green operator $G_{2}$, associated to $H_{2}$, yields (through a residue integration, similar to that for $G_{1} \left( {\bar{x}}-{\bar{x}}_{1},z-z_{1}\right)$) the equivalent Green function:

$$\begin{aligned}&G_{2} \left( {\bar{x}}-{\bar{x}}_{1},z-z_{1}\right) = \sum _{\alpha } \phi _{\alpha }\left( {\bar{x}}\right) \phi _{\alpha }\left( {\bar{x}}_{1}\right) ^{*} \frac{\left( -2mi\right) }{\left( 2mE/\hbar ^{2}+\chi _{\alpha }^{2}\right) ^{1/2}}\times \nonumber \\&\exp \left( i\left( 2m\left( E+i\epsilon \right) /\hbar ^{2}+\chi _{\alpha }^{2}\right) ^{1/2}\mid z-z_{1}\mid\right) +\nonumber \\&\int \frac{d^{2}{\bar{l}}}{\left( 2\pi \right) ^{2}} \phi _{{\bar{l}}}\left( {\bar{x}}\right) \phi _{{\bar{l}}}\left( {\bar{x}}_{1}\right) ^{*} \exp \left( i\left( 2m\left( E+i\epsilon \right) /\hbar ^{2} -{\bar{l}}^{2}\right) ^{1/2}\mid z-z_{1}\mid\right) \times \nonumber \\&\frac{\left( -2mi\right) }{\left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}} \end{aligned}$$

(32)

which displays the propagation modes along the 3D waveguide associated to the 2D bound states $\phi _{\alpha }\left( {\bar{x}}\right)$. For $2mE/\hbar ^{2}-{\bar{l}}^{2}< 0$, one has an evanescent behaviour for $\mid z-z_{1}\mid >0$.

3 3D integral equations

Throughout this section, use will be made of the initial condition in Sect. 1.2.

In order to analyse properly the physical phenomena indicated in the introduction, we shall study successively convenient scattering integral equations: first, the ones which are necessary in Sects. 3.1 and 3.2 and, then, the ones which combine the former two and account adequately for those phenomena, in Sects. 3.3 and 3.4.

3.1 $LS_{1}$ equation

Let $\psi \left( \mathbf {x}\right) =\psi \left( {\bar{x}},z\right)$ be the total neutron wave function, determined by the incoming wave $\psi _{in}\left( \bar{ x}\right)$. $\psi \left( {\bar{x}},z\right)$ fulfils the well-known 3D inhomogeneous linear integral Eq. [20, 21] for $-\infty<z<+\infty$ (the 3D Lippmann–Schwinger equation):

$$\begin{aligned}&\psi \left( {\bar{x}},z\right) =\psi _{in}\left( {\bar{x}},z\right) +\int d^{2}{\bar{x}}_{1}\int _{0}^{+\infty }dz_{1} G_{1} \left( {\bar{x}}-{\bar{x}}_{1},z-z_{1}\right) V\left( {\bar{x}}_{1}\right) \psi \left( {\bar{x}}_{1},z_{1}\right) \end{aligned}$$

(33)

The integration in Eq. (33) is extended over the whole domain in which $V\left( {\bar{x}}_{1}\right) \ne 0$. It follows upon combining the recipe $\psi \left( \bar{x},z\right) =\lim _{\epsilon \rightarrow 0}+i\epsilon G \left( E\right) \psi _{in}$, stated in Appendix A, and Eq. (14). Notice that $V_{1}\left( \mathbf {x}_{1}\right)$ has been replaced by $V\left( {\bar{x}}_{1}\right)$, by using Eq. (11).

Equation (33) has been used in a preliminary study aimed at characterizing the incoming waves which could give rise to propagation modes along the waveguide [8]: see also [22] for an extension to absorbing optical waveguides. However, in spite of [8, 22], neither Eq. (33) nor its iterations display explicitly the possibility that the neutron could propagate confined along the waveguide.

Equation (33), to be referred to as the $LS_{1}$ equation, is a useful representation for $\psi \left( {\bar{x}},z\right)$ in $-\infty<z<0$ in terms of all values of $\psi \left( {\bar{x}},z\right)$ in $0<z<+\infty$ and any ${\bar{x}}$. On the other hand, Eq. (33), even if a correct one, is not a suitable integral equation for $\psi \left( {\bar{x}},z\right)$ in $0<z<+\infty$ as it stands, since difficulties due to the infinite length of the semi-infinite waveguide (and the independence of $V\left( {\bar{x}}_{1}\right)$ on $z_1$) arise upon iterating it. Such difficulties will be named “secular terms”. In fact, for $0<z<+\infty$ the first iteration of Eq. (33) after integrating in $0\le z_{1}<+\infty$ (leaving aside other factors and contributions) gives rise to: $\int d^{2}{\bar{l}}[\exp ik_{z}z-\exp i(2m(E+i\epsilon )/\hbar ^{2}-{\bar{l}}^{2})^{1/2}z]/[i(k_{z}-(2mE/\hbar ^{2}-{\bar{l}}^{2})^{1/2})]$. The latter integral, upon integrating in a domain with $(2m(E+i\epsilon )/\hbar ^{2}-{\bar{l}}^{2})^{1/2}$ near $k_{z}$, yields a contribution proportional to z (a “secular term”), say, an increasing behaviour with length, neatly different from the physically natural ones (oscillatory or evanescent), hindering the interpretation of probabilities. The successive iterations of Eq. (33) give rise to increasing powers of z (higher “secular terms”), in direct correspondence with the repeated integrals $\int _{0}^{+\infty }dz_{1}\int _{0}^{+\infty }dz_{2}$ and so on, generated by those iterations. Although those difficulties could be dealt with by invoking a systematic order by order procedure [23], one should explore further alternatives aimed at obtaining probabilities in a more direct and manageable way.

In spite of the above shortcomings, Eq. (33) for $0<z<+\infty$ will be essential for the improving developments in Sects. 3.3 and 3.4.

We notice that the amplitude and probability for the slow neutron to be scattered by the actual waveguide along a direction parallel to the incoming wavevector diverge. The key is the semiinfinite waveguide length, which has to be maintained in the model.

To illustrate this statement, one may study the 3D scattering amplitude for the slow neutron with incoming wavevector $\left( {\bar{k}}, k_{z}\right)$ to be scattered with outgoing wavevector $\left( {\bar{k}}_{1}, k_{z,1}\right)$ ($E=\left( {\bar{k}}_{1}^{2}+k_{z,1}^{2}\right) /2m$), which follows from Eq. (33) in a standard way [21, 23]:

$$\begin{aligned}f \left( \left( {\bar{k}}_{1}, k_{z,1}\right) , \left( {\bar{k}}, k_{z}\right) \right) &=-\left( m/2\pi \hbar ^{2}\right) \int d^{2}{\bar{x}}_{1}\int _{0}^{+\infty }dz_{1}\exp \left[ - i\left( {\bar{k}}_{1}{\bar{x}}+k_{z,1}z\right) \right] \nonumber \\ &\qquad \times V\left( {\bar{x}}_{1}\right) \psi \left( {\bar{x}}_{1},z_{1}\right) \end{aligned}$$

(34)

where $\psi$ is given by the right-hand side of Eq. (33). In the lowest (Born) approximation, $\psi \left( {\bar{x}}_{1},z_{1}\right)$ in Eq. (34) is replaced by $\psi _{in}\left( {\bar{x}}_{1},z_{1}\right)$. The resulting (Born) scattering amplitude is easily seen to diverge as $\left( {\bar{k}}_{1}, k_{z,1}\right)$ approaches $\left( {\bar{k}}, k_{z}\right)$ (forward direction), due to the infinite length of the semi-infinite waveguide ($V\left( {\bar{x}}_{1}\right)$ being independent on $z_{1}$). The total scattering cross section diverges (see the end of Appendix C).

After the improving developments in Sects. 3.3 and 3.4, the new scattering amplitude will also be seen to diverge as $\left( {\bar{k}}_{1}, k_{z,1}\right) \rightarrow \left( {\bar{k}}, k_{z}\right)$. See Appendix C.

Notice that, contrary to the above 3D $LS_{1}$ in Eq. (33), the 2D Eq. (25) can indeed be solved by successive iterations without those difficulties (as it lacks structures like $\int _{0}^{+\infty }dz_{1}$).

3.2 $LS_{2}$ equation

As in the previous case, one can derive the corresponding (although less familiar) Lippmann-Schwinger equation associated to $G_{2}\left( E\right)$ (Eq. 21) and also determined by the incoming wave $\psi _{in}\left( \bar{ x}\right)$. See Appendix A. Use will be made of Eqs. (18–19) to avoid further writing of $V_{2}$. Then, in $-\infty<z<+\infty$ the total wavefunction $\psi \left( {\bar{x}},z\right)$ (satisfying Eq. 33) also fulfils the inhomogeneous linear integral equation (to be referred to as the $LS_{2}$ equation):

$$\begin{aligned}\psi \left( {\bar{x}},z\right) &=\phi _{{\bar{k}}}\left( {\bar{x}}\right) \exp ik_{z}z \nonumber \\& \qquad +\int d^{2}{\bar{x}}_{1}\int _{-\infty }^{0} dz_{1} G_{2} \left( {\bar{x}}-{\bar{x}}_{1},z-z_{1}\right) \left[ -V\left( {\bar{x}}_{1}\right) \right] \psi \left( {\bar{x}}_{1},z_{1}\right) \end{aligned}$$

(35)

Comparing Eqs. (33) and (35), two remarks are in order: a) in comparison with (the interaction-free) $H_{1}$ and $G_{1}$ for the $LS_{1}$ Eq. (33), for the actual $LS_{2}$ Eq. (35) one deals with $H_{2}$ and $G_{2}$ (containing interactions in 2D space), b) the role of the inhomogeneous term (incoming free plane wave) $\psi _{in}\left( \mathbf {x}\right)$ for Eq. (33) is now played by $\phi _{{\bar{k}}}\left( {\bar{x}}\right) \exp ik_{z}z$ (determined in turn by $\psi _{in}\left( \mathbf {x}\right)$) in the $LS_{2}$ Eq. (35). That is, the 2D interaction has to be included, for any $-\infty<z<+\infty$, in the incoming wave, which is a free wave only along the z direction.

Equation (35) has the good feature that it displays, through $G_{2} \left( {\bar{x}}-{\bar{x}}_{1},z-z_{1}\right)$, 2D bound-state contributions which give rise to 3D propagation modes. However, the successive iterations of the $LS_{2}$ Eq. (35), for $-\infty<z<0$, suffer of similar difficulties also due to the infinite length of the semi-infinite waveguide. To understand the last statement, notice that the successive iterations of Eq. (35), for $-\infty<z<0$, give rise to the repeated integrals $\int _{-\infty } ^{0}dz_{1}\int _{-\infty }^{0}dz_{2}$ and so on (the counterparts of $\int _{0}^{+\infty }dz_{1}\int _{0}^{+\infty }dz_{2}$ and so on, for the $LS_{1}$ Eq. (33)): such repeated integrals are associated in both cases to the “secular terms”). In spite of those shortcomings, Eq. (35) for $-\infty<z<0$, combined with Eq. (33), will provide the essential basis for the developments in Sects. 3.3 and 3.4.

The pair formed by Eqs. (33) and (35) suggest the following approximation method: a) in Eq. (33) for $-\infty<z<0$, one replaces inside the integral over $0<z_{1}<+\infty$ in its right-hand side $\psi \left( {\bar{x}}_{1},z_{1}\right)$ by $\phi _{{\bar{k}}}\left( {\bar{x}}_{1},\right) \exp ik_{z}z_{1}$, b) in Eq. (35) for $0<z<+\infty$, one replaces inside the integral over $-\infty<z<0$ in its right-hand side $\psi \left( {\bar{x}}_{1},z_{1}\right)$ by $\psi _{in}\left( {\bar{x}}_{1},z_{1}\right)$. The latter approximation in b) is different from the first iteration of Eq. (33) alone. In short: a) and b) constitute an alternative and improved approximation to that based upon iterating Eqs. (33) and (35) separately and amount to reorderings and resummations of the latter iterations. A systematic and consistent procedure generalizing a) and b) and generating all successive approximations, to all orders, in this improved alternative will be treated in Sects. 3.3 and 3.4.

3.3 The $LS_{1} \rightarrow LS_{2}$ equation, for $-\infty<z<0$

The $LS_{1}$ and the $LS_{2}$ equations will now be combined into a new scattering integral equation (to be referred to as the $LS_{1} \rightarrow LS_{2}$ equation) yielding the total wave function $\psi \left( {\bar{x}},z\right)$ in $-\infty<z<0$, as follows. Upon considering Eq. (33) for $-\infty<z<0$ and replacing in its right-hand side $\psi \left( {\bar{x}}_{1},z_{1}\right)$ by the right-hand side of Eq. (35) for $0<z<+\infty$, one arrives at the $LS_{1} \rightarrow LS_{2}$ in $-\infty<z<0$ :

$$\begin{aligned}\psi \left( {\bar{x}},z\right)& =\psi _{in}\left( \mathbf { x}\right) + \int d^{2}{\bar{x}}_{1}\int _{0} ^{+\infty }dz_{1} G_{1} \left( {\bar{x}}-{\bar{x}}_{1},z-z_{1}\right) V\left( {\bar{x}}_{1}\right) \phi _{{\bar{k}}}\left( {\bar{x}}_{1}\right) \exp \left( ik_{z}z_{1}\right) \nonumber \\&\quad + \int d^{2}{\bar{x}}_{1}\int _{0}^{+\infty } dz_{1}G_{1} \left( {\bar{x}}-{\bar{x}}_{1},z-z_{1}\right) V\left( {\bar{x}}_{1}\right) \nonumber \\&\quad \times \int d^{2}{\bar{x}}_{2}\int _{-\infty }^{0} dz_{2}G_{2} \left( {\bar{x}}_{1}-{\bar{x}}_{2},z_{1}-z_{2}\right) \left[ -V\left( {\bar{x}}_{2}\right) \right] \psi \left( {\bar{x}}_{2}, z_{2}\right) \end{aligned}$$

(36)

Equation (36) amounts to a reordering and a resummation of all iterations of the $LS_{1}$ and $LS_{2}$ ones. We shall now illustrate the latter feature: the second term in the right-hand side of Eq. (36) gives directly, through Eq. (40), $T_{ref}(\mathbf{l})_{0}$ in Eq. (41), containing $\phi _{\mathbf{k}}(\mathbf{x})$ and thereby resumming into it an infinite set of contributions. Equation (36), through $G_{2}$, displays explicitly the propagation modes.

Moreover, successive iterations of Eq. (36) contain $\int _{0}^{+\infty }dz_{1}$ and $\int _{-\infty }^{0}dz_{2}$ alternatively since the term $\psi \left( {\bar{x}}_{i}, z_{i}\right) , i=1...n$ will be alternatively replaced by its representation in $LS_{1}$ (Eq. 33) or $LS_{2}$ (Eq. 35) for each iteration.

This constitutes an improvement (regarding suppression of “secular terms” ) compared to the separate $LS_{1}$ and $LS_{2}$ equations. Some peculiarities still remain which, fortunately, yield finite results. We shall now illustrate those features. The third term in the right-hand side of Eq. (36) gives:

$$\begin{aligned}&\int d^{2}{\bar{x}}_{1}\int d^{2}{\bar{x}}_{2}V\left( {\bar{x}}_{1}\right) \left[ -V\left( {\bar{x}}_{2}\right) \right] \int \frac{d^{2}{\bar{l}}}{\left( 2\pi \right) ^{2}}\exp \left( i{\bar{l}}\left( {\bar{x}}-\bar{x}_{1}\right) \right) \exp \left( -iz\left( 2m\left( E+i\epsilon \right) /\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2} \right) \frac{\left( -2mi\right) }{2\hbar ^{2}\left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}}\times \end{aligned}$$

$$\begin{aligned}&\left( \sum _{\alpha } \phi _{\alpha }\left( {\bar{x}}_{1}\right) \phi _{\alpha }\left( {\bar{x}}_{2}\right) ^{*} \frac{\left( -2mi\right) }{2\hbar ^{2}\left( 2mE/\hbar ^{2}+\chi _{\alpha }^{2}\right) ^{1/2}} \frac{i}{\left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}+\left( 2mE/\hbar ^{2}+\chi _{\alpha }^{2}\right) ^{1/2}} \right. \nonumber \\&\times \int _{-\infty }^{0}dz_{2}\exp (-iz_{2}\left( 2m\left( E+i\epsilon \right) /\hbar ^{2}+\chi _{\alpha }^{2}\right) ^{1/2}) \psi \left( {\bar{x}}_{2}, z_{2} \right) +\int \frac{d^{2}{\bar{q}}}{\left( 2\pi \right) ^{2}} \phi _{{\bar{q}}}\left( {\bar{x}}\right) \phi _{{\bar{q}}}\left( {\bar{x}}_{1}\right) ^{*} \frac{\left( -2mi\right) }{2\hbar ^{2}\left( 2mE/\hbar ^{2}-{\bar{q}}^{2}\right) ^{1/2}} \nonumber \\&\left. \times \frac{i}{\left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}+\left( 2mE/\hbar ^{2}-{\bar{q}}^{2}\right) ^{1/2}} \int _{-\infty }^{0}dz_{2}\exp (-iz_{2}\left( 2m\left( E+i\epsilon \right) /\hbar ^{2}-\bar{q}^{2}\right) ^{1/2}) \psi \left( {\bar{x}}_{2}, z_{2} \right) \right) \end{aligned}$$

(37)

where the integration over $z_{1}$ has been carried out, amounting to eliminate one “secular” term. $i\epsilon$-terms have been omitted, except where needed. The integrals $\int _{-\infty }^{0}dz_{2}$ still remain and one could wonder if they could pose still convergence difficulties. How to overcome them will be exemplified through the first iteration. In the latter, one replaces $\psi \left( {\bar{x}}_{2}, z_{3} \right)$ in the right-hand side of the expression above by $\psi _{in}\left( {\bar{x}}_{2}, z_{2} \right)$ and performs both $\int _{-\infty }^{0}dz_{2}$. After that, $\frac{i}{k_{z}-\left( 2mE/\hbar ^{2}+\chi _{\alpha }^{2}\right) ^{1/2}}$ is directly seen to be finite. On the other hand, regarding $\frac{i}{k_{z}-\left( 2m\left( E+i\epsilon \right) /\hbar ^{2}-{\bar{q}}^{2}\right) ^{1/2}}$, the smoothing provided by $\int d^{2}{\bar{q}}$ and the crucial $i\epsilon$ makes

$$\begin{aligned}&\int d^{2}{\bar{q}}\phi _{{\bar{q}}}\left( {\bar{x}}\right) \phi _{{\bar{q}}}\left( {\bar{x}}_{1}\right) ^{*} \frac{i}{k_{z}-\left( 2m\left( E+i\epsilon \right) /\hbar ^{2}-{\bar{q}}^{2}\right) ^{1/2}} \frac{\left( -2mi\right) }{2\hbar ^{2}\left( 2mE/\hbar ^{2}-{\bar{q}}^{2}\right) ^{1/2}}\times \\&\quad \times \frac{i}{\left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}+\left( 2mE/\hbar ^{2}-{\bar{q}}^{2}\right) ^{1/2}} \end{aligned}$$

to be finite. And so on for higher order iterates.

3.4 The $LS_{2} \rightarrow LS_{1}$ equation, for $0<z<+\infty$

Next, the $LS_{1}$ and $LS_{2}$ equations will be combined into a new scattering integral equation (to be referred to as the $LS_{2} \rightarrow LS_{1}$ equation) giving the total wave function $\psi \left( {\bar{x}},z\right)$ in $0<z<+\infty$, as follows. Upon considering Eq. (35) for $0<z<+\infty$ and replacing in its right-hand side $\psi \left( {\bar{x}}_{1},z_{1}\right)$ by the right-hand side of Eq. (33) for $-\infty<z<0$, one gets the $LS_{2} \rightarrow LS_{1}$ equation in $0<z<+\infty$:

$$\begin{aligned}\psi \left( {\bar{x}},z\right) &=\phi _{{\bar{k}}}\left( {\bar{x}}\right) \exp \left( ik_{z}z\right) + \int d^{2}{\bar{x}}_{1}\int _{-\infty }^{0} dz_{1} G_{2} \left( {\bar{x}}-{\bar{x}}_{1},z-z_{1}\right) \left[ -V\left( {\bar{x}}_{1}\right) \right] \psi _{in}\left( {\bar{x}}_{1},z_{1}\right) + \nonumber \\& \qquad \int d^{2}{\bar{x}}_{1}\int _{-\infty }^{0} dz_{1} G_{2} \left( {\bar{x}}-{\bar{x}}_{1},z-z_{1}\right) \left[ -V\left( {\bar{x}}_{1}\right) \right] \times \nonumber \\&\qquad \int d^{2}{\bar{x}}_{2}\int _{0}^{+\infty } dz_{2} G_{1} \left( {\bar{x}}_{1}-{\bar{x}}_{2},z_{1}-z_{2}\right) V\left( {\bar{x}}_{2}\right) \psi \left( {\bar{x}}_{2},z_{2}\right) \end{aligned}$$

(38)

As in Sect. 3.3, the above equation also displays explicitly the propagation modes (through $G_{2}$ and its successive iterations contain $\int _{-\infty }^{0}dz_{1}$ and $\int _{0}^{+\infty }dz_{2}$ alternatively. So, Eq. (38) is more suitable for describing the wavefunction behaviour for $z>0$ (i.e. the waveguide).

4 Neutron wavefunction behaviour for different regions

4.1 Region $z<0$: reflection scattering amplitudes

For $z<0$, by using Eq. (23) for $G_{1}\left( {\bar{x}}-{\bar{x}}_{1},z-z_{1}\right)$, the $LS_{1} \rightarrow LS_{2}$ Eq. (36) yields:

$$\begin{aligned}&\psi \left( {\bar{x}},z\right) =\psi _{in}\left( {\bar{x}},z\right) + \int \frac{d^{2}{\bar{l}}}{\left( 2\pi \right) ^{2}}\exp i{\bar{l}}{\bar{x}}\nonumber \\&\times \exp \left[ -i\left( 2m\left( E+i\epsilon \right) /\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2} z\right] T_{ref}\left( {\bar{l}}\right) \end{aligned}$$

(39)

where $T_{ref}\left( {\bar{l}}\right)$ is interpreted as the reflection amplitude of the slow neutron by the waveguide.

The integral is convergent (due to $\int d^{2}{\bar{l}}$), so that $\psi \left( {\bar{x}},z\right)$ is indeed finite. The $+i\epsilon$ in the exponential in Eq. (39) warrants the correct (vanishing) behaviour of the evanescent contributions as $z\rightarrow -\infty$ (the corresponding comment will apply for Eq. (41) as $z\rightarrow +\infty$).

For $2mE/\hbar ^{2}-{\bar{l}}^{2}\ge 0$, one has oscillatory behaviour in $z<0$. For $2mE/\hbar ^{2}-{\bar{l}}^{2}< 0$, one has an evanescent behaviour in $z<0$. Equation (33) also yields Eq. (39) for $z<0$. It is far more convenient to express $T_{ref}\left( {\bar{l}}\right)$ in terms of $\psi$, by using Eqs. (36) and (23). When Eq. (36) in $-\infty<z<0$ is iterated successively, one generates an infinite series for $\psi$ into powers of V and the 2D eigenfunctions $\phi _{\mathbf{l}}$ ’s and $\phi _{\alpha }$ ’s (the latter two also depending on V). This series gives rise, as indicated above, to an infinite series for $T_{ref}\left( {\bar{l}}\right)$. All terms in such a series are finite if $E>0$, $k_{z}>0$, $\mathbf{k}^{2}>0$, $2mE/\hbar ^{2}-\mathbf{l}^{2}\ne 0$. The lowest approximation reads:

$$\begin{aligned}&T_{ref}(\mathbf{l})_{0}=\frac{(-im)}{\hbar ^{2}(2mE/\hbar ^{2}-\mathbf{l}^{2})^{1/2}} \frac{i}{k_{z}+(2mE/\hbar ^{2}-\mathbf{l}^{2})^{1/2}}\times \nonumber \\&\int d^{2}{} \mathbf{x} \phi _{\mathbf{k}}(\mathbf{x})\exp (-i\mathbf{l}{} \mathbf{x})V(\mathbf{x}) \end{aligned}$$

(40)

which is, indeed, finite and will be used in (2D) numerical simulations performed in Sect. 6.3.

4.2 Region $z>0$: propagation modes and scattering amplitudes

For $z>0$, by using Eq. (32) for $G_{2}\left( {\bar{x}}-{\bar{x}}_{1},z-z_{1}\right)$, the $LS_{2} \rightarrow LS_{1}$ Eq. (38) yields:

$$\begin{aligned}&\psi \left( {\bar{x}},z\right) =\phi _{{\bar{k}}}\left( {\bar{x}}\right) \exp \left(ik_{z}z\right) + \sum _{\alpha } \phi _{\alpha }\left( {\bar{x}}\right) \exp \left[ i\left( 2m\left( E+i\epsilon \right) /\hbar ^{2}+\chi _{\alpha }^{2}\right) ^{1/2}z\right] T_{pm,\alpha } \nonumber \\&+ \int \frac{d^{2}{\bar{l}}}{\left( 2\pi \right) ^{2}}.\phi _{{\bar{l}}}\left( {\bar{x}}\right) \exp \left[+i \left( 2m\left( E+i\epsilon \right) /\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2} z\right] T_{scat}\left( {\bar{l}}\right) \end{aligned}$$

(41)

$T_{pm,\alpha }$ is the amplitude for the slow neutron to propagate confined along the waveguide in the $\alpha$-th propagation mode. For $2mE/\hbar ^{2}-{\bar{l}}^{2}\ge 0$, one has oscillatory behaviour in $z>0$ and $T_{scat} \left( {\bar{l}}\right)$ is the amplitude for the slow neutron to be scattered by the waveguide. For $2mE/\hbar ^{2}-{\bar{l}}^{2}< 0$, one has evanescent behaviour in $z>0$. Equation (35) also yields Eq. (41) for $z>0$. Let $2mE/\hbar ^{2}-{\bar{l}}^{2}\ne 0$, $E>0$, $k_{z}>0$ ${\bar{k}}^{2}>0$. It is more adequate to express $T_{pm,\alpha }$ and $T_{scat}\left( {\bar{l}}\right)$ in terms of $\psi$, by using Eq. (38). When Eq. (38) in $0<z<+\infty$ is iterated successively, one generates an infinite series for $\psi$ into powers of V and the 2D eigenfunctions $\phi _{\mathbf{l}}$’s and $\phi _{\alpha }$’s . This series gives rise, as indicated above, to two separate infinite series for $T_{pm,\alpha }$ and $T_{scat}\left( {\bar{l}}\right)$. All terms in such a series for $T_{pm,\alpha }$ are finite. The lowest order approximation reads:

$$\begin{aligned}T_{pm,\alpha _{0}}&=\frac{\left( -2im\right) }{\left( 2mE/\hbar ^{2}+\chi _{\alpha }^{2}\right) ^{1/2}} .\frac{i}{\left( 2mE/\hbar ^{2}+\chi _{\alpha }^{2}\right) ^{1/2}-\left( 2mE/\hbar ^{2}-{\bar{k}}^{2}\right) ^{1/2}}\times \nonumber \\& \qquad \int d^{2}{\bar{x}} \phi _{\alpha }\left( {\bar{x}}\right) ^{*}\exp \left( i{\bar{k}}{\bar{x}}\right) \left( -V\left( {\bar{x}}\right) \right) \end{aligned}$$

(42)

By including the second iteration of Eq. (38), integrating over $z_{1}$ (thereby eliminating one “secular” term) and, then, integrating over $z_{1}$, one finds: $T_{pm,\alpha }\simeq T_{pm,\alpha _{0}}+T_{pm,\alpha _{1}}$, with:

$$\begin{aligned}&T_{pm,\alpha _{1}}=\frac{\left( -2im\right) }{2\hbar ^{2}\left( 2mE/\hbar ^{2}+\chi _{\alpha }^{2}\right) ^{1/2}}\int d^{2}{\bar{x}}_{1} \phi _{\alpha }\left( {\bar{x}}_{1} \right) ^{*} (-V\left( {\bar{x}}_{1} \right) ) \int d^{2}{\bar{x}}_{2} \phi _{\alpha }\left( {\bar{x}}_{2} \right) ^{*}\left( -V\left( {\bar{x}}_{2} \right) \right) \int \frac{d^{2}{\bar{l}}}{\left( 2\pi \right) ^{2}} \exp \left( i{\bar{l}}{\bar{x}}_{1}\right) \times \nonumber \\&\frac{\left( -2im\right) }{2\hbar ^{2}\left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}} \exp \left( i({\bar{k}}-{\bar{l}}){\bar{x}}_{2} \right) .\frac{i}{\left( 2mE/\hbar ^{2}+\chi _{\alpha }^{2}\right) ^{1/2}+\left( 2mE/\hbar ^{2}-{\bar{k}}^{2}\right) ^{1/2}}\frac{i}{k_{z} +\left( 2m\left( E+i\epsilon \right) /\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}} \end{aligned}$$

(43)

which is finite. For a semiquantitative estimate, we approximate ${\bar{l}}\simeq {\bar{k}}$ inside both integrals over ${\bar{x}}_{1}$ and ${\bar{x}}_{2}$ in $T_{pm,\alpha _{1}}$, majorize and perform the integration over ${\bar{l}}$. Then, the ratio $\mid T_{pm,\alpha _{1}}/T_{pm,\alpha _{0}}\mid$ is of order:

$$\begin{aligned}&\left(\left( 2mE/\hbar ^{2}+\chi _{\alpha }^{2}\right) ^{1/2}-\left( 2mE/\hbar ^{2}-{\bar{k}}^{2}\right) ^{1/2}\right) \left(m/2\pi \hbar ^{2}\right) \int d^{2}{\bar{x}}_{1} \mid V\left( {\bar{x}}_{1} \right) \mid \times \nonumber \\&\frac{1}{k_{z}}\left(\frac{1}{2\pi }\frac{\left( 2mE/\hbar ^{2} \right) ^{1/2}}{k_{z}+\left( 2mE/\hbar ^{2} \right) ^{1/2}}+\frac{1}{2}\right) \end{aligned}$$

(44)

which is dimensionless and smaller than unity for adequate $\int d^{2}{\bar{x}}_{1} \mid V\left( {\bar{x}}_{1} \right) \mid$.

In the case of $T_{scat}\left( {\bar{l}}\right)$, it is adequate to decompose it as:

$$\begin{aligned}&T_{scat}\left( {\bar{l}}\right) =T_{scat,1}\left( {\bar{l}}\right) +T_{scat,2}\left( {\bar{l}}\right) \end{aligned}$$

(45)

$$\begin{aligned}&T_{scat,1}\left( {\bar{l}}\right) = \frac{\left( -2im\right) }{\left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}} \frac{\left( -i\right) }{k_{z}-\left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}}\times \nonumber \\&\quad \int d^{2}{\bar{x}} \phi _{{\bar{l}}}\left( {\bar{x}}\right) ^{*}\exp \left( i{\bar{k}}{\bar{x}}\right) \left[ -V\left( {\bar{x}}\right) \right] \end{aligned}$$

(46)

$T_{scat,1}\left( {\bar{l}}\right)$ is the contribution due to the first term on the right-hand side of Eq. (38) in $0<z<+\infty$). $T_{scat,2}\left( {\bar{l}}\right)$ is the infinite series formed by all contributions to $T_{scat}\left( {\bar{l}}\right)$ except the lowest one, given in $T_{scat,1}\left( {\bar{l}}\right)$. That is, $T_{scat,2}\left( {\bar{l}}\right)$ arises from all higher iterations (except the first one) of Eq. (38) in $0<z<+\infty$. As Eq. (46) shows, due to the denominator $\left[ k_{z}-\left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}\right] ^{-1}$, $T_{scat,1}\left( {\bar{l}}\right)$ diverges as ${\bar{l}}\rightarrow {\bar{k}}$ (say, in the forward direction). $T_{scat,2}\left( {\bar{l}}\right)$ is finite for $2mE/\hbar ^{2}-{\bar{l}}^{2}\ne 0$, $E>0$, $k_{z}>0$, ${\bar{k}}^{2}>0$, as so are all terms in the infinite series contribution to it. In Eq. (41), the integration over $d^{2}{\bar{l}}$ overcomes the divergence of $T_{scat,1}\left( {\bar{l}}\right)$ as $2mE/\hbar ^{2}-{\bar{l}}^{2}\rightarrow 0$ and gives rise to a convergent integral (compare with the discussion in Appendix C).The contribution of $T_{scat,2}\left( \bar{l}\right)$ to Eq. (41) is also finite. Then, $\psi \left( {\bar{x}},z\right)$ in $z>0$ is indeed finite.

Summarizing, the $LS_{1}-LS_{2}$ and $LS_{2} \rightarrow LS_{1}$ equations enable to get rid of all difficulties in the successive iterations involved in obtaining $T_{ref}$, $T_{pm,\alpha }$ and $T_{scat,2}$, which are always finite for $E\ne 0$, $k_{z}\ne 0$ and ${\bar{k}}^{2}\ne 0$, at least. However, there is still just one contribution which is divergent in the special case ${\bar{l}}\rightarrow {\bar{k}}$ (forward direction), namely, $T_{scat,1}\left( {\bar{l}}\right)$. Then, due to $T_{scat,1}\left( {\bar{l}}\right)$, it follows that $T_{scat}\left( {\bar{l}}\right)$ also diverges as ${\bar{l}}\rightarrow {\bar{k}}$. In order to display explicitly the possible confined propagation, the Green operator $G_{2}\left( E\right)$ and the $LS_{2}$ equation have been employed. The divergence for the forward direction remains (as it is inherent to the infinite length of the semi-infinite waveguide), but the approach in Sects. 3.3 and 3.4 has enabled to isolate it compactly in $T_{scat,1}\left( {\bar{l}}\right)$. The contribution of the divergence of $T_{scat,1}$ in the forward direction to the total probability flux will be shown to cancel in Appendix C.

5 Probability fluxes

The probability current of the wavefunction $\psi \left( {\bar{x}},z\right)$ along the z-axis, at ${\bar{x}}$ is (Re and Im denoting real and imaginary parts, respectively):

$$\begin{aligned}&\frac{\hbar }{m}Re\left[ -i\psi \left( {\bar{x}},z\right) ^{*}\frac{\partial }{\partial z}\psi \left( {\bar{x}},z\right) \right] \end{aligned}$$

(47)

The probability flux of $\psi \left( {\bar{x}},z\right)$ across an infinite plane orthogonal to the z-axis at the position z is:

$$\begin{aligned}&Flux\left( z\right) =\int d^{2}{\bar{x}}\frac{\hbar }{m}Re\left[ -i\psi \left( {\bar{x}},z\right) ^{*}\frac{\partial }{\partial z}\psi \left( {\bar{x}},z\right) \right] \end{aligned}$$

(48)

For the incoming plane wave, upon replacing $\psi \left( {\bar{x}},z\right)$ by $\psi _{in}\left( \mathbf {x}\right)$:

$$\begin{aligned}&Flux_{in}\left( z\right) =\int d^{2}{\bar{x}}\frac{\hbar k_{z}}{m} \end{aligned}$$

(49)

which diverges due to the infinite extension of the ${\bar{x}}$ plane. The probability flux for the neutron to propagate confined as the $\alpha$-th propagation mode, normalized to the incoming flux per unit area, is:

$$\begin{aligned}&\frac{1}{\hbar k_{z}/m} \frac{\hbar }{m} \left( 2mE/\hbar ^{2}+\chi _{\alpha }^{2}\right) ^{1/2} \mid T_{pm,\alpha }\mid ^{2} \end{aligned}$$

(50)

By replacing $T_{pm,\alpha }$ by $T_{pm,\alpha _{0}}$ (Eq. 40), one gets the following approximate normalized probability flux for the neutron to propagate confined as the $\alpha$-th propagation mode

$$\begin{aligned}&\frac{1}{\hbar k_{z}/m} \frac{\hbar }{m} \left( 2mE/\hbar ^{2}+\chi _{\alpha }^{2}\right) ^{1/2} \mid T_{pm,\alpha _{0}}\mid ^{2} \end{aligned}$$

(51)

This is a first-order (Born) approximation. As discussed in Sect. 4.2, the error derived from this approximation is bounded since the ratio $\mid T_{pm,\alpha _{1}}/T_{pm,\alpha _{0}}\mid$ is smaller than unity for adequate $\int d^{2}{\bar{x}}_{1} \mid V\left( {\bar{x}}_{1} \right) \mid$. Equation (51) is a counterpart of a related approximation given in Snyder and Love [24] for an optical waveguide. In Molina de la Peña et al. [17], the probability for an incoming slow neutron to propagate confined along a semi-infinite waveguide has been studied briefly, without infinitely repulsive clads, in 2D space. No detailed theoretical justification was provided for the approximate formula employed in Molina de la Peña et al. [17]: such a formula turns out to be similar to Eq. (51).

6 Approximations and numerical results

This section will deal with numerical simulations for the scattering amplitudes including reflection ones ($T_{scat}\left( {\bar{l}}\right)$ and $T_{ref}\left( \bar{l}\right)$), for different impinging neutron angles. So far to this point, equations in the general 3D case have been developed: nevertheless, in order to obtain results, a 2D waveguide (i.e. thin film) disregarding the y coordinate will be considered. Those results obtained thus far for 3D are ready to be directly exported to the 2D case. In short, the 3D developments in Sects. 1.2, 2 and 3–5 will keep their validity for 2D, provided that previous generic symbols $\left( {\bar{u}}\right)$ (meaning thus far either 2D wavevectors or spatial coordinate), be understood in this section as one-dimensional (1D) ones, (u).

Thus, $\mathbf {x}$ will now correspond to a 2D vector $\left( x,z\right)$ (to avoid confusion with $\bar{x}=\left( x,y\right)$ in the 3D case). Correspondingly, typical wavefunctions for 2D are $\psi (\mathbf {x})=\phi \left( x\right) \exp ik_{z}z$ and superpositions thereof.

While, in previous equations, we displayed explicitly the dependences of the neutron wavefunctions in the z coordinate, if a simulation is to be performed, one must obtain first the corresponding behaviours in the transverse 1D coordinate (say, $\phi \left( x\right)$). They correspond to the 1D counterparts of the eigenfunctions $\phi _{{\bar{ q}}}\left( {\bar{x} }\right)$, $\phi _{\alpha }\left( {\bar{x} }\right)$ studied in Sect.2.4. In the cases represented in Fig. 2a and b, it is considered that, for $z>0$, $V_{core}$ is constant and negative (Titanium in this model), while $V_{clad}$ is constant and positive (Silica, in this model). The main difference between Fig. 2a and b is the presence in the latter of a substrate that we assume to be infinitely repulsive, $V_{substrate}=+\infty$. Both waveguides are assumed to be surrounded by an infinitely extended vacuum.

In both cases, for obtaining $\phi \left( x\right)$, these regions must be modelled as potential wells. Standard quantum-mechanical continuity conditions for $\phi \left( x\right)$ and $d\phi \left( x\right) /dx$ at the points where V has finite discontinuities (and so on for $\phi \left( x\right)$ at points with infinite discontinuities) will be imposed.

6.1 Propagation modes

Let us assume an incoming neutron beam represented by a plane wave of arbitrary angle of incidence; $\psi _{in}(\mathbf {x})=\psi _{in}\left( x,z\right) =e^{ik_{x}x}e^{ik_{z}z}=e^{i\mathbf {k_{in}x}}$ with associated 2D wavevector $\mathbf {k_{in}}=(k_{x},k_{z})$. For a thermal neutron: $E=0.025$ eV, $\mid \mathbf {k_{in}}\mid =\sqrt{k_{x}^{2}+k_{z}^{2}}=3.47$ Å$^{-1}$.

Two cases of layer arrangements (clad and core) will be simulated, as displayed in Fig. 2a (Si–Ti–Si symmetrical waveguide) and Fig. 2b (Si–Ti waveguide located over a highly repulsive substrate that will be understood as not allowing neutrons to penetrate inside) both of them in a relatively large domain surrounded by vacuum $V=0$. The first layers arrangement, Si–Ti–Si waveguide (Fig. 2a), matches with the waveguide proposals in previous works (see Molina de la Peña et al. [17, 18] and [5], Chapter 3) and is a natural extension of the analysis in Snyder and Love [24]. The second one, Si–Ti-substrate waveguide (Fig. 2b), is closer to experiments on neutron waveguiding (see, for example, [13] and [16]). There is a significant difference between our simulation and possible experiments; in the experiments, researchers exposed part of the Ti core and made the neutron beam impinge over the top part of the device. This is called lateral coupling (instead of front coupling). It is used for a better control of the angle of incidence and improves the waveguide efficiency. In the current study the thermal neutron beam impinges on the waveguide entrance, with front illumination, directly to the Ti core, as shown in Fig. 2a and b. We made this choice for convenience. Both cases, even if similar (as infinitely extended plane waves will continue to be employed) imply a different arrangement of layers (waveguide clad and core as well as symmetries) and, consequently, the arising propagation modes will be different ones.

Fig. 2

Layer arrangement for the simulated waveguides. Notice that in (a) the origin of coordinates is located at the core centre while in (b) is located in the Ti-substrate interlayer

The eigenfunctions that solve Eqs. (24) or (27) relate, in this case, with the angle of incidence of the neutron beam. As stated in Sect. 2.4, when examining the energy eigenvalues for these eigenfunctions, one finds three possibilities:

• Negative energies. These eigenfunctions constitute a discrete set and correspond (provided that the z-dependence be included) to confined propagation modes. They have the 2D structure: $\psi (\mathbf {x})= \phi _{\alpha }\left( x\right) e^{iz\left( 2m\left( E+i\epsilon \right) /\hbar ^{2}+\chi _{\alpha }^{2}\right) ^{1/2}}$. Since these modes cannot give rise to free propagation in vacuum, they propagate along the waveguide without losses (as no absorption is assumed in the material).

• Positive energy lower than $V_{clad,max}$. Their structure is: $\psi (\mathbf {x})=\phi _{\mathbf {q}}(x) e^{iq_{z}z}$. These eigenfunctions constitute a continuous set. In this energy region there may be a discrete subset of eigenfunctions that correspond to resonant levels and behave as quasidiscrete propagation modes. These states are different from those mentioned above, as they describe travelling neutrons trapped in the waveguide along some propagation distance, escaping from it (via tunnelling effect) and, finally, propagating in free space. Consequently, these excited modes amount to effective losses in the waveguide (even if there is no absorption in the material, since V is real).

• Positive energy higher than $V_{clad,max}$. These eigenfunctions are continuous and not trapped in the waveguide, so they will be disregarded here.

6.1.1 Structure of the energy levels

Introducing Si and Ti as suitable materials (clad and core, respectively) for neutron waveguiding, their experimental data to be applied in Eq. (2) for obtaining potential values, are in Table 1.

Table 1 Data and potential values for Ti and Si (see [2, 3])

Using the values in Table 1, the 1D transverse section of the 2D waveguide is characterized, as will the possible propagation modes and continuum wavefunctions that will arise. These functions are the eigenfunctions fulfilling Eqs. (24) and (27) and can be solved assuming the potential $V\left( x\right)$ as a combination of potential barriers and wells.

The standard procedure is to represent the various $\phi \left( x\right)$ as linear combinations of arbitrary amplitudes times suitable plane waves or real exponentials (linear in x), formulate the continuity equations for $\phi \left( x\right)$ and $d\phi \left( x\right) /dx$ at the points where V is discontinuous, and solve the resulting system of equations for the amplitudes (see for example [25]).

Let us consider Fig. 2a, Si–Ti–Si waveguide impinged by a thermal neutron beam with an arbitrary $\theta$ angle (directly to the Ti core). In this case, the potential is set to be a potential well 1000 Å  wide in the centre, corresponding to the Ti core negative potential, surrounded by two 2000 Å  potential barriers corresponding to the Si clad (see Fig. 3).

Consequently, the set of eigenfunctions $\phi \left( x \right)$ that solves this configuration is:

$$\begin{aligned} \phi _{\alpha }^{even}\left( x\right) = \left\{ \begin{array}{lcc} D cos(sx) &{} if &{} \vert x \vert \le a \\ \\ B e^{-rx}+C e^{+rx} &{} if &{} a \le \vert x \vert \le b \\ \\ A e^{-q\mid x \mid } &{} if &{} \vert x \vert \ge b \end{array} \right.&\phi _{\alpha }^{odd}\left( x\right) = \left\{ \begin{array}{lcc} D sin(sx) &{} if &{} \vert x \vert \le a \\ \\ B e^{-rx}+C e^{+rx} &{} if &{} a \le \vert x \vert \le b \\ \\ A e^{-q\mid x\mid } &{} if &{} \vert x \vert \ge b \end{array} \right. \nonumber \\ \phi _{\mathbf {q}}^{even}\left( x\right) = \left\{ \begin{array}{lcc} D cos(sx) &{} if &{} \vert x \vert \le a \\ \\ B e^{-rx}+C e^{+rx} &{} if &{} a \le \vert x \vert \le b \\ \\ A e^{-iqx} &{} if &{} \vert x \vert \ge b \end{array} \right.&\phi _{\mathbf {q}}^{odd}\left( x\right) = \left\{ \begin{array}{lcc} D sin(sx) &{} if &{} \vert x \vert \le a \\ \\ B e^{-rx}+C e^{+rx} &{} if &{} a \le \vert x \vert \le b \\ \\ A e^{-iqx} &{} if &{} \vert x \vert \ge b \end{array} \right. \end{aligned}$$

(52)

where $r=\root 2 \of {\mid q^2-4\pi b_{Si}\rho _{Si}\mid }$ and $s=\root 2 \of {\mid q^2-4\pi b_{Ti} \rho _{Ti}\mid }$ are the wave numbers in the Si clad and Ti core, respectively, and $a=500$ Å  and $b=2500$ Å. The superscripts even and odd refer to the symmetry properties (under $x\rightarrow -x$) of the wavefunctions in the core. A, B, C and D are arbitrary complex amplitudes. One finds those energy values that make the determinant of the homogeneous set of linear equations in A, B, C and D (arising from the continuity equations) vanish. Notice that, as the incoming wave has not been included so far in those wavefunctions, one is dealing with a homogeneous set of equations. The inclusion of the incoming wave in the wavefunctions and its consequences will be considered later in Sect. 6.1.2. The energy corresponding to each solution relates with the incoming neutron beam angle; $q=k_{x}=\mid \mathbf {k_{in}}\mid sin\theta$.

In this case, the above analysis yields three energy levels, represented in Fig. 3. Two of them are discrete bound-state levels, $\varSigma _{0}$, $\varSigma _{1}$, ($E_{\varSigma _{0}}<0$, $E_{\varSigma _{1}}<0$, so there is no wave propagation in free space). The third one corresponds to an unbound-state level, $\varSigma _{2}$. This level is not, in a strict sense, a discrete level since it has positive energy, but it could be regarded as a quasidiscrete solution of the system of equations. It will be interpreted in Sect. 6.1.2 as a resonance in the continuum of eigenfunctions and physically it will yield some sort of unstable propagation mode with neutron losses across the clad via tunnel effect. Finally, in those cases with energies higher that the clad potential, $V_{Si}=5.4\times 10^{-8}$ eV, there is a continuum of wavefunctions for any energy with different wavenumber depending on the region (free space, clad or core).

Fig. 3

Energy levels for a Si–Ti–Si waveguide. Ti core = 1000 Å  and Si clads = 2000 Å 

For the case of Fig. 2b, Si–Ti-substrate waveguide, when a thermal neutron beam impinges the Ti core with an arbitrary angle, $\theta$, multiple propagation modes rise. In this case, the scheme is rather closely related to (but does not coincide with) the proposal in [7] and the setup in [13]: a potential well 1000 Å  wide, corresponding to the negative potential of the Ti core, over a substrate of Si (assumed to be an infinite potential barrier, or infinitely repulsive clad, with vanishing wavefunctions at $x=0$, for convenience)¹. This potential well is covered with a 1500 Å  Si layer that acts as a potential barrier (finite $V_{clad,max}$) (see Fig. 4). In this case, the wavefunction cannot support symmetries under $x\rightarrow -x$ and it vanishes at $x=0$, due to the infinite potential barrier: then, only a sine function may describe the eigenfunction in the Ti core:

$$\begin{aligned} \phi _{\alpha }\left( x\right) = \left\{ \begin{array}{lcc} D sin(sx) &{} if &{} x \ge -a \\ \\ B e^{-rx}+C e^{+rx} &{} if &{} -b\le x \le -a \\ \\ A e^{-q\mid x\mid } &{} if &{} x\le -b \\ 0 &{} if &{} x\ge 0 \end{array} \right. \nonumber \\ \phi _{\mathbf {q}}\left( x\right) = \left\{ \begin{array}{lcc} D sin(sx) &{} if &{} x \ge -a \\ \\ B e^{-rx}+C e^{+rx} &{} if &{} -b\le x \le -a \\ \\ A e^{-iqx} &{} if &{} x\le -b \\ 0 &{} if &{} x\ge 0 \end{array} \right. \end{aligned}$$

(53)

Again, $r=\root 2 \of {\mid q^2-4\pi b_{Si}\rho _{Si}\mid }$ and $s=\root 2 \of {\mid q^2-4\pi b_{Ti} \rho _{Ti}\mid }$are the wave numbers in the Si clad and Ti core, respectively, and $a=500$ Å  and $b=2500$ Å. A, B, C and D are arbitrary complex amplitudes.

Fig. 4

Energy levels for a Si–Ti-substrate waveguide. Ti core = 1000 Å  and Si clad = 1500 Å

In this case, there are two discrete energy levels, represented in Fig. 4. Similarly to the previous case, $\varUpsilon _{0}$ represents a bound state level (giving rise to a propagation mode) and $\varUpsilon _{1}$ represents a resonant positive energy level (lossy propagation mode).

Notice that eigenfunctions corresponding to $\varSigma _{2}$ and $\varUpsilon _{1}$ cannot be normalized since the planewave functions extend to infinity. In any case, in order to compare the rising of propagation modes for different neutron beam impinging angles, one changes conveniently the normalization used to $N=\int _{-b}^{+b}\phi \left( \bar{x}\right) ^{*}\phi \left( \bar{x}\right) d\bar{x}$. So, physically, one normalizes the total probability of the wavefunction excited inside the waveguide (including clad and core) to unity.

6.1.2 Resonant states

As previously said, the eigenfunctions corresponding to energy levels $\varSigma _{2}$ and $\varUpsilon _{1}$ have positive values of energy. Consequently, they are not discrete states, as it happens with the eigenfunctions with negative energies. In fact, there is a continuous set of eigenfunctions (among them, either $\varSigma _{2}$ or $\varUpsilon _{1}$) for the corresponding Hamiltonian.

These eigenfunctions were described in Landau and Lifshitz [26] as resonances in quasidiscrete levels of energy. Since a slow neutron is susceptible to escape via tunnelling effect across the potential barrier (finitely extended clad), they do not belong to any discrete spectrum of energies. The neutron will eventually escape from the waveguide to vacuum (the infinitely extended clad). The main difference between $\varSigma _{2}$ or $\varUpsilon _{1}$ and any other negative energy eigenfunction (2D bound states, counterparts of those in Eq. 27) is that the former have a small probability of escaping from the waveguide.

For obtaining the continuous spectrum of solutions, instead of finding the Hamiltonian eigenfunctions, one must excite the system from the outside. It implies adding an inhomogeneous term (incoming wave, $A_{in}exp\left( ik_{x}x\right)$) to Eqs. 52 and 53, so as to obtain an inhomogeneous linear system of equations for the amplitudes, that will always have a solution for any value of $k_{x}$ (i.e. angle of incidence). By representing the ratio $\mid D/A_{in}\mid ^{2}$ versus energy, a peak appears, that matches with the resonant quasidiscrete eigenfunction obtained by finding a vanishing value for the determinant of the homogeneous system of equations (Sect. 6.1.1). It corresponds to those quasidiscrete propagation modes which escape from the waveguide by tunnelling effect. Notice that, in the case of negative energies, an inhomogeneous term $A_{in}exp\left( ik_{x}x\right)$ cannot be imposed since it would give rise to a divergent exponential.

This way of obtaining resonant states is quite interesting since it matches with the experimental result in papers [13] and [14]. In these experiments the excitation of the waveguide (neutron counts) is obtained for different incident beam angles. In these cases there is a resonant peak curve for a certain angle, a Lorentzian-shaped curve, that is interpreted as an excited propagation mode.

There is another interest in these Lorentzian-shaped curves, since their width at half height, $\varDelta _{1/2}E$ yields a measure of the particle (or neutron beam) half life in this quasistable state and, thus, a good estimation of the propagation distance of this lossy mode.

For the case of Si–Ti–Si waveguide, the simulations yield the results showed in Fig. 5. It can be seen that the maximum peak occurs at an energy of $E=4.6\times 10^{-8} eV$ (that for an incoming thermal neutron beam of energy 0.025 eV, corresponds to an impinging angle of $\theta =0.077243^{\circ }$) that totally matches with the values obtained for $\varSigma _{2}$, and a width at half height, $\varDelta _{1/2}E=8.65\times 10^{-12} eV$. Moreover, it is clear that this curve has a Lorentzian shape, as expected.

Fig. 5

Resonant level for Si-Ti-Si waveguide at $\theta =0.077^{\circ }$. Ti core = 1000 Å  and Si clads = 2000 Å

For the case of Si–Ti-substrate waveguide, the simulations are shown in Fig. 6. The maximum peak occurs at an energy of $E=1.005\times 10^{-8} eV$ (that corresponds to an impinging angle of $\theta =0.0360397^{\circ }$). It matches with the value obtained for $\varUpsilon _{1}$. Its width at half height is $\varDelta _{1/2}E=2.83\times 10^{-14} eV$. In this case, as expected, the curve has a Lorentzian shape too. Comparing those results with those in Feng et al. [13], they are found in good accordance (the maximum peak occurring at $\theta =0.098^{\circ }$ in the experiment). One should take into account that the incoming neutron beam had, in those experiments, a wavelength of 2.35 Å  and that the potential barrier simulated here is not exactly the same as in Feng et al. [13]. The scheme here is kept for internal comparison between the cases of Si–Ti–Si and Si–Ti-substrate waveguides.

Fig. 6

Resonant level for Si–Ti-substrate waveguide at $\theta =0.036^{\circ }$ . Ti core = 1000 Å  and Si clad = 1500 Å

Comparing results for the resonant states from Figs. 5 and 6, it is clear that the higher the energy of the state, the wider the associated Lorentzian curve and consequently the higher probability for escaping the waveguide (lower travelling distance) as it is expected. Indeed, there will be neutron losses via tunnelling effect and the results may be used to perform a rough estimation of the neutron travelling distance, $d_{\varSigma ,\varUpsilon }$ along the waveguide in a quasi-discrete propagation mode (resonant state). In fact, the fundamental time-energy uncertainty relationship $\varDelta E \varDelta t \approx \hbar$ combined with the width, $\varDelta _{1/2}E$ of each resonant peak (calculated for $\varSigma _{2}$, and $\varUpsilon _{1}$) may quantify the neutron beam propagation length in this mode. A thermal neutron with $\lambda _{db}=1.8$ Å has a velocity, $v=d_{\varSigma ,\varUpsilon } / \varDelta t \simeq 2.2$ km/s and, thus, it yields a propagation distance of $d_{\varSigma _{2}} \simeq 0.17$ m (for Si–Ti–Si waveguide) and $d_{\varUpsilon _{1}} \simeq 51.15$ m (for Si–Ti-substrate waveguide).

Notice that, unless similar, there is not total correspondence between the models simulated and those in Chen et al. [11] (i.e. absorption is not taken into account in our model). In an experiment, the impinging beam angle cannot be fixed a priori since it strongly depends on the illumination conditions. The source’s shape, in our model with ideal inclinated plane waves, is critical. Moreover, lateral illumination would change the peak structure, that may not be symmetric. Notice as well that the maximum peak would remain and our results are consistent with those experiments.

For last, in the experimental setup in Chen et al. [11], neutron counts are measured for the detector being in a different angle. The opposite setup may be possible (i.e. measuring counts for different impinging angles). As the peak in Figs. 5 and 6 represents an acceptance window, it implies that angles are close, but not equal to the resonance peak would excite (though less efficiently) the propagation mode. Consequently, the wider the peak the wider the phase range accepted by the waveguide.

6.2 Propagation mode amplitudes: $T_{pm,\alpha }$ and scattering amplitude ($T_{scat,1}$)

In Molina de la Peña et al. [17] a first approximation to the study of these systems was conducted. In that paper, the excitation of propagation modes for a Si-Ti-Si waveguide (with clad extending to infinity) as a function of the neutron beam angle of incidence was studied. That was made by using an approximation recipe given in Snyder and Love [24]. This recipe (omitted here for brevity) led to represent the solutions for $\int _{-\infty }^{\infty }\exp \left( ik_{in,x}x\right) ^{*}\phi _{\varSigma _{i}}\left( x\right) dx$ $i=0,1,2$.

Recalling the formulation developed in the previous Sect. 4.2, notice that the main difference of Eq. (42) with the equations used in Snyder and Love [24] and Molina de la Peña et al. [17] is the presence here of the denominators; $\left( \left( 2mE/\hbar ^{2}+\chi _{\alpha }^{2}\right) ^{1/2}\right) ^{-1}$ and $(\left( 2mE/\hbar ^{2}+\chi _{\alpha }^{2}\right) ^{1/2}$ $-\left( 2mE/\hbar ^{2}-{\bar{k}}^{2}\right) ^{1/2})^{-1}$ that will lead to interesting conclusions.

$\mid T_{pm,\alpha _{0}}\mid ^{2}$ (i.e. proportional to the probability for the excitation of the $\alpha _{0}$ -th propagation mode) versus the angle of incidence, for the case of a Si-Ti-Si waveguide, is represented in Fig. 7 for states $\varSigma _{0}$ and $\varSigma _{1}$. Notice that, since $\varSigma _{2}$ corresponds to a positive energy, the correct representation in this case is $\mid T_{scat,1}\mid ^{2}$, upon comparing Eqs. 42 and 46. The ordinate value is normalized for comparison, with the value for $\varSigma _{0}$, $\mid T_{pm,\varSigma _{0}}\mid ^{2}(0^{\circ })=1$. This figure is the counterpart of Fig. 10 in [17] and, since the former comes from a more realistic formulation here, expands its conclusions.

Fig. 7

$T_{pm,\alpha _{0}}$ and $T_{scat,1}$ for the Si–Ti–Si waveguide case. Ti core = 1000 Å  and Si clads = 2000 Å. The divergence of $T_{scat,1}$ in the forward direction is displayed

The underlying structure is $sinc\left( k_{in,x}+\chi _{\alpha }\right) +sinc\left( k_{in,x}-\chi _{\alpha }\right)$ for even modes (i.e. $T_{pm,\varSigma _{0}}$ and $T_{scat,1}$) and $sinc\left( k_{in,x}+\chi _{alpha}\right) -sinc\left( k_{in,x}-\chi _{alpha}\right)$ for odd modes (i.e. $T_{pm,\varSigma _{1}}$) and it is close with our results in Molina de la Peña et al. [17]. One of the most evident characteristics is that $\mid T_{scat,1}\mid ^{2}$ diverges for a certain angle. This has already been discussed in Sect. 4.2: it comes from the infinite length of the semi-infinite waveguide and it is inherent to this formulation used.

The other main characteristic is the high values related to $\mid T_{pm,\varSigma _{1}}\mid ^{2}$ in comparison with $\mid T_{pm,\varSigma _{0}}\mid ^{2}$ and is a different result from [17]. This is due to the factor $\left( \left( 2mE/\hbar ^{2}+\chi _{\alpha }^{2}\right) ^{1/2}-\left( 2mE/\hbar ^{2}-{\bar{k}}^{2}\right) ^{1/2}\right) ^{-1}$, since $\chi _{0}^{2}>\chi _{1}^{2}$ (because $\varSigma _{0}$ is a level lower than $\varSigma _{1}$). The physical implication of this result is that, since the closest to 0 is the energy of a bounded level, the more it may be excited, then. For a bounded (i.e. with no losses) mode, one can look for negative energy states as close to zero as possible so that they will be efficiently excited. This may be controlled via switching adequate values for clad and core transverse sections and could imply an improvement in the waveguide efficiency.

For the case of Si-Ti-substrate waveguide, similar results are obtained. The simulations for $\mid T_{pm,\alpha _{0}}\mid ^{2}$ versus angle of incidence are represented in Fig. 8 for $\varUpsilon _{0}$. Notice that, in this case, the result is represented in logarithmic scale. The corresponding $\mid T_{scat,1}\mid ^{2}$ (related to $\varUpsilon _{1}$) is also displayed. The main difference is that the sample substrate (assumed as an infinitely repulsive potential) breaks the $x\rightarrow -x$ symmetry (which holds for Fig. 7). In De Wames and Sinha [7] and Feng et al. [13] it is stated that only the positive energy propagation mode may arise, since neutrons must penetrate in the clad barrier via tunnelling effect, making the levels with negative energies not accessible. From the results in the present work, it is clear that both $\varUpsilon _{0}$ and $\varUpsilon _{1}$ are excited in the waveguide for any impinging angle, but with a low efficiency. Only in the case of an impinging angle that matches with $\varUpsilon _{1}$ the difference becomes significant by various magnitude orders. This is in good agreement with the results of the experiment, where only at a certain angle a peak is clearly visible.

Fig. 8

$T_{pm,\alpha _{0}}$ and $T_{scat,1}$ for Si–Ti-substrate waveguide. Ti core = 1000 Å  and Si clad= 1500 Å  over a substrate assumed to be infinitely repulsive. Notice that this case is represented in logarithmic scale for enhancing the structure. The divergence of $T_{scat,1}$ in the forward direction is displayed

Comparing the results for both cases, it is not clear which method would be preferable from the perspective of improving the waveguide efficiency (for wave packets). On one hand, lateral incidence (as in Feng et al. [13]) exposes a wider surface to the neutron beam, allowing more neutrons to be collected. Since impinging angles used here are extremely low, it implies a wider exposed surface: $\frac{W}{tan\left( \theta _{in}\right) }$ where W is the neutron beam width and $\theta _{in}$ is the neutron beam impinging angle. On the other hand, frontal incidence, simulated here, allows to excite more easily highly efficient propagation modes, at the cost of only exposing the waveguide entrance (100 $\mu$m in our case) to the thermal neutron beam. Probably a combination of both would yield the best results: lateral incidence at the entrance and frontal escaping at the end of the waveguide as, for example, in Kozhevnikov et al. [16].

6.3 Reflection amplitudes: $T_{ref}\left( \bar{l}\right)$

It is also interesting to focus attention on the reflection amplitudes, for the sake of completeness of the previous formulation (focused on propagation modes). Equation (40) in Sect. 4.1 allows to quantify the reflection amplitudes for each spatial frequency ($\bar{l}$) as a function of the impinging neutron beam angle (related to $\bar{k}$, in this case $k_{x}=k_{in}sin\left( \theta \right)$).

For the case of Si-Ti-Si waveguide, results are displayed in Fig. 9. These figures employ the same logarithmic representation of $\mid T_{ref}\left( l\right) \mid ^{2}$. Figure 9a and b is the same figure one being a waterfall mesh type and the other one being a contour plot, while Fig. 9c and d shows the scan line for a fixed value of the spatial frequency (at $\mid l\mid =2.05\times 10^{-3}$ Å$^{-1}$) (white dashed line at Fig. 9b) and the scan line for the resonance peak value, at $\theta =0.0772^{\circ }$ (white dotted line at Fig. 9b). Figure 9a, d and c clearly shows a strong peak at a certain incoming beam angle for any spatial frequency value, l. This peak corresponds to the resonant or quasibounded state, $\varSigma _{2}$ level and results in a decrease on the reflected value of the neutron beam (as expected). Upon examining Fig. 9b and d, a structure of peaks and valleys appears both in l and $k_{x}$ (impinging angle). This behaviour comes from the term $\int dx \phi _{k_{x}}\left( x\right) \exp \left( -ilx\right)$ (the scalar product of a wavefunction associated to the incoming beam times a possible plane wave reflected one).

Fig. 9

Reflection amplitudes for different neutron beam impinging angles, $\theta$, and reflecting angles ($\mid l\mid$) for a Si–Ti–Si waveguide. Notice that figures are represented in logarithmic scale

For the case of Si–Ti-substrate waveguide, a similar structure to the previous one is displayed in Fig. 10. In this case, the main structure shown is the resonance peak corresponding to $\varUpsilon _{1}$. In this case, Fig. 10d appears to be smoother than that of Fig. 9d. This is interpreted as that the waveguide presents a resonance in which it accepts all the spatial frequency values of the spectral decomposition. This behaviour difference is due to the presence of the infinite potential substrate.

Fig. 10

Reflection amplitudes for different neutron beam impinging angles, $\theta$, and $\mid l\mid$ for Si–Ti-substrate waveguide. Notice that both figures are represented in logarithmic scale

7 Conclusions and comments

This work focuses on the interaction of an incoming slow neutron with a straight semi-infinite material waveguide in the infinite three-dimensional (3D) space. Computational applications for two-dimensional (2D) waveguides also play a quite important role here.

The waveguide creates an attractive potential on the neutron. In the 3D case, there are neither infinitely extended clads with infinitely repulsive potentials nor Dirichlet boundary conditions nor extinction of the incoming wave. Two new 3D scattering integral equations ($LS_{1}\rightarrow LS_{2}$ and $LS_{2} \rightarrow LS_{1}$) are proposed and discussed for the two half-spaces using suitable Green functions, adequate for the semi-infinite waveguide. Those integral equations yield: 1) the reflection scattered amplitude ($T_{ref}\left( {\bar{l}}\right)$ ), 2) the amplitudes for the neutron to propagate confined along the waveguide in the $\alpha$-th propagation mode ($T_{pm,\alpha }$ ), 3) the scattering amplitude of the neutron by the waveguide ($T_{scat}$).

We focus on the propagation modes: an approximate formula for $T_{pm,\alpha }$ in 3D is given and studied in specific 2D cases.

The lowest 3D contribution $T_{scat,1}$ to $T_{scat}$ diverges as the direction of the scattered neutron tends to be parallel to the direction of the incoming one due to the infinite length of the semiinfinite waveguide.

The detailed computational studies for two-dimensional (2D) waveguides in Sect. 6 yield results: for one-dimensional (1D) bound and resonant states (Figs. 3, 4, 5 and 6), all of which lead to the generation of propagation modes along the 2D waveguides, for $T_{pm,\alpha }$ and $T_{scat,1}$ (Figs.7 and 8) and for $T_{ref}$ (Figs.9a and b and 10a and b. Figures 7 and 8 display the divergence of $T_{scat,1}$ in the forward direction ($\theta _{in}=\pm 0.077^{\circ }$ for $\varSigma _{2}$ and $\theta _{in}=0.0363^{\circ }$ for $\varUpsilon _{1}$, respectively).

This formulation focused on the rising of propagation modes in the waveguide, consequently, all terms in the Hamiltonian related to neutron losses (like nuclear absorption) beyond quantum-mechanical (tunnelling) effects were disregarded. Some terms quantifying for absorbing media could be easily added by considering a complex potential. In this case, the imaginary part of the potential would turn the propagating waves obtained here into damped waves. In any case, this formulation accounts for neutron beam losses in the waveguide via tunnelling effect in certain quasidiscrete propagation modes with positive transverse energy: this would provide an upper bound for the mode decay versus distance as in Sect. 6.1.2.

On the other hand, it is interesting to notice that, assuming no absorption in the waveguide material, those propagation modes associated with a strict negative energy state may travel indefinitely through the waveguide. As commented in the case of Fig. 7, some negative-energy propagation modes may be very efficiently raised in some waveguides. By inspecting Eq. (42), it is clear that the main condition for that is that they have a value for $\chi _{\alpha }$ as low as possible (i.e. the level should be as close to zero energy as possible). This propagation mode would rise efficiently for certain angles while, at the same time, propagate indefinitely. This may be accomplished by designing a waveguide with an appropriate transverse section (which is easier than finding an adequate isotope), making the corresponding bounded level as close as possible to zero. Resonances (like $\varSigma _{2}$ and $\varUpsilon _{1}$) and their widths enable to estimate the associated neutron propagation lengths along the waveguide. On the other hand, these widths represent an acceptance window (phase range accepted by the waveguide). Consequently, for those impinging angles close, but not equal, to the resonance peak would excite, (though less efficiently) the propagation mode. See Sect. 6.1.2.

The present formulation allows to quantify the generation of propagation modes. For an incoming neutron beam with certain angle of incidence a mixture of states (including the negative-energy levels) could arise. The propagation modes do not raise independently, but rather as a mixture of modes. Consequently, a monomodel behaviour it is not expected for any angle of incidence. This could give rise to some qualified controversy in comparison with [7], that stated that negative-energy levels were not accessible since there was no angle of incidence that would allow neutrons to penetrate the potential barrier.

For completeness, certain theoretical aspects are studied in Appendices B and C, namely, the total 3D probability fluxes of the total wave function along z-axis and their conservation. Those fluxes contain separately divergent contributions (arising from the infinite 2D area orthogonal to the z-axis). In Appendix C, conservation of the total probability flux along the z-axis yields directly the cancellation of the divergences associated to the area. After that, there remains in principle an additional divergence in the 3D equation expressing total probability flux conservation, due to the divergent $T_{scat,1}$. It turns out that such a total probability flux conservation equation has a 3D structure which resembles the 2D optical theorem (Eq. 62). Based upon such an analogy, the divergent contributions of $T_{scat,1}$ turn out to cancel out yielding a finite equation expressing 3D total probability flux conservation. At the end, conservation of total probability flux appears to yield a convergent generalization for the 3D semi-infinite waveguide of the standard optical theorem in 3D quantum scattering [21, 23].

The analysis and applications of open waveguides (namely, those which do not extend from $-\infty$ to $+\infty$ but start at some domain at finite distance) constitutes a subject of permanent interest in several physical and technological branches: see, for instance, [27,28,29,30]. One purpose of the present work is to contribute to that analysis.

Appendices

Appendix

A: Derivation of the $LS_{2}$ equation

Quantum scattering theory [23, 31, 32] provides a useful recipe justifying the 3D $LS_{2}$ equation. The recipe is based upon the formula: $\psi \left( \bar{x},z\right) =\lim _{\epsilon ^{+}\rightarrow 0}(+i\epsilon ) G \left( E\right) \psi _{in}$ ($\epsilon ^{+}$ meaning that $\epsilon >0$). As a consistency check, the application of the recipe provides the standard $LS_{1}$ equation [20, 21]. In fact, for that purpose, one replaces $G \left( E\right)$ by the right-hand side of Eq. (14) (in terms of $G_{1}\left( E\right)$). The limit of $+i\epsilon G_{1} \left( E\right) \psi _{in}$ gives the wavefunction $\psi _{in}\left( {\bar{x}},z\right)$. The second term in the right-hand side of Eq. (14) gives directly the one in Eq. (33). An entirely similar application of the 2D version of the recipe justifies directly the 2D scattering integral Eq.  (25), and this fact will be employed for the following justification of the $LS_{2}$ equation. One replaces, in the above recipe, $G \left( E\right)$ by the right-hand side of Eq. (21) (in terms of $G_{2}\left( E\right)$). Notice that, in terms of the 2D Hamiltonian in Sect. 2.4, $G_{2} \left( E\right) =\frac{1}{E+i\epsilon -\left[ -\frac{\hbar ^{2}}{2m}\varDelta _{{\bar{x}}}+ V\left( {\bar{x}}\right) \right] +\frac{\hbar ^{2}}{2m}\frac{\partial ^{2}}{\partial z^{2}}}$. Then, recalling Sect. 2.4, the above 2D version of the recipe directly implies for 3D that $\lim _{\epsilon ^{+}\rightarrow 0}(+i\epsilon ) G _{2} \left( E\right) \psi _{in} = \phi _{{\bar{k}}}\left( {\bar{x}}\right) \exp ik_{z}z$ (since only $\frac{\partial ^{2}}{\partial z^{2}}$ acts upon $\exp ik_{z}z$). The second term in the right-hand side of Eq. (21) gives directly the one in Eq. (35), which establishes the $LS_{2}$ equation. Notice that the application of the above recipe, just for scattering, is not affected by the bound states.

B: Probability fluxes for total wave function

For $z<0$ with $z\rightarrow -\infty$, Eqs. (39) and (48) yield the total flux for the total wave function $\psi \left( {\bar{x}},z\right)$:

$$\begin{aligned}&Flux\left( z, z<0\right) =\int d^{2}{\bar{x}}\frac{\hbar k_{z}}{m} \nonumber \\&\quad -\frac{\hbar }{m}\int _{ \left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}\ge 0}\frac{d^{2}{\bar{l}}}{\left( 2\pi \right) ^{2}} \left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2} \mid T_{ref}\left( {\bar{l}}\right) \mid ^{2} \end{aligned}$$

(54)

For $z>0$ with $z\rightarrow +\infty$, Eqs. (41) and (48) yield the total flux:

$$\begin{aligned}&Flux\left( z, z>0\right) =\int d^{2}{\bar{x}}\frac{\hbar k_{z}}{m}+\frac{\hbar }{m} \sum _{\alpha } \left( 2mE/\hbar ^{2}+\chi _{\alpha }^{2}\right) ^{1/2} \mid T_{pm,\alpha }\mid ^{2} \nonumber \\&\quad +\frac{\hbar }{m}\int _{ \left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}\ge 0}\frac{d^{2}{\bar{l}}}{\left( 2\pi \right) ^{2}}\left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2} \mid T_{scat}\left( {\bar{l}}\right) \mid ^{2}\nonumber \\&\quad + \frac{\hbar k_{z}}{m}Re\left[ T_{scat}\left( {\bar{k}}\right) +T_{scat}\left( {\bar{k}}\right) ^{*}\right] \end{aligned}$$

(55)

Notice that evanescent waves do not contribute to either $Flux\left( z, z<0\right)$ or $Flux\left( z, z>0\right)$. Both $Flux\left( z, z<0\right)$ and $Flux\left( z, z>0\right)$ contain divergent contributions. Their cancellations will be established in Appendix C.

C: Conservation of the total probability flux

Conservation of the total probability flux reads:

$$\begin{aligned}&Flux\left( \bar{x}, z<0\right) =Flux\left( \bar{x}, z>0\right) \end{aligned}$$

(56)

By using Eqs. (54), (55) and (56) and cancelling out the divergent $\int d^{2}{\bar{x}}\frac{\hbar k_{z}}{m}$ (incoming flux), Eq. (56) becomes:

$$\begin{aligned}&\frac{\hbar }{m} \int _{ \left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}\ge 0} \frac{d^{2}{\bar{l}}}{\left( 2\pi \right) ^{2}} \left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2} \mid T_{ref}\left( {\bar{l}}\right) \mid ^{2}+ \nonumber \\&\quad +\frac{\hbar }{m} \sum _{\alpha } \left( 2mE/\hbar ^{2}+\chi _{\alpha }^{2}\right) ^{1/2} \mid T_{pm,\alpha }\mid ^{2}+ F_{scat, fin}=0 \end{aligned}$$

(57)

$$\begin{aligned}&F_{scat, fin}=\frac{\hbar }{m} \int _{ \left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}\ge 0}\frac{d^{2}{\bar{l}}}{\left( 2\pi \right) ^{2}}\left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}\times \nonumber \\&\quad \mid T_{scat,1}\left( {\bar{l}}\right) +T_{scat,2}\left( {\bar{l}}\right) \mid ^{2} + \frac{\hbar k_{z}}{m}Re\left[ T_{scat}\left( {\bar{l}}={\bar{k}}\right) + T_{scat}\left( {\bar{l}}={\bar{k}}\right) ^{*}\right] \end{aligned}$$

(58)

In Eq. (57), the first two contributions in the left-hand side are finite. Then, the third contribution in the left-hand side, namely $F_{scat, fin}$, has to be also finite. A direct analysis of $F_{scat, fin}$ will be outlined, aimed at verifying explicitly that the various divergent terms contained in it cancel out so that, after the cancellation, $F_{scat, fin}$ is finite. It is easy to see that: i) The only divergent contributions in $F_{scat, fin}$ are contained separately in each of the two terms in:

$$\begin{aligned}&\frac{\hbar }{m} \int _{ \left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}\ge 0}\frac{d^{2}{\bar{l}}}{\left( 2\pi \right) ^{2}}\left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2} \mid T_{scat,1}\left( {\bar{l}}\right) \mid ^{2}\nonumber \\&\quad +\frac{\hbar k_{z}}{m}Re\left[ T_{scat,1}\left( {\bar{l}}={\bar{k}}\right) + T_{scat,1}\left( {\bar{l}}={\bar{k}}\right) ^{*}\right] \end{aligned}$$

(59)

(ii) The remaining contributions in $F_{scat, fin}$ (besides those in  59) are two integrals, which turn out to be finite. In fact, the one in (ii) containing $\mid T_{scat,2}\left( {\bar{l}}\right) \mid ^{2}$ is obviously finite. On the other hand, while $T_{scat,1}\left( {\bar{l}}\right)$ diverges, the integral in ii) containing the interference terms $T_{scat,1}\left( {\bar{l}}\right) T_{scat,2}\left( {\bar{l}}= {\bar{k}}\right) ^{*}+T_{scat,1}\left( {\bar{k}}\right) ^{*}T_{scat,2}\left( {\bar{l}}={\bar{k}}\right)$ is finite, due to the integration over $\int _{ \left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}\ge 0}d^{2}{\bar{l}}$. At this point (and in order to deal with i)), it is reminded that the right-hand side of the 2D Eq. (25) becomes, as $\mid {\bar{x}}\mid \rightarrow +\infty$ along a fixed direction (${\bar{x}}/\mid {\bar{x}}\mid$) (with ${\bar{q}}_{1}=\mid {\bar{q}}\mid \cdot \left( {\bar{x}}/\mid {\bar{x}}\mid \right) )$:

$$\begin{aligned}&\exp \left( {i\bar{q}}{\bar{x}}\right) +\mid {\bar{x}}\mid ^{-1/2} \exp \left( i\pi /4\right) \exp \left( i\mid {\bar{q}}\mid \mid {\bar{x}}\mid \right) f\left( {\bar{q}}_{1}, {\bar{q}}\right) \end{aligned}$$

(60)

$$\begin{aligned}&f\left( {\bar{q}_{1}}, {\bar{q}}\right) =-\left( m/2\hbar ^{2}\right) \left( 2/\pi \mid {\bar{q}}\mid \right) ^{1/2} \int d^{2}{\bar{x}}_{1}\exp \left( -i{\bar{q}}_{1}{\bar{x}}_{1}\right) \times \nonumber \\&\quad V\left( {\bar{x}}_{1}\right) \phi _{{\bar{q}}}\left( {\bar{x}}_{1}\right) \end{aligned}$$

(61)

$f\left( {\bar{q}}_{1}, {\bar{q}}\right)$ being the 2D scattering amplitude. The latter fulfils the 2D optical theorem:

$$\begin{aligned}&\frac{1}{2}\left( \mid {\bar{q}}\mid /2\pi \right) ^{1/2} \int _{0}^{2\pi } d\beta \mid f\left( {\bar{q}}_{1}, {\bar{q}}\right) \mid ^{2}-Im\left[ f\left( {\bar{q}}_{1}=\bar{q}, \bar{q}\right) \right] =0 \end{aligned}$$

(62)

$\beta$ and $f\left( \bar{q_{1}}=\bar{q},\bar{q}\right)$ being the angle between ${\bar{q}}_{1}$ and ${\bar{q}}$ and the 2D scattering amplitude in the forward direction, respectively. The important point here is that the two terms in the 3D expression Eq. (59) resemble, term by term, the two contributions in the left-hand side of the 2D Eq. (62), for a suitable 2D scattering amplitude f determined uniquely by $\int d^{2}{\bar{x}} \phi _{{\bar{l}}}\left( {\bar{x}}\right) ^{*}\exp \left( i{\bar{k}}{\bar{x}}\right) \left[ -V\left( {\bar{x}}\right) \right]$ in Eq. (46). This suggests that as the difference of the latter two vanishes, as Eq. (62) indicates, a cancellation could hold for the sum of the divergent terms in  (59). In fact, a detailed computation shows that, in the forward direction, each of the two divergent terms in the 3D expression Eq. (59) equals a constant divergent factor, namely, $w=(2\hbar /m)(2\pi \mid {\bar{k}}\mid )^{1/2}\int _{-\infty }^{0}dz$ (diverging as the infinite length of the semi-infinite waveguide) times its mate in the left-hand side of Eq. (62) (up to subdominant finite corrections). One finds directly $\frac{\hbar k_{z}}{m}Re\left[ T_{scat}\left( {\bar{l}}={\bar{k}}\right) + T_{scat}\left( {\bar{l}}={\bar{k}}\right) ^{*}\right] =-wIm\left[ f\left( {\bar{k}}, \bar{k}\right) \right]$, by using $\frac{\left( -i\right) }{k_{z}-\left( 2m(E+i\epsilon )/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}}=\int _{-\infty }^{0}dz\exp (iz(k_{z}-\left( 2m(E+i\epsilon )/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}))$. For the first term in Eq. (59), one argues as follows. After some simple algebra and a suitable complex conjugation, one concentrates on the divergence in the forward direction, determined by $\int _{-\infty }^{0}dz \frac{\hbar }{m} \int _{\mid {\bar{k}}\mid -\epsilon }^{\mid {\bar{k}}\mid +\epsilon }d\mid {\bar{l}}\mid \frac{\mid {\bar{l}}\mid }{2\pi i}\left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{-1/2} \frac{1}{-k_{z}-i\epsilon +\left( 2mE/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}}\exp (iz(k_{z}-\left( 2m(E+i\epsilon )/\hbar ^{2}-{\bar{l}}^{2}\right) ^{1/2}))$. To leading order near the forward direction and given z, the leading contribution in $\int _{ \mid {\bar{k}}\mid -\epsilon }^{\mid {\bar{k}}\mid +\epsilon }d\mid {\bar{l}}\mid$ comes from very large negative values of z (say, $z\rightarrow -\infty$) and, then, that leading contribution is shown to approach +1( by a change of variables and the relationship $\int _{ -a}^{+a}\frac{dx }{2\pi i(x-i\epsilon )} \exp ix\tau \rightarrow +1$, for given $a>0$ and large positive $\tau$, [23], page 81). It follows directly that the leading contribution to the first term in Eq. (59) in the forward direction equals $w\frac{1}{2}\left( \mid {\bar{k}}\mid /2\pi \right) ^{1/2} \int _{0}^{2\pi } d\beta \mid f\left( {\bar{l}}, {\bar{k}}\right) \mid ^{2}$, now with $\mid {\bar{l}}\mid =\mid {\bar{k}}\mid$. Then, by factoring out w and using Eq. (62), the divergent part of the expression  (59) vanishes. This establishes the finiteness of $F_{scat, fin}$. One can also show, through a detailed analysis, that the finite contribution $- \frac{\hbar k_{z}}{m}Re\left[ T_{scat,2} \left( {\bar{l}}= {\bar{k}}\right) +T_{scat,2}\left( {\bar{l}}={\bar{k}}\right) ^{*}\right]$ is non-negative.

Equation (57) is a generalization of the standard optical theorem [21, 23] for the actual 3D interaction of the slow neutron with the semi-infinite waveguide. Equation (57) is the counterpart for the actual 3D semi-infinite waveguide without any infinitely extended clad having an infinitely repulsive potential (no Dirichlet conditions) of another generalized optical theorem for a 2D semi-infinite waveguide with the opposite clad structure (namely, an infinitely extended clad with an infinitely repulsive potential and, so, with Dirichlet conditions), presented in Molina de la Peña et al. [18].

The (finite) total probability flux for reflection is given by the first contribution in the left-hand side of Eq. (57). A related computation of the total probability for reflection proceeds, in short, as follows. Starting from Eq. (38), one can introduce, in the standard way [21, 23], the 3D amplitude for the slow neutron to be scattered with outgoing wavevector $\left( {\bar{k}}_{1}, k_{z,1}\right)$ ($E=\left( {\bar{k}}_{1}^{2}+k_{z,1}^{2}\right) /2m$), with $k_{z,1}<0$ :

$$\begin{aligned}&f \left( \left( {\bar{k}}_{1}, k_{z,1}\right) , \left( {\bar{k}}, k_{z}\right) \right) =-\left( m/2\pi \hbar ^{2}\right) \int d^{2}{\bar{x}}_{1}\int _{0}^{+\infty }dz_{1}\exp \left[ - i\left( {\bar{k}}_{1}{\bar{x}}+k_{z,1}z\right) \right] \nonumber \\&\quad \times V\left( {\bar{x}}_{1}\right) \psi \left( {\bar{x}}_{1},z_{1}\right) \end{aligned}$$

(63)

where $\psi$ is now given by the right-hand side of Eq. (39). The integral in Eq. (63) converges, since $k_{z,1}<0$. The integral of $\mid f \left( \left( {\bar{k}}_{1}, k_{z,1}\right) , \left( {\bar{k}}, k_{z}\right) \right) \mid ^{2}$ by integrating over all angles corresponding to $k_{z,1}<0$ yields the total scattering cross section for backward scattering (which, in turn, is finite and corresponds to the total probability for reflection). The corresponding total scattering cross section, by integrating over all angles corresponding to $k_{z,1}<0$ and $k_{z,1}>0$, diverges in agreement with a similar statement in Sect. 3.1.