On the definition of the deuterium-tritium ion beam parameters for the SORGENTINA-RF fusion neutron source

Abstract

The SORGENTINA-RF project aims to develop a 14 MeV fusion neutron source to produce medical radioisotopes with special focus on $^{99}$Mo. The facility is based on a positive ion source with an acceleration stage to produce a deuterium (D$^{+})$ and tritium (T$^{+})$ ion beam that, impacting on a titanium-coated rotating target, allows fusion reactions to take place. Maximizing the neutron production rate is one of the main issues to be addressed in the project and the optimization of some key parameters of the ion beam is of paramount importance in this regard. In this study, a methodology is discussed to reach a definition of the beam characteristics for an effective and sustainable operation of the plant. The most convenient layout that has been found out is based on a single ion source fed by a deuterium and tritium gas mixture. Eventually, a series of considerations about the operation of the ion source and fuel cycle have been drawn.

1 Introduction

The objective of the SORGENTINA-RF project is to realize a 14 MeV fusion neutron source based on the deuterium-tritium fusion reaction, to produce $^{99}$Mo for nuclear medicine diagnostics [1]. The project relies on some experimental evidences obtained at the ENEA laboratories in recent years [2, 3] and aims at assessing the viability of producing $^{99}$Mo, by means of the studied processes, at a quasi-industrial scale. An efficient method to generate 14 MeV neutrons is to produce positive deuterium (D$^{+}$) and tritium (T$^{+}$) ions, accelerate them up to a convenient energy and make them impinge on a suitable target where they get implanted. The target is a titanium layer deposited onto a metallic material with compatible thermomechanical properties (i.e., copper or aluminum) which allows the implantation of the ion beam and the fusion reaction to occur when D/T loading of the titanium reaches a certain value. The reader is referred to Ref. [1] for a more detailed description. The ion source (here intended as the device capable of producing, accelerating and delivering to the target the ion beam) constitutes the “engine” of the neutron source, and it is an extremely critical component. Focusing on the transport and the stopping power of D$^{+}$ and T$^{+}$ into the titanium layer and the cross section of the fusion reaction of interest, a beam energy of 300 keV is considered necessary for an efficient neutron production. This comes from a series of experimental evidences obtained at smaller neutron sources, such as the Frascati Neutron Generator (FNG) [4, 5] and from some numerical considerations. The starting point for the numerical and analytical results presented in the following relies on the work done by Martone for a larger-scale neutron source [6]. The beam power of 250 kW at the target was fixed after evaluating a number of general aspects of the project, among which the maximum power input of the facility, the electrical consumption and the expected volume production of $^{99}$Mo. This derives that the nominal value of the beam current (at the target) is 833 mA (416.5 mA each of deuterium and tritium ions). Moreover, it is envisaged to produce the two beams of positive ions with precise requirements and with high reliability and efficiency. As one of the aims of this component of the SORGENTINA-RF plant is to demonstrate continuous and sustainable operation, availability and maintainability are just as important. Four aspects make the realization of such device critical and peculiar:

• Continuous cycle of several thousands of hours of operation between maintenance services;

• Mixed beam of D$^{+}$ and T$^{+}$ with controlled composition, within a specific range, to preserve the neutron production rate;

• Use of a radioactive gas as tritium, which brings to a number of issues related to tritium-handling and contamination of some components of the device which prevents from exploiting standard design solutions;

• Atypical beam characteristics: high-energy/high-current are not common among existing positive ion sources (generally these are low-energy/high-current or high-energy/low-current devices). This increases the workload in the design phase, in particular for the 300 kV acceleration stage.

2 Modeling the ion source-target system

The definition of the beam parameters has to be established along with the optimized tritium cycle to guarantee an economically profitable production of $^{99}$Mo. To this aim, a simplified time-dependent numerical model was developed to calculate: (1) the amount of deuterium and tritium implanted in the titanium layer; (2) the amount of deuterium and tritium released in the vacuum chamber housing the rotating target and that has to be removed and recycled; (3) the amount of helium generated by fusion reactions; (4) the neutron production rate, Y$_{n}$, of the facility as a function of some relevant parameters of the machine. The preliminary results achieved from the model are valid within some simplifying assumptions. Nevertheless, some clear and important indications emerge, such as the most effective layout of the ion source. The ion source-target system was modeled according to the scheme shown in Fig. 1.

Fig. 1

Scheme of the model ion source-target system: time length of D$^{+}$ and T$^{+}$ beams within the time cycle of the machine are defined as inputs, as well as their current (I$_{D}$ and I$_{T}$), bigger vertical arrows). The smaller vertical arrows indicate the fraction of D and T implanted in the Ti layer. Horizontal arrows indicate the particles leaving the target (see text for details)

The model relies on the balance of D$^{+}$, T$^{+}$ and $^{4}$He (the latter being produced by the $^{2}$H($^{3}$H,n)$^{4}$He fusion reactions) in the rotating target and in the vacuum chamber. The particle source terms, either positive or negative, are indicated below as referred to the target and the vacuum chamber.

Positive source terms for the target:

• Deuterium/Tritium, $\propto$ T$^{+}$/D$^{+}$ implanting rate;

• Helium, $\propto$ $^{2}$H($^{3}$H,n)$^{4}$He reaction rate.

Negative source terms for the target:

• Deuterium/Tritium, $\propto$ T$^{+}$/D$^{+}$ release rate;

• Helium, $\propto$ $^{2}$H($^{3}$H,n)$^{4}$He reaction rate $\times$ $^{4}$He release rate.

Positive source terms for the vacuum chamber:

• Deuterium/Tritium, $\propto$ T$^{+}$/D$^{+}$ release rate + T$^{+}$/D$^{+}$ not implanted per unit time;

• Helium, $\propto$ $^{2}$H($^{3}$H,n)$^{4}$He reaction rate $\times$ release rate.

Negative source terms for the vacuum chamber:

• Deuterium/Tritium, $\propto$ T$^{+}$/D$^{+}$ pumping rate;

• Helium, $\propto$ $^{4}$He pumping rate.

The physical quantities used in the model are listed in the following, keeping in mind that capital letter means total number of atoms, whereas lowercase letters means atomic density (number of atoms per cubic centimeter).

• Y$_{n}$(t): neutron production rate at the target;

• I$_{H}$ (H=D,T): ion beam current;

• $\epsilon _{imp}^{H}$: implantation efficiency, i.e., fraction of implanted ions with respect to the impinging ones;

• $\epsilon _{rel}^{H}$: release rate from the Ti layer under ion beam irradiation;

• $\epsilon _{rel}^{^{4}He}$: release rate of helium generated by fusion reactions from the target;

• N$_{H,^{4}He}$: number of atoms of the target;

• $e$: elementary electric charge;

• $\sigma _{DT}$,$\sigma _{TD}$: fusion cross section of D-T and T-D reactions;

• R$_{H,^{4}He}$: particle range in the Ti layer for H=D,T and helium.

The beam model relies on two D$^{+}$ and T$^{+}$ independent beams with a certain ion current I$_{D}$ and I$_{T}$, respectively. Each beam is characterized by an independent time duration within the operating cycle of the ion source, as shown in Fig. 1. Such input parameters can be modified for the sake of the optimization process. Thus, the two beams can be simulated as simultaneous (partially or fully) or not. This allows to explore even the alternate use of a low intensity T$^{+}$ beam to load the titanium layer by tritium and a more intense D$^{+}$ beam for neutron production. In principle, a similar layout could be beneficial as a low intensity T$^{+}$ ion source means a lower tritium flow rate and thus a reduced tritium inventory, with advantages in terms of cost saving and safety. The two beams are characterized by a given implantation efficiency in the titanium layer that in turn has a limited deuterium, tritium and helium retention. More specifically, the loading factors in terms of maximum number of atoms which are retained in the target, respectively (N$_{D}$+N$_{T}$) for hydrogen and (N$_{^{4}He}$) for helium, are set as described in the following and with respect to the number of Ti atoms (N$_{Ti}$). The 14 MeV neutron production rate is calculated as follows:

$$\begin{aligned} Y_{n}(t)=\frac{I_{D} (t)}{e} \epsilon _{impl}^{D} \cdot n_{T} (t) \cdot \sigma _{DT} \cdot R_{D}+ \frac{I_{T} (t)}{e} \epsilon _{impl}^{T} \cdot n_{D} (t) \cdot \sigma _{TD} \cdot R_{T} \end{aligned}$$

(1)

In this preliminary assessment of the neutron production rate, the energy dependence of cross section is neglected, and a more accurate calculation considering the ion energy profiles along the target layer will be given in the future. Here, the main purpose is a comparative study of the different beam configurations. The time variation of the amount of D, T and $^{4}$He in the Ti layer can be calculated as:

$$\begin{aligned} \frac{dN_H}{dt}= ~& {} \frac{I_{H} (t)}{e} \cdot \epsilon _{impl}^{H} - Y_{n}(t)- [( I_{D} (t) \cdot \epsilon _{impl}^{D}+I_{T} (t) \cdot \epsilon _{impl}^{T}) \cdot \epsilon _{rel}^{H}] \cdot \frac{n_{H}}{n_{T}+n_{D}} \end{aligned}$$

(2)

$$\begin{aligned} \frac{dN_{^{4}He}}{dt}=~ & {} Y_{n}(t)(1-\epsilon _{rel}^{^{4}He}) \end{aligned}$$

(3)

The time variation of the amount of D, T and $^{4}$He in the vacuum chamber to be pumped out can be calculated as:

$$\begin{aligned} \frac{dN_{H}^{out}}{dt}=~ & {} \frac{I_{H} (t)}{e} \cdot (1- \epsilon _{impl}^{H}) + [ (I_{D} (t) \cdot \epsilon _{impl}^{D}+I_{T} (t)) \cdot \epsilon _{impl}^{T}) \cdot \epsilon _{rel}^{H}] \cdot \frac{n_{H}}{n_{T}+n_{D}} \end{aligned}$$

(4)

$$\begin{aligned} \frac{dN_{^{4}He}^{out}}{dt}=~ & {} Y_{n}(t)\cdot \epsilon _{rel}^{^{4}He} \end{aligned}$$

(5)

Table 1 Tritium release rate from literature

The tritium release rate from the Ti target under deuterium ion bombardment is taken from Ref. [6] (see also Table 1) and is intended as per unit of ion current penetrating the target layer. This value is in line with the experience at FNG on the depletion of tritiated targets [8] (where the impinging atoms are only D$^{+}$) and also with INGE-1 [10]. Assuming a similar chemistry for D$^{+}$ and T$^{+}$ in the titanium layer, and neglecting mass-dependent physical processes such as diffusion, it is expected that hydride formation and destruction rates are equivalent for the two species. This value is assumed as the release rate per unit beam current both for deuterium and tritium from the target, namely $\epsilon _{rel}^{H}$=8.354 $\times$ 10$^{17}$ A$^{-1}$ s$^{-1}$.

The total number of released hydrogen atoms is shared between tritium and deuterium depending on their density in the target. The estimation of the helium release is performed in the assumption that it is independent from the ion bombardment. The number of $^{4}$He nuclei per unit time equals the neutron yield rate, since a single 3.5 MeV $^{4}$He nucleus and a single neutron are produced in a fusion reaction. The D-D and T-T fusion reactions are neglected as their reaction rates are several orders of magnitude lower than the D-T one. As the range of a 3.5 MeV $^{4}$He is about 9 $\mu$m in titanium [6], considering a depth of 2 $\mu$m titanium, a fraction of 11% can be considered as implanted, with the others being released almost immediately into the vacuum chamber. The helium release is considered as 89% of the neutron yield rate, i.e., $\epsilon _{rel}^{^{4}He}$=0.89.

The implantation efficiency of tritium and deuterium ions is assumed to be $\epsilon _{imp}^{D}$=$\epsilon _{imp}^{T}$=0.99.

This means that 1% of the D$^{+}$ and T$^{+}$ beams is supposed not to enter in the titanium layer, thus remaining in the vacuum chamber. Although arbitrarily chosen, nevertheless it is considered reasonable. The maximum loading factor for hydrogen in Ti (i.e., H atoms per Ti atom) is set to 1.8 according to Ref. [6]. This is valid below 200 $^{\circ }$C, temperature below which D and T form stable compounds (hydrides) with titanium, although some experimental evidence of the same retention capability is reported even above 200 $^{\circ }$C for a titanium target under high ion flux. For helium, a loading factor of 0.3 is considered in this model, as reported for metals at one third of their fusion temperature in [6]. The other values assigned are: $\sigma _{DT}$=$\sigma _{TD}$=5 $\cdot$ 10$^{-24}$ cm$^{2}$; $R_{T}$=$R_{D}$=2 $\mu$m (at 300 keV energy); n$_{Ti}$=5.68 $\cdot$ 10$^{22}$ cm$^{-3}$. In a preliminary rotating target design, the volume of the titanium layer involved in the deposition is a circular crown with a depth of $R_{T}$=$R_{D}$, outer diameter of 90 cm and inner diameter of 75 cm, as a uniform beam of 15 cm diameter is considered. Such volume allows to store about 1.2 $\cdot$ 10$^{22}$ $^{4}$He nuclei and 7.23 $\cdot$ 10$^{22}$ hydrogen (deuterium and tritium). After the definition of the above-mentioned physical quantities and a proper finite time step (0.1 s was found adequate in the calculations here presented), the routine is launched to execute the following steps:

• 1 Set initial values, namely

  • N$_{T}$(t = 0)

  • N$_{D}$(t = 0)

  • N$_{^{4}He}$(t = 0)

  • N$_{T}^{out}$(t = 0)

  • N$_{D}^{out}$(t = 0)

  • N$_{^{4}He}^{out}$(t = 0)

  • I$_{D}$(t = 0)

  • I$_{T}$(t = 0)

• 2 Calculate the neutron production rate at $t$ = 0:$Y_{n}(t=0)=\frac{I_{D}(t=0)}{e} \epsilon _{impl}^{D} \cdot n_{T} (t=0) \cdot \sigma _{DT} \cdot R_{D}+ \frac{I_{T}(t=0)}{e} \epsilon _{impl}^{T} \cdot n_{T}(t=0) \cdot \sigma _{DT} \cdot R_{T}$.

• 3 Calculate the number of atoms at the time t+$\Delta$t, i.e.,:

  • $N_{T}(t+\Delta t)=N_{T}(t)+\left[\left(\frac{I_{T}(t)}{e}\right) \cdot \epsilon _{imp}^{T}-Y_{n}(t) -(I_{D}(t) \cdot \epsilon _{imp}^{D}+I_{T}(t) \cdot \epsilon _{imp}^{T}) \cdot \epsilon _{rel}^{H} \cdot \frac{n_{T}}{(n_{T}+n_{D} )}\right]\Delta t$;

  • $N_{D} (t+\Delta t)=N_{D} (t)+\left[\left(\frac{I_{D}}{e}(t)\right) \cdot \epsilon _{imp}^{D}-Y_{n}(t) -[(I_{D}(t)\cdot \epsilon _{imp}^{D}+I_{T}(t) \cdot \epsilon _{imp}^{T}) \cdot \epsilon _{rel}^{H} \cdot \frac{n_{D}}{(n_{T}+n_{D} )}\right]\Delta t$;

  • $N_{^{4}He}(t+\Delta t)=N_{^{4}He}(t)+\left[Y_{n} (t) \cdot \epsilon _{imp}^{^{4}He}\right]\cdot \Delta t$.

• 4 Calculate the integral amounts to be pumped out:

  • $N_{T}^{out}(t+\Delta t)=N_{T}^{out}(t)+\left[(\frac{I_{T}(t)}{e} \cdot (1-\epsilon _{imp}^{T})+(I_{D}(t) \cdot \epsilon _{imp}^{D}+I_{T}(t) \cdot \epsilon _{imp}^{T}) \cdot \epsilon _{rel}^{H} \cdot \frac{n_{T}}{(n_{T}+n_{D} )}\right] \Delta t$

  • $N_{D}^{out}(t+\Delta t)=N_{D}^{out}(t)+\left[(\frac{I_{D}(t)}{e} \cdot (1-\epsilon _{imp}^{D})+(I_{D}(t) \cdot \epsilon _{imp}^{D}+I_{T}(t) \cdot \epsilon _{imp}^{T}) \cdot \epsilon _{rel}^{H} \cdot \frac{n_{D}}{(n_{T}+n_{D})}\right] \Delta t$

  • $N_{^{4}He}^{out}(t+\Delta t)=N_{^{4}He}^{out}(t)+\left[Y_{n}(t) (1- \epsilon _{imp}^{^{4}He})\cdot \Delta t\right]$

• 5 Calculate the Pumping rates:

  • $\frac{N_{T}^{out}(t+\Delta t)-N_{T}^{out}(t)}{\Delta t})=\left[\frac{I_{T}(t)}{e} (1-\epsilon _{imp}^{T})+(I_{D}(t) \epsilon _{imp}^{D}+I_{T}(t) \epsilon _{imp}^{T}) \cdot \epsilon _{rel}^{H} \cdot \frac{n_{T}}{(n_{T}+n_{D} )}\right]$

  • $\frac{N_{D}^{out}(t+\Delta t)-N_{D}^{out}(t)}{\Delta t})=\left[\frac{I_{D}(t)}{e} (1-\epsilon _{imp}^{D})+(I_{D}(t) \epsilon _{imp}^{D}+I_{T}(t) \epsilon _{imp}^{T}) \cdot \epsilon _{rel}^{H} \cdot \frac{n_{D}}{(n_{T}+n_{D} )}\right]$

  • $\frac{N_{^{4}He}^{out}(t+\Delta t)}{\Delta t}=Y_{n}(t)(1-\epsilon _{imp}^{^{4}He})$.

At each time step, it is checked if (N$_{T}$+N$_{D}$) and N$_{^{4}He}$ are below the concentrations which would saturate the titanium layer. If the number of atoms exceeds the maximum loading factor, the surplus diffuses into the vacuum chamber. The fraction of surplus of each species is calculated as a weighted average where weights are their growth rates. Then, the number of atoms at the time $t$ are updated. Time is then increased by $\Delta t$ , and the cycle is repeated from step-2 until the operation time length is reached. This model has been implemented in a MATLAB computer routine. The flexibility given to the model (by defining a number of parameters for each species and for each process involved) allows to improve the detail of the calculation if necessary and also to perform some parametric and sensitivity studies.

3 Ion source operation

The results reported in this section include the main findings which contributed to determine some relevant parameters characterizing the ion source. In the following sections, the criteria to choose the optimized beam configuration are provided.

3.1 Alternate operation of D$^{+}$ and T$^{+}$ ion beams

An ion source foreseeing the alternate use of a low intensity T$^{+}$ beam to load the titanium target and a more intense $D^{+}$ beam to trigger the fusion reactions would allow to reduce the cost due to a higher tritium flow rate. To explore this possibility, some simulations have been done. In Fig. 2, a representative case is reported of a 100 mA T$^{+}$ beam (an ion source with such a current is not far from some devices available on the market for deuterium, and it would require some adaptation to radioactive gas as tritium, without an extensive design activity) operated alternatively to a 700 mA D$^{+}$ beam.

Fig. 2

Neutron production rate (a), number of atoms in the titanium layer (b) and atoms to be pumped out from vacuum chamber (c) obtained in a simulation of T$^{+}$ ion beam of 100 mA and D$^{+}$ ion beam of 700 mA operated alternatively for 40 hours each

Considering that 7.23$\times$10$^{22}$ hydrogen atoms are necessary to saturate the titanium target, about 38 hours are necessary to reach the saturation also accounting for the tritium release. The simulation considers 40 hours of T$^{+}$ irradiation followed by 40 hours of D$^{+}$ irradiation. The decrease in neutron production (neutron rate is halved in about 24 hours) would make impossible to operate the machine with a quasi-constant neutron production rate. This is mainly due to the large amount of tritium and deuterium released as a consequence of the ion bombardment of the target, while the amount of tritium implanted which reacts to produce fusion neutrons is an extremely small fraction of the amount released in the vacuum chamber, i.e., about 10 orders of magnitude lower. Apparently, a pure loading phase with a low intensity T$^{+}$ beam is not effective.

3.2 Optimum D$^{+}$ and T$^{+}$ beam ion currents

Foreseeing the necessity of having the two beams in simultaneous operation, it is important to determine the fraction of D$^{+}$ and T$^{+}$ in the total beam current. It has been decided to take as a criterion the maximization of the neutron production rate. Figure 3 reports the comparison of the performance of the neutron source as the fraction of T$^{+}$ varies from 0.1 (in this case D$^{+}$ fraction is 0.9) to 0.9 (in this case D$^{+}$ fraction is 0.1).

Fig. 3

Neutron production rate in the first 10 hours of functioning as the T$^{+}$ current fraction varies from 0.1 to 0.9

It is worth noting that here the purpose is the comparative assessment of the achievable neutron yield as the fraction of T$^{+}$ and D$^{+}$ varies, while a more precise evaluation of the neutron yield rate will be provided elsewhere. All the curves show the onset of a flat top in correspondence of the saturation time of deuterium and tritium implanted in the titanium layer. From that time on, n$_{T}$ and n$_{D}$ cannot increase further and this limits the fusion reaction rate. Assuming $\epsilon _{rel}^{D}$ = $\epsilon _{rel}^{T}$ and $\sigma _{DT}$ = $\sigma _{TD}$, it follows that the maximum neutron yield rate is obtained when T$^{+}$ and D$^{+}$ fractions are 0.5. In facts, the fusion reaction rate is proportional to the flux of the impinging ions by the density of the target nuclei in the titanium layer and in the specific case there are two contributions to the total neutron production rate, i.e., T(D) ions impinging on the implanted D(T) ions. Considering that both ion flux and density of ions implanted are proportional to the current fraction of that kind of ions in the beam, it can be easily demonstrated that maximizing the neutron production means simply maximizing the product of the ion current fractions of D and T, which brings to an ion beam made by 50% of D$^{+}$ and 50% of T$^{+}$ (in terms of ion current fraction).

3.3 Simultaneous operation of D$^{+}$ and T$^{+}$ ion beams

Relying on the previous results, the most effective configuration of the ion source is the simultaneous use of the D$^{+}$ and T$^{+}$ ion beams with a current of 416.5 mA each. Figure 4 shows the resulting neutron production rate across the first 24 hours of operation.

Fig. 4

Neutron yield rate (Y$_{n}$) obtained in a simulation of a 833 mA T$^{+}$ and D$^{+}$ (50/50) ion beam over 24 hours of operation

Figure 5 shows the cumulative mass of D, T and $^{4}$He in the vacuum chamber (a), i.e., as there was not any removal system, and the mass of D, T and $^{4}$He into the Ti layer (b). In Fig. 6, the pumping rates for D and T in terms of mass per unit of time are plotted. About 13 $\mu$g s$^{-1}$ of tritium, 8.7 $\mu$g s$^{-1}$ of deuterium and 1.6 ng s$^{-1}$ of helium are released into the vacuum chamber that in turn have to be removed. This means that after the initial transient of about 5 hours, when the steady state is reached, 1.12 g of tritium and 0.75 g of deuterium have to be used to produce the nominal ion beam for the next 19 hours. Noteworthy, these figures are valid in the ideal case of an ion source featuring a 100% gas efficiency, i.e., all the deuterium and tritium being ionized into the plasma chamber and extracted and accelerated without any loss. Moreover, some amount of deuterium and tritium are necessary to sustain the density profile along the device, i.e., they have to circulate as a background gas to guarantee the necessary pressure inside the device. The gas efficiency depends on the design of the machine. Typically, big positive ion sources feature a gas efficiency of 20–40% [11]. Conservatively, a similar gas efficiency is expected for the SORGENTINA-RF ion source, meaning that the minimum gas flow rates of tritium and deuterium earlier mentioned should be at least doubled. The evaluation of the cumulative masses is important to determine how to recirculate deuterium and tritium for the system. The pumping rates also provide a first estimation of the amounts to be recirculated. In order to better appreciate the results, Fig. 6 shows a blow up of the mass pumping rate in the first hours of operation: the discontinuity there visible is due to the saturation of the titanium layer.

Fig. 5

a Mass of D, T and He atoms cumulated in the vacuum chamber (as if there was not a pumping system); b Mass of D, T and He atoms in the titanium layer. The quantities are obtained considering 833 mA ion current (50% T$^{+}$ and 50% D$^{+}$) operating over 24 hours

Fig. 6

Mass of D and T atoms to be pumped out per unit of time from vacuum chamber, calculated in a simulation with the same conditions of Fig. 5

3.4 Recirculation system and layout of the device

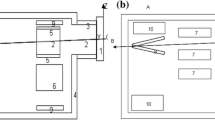
As for the evaluation of the necessity to recirculate deuterium and tritium, it appears that a single day of operation in steady state, requires 1.12 g of tritium (in the ideal case of gas efficiency 100%), which corresponds to a value of about 30 kEuro [1]. This prohibitive cost makes the use of a recirculation system necessary for the economic viability of the plant. The need of a recirculation system and the fact that the isotopic separation of deuterium from tritium is too costly, supported the choice of a single ion source fed by a gas mixture of deuterium and tritium. A recirculation line is under design to separate the outflowing deuterium and tritium from helium and other gas impurities before reinjection. For these reasons, the primitive layout of the machine with two separate ion sources was abandoned in favor of a layout with a single device (see Fig. 7).

Fig. 7

(Left) Primitive conceptual scheme with two separate ion sources; (right) a more refined model with a single ion source providing a mixed D/T ion beam

3.5 Sensitivity of the device to the variation of D$_{2}$ and T$_{2}$ fractions at the gas inlet

The simplified model earlier described can be also applied to assess the sensitivity of the system to the concentration of D$_{2}$ and T$_{2}$ at the gas inlet. The recirculation system must separate the hydrogen fraction (D$_{2}$ and T$_{2}$) from helium and other gases (e.g., O$_{2}$, N$_{2}$), then it has to restore the proper concentration of D$_{2}$ and T$_{2}$ at the gas inlet of the ion source. The effect of the time variation of the composition of the inflowing gas of D$_{2}$ and T$_{2}$ on the neutron production rate was studied with the same model. D$_{2}$ and T$_{2}$ concentrations in the gas mixture injected in the plasma chamber to produce the nominal ion current of 833 mA are here assessed by imposing equal ion flux for the two ion beams, i.e., $n_{D}$ $\cdot$ $v_{D}$ = $n_{T}$ $\cdot$ $v_{T}$. From this relation, the ratio of ion densities can be derived as the square root of atomic masses, i.e., $\frac{n_{D}}{n_{T}} = \frac{v_{T}}{v_{D}} = \sqrt{\frac{m_{D}}{m_{T}}}$ = 0.817, where $m_{D}$=3.3437 $\times$10$^{-27}$ kg, $m_{T}$ =5.0083 $\times$10$^{-27}$ kg, providing $v_{D}$ = 5.36 $\times$ 10$^{6}$ m s$^{-1}$ and $v_{T}$= 5.36 $\times$ 10$^{6}$ m s$^{-1}$. This is also valid for the normalized densities defined to satisfy the closure relation ${\overline{n}}_{D}$ + ${\overline{n}}_{T}$=1, that in turn provides ${\overline{n}}_{D}$=0.45 and ${\overline{n}}_{T}$=0.55, respectively. Assuming that both D$_{2}$ and T$_{2}$ are ionized and extracted from the plasma chamber with the same efficiency (i.e., considering the atomic mass difference negligible in these processes), the gas D$_{2}$:T$_{2}$ mixture has to be 45:55. This would be the nominal composition and the reference of the concentration control system. Some preliminary considerations on how the performance of the real-time monitoring and control of the gas composition reflects on the neutron source performance can be done by exploiting this simple model. A time variation of the gas composition is given as input and the deuterium and tritium beam currents are calculated from the normalized currents which can be written as follows:

$$\begin{aligned} {\overline{I}}_{D}= & {} \frac{{\overline{n}}_{D}\cdot v_{D}}{{\overline{n}}_{D}\cdot v_{D}+{\overline{n}}_{T}\cdot v_{T}} \end{aligned}$$

(6)

$$\begin{aligned} {\overline{I}}_{T}= & {} \frac{{\overline{n}}_{T}\cdot v_{T}}{{\overline{n}}_{D}\cdot v_{D}+{\overline{n}}_{T}\cdot v_{T}} \end{aligned}$$

(7)

These two relations are used to calculate I$_{D}$ and I$_{T}$ as they appear in the model, for each time step.

In Fig. 8, Y$_{n}(t)$ is plotted as a function of the operation time, assuming different decreasing rates (in units of % hr$^{-1}$) of T$_{2}$ at the gas inlet.

Fig. 8

Y$_{n}(t)$ as a function of the operation time for different T$_{2}$ decreasing rates up to −50% hr$^{-1}$

Values up to −50%/hour are considered. The decrease in the neutron yield reflects directly on the reduction of production of $^{99}$Mo and on the basis of this, considering also the cost of the control system, some considerations on how quickly the set point has to be restored can be done. What seems clear from the results of this preliminary evaluation is that the rotating target act as a tritium reservoir and mitigates significantly the decrease in T$^{+}$ ions impinging on it. This effect can contribute to reduce, if necessary, the intervention speed of the control system to restore the T$_{2}$ concentration at the gas inlet.

4 Conclusions and future works

The present work describes the approach followed to define some basic and fundamental properties of the deuterium (D$^{+}$) and tritium (T$^{+}$) ion beam impacting on the rotating target of the SORGENTINA-RF neutron source, once provided the geometrical constraints (ion source-target distance and beam spot). Some of the most important physical quantities have been here defined and the basic features of the ion source outlined. According to the numerical considerations derived from the ion source-target model, it can preliminarily concluded that:

• D$^{+}$ and T$^{+}$ ion beams have to be simultaneous, each providing half of the total current;

• The layout foresees a single ion source fed by a gas mixture of deuterium and tritium species;

• More than 1.12 g day$^{-1}$ (depending on the actual gas efficiency) of tritium is needed, thus imposing the need of a recirculation system;

• The rotating target acts as a tritium reservoir, and it would mitigate the decrease in T$_{2}$ concentration at the gas inlet. This effect can contribute to reduce, if necessary, the intervention speed of the control system of inflowing gas composition.

Some assumptions, such as the tritium release rate that here was taken from literature, require to be confirmed experimentally and some experiments are already planned at FNG. Moreover, a more precise assessment of the SORGENTINA-RF’s neutron yield must account for the D and T density profiles as well as for the energy profile of the impinging D$^{+}$ and T$^{+}$ ions across the titanium layer. To determine the density of target nuclei, some codes allow to simulate the ion deposition; however, it is believed that evolution and thermal stability of tritium and deuterium ions in the titanium layer must be better characterized by means of dedicated experiments.