1 Introduction

Nanoporous metals (NPM) form a broad class of monolithic solids that are currently under intense scrutiny. With their architecture consisting of an elegant, and yet confusing, tangle of voids and solid [1], in the past 20 years, these materials received considerable attention from scientists of very different backgrounds.

The main synthetic route to NPM is based on the selective dissolution of less noble metals from a parent alloy. Dealloying is, indeed, a relatively simple process [2] where the alloy is exposed to an acidic aqueous solution and less noble elements are progressively removed by a free corrosion process [3,4,5]. At present, electrochemical methods are often applied to achieve better control of the dissolution process [4, 6], but this leaves the key features of the corrosion process unaffected.

The result of dealloying is a homogeneous, interpenetrating, bi-continuous disordered network of ligaments and pores [1, 4, 7]. In this regard, NP Au represents the most typical example [8]. Easy to obtain because of Au chemical nobility, it has provided the ideal model system to explore the structure–property relationships for NPM and has rapidly risen to the role of absolute protagonist in the field of study. Gradually, it has shown promise for actuation, catalysis, energy, and sensing-related applications, just to cite a few [8,9,10,11,12,13,14,15,16,17].

A key enabling technology issue stands, nonetheless, in the way to the practical exploitation of NP Au, and NPM in general, namely their mechanical properties [18,19,20,21,22,23,24,25,26,27]. Actuators, self-supported catalysts and scaffolds for surface-enhanced Raman spectroscopy, thermal insulators and structural materials all need long-term mechanical stability and, therefore, a satisfactory characterization of the NPM response to elastic and plastic deformation. However, the subject is also per se extremely interesting. Porosity degree and characteristic lengths severely affect the response to mechanical loads. Particularly intriguing is the evidence that the reduction in ligament and pore size to a few nanometers can induce a significant hardening and stiffening of NP architectures. Although literature data are still fragmentary and contradictory, there is no doubt, at least for NP Au, that size effects affect the mechanical properties.

Concerning the elastic properties in particular [26, 28,29,30,31,32], experiments and atomistic simulations have been used to investigate Young’s modulus and Poisson ratio. Constitutive models have been mostly based on the Gibson-Ashby scaling laws [33, 34], but their validity has been questioned. Typically, ligaments have aspect ratios far from those compatible with Gibson-Ashby’s models, and other structural and topological factors have been shown to play a role [29, 35]. For instance, several experiments have provided robust evidence that the NP Au Young’s modulus increases as the ligament thickness is reduced approximately from 200 nm to 5 nm [28, 29, 36]. Surface stress has been invoked to explain experimental observations as well as the enhanced moment of inertia of finer structures [29] and the content of lattice defects [37]. In this latter case, it is worth recalling that while point defects can induce a significant reduction in the elastic moduli [38, 39], extended defects may affect local interatomic bonding [37].

Motivated by this intriguing and open scenario, in this work, we investigate the Young’s modulus of NP Au by combining experimental, simulative, and theoretical methods. To this aim, we have generated in silico replicas of NP Au structures with atomistic resolution by mapping the initial volumetric data obtained by experimental tomographic evidence. Re-scaling the characteristic lengths of the atomistic sample, we have systematically explored the impact of size effects, keeping constant the degree of porosity. Our findings confirm that the Young’s modulus significantly increases as the ligament size decreases. Further, we prove that the observed stiffening cannot be ascribed to surface stress or grain-boundary effects. Rather, our results indicate a quantitative correlation with the dislocation density. Specifically, we show that local stress and strain fields in the neighborhood of dislocation cores allow dislocations to induce reinforcing effects comparable with those originated by dispersoids with the shape of whiskers or fibers. These are known since long to determine a significant increase in Young’s modulus and shear modulus, somehow hindering atomic and dislocation mobility. Shortly, the effects induced by dislocations are enhanced by the small length scale involved in the NP Au ligaments, and the result is a mechanical behavior that can be equated, to a first approximation, to the one observed in fiber-reinforced materials.

2 Materials and experimental methods

2.1 Fabrication

NP Au samples have been fabricated by electrochemical dealloying of a homogeneous chemically disordered polycrystalline Ag\(_{70}\)Au\(_{30}\) solid solution. The parent alloy was prepared by mechanical alloying of Ag\(_{50}\)Au\(_{50}\) powder mixtures followed by melting in an induction furnace and magnetic stirring. Elemental Ag and Au powders with particle size below 45 \(\mu \)m and 99.99% purity were manually mixed to obtain powder mixtures with Ag\(_{50}\)Au\(_{50}\) stoichiometry. Mechanical alloying was carried out on powder batches of 10 g. The powders were sealed in a hardened-steel cylindrical reactor together with two 8-g stainless steel balls under inert Ar atmosphere with oxygen and humidity contents below 2 ppm. The reactor was clamped to the mechanical arm of a SPEX Mixer/Mill 8000 ball mill and swung back and forth along a three-dimensional trajectory at about 875 rotations per minute. The mechanical processing resulted in the mutual dissolution of Ag and Au and the formation of a homogeneous chemically disordered nanocrystalline solid solution with Ag\(_{50}\)Au\(_{50}\) chemical composition.

The obtained powders were placed in a quartz crucible and molten inside a laboratory Nabertherm N60/ER furnace. The melt was kept at 1050 °C for 5 days under magnetic stirring and Ar flux conditions. Then, the molten phase was cast into cylindrical pellets about 1 mm high and with a diameter of about 1 cm. The surfaces of cylindrical pellets were finely polished and annealed for 10 h at about 400 °C to relieve residual stresses.

Structural and microstructural transformations of powders and bulk solids along with the different steps of the preparation process of the Ag\(_{50}\)Au\(_{50}\) solid solution were investigated by X-ray diffraction (XRD). To this aim, a Rigaku SmartLab diffractometer equipped with a PhotonMax high-flux 9 kW rotating anode X-ray source was used. Not shown for brevity, XRD patterns were analyzed according to the Rietveld method. Mechanical alloying confirms its ability to induce the formation of homogeneous nanocrystalline solid solutions. Although we do not have direct evidence in this regard, melting and magnetic stirring can be expected to enhance the homogeneity of the final polycrystalline Ag\(_{50}\)Au\(_{50}\) solid solution on the atomic scale.

NP Au structures were obtained from the parent alloy by electrochemically assisted dealloying. The cylindrical pellets were exposed to an aqueous solution 0.75 M in HNO\(_{3}\) and 0.01 M in AgNO\(_{3}\). Selective Ag dissolution was carried out at room temperature inside a three-electrode electrochemical cell controlled by a Metrohm Autolab 302N potentiostat-galvanostat. A potential of about 600 mV was applied, using a Pt wire and an Ag electrode as counter and reference electrodes, respectively. Dealloying was interrupted after 10 days. To this aim, the cylindrical pellets were repeatedly rinsed with high-purity water and, finally, dried using an Ar flux at room temperature for 4 days. X-ray fluorescence measured a residual Ag content lower than 1 at %. To eliminate internal residual stresses due to the dealloying process, the NP Au structures were subjected to 5-day long annealing at 400 K under Ar flux conditions.

2.2 Serial Block Face-SEM sectioning and imaging

The NP Au sample was embedded in Epon epoxy resin using small silicon mold by polymerization at 65 \(^{\circ }\)C for 72h. Resin blocks were mounted on aluminum specimen pins (10-006002-10, Micro to Nano) using cyan acrylic glue and trimmed with a glass knife to a rectangle 0.5 \(\times \) 0.75 mm, with the gold sample exposed on all four sides. Silver paint (16 062-PELCO Conductive Silver Pain, TedPella) was used to favor the electrically grounding of the block edges to the aluminum pin. The entire, glued block was then sputter-coated with a thin (25 nm) layer of gold (Cressington 208 HR sputter coater) to make its surface reflect. After the block alignment into the SEM chamber, block cutting and serial block-face (SBF)-SEM images collection was performed using a dedicated VolumeScope (Thermo Scientific) cutting device mounted in a Teneo (Thermo Scientific) variable pressure SEM, the latter operating at an acceleration voltage of 2 kV, and with a probe current of 50 pA and an in-chamber pressure of 20 Pa of water vapor. The sample was imaged at a magnification and with a pixel number that could allow obtaining an ultimate voxel size of 6 \(\times \) 6 \(\times \) 50 nm (x-y-z), where the z-one is the thickness chosen for the block cutting. The SEM images were collected using a dedicated backscattered electron (BSE) detector, provided for working with the VolumeScope cutting device. We carried out X-ray fluorescence measurements to evaluate the impurity level. This is a standard procedure we adopted since ball milling can be really, and often it is, source of considerable contamination due to milling tools abrasion. However, we have shown with our previous work on mechanical alloying, and mechanochemistry in general, that the mechanical processing in the presence of relatively large amounts of powder almost completely suppresses undesired contamination. Fe levels keep well below 4 ppm even after days of uninterrupted mechanical treatment.

2.3 3D reconstruction and rendering

Serial SBF-SEM images were assembled into volume files using AVIZO software package (Thermo Scientific). NP Au ligaments and pores were segmented using Ilastik software. The models extracted were assembled into volume and rendered using again AVIZO software package. By using the reconstructed volume, the porosity (i.e., the volume of the pores) was also determined slice by slice over the whole thickness of the reconstructed sample.

2.4 Nanoindentation

The Young’s modulus of NP Au structures obtained by dealloying was measured using depth-sensing nanoindentation. A calibrated three-sided pyramid diamond Berkovich tip with radius of about 200 nm was used. Indentation was carried out using a constant loading rate of 500 \(\mu \)N s\(^{-1}\). The load was varied between 200 and 2000 \(\mu \)N. Up to 100 loading–unloading curves were measured per sample. The Young’s modulus was estimated by measuring the slopes of the linear part for any unloading curve and averaging over all unloading curves.

3 Simulations

3.1 3D reconstruction and rendering of NP Au samples.

We used serial block-face (SBF) scanning electron microscopy (SEM) to collect two-dimensional images of NP Au samples through a SEM-dedicated VolumeScope cutting device (see Materials and Methods for details). A typical SEM image is shown in Fig. 1 (Panel a) for illustration purposes. The typical appearance of a NP architecture is immediately evident, with irregularly shaped ligaments and ligament junctions forming condensed open cells finally resulting in an inherently distorted three-dimensional lattice. The two-dimensional images were assembled into a single three-dimensional structure via a suitable volume reconstruction method (see Materials and Methods for details). A representative tomographic reconstruction of the NP Au structure is shown in Fig. 1 (Panel b). It allows clearly appreciating how solid and void give rise to a maze of rounded shapes, where ligaments interconnecting at massive junctions form an interpenetrating, bi-continuous network of pores and ligaments and nodes. Ligaments and pores have similar diameter of about 42 ± 3 nm. Porosity evaluation throughout the reconstructed sample volume indicates a solid volume fraction of 0.48 ± 0.03.

3.2 “In silico” sample generation with atomistic resolution

Starting from the volumetric data previously obtained, we proceeded to decorate the corresponding SBF-SEM images with an atomistic structure corresponding to face-centered-cubic (fcc) Au lattice with spacing a = 0.40782 nm. The procedure has been performed by following three consecutive steps:

  1. 1.

    Homothetic transformation—We used the Meshmixer code [40] to apply a series of homothetic transformations to the selected experimental cubic NP Au sub-volumes. Preserving shape and inner geometries while changing the volume, we generated nine NP Au samples with side length \(L_{cell}\) ranging from 5.5 to 40.7 nm per each selected sub-volume. Figure 1 (Panel c) shows the NP Au sample with \(L_{cell}\) = 19.7 nm;

  2. 2.

    Solid phase identification—We used the Nanosculpt software [41] to identify the NP Au volume occupied by the solid phase, and build the surface mesh that encloses it;

  3. 3.

    Crystallographic information addition—We filled the selected volume with Au atoms arranged in a perfect fcc lattice with a guessed crystallographic orientation obtained by rotating the primitive lattice vectors and positioning all the atoms at integer multiples of the lattice vectors. The procedure has been repeated for several orientations observing no sizeable effects on the physics discussed below. The NP Au samples contain a number of atoms ranging from 4.95\(\times \)10\(^3\) up to 1.85\(\times \)10\(^6\).

Fig. 1
figure 1

Panel (a), a typical SEM two-dimensional image of an NP Au sample. Panel (b), representative tomographic reconstruction of an NP Au structure. Panel (c), cyan color: volumetric structure of an NP Au sample with \(L_{cell}\) = 19.7 nm. Panel (d), yellow color: corresponding structure obtained by using the “in silico” procedure described in the main text. Panel (e): superposition of the volumetric and atomistic pictures, proving the almost perfect matching between the two structures

Full size image

One out of the nine cubic NP Au samples with \(L_{cell}\) = 19.7 nm we have generated is shown in Fig. 1 (Panel d). The comparison with the corresponding experimental SBF-SEM tomographic reconstruction reported in Fig. 1 (Panel e) clearly shows how accurate is the atomistic decoration in reproducing the characteristic shapes of NP Au samples.

3.3 Molecular dynamics simulations

Once the atomistic NP Au structures have been generated, we performed a series of molecular dynamics (MD) simulations aimed at relaxing the atomic structure down to its minimum configurational energy and at calculating their elastic properties as a function of the actual atomic-scale structure. MD runs have been performed using the LAMMPS [42] simulation code and modelling the interatomic interactions by means of an embedded-atom model (EAM) potential [43] which has been previously validated as a good quantitative predictor of the elastic properties of gold systems [32]. Atomic trajectories have been aged by the velocity-Verlet algorithm with a discretization of time evolution based on a time-step as small as 1.0 fs; temperature and pressure control were operated by a Nosé-Hoover thermostat and barostat, respectively.

Upon “in silico” generation, NP Au samples have been at first relaxed by performing a conjugate-gradient minimization, until the modulus of the maximum force on each atom was less than 10\(^{-6}\) eV/Å. The samples were then equilibrated at temperature T = 300 K and pressure P = 1 Atm for 100 ps and eventually cooled down to zero temperature by a gentle simulated annealing.

After such a careful equilibration procedure, we statically applied a uniaxial tensile strain \(\epsilon _{ii}\) (where i = x, y or z) on each NP Au sample in the range \(0\%\le \epsilon _{ii}\le 2\)% at incremental steps as small as \(\Delta \epsilon _{ii}= 0.1\%\). After another conjugate-gradient minimization of each deformed configuration, we eventually calculated the resulting stress value \(\sigma _{ii}\) by averaging the per-atom stress tensor [44, 45] throughout the whole simulated structure. Due to the relatively small maximum strain applied, we assume a regime of linear elastic response and we accordingly estimate the Young’s modulus by fitting the stress–strain curve. Panel b of Fig. 3 shows a typical stress–strain curve with the corresponding fitting line obtained for a cubic NP Au sample with 40.7 nm lateral size (see next section for details). In order to further confirm that a truly linear elastic regime is indeed explored, we repeated the calculation of the Young’s modulus by reducing the maximum strain down to 1\(\%\). The estimated Young’s moduli show variations with respect to the previous case < 1\(\%\) thus confirming the absence of any plasticity effects. All the simulations have been performed using free boundary conditions by fixing the coordinates of the boundary atoms in order to avoid any spurious effect due the presence of free surfaces.

4 Results and discussion

4.1 Young’s modulus of atomistic NP Au samples

We used the Ovito software to evaluate the specific surface area \(\alpha \) of the different NP Au samples. The corresponding values obtained from the nine different NP Au sub-volumes selected per each NP Au sample size considered are plotted in Fig. 2 (Panel a) as a function of the side length \(L_{cell}\) of the cubic NP Au sample. It can be seen that \(\alpha \) monotonically decreases as function of \(L_{cell}\), in the range of the explored \(L_{cell}\) values.

The specific surface area can be used to estimate the apparent ligament diameter \(L_{ap}\). The calculation is immediate if the structure is assumed to consist of long circular rods. Accordingly,

$$\begin{aligned} L_{ap}=\frac{4}{\alpha } \end{aligned}$$
(1)

other estimates can be obtained assuming that the NP Au samples have a periodic diamond-like cubic structure interconnected by cylindrical ligaments of diameter \(D_L\) [32, 46]:

$$\begin{aligned} D_L=\frac{1.63(1.25-\phi )[1.89+\phi (0.505+\phi )]}{\alpha } \end{aligned}$$
(2)

where \(\phi \) is the solid volume fraction \(\sim \)0.49 for all samples. A more quantitative topological measure, which involves an exact relationship with the specific surface area, is the characteristic spacing \(\tilde{L}\) between the centers of neighboring ligaments. Since ligaments and pores most often have the same characteristic length, \(\tilde{L}\) can be also regarded as a measure of the ligament size [47]. In particular, \(\tilde{L}\) can be expressed as [26, 47]:

$$\begin{aligned} \tilde{L}=\left( \frac{g V_{total}}{G}\right) ^{1/3} \end{aligned}$$
(3)
Fig. 2
figure 2

Panel (a): specific surface area \(\alpha \) as a function of the side length \(L_{cell}\) of the cubic NP Au sample. Panel (b): apparent ligament diameter (\(L_{ap}\)), characteristic spacing between local centers of the solid or the pore space (\(\tilde{L}\)) and average ligament diameter (\(D_{L}\)) as a function of the cubic NP Au sample side length \(L_{cell}\)

Full size image

where G is the topological genus measuring the number of connections in a specific network, g is the scaled genus representing the number of connections in a representative volume element with size \(\tilde{L}^3\) and \(V_{total}\) is the total volume of the sample [26]. The calculations of G have been performed by estimating, using the CHomP [48] open-source code, the corresponding Betti numbers \(B_0\) and \(B_1\), representing a characteristic topological invariant of the NP Au samples. In particular, \(B_0\) is an estimate of the number of connected components while \(B_1\) represents the number of handles a the specific structure. The genus is obtained as \(G = B_1\). The calculation of the scaled genus g has been performed as [26]:

$$\begin{aligned} g=\frac{2\pi \alpha ^3}{3\sqrt{3}}(1-\xi ^2)e^{-\xi ^2/2} \end{aligned}$$
(4)

where \(\alpha \) is the specific surface area and \(\xi \) a characteristic function of the volume fraction \(\phi \):

$$\begin{aligned} \xi (\phi )=\sqrt{2}erf^{-1}(2\phi -1) \end{aligned}$$
(5)

The estimated values of \(L_{ap}\), \(D_L\) and \(\tilde{L}\) are reported in Fig. 2 (panel b) as a function of \(L_{cell}\). The estimated ligament size undergoes a consistent change with the total sample volume. In fact, they increase with \(L_{cell}\) up to a maximum value of \(\sim \)16 nm. \(L_{ap}\) represents the most straightforward as well as approximate estimate of the ligament diameter from the specific surface area \(\alpha \) (see Eq. 1), roughly assuming an NP Au microstructure made of long circular rods. A more realistic representation of the NP Au microstructure can be achieved by considering \(D_L\) (see Eq. 2), where NP Au is represented as a periodic diamond-like structure with cylindrical ligaments. However, also Eq. 2 involves an approximate relationship with the specific area giving rise to large uncertainties in the calculation of the ligament diameters. In this perspective, the most accurate estimate of the ligament diameter which involves an exact relationship with the specific surface area is the characteristic spacing \(\tilde{L}\) between the centers of neighboring ligaments (see Eq. 3) which we eventually used as the characteristic length of the selected NP Au structures.

Performed within the elastic limit, the simulated uniaxial compression determines a gradual deformation of the NP Au samples. A typical stress–strain curve is shown in Fig. 3 (panel b). Almost perfectly linear, its slope allows to univocally evaluate the Young’s modulus of the corresponding NP Au structure. The Young’s modulus E is plotted in panel a of Fig. 3 as a function of \(\tilde{L}\). It exhibits a clean dependence on the length scale. In particular, E increases approximately from 18.0 GPa to 25.3 GPa as \(\tilde{L}\) decreases.

An experimental estimate of the Young’s modulus, obtained by nanoindentation of the NP Au sample (see Materials and Methods for details), is also shown in Fig. 3 (panel a), shaded area. It is equal to 20.8 ± 2.3 GPa, in pretty good agreement with the value of 18.3 GPa estimated by atomistic simulations for large \(\tilde{L}\) values. We argue that such an agreement can be attributed to the high purity of the experimental NP Au sample and to the low level of local stresses achieved by the low-temperature thermal annealing to which the NP Au sample has been subjected.

Fig. 3
figure 3

Panel (a): calculated Young’s modulus E for the computer-generated NP Au gold samples as a function of the characteristic spacing between local centers of the solid or the pore space \(\tilde{L}\); the shaded black area represents the experimental estimate of the Young’s modulus obtained by nanoindentation. Panel (b): a typical calculated linear elastic stress-strain curve (back squares) for a sample with \(L_{cell}\) = 40.7 nm; the Young’s modulus is obtained by linear interpolation (thin red line)

Full size image

As outlined in the Introduction, several mechanisms can been taken into account in order to explain the \(E=E(\tilde{L})\) dependence reported in Fig. 3. In the following we thoroughly analyze in detail all of them, by focusing on the primary NP Au elements, namely the single ligament, which we mimic as Au fcc-nanowire with a constant diameter \(D_{nw}\).

We believe that this systematic investigation is worthy since a variation of Young’s modulus similar to the one reported in Fig. 3 has been already observed in several cases, but it has not been interpreted univocally [28, 29, 36]. In contrast, various factors have been invoked to rationalize the experimental and numerical evidence.

In the following (see Section 5), we examine the different possible mechanisms that can be expected to play a role in determining the observed mechanical response. Here, we better define the purpose of this work as follows. If we consider a porous medium composed of a linear and isotropic material without defects (dislocations, inhomogeneities, grain boundaries, and so on), the effective elastic properties are given by the classical homogenization theory [49, 50]. Now, if we consider the specific case of a porous material with a volume fraction equal to 0.5, we obtain that the effective Young’s modulus is approximately divided by 5 with respect to its bulk value, and this is true for a rather large class of microstructures [51, 52]. For bulk gold, the measured Young modulus is around 80 GPa [53,54,55], and therefore the NP Au sample with a volume fraction equal to 0.5 should have a Young’s modulus of about 16 GPa (without scale effects or defects). Thus, higher and lower values than this reference should be explained by intrinsic scale effects or by the presence of local or surface defects induced by the length scale itself. In the literature, we find experimental values of the Young’s modulus that are much larger than 16 GPa for NP Au (ligament size less than 15 nm), and therefore this point should be explained by some specific micromechanical phenomena [29, 56]. The investigation of this issue represents the main aim of the present work.

5 Discussion

5.1 Effect of surface-stress on fcc-nanowires

Free surfaces are made of low-coordinated atoms. Reduced coordination numbers imply a redistribution of electronic charge and potential energy, possibly resulting in a change of local elastic moduli near the surface region compared with bulk ones. These effects have been extensively reported for clusters, wires and films [57,58,59,60]. While the general formalism for the theoretical description of surface mechanics is fully established [60,61,62,63,64,65,66], the surface constitutive equation and its parameters are still a matter of investigation [67]. In particular, surface effects, and the resulting size-dependent elastic behavior of Au nanowires remain unexplored.

To elucidate this effect, we theoretically evaluated the Young’s modulus of three macroscopic Au wires with their main axis aligned, respectively, to the three main crystallographic directions of the fcc lattice, namely (100), (110) and (111). To do this, we assume to apply a stress of the form \(\hat{T}=T_0\mathbf {n}\otimes \mathbf {n}\), where \(\mathbf {n}\) can assume the values (100), (110) or (111) directions. It means that \( \hat{T}\vec{m} = 0 \) if \( \vec{m} \bot \vec{n} \), and therefore the lateral surfaces of the wire are supposed to be free. For the cubic structure, the stress–strain relation can be summarized as

$$\begin{aligned} T_{ii} \,=\, & {} (C_{11}-C_{12})\varepsilon _{ii}+C_{12}(\varepsilon _{11}+\varepsilon _{22}+\varepsilon _{33}), \end{aligned}$$
(6)
$$\begin{aligned} T_{ij} \,=\, & {} 2C_{44}\varepsilon _{ij}\,\,\,(\text{ if } i\ne j), \end{aligned}$$
(7)

where \(C_{11}\), \(C_{12}\) and \(C_{44}\) are the bulk elastic constants. It should be noted that Eqs. 6 and 7 reduce to the constitutive relation for an isotropic solid when \(2C_{44}=C_{11}-C_{12}\). The embedded-atom model (EAM potential) potential used for the present atomistic simulations predicts \(C_{11}\) = 78.1 GPa, \(C_{12}\) = 66.2 GPa and \(C_{44}\) = 21.2 GPa, in good agreement with experimental data [68]. By using Eqs.6 and 7, we determine the strain tensor \(\hat{\varepsilon }\), and we evaluate the directional strain \( \varepsilon _{0} = \vec{n} \cdot \hat{\varepsilon }\vec{n} \). This allows to calculate the directional Young modulus as \( E_{{\vec{n}}} = T_{0} /\varepsilon _{0} \). The Young modulus for three differently oriented wires has been eventually obtained in the following form:

$$\begin{aligned}&E_{(100)}=\frac{(C_{11}-C_{12})(C_{11}+2C_{12})}{C_{11}+C_{12}}, \end{aligned}$$
(8)
$$\begin{aligned}&E_{(110)}=\frac{4(C_{11}-C_{12})(C_{11}+2C_{12})C_{44}}{2C_{11}C_{44}+(C_{11}+2C_{12})(C_{11}-C_{12})}, \end{aligned}$$
(9)
$$\begin{aligned}&E_{(111)}=\frac{3(C_{11}+2C_{12})C_{44}}{2C_{12}+C_{11}+C_{44}}. \end{aligned}$$
(10)

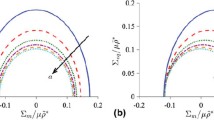
The results (dashed lines of Fig. 4, panel a) represent the asymptotic Young modulus values obtained for macroscopic \(D_{nw}\) values for which surface effects becomes less critical.

Fig. 4
figure 4

Panel (a): Young’s modulus E of gold-fcc nanowires with length \(L_z\) = 20 nm oriented along the (100), (110) and (111) directions as a function of the diameter \(D_{nw}\). Panel (b): color map of the local von Mises stress calculated on a gold-fcc nanowires with \(D_{nw}\) = 3 nm. Panel (c): Young’s modulus E vs. \(D_{nw}\) of gold-fcc nanowires containing two grain-boundaries obtained by rotating by an angle \(\theta \) the central part (half) of the NW with respect to the two top and bottom quarters

Full size image

These values have to be compared with the Young’s modulus of Au nanowires with diameter on the nanometer scale, which can be significantly affected by surface-stress effects. To this aim, we performed molecular MD simulations on fcc Au nanowires with the main axis parallel to the (100), (110) and (111) directions. We considered Au nanowires with total length \(L_z\) of 20 nm and diameter varying in the range 1.5 nm \(\le \) \(D_{nw}\) \(\le \) 15 nm. After a geometry optimization based on the conjugate-gradients algorithm, we obtained the Young’s modulus values summarized in Fig. 4 (panel a), where E is plotted as a function of the nanowire diameter \(D_{nw}\). The dashed lines account for the theoretical Young’s moduli of macroscopic Au wires.

The Young’s modulus of Au nanowires exhibits significant deviation from the macroscopic counterparts, decreasing down to 60% as the nanowire size decreases below 10 nm. Such a reduction can be entirely ascribed to surface effects. This means that surface stresses induce a softening of the Au nanowire, not a stiffening. It follows that surface effects cannot explain the Young’s modulus increase observed when the characteristic length of NP Au structure decreases. Figure 4 (panel b) shows a color map of the local von Mises stress calculated on a Au-fcc nanowires with \(D_{nw}\) = 3 nm.

5.2 Effect of grain boundaries on fcc Au nanowires

We applied the methodology described above to evaluate the Young’s modulus of an Au nanowire containing two grain boundaries obtained by the rotation of the central region of the nanowire with respect to the end regions. In this way, grain boundaries are perpendicular to the nanowire main axis. The Young’s modulus values are plotted in Fig.4 (panel c) as a function of the nanowire diameter for the different rotation angles considered. It can be seen that the presence of grain boundaries determines a reduction in the Young’s modulus as the nanowire diameter decreases. Therefore, similar to surface effects, grain boundaries cannot justify the observed stiffening of NP Au structures with increasingly reduced ligament size.

In this regard, it is worth noting that the case study we examined is the most favorable to observe a modification of the elastic properties. For instance, let us consider the uniaxial compression of the fcc Au nanowire along its main axis. It is intuitively clear that grain boundaries perpendicular to the main axis have a minor impact compared with grain boundaries with a different orientation. In particular, oblique grain boundaries are likely to give rise to grain boundary sliding events upon compression that make the Au nanowire much softer and deformable. Similar behavior has been reported for several metal nanowires [69,70,71]. For this reason, we did not investigate further along this direction.

5.3 Effect of extended defects: dislocations

Dislocations can be also expected to affect the elastic properties of NPM [72,73,74]. Many experimental works pointed out the effects of extended defects on the Young’s modulus of nanowires [75,76,77,78]. For instance, it has been shown that a high density of stacking faults in GaAs nanowires can determine a Young’s modulus enhancement up to 13% compared with the one of defect-free structures [76].

Dislocations are also expected to affect the elastic properties because of the associated stress and strain fields. We detected the presence of dislocations in the nine NP Au structures previously generated by means of the dislocation extraction algorithm [79, 80]. By analyzing the final structures obtained after the simulated annealing procedure described in Sect. 3.3, we detected the presence of a large number of different types of dislocations. A clear explanation of the mechanism ruling the dislocation nucleation is still under debate; however, different works underlined the critical role played by surface stress in triggering the nucleation of dislocations [81, 82]. In particular, we identified the total length of dislocation lines within the simulation cell by considering all type of dislocations (full dislocations, Frank partials, Shockley partials, and stair rods). The dislocation density \(\rho _D\) has been then calculated as the total dislocation length divided by simulation cell volume [83]. The estimated \(\rho _D\) values are in good agreement with previous works on NP Au [84, 85].

Fig. 5
figure 5

Panel (a): dislocation density \(\rho _D\) as a function of the characteristic spacing between local centers of the solid or the pore space \(\tilde{L}\). Panel (b): Young’s modulus as a function of the dislocation density \(\rho _D\) showing a reasonable linear dependence (red dashed line)

Full size image

Figure 5 (panel a) shows the dislocation density \(\rho _D\) as a function of the characteristic spacing between local centers of the solid or the pore space \(\tilde{L}\) calculated for the nine NP Au samples under investigation. We clearly observe a sizeable \(\rho _D\) reduction by increasing \(\tilde{L}\); this suggests that the occurrence of large \(\rho _D\) values, observed for samples with relatively small \(\tilde{L}\), gives rise to a stiffening effect, in turn resulting as an increase of the Young’s modulus. This is fully confirmed in Fig. 5 (panel b), where a reasonable linear correlation is observed between the Young’s modulus and the corresponding \(\rho _D\) value, providing evidence that high dislocation densities can lead to a sample stiffening.

The observed increasing \(\rho _D\) value upon decreasing \(\tilde{L}\) in Fig. 5 (panel a) can be attributed to the effect of surface stress: dislocations are firstly generated at the surface and then migrate into the bulk. Since, as shown in Fig. 2 , the specific surface area \(\alpha \) also increases by decreasing \(\tilde{L}\), and we can reasonably expect a corresponding increase in the number of nucleated dislocations at the ligament surfaces, thus increasing the \(\rho _D\) value.

In order to explain the increase of the Young’s modulus as a function of \(\rho _D\) observed in Fig. 5 (panel b), we further investigated the effect of dislocations on the mechanical response of individual ligaments, by considering an Au nanowire with the main axis oriented along the (100) crystallographic direction, a diameter of 3 nm and a total length of 20 nm. Specifically, we evaluated the Young’s modulus of the nanowire decorated with an increasing number of dislocations.

Fig. 6
figure 6

Young’s modulus E of a gold fcc nanowire (oriented along the (100) direction with D\(_{nw}\) = 3 nm and L\(_{z}\) = 20 nm) as a function of the edge-dislocation density \(\rho _D\). Black dots and line: dislocations are positioned so as to maximize their distance. Red dots and lines: dislocations are placed in totally random positions

Full size image

Although different types of dislocations can be present in a typical NP Au sample, for this proof-of-concept calculation, we restricted our investigation to edge dislocations, which can be easily generated in any specific position of the crystalline lattice [86].

We carried out calculations using two different dislocation arrangements. In one case, dislocations were suitably placed to maximize the distance between them. In the other one, their positions were selected randomly. As shown in Fig. 6, in both cases, the Young’s modulus E undergoes a marked increase up to \(\sim \)25% for dislocation densities of \(\sim \)2\(\times \)10\(^{17}\) m\(^{-2}\), showing that dislocations can induce a significant stiffening of NP Au ligaments.

We finally investigated the stiffening effect further estimating the local Young’s modulus of a fcc Au nanowire containing a single edge dislocation. For each atom i of a gold-fcc nanowire containing a single edge-dislocation positioned at z = 6.3 nm, we estimated the local Young modulus \(E^{i}\) by calculating the ratio between the modulus of the per-atom stress tensor \(\sigma ^i\) as implemented in the LAMMPS package and the corresponding per-atom elastic strain tensor \(\epsilon ^i\) as implemented in the Ovito package. Figure 7 (panel a) shows a map of the corresponding local Young modulus (i.e., \(\sigma ^i_{zz}\)/\(\epsilon ^i_{zz}\)) showing a sudden increase up to a value \(\sim \) 40 GPa in the region surrounding the dislocation confirming that the presence of dislocations locally increases the elastic properties of the ligaments. This is a clear evidence that dislocation effects stem from the local enhancement of elastic properties.

5.4 Theoretical considerations on dislocation effects

Based on the numerical evidence concerning individual dislocations, we developed an elastic model to estimate the effects of multiple dislocations. We considered a nanowire with n edge dislocations generating a surface \(s_d\) over the total wire section S. We supposed that the effective longitudinal width of each dislocation is \(\ell _d\) over the total wire length L. Additionally, we assumed that the effective volume of the dislocation \(\ell _ds_d\) corresponds to an inhomogeneity with Young’s modulus \(E_d>E\). A procedure of elastic homogenization [87, 88] of the nanowire elastic response with the population of dislocations eventually leading to the effective Young’s modulus as

$$\begin{aligned} \frac{1}{E_{eff}}=\frac{1}{E}\left( 1-n\frac{\ell _d}{L}\right) +\frac{1}{E_d\frac{s_d}{S}+E\left( 1-\frac{s_d}{S}\right) } n\frac{\ell _d}{L}, \end{aligned}$$
(11)

Eq. 11 is correct for \(n\ll L/\ell \) as far as interactions between the elastic fields of nearby dislocations are negligible.

Fig. 7
figure 7

Panel (a): map of the Young’s modulus (i.e., \(\sigma ^i_{zz}\)/\(\epsilon ^i_{zz}\)), calculated as the ratio between the local stress and local strain values on a gold-fcc nanowire (oriented along the (100) direction with D\(_{nw}\) = 3 nm and L\(_{z}\) = 20 nm) with a single edge-dislocation positioned at z = 6.3 nm. Panel (b): black squares: Young’s modulus E of a gold fcc nanowire (oriented along the (100) direction with D\(_{nw}\) = 3 nm and L\(_{z}\) = 20 nm) as a function of the number of edge-dislocations. Red line: effective Young’s modulus obtained from Eq. 11 by considering \(L=20\)nm, \(\ell _d/L\simeq 1/10\), \(s_d/S\simeq 1/2\), \(E=20.5\) GPa and \(E_d=40\) GPa

Full size image

Theoretical predictions are compared with numerical findings in Fig. 7 (panel b). Data refer to an Au nanowire with total length L = 20 nm and diameter \(D_{nw}\) = 3 nm, dislocation width \(\ell _d\) = 2 nm, surface associated with dislocations \(s_d\) = 14.1 nm\(^2\), bulk Au Young’s modulus E = 20.5 GPa and locally enhanced Young’s modulus \(E_d\) = 40 GPa. It can be further seen that homogenized elastic theory satisfactorily best fits the atomistic data, thus supporting the hypothesis that edge dislocations act as reinforcing dispersoids in the Au nanowire. We note that atomistic simulations involving more than seven dislocations indicate that the Young’s modulus reaches a plateau value of about 24 GPa. We argue that interactions among dislocations, not included in the homogenized elastic model, become increasingly more intense as the dislocation density increases, thus depressing the reinforcing effect.

6 Conclusions

In conclusion, we used experimental, simulative and theoretical methods to investigate the mechanical behavior of nanoporous Au by addressing the long-standing debate of the observed Young’s modulus increases upon characteristic length reduction. To this aim, we have used an experimental tomographic reconstruction to generate NP Au samples with atomistic resolution by mapping the initial volumetric data. Atomistic simulations confirm that nanoporous Au stiffens as ligaments become finer, reproducing the experimental results obtained by nanoindentation. A combination of numerical and theoretical findings allows to rule out the effect of surface stress and grain boundaries. In contrast, we argue that dislocations may act as strengthening agents that enhance the nanoporous Au Young’s modulus. The results obtained emphasize the importance of line defects and can address future research to investigate the mechanical properties of nanoporous metals.