Learning to increase matching efficiency in identifying additional b-jets in the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ process

Abstract

The $\text {t}\bar{\text {t}}\text {H}(\text {b}\bar{\text {b}})$ process is an essential channel in revealing the Higgs boson properties; however, its final state has an irreducible background from the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ process, which produces a top quark pair in association with a b quark pair. Therefore, understanding the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ process is crucial for improving the sensitivity of a search for the $\text {t}\bar{\text {t}}\text {H}(\text {b}\bar{\text {b}})$ process. To this end, when measuring the differential cross section of the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ process, we need to distinguish the b-jets originating from top quark decays and additional b-jets originating from gluon splitting. In this paper, we train deep neural networks that identify the additional b-jets in the ${\text {t}}{\bar{\text {t}}}{\text {b}}{\bar{\text {b}}}$ events under the supervision of a simulated $\text{t}\bar{\text{t}}\text{b}\bar{\text{b}}$ event data set in which true additional b-jets are indicated. By exploiting the special structure of the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event data, several loss functions are proposed and minimized to directly increase matching efficiency, i.e., the accuracy of identifying additional b-jets. We show that, via a proof-of-concept experiment using synthetic data, our method can be more advantageous for improving matching efficiency than the deep learning-based binary classification approach presented in [1]. Based on simulated $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event data in the lepton+jets channel from pp collision at $\sqrt{s}$ = 13 TeV, we then verify that our method can identify additional b-jets more accurately: compared with the approach in [1], the matching efficiency improves from 62.1$\%$ to 64.5$\%$ and from 59.9$\%$ to 61.7$\%$ for the leading order and the next-to-leading order simulations, respectively.

1 Introduction

Since discovering the Higgs boson at the large hadron collider (LHC) [2, 3], its consistency with the standard model has been tested extensively in many different channels. In 2018, there were observations of Higgs boson production in association with a top quark pair ($\text {t}\bar{\text {t}}\text {H}$), which is an important channel in revealing the Higgs boson properties [4, 5]. As the branching fraction of the Higgs boson to $\text {b}\bar{\text {b}}$ is the largest, among $\text {t}\bar{\text {t}}\text {H}$, the $\text {t}\bar{\text {t}}\text {H}(\text {b}\bar{\text {b}})$ process can be measured with the best statistical precision. However, the final state of the $\text {t}\bar{\text {t}}\text {H}(\text {b}\bar{\text {b}})$ process has an irreducible background from the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ process, which produces a top quark pair in association with a b quark pair. Therefore, understanding the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ process precisely is essential for improving the sensitivity of a search for the $\text {t}\bar{\text {t}}\text {H}(\text {b}\bar{\text {b}})$ process.

For the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ process, the theoretical next-to-leading-order (NLO) calculation was done [6] in the same phase space where the inclusive cross sections were measured at $\sqrt{s}$ = 8 TeV in the CMS experiment [7]. This analysis was updated with more data at $\sqrt{s}$ = 13 TeV recently, including inclusive cross section measurements in the dilepton channel [8], the lepton+jets channel [9], and the hadronic channel [10]. The inclusive and the differential $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ cross sections were also measured in the ATLAS experiment [11]. However, these measurements in different channels show consistently that the measured inclusive cross sections are higher than the theoretical predictions and that there are large uncertainties in both theoretical and experimental results.

Fig. 1

Feynman diagram of the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ process in the lepton+jets channel

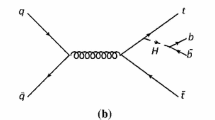
The final state of the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ process contains b-jets from top quark decays and additional b-jets from gluon splitting, as shown in the Feynman diagram in Fig. 1. By identifying the origin of the b-jets in the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ process and measuring their respective differential cross sections, we can provide more information to the theorists to lessen the mismatch between the theoretical and experimental results and the uncertainties in both results. In this regard, we consider the problem of predicting which b-jets correspond to the additional b-jets originating from gluon splitting based on the kinematic observables derived from the final state objects in the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ process.

Due to the high-dimensional nature and complicated stochastic generative processes of the relevant observables, however, there are no simple rules to distinguish between the b-jets from top quark decays and those from gluon splitting in real $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event data. It is also challenging to manually engineer features useful for the task, even if we have some knowledge of the underlying physics model. Fortunately, recent advances in neural networks and deep learning have enabled discovering useful discriminative patterns in the data by using multiple network layers. The process in the learning algorithm via multiple layers finds simple and disentangled representations of data and improves the predictions [12].

In various high-energy physics problems under similar challenges mentioned above, deep learning techniques have been applied to analyze high-dimensional and complex data obtained from the LHC experiments [13,14,15,16]. In jet identification problems, of which the goal is to classify the type of jets from data, many deep learning methods have been successful in flavor tagging, jet substructure tagging, and quark/gluon tagging [17,18,19,20,21,22,23,24]. More relevant to our problem are the jet-parton assignments for the $\text {t}\bar{\text {t}}$ process [25] and the $\text {t}\bar{\text {t}}\text {H}$ process [26], but they have not specifically attempted to identify the additional b-jets in the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ process.

In this paper, we apply deep learning techniques to identify the two additional b-jets originating from gluon splitting from the other b-jets originating from top quark decays in the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ process. Specifically, we train deep neural networks (DNNs) that identify additional b-jets under the supervision of a simulated $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event data set in which true additional b-jets are indicated.

A few learning-based attempts have already been made to tackle this problem. In the CMS experiment, using early data at $\sqrt{s}$ = 8 TeV, identifying the additional b-jets was attempted for the first time with a boosted decision tree (BDT) in the dilepton channel [27]. Another recent work trained a deep neural network (DNN) as a binary classifier to determine whether a pair of b-jets is a pair of additional b-jets in the lepton+jets channel [1]. However, during training, these methods do not exploit the fact that every $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event has at least a pair of additional b-jets and only a single pair for most cases, thus giving up further possible improvements in the identification performance. More strictly speaking, these binary classification approaches cannot even be considered as exactly solving the targeted problem. This is because we do not have to classify for every b-jet pair if it is an additional b-jet pair; instead, only one additional b-jet pair needs to be correctly identified among the b-jets contained in each event.

In this study, by defining a learning problem that is much more specialized to the problem of identifying additional b-jets in the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ process, we further improve the identification performance than the previous binary classification approach. Specifically, we design a DNN-based model whose prediction conforms to the special structure of $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event data, where (in most cases) there is only one additional b-jet pair in each event. We then train this model to directly maximize the matching efficiency, i.e., the ratio of successfully identified events to the total number of events, the improvement of which precisely matches our goal. Since the matching efficiency itself is a highly non-smooth objective, we suggest surrogate objective functions suitable for gradient-based optimization. We discuss the advantages our method can have over the binary classification approach via a proof-of-concept experiment using synthetic data. We then show that we can identify additional b-jets more accurately by increasing matching efficiency directly rather than the binary classification accuracy via experiments using simulated $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event data. In the experiments, we follow the data simulation scheme of [1] for both leading order and next-to-leading order calculations and consider the lepton+jets channel, which is advantageous for precise measurements due to its large branching fraction, as discussed in [1].

The paper is organized as follows. We define the deep learning-based additional b-jet identification problem in Sect. 2. We then propose methods to maximize matching efficiency directly in Sect. 3, discussing its difference to the binary classification approach. Section 4 presents experimental results on simulated $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event data in the lepton+jets channel.

2 Deep learning-based additional b-jet identification

2.1 Problem definition

Our purpose is to precisely predict which of the b-jets in a $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event correspond to the additional b-jets from gluon splitting. To achieve this goal, we train deep neural networks that can identify additional b-jets using a simulated $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event data set in which true additional b-jets are indicated.

We now describe how the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event data are defined. We regard a $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event datum as the collection of every pair of b-jets in the event. Each b-jet pair is represented by a multi-dimensional vector consisting of kinematic observables derived from its b-jets and other final state objects in the event. (Further details on the considered kinematic observables are provided in Sect. 4.1.) Suppose there are N $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event data. Denote by $c_i$, $i=1,\ldots ,N$ the numbers of b-jet pairs in each event and by F the dimension of the vector representing each b-jet pair. Then denote the event matrices comprised with all b-jet pairs (or vectors) in each event as $M_i \in {\mathbb {R}}^{c_i \times F}$, $i=1,\ldots ,N$. Most $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ events contain a single pair of additional b-jets among the b-jet pairs in the event, which are the cases that our model assumes. When an event in our data has more than one pair of additional b-jets, e.g., from two gluon splittings [28], we consider the pair consisting of the two additional b-jets with the highest transverse momentum $p_{\mathrm{T}}$ as the single pair of additional b-jets to identify.¹ Let $y_i \in \{1, \ldots , c_i\}$, $i=1,\ldots ,N$ be the indices to indicate the pair of additional b-jets in each event. Here, the additional b-jet pair becomes the signal to be sought, while the other pairs form the background.

Our performance criterion is the matching efficiency, i.e., the accuracy of identifying additional b-jet pair (or the signal) from each event. Given N $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event data $\{(M_1, y_1),$ $\ldots ,$ $(M_N, y_N)\}$, matching efficiency is defined as follows:

$$\begin{aligned} \text {Matching efficiency} = \frac{1}{N}\sum _{i=1}^N \delta (y_i, \hat{y}(M_i)), \end{aligned}$$

(1)

where $\delta (\cdot , \cdot )$ denotes the Kronecker delta function, i.e., $\delta (y, \hat{y}) = 1$ if $y = \hat{y}$ and zero otherwise, and $\hat{y}(M_i)$ denotes the index predicted on the event matrix $M_i$. Increasing matching efficiency becomes our ultimate goal to train the identification models.

2.2 Previous approach

Based on deep learning methods, there has been an attempt to identify additional b-jets in the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ events [1]. Specifically, they trained a binary classifier to discriminate whether each pair of b-jets is an additional b-jet pair or not. For this purpose, all the training event data $\{(M_1, y_1), \ldots , (M_N, y_N)\}$ are separated to construct the b-jet pair data $\{(x_1, \xi _1), \ldots , (x_{N_p}, \xi _{N_p})\}$, where $x_i \in {\mathbb {R}}^F$ and $\xi _i \in \{0, 1\}$ for $i = 1, \ldots , N_p$ are, respectively, individual b-jet pairs and their corresponding labels, and $N_p = \sum _{i=1}^N c_i$ is the total number of b-jet pairs. Here, the labels are 1 for additional b-jet pairs and 0 otherwise. Note that, when collecting pairs from a single event, there is only one pair with the label of 1 according to the assumption used in Sect. 2.1.

The binary classifier is modeled as a deep feedforward neural network $f: {\mathbb {R}}^F \rightarrow [0,1]$ as detailed in Appendix B. Given an input b-jet pair, it returns the value between zero and one, which can be conceptually interpreted as the probability for the input pair to be label 1. The model parameters are trained to minimize the binary cross-entropy loss ($L_{BCE}$) defined as follows:²

$$\begin{aligned} L_{BCE} = -\frac{1}{N_p} \sum _{i=1}^{N_p} \left( \xi _i \log f(x_i) + (1-\xi _i) \log (1-f(x_i)) \right). \end{aligned}$$

(2)

After training the model, when a prediction is to be made for an event data unseen during training, e.g., that from a test data set, they select the pair with the highest model output value to be the pair of additional b-jets.

Although the suggested method showed better performance than another method using a physics-based feature, it is difficult to say that this method is optimally designed to increase the matching efficiency for a couple of reasons. First, there is no need to classify for every b-jet pair if it is an additional b-jet pair as in this approach. Instead, only one additional b-jet pair must be correctly identified in each event. In terms of training objectives, the approach in [1] is to maximize the binary classification accuracy for b-jet pairs, whereas it is desired to maximize the matching efficiency for $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ events; thus, the objective pursued in [1] does not precisely match our goal. Methods that maximize the binary classification accuracy would not generally achieve better matching efficiency than methods that directly maximize the matching efficiency. Second, while training the DNNs on how to process each b-jet pair in [1], they do not utilize information on the other b-jets involved in the corresponding event. If such information is provided during training, further performance improvements will be available by allowing the DNNs to extract more useful features for identifying additional b-jet pairs from comparing b-jets (or b-jet pairs) within each $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event. Considering the above discussion, in the next section, we propose a learning method much more specialized for this problem, which directly maximizes the matching efficiency and utilizes more information available in each $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event data during training.

3 Directly maximizing matching efficiency

3.1 Prediction model

We first propose the form of our prediction model to be used in maximizing matching efficiency directly. Given event matrices $M_i \in {\mathbb {R}}^{c_i \times F}$, $i=1,\ldots ,N$ as the input, our model $f: {\mathbb {R}}^{c_i \times F} \rightarrow [0,1]^{c_i}$ is set to³

$$\begin{aligned} f = (f_1, \ldots , f_{c_i}), \end{aligned}$$

(3)

where the output of each $f_j: {\mathbb {R}}^{c_i \times F} \rightarrow [0,1]$ can be interpreted as the probability of the j-th b-jet pair (or the j-th row of $M_i$) being the pair of additional b-jets for $j=1,\ldots ,c_i$. Here, the output elements should sum to one, i.e., $\sum _{j=1}^{c_i} f_j(M_i) = 1$, so that the output $f(M_i)$ can be a proper distribution for $i=1,\ldots ,N$. By defining the output as such a probability distribution, this model inherently assumes the presence of one additional b-jet pair in every $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event. Moreover, the additional b-jet pair is straightforwardly predicted to be the pair that returns the highest probability, i.e.,

$$\begin{aligned} \hat{y}(M_i) = \mathop{{\mathrm{argmax}}}\limits_{j \in \{1, \ldots , c_i\}} f_j(M_i), \quad i=1,\ldots ,N. \end{aligned}$$

(4)

We now briefly explain how to model such an f using deep neural networks. The constraint $\sum _{j=1}^{c_i} f_j(M_i) = 1$ on the prediction model in eq. (3) is usually realized by using the softmax function on some activation value $(g_1(M_i), \ldots , g_{c_i}(M_i)) \in {\mathbb {R}}^{c_i}$ as

$$\begin{aligned} f_j(M_i) = \frac{\exp (g_j(M_i))}{\sum _{k=1}^{c_i}\exp (g_k(M_i))}, \quad j=1,\ldots , c_i, \end{aligned}$$

(5)

where $g_j: {\mathbb {R}}^{c_i \times F} \rightarrow {\mathbb {R}}$ denotes a function to return the j-th activation value. In modeling $g_j$, $j=1,\ldots ,c_i$, we can make another simplification to deal with different $c_i$s (or the numbers of b-jet pairs) for each datum as follows:

$$\begin{aligned} g_j(M_i) = g(M_{i,j:}), \quad j=1,\ldots ,c_i, \end{aligned}$$

(6)

where $M_{i,j:} \in {\mathbb {R}}^F$ denotes the j-th row of $M_i\in {\mathbb {R}}^{c_i \times F}$, and $g: {\mathbb {R}}^{F} \rightarrow {\mathbb {R}}$ can be modeled as a deep neural network as explained in Appendix B. Note that this model applies identical operations to each b-jet pair (or row vector); hence permutation-equivariant, i.e., the output $f(M_i) \in [0,1]^{c_i}$ is permuted identically according to the permutation of rows of the input $M_i \in {\mathbb {R}}^{c_i \times F}$. Moreover, this model allows processing each b-jet pair in conjunction with the other b-jet pairs included in the corresponding event during training, while having similar modeling complexity to the binary classifier explained in Sect. 2.2.

3.2 Surrogate loss functions

When training the prediction model f, it is not easy to maximize the matching efficiency in eq. (1) itself since it is a highly non-smooth objective, i.e., not differentiable in many different regions of the model parameter space, and even returns zero gradients when differentiable. Therefore, we propose appropriate relaxations or surrogates of eq. (1) which can be optimized by usual gradient-based methods to increase matching efficiency directly.

In terms of our model presented in the previous section, observe that the $\delta (y_i, \hat{y}(M_i))$ value in eq. (1) becomes one if $f_{y_i}(M_i)$ is the largest among $\{f_1(M_i), \ldots , f_{c_i}(M_i)\}$ and zero otherwise according to eq. (4). Hence, we can maximize $f_{y_i}(M_i)$ instead of $\delta (y_i, \hat{y}(M_i))$ while minimizing $f_{j}(M_i)$ for $j \ne y_i$ to make the $\delta (y_i, \hat{y}(M_i))$ value one and consequently increase the matching efficiency. Since the usual machine learning problems are formulated as ‘minimizing losses,’ we define our first surrogate loss function (denoted $L_1$) as follows:⁴

$$\begin{aligned} L_1 = -\frac{1}{N}\sum _{i=1}^N \left( f_{y_i}(M_i) - \sum _{j\ne y_i} f_j(M_i) \right) . \end{aligned}$$

(7)

Our problem can also be considered as a ranking problem, in which the goal is to assign the highest rank (or score) to the additional b-jet pair in each event matrix. To tackle the ranking problem, the authors in [29] first model the posterior probability that a datum is ranked higher than another based on the score difference between the two data, with the score obtained from a neural network. They then propose a probabilistic ranking loss function that compares the posterior to the target posterior (reflecting the desired ranking) via the cross-entropy loss and minimize the loss on the available training data pairs to obtain neural network parameters. Similarly, we can guide our model to return a higher rank for the additional b-jet pair rather than the other pairs in each event by minimizing the following loss function (denoted $L_2$):

$$\begin{aligned} L_2 = -\frac{1}{N}\sum _{i=1}^N \sum _{j\ne y_i} \log \left( \frac{f_{y_i}(M_i)}{f_{y_i}(M_i) + f_j(M_i)}\right) , \end{aligned}$$

(8)

where the posterior inside the log can be interpreted as the probability of the $y_i$-th b-jet pair being ranked higher than the j-th b-jet pair.

From a slightly different perspective, it is possible to deem an event matrix’s row indices as distinctive categories to which the additional b-jet pair belongs. The problem can then be viewed as a multi-class classification problem to predict the class, i.e., the additional b-jet pair index, for each event matrix; corresponding classification accuracy becomes exactly the same as the matching efficiency in eq. (1). Hence, the widely used (categorical) cross-entropy loss (denoted $L_3$) for these classification problems can also serve as our surrogate loss:

$$\begin{aligned} L_{3} = -\frac{1}{N}\sum _{i=1}^N \log f_{y_i}(M_i). \end{aligned}$$

(9)

Based on this interpretation, though not used as often as the cross-entropy loss in classification problems, we can also consider minimizing the mean squared error loss (denoted $L_4$) defined as:

$$\begin{aligned} L_{4} = \frac{1}{N} \sum _{i=1}^N \Vert f(M_i) - \text {one}\_ \text {hot}(y_i)\Vert ^2, \end{aligned}$$

(10)

where $\text {one}\_\text {hot}(y_i) = [0, \ldots , 1, \dots , 0] \in {\mathbb {R}}^{c_i}$ is the one-hot encoding whose $y_i$-th element is one.

3.3 A proof-of-concept experiment

We now conduct a proof-of-concept experiment using synthetic data to provide an insight into how minimizing the proposed loss functions can be advantageous over the binary classification approach. For this purpose, we generate two-dimensional data points and construct matrices from them to follow the assumption in the structure of the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event data, which have only a single row vector of label 1 (as the signal) in each matrix. Specifically, each matrix consists of a signal vector in class 1 sampled from the two-dimensional normal distribution and three background vectors in class 0 obtained by translating the class 1 vector to the left slightly and injecting noise along the vertical axis, as shown in Fig. 2a. This setup will make the binary classification approach suffer from a significant overlap between data from classes 0 and 1 since, during training, all vectors are given mixed regardless of their originated matrices, as shown in Fig. 2b.

Fig. 2

Experimental results from synthetic data. (a) An example matrix is illustrated. (b) The level sets of the trained models are drawn over the data scatter plot. (c) Matching efficiencies (evaluated on a test data set) for each of the loss functions are shown

We train simple linear models to identify class 1 data by minimizing the suggested loss functions in eqs. (7), (8), (9), (10), and the binary cross-entropy loss in eq. (2). (Further details of the experiments are explained in Appendix C.) For each of the trained models, we plot their decision boundaries or level sets, i.e., the set of input points with identical output values, in Fig. 2b. Considering the structure of the matrices, the models should return larger outputs for the points with larger horizontal axis values for a successful identification; hence, the vertical decision boundaries or level sets are desired. However, the binary classification approach gives a somewhat arbitrary decision boundary due to the significant overlap between classes. On the other hand, observe that the level sets of the models obtained from minimizing eqs. (7), (8), (9), (10) are almost vertical as desired. Thanks to the loss functions formulated to exploit the special structure of the data, these models can learn how to discriminate the data inside each matrix.

The matching efficiency of each model is evaluated on a test data set sampled in the same way as the training data set. According to Fig. 2c, the models trained using the proposed loss functions obtain matching efficiency of one, i.e., identify the class 1 data perfectly for all matrices, while that from the binary classification approach shows a much lower value. Although the setup is dexterously designed to reveal the difference between the approaches apparently, this experiment effectively verifies the concept that minimizing the suggested loss functions can be more beneficial than the binary classification approach in identifying a single signal vector from each matrix where all other vectors belong to the backgrounds.

4 Experiments on simulated $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event data

4.1 Simulated data set

We now examine if the proposed methods can achieve better matching efficiency than the binary classification approach on simulated $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event data. Here, we follow the overall simulation scheme of [1] to generate data. The simulated $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ events in pp collisions are produced at a center-of-mass energy of 13 TeV. Using the MadGraph5_aMC@NLO program (v2.6.6) [30], we generated 31 million events and 8.2 million events for the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ samples at the leading order and the next-to-leading order, respectively. These events are further interfaced to Pythia (v8.240) [31] for the hadronization. A W boson decays through MadSpin [32] with explicitly specifying leptonic or hadronic decay, and the events are generated in a 4-flavor scheme, where the b quark has mass.

The generated events are processed using the detector simulation with the DELPHES package (v3.4.1) [33] for the CMS detector. The physics objects used in this analysis are reconstructed based on the particle-flow algorithm [34] implemented in the DELPHES framework. In the DELPHES fast simulation, the final momenta of all the physics objects, such as electrons, muons, and jets, are smeared as a function of both the transverse momentum $p_{\mathrm{T}}$ and the pseudorapidity $\eta$ so that they can represent the detector effects. The efficiencies of identifying the electrons, muons, and jets are parameterized as functions of $p_{\mathrm{T}}$ and $\eta$ based on information from the measurements made by using the CMS data [33]. The particle-flow jets used in this analysis are reconstructed using the anti-$k_{\mathrm{T}}$ algorithm [35] with a distance parameter of 0.5 to cluster the particle-flow tracks and particle-flow towers.

The b-tagging efficiency is around 50$\%$ at the tight-working point of the deep combined secondary vertex (DeepCSV) algorithm [20], which shows the best performance in the CMS measurement [36]. The corresponding fake b-tagging rates from the c-flavor and the light flavor jets are set to around 2.6$\%$ and 0.1$\%$, respectively.

Once events are produced, the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ process is defined based on the particle-level jets obtained by clustering all final-state particles at the generator level. A jet is considered as an additional b-jet if the jet is matched to the last b quark (before hadronization in the decay chain) that is not directly from a top quark decay within $\Delta R(j, q) = \sqrt{\Delta \eta (j, q)^2 + \Delta \phi (j, q)^2} < 0.5$, where j denotes jets at the generator level, and q denotes the last b quark. The additional b-jets are required to be within the experimentally accessible kinematic region of $p_{\mathrm{T}} >$ 20 GeV and $|\eta | < 2.5$. An event is considered a valid $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event when there are at least two additional b-jets at the generator level that satisfy these kinematic acceptance requirements. Under this condition to be a valid $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event, 67$\%$ of the generated samples remain. The other 33$\%$ of the events do not pass the acceptance requirement and are not considered as signal events in our analysis.

We applied the following event selection to remove the main backgrounds from the multi-jet events and W+jet events. At the reconstruction level of the lepton+jets channel, the event must have exclusively one lepton with $p_{\mathrm{T}} >$ 30 GeV and $|\eta | < 2.4$. According to this condition, 19.7$\%$ of the generated events survive. Jets are selected with a threshold of $p_{\mathrm{T}} >$ 30 GeV and $|\eta | < 2.5$. The $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event has the final state of four b-jets (including the two additional b-jets) and two jets from one of the two W bosons in top quark decays. However, the detector acceptance and the efficiencies of the b-jet tagging algorithms are not 100$\%$; hence, some of the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ events have fewer jets at the reconstruction level. We discarded the events containing b-jets fewer than three or jets fewer than six in our experiments, resulting in 212,095 and 25,985 matchable events at the leading order and the next-to-leading order, respectively. Here, matchable events denote our signal events containing two additional b-jets at the detector level, which match any additional b-jet at the generator level within $\Delta R < 0.4$.

After the event selection, we construct data for each $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event by gathering every pair of b-jets in the event, as explained in Sect. 2.1. Specifically, the variables representing a pair of b-jets are selected considering all possible combinations of the four-vectors (as low-level features) of the final state objects, such as selected two b-tagged jets, a lepton, a reconstructed hadronic W boson, and missing transverse energy (MET). We consider the total of 78 variables as listed in Section V of [1], which consists of two sets of 27 variables involving each b-tagged jet only and 24 variables involving both b-tagged jets together.

4.2 Experimental details

We train our model defined in Sect. 3.1 on simulated $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event data by minimizing the proposed loss functions. We also consider two models trained to minimize the binary cross-entropy loss under different input feature compositions for comparison purposes. For the first model denoted by ‘Model 1,’ we follow the previous binary classification approach in [1] and use 78 variables to represent each b-jet pair as explained in Sect. 4.1. The second model is inspired by [25, 26], which formulate the jet-parton assignment problem as a binary classification one that determines whether each permutation of jets within an event is in the desired parton order. In this model denoted by ‘Model 2,’ we expand variables for each b-jet pair to contain those involving the other b-jets in the corresponding event, thereby utilizing the information inside the event not used in Model 1. Specifically, the variables to represent each b-jet pair are expanded as $x'_i = [x_i^{\top }, z_{i,1}^{\top }, \ldots , z_{i,{B-2}}^{\top }]^{\top } \in {\mathbb {R}}^{78+27\times (B-2)}, i=1, \ldots , N_p$, where $x_i \in {\mathbb {R}}^{78}$ is the variable for individual b-jet pairs used in Model 1, $z_{i,j} \in {\mathbb {R}}^{27}, j = 1, \ldots , B-2$ denote the variables involving distinct single b-jets which are included in the event containing $x_i$ but are not included in the pair $x_i$, and B is the maximum value of the number of b-jets in the events in the data set.⁵ Since there are no specified rules to determine the order of single b-jets in each event, we consider all possible permutations during training by randomly shuffling the order and constructing different input values for every iteration. To predict the additional b-jet pair in an event using this model, we collect the output values from all possible permutations (of single b-jet variables) for each pair and choose the pair with the highest model output value. Note that, despite utilizing more information from $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event data than Model 1, using Model 2 ends up maximizing the binary classification accuracy by minimizing $L_{BCE}$. Therefore, it would be difficult for this method to yield a better matching efficiency than our method of directly maximizing the matching efficiency, in a similar context discussed in Sect. 2.2.

When constructing deep neural networks (DNNs) for eq. (3) (or g in eq. (6) to be specific) and eq. (11) (in Appendix B), we utilize the L2 regularizer (only for the parameters in the first layer of DNNs) with a coefficient of 0.01 and the dropout layer [37] with a dropout rate of 0.08 to prevent overfitting on training data, and the batch normalization layer (except for the case of $L_2$) [38] to increase the training speed. Adam optimizer [39] is applied to train the models with a batch size of 2,048 and a learning rate of 1e-3. We conducted all the experiments using Keras [40].

The data set is split into training, validation, and test sets with varying sizes. The considered training/validation/test data split configurations are (i) 10,000/2,500/10,000 events, (ii) 40,000/10,000/10,000 events, (iii) 161,676/40,419/10,000 events for the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ samples at the leading order (LO), and (iv) 4,000/1,000/5,000 events, (v) 8,000/2,000/5,000 events, (vi) 16,788/4,197/5,000 events for the samples at the next-to-leading order (NLO). We use the validation set to determine hyperparameters required for training the deep neural network, such as the number of hidden layers L, the dimension of hidden variables d, and the number of training epochs T; we consider $L \in \{2, 4, 6, 8, 10\}$, $d \in \{25, 50, 100, 200\}$, and $T \in \{50, 100, 150,$ $200\}$ in the search. For each data split condition and loss function, we first train the models according to each hyperparameter setting using the training set and select the hyperparameter that gives the best matching efficiency on the validation set, averaged over five runs for different random seeds to split the data sets. The hyperparameter tuning results are reported in Appendix D.

After the hyperparameter tuning, we train models by minimizing the loss functions using both training and validation sets from each data split configuration. The final performance on the test set is then averaged over fifty runs (with ten different random initializations of the model parameters for five different random seeds to split the data sets). For the performance metric, we consider the matching efficiency defined in eq. (1) and the area under the ROC curve (AUC), a widely used metric for the binary classification. Note that for the models minimizing the surrogate loss functions, the AUC is calculated for a binary classifier that classifies each b-jet pair to class 1 when the model output for the pair, e.g., values from eq. (6), exceeds a given threshold and to class 0 otherwise.

4.3 Experimental results

The matching efficiency and the AUC score of the trained models are reported in Tables 1 and 2 for the leading-order (LO) samples and the next-to-leading order (NLO) samples, respectively. The first row in each table represents the sample configurations with the number of data used to train the models in parentheses.

From the tables, we can make a few observations. First, minimizing the binary cross-entropy loss ($L_{BCE}$) using Model 2 yields the best AUC score, but this does not necessarily lead to the best matching efficiency. Comparing Model 1 and Model 2 (both minimizing $L_{BCE}$) shows that the matching efficiency can be improved by simply extending the input features to provide more information about the event to which each b-jet pair belongs. However, such an improvement is not as much as minimizing our proposed loss functions designed to maximize the matching efficiency directly; Model 2 shows performance gains in average matching efficiency up to 1.3 percent points from Model 1, while minimizing our loss functions shows those up to 2.4 percent points. As the number of training data grows, the overall identification performance increases, and the performance advantage of our methods over the binary classification approaches is maintained in most cases. (Only when the number of training data is small for NLO samples, minimizing $L_{BCE}$ using Model 2 shows a comparable matching efficiency to our methods.) For most of the considered training configurations, minimizing the probabilistic ranking loss ($L_2$) or the cross-entropy loss ($L_3$) shows the best matching efficiency. Compared to minimizing $L_{BCE}$ using Model 1, which corresponds to the previous approach in [1], the matching efficiency improves from 62.1$\%$ to 64.4-64.5$\%$ and from 59.9$\%$ to 61.6-61.7$\%$ for the LO and NLO samples, respectively, under the configurations with the largest number of training samples. From these observations, we can conclude that simply changing the loss functions to directly maximize matching efficiency (especially using the $L_2$ or $L_3$) shows a definite performance improvement in identifying additional b-jets in the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event data samples both at the leading order and the next-to-leading order.

Table 1 Average matching efficiency (Mat. eff.) and AUC on the test set from different training configurations for the LO samples with the standard deviations in parentheses. Bolds represent the best and comparable methods from the t-test with a significance level of 5$\%$

Table 2 Average matching efficiency (Mat. eff.) and AUC on the test set from different training configurations for the NLO samples with the standard deviations in parentheses. Bolds represent the best and comparable methods from the t-test with a significance level of 5$\%$

We can also examine the identification performance qualitatively by observing distributions of kinematic observables derived from b-jet pairs. In Fig. 3, we obtain reconstructed-level distributions of both $\Delta R$ (the angular difference) and the invariant mass for the additional b-jet pairs and the other pairs identified from the test sets of both the LO and NLO samples. Here, we consider three different identification results based on (i) the true label (matched to the generator-level information at the LO or NLO), (ii) the prediction from the binary classification approach (using Model 1), and (iii) the prediction from our method using $L_3$ (the cross-entropy loss); all the considered prediction models are trained according to the data split conditions with the largest training set size in Sect. 4.2. Compared to the binary classification approach, the distributions acquired from our method using $L_3$ get closer to the true distribution, which can be considered the ideal case of 100$\%$ accuracy. Since observable improvements in the distributions occur relatively uniformly across the entire bins, our identification performance improvements can be considered plausible from a physical viewpoint as well.

Fig. 3

Reconstructed-level distributions of $\Delta R$ (angular distance) and invariant mass of b-jet pairs in the test sets of LO samples (for (a) and (b)) and NLO samples (for (c) and (d)). The additional b-jet pairs are denoted the signal (sig), and the other b-jet pairs are denoted the background (bkg). Additional b-jet pairs are identified according to three different criteria (true: matched to the generator-level information at the LO or NLO, BCE: the prediction from the binary classification approach, CE: the prediction from our method using $L_3$, i.e., the cross-entropy loss)

5 Conclusions

In measuring the differential cross sections of the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ process from the properties of its b-jets, it is crucial to identify additional b-jets originating from gluon splitting correctly. In this paper, we have proposed different loss functions to directly maximize matching efficiency, i.e., the accuracy of identifying additional b-jets. Unlike the previous deep learning-based binary classification approach in [1], these loss functions are designed to fully exploit the special structure of the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event data, as discussed via a simple synthetic data experiment. Using the simulated $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event data in the lepton+jets channel from pp collision at $\sqrt{s}$ = 13 TeV, we have also verified that directly maximizing the matching efficiency via our method shows better performance in identifying additional b-jets than the previous approach.

In the future, our simulation can be extended in line with the settings of Run-3 at the LHC or the High Luminosity LHC (HL-LHC) to verify our method’s applicability. To improve the identification performance further, we can consider utilizing more sophisticated high-level features such as the b-tag discriminator or modifying the neural network architectures to obtain better discriminative features. Another topic worthy of further study is learning to improve the sensitivity of the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ and $\text {t}\bar{\text {t}}\text {H}(\text {b}\bar{\text {b}})$ processes by utilizing the additional b-jet identification models trained on each of the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ and $\text {t}\bar{\text {t}}\text {H}(\text {b}\bar{\text {b}})$ event data as sorts of feature extractor. These future works would ultimately lead to a more precise understanding of the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ process and help search the $\text {t}\bar{\text {t}}\text {H}(\text {b}\bar{\text {b}})$ process to study the properties of the Higgs boson.

Appendices

Appendix

A The histograms for the number of additional b-jets in simulated $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ events

Figure 4 depicts the histograms for the number of generator-level additional b-jets in simulated $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ events (as explained in Sect. 4.1) at both the leading order (LO) and the next-to-leading order (NLO). Here, we denote the b-jets which do not originate from top quark decays as the generator-level additional b-jets. When counting events in the histograms, we have considered only the events that satisfy the kinematic constraints of the $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ event data in the lepton+jets channel, e.g., the requirements for at least two additional b-jets as well as the constraints on the transverse momentum $p_{\mathrm{T}}$ and the pseudorapidity $\eta$ values of a lepton and jets, as explained in Sect. 4.1. Such a kinematic selection has not been applied to the generator-level additional b-jets, the numbers of which have to be counted. In the histograms, the numbers of events are normalized with respect to the total number of considered $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ events in each simulation, and events with more than five additional b-jets are included in the last bin.

Fig. 4

Histograms for the number of generator-level additional b-jets in simulated $\text {t}\bar{\text {t}}\text {b}\bar{\text {b}}$ events at both the leading order (LO) and the next-to-leading order (NLO). Note that most events have two additional b-jets (82.8$\%$ for LO and 77.4$\%$ for NLO)

B The deep feedforward neural network

A deep feedforward neural network $f: {\mathbb {R}}^m \rightarrow {\mathbb {R}}^n$ with L hidden layers can be modeled as follows:

$$\begin{aligned} \begin{aligned} h_{i}&= \sigma _{i}(W_i h_{i-1} + b_i), \qquad i = 1, \ldots , L, \\ f(x)&= \sigma (W_{L+1} h_{L} + b_{L+1}), \end{aligned} \end{aligned}$$

(11)

where $h_i \in {\mathbb {R}}^d$, $i=1,\ldots ,L$ denote the hidden variables, $h_0$ is set to be the input $x \in {\mathbb {R}}^m$, $\sigma _i(\cdot )$, $i=1,\ldots ,L$ denote nonlinear activation functions, and $W_i, b_i$ for $i = 1, \ldots , L+1$, respectively, denote the matrix and vector parameters with sizes defined accordingly as above. In the case of binary classification, the output dimension n is set to one and the activation function $\sigma (\cdot )$ for the output is usually chosen to be the sigmoid function $\sigma (s) = \frac{1}{1+\exp (-s)}$. For general n-dimensional vector outputs, $\sigma (\cdot )$ is set to be an identity.

C Details for the proof-of-concept experiment

To generate synthetic data in Sect. 3.3, we first sample N data in class 1 from the two-dimensional normal distribution, i.e., $x_{1i} \sim N(0,I)$, $i=1,\ldots ,N$ with $I\in {\mathbb {R}}^{2\times 2}$ as the identity matrix. We draw three data points in class 0 by translating each class 1 datum along the horizontal axis for a constant and then inject the Gaussian noise along the vertical axis, in specific, $x_{0i,j} = x_{1i} + (-0.03, \epsilon _j) \in {\mathbb {R}}^2$ with $\epsilon _j \sim N(-0.01,0.1)$ for $i = 1, \ldots , N$, $j = 1,2,3$. We then randomly stack the vectors $x_{0i,1}, x_{0i,2}, x_{0i,3}, x_{1i}\in {\mathbb {R}}^2$ to construct each matrix $M_i \in {\mathbb {R}}^{4\times 2}$ for $i = 1, \ldots , N$.

For the approaches directly maximizing matching efficiency using the surrogate losses in Eqs. (7), (8), (9), (10), the function $g: {\mathbb {R}}^{2} \rightarrow {\mathbb {R}}$ in Eq. (6) is defined as $g(x) = x W + b$, where $W \in {\mathbb {R}}^{2\times 1}, b \in {\mathbb {R}}$ are the model parameters. For the binary classification approach that minimizes Eq. (2), we consider the model $f: {\mathbb {R}}^2 \rightarrow [0,1]$ defined as $f(x) = \sigma (xW + b)$, where W, b are the model parameters of identical size as the above, and $\sigma (\cdot )$ denotes the sigmoid function.

D The hyperparameter tuning results

We report in Tables 3 and 4 the hyperparameter tuning results in Sect. 4.2 for each data split condition and loss function. The first row in each table represents the sample configurations with the number of data used to train the models in parentheses.

Table 3 Hyperparameter tuning results for each data split condition and loss function for the LO samples. L, d, and T represent the number of hidden layers, the dimension of hidden variables, and the number of training epochs, respectively

Table 4 Hyperparameter tuning results for each data split condition and loss function for the NLO samples. L, d, and T represent the number of hidden layers, the dimension of hidden variables, and the number of training epochs, respectively