Calibration of a large-size wide-range neutron spectrometer

Abstract

Over the last year, Politecnico di Milano has developed the W-PIE, a cosmic neutron spectrometer employed for environmental measurements. The W-PIE is based on the Artkis M800 thermal neutron detector and works as a 4-channel spectrometer for detecting neutrons in the energy range 0.01eV – 1GeV. In this paper, the calibration of the instrument in monoenergetic neutron fields at the PIAF facility of PTB is discussed. These measurements were intended to calibrate the detector and validate the response functions. Despite obtaining satisfactory results in terms of fluence and dose calculations, the irradiation in the monoenergetic fields suggested that the detector sensitivity to fast neutrons was greater than expected by the calculated response functions. This discrepancy was investigated and a reasonable explanation for it was proposed.

1 Introduction

Since the beginning of the previous decade, several studies have proven the possibility of investigating changes in the water content over an area of hectares and depth of tens of centimeters, measuring the cosmic neutrons flux [1, 2]. Earth is constantly irradiated by protons and other charged particles originated in our galaxy. Some of them reach the atmosphere of the planet and interact with nitrogen and oxygen via intranuclear cascades. Many different products are generated from these reactions, including neutrons. Some of them are emitted immediately after the interaction in almost the same direction as the incoming particle and with energy around 100 MeV. Others originate in a second moment due to the de-excitation of the residue nucleus in an isotropic mechanism called evaporation and have energies around 1 MeV. After reaching the earth’s surface, the high-energy neutrons can interact with the nuclei in the soil via inelastic reactions, from which other neutrons are emitted via evaporation. These neutrons interact with soil and air mainly via elastic scattering, and in this way they are moderated until thermalizing and reaching the equilibrium state with the surroundings. The neutron energy spectrum observed at the ground level (Figure 1) is the result of these interactions: the red peak is associated with the high-energy neutrons emitted in the first phase of the intranuclear cascade, the green peak is caused by the evaporation processes, the blue region represents the neutron which are being slowed down via collisions, and the gray peak includes thermal neutrons at equilibrium.

Fig. 1

Cosmic neutrons energy spectrum, from [2]. The gray peak represents the energy distribution of thermal neutrons at equilibrium with the environment, the blue region represents the epithermal neutrons, the green peak includes the fast neutrons generated by evaporation, and the red peak is the distribution of high-energy neutrons generated in the upper atmosphere

The epithermal and fast parts of the spectrum are extremely sensitive to the moderation of water in soil, as shown in Fig. 2. Indeed, the epithermal neutron flux is an excellent probe for measuring changes in water content in soil or any other water basin. The area investigated depends on the distance travelled by neutrons (around hundreds of meters) and the depth at which they are generated in the soil (up to 70 cm) [3]. The volume investigated by this technique is of great interest for irrigation, farming and for validating weather, climate, and hydrological forecasts.

Fig. 2

The effect of water content in soil ($\theta$) on the cosmic neutrons energy spectrum, from [2]. Dry soils show greater fluxes especially in the epithermal ($10^{-6}$–$10^{-1}$MeV) and fast ($10^{-1}$–20Mev) energy ranges

The technique for assessing soil moisture via cosmic neutron measurements employs neutron counters coated with moderators to enhance their sensitivity over the epithermal range. The variation in the count rate recorded can be correlated to the average water content over the investigated volume via an universal calibration function [1] which is independent from the soil characteristics. Neutron counters are effective and quite easy to employ, but show some drawbacks, above all they cannot monitor variations in the primary cosmic rays’ flux, and suffer contamination from thermal and fast neutrons, which are not correlated to soil moisture by the same function as epithermal ones. For these reasons, we developed a neutron spectrometer called WEDDING-PIE (or W-PIE), which can be employed for soil moisture measurements and exceed the limits of conventional counters. The instrument is sensitive to the entire range of energies at which cosmic neutrons are generated (i.e., it is a “wide-range” spectrometer). In this paper, the calibration of the device with monoenergetic neutron fields generated at the PIAF facility of PTB will be discussed.

2 Materials and methods

2.1 The W-PIE

The WEDDING-PIE (Wide Energy Detector for Direct Investigation of Neutron spectrum at Ground level for Precise moIsture Evaluation), abbreviated as W-PIE, was developed starting from the thermal nuclear detector M800 manufactured by Arktis. The M800 is a cylinder in which a thin layer of LiF enriched in $^{6}\hbox {Li}$ is present. The remaining part of the volume is filled with ${}^{4}\hbox {He}$ at the pressure of 8 atmospheres. The products of the reaction $^6\text {Li}(n,\alpha )^3H$ excite the gas which de-excites emitting scintillation photons in the UV range, and the collection of the light emitted via silicon photomultipliers (SiPMs) allows the detection of the neutron. The tube is divided into eight segments which can be read independently by 24 SiPMs (one triplet per segment). Gamma rejection is obtained accepting only the counts in coincidence of at least two SiPMs belonging to the same segment, and exploiting the amplitude and time characteristics of the pulse recorded [4]. Precisely, the detector allows setting an amplitude threshold and records the time over threshold (TOT) for each pulse, which means that neutrons and $\gamma$ interactions can be distinguished choosing only the pulses which spent an adequate time above the threshold. The M800 is power supplied via Power over Ethernet (PoE) and is IP addressable, which allows a straightforward transmission of the data to the acquisition system. The cylinder was divided in 4 sectors (each constituted of two adjacent segments) called thermal, epithermal, fast, and high energy. Each sector was covered with moderator layers to maximize its sensitivity over the corresponding range of the energy spectrum [5]. The response functions of the sectors were calculated employing the MCNP6.2 code and are given as an input to an unfolding algorithm implemented in Python and based on the GRAVEL algorithm [6]. In this way, after measuring the count rate in each sector with a reasonable uncertainty (1–5%), the neutron energy spectrum is calculated. GRAVEL is an iterative unfolding algorithm and belongs to the class of nonlinear square gradient methods. For this application, the user can give as an input to the code a $\chi ^2$ threshold value: The algorithm continues iterating until the calculated spectrum has a lower $\chi ^2$ than the one given as an input. Figure 3 schematically represents the detector and the coatings, and Fig. 4 shows the calculated response functions.

Fig. 3

Coatings for the four sectors. The thermal sector is bare. The epithermal sector is covered with a 2-cm layer of HDPE (high-density polyethylene). The fast sector is covered with a 7.2 cm layer of HDPE. The high-energy sector features the following layers (from the inner to the outer part): (1) 4.8 cm of HDPE; (2) 0.2 cm of cadmium; (3) 2 cm of lead; (4)5.9 cm of HDPE. The cadmium layer is too thin to be appreciated in the figure. The inelastic reactions occurring in Pb allow the detection of neutrons with energy above 20 MeV

Fig. 4

Response functions for the four sectors. The ordinate axis show the cps per unit flux ($\frac{cps}{nv}$) as a function of the neutron energy. The responses are found in case of an expanded aligned neutron field

2.2 Monte Carlo simulations

Monte Carlo simulations allowed to calculate the response function of each sector and, in the design phase of the instrument, were crucial to optimize the moderator’s thicknesses for reaching the best configuration in terms of sensitivity to neutrons in a specific energy range. They were performed via the MCNP ver 6.2 code. MCNP is a general-purpose Monte Carlo N-Particle code that can be used for neutron, photon, electron, or coupled neutron/photon/electron transport [7].

For these calculations, the M800 geometry and the coatings employed were simulated. The source was represented by an expanded aligned field of neutrons. The code allowed the estimation of the capture reactions occurring in the LiF lamina and the incident neutron flux. The response function was given in terms of cps per unit neutron flux. Still, some essential information for a correct modeling was unknown, above everything the exact content of ${}^{6}\hbox {Li}$, about which the manufacturer keeps confidentiality. For this reason, a guess concentration of ${}^{6}\hbox {Li}$ was employed for these simulations, meaning that the calculated response functions are known, save for a multiplicative constant which was determined after the calibration discussed in this paper.

2.3 PIAF

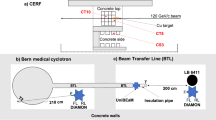
The measurements were performed at the Physikalisch-Technische Bundesanstal (PTB) accelerator irradiation facility PIAF [8]. The facility allows the irradiation and calibration of neutron detectors in monoenergetic neutron fields with energies from 24 keV to 20 MeV. The monoenergetic fields are obtained exploiting the nuclear reactions occurring between charged particles (protons or deuterons) and a target containing lithium, deuterium, or tritium. The charged particles are accelerated by a 2 MV tandetron or by a CV28 cyclotron. The neutron emission from the target is almost monoenergetic and only depends on the emission angle and target thickness. The experimental area of the accelerator facility is a free scattering room, and the shadow cone technique is employed for further reducing the counts induced by the scattered component of the neutron flux [9]. Given the particular size of the W-PIE, a specific shadow cone was designed and manufactured at PSI. The shadow cone should ideally cast a shadow tailored to the shape of the detector, but, to achieve a simpler design and faster realization, a rectangular shape was chosen. Figure 5 shows a picture of the shadow cone and compares the generated shadow with the detector size.

Fig. 5

Picture showing the shadow cone manufactured at PSI and comparison between the generated shadow and the detector cross section

During the irradiation in monoenergetic fields, the detector was placed on an aluminium plate manufactured by PTB at a distance of 3.7 meters from the target generating neutrons. The plate was supported employing the crane inside the irradiation room, which also allowed the movement and positioning of the instrument. Figure 6 shows the positioning of the detector in the irradiation room. For each monoenergetic field, the W-PIE was irradiated both without and with the shadow cone. In the first configuration, the spectrometer is sensitive both to the foreground (monoenergetic) and the background (scattered) component of the field, while in the second one it only interacts with scattered neutrons. The counts recorded in both configurations were normalized to the overall charge of the accelerated protons or deuterons, and the difference between them is used for performing the unfolding of the spectrum.

Fig. 6

Positioning of the detector at the PIAF facility: The detector is placed at a distance of 3.7 meters from the target on an aluminum plate and supported with the aid of a crane

3 Results

For each monoenergetic field, the reconstructed spectrum was compared to the nominal neutron energy to assess the spectrometer capability to correctly identify the neutron energy distribution. Figure 7 compares the reconstructed spectra with the monoenergetic emission of the source. For emissions from 71 keV to 2.5 MeV, the guess spectrum was flat. For the 14.8 MeV field, the guess spectrum was flat from 0 to 25 MeV, and null above that value.

Fig. 7

Reconstructed energy spectra. The red dashed line represents the channel corresponding to the monoenergetic emission of the source. The spectra are normalized for having unitary integral

In a second moment, the calculated fluence was compared to the reference one. As already mentioned in Sect. 2.2, the response functions were known, save for a multiplicative constant depending on the absolute quantity of ${}^{6}\hbox {Li}$ in the LiF lamina. The ratio between the reference values for the fluence and the calculated one was found to be almost constant and allowed determining the unknown multiplicative constant. In this way, the response functions were corrected. Table 1 compares the calculated fluences with the reference values. Table 2 shows the same comparison in terms of ambient dose equivalent.

Table 1 Comparison between the calculated neutron fluence and the reference values for the monoenergetic fields

Table 2 Comparison between the calculated ambient dose equivalent and the reference values for the monoenergetic fields

4 Discussion

The measurements performed in monoenergetic fields proved the detector capability of fairly identifying the energy at which neutrons are emitted. Even though the results never show a perfect agreement, the main component of the beam is always identified with little error. The environmental application for which the spectrometer is intended only requires to correctly classify a neutron as thermal, epithermal, fast or above 20 MeV. With this in mind, the results look fully satisfactory. Still, some aspects emerged which require further investigation: in the 1.2 MeV, 2.5 MeV, and 14.8 MeV fields, the thermal and epithermal sectors of the W-PIE recorded many more counts than predicted by the response functions, as shown in Fig. 8. Nevertheless, these counts are far less than the ones in the fast and high-energy sectors, and the reconstruction of the spectrum and the calculated quantities remain accurate. On the other hand, it seems adequate to understand the reason behind this discrepancy to possibly correct the response functions and have better results.

Fig. 8

Comparison between the measured counts and the ones predicted by the response functions for the four sectors of the W-PIE. For these fields, the Monte Carlo severely underestimates the responses of the epithermal and thermal sectors

Two possible effects might justify the underestimation of the counts recorded:

• 1. Overshadowing: the shadow cone was designed for having a rectangular shape, for which the lower part (high-energy sector), is precisely shadowed, whereas the upper one (thermal sector) is overshadowed (as shown in Figure 5b). Overshadowing is indeed a negative effect, but its magnitude is not expected to change the counts recorded of a factor 10. That is why we believe it is not sufficient to explain the recorded discrepancy.

• 2. Scattering interactions between neutrons and ${}^{4}\hbox {He}$: the scattering reaction can supply enough energy to the helium nuclei to trigger scintillation. This mechanism is also the basis of some detectors for neutrons from fission sources in the MeV energy range [10].

The second aspect looks a better candidate for explaining the discrepancy and was investigated in better detail. To begin, it is worth considering that the overall amount of helium inside the detector is comparable to the ${}^{6}\hbox {Li}$ content and that, at the energies of interest, the neutron capture of  ${}^{6}\hbox {Li}$ has a much lower cross section with respect to ${}^{4}\hbox {He}$ scattering (see Figure 9).

Fig. 9

Comparison between ${}^{6}\hbox {Li}$ capture cross section and ${}^{4}\hbox {He}$ scattering cross sections. Data from ENDF/B VIII library

Assuming that the scattering reaction between a neutron and a ${}^{4}\hbox {He}$ nucleus can trigger scintillation; the event is counted if the output signal is above the TOT threshold. This means that, for a scattering event to be recorded, a minimum amount of energy should be deposited in the gas.

For validating this hypothesis, another irradiation was performed in the neutron laboratory of Politecnico di Milano with an AmBe source. The aim of this experiment was understanding if the counts recorded by the instrument arise only from capture reactions on ${}^{6}\hbox {Li}$, or also from fast neutrons detected via scattering reactions. For this experiment, the M800 counter was irradiated without any moderator and the shadow cone technique was employed. The detector measured a foreground contribution of on average 0.5 cps per sector, whereas the response functions predicted ten times fewer counts. This suggested that the detector itself is more sensitive to fast neutrons than expected and that the neutron scattering could actually enhance its sensitivity.

A further proof to this hypothesis can be found looking at the measured TOT spectra. Figure 10a, b shows the TOT distributions for the pulses recorded by the thermal sector in monoenergetic fields. The counts account for the foreground contribution only. Figure 11 shows the same spectra for the background contribution. In this case, the thermal neutron component is relevant, and the signal mainly arises from the ${}^{6}\hbox {Li}$(n,$\alpha$)${}^{3}\hbox {H}$ reactions, while scattering is negligible.

Fig. 10

TOT spectra in the thermal sector for the monoenergetic neutron fields. The spectra refer to the foreground component of the neutron flux and are normalized for having unitary integral

Fig. 11

TOT spectra in the thermal sector for the background component of the monoenergetic fields. All the spectra are normalized for having unitary integral

Some important aspects should be noticed:

• 1. The TOT spectra in Fig. 11 are identical to each other.

• 2. The TOT spectra in Fig. 10a are overlapped to the ones in Fig. 11.

• 3. The TOT spectra in Fig. 10b are different from the previous ones: the pulses recorded in these measurements have different amplitude with respect to the other fields. Moreover, the spectra shift towards right increasing the energy of the neutron beam.

Therefore, some conclusions can be drawn:

• 1. When neutrons are detected via the neutron capture on ${}^{6}\hbox {Li}$, the TOT spectrum has the shape reported in Fig. 11.

• 2. This shape is different from the one recorded for neutrons above 1 MeV (Fig. 10b). In these cases, the scintillation in the gas is mainly caused by the scattering between a Helium nucleus and a neutron, which leads to a different light output from the ${}^{6}\hbox {Li}$(n,$\alpha$)${}^{3}\hbox {H}$ reaction products. Moreover, higher energy neutrons tend to deposit more energy in the mean, giving rise to higher pulses, which explains the shift towards right increasing the beam energy.

• 3. Conversely, the shape of the TOT spectra for the 71 keV and 144 keV emissions (Figure 10a) is compatible to the one of neutron captures. This implies that neutrons up to some hundreds of keV do not deposit enough energy in the medium to generate a pulse above the detector threshold, and the only reaction of interest is the ${}^{6}\hbox {Li}$(n,$\alpha$)${}^{3}\hbox {H}$.

In summary, neutrons with adequate energy can generate pulses via scattering reactions. Neglecting this mechanism in the calculation of the response functions can lead to the underestimation of the counts recorded. The TOT spectra provide a tool to understand the magnitude of this error: If their shape is the same as the one in Fig. 11, neutron scattering has little relevance.

The magnitude of this effect is different among the four sectors of the W-PIE: Fig. 12 shows the TOT spectra recorded by the high-energy sector for the foreground component of the monoenergetic fields. This sector is in the lowest part of the spectrometer and is the most shielded one (see Fig. 3). The thick moderator thermalizes the incoming neutrons, which are then captured in the ${}^{6}\hbox {LiF}$ lamina. The shape of the spectrum suggests that neutron scattering is always negligible, which explains why the response functions fairly predicted the counts recorded in this sector.

Fig. 12

TOT spectra for the foreground component of the monoenergetic fields measured by the high-energy sector. All the spectra are normalized for having unitary integral

The response functions were then corrected to take into account neutron scattering. They were calculated under these assumptions:

• The overall response function is the sum of a contribution related to ${}^{6}\hbox {Li}$(n,$\alpha$)${}^{3}\hbox {H}$ reaction and one related to ${}^{4}\hbox {He}$(n,n)${}^{4}\hbox {He}$.

• The contribution related to the ${}^{6}\hbox {Li}$(n,$\alpha$)${}^{3}\hbox {H}$ reaction was assessed via Monte Carlo simulations as described in Sect. 2.2. It is calculated as the ratio between the number of neutron captures occurring and the incident neutron flux, as functions of the neutron energy.

• The contribution related to ${}^{4}\hbox {He}$(n,n)${}^{4}\hbox {He}$ was calculated in a similar way, but the neutron scattering reaction rate was corrected for a multiplicative factor. This factor represents the probability that a neutron deposits enough energy via the scattering reaction, to generate a pulse above the threshold. The results obtained for the monoenergetic fields allow estimating the minimum energy deposition for which neutron scattering triggers detectable scintillation. It was observed that for the 71 keV and 144 keV fields the counts arise only from neutron capture, whereas neutron scattering becomes relevant above 1 MeV. Therefore, it can be assumed that the neutron should deposit some tens or hundreds of keV in the helium gas for being detected. The correction factor chosen represents the probability that the neutron scattering deposits at least 300 keV in the mean. This energy value is the one that gives the best agreement with the results obtained in the 1.2 MeV, 2.5 MeV, 14.8 MeV, and AmBe fields. Its values are shown in Fig.  13.

The expected counts for each region were calculated with the new response functions. They are compared to the measured ones in Fig.  14.

Fig. 13

Correction factor representing the probability that an incident neutron deposits at least 300 keV in the helium gas. This factor is especially important for fast neutrons interacting in the thermal sector of the W-PIE. If all neutrons had energy below 300 keV, no correction would be required. Conversely, neutrons above 1 MeV can deposit enough energy via elastic scatteing to be misinterpreted as a thermal neutron signal. In the other sectors of the W-PIE, neutrons are slowed down before reaching the detector active volume and this correction is negligible. The correction factor shape is determined by two different factors. To begin, neutrons with higher energy can deposit more energy inside the gas. At the same time, the neutrons up to 1-2 MeV scattering on the helium nucleus are more likely to have a backward scattering, whereas neutron above this values are more likely to scatter forward. These aspects explain the maximum around 1.5MeV for the correction factor

Fig. 14

Comparison between the measured counts and the ones predicted by the corrected response functions for the four sectors of the W-PIE

Once the response functions were corrected, the neutron spectra for the irradiation in PIAF were recalculated. Results are shown in Table 3. It can be immediately noticed that, with the updated response functions, the calculated neutron fluences only slightly change. The correction of the dose equivalent, on the other hand, is more relevant: comparing the values reported in Tables 2 and  3 it is clear that the previous response functions systematically underestimated the dose equivalent, whereas the new ones show a zero-average error and a better agreement with the reference values, especially at high energies.

Table 3 Calculated values for neutron fluence and ambient dose equivalent in the PIAF facility using the updated response functions

5 Conclusions

This paper discusses the calibration of a novel spectrometer in some neutron reference fields. The peculiarities of this device are the neutron counter on which it is based and the application for which it is intended. To begin, the M800 thermal neutron detector can be easily and effectively employed as a spectrometer in the configuration described. The W-PIE achieves a fair reconstruction of the neutron spectrum in a single measurement, and its sensitivity allows its employment even for very weak sources. In this work, we also highlighted that the sensitivity of the M800 to fast neutrons must be accounted for during the calibration with monoenergetic fast neutron fields.