1 Introduction

The formation of an electron cloud (e-cloud) due to secondary electron emission from the surfaces of the vacuum chambers can introduce significant limitations for the performance of particle accelerators operating with bunched beams of positively charged particles, as observed in several circular accelerators, storage rings and colliders over the past decades  [1]. The mechanism through which e-clouds are generated at a certain accelerator location can be described as follows  [2, 3]. Each passing bunch generates a number of primary electrons (e.g. photoelectrons), which are accelerated by the beam field and fly across the chamber cross section. These electrons produce secondary electrons when they hit the inner wall of the vacuum chamber. In case the Secondary Electron Yield (SEY) is greater than unity at the impact energy, net electron production occurs. With a sufficiently small bunch spacing, the emitted low-energy electrons can survive until the following bunch passage and in turn be accelerated by the beam, triggering an avalanche multiplication phenomenon. This leads to an exponential e-cloud build-up that can only stop when a dynamical steady state is reached, at which the space charge repulsion of the e-cloud itself pushes the newly emitted electrons back to the surface and the net electron production and loss rates become equal. E-cloud build-up in an accelerator is associated with undesirable phenomena such as vacuum pressure rise, excessive heat load in cryogenic regions, RF stable phase shift, as well as beam quality degradation manifesting itself through transverse instabilities, losses and emittance growth  [4].

Observations and first studies of beam-induced multipacting at CERN date back to 1977, when a pressure rise at the Intersecting Storage Rings (ISR) after installation of an aluminum test chamber was ascribed to electron accumulation [5]. Based on the ISR experience, concerns about the Large Hadron Collider (LHC) operation already started at the very early design stages in the 1980’s. These worries were then reinforced over the next two decades, when beam instabilities due to photoelectrons were observed at the KEK Photon Factory [6, 7] and a series of e-cloud studies including both simulations and experiments were launched both at the Beijing Electron Positron Collider [8] and for the positron ring (LER) of the PEP-II B Factory [9]. Since 1998, e-cloud effects have been directly observed at the CERN Super Proton Synchrotron (SPS) with the LHC-type beam (25 ns bunch spacing) [10]. By the first decade of the 2000’s, e-cloud was systematically observed not only in the SPS but also in its upstream injector, the Proton Synchrotron (PS), in the late stages of the preparation of the 25 ns spaced beams [11,12,13]. After 2010, e-cloud effects have been observed at the Large Hadron Collider (LHC). These effects were visible only in the interaction regions, where the two beams circulate in the same pipe, as long as the collider operated with 150 ns bunch spacing (2010), but then became more and more evident as the bunch spacing was gradually reduced to 75, 50 and finally 25 ns [14, 15]. One of the most important effects, which survives even after extensive machine conditioningFootnote 1, is the heat load deposited by the impacting electrons on the beam screens of the superconducting magnets. In Fig. 1, a cross-sectional cut of an LHC dipole magnet shows the beam screens of the two counter-rotating beams, which are cooled to a temperature between 5 and 20 K through a helium circuit attached to the external wall. Each of the arc beam-screen cooling circuits covers a 53 m long portion of the accelerator, which is usually called a “half cell“ as it corresponds to half of an arc FODO cell. Each half cell includes three main bending magnets and one main quadrupole magnet. By measuring the thermodynamic properties of the cooling fluid at the entrance and the exit of the cooling circuit, it is possible to obtain accurate measurements of the heat loads deposited on the beam screens of each half cell  [18]. The heat loads measured in the half-cells of each LHC sector (octant) can be summed up to provide the global heat load per sector.

Fig. 1
figure 1

A cut of an LHC dipole magnet

Full size image

Figure 2 corresponds to a typical Run 2 (2015-18) LHC fill, with a 25 ns bunch spacing, and a fill with a 50 ns beam (which was the typical configuration in the LHC Run 1, 2010-13), made in sequence for direct comparison. The top plot shows the beam intensity (Beam 1 in blue and Beam 2 in red, vertical axis on the left) as well as the beam energy (dashed line, vertical axis on the right). The bottom plot shows the average heat load per half cell correspondingly measured in the LHC sectors (as labeled) as well as the calculated value assuming only the contributions from impedance and synchrotron radiation (dashed line). It is clear that, while with the 50 ns beam the heat load measured is the same for all sectors and falls very close to the expected load from impedance and synchrotron radiation (dashed line), in the case of 25 ns beam the measured values significantly differ sector by sector and they all sit above the expected line. Such a dependence on the bunch spacing gives a strong indication that the source of the additional heating is the e-cloud as confirmed by several other observations [19]. Laboratory analyses conducted on beam screens extracted from the LHC during the Long Shutdown 2 (LS2), in 2019-2020, showed that these differences in the heat load are correlated with chemical alterations of the surface, which result in a different SEY  [20].

The High Luminosity LHC project (HL-LHC)  [21] foresees a twofold increase of the LHC beam intensity to be obtained by keeping the 25 ns bunch spacing and doubling the bunch population. It is therefore important to accurately predict how the heat loads on the beam screen behave as a function of the bunch population in order to ensure that they will remain compatible with the available cryogenic capacity. In this paper, we will show that the dependence of e-cloud induced heat loads on the bunch population can be nontrivial, showing a non-monotonic behavior in the range of interest for HL-LHC. The mechanism leading to such a dependence is investigated with simulations and probed experimentally by means of heat load measurements at the LHC. Table 1 lists the most relevant LHC parameters and their typical values during operation in Run 2. Except where otherwise stated, these correspond to the values used in the presented simulations and measurements.

Fig. 2
figure 2

Intensities of the two LHC beams (top) and evolution of the heat loads in the eight LHC arcs (bottom) during two consecutive fills with different bunch spacing. The expected load from impedance and synchrotron radiation is indicated by the dashed curve

Full size image
Table 1 Typical LHC parameters during Run 2
Full size table

2 Modelling of the e-cloud heat loads

To model the generation of an e-cloud inside a beam chamber in the presence of circulating beam, we use the PyECLOUD simulation code, developed at CERN since 2011 as an evolution of the ECLOUD code  [22]. The PyECLOUD modeling is of weak-strong type, with the beam represented by a rigid Gaussian distribution, and the electrons modelled by means of macroparticles. The Particle-In-Cell (PIC) method is used for computing the electromagnetic forces generated by the e-cloud itself, which are applied to the electrons in the solution of their equations of motion. When the electrons hit the beam chamber, the secondary emission process is simulated by generating new macroparticles. The model used for this purpose is based on laboratory measurements conducted to characterize the secondary emission from the LHC beam screen surface  [23, 24].

The presence of an externally applied magnetic field strongly influences the dynamics of the electrons. This is visible in the distribution of the electron density in the chamber as shown in Fig. 3 for the case of dipoles (left) and quadrupoles (right) in the LHC arcs. In both cases, electrons are subject to a Lorentz force by the strong magnetic fields and therefore tend to spiral along the magnetic field lines. In the quadrupoles, due to the presence of magnetic gradients, the electrons can be “reflected” along their motion giving rise to magnetic trapping phenomena through which they can be accelerated by several bunch passages before eventually hitting the beam-screen wall  [25]. In order to well resolve the cyclotron motion over the duration of the simulations, PyECLOUD employs the Boris algorithm for the electron motion [26, 27].

Fig. 3
figure 3

Snapshots of the electron distribution between bunch passages in the LHC arc dipoles (left figure) and quadrupoles (right figure) at injection energy (from PIC simulation)

Full size image
Fig. 4
figure 4

E-cloud-induced heat load as a function of the bunch population for different values of SEY\(_{\mathrm {max}}\), in the arc dipole (left) and quadrupole (right) with the standard 25 ns beam at 7 TeV

Full size image
Fig. 5
figure 5

Electron mean energy when hitting the wall (a), electron mean flux to the wall (b), average electron density at saturation in the beam chamber (c) and heat load onto the wall (d) are plotted as a function of the bunch population for SEY\(_{\mathrm {max}}\)=1.35. The blue lines have been calculated in the presence of a dipole field, the orange lines correspond to a quadrupole field

Full size image
Fig. 6
figure 6

Secondary Electron Yield curve (top figure) and energy spectra of impacting electrons as functions of the bunch population for both dipoles (middle figure) and quadrupoles (bottom figure)

Full size image

PyECLOUD simulations have been widely used to perform detailed calculations of the heat load deposited by an e-cloud on the inner walls of the beam chamber, and are being used in this paper to predict and study the nontrivial dependence of the heat load generated by the e-cloud on the bunch population. For this purpose, the heat load generated by electrons on the beam screen of the LHC dipole and quadrupole magnets has been calculated as a function of the bunch population for different values of the “SEY\(_{\mathrm {max}}\)” parameter, which is defined as the maximum of the secondary electron yield curve and corresponds to the parameter \(\delta _{\mathrm {max}}\) in  [23]. The simulations assume the HL-LHC beam configuration with 2748 bunches in trains of 72 bunches in each LHC ring, at the foreseen HL-LHC collision energy of 7 TeV. Figure 4 shows the results of such simulations. For the same bunch population and the same SEY\(_{\mathrm {max}}\) the heat load in the quadrupoles is significantly larger than in the dipoles. This is a direct consequence of the magnetic trapping that occurs in quadrupoles due to the presence of the magnetic field gradient, which largely increases the number of electrons that accumulate in the chamber. Furthermore, the dependence of the heat loads on the bunch population is not that of a simply monotonically increasing function, as one could have naively guessed, but exhibits a rather complex pattern. More specifically, in most configurations, and in particular for SEY\(_{\mathrm {max}}\) in the range 1.2-1.4 (which is representative for the LHC surfaces in Run 2 [28]), when increasing the bunch population the heat load only increases up to a certain value, above which it either remains constant or decreases. This turning point is close to \(10^{11}\) p\(^+\) for the dipoles, almost independently of SEY\(_{\mathrm {max}}\), while it moves from \(10^{11}\) p\(^+\) to \(2\times 10^{11}\) p\(^+\) for the quadrupoles according to SEY\(_{\mathrm {max}}\). This finding has significant implications for the HL-LHC project in particular in defining the upgrade of the LHC cryogenic system needed to cope with the increased intensity. It is therefore important to identify the root cause of the trend observed in simulations and to validate the results with experimental data.

We recall that the heat load deposited on the beam pipe can be written as:

$$\begin{aligned} P = \varPhi \overline{E} \, , \end{aligned}$$
(1)

where P is the heat load, \(\varPhi\) is mean flux of electrons impinging on the walls and \(\overline{E}\) is their average energy. The average electron energy \(\overline{E}\) is shown as a function of the bunch population in Fig. 5a for the dipoles (blue curves) and quadrupoles (orange curves) and for SEY\(_{\mathrm {max}}\)=1.35. It is much larger for the quadrupoles than for the dipoles, as a result of the magnetic trapping which allows electron in the quadrupoles to accumulate energy from several bunch kicks. Both for dipoles and quadrupoles the average electron energy \(\overline{E}\) scales monotonically with the bunch population. Hence, the non-monotonic behavior of the heat load is not driven by the energy of the impacting electrons but by their number. This is confirmed by Fig. 5b, which shows that it is indeed the average impinging electron flux \(\varPhi\) that exhibits a flat or decreasing trend above a certain bunch population, leading to the observed non-monotonic behavior of the heat loads. The decrease of the impinging electron flux \(\varPhi\) for high bunch population is in turn related to a decrease of the average electron density in the chamber as illustrated in Fig. 5c.

The root cause of such a behavior can be understood recalling that the number of electrons emitted by the surface can be written as:

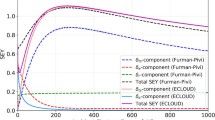
$$\begin{aligned} N_{\text {ele}} = \int _0^\infty \delta (E) \varphi (E)dE \quad , \end{aligned}$$
(2)

where \(\delta (E)\) is the SEY curve, represented in Fig. 6 (top) and \(\varphi (E)=dN/dE\) is the energy spectrum of the impinging electrons, which is displayed for different bunch populations in the middle and bottom parts of Fig. 6 for dipoles and quadrupoles respectively. It can be observed that as the bunch population increases the electron spectrum shifts towards higher energies as a result of the stronger electromagnetic forces exerted by the bunch. For high enough values of the bunch population, most of the electrons reach energies well above 350 eV for which the SEY curve has a decreasing trend and therefore the probability of emitting secondary electrons becomes significantly lower.

Another non-monotonic behavior with bunch population that stems from the shape of the SEY curve has also been observed in the LHC during Run 2, when electron-cloud-induced beam instabilities were suddenly triggered with decreasing bunch population during luminosity production [29]. In this case, the root cause is the increase in electron density around the beam location in dipole fields, caused by the electrons in that area approaching from above the energy corresponding to the peak of the SEY curve as the strength of the beam kick decreases with the decreasing bunch population.

3 Experimental confirmation

The experimental verification of the non-monotonic dependence of the electron-cloud-induced heat load on the bunch population, described in the previous section, could not easily be carried out in the machine mainly because of the limited range of achievable beam parameters before the upgrade of the LHC injectors, which was implemented during LS2. In particular, so far 25 ns beams with long bunch trains (e.g., 48 or 72 bunches) and bunch populations above \(1.2\times 10^{11}\) p\(^+\) were not available for LHC operation, as such beams could not be accelerated to 450 GeV in the last ring of the LHC injectors chain, the SPS, due to limitations in the RF power and longitudinal beam stability [30]. In spite of this limitation, heat load measurements could be collected during both LHC physics runs and dedicated experiments providing a rich set of data, which can be compared against PyECLOUD simulations. All data discussed in this paper were collected in the period 2017-18, during which the SEY of the beam screens could be considered unchanged, as indicated by the measured heat loads   [31].

For most of Run 2 the LHC was filled with trains of 48 bunches and a bunch population of about \(1.2\times 10^{11}\) p\(^+\). Therefore, a large set of measurements at beam energies of 450 GeV and 6.5 TeV for this specific case are available, showing that heat load measurements are very reproducible for the same beam configuration  [31]. A dedicated machine study was conducted filling the LHC with the same filling pattern used for luminosity production runs and varying the bunch population from \(3\times 10^{10}\) p\(^+\)+ to \(1.2\times 10^{11}\) p\(^+\) in order to explore the accessible intensity range at 450 GeV. The results of this experiment can be seen in the left graph of Fig. 7. Here the heat loads measured in the different LHC sectors are plotted as a function of the bunch population. One can clearly see that in the explored range of bunch population, the heat load is monotonically increasing in all sectors, and that a threshold effect at about \(4\times 10^{10}\) p\(^+\) occurs in all sectors.

In studies aimed at determining the RF power limitations of the SPS, trains of 12 bunches with bunch population up to \(1.9\times 10^{11}\) p\(^+\) were successfully accelerated to 450 GeV and could be used in the LHC to probe for the first time the behavior of the e-cloud in the range of bunch population for which the non-monotonic behavior discussed in Sect. 2 should be visible. Four measurements were done with trains of 12 bunches and 1020 bunches per ring, varying the bunch population from \(7\times 10^{10}\) p\(^+\) to \(1.9\times 10^{11}\) p\(^+\). The result of this experiment can be seen in the right graph of Fig. 7. It is clear that pushing the bunch population beyond \(1.2\times 10^{11}\) p\(^+\) the measured heat load either levels off or even starts to decrease. These measurements provide the first clear experimental evidence of the non-monotonic dependence of the heat loads on bunch population in the LHC.

Another filling pattern that was used for short periods during LHC operation is the “8b+4e” scheme, made of short trains of 8 bunches with 25 ns bunch spacing separated by gaps made of four empty 25 ns bunch slots. Heat load measurements for this bunch pattern are available for 1.2\(\times 10^{11}\) p\(^+\)/bunch and for 1.5\(\times 10^{11}\) p\(^+\)/bunch.

Fig. 7
figure 7

Heat loads measured at 450 GeV with different bunch populations with trains of 48 bunches (left) and with trains of 12 bunches (right). In the plots the contributions from impedance and synchrotron radiation are subtracted

Full size image

In order to compare the experimental data discussed above with PyECLOUD simulations it is necessary to estimate the SEY of the beam screens. This is done for each of the LHC half cells by comparing against PyECLOUD simulations the heat load measured at 450 GeV using the nominal bunch population of 1.2\(\times\)10\(^{11}\) p\(^+\). An example of the result of this exercise is shown in Fig. 8 for one of the sectors showing the highest loads, for which we find that SEY\(_{\mathrm {max}}\) mainly ranges between 1.2 and 1.45 (with a few outliers) averaging around 1.35.

Based on the estimated SEY\(_{\mathrm {max}}\) values, it is possible to simulate the expected heat load as a function of the bunch population for different bunch patterns and beam energies. The results of such simulations are shown by the continuous lines in Fig. 9. The red circle in Fig. 9 indicates the heat load corresponding to the measurement point used to infer SEY\(_{\mathrm {max}}\). The other points in Fig. 9 show the heat loads measured with other beam intensities and bunch patterns. These measurements are not used in any way to tune the simulation model and can therefore be used as an independent crosscheck of the simulation results. Very good agreement is observed between the simulations and the measured heat loads. This provides an important confirmation of both the fact that the observed heat loads are generated by electron cloud and of the estimated SEY\(_{\mathrm {max}}\) values. Furthermore, the measurements with the 12-bunch and the 8b+4e schemes confirm that the heat loads do not increase significantly for bunch populations above 1.2\(\times\)10\(^{11}\) p\(^+\), as predicted by the simulations due to the mechanism discussed in Sect. 2.

Fig. 8
figure 8

SEY\(_{\mathrm {max}}\) estimates for the half cells in sector 81, which shows the highest heat loads

Full size image
Fig. 9
figure 9

Heat loads per half cell as a function of the bunch population for one of the sectors showing the highest heat loads (S81) at 450 GeV (left) and 6.5 TeV (right). Simulation results are represented by lines while the markers represent measurement points. Different filling patterns are shown in different colors. The data point used to infer SEY\(_{\mathrm {max}}\) is circled in red

Full size image

4 Conclusions

During LHC operation in Run 2, large heat loads induced by electron cloud were systematically observed in the machine. In order to understand their behavior, e-cloud heat loads have been modelled with simulations for different beam and machine parameters. The simulations predict a nontrivial, non-monotonic behavior of the heat load as a function of bunch population. In-depth analysis of the simulation results shows that the reduction in heat load observed above a certain bunch population is linked to a reduction of the number of electrons in the chamber. This is driven by a shift of the energy spectrum of the impacting electrons towards higher energies, for which the SEY curve has a decreasing slope. Heat load measurements collected at the LHC allowed validating experimentally the simulation model and confirmed the non-monotonic behavior of the heat loads foreseen by simulations. Since the non-monotonic behavior of the heat loads is crucial for the HL-LHC in order to keep the heat loads within the available cryogenic capacity, the importance of these results cannot be overstated. Over the next few years, as the readiness of the CERN accelerator complex for the HL-LHC increases, larger bunch populations in longer bunch trains will become available also in the LHC, which will allow to further verify the results presented here. The benchmarking of the simulation tools with experimental data will continue as further measurements become possible.