Manipulation of transverse emittances in circular accelerators by crossing nonlinear 2D resonances

Abstract

Controlling nonlinear effects in the transverse dynamics of charged particle beams in circular accelerators opens new possibilities for controlling some of the beam properties. Beam splitting by crossing a stable 1D nonlinear resonance is part of the routine operation of the CERN Proton Synchrotron. The beam undergoes trapping and transport inside stable islands created in the horizontal plane to allow multi-turn extraction toward the Super Proton Synchrotron, where the beam is used for fixed-target experiments. This process acts only on the horizontal beam emittance, inducing a reduction of its initial value. In this paper, we present a generalization of this approach, in which both transverse planes are affected by the proposed technique. We will discuss in detail how to manipulate the transverse emittances by means of a controlled crossing of a 2D nonlinear resonance. The novel technique will be presented by discussing the theoretical analysis of a Hamiltonian model, as well as simulating the performance of the proposed manipulation using a more realistic nonlinear symplectic map.

Introduction

In circular particle accelerators, the beam dynamics is governed by a number of invariants. This is the case of transverse emittances, which are preserved under the condition that radiation effects can be neglected, which is often the case for hadron accelerators at intermediate beam energy, and time-dependent effects are absent. The very existence of these invariants is related to the existence of integrals of motion of the Hamiltonian character of the beam dynamics.

This picture, however, has to be completely reviewed whenever nonlinear resonances and time-dependent effects are introduced in the system. In this case, the invariance of the transverse emittances is broken, which implies a potential harmful impact on the accelerator performance due to the diffusion of orbits in phase space [1,2,3,4].

Perturbative theory [5] has shown that for quasi-integrable systems one can define quasi-invariant quantities whose value changes by a small amount even after extremely long times. In the presence of nonlinear effects, nonlinear invariants can be found, which represent the generalization of the Courant–Snyder invariant [6] for the case of linear dynamics. In this respect, the theory of Normal Forms (see, e.g. , [7,8,9,10,11,12] for an overview) provides exactly the tools to evaluate, among other observables, these invariants for a nonlinear symplectic map near an elliptic fixed point.

Indeed, the lack of invariance for the transverse emittances implies a degraded accelerator performance in terms, e.g. , of emittance growth and particle loss. There are, however, also some advantages that we would like to highlight and explore. One could devise appropriate beam manipulations in which the transverse emittances are acted upon in a controlled way.

In recent years, the proposal of the so-called Multi-Turn Extraction (MTE) at the CERN Proton Synchrotron (PS) [13,14,15,16] and its successful operational implementation [17,18,19,20] opened the way to a novel attitude toward applications of nonlinear beam dynamics. The principle of MTE relies on the adiabatic crossing of a nonlinear resonance in the horizontal plane, with the goal to trap particles inside the stable islands of the phase space and then transport them toward high amplitudes prior to extraction without any beam loss. This manipulation generates a beam structure that extends beyond the length of the PS circumference, which is an essential feature of MTE. However, the beam splitting, achieved when particles are trapped inside the stable islands, induces a reduction of the horizontal emittance only, i.e. , the emittance of each of the five generated beamlets is smaller than that of the initial single-Gaussian beam, which is related to the 1D character of the resonance used.

We would like to extend this approach by considering the adiabatic crossing of a nonlinear coupled resonance, which should provide a control of the emittances in the horizontal and vertical planes. It is worth mentioning that an intermediate step in this direction is performed by crossing the coupling resonance in the presence of linear coupling. In this case, it is well known [21,22,23] that the transverse emittances can be exchanged between the two planes. Furthermore, a recent paper showed how the process of resonance crossing in the presence of linear coupling can be best understood by means of the Hamiltonian theory [24].

Crossing a nonlinear 2D resonance provides extended capabilities in terms of control and manipulation of transverse emittances and could be pursued both from the theoretical and experimental point of view. The source of inspiration is the analysis of the impact of crossing the Walkinshaw, i.e. , $\omega _x-2\omega _y=0$, resonance [25, 26], and for the $2\omega _x-\omega _y$ resonance [27]. However, the focus of the analysis performed in Ref. [25] was to estimate the undesired emittance growth due to the resonance crossing, whereas our aim is to intentionally manipulate the transverse emittances for specific applications.

In this paper, we propose a general approach to emittance sharing based on adiabatic invariance and separatrix-crossing theory. If the linear frequencies are slowly modulated to cross the selected resonances, the area of the phase space enclosed by the separatrix changes and particles can jump between different phase-space regions, which results in a change of their adiabatic invariant. The statistical analyses show that, starting from a Gaussian distribution of initial conditions with emittances $\varepsilon _{x,\text {i}}$, $\varepsilon _{y,\text {i}}$, at the end of the resonance crossing process the emittances are given by $\varepsilon _{x,\text {f}}\propto \varepsilon _{y,\text {i}}$ and $\varepsilon _{y,\text {f}}\propto \varepsilon _{x,\text {i}}$, with factors depending on the order of the crossed resonance.

The approach presented in this paper has been assessed by means of a detailed analysis of the phase-space topology of simple Hamiltonian systems, which is the basis for applying the adiabatic theory. The technique is then probed using more realistic map models. Extensive numerical simulations have been performed to determine the dependence of the results on the various system parameters.

The structure of the paper is the following: in Sect. 2, the models are introduced, and the phase-space topology of the Hamiltonians described is studied in detail, including considerations on some specific low-order resonances, which are useful for applications. The results of numerical simulations are presented and discussed in Sect. 3, while some conclusions are drawn in Sect. 4. Moreover, a discussion on which type of magnet excites a given resonance is given in Appendix A, while a short digression on the motion in the resonant condition is reported in Appendix B.

Theoretical framework

General considerations

The starting point is the choice of the model used for our analyses, which is the Hénon-like [28] 4D symplectic map that describes the transverse betatron motion in a FODO cell with nonlinearities [7]. Such a map, written in Courant–Snyder normalized co-ordinates, is composed of rotations of frequencies $\omega _x$ and $\omega _y$ and a $2(r+1)$-polar kick, i.e. ,

$$\begin{aligned} \begin{pmatrix} x'\\ p'_x\\ y' \\ p'_y \end{pmatrix} = R(\omega _x,\omega _y) \begin{pmatrix} x &{}\\ p_x &{}+ \sqrt{\beta _x} {\text {Re}}\left[ \left( \dfrac{ K_r + i J_r}{r!} \right) \left( \sqrt{\beta _x}\, x+i\sqrt{\beta _y}\,y \right) ^r\right] \\ y &{}\\ p_y &{}- \sqrt{\beta _y} {\text {Im}}\left[ \left( \dfrac{ K_r + i J_r}{r!} \right) \left( \sqrt{\beta _x}\,x+i\sqrt{\beta _y}\,y \right) ^r\right] \end{pmatrix}\, , \end{aligned}$$

(1)

where $R(\omega )$ is a 2D rotation matrix and $R(\omega _x,\omega _y)=\mathrm {diag}\left( R(\omega _x),R(\omega _y)\right)$, while $K_r$ and $J_r$ are the normal and the skew integrated strength of the $2(r+1)$-polar magnet, respectively. They are obtained by considering the following expression for the transverse magnetic field

$$\begin{aligned} B_y +i B_x = B\rho \sum _{r=1}^{M} \left( k_r+ij_r\right) \frac{\left( x+i y\right) ^r}{r!} \, , \end{aligned}$$

(2)

where $B\rho$ is the beam magnetic rigidity and $K_r=k_r \ell$, $J_r = j_r \ell$, where $\ell$ is the length of the magnetic element.

In certain situations, it is interesting to introduce an explicit amplitude-detuning effect in the map of Eq. (1) that models the case where a magnetic multipole excites the resonance, whereas the effect of other magnetic elements, not modeled as kicks in the map, is to generate an amplitude-dependent detuning. In this case, the rotation matrix in Eq. (1) is replaced by a rotation matrix $R(\omega _x+\alpha _{xx}J_x + \alpha _{xy}J_y, \omega _y+\alpha _{xy}J_x + \alpha _{yy}J_y)$, where the linear actions $J_x=(x^2+p_x^2)/2$, and $J_y=(y^2+p_y^2)/2$ have been used, which defines an amplitude-dependent 4D rotation.

We say that $\omega _x, \omega _y$ satisfy a $(m,\, n)$ difference resonance condition if the following holds

$$\begin{aligned} m\omega _x - n\omega _y = 2\pi k \qquad m, n \in \mathbb {N}, k \in \mathbb {Z} \, , \end{aligned}$$

(3)

and the resonance order is given by $m+n$.

Normal Form theory applied to the map of Eq. (1) close to a $(m,\, n)$ resonance condition allows a resonant Normal Form to be built, from which a quasi-resonant interpolating Hamiltonian can be derived [7]. The analysis focuses on the resonances of orders 3 and 4 that, at the leading order in the actions, are possible to excite using common magnetic elements (the details about which magnet type can excite a given resonance are given in Appendix A) according to the following scheme

• (1, 2) resonance: normal sextupole ($j_2=0$);

• (2, 1) resonance: skew sextupole ($k_2=0$);

• (3, 1) resonance: skew octupole ($k_3=0$);

• (1, 3) resonance: skew octupole ($k_3=0$).

We remark that the Normal Form approach provides the resonant terms due to a given nonlinearity as perturbations in the actions $J_x$ and $J_y$, instead of using the resonance strength as the perturbation parameter.

We also remark that the correspondence between magnet type and resonance is valid for the case of a single kick, i.e. , for a map of the form of Eq. (1). In the case of a system with two nonlinear kicks, the fourth-order resonances can also be excited by using a combination of normal and skew sextupoles.

Phase-space topology of the Hamiltonian model

The Normal Form Hamiltonian in the resonant case, written in action-angle variables reads

$$\begin{aligned} \mathcal {H}(\phi _x,\,J_x,\,\phi _y,\,J_y) = \omega _x J_x + \omega _y J_y + \alpha _{xx}J_x^2 + 2\alpha _{xy} J_x J_y + \alpha _{yy} J_y ^2 + G J_x^{m/2} J_y^{n/2}\cos (m\phi _x-n\phi _y) \, , \end{aligned}$$

(4)

where the amplitude-detuning parameters $\alpha _{xx}$, $\alpha _{xy}$, $\alpha _{yy}$ have been introduced and the quasi-resonance condition is given by $m\,\omega _x - n\,\omega _y\approx 0$. The resonance-strength parameter G is directly proportional to the magnet strength $k_r$ or $j_r$, as one can verify by computing the resonant Normal Form Hamiltonian for map (1) using, e.g. , software presented in Ref. [29].

The canonical transformation (see [30, p. 410])

$$\begin{aligned} \begin{aligned} J_x&= mJ_1\,,&\phi _1&= m \phi _x -n \phi _y\,, \\ J_y&= J_2-nJ_1\,,&\phi _2&= \phi _y\,, \ \end{aligned} \end{aligned}$$

(5)

introduces the fast and slow phases and casts the Hamiltonian into the form

$$\begin{aligned} \mathcal {H}(\phi _1,J_1) =\delta J_1 +\alpha _{12} J_1 J_2 +\alpha _{11}J_1^2 +G(mJ_1)^{\frac{m}{2}}(J_2-nJ_1)^{\frac{n}{2}}\cos \phi _1 + \Big [\omega _yJ_2+ \alpha _{22}J_2^2\Big ]\,, \end{aligned}$$

(6)

where $\delta =m\,\omega _x-n\,\omega _y$ is the resonance-distance parameter, and the new constants $\alpha _{11}$, $\alpha _{12}$, and $\alpha _{22}$ are functions of $\alpha _{xx}$, $\alpha _{xy}$ and $\alpha _{yy}$ according to

$$\begin{aligned} \begin{aligned} \alpha _{11}&= m^2\alpha _{xx} - 2m\, n\, \alpha _{xy}+n^2\alpha _{yy}\, ,\\ \alpha _{12}&= 2(m\, \alpha _{xy}-n\, \alpha _{yy})\, ,\\ \alpha _{22}&= \alpha _{yy}\, . \end{aligned} \end{aligned}$$

(7)

We remark that the term in square brackets of Eq. (6) can be discarded as it is a function of $J_2$ only, which is an integral of motion since ${\partial \mathcal {H}}/{\partial \phi _2}=0$. Hence, it represents a constant additive term of the Hamiltonian. Furthermore, the term $\alpha _{12}$ induces a shift in the location of the resonance crossing, which occurs for $\delta + \alpha _{12} J_2=0$, thus making the resonance-crossing process dependent on the value of $J_2$ ( a time-independent quantity). We remark also that the condition $J_y>0$ constrains the motion within the circle $J_1 < J_2/n$, which we call the allowed circle. The existence of the allowed circle is a consequence of having chosen a difference resonance, i.e. , with the minus sign in Eq. (3). Sum resonances do not fulfil this property that is essential for emittance exchange.

It is worth mentioning that if instead of the resonance (m, n) one would like to analyze the (n, m) resonance, an exchange of the two transverse directions x and y can be applied to Eqs. (4), (5), and (7). However, the resulting Hamiltonian (6) will contain a term $-\delta J_1$, instead. Hence, the direction of the resonance crossing is reversed between the two resonances. Moreover, the amplitude-detuning terms will be different for the two resonances, which in turns implies that the actual crossing time will be different. Given the complexity of the symmetry induced, in the following the analysis of the resonances (m, n) and (n, m) is carried out by only exchanging m and n in Eq. (4).

To study the phase-space structure, it is convenient to express Eq. (6) using the rescaled variable $\tilde{J}_1 =J_1/J_2$, that gives the Hamiltonian

$$\begin{aligned} \tilde{\mathcal {H}}(\phi _1,\tilde{J}_1) =\frac{\delta }{G J_2^{\frac{m+n-2}{2}}} \tilde{J}_1 +\frac{\alpha _{12}}{G J_2^{\frac{m+n-4}{2}}} \tilde{J}_1 +\frac{\alpha _{11}}{G J_2^{\frac{m+n-6}{2}}} \tilde{J}_1^2 +(m\tilde{J}_1)^{\frac{m}{2}}(1-n\tilde{J}_1)^{\frac{n}{2}}\cos \phi _1\, . \end{aligned}$$

(8)

It appears that the resonance-crossing process is actually governed by the parameter

$$\begin{aligned} \eta = \frac{\delta }{G J_2^{\frac{m+n-2}{2}}} \, . \end{aligned}$$

(9)

Therefore, there is an interplay between the distance from resonance, $\delta$, the multipole strength, proportional to G, and the invariant action $J_2$. We also remark that the coefficients $\alpha _{12}, \alpha _{11}$ are rescaled by the quantity $1/(G J_2^{\frac{m+n-6}{2}})$.

The equations of motion for the Hamiltonian of Eq. (6) are

$$\begin{aligned} \begin{aligned} \dot{\phi }_1&= \frac{\partial \mathcal {H}}{\partial J_1}= \delta +2\alpha _{11}J_1+\alpha _{12} J_2 +\frac{m}{2}G(mJ_1)^{\frac{m}{2}-1} (J_2-nJ_1)^{\frac{n}{2} -1} \Big [ mJ_2 -n (m+n)J_1 \Big ]\cos \phi _1\,,\\ \dot{J}_1&= -\frac{\partial \mathcal {H}}{\partial \phi _1}=G \, (mJ_1)^{\frac{m}{2}}(J_2-nJ_1)^{\frac{n}{2}}\sin \phi _1\,, \end{aligned} \end{aligned}$$

(10)

and the phase-space topology that is originated by them depends both on m and n, although some features do not.

The knowledge about the existence of the fixed points of Eq. (10) and their stability is essential for understanding the phase-space topology. The solutions of the equation ${\partial \mathcal {H}}/{\partial \phi _1}=0$ that satisfy the condition $J_2-nJ_1=0$ are particularly relevant for our study, since they lie on the border of the allowed circle, and for this reason, these solutions have to be unstable fixed points and are computed by solving

$$\begin{aligned} \cos \phi _1=\frac{2(\delta +2\alpha _{11} J_1+\alpha _{12} J_2)}{Gm^{m/2}\left[ n^2J_1-m(J_2-nJ_1)\right] J_1^{\frac{m}{2}-1}(J_2-nJ_1)^{\frac{n}{2}-1}}\, . \end{aligned}$$

(11)

When imposing the condition $J_1-nJ_2=0$, the r.h.s. of Eq. (11) is not singular only if $n=1$ or $n=2$ (the exactly resonant case will be discussed later).

The separatrix that passes through the unstable fixed points on the border of the allowed circle is called coupling arc (as in Ref. [25]) and is found by solving the equation

$$\begin{aligned} \mathcal {H}(\phi _1, J_1) = \delta \frac{J_2}{n} + \left( \frac{\alpha _{11}}{n} + \frac{\alpha _{12}}{n}\right) J_2^2\,, \end{aligned}$$

(12)

which can be rewritten as

$$\begin{aligned} n\delta + \alpha _{11}n^2(J_2+nJ_1) + n\alpha _{12}J_2= G m^{m/2} J_1^{m/2}(J_2-nJ_1)^{\frac{n}{2}-1}\cos \phi _1\, . \end{aligned}$$

(13)

For $n=1$, the term $(J_2-nJ_1)^{1/2}$ appears in the numerator of Eq. (11) with a positive power, and when $J_1=J_2$, i.e. , on the allowed circle, $\cos \phi _1=0$, so $\phi _1=\pm \pi /2$. With no amplitude detuning, the equation of the coupling arc reads

$$\begin{aligned} \delta (J_2-J_1)^{1/2} = Gm^{m/2} J_1^{m/2} \cos \phi _1\, , \end{aligned}$$

(14)

and the existence of solutions requires $\delta \cos \phi _1 > 0$. If $\delta >0$ the coupling arc lies in the right hemicircle, while for $\delta <0$ it lies in the left one. Furthermore, for large values of $|\delta |$ the coupling arc is very close to the allowed circle, as it can be seen from the equation in the limit $|\delta | \rightarrow +\infty$.

For $n=2$, the term $(J_2-2J_1)$ disappears from the denominator of Eq. (11), and the coupling-arc intersections are found for

$$\begin{aligned} \cos \phi _1 = 2^{\frac{m}{2}-1}\frac{\delta + (\alpha _{11}+\alpha _{12})J_2}{Gm^{m/2}J_2^{m/2}} \, , \end{aligned}$$

(15)

which exist as long as $|\cos \phi _1|\le 1$, and they do not depend on $J_1$. In this case, in the absence of amplitude detuning, we obtain a simple expression for the coupling arc

$$\begin{aligned} J_1 = \left( \frac{\delta }{2 Gm^{m/2}\cos \phi _1}\right) ^{2/m}\, . \end{aligned}$$

(16)

Once the Hamiltonian of Eq. (6) is recast in Cartesian coordinates $(X=\sqrt{2J_1}\cos \phi _1,\,Y=\sqrt{2J_1}\sin \phi _1)$, one can observe that the other fixed points, which could be associated to the presence of other separatrices, can be found only on the X axis due to symmetry reasons.

First of all, we remark that the origin $(X=0,\,Y=0)$ is a fixed point only if $m > 1$. In this case, we can study the isoenergetic surface of the origin from the equation $\mathcal {H}(\phi _1,J_1)=0$, i.e. ,

$$\begin{aligned} J_1(\delta + \alpha _{11}J_1 + \alpha _{12}J_2 + Gm^{m/2}J_1^{m/2 - 1}(J_2-nJ_1)^{n/2}\cos \phi _1) = 0 \, , \end{aligned}$$

(17)

which is solved for $J_1=0$ or for

$$\begin{aligned} \delta + \alpha _{12}J_2 = - \alpha _{11}J_1 - Gm^{m/2}J_1^{m/2 - 1}(J_2-nJ_1)^{n/2}\cos \phi _1 \, . \end{aligned}$$

(18)

For $m=2$, we can solve analytically the case without amplitude-detuning terms, as the equation becomes

$$\begin{aligned} \delta = - 2G(J_2-nJ_1)^{n/2}\cos \phi _1\, . \end{aligned}$$

(19)

A solution $J_1(\phi _1)$ that passes through the origin when $\mathrm{acos}(\delta /(2GJ_2^{n/2}))$ exists, i.e. , for $|\delta |\le 2GJ_2^{n/2}$. The solution lies in the positive-X domain if $\delta <0$, and in the negative one if $\delta >0$. For $m>2$, the origin is a genuine fixed point and the Hamiltonian can be linearized around the origin using the coordinates X, Y. One obtains a simple rotator Hamiltonian, i.e. , $\mathcal {H}_\text {lin} = \delta (X^2+Y^2)/2$, which shows that the origin is an elliptic fixed point.

Finally, additional fixed points might exist on the axis $Y=0$, and they should be solutions of ${\partial \mathcal {H}}/{\partial X}=0$, having set $Y=0$. The equation reads

$$\begin{aligned} \delta + \alpha _{11}X^2 + \alpha _{12}J_2 + \frac{G}{2}\left( \frac{m}{2}\right) ^\frac{m}{2} \left( J_2-\frac{n}{2}X^2\right) ^{\frac{n}{2}-1}\,X^{m-2}\left[ 2mJ_2-2-n(m+n)X^2\right] =0\, . \end{aligned}$$

(20)

The number of real solutions of Eq. (20) that lie inside the allowed circle depends on the degree of the resulting polynomial in X, which is determined by the order of the resonance condition. Therefore, the topology of the phase space of higher-order resonances can be very complicated, and its detail is a crucial element for the feasibility of emittance sharing. A specialized discussion on fixed points on the $Y=0$ axis is carried out for each resonance taken into consideration in our study in Sect. 2.3.

We remark that when $\delta +\alpha _{12}J_2=0$, i.e. , the resonance condition is met, and $\alpha _{11}=0$, the nontrivial solutions of Eq. (20) are given by

$$\begin{aligned} 2mJ_2 -n(m+n)X^2 = 0\,, \qquad \text {or} \qquad X = \pm \sqrt{\frac{2mJ_2}{n(m+n)}}\, . \end{aligned}$$

(21)

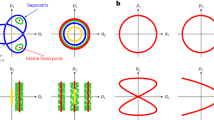
The two symmetrical solutions are both stable fixed points. For the origin, the previous discussion holds, having set $\delta =0$. Moreover, the coupling arc equation at resonance becomes $\cos \phi _1 =0$, and the coupling arc is reduced to the diameter of the allowed circle passing through $\phi _1 = \pm \pi /2$, for any value of m and n. Separatrices that are not coupling arcs approximate the behavior of a coupling arc close to the resonance (see, e.g. , the top-right phase-space portrait of Fig. 4).

In general, at resonance, the allowed circle is symmetrically divided in two regions. Hence, whatever the resonance is crossed, if $\alpha _{11}=0$ there is always a neighborhood of the resonant condition $\delta +\alpha _{12}J_2=0$ where the phase space is divided into two regions. This is the ideal condition to perform emittance sharing, as it will be shown in Sect. 2.4.

In the following, we analyze some resonances that can be excited using magnetic elements commonly installed in particle accelerators.

Motion close to low-order resonances

We now compute the most important features of the phase space of the resonant Normal Form Hamiltonian for low-order resonances excited by sextupole or octupole magnets. The theory of emittance sharing relies on separatrix crossing; therefore, we need to know which fixed points exist in the phase space, their stability, and where separatrices exist. In general, we will search for unstable fixed points on the allowed circle, which give rise to a coupling arc, for stable fixed points on $\phi _1=0$ or $\phi _1=\pi$, and for possible extra separatrices.

Resonance (1,2)

Resonance (1, 2) Hamiltonian in $(\phi _1, J_1)$ coordinates, corresponding to the resonant Normal Form of a Hénon-like map with a normal sextupolar kick, reads [25, 26],

$$\begin{aligned} \mathcal {H}(\phi _1,J_1) = \delta J_1 + \alpha _{11}J_1^2 + \alpha _{12}J_1 J_2 + GJ_1^{1/2}(J_2-2J_1)\cos \phi _1\, . \end{aligned}$$

(22)

The phase-space features an allowed circle given by $J_1<J_2/2$, and a coupling arc. From Eq. (11), one obtains the unstable fixed points as solutions of

$$\begin{aligned} \cos \phi =\frac{\delta + (\alpha _{11} + \alpha _{12})J_2}{G\sqrt{2J_2}} \end{aligned}$$

(23)

and a coupling arc (see Eq. (13)) that, expressed in Cartesian coordinates, reads

$$\begin{aligned} 4\alpha _{11}(X^2+Y^2) - \frac{G}{\sqrt{2}}X + 2(\delta + \alpha _{12}J_2+2\alpha _{11}J_2)=0\, . \end{aligned}$$

(24)

This represents a circumference that crosses the allowed circle when

$$\begin{aligned} \left| \frac{\delta + (\alpha _{11} + \alpha _{12})J_2}{G\sqrt{2J_2}}\right| \le 1 \end{aligned}$$

(25)

dividing it in two regions. When $\alpha _{11}=0$, the coupling arc reduces to the straight line

$$\begin{aligned} X = \frac{\sqrt{2}(\delta + \alpha _{12}J_2)}{2G} \end{aligned}$$

(26)

that sweeps through the phase space if $\delta$ is varied, defining two equal regions when $\delta =-\alpha _{12} J_2$. The equation of the stable fixed points for $\phi _1=0$ or $\phi _1=\pi$ reads

$$\begin{aligned} (\delta + 2\alpha _{11}J_1 + \alpha _{12}J_2)J_1^{1/2} \pm G(J_2-6J_1)=0 \, , \end{aligned}$$

(27)

and we obtain two real solutions inside the allowed circle, one for each side of the coupling arc. Therefore, the phase space is always divided into no more than two regions. Some phase-space portraits are shown in Fig. 1.

Fig. 1

Phase-space portraits of Eq. (22) (resonance (1, 2)) with $G=J_2=1$, $\alpha _{12}=0$. The red line delimits the allowed circle, the blue line is the coupling arc

Resonance (2,1)

The starting point is the Hénon-like 4D map with a skew sextupole kick and the resonant Normal Form provides an interpolating Hamiltonian up to order 3 of the form

$$\begin{aligned} \mathcal {H}(\phi _1,J_1) = \delta J_1 + \alpha _{11}J_1^2 + \alpha _{12}J_1J_2+ 2G J_1\sqrt{J_2-J_1}\cos \phi _1 \, , \end{aligned}$$

(28)

and the motion is limited to the allowed circle $J_1<J_2$. The fixed points on the allowed circle are given by $\cos \phi _1=0$, i.e. , $\phi _1=\pm \pi /2$, whereas the expression of the coupling arc is obtained by solving $\mathcal {H}(J_1,\phi _1) - \mathcal {H}(J_1=J_2,\phi _1=\pm \pi /2)$, i.e. ,

$$\begin{aligned} (\delta +\alpha _{11}(J_2+J_1)+\alpha _{12}J_2)\sqrt{J_2-J_1} = 2GJ_1\cos \phi _1\,, \end{aligned}$$

(29)

which is easily solved when $\alpha _{11}=0$:

$$\begin{aligned} J_1(\phi _1) = -\frac{{\hat{\delta }}^{2} - {\hat{\delta }} \sqrt{16 G^{2} J_{2} \cos \left( \phi _{1}\right) ^{2} + {\hat{\delta }}^{2}} }{8 G^{2} \cos \left( \phi _{1}\right) ^{2}} \qquad \text {with} \qquad {\hat{\delta }} = \delta +\alpha _{12}J_2 \, . \end{aligned}$$

(30)

We remark that if ${\hat{\delta }}>0$ we must have $\cos \phi _1>0$, i.e. , the coupling arc lies in the positive domain of X, whereas for ${\hat{\delta }}<0$ in the negative one. Moreover, for ${\hat{\delta }}=0$ the coupling arc reduces to a line that evenly divides the allowed circle. On the other hand, we can look for solutions when $\phi _1=0$ and $\phi _1=\pi$, and when $\alpha _{11}=0$, Eq. (30) reads

$$\begin{aligned} {\hat{\delta }}\sqrt{J_2-J_1} \pm G(2J_2-3J_1) = 0\, . \end{aligned}$$

(31)

Assuming $G>0$, we need to impose conditions on the existence of the solutions before squaring: for $\phi _1=0$ and ${\hat{\delta }}>0$, the condition $2J_2/3<J_1<J_2$ holds, while for ${\hat{\delta }}<0$ we require $J_1<2J_2/3$. For $\phi _1=\pi$, the conditions are reversed. Finally, we obtain the solutions

$$\begin{aligned} J_1^\pm = \frac{2}{3}J_2 \pm \frac{{\hat{\delta }}}{18G^2} \left( \sqrt{12G^2 J_2+{\hat{\delta }}^2}\mp {\hat{\delta }}\right) \, . \end{aligned}$$

(32)

No matter the sign, the quantity inside the brackets is always positive, which implies $J_1^+>2J_2/3$ if ${\hat{\delta }}>0$ and $J_1^+<2J_2/3$ if ${\hat{\delta }}<0$, and this solution is acceptable only for $\phi _1=0$. Conversely, $J_1^->2J_2/3$ if ${\hat{\delta }}<0$ and $J_1^-<2J_2/3$ if ${\hat{\delta }}>0$. This solution is only acceptable when $\phi _1=\pi$. Finally, we always have a solution in the positive X semi-axis and one in the negative one, as long as the solution for $J_1$ inside the allowed circle, but, as $J_1^+ \rightarrow J_2$ when ${\hat{\delta }} \rightarrow \infty$, and $J_1^- \rightarrow J_2$ as ${\hat{\delta }}\rightarrow -\infty$, this never occurs.

Let us study the trajectory of a point whose initial condition is at the origin. We have to solve the equation $\mathcal {H}(\phi _1,J_1) = 0$, i.e. ,

$$\begin{aligned} J_1\left( \delta + 2G\sqrt{J_2-J_1}\cos \phi _1\right) =0\,, \end{aligned}$$

(33)

and we have the solutions $J_1=0$ and $\delta + 2G\sqrt{J_2-J_1}\cos \phi _1=0$. The latter can only be solved for $\cos \phi _1<0$ if $\delta >0$, and $\cos \phi _1>0$ if $\delta <0$. Therefore, there is only one trajectory passing through the origin: it does not alter the topology of the phase space introducing new islands (see Fig. 2), and the allowed circle is always divided into two regions, thus making the emittance sharing possible.

Fig. 2

Phase-space portrait of Eq. (28) (resonance (2, 1)) with $\delta =G=J_2=1$, $\alpha _{11}=\alpha _{12}=0$. The red line delimits the allowed circle, the blue line is the coupling arc

We remark that in Fig. 2 and in general in the phase-space portraits of the Hamiltonian functions discussed in this paper, we used large values of $\delta$ and $J_2$, compared to those chosen for the numerical simulations that will be later discussed. This is justified by the fact that the Hamiltonian models depend on the unique parameter $\eta =\delta /(G\sqrt{J_2})$, for third order resonances, and $\eta =\delta /(GJ_2)$, for fourth-order ones (see Eq. 9), hence it is perfectly justified to choose conditions with $\eta \sim 1$.

Resonance (1,3)

For the (1, 3) resonance, which is excited by a skew octupole, we have the quasi-resonant Hamiltonian

$$\begin{aligned} \mathcal {H}(\phi _1,J_1) = \delta J_1 + \alpha _{12}J_1 J_2 + \alpha _{11}J_1^2 + GJ_1^{1/2}(J_2-3J_1)^{3/2}\cos \phi _1 \, . \end{aligned}$$

(34)

If we set $\alpha _{11}=\alpha _{12}=0$, which is the case when the resonance is excited without sextupolar kicks, we have fixed points for $\phi _1=0$ or for $\phi _1=\pi$ that are the solutions of

$$\begin{aligned} \frac{\partial \mathcal {H}}{\partial J_1}\Big |_{\phi _1=0,\pi } = \delta \pm \frac{G}{2}\left( J_1^{-1/2}(J_2-3J_1)^{3/2} - 9J_1^{1/2}(J_2-3J_1)^{1/2}\right) =0 \, , \end{aligned}$$

(35)

that gives

$$\begin{aligned} \delta J_1^{1/2} = \pm \frac{G}{2}\left( 9 J_1 (J_2-3J_1)^{1/2} - J_1^{1/2}(J_2-3J_1)^{3/2}\right) \, . \end{aligned}$$

(36)

The r.h.s. of Eq. 36 is positive when $\pm G\left( J_1-\frac{J_2}{12}\right) > 0$, and we will compare it to the sign of $\delta$. Let us choose $G>0$. For $\phi _1=0$, we have solutions for $\delta >0$ and $J_2/12<J_1<J_2/3$, or for $\delta <0$ and $0<J_1<J_2/12$. For $\phi =\pi$, the conditions are reversed. By squaring the equation, which gives a cubic polynomial, we compute its roots, taking into account all conditions. The solutions are given in Fig. 3. There are the following possibilities:

• if $\delta /(GJ_2)>1$, there exists only one stable fixed point for $\phi _1=\pi$ that tends to the origin when $\delta /(G J_2)\gg 1$;

• if $0< \delta /(GJ_2) < 1$, there are two fixed points on $\phi _1=0$ and one on $\phi _\pi$. The inner solution on $\phi _1=0$ ($J_1^+$) and the solution on $\phi _1=\pi$ ($J_1^-$) are stable, while the outer fixed point on $\phi _1=0$ is unstable, and generates a separatrix. The phase space is divided into three regions: $S^\pm$ around $J_1^\pm$, and ${\hat{S}}$ that is the area between the separatrix which crosses ${\hat{J}}_1$ and the allowed circle. Portraits with $\delta /(GJ_2)=0.1$ and $\delta /(GJ_2)=0.8$ are shown in Fig. 4;

• if $\delta =0$, two fixed points are present in $J_2/12$, at $\phi _1=0$ and $\phi _1=\pi$. The separatrix degenerates to the diameter of the allowed circle.

• if $\delta <0$, one has the same situation as for $\delta >0$, but exchanging $\phi _1=0$ and $\phi _1=\pi$.

Resonance (3,1)

From the general properties stated before, the allowed circle is $J_1 <J_2$ and the coupling arc intersects the border of the allowed circle at $\phi _1=\pm \pi /2$. Then, we have the origin that, being $m>2$, is a stable fixed point.

Fig. 3

Fixed points of Eq. (34) (resonance (1, 3)) with $\alpha _{11}=\alpha _{12}=0$ for $\phi _1=0$ (solid line) and $\phi _1=\pi$ (dashed line) as a function of $\delta$

Fig. 4

Phase-space portraits of Eq. (34) (resonance (1, 3)) for different values of $\delta$ with $G=J_2=1$, $\alpha _{11}=\alpha _{12}=0$. The red line delimits the allowed circle, while the blue line is the separatrix. In the bottom-left plot, the extended region on the left is $S^+$, the one inside the separatrix on the right is $S^-$ while the small region between the separatrix and the allowed circle is ${\hat{S}}$

For what concerns the fixed points on the X axis, we initially consider the case with $\alpha _{11}=\alpha _{12}=0$. For $\phi _1=0$ or $\phi _1=\pi$, the equation ${\partial H}/{\partial J_1}=0$ reads

$$\begin{aligned} 2\delta \sqrt{J_2-J_1}=\pm 3\sqrt{3}GJ_1^{1/2}(4J_1-3J_2)\, . \end{aligned}$$

(37)

Assuming $G>0$, for $\delta >0$ we can accept solutions on $\phi _1=0$ for $J_1<3J_2/4$ and on $\phi _1=\pi$ for $3J_2/3<J_1<J_2$, and the opposite for $\delta <0$. By squaring, we obtain the cubic equation

$$\begin{aligned} 4\delta ^2(J_2-J_1)=27 G^2 J_1(4J_1-3J_2)^2 \end{aligned}$$

(38)

whose roots can be studied by rewriting the equation as

$$\begin{aligned} \frac{4\delta ^2}{27G^2}=\frac{J_1(4J_1-3J_2)^2}{J_2-J_1}=f\left( \frac{J_1}{J_2}\right) \,, \end{aligned}$$

(39)

and by studying $f(J_1/J_2)$ as a function of $J_1$ in $[0,J_2]$. This function has zeroes in $J_1=0$ and $J_1=3J_2/4$ and diverges to $+\infty$ as $J_1\rightarrow J_2$. From its derivative, we find that a local maximum exists for $J_1=(3-\sqrt{3})J_2/4$ and the corresponding value of $\delta$ is (see Eq. (39))

$$\begin{aligned} \delta ^* =\pm \frac{9G}{2}\sqrt{2\sqrt{3}-3}J_2\approx \pm 3.1GJ_2\, . \end{aligned}$$

(40)

Fig. 5

Plot of $f(J_1/J_2)= \dfrac{(J_1/J_2)\left( 4J_1/J_2-3\right) ^2}{1-J_1/J_2}$, as introduced in Eq. (39). The real solutions of the equation are found as $f(J_1/J_2) = 4\delta ^2/(27G^2J_2)$

Fig. 6

Phase-space portraits of Hamiltonian of Eq. (6), with $m=3$, $n=1$, expressed in ($X=\sqrt{2J_1}\cos \phi _1$, $Y=\sqrt{2J_1}\sin \phi _1$) coordinates, for three values of $\delta$, having set $G=J_2=1$ and the amplitude detuning coefficients to zero. The red line delimits the allowed circle while the blue line is the coupling arc. In plot for $\delta =2$, the green line is the extra separatrix which delimits the regions $S_1$ and $S_2$

The plot of $f(J_1/J_2)$ is shown in Fig. 5. Considering the sign conditions on the solution, one has the following possibilities (some examples of phase-space portraits are shown in Fig. 6):

• if $\delta >\delta ^*$, there are a stable fixed point at the origin and a stable fixed point at the right of the coupling arc for $\phi _1=0$ and $J_1>3J_2/4$ (see Fig. 6, right);

• if $0<\delta <\delta ^*$, a stable fixed point at the origin, an unstable fixed point for $\phi _1=\pi$, $0<J_1<(3-\sqrt{3})J_2/4$, and a stable fixed point for $\phi _1=\pi$ and $(3-\sqrt{3})J_2/4<J_1<3J_2/4$, plus a stable fixed point at the right of the coupling arc, for $\phi _1=0$ and $J_1>3J_2/4$. The separatrix that passes through the unstable fixed point is the green line in Fig. 6 (centre) delimiting the regions $S_1$ and $S_2$;

• if $\delta =0$, two stable fixed points at $J_1=3J_2/4$; the coupling arc is a line that passes through the origin (see Fig. 6, left);

• if $-\delta ^*<\delta <0$, a stable fixed point at the origin, an unstable fixed point for $\phi _1=0$, $0<J_1<(3-\sqrt{3})J_2/4$, and a stable fixed point for $\phi _1=0$ and $(3-\sqrt{3})J_2/4<J_1<3J_2/4$, plus a stable fixed point at the left of the coupling arc, for $\phi _1=\pi$ and $J_1>3J_2/4$. The topology is the same of Fig. 6 (centre), but horizontally reversed;

• $\delta <-\delta ^*$: a stable fixed point at the origin and a stable fixed point at the left of the coupling arc for $\phi _1=\pi$ and $J_1>3J_2/4$. Once more, the topology is mirrored w.r.t. the rightmost plot of Fig. 6.

Emittance-sharing process

General considerations

Let us consider a process described by the Hamiltonian of Eq. (4), with either $\omega _x$ or $\omega _y$, or both, slowly changing as a function of time to cross the $(m,\,n)$ resonance. According to the transformations that led to Eq. (6), this is modeled varying $\delta$ from a case where ${\hat{\delta }}=\delta +\alpha _{12}J_2\gg 0$ to one where ${\hat{\delta }}\ll 0$, i.e. , ${\hat{\delta }}$ is adiabatically changed from $+\delta _\text {max}$ to $-\delta _\text {max}$ during a time interval T. The variation of ${\hat{\delta }}$ changes the position of the coupling arc, that sweeps the disk $J_1<J_2/n$ within which the dynamics is constrained.

A particle starts its orbit far from the resonance, with an action $J_{1,\text {i}} = J_{x,\text {i}}/m$, where the only fixed point is close to the origin and the particle orbit is almost a circle, of area $2\pi J_{1,\text {i}}$. This area is an adiabatic invariant, and it is conserved when ${\hat{\delta }}$ is slowly varied. As ${\hat{\delta }}$ is decreased, the moving coupling arc reduces the extent of the region the particle is orbiting in, dividing the allowed circle in two parts that have equal area when ${\hat{\delta }}=0$. When the area of the initial region is equal to $2\pi J_{1,\text {i}}$, according to separatrix crossing theory [31], the particle will cross the coupling arc and enter the other phase-space region with an action corresponding to the area of the arrival region at the jump time divided by $2\pi$.

Since the allowed circle has an area $2\pi J_2/n$, the resulting action will be

$$\begin{aligned} J_{1,\text {f}} = \frac{J_2}{n}-J_{1,\text {i}}\,, \end{aligned}$$

(41)

and, transforming back to the initial actions

$$\begin{aligned} J_{x,\text {f}} = m J_{1,\text {f}} = m \left( \frac{J_{y,\text {i}}+ n J_{x,\text {i}}/m}{n}-\frac{J_{x,\text {i}}}{m}\right) = \frac{m}{n}J_{y,\text {i}} \end{aligned}$$

(42)

and

$$\begin{aligned} J_{y,\text {f}} = \frac{n}{m} J_{x,\text {i}}\, . \end{aligned}$$

(43)

As $\delta$ continues decreasing, the area of the region containing the particle orbit increases and, at the end of the variation of $\delta$ (far from the resonance), the orbit is a circle around the origin whose area corresponds to the new action.

For each particle, this process realizes an action sharing between the two degrees of freedom. The product $J_x J_y$ remains constant, but the two values are, at the end of the process, reallocated according to a n/m ratio. Note that for the case of the linear coupling resonance, i.e. , $n=m=1$, this corresponds to the well-known emittance exchange process [21, 23, 24]. It is essential to stress that the analysis outlined before holds true only when the phase space is exactly divided into two regions by the coupling arc, and no other separatrices are present. Otherwise, a different analysis is needed to assess whether the additional phase-space regions, such as the ones visible in the centre plot of Fig. 6, interfere with the trapping process leading to the emittance sharing. A discussion on this and how to mitigate such effects is carried out in Sect. 2.4.2. If the action sharing is successful, it is possible to verify what happens in the presence of a set of initial conditions that are Gaussian distributed in both planes $(x, p_x)$ and $(y,p_y)$, i.e. , an exponential distribution in $J_x$ and $J_y$. Using the standard definition, i.e. , $\varepsilon _x = \langle {J_x}\rangle$, $\varepsilon _y = \langle {J_y}\rangle$, the initial distribution reads

$$\begin{aligned} \rho _\text {i}(J_x,J_y) = \frac{1}{\varepsilon _{x}\varepsilon _{y}}\exp ( -\frac{J_x}{\varepsilon _{x}} - \frac{J_y}{\varepsilon _{y}}) \end{aligned}$$

(44)

and, after the exchange process using Eqs. (42, 43), we obtain the final distribution

$$\begin{aligned} \rho _\text {f}(J_x,J_y) = \frac{1}{\varepsilon _{x}\varepsilon _{y}}\exp ( -\frac{m}{n}\frac{J_y}{\varepsilon _{x}} - \frac{n}{m}\frac{J_x}{\varepsilon _{y}}) \, . \end{aligned}$$

(45)

The new averages are given by the integrals

$$\begin{aligned} \begin{aligned} \varepsilon _{x,\text {f}} = \langle {J_{x,\text {f}}}\rangle&= \int _0^\infty \mathrm{d}J_x\int _0^\infty \mathrm{d}J_y\, J_x\, \rho _\text {f}(J_x,J_y)&= \frac{m}{n}\langle {J_{y,\text {i}}}\rangle = \frac{m}{n}\varepsilon _{y,\text {i}} \\ \varepsilon _{y,\text {f}} = \langle {J_{y,\text {f}}}\rangle&= \int _0^\infty \mathrm{d}J_x\int _0^\infty \mathrm{d}J_y\, J_y\, \rho _\text {f}(J_x,J_y)&=\frac{n}{m}\langle {J_{x,\text {i}}}\rangle = \frac{n}{m}\varepsilon _{x,\text {i}} \, , \end{aligned} \end{aligned}$$

(46)

and it is evident that an emittance sharing occurred.

It is also possible to compute the initial distributions in terms of $J_1$ and $J_2$

$$\begin{aligned} \begin{aligned} \rho _1(J_1)&=\int _0^\infty \mathrm{d}J_y \, \rho _\text {i}(mJ_1,J_y) = \frac{1}{\varepsilon _x} \exp (-\frac{mJ_1}{\varepsilon _x}) \\ \rho _2(J_2)&= \int _0^{\frac{m}{n}J_2}\mathrm{d}J_x\, \rho _\text {i}\left( J_x,J_2-\frac{n}{m}J_x\right) = \frac{m}{m\,\varepsilon _x-n\,\varepsilon _y} \left[ \exp \left( -\frac{J_2}{\varepsilon _y}\right) - \exp \left( -\frac{m\,J_2}{n\,\varepsilon _x}\right) \right] \, . \end{aligned} \end{aligned}$$

(47)

Then, given the dependence of the phase-space topology on the conserved parameter $J_2$, it is useful to consider the initial Gaussian distribution in $J_x$ and $J_y$ as an ensemble of distributions in $J_1$ dependent on the parameter $J_2$ distributed as $\rho _2(J_2)$: the distribution of $J_1$ for a given $J_2$ reads

$$\begin{aligned} \rho _{12}(J_1|J_2) = \frac{\rho (mJ_1, J_2-nJ_x/m)}{\rho _2(J_2)} = \frac{m\,\varepsilon _y - n\,\varepsilon _x}{m\,\varepsilon _x \varepsilon _y} \frac{\exp (\frac{n-m}{\varepsilon _x}J_1)}{1 - \exp (\frac{n\,\varepsilon _x-m\,\varepsilon _y}{n\,\varepsilon _x\varepsilon _y}J_2)} \end{aligned}$$

(48)

where the normalization

$$\begin{aligned} \int _0^\infty \mathrm{d}J_2\, \rho _2(J_2) \int _0^{J_2/n} \mathrm{d}J_1 \, \rho _{12}(J_1|J_2) = 1 \end{aligned}$$

(49)

holds.

During the emittance-sharing process, $\delta$ is varied between $\pm \delta _\text {max}$, and correspondingly, $\eta$ (see Eq. (9)) varies between $\pm \eta _\text {max}$, where $\eta _\text {max}=\eta (\delta _\text {max})$. For any pair $(J_{1,\text {i}},J_{2,\text {i}})$, there exists a value $\eta ^*$ for which the area of the phase-space region $A_{J_{_,\text {i}}{2}}(\eta )$ satisfies $2\pi J_{1,\text {i}}=A_{J_{2,\text {i}}}(\eta ^*)$, and whenever the phase space is divided into two regions, $A_{J_{2,\text {i}}}(\eta )$ is a monotonic decreasing function of $\eta$ (and of $\delta$) during the resonance-crossing process. Therefore, the function $J_1(\eta ^*)=A(\eta ^*)/(2\pi )$ is monotonic as well. During the resonance crossing, the fraction $\tau$ of particles that effectively undergoes emittance sharing is given by all particles for which $\eta ^*\in [-\eta _\text {max},\eta _\text {max}]$ and it can be obtained by

$$\begin{aligned} \tau = \int _0^\infty \mathrm{d}J_2 \,\rho _2(J_2) \int _{J_1(-\eta _\text {max})}^{J_1(\eta _\text {max})}\mathrm{d}J_1\,\rho _{12}(J_1) \, . \end{aligned}$$

(50)

The sharing fraction $\tau$ will also be a monotonic function of $\eta _\text {max}$. The parameter $\eta _\text {max}$ determines the effectiveness of the emittance sharing due to geometrical reasons: under the assumption that the initial beam distributions are Gaussian, one can define the following parameter

$$\begin{aligned} \kappa _\text {geom} = \frac{\delta _\text {max}}{G \langle {J_{2,\text {i}}}\rangle ^{(m+n-2)/2}} \, . \end{aligned}$$

(51)

as the relevant quantity to study the performance of the emittance-sharing process.

The phase-space geometry is certainly important in the emittance-sharing process, but the efficiency is also influenced by the adiabaticity of the resonance-crossing process. A form for the adiabaticity parameter should therefore be determined. For this purpose, we remark that the Hamiltonian of Eq. (6) can be written, while $\delta$ is varied, as

$$\begin{aligned} \mathcal {H}= \epsilon t J_1 + H_0(J_1) + G H_1(\phi _1,J_1)\,, \end{aligned}$$

(52)

where $\epsilon =2\delta _\text {max}/T$, and $H_0, H_1$ represent the amplitude-dependent and resonant terms, respectively, that appear in the equations of motion

$$\begin{aligned} \begin{aligned} \dot{J}_1&= -G \, \frac{\partial H_1}{\partial \phi } \\ {\dot{\phi }}_1&= \epsilon t + \frac{\partial H_0}{\partial J} + G \, \frac{\partial H_1}{\partial J} \, . \end{aligned} \end{aligned}$$

(53)

As shown in Ref. [24], under the rescaling of time ${\bar{t}} = Gt$, one obtains the equations

$$\begin{aligned} \begin{aligned} \frac{\partial J_1}{\partial {\bar{t}}}&= -\frac{\partial H_1}{\partial \phi } \\ \frac{\partial \phi _1}{\partial {\bar{t}}}&= \frac{\epsilon }{G^2} {\bar{t}} + \frac{1}{G}\frac{\partial H_0}{\partial J} + \frac{\partial H_1}{\partial J} \, . \end{aligned} \end{aligned}$$

(54)

Therefore, the appropriate adiabaticity parameter is given by $\epsilon /G^2$, i.e. , one obtains the same emittance sharing if G scales as $G\sim \sqrt{\epsilon }$, while the amplitude-detuning terms are rescaled by a factor G. Parenthetically, as discussed in Ref. [24], it is possible to improve the adiabaticity of the resonance-crossing process by using $\delta \sim (\epsilon t)^p$ with $p>1$. If $\epsilon$ is kept constant and the sharing efficiency is evaluated for different values of $\delta _\text {max}$, then the parameter that controls the emittance sharing, including the dynamical effects, is given by

$$\begin{aligned} \kappa _\text {dyn} = \frac{\sqrt{\delta _\text {max}}}{G \langle {J_{2,\text {i}}}\rangle ^{(m+n-2)/2}}\, . \end{aligned}$$

(55)

We remark that $\kappa _\text {geom}/\kappa _\text {dyn} = \sqrt{\delta _\text {max}}$.

Note that an effective resonance strength, which corresponds to the inverse of the parameter $\kappa _\text {dyn}$ defined above, was introduced in Ref. [25] and [26] as the unique parameter needed to describe the emittance sharing due to the crossing of the resonance (1, 2). Our discussion shows that the purely phenomenological choice can be explained by means of rigorous mathematical arguments.

Effect of phase-space topology on emittance sharing

A general assumption on emittance sharing requires that the allowed circle is divided by the coupling arc in two regions. From the considerations reported in Sect. 2.3, this is always true for third-order resonances. However, for fourth-order resonances, such as (1, 3) and (3, 1), the situation is more complex. Indeed, close to the resonance (1, 3), an extra phase-space region is present (see Fig. 4), although it does not affect the emittance sharing.

Let us follow the evolution of the system from a state when $\delta \gg GJ_2$ and one with $\delta \ll -GJ_2$. At the beginning, only a fixed point is present, around which the particle orbits. When $\delta <GJ_2$, the region ${\hat{S}}$ appears (see Fig. 4) and particles orbiting outside the new separatrix are automatically captured into that region, without any jump in $J_1$, since the area they enclose within their orbit remains the same.

While $\delta$ further decreases, however, ${\hat{S}}$ is pushed toward the outer circle. Particles inside it are then captured into $S^+$, for which $\varTheta ^+={\mathrm{d}A(S^+)}/{\mathrm{d}\delta }>0$, with the expected change in the adiabatic invariant. However, since in the crossing of the outer separatrix no change of adiabatic invariant occurs, the passage from ${\hat{S}}$ to $S^-$ is perfectly equivalent to the passage between $S^+$ and $S^-$. Once $\delta$ reaches zero, the situation is perfectly symmetric, with two stable fixed points and a separatrix dividing the allowed circle in two equal parts.

We then continue reducing $\delta$ in the negative domain. A new unstable fixed point appears at $\phi _1=\pi$, and a topology akin to the third plot of Fig. 4, although mirrored, appears. The problem is whether the new outer region will trap particles, and this turns out not to be possible. The outer region is maximal at $\delta =-G J_2$, and the unstable fixed point is at $J_1=J_2/4$ and $\phi _1=\pi$. We can thus estimate the area of the outer region as the difference between the outer circle at $J_1=J_2/3$, and the circle at $J_1=J_2/4$, which gives $\pi J_2/6$. On the contrary, particles inside ${\hat{S}}$ have a minimum action of $J_2/4$, i.e. , their orbit area is at least $\pi J_2/2$. Hence, since the area of ${\hat{S}}$ is always smaller than $\pi J_2/2$, no particle can reach the minimum action required when crossing from $S^+$ to ${\hat{S}}$. Thus, ${\hat{S}}$ remains void until, at $\delta =-GJ_2$ it disappears completely.

Finally, the extra fixed point does not affect the emittance exchange process, as all particles pass from $S^-$ to $S^+$, which results, according to our previous generic analysis, in an emittance exchange.

In the case of the resonance (3, 1), the presence of extra stable fixed points (see Fig. 6) translates in an extra (and unavoidable) phase-space region that can, in principle, trap particles, thus spoiling the emittance sharing. Nevertheless, the numerical observations discussed in Sect. 3) show that emittance sharing is still feasible, although with some reduction in performance due to the particles trapped in the extra region.

Results of numerical simulations

To assess the performance of the emittance-sharing process for different resonances, we compute the evolution of a Gaussian distribution of initial conditions $\rho (J_x,J_y)$ under the dynamics generated by the map of Eq. (1) ¹ iterated for a number N of turns, with or without amplitude-detuning terms, where $\omega _x$ is kept constant while $\omega _y$ is linearly varied between an initial value $\omega _{y,\text {i}} = m\omega _x/n + \delta _\text {max}$ and the final one $\omega _{y,\text {f}} = m\omega _x/n - \delta _\text {max}$, to cross the $(m,\, n)$ resonance. The initial and final emittance values are then compared, and a figure of merit is introduced to evaluate how well the emittance sharing occurred. To do so, we adapt the definition of $P_\text {na}$, introduced in Ref. [23] for the $(1,\, 1)$ resonance crossing leading to emittance exchange when a $(m,\, n)$ resonance is crossed, and emittance sharing occurs. The generalized definition is

$$\begin{aligned} P_\text {na} = 1 - \frac{ \langle {J_{x,\text {f}}}\rangle - \langle {J_{x,\text {i}}}\rangle }{(m/n)\langle {J_{y,\text {i}}}\rangle - \langle {J_{x,\text {i}}}\rangle } \, . \end{aligned}$$

(56)

The value of $P_\text {na}$ is 1 when no emittance sharing is achieved and zero when the sharing is perfect, i.e. , according to Eq. (46).

Note that in Ref. [25] a different figure of merit is introduced, the so-called fractional emittance growth (FEG), defined as

$$\begin{aligned} \mathrm {FEG} = \left| \frac{\langle {J_{x,\text {f}}}\rangle }{\langle {J_{x,\text {i}}}\rangle }-1\right| +\left| \frac{\langle {J_{y,\text {f}}}\rangle }{\langle {J_{y,\text {i}}}\rangle }-1\right| \, , \end{aligned}$$

(57)

which is 0 when no exchange is performed and $\displaystyle {\left| \frac{m\langle {J_{y,\text {i}}}\rangle }{n\langle {J_{x,\text {i}}}\rangle } - \frac{n\langle {J_{x,\text {i}}}\rangle }{m\langle {J_{y,\text {i}}}\rangle }\right| }$ for a perfect emittance sharing. The reason of this definition is that the goal of [25] is to avoid emittance sharing, and therefore to minimize the FEG, whereas our goal is the opposite, as we are looking to perform emittance sharing, and hence $P_\text {na}$ is the best choice for our study.

When not stated differently, we set $\beta _x=\beta _y=1$ and $\langle {J_{x,\text {i}}}\rangle =\langle {J_{y,\text {i}}}\rangle =1 \times 10^{-4}$, $\omega _x={2.602}$, and $\alpha =0$, generating distributions of initial conditions with $N_\mathrm {p}=1 \times 10^{4}$ particles. For the (1, 2) and (2, 1) resonances we use $\delta _\text {max}=0.1$, $k_2$ (or $j_2)$ equal to 1, $N=1 \times 10^{6}$. For the (1, 3) and (3, 1) resonances we set $\delta _\text {max}=0.01$, $j_3=10$, $N=1 \times 10^{7}$. The initial and final distributions of x, y, $p_x$, $p_y$ for the four resonances are plotted in Fig. 7, and they show clearly the effectiveness of the emittance sharing using these default parameters. Fits of Gaussian distributions with zero average are performed for the final distributions of the phase-space variables. The excellent agreement between the numerical results and the fitted functions shows that the emittance-sharing process preserves the Gaussian nature of the beam, acting only on the standard deviation.

Fig. 7

Histograms of the initial and final distribution of x, y (left plots) and $p_x$, $p_y$ (right plots) after the resonance-crossing process for the four resonances under study. The initial distribution is Gaussian, with a standard deviation $\langle {J_{x,\text {i}}}\rangle =\langle {J_{y,\text {i}}}\rangle =0.01$. The map of Eq. (1) has been used, with parameters $\delta _\text {max}=0.1$, $j_2=1$ or $k_2=1$, $N=10^6$, $\alpha =0$ for the third-order resonances; $\delta _\text {max}=0.01$, $j_3=10$, $N=10^7$, $\alpha =0$ for the fourth-order ones. The thick blue and green lines represent the Gaussian fits with zero average of the final distributions. The values of $\sigma$ printed on the plots represent the standard deviation of the Gaussian fits of the final distributions (for the initial distributions, $\sigma (x)=\sigma (y)=\sigma (p_x)=\sigma (p_y) = (100 \pm 1) \times 10^{-4}$)

We proceed with the quantitative evaluation of the performance of the proposed technique by analyzing how $P_\text {na}$ changes as a function of the parameters. In particular, we have concentrated our analyses on the dependence of $P_\text {na}$ on: (i) the excursion of $\omega _y$, i.e. , $\delta _\text {max}$; (ii) the strength of the nonlinear magnets $j_2$, $k_2$, and $j_3$, depending on the resonance crossed; (iii) the number of map iterations (turns) N; (iv) the detuning parameter $\alpha$ (that has been chosen as $\alpha =\alpha _{xx}=\alpha _{yy}=-2\alpha _{xy}$ to mimic the amplitude detuning generated by normal octupoles as done in Ref. [24]); (v) the initial values of $\langle {J_x}\rangle$ and $\langle {J_y}\rangle$; (vi) the ratio between $\langle {J_{y,\text {i}}}\rangle$ and $\langle {J_{x,\text {i}}}\rangle$. It is worth stressing that in our numerical investigation of the 4D parameter space, the dependence of $P_\text {na}$ is probed by changing one parameter at a time while keeping the others set to their nominal values.

Figure 8 (left) shows the plot of $P_\text {na}$ as a function of $\delta _\text {max}$ whereas in the right part the dependence on the strength of the nonlinear magnets is reported for the various resonances considered. A difference between the behavior of the third- and fourth-order resonances is clearly seen. While for the former it is possible to determine the optimal value of $\delta _\text {max}$, or the strength of the nonlinear magnets, such that $P_\text {na}=0$, i.e. , the emittance sharing is perfect, this is not the case for the latter resonances, for which $P_\text {na}$ reaches a non-zero minimum value.

Fig. 8

Left: $P_\text {na}$ as a function of the excursion $\omega _y$, i.e. , $\delta _\text {max}$. Right: $P_\text {na}$ as a function of the strength of the nonlinear magnets ($k_2$, $j_2$ or $j_3$ depending on the resonance used). In both plots the map (1) has been used, setting $\alpha =0$, and $N=10^6$ (for the third-order resonances) and $N=10^7$ (for the fourth-order ones), and using initial distributions with $\langle {J_{x,\text {i}}}\rangle =\langle {J_{y,\text {i}}}\rangle =0.01$. In the left plot, depending on the resonance, we set either $k_2=1$, $j_2=1$, or $j_3=10$. In the right plot, $\delta _\text {max}=0.1$ has been chosen for $(1,\, 2)$ and $(2,\, 1)$ while $\delta _\text {max}=0.01$ for $(1,\, 3)$ and $(3,\, 1)$

We remark that when $\delta _\text {max}$ approaches 0, $P_\text {na}$ does not converge to 1. This is due to the fact that, when $\delta \approx 0$, the motion of all particles is very close to resonant conditions, and all particles revolve around one of the two stable fixed points in the phase space. Taking the average of the coordinate $J_1$ along the orbit allows estimating the value of $P_\text {na}$ when $\delta _\text {max}\rightarrow 0$ (the details are found in Appendix B).

Other effects need to be taken into account, e.g. , the adiabaticity of the system. Weak nonlinear coupling, which corresponds to a small value of G in the Hamiltonian of Eq. (6), means a faster resonance crossing. For instance, for a particle moving close to the $(1,\, 2)$ resonance, the coupling arc, given by the line of equation $X=\delta /(\sqrt{2}G)$, moves, over one map iteration, by $\delta X = \delta _\text {max}/(\sqrt{2}G N)$. This means that the adiabaticity condition is not met when the strength of the nonlinear magnets is small, and for this reason $P_\text {na}$ goes to 1. The same effect accounts for the lower sharing efficiency at large $\delta _\text {max}$, when N is kept constant.

We remark that when the strength of the nonlinear magnets becomes large, the quasi-resonant Hamiltonian may be no longer a good approximation of the dynamics generated by the map as the higher-order terms cannot be neglected anymore. This observation will be particularly relevant when we will discuss the results shown in Fig. 10 later in this section.

Figure 9 shows the dependence of $P_\text {na}$ on the initial emittance values and the ratio between vertical and horizontal emittances. On the left plot, we keep $\langle {J_{x,\text {i}}}\rangle =\langle {J_{y,\text {i}}}\rangle$ and we change their value, while on the right plot we keep $\langle {J_{x,\text {i}}}\rangle =1 \times 10^{-4}$ and we vary $\langle {J_{y,\text {i}}}\rangle$ from $1 \times 10^{-6}$ to $1 \times 10^{-2}$. As observed before, the behavior for the third- and fourth-order resonances are different. The first type of resonances features a virtually zero $P_\text {na}$ over a rather wide range of parameters under consideration. On the other hand, the fourth-order resonances feature a non-zero minimum for $P_\text {na}$, and that is achieved for well-defined values of the parameters under consideration.

Furthermore, for all four resonances, $P_\text {na}$ increases (therefore that the emittance sharing is less effective) for large values of the initial emittances. This is due to a lower number of particle effectively performing the adiabatic jump. It also increases for small values of the initial action, as this translates to a more difficult onset of adiabatic conditions. It is also observed that achieving emittance sharing for fourth-order resonances is far more difficult than for the third-order ones when $\langle {J_{y,\text {i}}}\rangle \ne \langle {J_{x,\text {i}}}\rangle$. In particular, we remark that for $(1,\, 3)$ and $(3,\, 1)$ the situation is reversed, as emittance sharing fails for $(1,\, 3)$ when $\langle {J_{y,\text {i}}}\rangle \ll \langle {J_{x,\text {i}}}\rangle$, whereas this occurs for $\langle {J_{y,\text {i}}}\rangle \gg \langle {J_{x,\text {i}}}\rangle$ in the case of the $(3,\, 1)$ resonance. This fact will be discussed later.

Note that, in Fig. 9 (right), some discontinuities are present. They are due to the initial condition, for which $J_{x,\text {i}}\approx n/m\,J_{y,\text {i}}$ and then $P_\text {na}$ (see Eq. (56)) has a small denominator and tends to diverge.

Fig. 9

Left: $P_\text {na}$ as a function of the initial $\langle {J_{x,\text {i}}}\rangle$ (chosen to be equal to $\langle {J_{y,\text {i}}}\rangle$), for the four resonances. Right: $P_\text {na}$ as a function of the ratio between $\langle {J_{y,\text {i}}}\rangle$ and $\langle {J_{y,\text {i}}}\rangle$, using $\langle {J_{x,\text {i}}}\rangle =0.01$. In both plots the map (1) has been used, setting $\alpha =0$, and $\delta _\text {max}=0.1$, $j_2=1$ or $k_2=1$, $N=10^6$ (for the third-order resonances) and $\delta _\text {max}=0.01$, $j_3=10$, $N=10^7$ (for the fourth-order ones)

Some common observations can be drawn from Figs. 8 and 9 . First of all, it is clear that, in general, third-order resonances achieve smaller values of $P_\text {na}$, than fourth-order ones. In the observed conditions, the best results for resonances $(1,\, 2)$ and $(2,\, 1)$ correspond to$P_\text {na}\approx 0.01$, while for $(1,\, 3)$ and $(3,\, 1)$ the best performance corresponds to $P_\text {na}\approx 0.06$. This is explained by the fact, as can be seen from the higher values of $P_\text {na}$ at low initial action in the left plot of Fig. 9, that fourth-order resonances are more affected than third-order ones by adiabaticity (note that the numerical simulations for fourth-order resonances were performed with a number of turns an order of magnitude higher than those of the third-order resonances).

Fig. 10

Plots obtained by combining the numerical data presented in Fig. 8 (left and right) and in Fig. 9 (left), using, as independent variable, ${\hat{\kappa }}_\text {geom}$, introduced in Eq. (58a), for the left plots, and ${\hat{\kappa }}_\text {dyn}$, from Eq. (58b), for the right ones. The top plots refer to third-order while the bottom plots to fourth-order resonances. The colors encode the resonance considered, while the different point styles the variable that is varied in the data set, namely $\delta _\text {max}$, the strength of the nonlinear magnets or the initial distribution width

In Fig. 10, we combine the data from both plots of Fig. 8 and the left plot of Fig. 9, using as independent variables one of

$$\begin{aligned} {\hat{\kappa }}_\text {geom}&= \frac{\delta _\text {max}}{g \sqrt{\langle {J_{x,\text {i}}}\rangle ^{m+n-2}}} \end{aligned}$$

(58a)

$$\begin{aligned} {\hat{\kappa }}_\text {dyn}&= \frac{1}{g}\sqrt{\frac{{\delta _\text {max}}}{{\langle {J_{x,\text {i}}}\rangle ^{m+n-2}}}} \, , \end{aligned}$$

(58b)

where g stands for the generic strength of the nonlinear magnets, which, according to the resonance, is $k_2$, $j_2$ or $j_3$. The two new parameters differ from those introduced in Eqs. (51) and (55) only for their adaptation to the configuration of the numerical simulations that feature initial distributions where $\langle {J_{x,\text {i}}}\rangle =\langle {J_{y,\text {i}}}\rangle$. The goal of this analysis is to identify in which regime these global parameters are the relevant quantities to describe the emittance-sharing process: in that case, the data obtained by varying each parameter entering in the expression of the global parameters should lie on the same curve.

It is clearly visible that, when ${\hat{\kappa }}_\text {geom}$ and ${\hat{\kappa }}_\text {dyn}$ are small (i.e. , $\delta _\text {max}$ is small, the strength of the nonlinear magnets is large, and the distribution of initial conditions is wide), $P_\text {na}$ depends primarily on ${\hat{\kappa }}_\text {geom}$: the performance of the emittance sharing is only limited by the fact that the tune is varied only over a finite range.

The disagreement between the data collected while varying $\delta _\text {max}$ and the other quantities is visible when considering the resonance $(1,\, 2)$, but it can be understood by considering that when transforming the map (1) with a normal sextupole to a resonant normal form, and truncating at second order in the action variables, contributions to the amplitude detuning are present, even in the absence of an octupolar term. Indeed, the coefficients $\alpha _{11}$ and $\alpha _{12}$ are proportional to $k_2^2$. As $\alpha _{12}\ne 0$, the separatrix crossing in $[\delta _\text {max},-\delta _\text {max}]$ is no longer symmetric, and a lower number of particles undergoes emittance sharing.

For large values of the two parameters, ${\hat{\kappa }}_\text {dyn}$ captures the correct scaling, as in this regime, corresponding to large $\delta _\text {max}$, low g, and small initial emittance with constant value of 1/N, the emittance sharing effectiveness is limited by the degree of adiabaticity of the process.

We remark that the scaling $g\langle {J_{x,\text {i}}}\rangle ^{(r-2)/2}$ always holds, since the strength of the nonlinear magnets, for the model considered in this paper that features a single multipole, can always be normalized to unity under a convenient co-ordinate rescaling, therefore changing the average value of $J_{x,\text {i}}$.

Fig. 11

Top-left: $P_\text {na}$ as a function of the amplitude-detuning parameter $\alpha$, for the four resonances. Top-right: $P_\text {na}$ as a function of the number of turns N. Power-law fits $P_\text {na}=a_{m,n}N^{-b_{m,n}}+c_{m,n}$ are provided for each $(m,\, n)$ resonance. Bottom: the inverse of the number of turns for which $P_\text {na}$ reaches the value $P_\text {na}=0.2$ (for third-order resonances) and $P_\text {na}=0.3$ (for fourth-order ones) as a function of the strength of the nonlinear magnets. Quadratic fit between $N^{-1}$ and the strength of the nonlinear magnets are presented, confirming the scaling of Eq. (54). The parameters used for the plots are: $\langle {J_{x,\text {i}}}\rangle =0.01$, $\delta _\text {max}=0.1$ for resonance (1, 2) and (2, 1) and $\delta _\text {max}=0.01$ for (1, 3) and (3, 1). For the top-left plot $N=10^6$, $k_2=1$ or $j_2=1$ (for third-order resonances), $N=10^7$, $j_3=10$ (for fourth-order ones) are used. The same values for the strength of the nonlinear magnets are used in the to-right plot. Both the top-right and the bottoms plots use $\alpha =0$

Fig. 12

Average (left column) and variance (right column) of $J_{x,\text {f}}$, from initial uniform distributions at fixed $J_{x,\text {i}}$ chosen in the allowed interval $0\le J_{x,\text {i}} \le J_{2,\text {i}}/n$, having fixed $J_2=1 \times 10^{-4}$. The average of $J_{x,\text {f}}$ is compared to the theoretical value $J_{x,\text {f}}=mJ_2/n -J_{x,\text {i}}$. The map (1) has been used with no amplitude-detuning terms, using different numbers of turns N. For the third-order resonances, $\delta _\text {max}=0.1$, $j_2=1$ or $k_2=1$ have been used, whereas for the fourth-order ones $\delta _\text {max}=0.01$, $j_3=10$ have been used

In Fig. 11 (top-left), the role of the amplitude-detuning parameter $\alpha$ is probed. Very different behaviors are observed depending on the resonance order. For the case of third-order resonances, a rather broad minimum of $P_\text {na}$ is observed around $\alpha =0$, which indicates that the presence of amplitude-detuning effects does not spoil the emittance sharing process. The situation is radically different for the case of the fourth-order resonances, where the presence of a non-zero amplitude detuning changes the number and the stability type of the fixed points of the systems under consideration. This is indicated by the presence of a very sharp minimum of $P_\text {na}$ around $\alpha =0$ with a steep increase in the close neighborhood.

In the top-right plot of Fig. 11, the dependence of $P_\text {na}$ on the number of turns N is shown. A fit using a power law $P_\text {na}=a_{m,n}N^{-b_{m,n}}+c_{m,n}$ provides an excellent agreement with the numerical data. This observation is crucial, as it reveals the intrinsic difference between the behavior of the crossing of these nonlinear 2D resonances with respect to that of the linear $(1,\, 1)$ resonance studied in Ref. [24]. For the case of the linear coupling resonance, an exponential law for $P_\text {na}$ was found in the absence of amplitude detuning. The difference can be explained since the Hamiltonian describing the crossing of the linear coupling resonance is analytic, as the unstable fixed points in the action-angle coordinates are only a pathology of the coordinate system, while the Hamiltonian describing the 2D nonlinear resonances features real unstable fixed points, The separatrices related with these unstable fixed points introduce an error in the action, which is the adiabatic invariant of the system, after the jump from one region to the other one of the phase space. Such a jump in the value of the adiabatic invariant has a power-law dependence on the number of turns. The values of the exponent of the fit law for $P_\text {na}$ are: $b_{1,2}= {1.56\pm 0.02}$, $b_{2,1}={1.84\pm 0.08}$, $b_{1,3}={0.43\pm 0.01}$ and $b_{3,1}={0.60\pm 0.01}$, which reveal that they are strongly model dependent.

The bottom plot of Fig. 11 shows the scaling between the strength of the nonlinear magnets and the inverse of the number N of turns, which is a direct measurement of the adiabaticity of the emittance sharing process. The data show, for different values of $k_2$, $j_2$ and $j_3$ (depending on the resonance considered), the value of N for which one obtains a small value for $P_\text {na}$, i.e. , $P_\text {na}=0.2$ for third-order resonances and $P_\text {na}=0.3$ for fourth-order ones. The curves represent quadratic functions that fit in an excellent way the numerical data, thus confirming the quadratic scaling found in Eq. (54), which is independent on m and n.

Finally, in Fig. 12 we analyze the emittance sharing process by generating uniform distributions of $10^4$ initial conditions at a fixed value of $J_{x,\text {i}}$, in the range $0\le J_{x,\text {i}} \le mJ_2/n$, having fixed $J_2=1 \times 10^{-4}$. In the plots in the left column, we compare, for each resonance $(m,\, n)$, $\langle {J_x}\rangle$ at the end of the process with the expected value from the theory, namely

$$\begin{aligned} J_{x,\text {f}} = \frac{m}{n}J_2 - J_{x,\text {i}} \, , \end{aligned}$$

(59)

computed for the case of a perfect emittance-sharing process. The results of numerical simulations are presented for different number of turns N (for $N=1 \times 10^{8}$, only $10^3$ initial conditions have been used due to constraints on the available CPU time). In the plots in the right column, the standard deviation of the values of $J_{x,\text {f}}$ is shown. The rows correspond to the various resonances considered. When increasing the number of turns, the average jump becomes closer to the theoretical expectation. For the resonances $(1,\, 2)$ and $(2,\, 1)$, we remark that the data oscillate around the expected value, in a similar fashion to what was observed in Ref. [24] for an analogous situation with linear coupling. For the fourth-order resonances, the effects of the more complicated phase-space topology are clearly visible. For instance, resonance $(1,\, 3)$ suffers from a slow convergence of the data toward the expected values for large $J_{x,\text {i}}$, while for resonance $(3,\, 1)$ the same occurs, but rather at low values of $J_{x,\text {i}}$. This is consistent with what found when analyzing initial conditions with $\langle {J_{x,\text {i}}}\rangle \ne \langle {J_{y,\text {i}}}\rangle$: resonance $(1,\, 3)$ fails at high values of $J_{x,\text {i}}$, while $(3,\, 1)$ at small ones. In the latter case, also, a variance bump is observed for $J_{x,\text {i}}>1.5 \times 10^{-4}$ also at high adiabaticity: this is an effect of the presence of extra regions in the phase space. Finally, the plots of fourth-order resonances show how slowly the emittance sharing converges to the expected value when the number of turns is increased, which explains the lower performance for emittance sharing for fourth-order resonances.

Conclusions

In this paper, a novel beam manipulation technique is presented, based on the crossing of a 2D nonlinear resonance to induce a sharing of the transverse emittances. The foundations of this technique have been discussed using Hamiltonian models and the adiabatic theory applied to resonance crossing. The performance of this manipulation has been assessed by means of detailed numerical simulations using map models, which are more realistic than the Hamiltonian ones. The results of the numerical simulations indicate that it is indeed possible to control the proposed process so to achieve a sharing of the transverse emittances. The final distributions of initial conditions retain the Gaussian character of the initial ones, which is an excellent feature. Scans of the various system parameters have been performed, thus achieving a good understanding of the details of the proposed mechanism.

Differences in the behavior and performance of the emittance-sharing process have been found and when comparing third- and fourth-order resonances, although these observations can be fully understood and explained in terms of the phase-space topology linked with each of the resonances under study.

As far as applications are concerned, this study shows clearly the theoretical feasibility of an emittance sharing process where the target emittance is met at up to $\approx 99\%$, using third-order resonances, and up to $\approx 90\%$, using fourth-order ones. These results are extremely encouraging, also in consideration of the fact that the resonances under consideration can be excited by widespread magnetic elements, such as normal and skew sextupoles, or skew octupoles (that can also be substituted by pairs of normal and skew sextupoles).

In summary, the novel beam manipulation passed successfully through theoretical and numerical tests and it is now ready for experimental validation.

Appendices

Magnet type and resonances: analysis using normal forms

The goal of this appendix is to compute, using Normal Form theory, which resonance can be excited by a certain nonlinearity in an Hénon-like map as the one of Eq. (1).

We start the analysis by considering which monomial appears in the complex representation of the generic polynomial map. When dealing with 4D complex coordinates $(z_1,z_1^*,z_2,z_2^*)$, we use the vector notation $(\ell _1,m_1,\ell _2,m_2)$ to identify a monomial $z_1^{\ell _1}\,{z_1^*}^{m_1}\,z_2^{\ell _2}\,{z_2^*}^{m_2}$, and we indicate a 4D complex function as $\mathbf {F}=(F_1, F_1^*, F_2, F_2^*)$.

Starting from an Hénon-like map, we replace the real variables with complex ones, defined according to $z_1 = x - ip_x$, $z_2 = y - ip_y$, together with the corresponding complex conjugate relationships, and we obtain, expanding all binomials, the following complex map

$$\begin{aligned} z_1'= & {} e^{i\omega _1}\Bigg [ z_1 + \sqrt{\beta _x} \frac{k_r\beta _x^\frac{r}{2}}{2^r r!}\sum _{q\le r/2}\sum _{\ell =0}^{r-2q}\sum _{p=0}^{2q} (-1)^q \left( \frac{\beta _y}{\beta _x} \right) ^q \left( {\begin{array}{c}r\\ 2q\end{array}}\right) \left( {\begin{array}{c}r-2q\\ \ell \end{array}}\right) \nonumber \\&\times \left( {\begin{array}{c}2q\\ p\end{array}}\right) z_1^{r-2q-\ell }{z_1^*}^\ell z_2^{2q-p} {z_2^*}^p \nonumber \\&-\sqrt{\beta _y} \frac{j_r \beta _x^\frac{r}{2}}{2^r r!}\sum _{q\le (r-1)/2}\sum _{\ell =0}^{r-2q-1}\sum _{p=0}^{2q+1} (-1)^q \left( \frac{\beta _y}{\beta _x} \right) ^q \left( {\begin{array}{c}r\\ 2q+1\end{array}}\right) \nonumber \\&\times \left( {\begin{array}{c}r-2q-1\\ \ell \end{array}}\right) \left( {\begin{array}{c}2q+1\\ p\end{array}}\right) z_1^{r-2q-\ell -1}{z_1^*}^\ell z_2^{2q-p+1} {z_2^*}^p \Bigg ] \end{aligned}$$

(60)

and

$$\begin{aligned} z_2'= & {} e^{i\omega _2}\Bigg [ z_2 - \frac{\beta _y}{\sqrt{\beta _x}} \frac{k_r \beta _x^\frac{r}{2}}{2^r r!}\sum _{q\le (r-1)/2}\sum _{\ell =0}^{r-2q-1}\sum _{p=0}^{2q+1} (-1)^q \left( \frac{\beta _y}{\beta _x} \right) ^{q} \left( {\begin{array}{c}r\\ 2q+1\end{array}}\right) \nonumber \\&\times \left( {\begin{array}{c}r-2q-1\\ \ell \end{array}}\right) \left( {\begin{array}{c}2q+1\\ p\end{array}}\right) z_1^{r-2q-1-\ell }{z_1^*}^\ell z_2^{2q+1-p} {z_2^*}^p \nonumber \\&- \sqrt{\beta _y} \frac{j_r \beta _x^\frac{n}{2}}{2^r r!}\sum _{q\le r/2}\sum _{\ell =0}^{r-2q}\sum _{p=0}^{2q} (-1)^q \left( \frac{\beta _y}{\beta _x} \right) ^{q}\left( {\begin{array}{c}r\\ 2q\end{array}}\right) \left( {\begin{array}{c}r-2q\\ \ell \end{array}}\right) \nonumber \\&\times \left( {\begin{array}{c}2q\\ p\end{array}}\right) z_1^{r-2q-\ell }{z_1^*}^\ell z_2^{2q-p} {z_2^*}^p \Bigg ] \, , \end{aligned}$$

(61)

and we express the map action as $\mathbf {z}' = \mathbf {F}(\mathbf {z})$. $F_1$ includes the following monomials

• for a normal multipole $k_r$, the generic term $(r-2q-\ell ,\,\ell ,\,2q-p,\,p)$ with

  $$\begin{aligned} 0\le q\le \frac{r}{2}, \qquad 0\le \ell \le r-2q, \qquad 0\le p\le 2q \, ; \end{aligned}$$

• for a skew multipole $j_r$, the generic term $(r-(2q+1)-\ell ,\,\ell ,\,2q+1-p,\,p)$ with

  $$\begin{aligned} 0\le q\le \frac{r-1}{2}, \qquad 0\le \ell \le r-(2q+1), \qquad 0\le p\le 2q+1 \, ; \end{aligned}$$

while for $F_2$ we obtain

• for a normal multipole $k_r$, the generic term $(r-(2q+1)-\ell ,\,\ell ,\,2q+1-p,\,p)$ with

  $$\begin{aligned} 0\le q\le \frac{r-1}{2}, \qquad 0\le \ell \le r-(2q+1), \qquad 0\le p\le 2q+1 \, ; \end{aligned}$$

• for a skew multipole $j_r$, the generic term $(r-2q-\ell ,\,\ell ,\,2q-p,\,p)$ with

  $$\begin{aligned} 0\le q\le \frac{r}{2}, \qquad 0\le \ell \le r-2q, \qquad 0\le p\le 2q \, , \end{aligned}$$

and we remark that the form of the monomials for the normal and skew components exchanges between $F_1$ and $F_2$.

The Normal Form map $\mathbf {U}$ contains all the terms that are needed to solve the functional equation $\mathbf {F} \circ \varvec{\varPhi } = \varvec{\varPhi } \circ \mathbf {U}$, and, at order k, we have the functional equation

$$\begin{aligned} \varDelta [\varvec{\varPhi }]_k(\varvec{\zeta }) + [\mathbf {U}]_k(\varvec{\zeta }) = [\mathbf {Q}]_k(\varvec{\zeta }) \end{aligned}$$

where $[\mathbf {Q}]_k=[\mathbf {F} \circ \varvec{\varPhi }]_k$, the symbol $[ \cdot ]_k$ indicates the truncation of the homogeneous polynomial at order k, while $\mathbf {U}$ contains all monomials that are in the kernel of the Normal-Form operator $\varDelta$, defined as $\varDelta \mathbf {\varPhi }(\mathbf {\zeta })= e^{i \mathbf {\omega }} \mathbf {\varPhi }(\mathbf {\zeta })-\mathbf {\varPhi }(e^{i \mathbf {\omega }} \mathbf {\zeta })$, which, following [7, p. 128], occurs for monomials satisfying

$$\begin{aligned} \begin{aligned} F_1: \qquad \omega _x (\ell _1-m_1) + \omega _y(\ell _2 - m_2) = \omega _x\,,\\ F_2: \qquad \omega _x (\ell _1-m_1) + \omega _y(\ell _2 - m_2) = \omega _y\, . \end{aligned}\end{aligned}$$

(62)

For a $(m,\, n)$ resonance (with m, n coprimes), we can rewrite the previous relations as

$$\begin{aligned} F_1:&\qquad \ell _1 - m_1 + \frac{m}{n}(\ell _2 - m_2) = 1 \, , \end{aligned}$$

(63a)

$$\begin{aligned} F_2:&\qquad \frac{n}{m}(\ell _1 - m_1) + \ell _2 - m_2 = 1 \, . \end{aligned}$$

(63b)

A condition for the resonant terms to be present in the interpolating Hamiltonian is that the corresponding monomials in the kernel of $\varDelta$ are present in either $F_1$ or $F_2$ at order r.

To satisfy the condition for $F_1$, we need

$$\begin{aligned} \ell _2 - m_2 \equiv 0 \pmod n \, , \end{aligned}$$

(64)

which for a normal multipole translates to

$$\begin{aligned} 2(q-p) \equiv 0 \pmod n\, , \end{aligned}$$

(65)

while for a skew one to

$$\begin{aligned} 2(q-p)+1 \equiv 0 \pmod n\, . \end{aligned}$$

(66)

The condition is always satisfied when $\ell _2=m_2$ and in this case $\ell _1=m_1+1$ and the form of the corresponding monomial is

$$\begin{aligned} \left( \frac{m+n}{2}-p,\, \frac{m+n}{2}-p-1,\, p,\, p \right) \, , \end{aligned}$$

(67)

which is a valid solution only if m and n are both odd.

Solutions are also found whenever $\ell _2-m_2=s\,n$ with $s \ne 0$. For a normal multipole, $2(m-p)\le 2(m+p) \le r$ and we can restrict s to $0< s \le (m-1)/n + 1$.

If $m < n$, then only $s=1$ is possible and if n is odd, no other solution can be found. If n is even, we have $2(q-p) = n$ for which the resonant condition (63a) becomes $m-p-\ell =1$ and the form of the generic monomial reads $(-p,\,m-p-1,\,p+n,\,p)$, from which we can only choose $p=0$, so that the solution for n even and $m < n$ reads

$$\begin{aligned} (0,\,m-1,\,n,\,0) \, . \end{aligned}$$

(68)

If $m>n$, again two cases should be considered. If n is odd, then s must be even and the resonant condition (63a) is

$$\begin{aligned} m+n+s(m-n)=2(1 +p+\ell ) \end{aligned}$$

(69)

and m must be odd. Let $m=2m'+1$, $n=2n'+1$ and $s=2s'$. Substituting, we get the relation $p+\ell = m'+n'+2s'(m'-n')$, and $\ell _1$ becomes $\ell _1=m'(1-2s') + n'(1-2s') - p + 1 - 2 s'$. Since $s'>0$, $\ell _1$ is always negative and no solution can be found.

If, on the other hand, n is even, then m has to be odd, and from Eq. (69), s is necessarily odd. Therefore, we substitute $n=2n'$, $m=2m'+1$, $s=2s'+1$ and we obtain $p+\ell =2m'+2m's'+s'-2n's'$ and $\ell _1 = -p-2n's'-2m's'-s'$. The only possibility, since $\ell _1\ge 0$, is given by $p=0$ and $s'=0$ (i.e. , $s=1$), which gives $\ell = 2m' = m-1$, $2q= n$, and the general form of the resonant monomial is therefore

$$\begin{aligned} (0,\,m-1,\,n,\,0) \, , \end{aligned}$$

(70)

which is the same as for the previous case (68)

We proceed in a similar fashion in the case of a skew multipole. The first point to note is that the special solution of Eq. (64) for $s=0$ does not exist in this case. Hence, the resonant condition (66) $2q-2p+1=s\,n$ provides a solution only if both s and n are odd. Hence, letting $n=2n'+1$ and $s=2s'+1$ and performing the usual substitutions, we get $q = 2s'n'+s'+n'+p$ and $\ell = m-2s'n'-s'-p-1+s'm$ and the condition $\ell _1\ge 0$ becomes $-2s'n'-p-s'm\ge 0$, which requires $p=0$ and $s'=0$, and the generic skew monomial is of the form

$$\begin{aligned} (0,\,m-1,\,n,\,0) \, . \end{aligned}$$

(71)

In summary, the monomials of $U_1$ are:

$$\begin{aligned} \begin{aligned} \text {Normal multipoles:}&\quad {\left\{ \begin{array}{ll} \displaystyle {\left( \frac{m+n}{2}-p,\,\frac{m+n}{2}-p-1,\,p,\,p\right) }, \quad 0\le p \le \frac{r-1}{2} &{}\qquad \text {if} \quad m, n \; \text {are odd,} \\ \\ (0,\,m-1,\,n,\, 0) &{}\qquad \text {if} \quad n \; \text {is even} \,, \end{array}\right. } \\ \text {Skew multipoles:}&\quad (0,\,m-1,\,n,\, 0) \qquad \text {if} \quad n \; \text {is odd.} \end{aligned} \end{aligned}$$

(72)

Thus far, only Eq. (63a) has been considered. For $F_2$, we proceed in the same way. We need to apply the resonant condition (63b), which requires $\ell _1-m_1 \equiv 0 \pmod m$, i.e. ,

$$\begin{aligned} \frac{n}{m}(\ell _1-m_1)=s\, n\, . \end{aligned}$$

(73)

For a normal multipole, the divisibility condition and the resonant correspond to

$$\begin{aligned} {\left\{ \begin{array}{ll} m(1-s) + n &{}= 2(q + \ell + 1)\\ 2(q-p) &{}= s\,n\,, \end{array}\right. } \end{aligned}$$

(74)

and solving for $\ell$ and q, and substituting in $\ell _1$ we obtain $\ell _1 = \frac{1}{2}(m+n)(1+s) - 1 - p$. We have $0\le \ell _1\le r=m+n-1$, because $(m+n)(1+s) \ge 2(p+1) \ge 0$ implies $s\le 0$, and $(m+n)(1+s) \le 2(r+1+p)$ implies $1+s \le 2( 1 + r/(r-1)) \le 2$, therefore $s\le 1$. This means that we can restrict s to the two values $s=0$ or $s=1$.

For $s=0$, we obtain the solution

$$\begin{aligned} \left( \frac{m+n}{2}-p-1,\,\frac{m+n}{2}-p-1,\,p+1,\,p\right) \qquad \text {for} \quad 0\le p\le r/2\,, \end{aligned}$$

(75)

which only exists if $m+n$ is even, so both m and n must be odd, while, for $s=1$

$$\begin{aligned} (m+n-p-1,\,n-p-1,\,p-n+1,\, p)\, . \end{aligned}$$

(76)

The only way to ensure both $m_1\ge 0$ and $\ell _2\ge 0$ is setting $m_1=\ell _2=0$, so $p=n-1$, whence we obtain the resonant solution

$$\begin{aligned} (m,\,0,\,0,\, n-1) \end{aligned}$$

(77)

In the case of a skew multipole, we have the equations

$$\begin{aligned} {\left\{ \begin{array}{ll} m+n-1-2q-2\ell &{}= sm\\ 2q &{}= 1 + 2p - sn \end{array}\right. } \end{aligned}$$

(78)

and the same condition for $\ell _1$, which imposes as before, $s=0$ or $s=1$. For $s=0$, we have the same solution (if m and n are odd)

$$\begin{aligned} \left( \frac{m+n}{2}-p-1,\,\frac{m+n}{2}-p-1,\,p+1,\,p\right) \,, \end{aligned}$$

(79)

while, for $s=1$, as before

$$\begin{aligned} (m,\,0,\,0,\, n-1)\, . \end{aligned}$$

(80)

Now, if we substitute $\ell _1=m$, $m_1=\ell _2=0$ and $m_2=n-1$ in the generic Normal Form term in $U_2$, we need $2q=n-2$, so $q = (n-2)/2$, which is possible only if n is even. In the skew case, on the other hand, we have $2q=n-1$, which is solved only for odd n. Thus, summarizing:

$$\begin{aligned} \text {Normal multipoles:} {\left\{ \begin{array}{ll} \displaystyle {\left( \frac{m+n}{2}-p-1,\,\frac{m+n}{2}-p-1,\,p+1,\,p\right) } \qquad \text {if} \quad m, n \; \text {are odd} \\ \\ (m,\,0,\,0,\, n-1) \qquad \text {if} \quad n \; \text {is even} \,, \end{array}\right. } \end{aligned}$$

(81)

$$\begin{aligned} \text {Skew multipoles:} {\left\{ \begin{array}{ll} \displaystyle {\left( \frac{m+n}{2}-p-1,\,\frac{m+n}{2}-p-1,\,p+1,\,p\right) } \qquad \text {if} \quad m, n \; \text {are odd} \\ \\ (m,\,0,\,0,\, n-1) \qquad \text {if} \quad n \; \text {is odd} \,, \end{array}\right. } \end{aligned}$$

(82)

The next step is to consider how the resonant monomials in the Normal Form $\mathbf {U}$ contribute to the interpolating Hamiltonian. The first point consists in showing that monomials of type

$$\begin{aligned} \left( \frac{m+n}{2} - p,\, \frac{m+n}{2} - p-1,\, p,\,p \right) \end{aligned}$$

(83)

do not contribute to the resonant part of the interpolating Hamiltonian. In fact, given a 4D Normal Form $\mathbf {U}(\varvec{\zeta },\varvec{\zeta }^*)=(U_1,U^*_1,U_2,U^*_2)$, and writing polynomials as:

$$\begin{aligned} A(\zeta _1,\zeta _1^*,\zeta _2,\zeta _2^*) = \sum _{\ell _1,\,m_1,\,\ell _2,\,m_2} A(\ell _1,\,m_1,\,\ell _2,\,m_2)\zeta _1^{\ell _1}{\zeta _1^*}^{m_1}\zeta _2^{\ell _2}{\zeta _2^*}^{m_2}\,, \end{aligned}$$

(84)

the construction of the interpolating Hamiltonian of order r is done as follows:

$$\begin{aligned} \mathcal {H}(\ell _1+1,\,m_1,\,\ell _2,\,m_2)&= -\frac{1}{\ell _1+1}U_1^*(\ell _1,\,m_1,\,\ell _2,\,m_2)&\qquad \text {for } \ell _1+m_1+\ell _2+m_2=r\,,\\ \mathcal {H}(0,\,m_1+1,\,\ell _2,\,m_2)&= \frac{1}{m_1+1}U_1(0,\,m_1,\,\ell _2,\,m_2)&\qquad \text {for } m_1+\ell _2+m_2=r\,,\\ \mathcal {H}(0,\,0,\,\ell _2+1,\,m_2)&= -\frac{1}{\ell _2+1}U_2^*(0,\,0,\,\ell _2,\,m_2)&\qquad \text {for } \ell _2+m_2=r\,,\\ \mathcal {H}(0,\,0,\,0,\,r+1)&= \frac{1}{r+1}U_2(0,\,0,\,0,\,r)\, . \end{aligned}$$

The monomials in $U_1^*$ and $U_2^*$ are the same in $U_1$ and $U_2$, but with the exchanges $\ell _1\leftrightarrow m_1$ and $\ell _2 \leftrightarrow m_2$. Hence, the $U_1$ terms can be $(0,\,m-1,\,n,\,0)$ or $(\ell _2+1,\,\ell _2,\,m_1,\,m_1)$ and in $U^*_1$ we will have either $(m-1,\,0,\,0,\,n)$ or $(\ell _2,\,\ell _2+1,\,m_1,\,m_1)$. If this latter form is present in $U^*_1$, it gives rise to the Hamiltonian coefficient $\mathcal {H}(\ell _2+1,\,\ell _2+1,\,m_1,\,m_1)$, and by performing the transformation to the action-angle coordinates $(\varvec{J},\,\varvec{\phi })$, i.e. , $\zeta _1 = \sqrt{J_x}e^{i\phi _x}$, $\zeta _2 = \sqrt{J_y}e^{i\phi _y}$, the angular parts of these terms vanish, and we obtain a $J_x^{\ell _2/2}J_y^{m_1/2}$ monomial, which is clearly non resonant.

For what concerns the second component of the map, we see from the construction of the interpolating Hamiltonian that we need to restrict our search to monomials with $\ell _1=m_1=0$. We can have terms in $U_2$ of the form

$$\begin{aligned} \left( 0,\,0,\,\frac{r+1}{2},\,\frac{r-1}{2}\right) \end{aligned}$$

(85)

owing to the resonant condition $\ell _2-m_2=1$ with $\ell _2+m_2=r$. Since such a term contributes to the Hamiltonian via $U_2^*$, it gives rise to the Hamiltonian term $\mathcal {H}(0,0,(r-1)/2 + 1, (r+1)/2) = \mathcal {H}(0,0,(r+1)/2, (r+1)/2)$, and, as we discussed before, this does not give origin to a resonant term since the angular parts of $\zeta _2$ and $\zeta _2^*$ are cancelled. Finally, we could look for monomials in $U_2$ of the form $(0,\,0,\,0,\,r)$, but the resonant condition would be $-r=1$ which is never satisfied.

In conclusion, we have the following relationships between the parity of m and n and the type of multipole element that gives origin to quasi-resonant Hamiltonian terms:

Multipole type	m	n	$U_1$ non-trivial monomials	$\mathcal {H}$ resonant monomials
Normal	even	odd	no	no
	odd	odd	no	no
	odd	even	$(0,\,m-1,\,n,\,0)$	$(0,\,m,\,n,\,0);\,(m,\,0,\,0,\,n)$
Skew	even	odd	$(0,\, m-1,\, n,\,0)$	$(0,\,m,\,n,\,0);\,(m,\,0,\,0,\,n)$
	odd	odd	$(0,\, m-1,\, n,\,0)$	$(0,\,m,\,n,\,0);\,(m,\,0,\,0,\,n)$
	odd	even	no	no

Therefore, if we restrict our search to sextupoles and octupoles ($r=2$ or $r=3$) we find that a normal sextupole can excite the (1, 2) resonance, while a skew sextupole the (2, 1) one. A skew octupole, on the other hand, is needed for both the (1, 3) and (3, 1) resonances.

Computation of $P_\text {na}$ in resonant conditions

The motion in the resonant condition is governed by the Hamiltonian (6) with $\delta =0$ (for the sake of simplicity, we neglect the amplitude-detuning terms in the following considerations). The analysis of the phase-space topology shows that, independently of the resonance order, the allowed circle is symmetrically divided in two regions by the coupling arc. The trajectory of a particle with initial condition $(\phi _{1,\text {i}},J_{1,\text {i}})$, in one of the two hemicircles (let us choose $\cos \phi >0$) is given by the solution of the equation $\mathcal {H}(\phi _1,J_1)=\mathcal {H}(\phi _{1,\text {i}},J_{1,\text {i}})$, i.e. ,

$$\begin{aligned} J_1^{m/2}(J_2-nJ_1)^{n/2}\cos \phi _1 = J_{1,\text {i}}^{m/2}(J_2-nJ_{1,\text {i}})^{n/2}\cos \phi _{1,\text {i}} \end{aligned}$$

(86)

whose solution gives rather straightforwardly the function $\phi _1(J_1)$ given the initial conditions.

To compute $P_\text {na}$ for an emittance sharing process when $\delta _\text {max}\rightarrow 0$, ultimately, we should consider a motion when $\delta$ is equal to zero, and since $P_\text {na}$ depends on $\langle {J_{x,\text {i}}}\rangle$, our goal is to compute the trajectory $J_1(\phi _1)$.

For generic values of $(m,\, n)$ one cannot easily invert analytically $\phi _1(J_1)$ from Eq. (86), yet this task can be carried out numerically. To compute the final mean $J_1$ for a given initial distribution, we can use the time average of $J_1$ over a (long) time interval T. This is given by

$$\begin{aligned} \overline{J_1} = \frac{1}{T}\int _0^T \mathrm{d}t\, J_1(\phi _1) = \frac{1}{T}\int _{\phi _-}^{\phi _+}\mathrm{d}\phi _1\, \frac{J_1(\phi _1)}{\dot{\phi }_1} = \frac{\displaystyle {\int _{\phi _-}^{\phi _+}\mathrm{d}\phi _1\, \left( J_1\left( \phi _1\right) /\dot{\phi }_1\right) }}{\displaystyle {\int _{\phi _-}^{\phi _+}\mathrm{d}\phi _1\, (1/\dot{\phi }_1)}},\, \end{aligned}$$

(87)

where $\phi _\pm$ are the inversion points of the trajectory and ${\dot{\phi }}_1$ is taken from the equations of motion with $\delta =0$. Note that the strength G of the resonant term never appears in the integral.

Then, the averaging of the result of $\overline{J_1}$ over the initial conditions $(\phi _{1,\text {i}}, J_{1,\text {i}})$ provides the expected value of $\langle {J_{x,\text {i}}}\rangle$ as $\delta \rightarrow 0$, and therefore of $P_\text {na}$.

For resonance (1, 2), if the Cartesian coordinate X is used instead of the angle $\phi _1$ to parametrize the motion, $J_1(X)$ can be written as

$$\begin{aligned} J_1 = \frac{1}{2}\left( J_2 - \frac{X_\text {i}(J_2 - X_\text {i}^2)}{X}\right) \end{aligned}$$

(88)

and the time average $\overline{J_1}$

$$\begin{aligned} \overline{J_1} = \frac{J_2}{2} + \frac{C_\text {i}}{2}\frac{\displaystyle {\int _{X_-}^{X_+}\mathrm{d}X\, \frac{1}{X^2\sqrt{J_2-X^2+C_\text {i}/X}}} }{\displaystyle {\int _{X_-}^{X_+}\mathrm{d}X\, \frac{1}{X\sqrt{J_2-X^2+C_\text {i}/X}}}} \end{aligned}$$

(89)

where $C_\text {i}=X_\text {i}\sqrt{X_\text {i}^2-J_2}$ and the inversion points are $X_-=X_\text {i}=\sqrt{2J_{1,\text {i}}}\cos \phi _{1,\text {i}}$, $X_+ = -(X_\text {i}+\sqrt{4J_2 - 3X_\text {i}^2})/2$.

A numerical evaluation of this integral, averaged on a Gaussian distribution for $(\phi _{1,\text {i}},J_{1,\text {i}})$ with $\langle {J_{x,\text {i}}}\rangle =1 \times 10^{-4}$ gives $\overline{J_1}=8.115 \times 10^{-5}$, which replaced into the definition of $P_\text {na}$ gives a values, when $\delta \rightarrow 0$

$$\begin{aligned} P_\text {na}=0.623,\, \end{aligned}$$

(90)

which is consistent with the value observed in Fig. 8 (left). This procedure can be used to explain the values observed for other resonances, too.