Some new wave profiles and conservation laws in a Pre-compressed one-dimensional granular crystal by Lie group analysis

Abstract

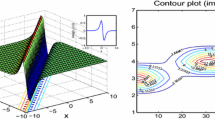
In the present exploration, some new wave profiles are constructed via Lie symmetry of transformations scheme by the one-dimensional optimal system in a pre-compressed one-dimensional granular crystal. Lie group scheme is used to construct the infinitesimal generators, entire vector field, commutation relations, and adjoint representations. Infinitesimal generators are used to construct one optimal system of the one-dimensional sub-algebras. Employing the optimal system, similarity reductions are obtained for the considered nonlinear model. Translational vectors and their linear combination are used to covert the assumed model in a nonlinear ordinary differential equation. These methods give us some new and interesting solutions which contain the trigonometric, hyperbolic trigonometric, and exponential type functions. To represent the physical significance of the assumed model, some 3D and 2D diagrams of acquired results are plotted by using Mathematica under the suitable choice of involving parameters values. The multiplier scheme is employed to describe the conserved vectors of the assumed problem.

Appendix

1.1 Multiplier approach

Here, we will describe the general method in detail (see [53]):

Suppose, we have a general nonlinear partial differential equation of integer order:

$$\begin{aligned} F({\Phi },{\Phi }_\tau ,{\Phi }_\theta ,{\Phi }_{\theta \theta },{\Phi }_{\theta \tau },...)=0, \end{aligned}$$

(71)

where $\Phi =\Phi (\theta ,\tau )$ and $\theta$ and $\tau$ are space and temporal components. Some steps of the technique are given below.

(1) The total differential operator may be defined as:

$$\begin{aligned} D_{i}=\frac{\partial }{\partial \theta ^{i}}+{\Phi }_{i}\frac{\partial }{\partial {\Phi }}+{\Phi }_{ij}\frac{\partial }{\partial {\Phi }_{j}}+...,~~~i=1,2,3...m, \end{aligned}$$

(72)

where ${\Phi }_{i}$ indicates the derivative w.r.t $\theta ^{i}$ and ${\Phi }_{ij}$ displays the derivative w.r.t $\theta ^{i}$ and $\theta ^{j}$.

(2) The Euler operator is defined as:

$$\begin{aligned} \frac{\delta }{\delta {\Phi }}=\frac{\partial }{\partial {\Phi }}-D_{i}\frac{\partial }{\partial {\Phi }_{i}}+D_{ij}\frac{\partial }{\partial {\Phi }_{ij}}-D_{ijk}\frac{\partial }{\partial {\Phi }_{ijk}}+...~. \end{aligned}$$

(73)

$\mathbf {(3)}$ An n-tuple ${\mathfrak {f}}=({\mathfrak {f}}^{1},{\mathfrak {f}}^{2},{\mathfrak {f}}^{3},...,{\mathfrak {f}}^{m})$, $i=1,2,...m$, we get

$$\begin{aligned} D_{i}{\mathfrak {f}}^{i}=0, \end{aligned}$$

(74)

which satisfies the entire solutions of Eq. (77), and Eq. (74) is named as the local conserved vectors.

(4) The property of $\Lambda (\theta , \tau , {\Phi })$ of Eq. (77):

$$\begin{aligned} D_{i}{\mathfrak {f}}^{i}=\Lambda (\theta ,\tau ,{\Phi }) H, \end{aligned}$$

(75)

for some function ${\Phi }(\mu ^{1},\mu ^{2},...,\mu ^{m})$.

(5) We obtain the determining equations for multiplier $\Lambda (\theta , \tau , {\Phi })$ when we take the derivative of Eq. (75):

$$\begin{aligned} \frac{\delta }{\delta {\Phi }}(\Lambda (\theta , \tau , {\Phi }) H)=0. \end{aligned}$$

(76)

Equation (76) contains for few function ${\Phi }(\mu ^{1}, \mu ^{2}, . . . , \mu ^{m})$ not just for solutions of Eq. (77).

When the multiplier $\Lambda (\theta , \tau , {\Phi })$ are achieved by use of Eq. (76), the conserved vectors may be obtained by Eq. (75) just as the determining equation.

1.2 New auxiliary method

Suppose, we have a general nonlinear partial differential equation in the following expression:

$$\begin{aligned} {\mathcal {R}}(\Phi ,\Phi _\tau ,\Phi _{\theta },\Phi _{\theta },...)=0, \end{aligned}$$

(77)

where $\Phi =\Phi (\theta ,\tau )$, $\theta$ and $\tau$ are space and temporal components, respectively. Some steps of the technique are given below.

Step: 1 Assuming the new dependent and independent variables

$$\begin{aligned} \Phi (\theta ,\tau )={U}(\rho ),\qquad \rho =k_1\theta +c\tau . \end{aligned}$$

(78)

Here, $\rho$ is new independent variable, where $k_1$ and c are real parameter for Eq. (77). Using Eq. (78) into Eq. (77), we obtain the following ordinary differential equation of the form:

$$\begin{aligned} {\mathcal {Q}}(U,U^\prime ,U^{\prime \prime },...)=0. \end{aligned}$$

(79)

Step: 2 Assume the solution for Eq. (79) of the type

$$\begin{aligned} U(\rho )=\sum _{i=0}^{k}{\mathfrak {F}_{i}}{\mathfrak {F}^{if(\rho )}}, \end{aligned}$$

(80)

where $b_i$’s are constants which are to be found later, and also first-order ODE satisfy $f(\rho )$.

$$\begin{aligned} p^{\prime }(\rho )=\frac{1}{\ln ({\mathfrak {F})}}\{{\kappa _{2}}{\mathfrak {F}^{-f(\rho )}}+{\kappa _{1}}+{\kappa _{3}}{\mathfrak {F}^{f(\rho )}}\},~~{\mathfrak {F}}>0,~~{\mathfrak {F}}\ne 1. \end{aligned}$$

(81)

Step: 3 To find the value of k in Eq. (80), we use the balancing procedures, i.e., the highest-order derivative is balanced by the highest degree nonlinear term.

Step: 4 Substituting Eq. (80) and Eq. (81) into Eq. (77) and collecting the coefficients of the powers of ${\mathfrak {F}}^{f(\rho )} (i=0,1,2,3..)$. After collecting the like term, we put them equal to zero and we have a collection of equations and then solving these by computer algebra system (CAS), i.e., Mathematica.

Step: 5 The category of solutions for Eq. (81) may be obtained as:

Family:1 When ${\kappa _{1}}^2-{\kappa _{2}}{\kappa _{3}}<0$ and ${\kappa _{3}}\ne 0$

$$\begin{aligned} {\mathfrak {F}^{f(\rho )}}=\frac{-{\kappa _{1}}}{{\kappa _{3}}}+\frac{\sqrt{-({\kappa _{1}}^2-{\kappa _{2}}{\kappa _{3}})}}{{\kappa _{3}}}\tan \bigg (\frac{\sqrt{-({\kappa _{1}} ^2-{\kappa _{2}}{\kappa _{3}})}}{2}\rho \bigg ), \end{aligned}$$

(82)

$$\begin{aligned} {\mathfrak {F}^{f(\rho )}}=\frac{-{\kappa _{1}}}{{\kappa _{3}}}+\frac{\sqrt{-({\kappa _{1}}^2-{\kappa _{2}}{\kappa _{3}})}}{{\kappa _{3}}}\cot \bigg (\frac{\sqrt{-({\kappa _{1}} ^2-{\kappa _{2}}{\kappa _{3}})}}{2}\rho \bigg ). \end{aligned}$$

(83)

Family:2 When ${\kappa _{1}}^2-{\kappa _{2}}{\kappa _{3}}>0$ and ${\kappa _{3}}\ne 0$

$$\begin{aligned} {\mathfrak {F}^{f(\rho )}}=\frac{-{\kappa _{1}}}{{\kappa _{3}}}+\frac{\sqrt{({\kappa _{1}}^2-{\kappa _{2}}{\kappa _{3}})}}{{\kappa _{3}}}\tanh \bigg (\frac{\sqrt{({\kappa _{1}} ^2-{\kappa _{2}}{\kappa _{3}})}}{2}\rho \bigg ), \end{aligned}$$

(84)

$$\begin{aligned} \mathfrak {F}^{f(\rho )}=\frac{-{\kappa _{1}}}{{\kappa _{3}}}-\frac{\sqrt{({\kappa _{1}}^2-{\kappa _{2}}{\kappa _{3}})}}{{\kappa _{3}}}\coth \bigg (\frac{\sqrt{({\kappa _{1}} ^2-{\kappa _{2}}{\kappa _{3}})}}{2}\rho \bigg ). \end{aligned}$$

(85)

Family:3 When ${\kappa _{1}}^2+{\kappa _{2}}^2>0$ and ${\kappa _{3}}\ne 0$ and ${\kappa _{3}}\ne -{\kappa _{2}}$

$$\begin{aligned} \mathfrak {F}^{f(\rho )}=\frac{{\kappa _{1}}}{{\kappa _{3}}}+\frac{\sqrt{({\kappa _{1}}^2+{\kappa _{2}}^2)}}{{\kappa _{3}}}\tanh \bigg (\frac{\sqrt{({\kappa _{1}}^2+{\kappa _{2}}^2)}}{2}\rho \bigg ), \end{aligned}$$

(86)

$$\begin{aligned} \mathfrak {F}^{f(\rho )}=\frac{{\kappa _{1}}}{{\kappa _{3}}}+\frac{\sqrt{({\kappa _{1}}^2+{\kappa _{2}}^2)}}{{\kappa _{3}}}\coth \bigg (\frac{\sqrt{({\kappa _{1}}^2+{\kappa _{2}}^2)}}{2}\rho \bigg ). \end{aligned}$$

(87)

Family: 4 When ${\kappa _{1}}^2+{\kappa _{2}}^2<0$, ${\kappa _{3}}\ne 0$ and ${\kappa _{3}}\ne -{\kappa _{2}}$

$$\begin{aligned} \mathfrak {F}^{f(\rho )}=\frac{{\kappa _{1}}}{{\kappa _{3}}}+\frac{\sqrt{-({\kappa _{1}}^2+{\kappa _{2}}^2)}}{{\kappa _{3}}}\tan \bigg (\frac{\sqrt{-({\kappa _{1}}^2+{\kappa _{2}}^2)}}{2}\rho \bigg ), \end{aligned}$$

(88)

$$\begin{aligned} \mathfrak {F}^{f(\rho )}=\frac{{\kappa _{1}}}{{\kappa _{3}}}+\frac{\sqrt{-({\kappa _{1}}^2+{\kappa _{2}}^2)}}{{\kappa _{3}}}\cot \bigg (\frac{\sqrt{-({\kappa _{1}}^2+{\kappa _{2}}^2)}}{2}\rho \bigg ). \end{aligned}$$

(89)

Family: 5 When ${\kappa _{1}}^2-{\kappa _{2}}^2<0$ and ${\kappa _{3}}\ne -{\kappa _{2}}$

$$\begin{aligned} \mathfrak {F}^{f(\rho )}=\frac{-{\kappa _{1}}}{{\kappa _{3}}}+\frac{\sqrt{-({\kappa _{1}}^2-{\kappa _{2}}^2)}}{{\kappa _{3}}}\tan \bigg (\frac{\sqrt{-({\kappa _{1}}^2-{\kappa _{2}}^2)}}{2}\rho \bigg ), \end{aligned}$$

(90)

$$\begin{aligned} \mathfrak {F}^{f(\rho )}=\frac{-{\kappa _{1}}}{{\kappa _{3}}}+\frac{\sqrt{-({\kappa _{1}}^2-{\kappa _{2}}^2)}}{{\kappa _{3}}}\cot \bigg (\frac{\sqrt{-({\kappa _{1}}^2-{\kappa _{2}}^2)}}{2}\rho \bigg ). \end{aligned}$$

(91)

Family: 6 When ${\kappa _{1}}^2-{\kappa _{2}}^2>0$ and ${\kappa _{3}}\ne -{\kappa _{2}}$

$$\begin{aligned} \mathfrak {F}^{f(\rho )}=\frac{-{\kappa _{1}}}{{\kappa _{3}}}+\frac{\sqrt{({\kappa _{1}}^2-{\kappa _{2}}^2)}}{{\kappa _{3}}}\tanh \bigg (\frac{\sqrt{({\kappa _{1}}^2-{\kappa _{2}}^2)}}{2}\rho \bigg ), \end{aligned}$$

(92)

$$\begin{aligned} \mathfrak {F}^{f(\rho )}=\frac{-{\kappa _{1}}}{{\kappa _{3}}}+\frac{\sqrt{({\kappa _{1}}^2-{\kappa _{2}}^2)}}{{\kappa _{3}}}\coth \bigg (\frac{\sqrt{({\kappa _{1}}^2-{\kappa _{2}}^2)}}{2}\rho \bigg ). \end{aligned}$$

(93)

Family: 7 When ${\kappa _{2}}{\kappa _{3}}<0$, ${\kappa _{3}}\ne 0$ and ${\kappa _{1}}=0$

$$\begin{aligned} \mathfrak {F}^{f(\rho )}=\sqrt{\frac{-{\kappa _{2}}}{{\kappa _{3}}}}\tanh \bigg (\frac{\sqrt{-{\kappa _{2}}{\kappa _{3}}}}{2}\rho \bigg ), \end{aligned}$$

(94)

$$\begin{aligned} \mathfrak {F}^{f(\rho )}=\sqrt{\frac{-{\kappa _{2}}}{{\kappa _{3}}}}\coth \bigg (\frac{\sqrt{-{\kappa _{2}}{\kappa _{3}}}}{2}\rho \bigg ). \end{aligned}$$

(95)

Family: 8 When ${\kappa _{1}}=0$ and ${\kappa _{2}}=-{\kappa _{3}}$

$$\begin{aligned} \mathfrak {F}^{f(\rho )}=\frac{-(1+e^{2{\kappa _{2}}\rho })\pm \sqrt{2(1+e^{2{\kappa _{2}}\rho })}}{e^{2{\kappa _{2}}\rho }-1}. \end{aligned}$$

(96)

Family: 9 When ${\kappa _{1}}^2={\kappa _{2}}{\kappa _{3}}$

$$\begin{aligned} \mathfrak {F}^{f(\rho )}=\frac{-{\kappa _{2}}({\kappa _{1}}\rho +2)}{{\kappa _{1}}^2\rho }. \end{aligned}$$

(97)

Family: 10 When ${\kappa _{1}}=k$, ${\kappa _{2}}=2k$ and ${\kappa _{3}}=0$

$$\begin{aligned} \mathfrak {F}^{f(\rho )}=e^{\rho }-1. \end{aligned}$$

(98)

Family: 11 When ${\kappa _{1}}=k$, ${\kappa _{3}}=2k$ and ${\kappa _{2}}=0$

$$\begin{aligned} \mathfrak {F}^{f(\rho )}=\frac{e^{\rho }}{1-e^{\rho }}. \end{aligned}$$

(99)

Family: 12 When $2{\kappa _{1}}={\kappa _{2}}+{\kappa _{3}}$

$$\begin{aligned} \mathfrak {F}^{f(\rho )}=\frac{1+{\kappa _{2}} e^{\frac{1}{2}({\kappa _{2}}-{\kappa _{3}})\rho }}{ 1+{\kappa _{3}} e^{\frac{1}{2}({\kappa _{2}}-{\kappa _{3}})\rho }}. \end{aligned}$$

(100)

Family: 13 When $-2{\kappa _{1}}={\kappa _{2}}+{\kappa _{3}}$

$$\begin{aligned} \mathfrak {F}^{p\rho )}=\frac{{\kappa _{2}}+{\kappa _{2}} e^{\frac{1}{2}({\kappa _{2}}-{\kappa _{3}})\rho }}{ {\kappa _{3}}+{\kappa _{3}} e^{\frac{1}{2}({\kappa _{2}}-{\kappa _{3}})\rho }}. \end{aligned}$$

(101)

Family: 14 When ${\kappa _{2}}=0$

$$\begin{aligned} . \mathfrak {F}^{f(\rho )}=\frac{{\kappa _{1}} e^{{\kappa _{1}}\rho }}{ 1+\frac{{\kappa _{3}}}{2}e^{{\kappa _{1}}\rho }}. \end{aligned}$$

(102)

Family: 15 When ${\kappa _{2}}={\kappa _{1}}={\kappa _{3}}\ne 0$

$$\begin{aligned} \mathfrak {F}^{f(\rho )}=\frac{-({\kappa _{2}}\rho +2)}{{\kappa _{2}}\rho }. \end{aligned}$$

(103)

Family: 16 When ${\kappa _{2}}={\kappa _{3}}$, ${\kappa _{1}}=0$

$$\begin{aligned} \mathfrak {F}^{f(\rho )}=\tan \bigg (\frac{{\kappa _{2}}\rho +c}{2}\bigg ). \end{aligned}$$

(104)

Family: 17 When ${\kappa _{3}}=0$

$$\begin{aligned} \mathfrak {F}^{f(\rho )}=e^{{\kappa _{1}}\rho }-\frac{{\kappa _{2}}}{2{\kappa _{1}}}. \end{aligned}$$

(105)

Step: 6 Using all the values of $\mathfrak {F}^{f(\rho )}$ from step: 5 into Eq. (80), we get the results for Eq. (77).