1 Conventional planer AG focusing lattice

Alternating gradient (AG) or strong focusing principle was initially realised by the magnets with a large field index n, which is called a gradient magnet [1]. A pair of gradient magnets with an opposite sign of n gives much stronger net focusing in both horizontal and vertical directions compared with a single magnet with n between 0 and 1 that gives focusing in both directions but weak. In modern accelerator optics, however, dipole magnets for bending and quadrupole magnets for focusing are used instead of gradient magnets. The lattice design based on dipole and quadrupole magnets is called a separated function lattice in contrast to a combined function lattice with gradient magnets. A design orbit goes through the centre of quadrupole magnets without bending and dipole magnets do not give strong focusing.

Although it is backward in a sequence of developments, a combined function lattice can be made with quadrupole magnets by designing the orbit going off the centre. A feed-down dipole component from the shifted quadrupole bends the beams as well as focuses them. By shifting a defocusing quadrupole (QD) outward with respect to the centre of a circular accelerator lattice and a focusing quadrupole (QF) inward, both quadrupole magnets gives the normal bending action. That configuration is equivalent to having gradient magnets.

Both QD and QF do not have to bend the beams inward to close the orbit. If one of the quadrupoles provides more normal bending than the other, there is a net bending angle per lattice period and eventually the orbit closes. A fixed-field alternating gradient accelerator (FFA) uses this principle [2,3,4]. The local gradient is kept constant only as a function of the distance measured from the machine centre. AG focusing is realised by changing the polarity of magnets. One magnet bending the beam inward has focusing action, and the other bending the beam outward has defocusing. When the angle of normal bending is larger than that of reverse bending, the orbit closes. Magnets for a FFA is not a simple quadrupole because the field gradient should be scaled to give constant focusing action for the beams with a wide range of momentum spreading in a horizontal direction. However, it can be regarded as a quadrupole locally for a fixed momentum and the lattice is made of both signs of quadrupoles without horizontal shift.

There is a different kind of a FFA lattice which uses literally quadrupole magnets. Since the field gradient does not scale with the beam momentum, effective focusing strength varies depending on the beam momentum. This FFA is called a non-scaling FFA (nsFFA) in contrast to the conventional FFA which is called a scaling FFA (sFFA). In a nsFFA, relatively large horizontal shift between focusing and defocusing magnets is utilised to force the normal bending action at QD and the reverse bending at QF. In this way, the momentum compaction factor can be reduced or even zero at a particular momentum as described below. That is particularly important as a nsFFA lattice. With fixed-field magnets, the orbit moves in the direction according to the dispersion function with acceleration. A large orbit excursion such as in a cyclotron should be avoided in order to squeeze the magnet aperture. A small momentum compaction factor helps to reduce the orbit excursion. It is a normal exercise to make the momentum compaction factor zero at the central momentum when a nsFFA is designed although it is not possible to make it zero for the whole range of momenta from injection to extraction [5].

Fig. 1
figure 1

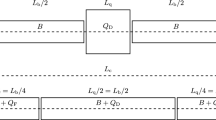
Orbit and vertical field in a normal quadrupole lattice. In this example, bending angle per cell is 7.2 degree. Red box shows a defocusing quadrupole and blue box shows a focusing quadrupole. A straight line at the centre shows the quadrupole axis. a, d sFFA like lattice without horizontally shifted quadrupoles. b, e combined function focusing lattice with shifted quadrupoles. c, f nsFFA lattice with large horizontal shift of quadruples than a combined function lattice

Full size image
Table 1 Main parameters of three lattices of Fig. 1
Full size table

Three different lattice configurations discussed above are illustrated in Fig. 1 and their main parameters are listed in Table 1. In terms of horizontal shift of QD and QF, a lattice becomes a sFFA like with zero shift (Fig. 1a). With a proper amount of shift, it becomes a combined function lattice (Fig. 1b). Further increase in the horizontal shift creates a reverse bending at QF and the lattice becomes a nsFFA (Fig. 1c). Vertical magnetic field along the orbit for each lattice is depicted in Fig. 1d–f.

It should be noted that the effect of horizontal shift of quadrupole magnets is equivalent to adding a bending component at quadrupole magnets. With a normal bending component added to both QD and QF, it becomes the conventional combined function lattice. A reverse bending component at QD and a normal bending component at QF make a sFFA like lattice. A normal bending component at QD and a reverse bending component at QF make a nsFFA lattice.

2 Momentum compaction factor in a normal quadrupole lattice

Let us look at more details on the last example where normal bending occurs at QD and reverse bending at QF. Let us see how the momentum compaction factor is controlled. The magnets are aligned in the horizontal direction and there is no displacement of the orbit in the vertical direction. The dispersion function is finite only in the horizontal direction. As shown in Fig. 1c, the beams go through the inside (towards the machine centre) of the quadrupole centre of QD and QF. As a result, QD gives normal bending and QF gives reverse bending. On the other hand, the dispersion function is determined by the optics. It is small at QD and large at QF as shown in Fig. 2 that is independent of the orbit location.

With a slight increase in the beam momentum, the orbit moves outward according to the dispersion function. A smaller dispersion function at QD than that at QF makes a horizontal orbit oscillation amplitude smaller with momentum. That effect itself reduces the path length. An increase in the horizontal position and a decrease in a horizontal orbit oscillation amplitude counteract the change of the path length. When they are equal at a particular momentum, the momentum compaction factor becomes zero (Fig. 3).

Fig. 2
figure 2

Dispersion function of a normal quadrupole lattice in the unit of [m]. Lattice parameters are the same as Fig. 1c. “disp1” shows the dispersion function in the horizontal plane and “disp3” shows that in the vertical plane

Full size image
Fig. 3
figure 3

Path length difference dC as a function of momentum deviation in the lattice of Fig. 1c

Full size image
Fig. 4
figure 4

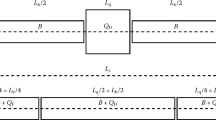
Horizontal and vertical orbits and vertical and horizontal fields in a skew quadrupole lattice. In this example, bending angle per cell is 7.2 degree. Red box shows a defocusing skew quadrupole and blue box shows a focusing skew quadrupole. A straight line at the centre shows the quadrupole axis. a horizontal orbit without vertical shift. b Horizontal orbit with certain vertical shift. The beams go through almost at the centre of skew quadrupoles in the horizontal direction. c Horizontal orbit with more vertical shift. The beams go inside of skew quadrupoles. d Vertical orbit without vertical shift. e Vertical orbit with certain vertical shift. f Vertical orbit with more vertical shift. The vertical bending direction is swapped compared with d. g–i are vertical fields of each lattice. j–l Horizontal fields of each lattice

Full size image

3 AG focusing lattice with skew quadrupoles

Most of circular accelerator lattice designs are based on normal quadrupoles although there are some exceptions [6]. The orbit is confined in the horizontal direction unless a vertical bending magnet exists along the orbit. In other words, the particle motion in horizontal and vertical direction is decoupled. Thus, an invariant of the motion exists in horizontal and vertical direction independently. Introducing a coupled optics partially or in the entire lattice seems unnecessary confusion which is normally avoided as possible.

Here we will show a circular accelerator based on skew quadrupoles for the whole lattice has interesting characteristics. The key ingredient that makes a skew quadrupole lattice stand out is the relative vertical shift of skew quadrupoles or equivalently polarity and strength of a vertical bending component along the orbit. Let us look at a lattice with a combination of simple focusing and defocusing skew quadrupoles, denoting SQF and SQD respectively. Because it is somewhat arbitrary unlike normal quadrupoles, for the rest, we define in a way that SQF gives the normal bending in the upper half of a magnetic.

Without relative vertical shift of SQD and SQF, the orbit moves outward with respect to the quadrupole centre (opposite to the machine centre) in the horizontal direction (Fig. 4a). The finite horizontal field bends the orbit in such a way that the beams go through the lower half of SQD and the upper half of SQF (Fig. 4d). Thus, both quadrupoles bend the beams inward.

With a certain amount of the vertical shift, upward of SQD and downward of SQF, the beams go through at the centre of both quadrupole magnets in the horizontal plane (Fig. 4b). The vertical orbit oscillation disappears (Fig. 4e) because no horizontal field exists along the vertical axis.

With more vertical shift, the orbit moves inward with respect to the quadrupole centre (towards the machine centre) in the horizontal plane. The beams go through the lower half of SQD and the upper half of SQF as in the previous case. Thus, both quadrupoles bend the beams inward as shown (Fig. 4c). However, the sign of the horizontal field which depends on the sign of the horizontal coordinate changes. The beam bends downward in SQD and upward in SQF (Fig. 4f). Vertical and horizontal fields along the orbit is depicted in Fig. 4g–l. Main parameters of three lattices are listed in Table 2.

The vertical dispersion function does not change due to the vertical shift whereas the horizontal dispersion is almost constant along the orbit as shown in Fig. 5.

Table 2 Main parameters of three lattices of Fig. 4
Full size table

4 Momentum compaction factor in a skew quadrupole lattice

The momentum compaction factor in a normal quadrupole lattice can be controlled and set to zero by choosing parameters. In a skew quadrupole lattice, the horizontal position increases with momentum due to the horizontal dispersion function which is positive and finite. However, a vertical oscillation amplitude of the orbit depends on a shape of the vertical orbit and the vertical dispersion function. Without vertical shift of SQD and SQF, the vertical orbit is lower at SQD and higher at SQF. The vertical dispersion function which is determined by the optics and always low at SQD and high at SQF increases vertical orbit oscillation amplitude with momentum. When vertical shift exceeds some certain value (Fig. 4c), an oscillation pattern of the vertical orbit flips. A vertical orbit oscillation amplitude reduces with momentum. Combined with the vertical dispersion function, an increase in the path length due to shift of the horizontal position can be cancelled. Thus, the momentum compaction factor will be zero at a certain momentum (Fig. 6).

Fig. 5
figure 5

Dispersion function of a skew quadrupole lattice in the unit of [m]. Lattice parameters are the same as Fig. 4c. “disp1” shows the dispersion function in the horizontal plane and “disp3” shows that in the vertical plane

Full size image
Fig. 6
figure 6

Path length difference dC as a function of momentum deviation in the lattice of Fig. 4c

Full size image

The way to make the momentum compaction factor zero in a normal and a skew quadrupole lattice is similar. Both use shape of the orbit counteracting the dispersion function with momentum. One of noticeable differences between two is the existence of reverse bending in a normal quadrupole lattice which increases either the circumference or the bending magnet strength of a circular accelerator lattice. On the contrary, the momentum compaction factor can be zero without having reverse bending in a skew quadrupole lattice.

5 Chromaticity correction in a skew quadrupole lattice

Correction of chromaticity can be done in the same way as in a normal quadrupole lattice. The difference is that the dispersion function is finite both in the horizontal and vertical directions. A sextupole component in the magnets has to be either tilted or equivalently a combination of normal and skew sextupoles.

As a demonstration of chromaticity correction of the skew quadrupole lattice, we take the zero momentum compaction factor lattice (Fig. 4c). A sextupole component should not affect the tune of the on-momentum particle. The axis of the sextupole magnet is supposed to be aligned with the on-momentum beam orbit. To make positioning of a sextupole component easier, we first added horizontal and vertical bending components in the skew quadrupole magnets. With proper adjustment of bending strength, its strength can be calculated from the horizontal and vertical displacements and skew quadrupole strength, the same optics of the zero momentum compaction factor lattice without vertical shift of SQD and SQF is realised. Figure 7 demonstrates that the beam goes through on the axis of skew quadrupole magnets when the bending components are added.

Fig. 7
figure 7

Skew quadrupole lattice with bending components makes the beam go through the skew quadrupole centre. a Horizontal orbit, b vertical orbit

Full size image

There are four parameters to be adjusted to achieve chromaticity correction. Normal and skew sextupole components in SQD and SQF respectively. Together with dipole, skew quadrupole and normal and skew sextupole components, the horizontal and vertical fields in the combined focusing magnet (CFM) and the combined defocusing magnet (CDM) are described by Eq. (1).

$$\begin{aligned} b_x= & {} b_{0s}-b_{1s} x - b_{2s} \left( 3 x^2-3 y^2 \right) + b_{2n} \left( 6xy \right) , \nonumber \\ b_y= & {} b_{0n}+b_{1s} y + b_{2s} \left( 6xy \right) + b_{2n} \left( 3x^2-3y^2 \right) . \end{aligned}$$
(1)

With a set of values listed in Table 3, momentum dependence of two eigentunes of the cell is reduced as shown in Fig. 8.

Table 3 Strength of multipoles
Full size table
Fig. 8
figure 8

Chromaticity correction in a skew quadrupole lattice achieved with normal and skew sextupole components. Left figure is before correction and right after correction. “qu” and “qv” denote two eigentunes of a focusing unit

Full size image

6 Application to a muon collider ring

One possible direction of particle accelerators for energy frontier physics is a muon collider. Unlike electrons, the mass of muons is large enough so that the synchrotron radiation at bending magnets is small. That makes a design of a circular collider of muons around 10 TeV energy. On the other hand, the life time of muons at rest is 2.2 \(\mu \)s and acceleration and collision have to be done as quick as possible. The concept has been studied several times in the past [7] and the new initiative [8] has been launched recently.

Fig. 9
figure 9

Orbits and magnetic field of a muon collider arc with a normal quadrupole lattice. a Horizontal b vertical c magnetic field along the orbit. \(B_y\) is the vertical field and \(B_x\) is the horizontal field

Full size image
Fig. 10
figure 10

Orbits and magnetic field of a muon collider arc with a skew quadrupole lattice. a Horizontal b vertical c magnetic field along the orbit. \(B_y\) is the vertical field and \(B_x\) is the horizontal field

Full size image
Table 4 Parameters of a muon collider ring (only arc) with normal and skew quadrupoles. With the same arc length, the maximum field strength is significantly lower in a skew quadrupole lattice without reverse bending magnets
Full size table

To keep the bunch length short, a collider ring has to have almost zero momentum compaction factor. Another requirement of a collider ring comes from the decay of muons. While the muon beams are colliding at a collider ring, a fraction of circulating muons decays due to its lifetime. Muon decay emits neutrinos and they cause radiation hazard with interaction with material in the direction of the neutrino radiation. In a conventional collider ring design, the orbit is in the horizontal plane so that the direction of the neutrino radiation is also confined in the plane with some small angle coming from the beam divergence. One of the mitigation measure of the radiation is to introduce a vertical orbit oscillation in a lattice design so that the radiation spreads out more than a single horizontal plane.

With a skew quadrupole lattice, two requirements above are satisfied at the same time. Figures 9 and 10 compare the orbits and magnetic field strength long the orbits in two lattices. Parameters are given in Table 4.

7 Summary

An AG lattice with skew quadrupole magnets for the whole ring is designed. Combined with vertical shift of SQD and SQF, the vertical orbit oscillation is excited. The dispersion function becomes finite in both horizontal and vertical directions. The momentum compaction factor is controlled in the similar way in a normal and skew quadrupole lattice. A skew quadrupole lattice can make the zero momentum compaction factor lattice without reverse bending magnets or the negative dispersion function. It was shown that normal and skew sextupole components can be used to correct chromaticity in a skew quadrupole lattice. As a demonstration of the concept, a collider ring arc design of a muon collider facility is illustrated.