1 Introduction

When positive and negative dust exists in plasmas, a new dusty plasma system termed “opposite polarity dusty plasma” (OPDP) arises [1,2,3,4,5,6,7,8,9]. Generally, the collection of electrons from the surrounding medium and the thermal speeds of electrons that far exceed that of ions cause dust grains to be negatively charged. However, there are some observations of positively charged dust grains in different parts of space (Jupiter’s magnetosphere [10], upper mesosphere [11], cometary tails [12], thick molecular clouds [13], and in the Martian atmosphere [3]). The charging processes of the positive dust are achieved by different mechanisms, such as the secondary emission of electrons from the surface of the dust grains [3], the thermionic emission from particles heated by radiative sources [3], and the photoemission under ultraviolet radiation [14].

Usually, the size of positively charged particles compared to negatively charged dust might be smaller or larger than unity in the dusty plasma, and it can even be equal to unity. This important feature of dust particles makes the OPDP distinguished from electron–ion and electron–positron plasmas. Depending on the dust size, the mass and the magnitude of the charge of the dust are determined. Chow et al. [15] studied theoretically the effect of dust species size (the size of positively charged dust grains is smaller than that of the negatively charged dust grains) on the charging of insulated dust grains by the secondary electron emission. Also, Mendis and Rosenberg [16] and Zhao et al. [17] studied the opposite situation (the size of positively charged dust grains is larger than that of the negatively charged dust grains).

The investigation of the linear [1,2,3] and nonlinear [2, 4,5,6,7,8,9] propagation of electrostatic waves in the OPDP systems with or without [2,3,4,5,6,7,8,9] external static magnetic field have been performed. These works are valid only when the effect of the self-gravitational force is negligible in comparison with the electrostatic force or the effect of self-gravitational force is insignificant.

Dust-acoustic waves (DAWs) propagating in a multicomponent, collisional, magnetized dusty plasma have been investigated, recently by Tolba [18], and found that relative densities and temperatures parameters affect the behavior of the obtained waves. The extremely massive charged dust particles may be affected by both the electromagnetic force [19] and the gravitational field [20] in astrophysical environments when compared to charged electrons and ions, which are controlled by electromagnetic fields only. The gravitational and the electric forces for a massive dust grain in this case become nearly comparable in their values. Therefore, they play an important role in dust particles dynamics [20, 21] in space plasmas containing dust grains with a radius larger than 1 \(\upmu \)m [22]. Accordingly, for the dust species with radius \(r_{d}>1 \upmu \)m the gravitational force is important for the dynamical properties. On the other hand, for \(r_{d}<1 \upmu \)m, the electrostatic (repulsion) force must be considered [23, 24]. Both electrostatic and gravitational forces govern the massive and highly charged dust grain dynamics since the dust sizes vary from 1 to 15 \(\upmu \)m. In this situation, both forces are in competition. The physical explanation of the star formation and the mechanism of self-gravitational collapse occur due to the combination of these two forces. This is the reason to study the self-gravitating dusty plasma associated with the nonlinear structures, such as dust-acoustic (DA) solitary and periodic waves and other associated nonlinear features. The coupling of electromagnetic and gravitational forces is essential for the investigation of various astrophysical objects like circumstellar disks, nebulae, and supernova remnants [19, 21, 25, 26], where the combined effects of these two dominant forces are important [19, 20]. The nonlinear structure of self-gravito-acoustic (SGA) mode rises as a result of the gravitational force. In this mode, the inertia and the restoring force are provided by the mass density of mobile heaviest nuclei and degenerate pressure of lightest particles, respectively. This situation motivated astrophysicists to discover the SGA modes and associated nonlinear structures that exist in such compact objects.

The self-gravitational effects have been taken in many OPDP systems [24, 27,28,29,30,31,32,33], such as dust-acoustic (DA) solitary and shock waves investigations [24, 27]. The polarization force effect on the small amplitude of gravito-electrostatic excitations was investigated [28]. Prajapati and Chhajlani [29] analyzed the Jeans’ instability in a magnetized self-gravitating dusty plasma. This Jeans instability was affected by the magnetic field and dust temperature. Later on, Sabetkar and Dorranian [30] found that the increase in the width of the DA double layers resulted due to the considered self-gravitational field enhancement. Sumi et al. [32] found also that the amplitude of DA waves was modified by the presence of opposite polarity charged dust and their self-gravitational force. Mannan et al. [33] found that the positive dust number density decrease leads to enhancing the amplitude of the self-gravitational solitary wave.

The bifurcation analysis has been employed for traveling waves investigation through perturbative and non-perturbative approaches [34,35,36,37,38]. Saha et al. [34] investigated the periodic waves in a plasma with q-nonextensive electrons. By applying the bifurcation theory, they analyzed all possible dynamical system phase portraits[34,35,36,37,38]. Moreover, Saha and Chatterjee[36] investigated the dynamical behavior of electron acoustic waves in plasmas with nonextensive electrons using the non-perturbative approach. DA waves phase planes were checked also for the evolved Burgers equation in a strongly coupled system of dusty plasma [39]. Periodic waves in quantum plasma were reported in the case of absence of dissipation in the Thomas Fermi dusty plasmas [40] and were analyzed also through bifurcation analysis [23]. The bifurcation theory of planar dynamical systems was applied for an OPDP to investigate the dust-ion-acoustic solitary structures [41]. OPDP systems have been employed also to investigate the elliptic periodic waves that were affected by the system parameters [42].

However, to the best of the authors’ knowledge, no attempt has been made considering the phase plane theory of dynamical systems on the magnetized self-gravitating dusty plasma. Therefore, in this work, we investigate the phase portrait profiles to study the solitary and periodic waves associated with SGA mode.

Our work is organized as follows. The basic set of equations that govern the dynamics of DA waves are presented in Sect. 2. The nonlinear analysis, the Korteweg–de Vries–Burger (KdVB) equation, and its solution are derived in Sect. 3. The modified Korteweg–de Vries equation (mKdV) and its solution are presented in Sect. 4. The bifurcations of the corresponding phase portraits are also included in Sect. 5. The periodic wave solution is mentioned in Sect. 6. Finally, the discussion and conclusions are provided in Sect. 7.

2 The model

We consider the propagation of the DA waves in a self-gravitating OPDP consisting of negatively and positively charged dust grains and inertialess ions (following the Maxwellian distribution). We neglect the contribution of the free electrons since the latter were almost completely depleted to the surface of the negative dust species; also, we neglect the effect of the self-gravitational field on the ions since the number density of ions is neglected in comparison with that of positive or negative dust species. Since the charged dust grains are highly massive particles, the self-gravitational, electrical forces should be taken into account and in the presence of an external static magnetic field \(B_{0}{\hat{z}}\) which is aligned in the z-direction, where \(B_{0}\) is its magnitude and \({\hat{z}}\) is the unit vector along the z-direction. The nonlinear gravito-electrodynamics [19] of the DA waves are described by the normalized equations in the form [24, 43,44,45]

$$\begin{aligned} \left. \begin{array} [c]{c} \frac{\partial n_{1}}{\partial t}+\nabla \cdot (n_{1}u_{1})=0,\\ \text {\ }\frac{\partial u_{1}}{\partial t}+\left( u_{1}\cdot \nabla \right) u_{1}+\frac{\alpha }{\beta }\nabla \phi +\nabla \psi =\eta _{1}\nabla ^{2}u_{1} +\frac{\alpha }{\beta }\omega _{c1}(u_{1}\times {\hat{z}}),\\ \frac{\partial n_{2}}{\partial t}+\nabla \cdot (n_{2}u_{2})=0,\text { }\\ \frac{\partial u_{2}}{\partial t}+\left( u_{2}\cdot \nabla \right) u_{2}-\nabla \phi +\nabla \psi =\eta _{2}\nabla ^{2}u_{2}-\omega _{c2}(u_{2} \times {\hat{z}}),\\ \nabla ^{2}\phi =n_{2}-\alpha \mu n_{1}-(1-\alpha \mu )(e^{-\phi }-1),\\ \nabla ^{2}\psi =\gamma (n_{2}+\beta \mu n_{1}), \end{array} \right\} \end{aligned}$$
(1)

where \(n_{1}\)(\(n_{2}\)) represents the positive (negative) dust number density normalized by its equilibrium value \(n_{10}\)(\(n_{20}\)); \(u_{1}\) (\(u_{2}\)) is the positive (negative) dust fluid speed normalized by the negative DA speed \(C_{d2}=\sqrt{Z_{2}k_{B}T_{i}/m_{2}}\) (\(T_{i}\) being the ion temperature, and \(k_{B}\) being the Boltzmann constant); \(\alpha =Z_{1}/Z_{2}\) with \(Z_{1}\) being the number of electrons depleted from the positive dust and \(Z_{2}\) being the number of electrons residing in the negative dust. \(\beta =m_{1}/m_{2}\) with \(m_{1}\)(\(m_{2}\)) being the mass of positive (negative) dust; \(\eta _{1,2}\) being the normalized longitudinal viscosity coefficient which is normalized by \(m_{1,2}n_{10,20}\omega _{p2}\lambda _{D2}^{2}\); \(\phi \) is the electrostatic wave potential normalized by \(k_{B}T_{i}/e\) (with e being the charge of an electron); \(\psi \) is the self-gravitational potential normalized by \(C_{d2}^{2}\); the space variables \(\left( x,y,z\right) \) in \(\nabla ={\hat{x}}\frac{\partial }{\partial x}+{\hat{y}} \frac{\partial }{\partial y}+{\hat{z}}\frac{\partial }{\partial z}\) are normalized by Debye length \(\lambda _{D2}=\sqrt{K_{B}T_{i}/4\pi Z_{2}n_{20}e^{2}}\); and t is the time variable normalized by \(\omega _{p2}^{-1}=\sqrt{m_{2}/4\pi Z_{2}^{2}n_{20}e^{2}}\); \(\omega _{c1,2}=Z_{1,2}eB_{0}/m_{1,2}\omega _{p2}\) is the cyclotron frequency for the positive and negative dust which are normalized by negative dust plasma frequency \(\omega _{p2}\); \(\mu =\) \(n_{10}/n_{20}\); and \(\gamma =\omega _{J2}^{2}/\omega _{p2}^{2}\) (with \(\omega _{J2}=\sqrt{4\pi Gn_{20}m_{2}}\) being the Jeans frequency for the negative dust component and G being the universal gravitational constant).

3 Derivation and solution of the KdVB equation

To study the characteristics of the nonlinear DAWs propagating in this magnetized plasma system, we derive the nonlinear KdVB equation by using the reductive perturbation method [46]. So, we first introduce the stretched coordinates as

$$\begin{aligned} \left| \begin{array} [c]{c} \eta =\epsilon ^{\frac{1}{2}}(L_{x}x+L_{y}y+L_{z}z-V_{p}t),\\ T=\epsilon ^{\frac{3}{2}}t,\eta _{i}=\epsilon ^{\frac{1}{2}}\eta _{i0}, \end{array} \right\} \end{aligned}$$
(2)

The viscosity coefficient is rescaled as \(\eta _{i}=\epsilon ^{\frac{1}{2}} \eta _{i0}\), i.e., low viscosity is needed, where \(\epsilon \) is the smallness parameter measuring the perturbation amplitude. \(V_{p}\) is the phase speed of the perturbation wave. The wave vector k has directional cosines given by \(L_{x}\), \(L_{y}\), and \(L_{z}\) along x, y, and z axes, respectively, satisfying the relation \(L_{x}^{2}+L_{y}^{2}+L_{z}^{2}=1\). We expand the dependent parameters \(n_{1,2}\), \(u_{1,2x,1,2y,1,2z}\), \(\psi \) and \(\phi \) in power series of \(\epsilon \) as [47]

$$\begin{aligned} \left| \begin{array} [c]{c} n_{1,2}=1+\epsilon n_{1,2}^{(1)}+\epsilon ^{2}n_{1,2}^{(2)}+\epsilon ^{3} n_{1,2}^{(3)}+.....,\\ u_{1,2x}=\epsilon ^{\frac{3}{2}}u_{1,2x}^{(1)}+\epsilon ^{2}u_{1,2x} ^{(2)}+.....,\\ u_{1,2y}=\epsilon ^{\frac{3}{2}}u_{1,2y}^{(1)}+\epsilon ^{2}u_{1,2y} ^{(2)}+.....,\\ u_{1,2z}=\epsilon u_{1,2z}^{(1)}+\epsilon ^{2}u_{1,2z}^{(2)}+.....,\\ \phi =\epsilon \phi ^{(1)}+\epsilon ^{2}\phi ^{(2)}+.....,\\ \psi =\epsilon \psi ^{(1)}+\epsilon ^{2}\psi ^{(2)}+.....{{.}} \end{array} \right\} \end{aligned}$$
(3)

Now, substituting Eqs. (2) and (3) into the set of basic Eqs. (1) and collecting equations having the same power, the lowest order coefficients of \(\epsilon \) lead to

$$\begin{aligned} \left. \begin{array} [c]{c} n_{1}^{(1)}=\frac{L_{z}^{2}}{V_{p}^{2}}\left( \frac{\alpha }{\beta }\phi ^{(1)}+\psi ^{(1)}\right) ,n_{2}^{(1)}=\frac{L_{z}^{2}}{V_{p}^{2}}\left( \psi ^{(1)}-\phi ^{(1)}\right) ,\\ u_{1z}^{(1)}=\frac{L_{z}}{V_{p}}\left( \frac{\alpha }{\beta }\phi ^{(1)} +\psi ^{(1)}\right) ,u_{2z}^{(1)}=\frac{L_{z}}{V_{p}}\left( \psi ^{(1)} -\phi ^{(1)}\right) ,\\ \psi ^{(1)}=\frac{\left( 1-\alpha \mu \right) }{\left( \beta \mu +1\right) }\phi ^{(1)}. \end{array} \right\} \end{aligned}$$
(4)

The first-order perturbed quantities accompanied in the Poisson’s equation lead to the following expression for the phase speed of the DA waves:

$$\begin{aligned} V_{p}=L_{z}\left( \alpha +\beta \right) \sqrt{\frac{\mu }{\beta \left( \beta \mu +1\right) (1-\alpha \mu )}}. \end{aligned}$$
(5)

It is obvious that the phase speed, \(V_{p}\), is affected by the system parameters, such as the positive and negative dust equilibrium densities, charges, masses ratios, and magnetic field obliquity angle. Accordingly, Fig.  1 shows how the DA phase speed varies with four important parameters \(\mu ,\alpha ,\beta \), and \(\theta \). It is depicted from Fig. 1 that the phase speed increases as \(\mu ,\alpha ,\) and \(\beta \) increase, while it decreases as \(\theta \) increases. The next order equations in \(\epsilon \) lead to

$$\begin{aligned} \left| \begin{array} [c]{c} u_{1x}^{(1)}=\frac{\beta L_{y}}{\omega _{c1}\alpha }\left( \frac{\alpha }{\beta }\frac{\partial \phi ^{(1)}}{\partial \eta }+\frac{\partial \psi ^{(1)}}{\partial \eta }\right) ,\\ u_{2x}^{(1)}=\frac{L_{y}}{\omega _{c2}}\left( \frac{\partial \phi ^{(1)} }{\partial \eta }-\frac{\partial \psi ^{(1)}}{\partial \eta }\right) ,\\ u_{1y}^{(1)}=-\frac{L_{x}\beta }{\alpha \omega _{c1}}\left( \frac{\alpha }{\beta }\frac{\partial \phi ^{(1)}}{\partial \eta }+\frac{\partial \psi ^{(1)}}{\partial \eta }\right) ,\\ u_{2y}^{(1)}=\frac{L_{x}}{\omega _{c2}}\left( \frac{\partial \psi ^{(1)} }{\partial \eta }-\frac{\partial \phi ^{(1)}}{\partial \eta }\right) . \end{array} \right\} \end{aligned}$$
(6)
Fig. 1
figure 1

The variation of the phase speed \(V_{p}\), represented by Eq. (5) at \(\gamma =0.3\) a against \(\alpha \) for different values of \(\beta \) at \(\mu =0.6\) with \(\theta =20\), and b against \(\mu \) for different values of \(\theta \) at \(\alpha =0.5\) with \(\beta =5\)

Full size image

Similarly, proceeding to higher order in the reductive perturbation theory, we get

$$\begin{aligned} \left| \begin{array} [c]{c} \frac{\partial n_{1}^{(1)}}{\partial T}-V_{p}\frac{\partial n_{1}^{(2)} }{\partial \eta }+L_{x}\frac{\partial u_{1x}^{(2)}}{\partial \eta }+L_{y} \frac{\partial u_{1y}^{(2)}}{\partial \eta }+L_{z}\frac{\partial u_{1z}^{(2)} }{\partial \eta }+L_{z}\frac{\partial }{\partial \eta }\left( n_{1}^{(1)} u_{1z}^{(1)}\right) =0,\\ \frac{\partial u_{1z}^{(1)}}{\partial T}-V_{p}\frac{\partial u_{1z}^{(2)} }{\partial \eta }+u_{1z}^{(1)}L_{z}\frac{\partial u_{1z}^{(1)}}{\partial \eta }+\frac{\alpha }{\beta }L_{z}\frac{\partial \phi ^{(2)}}{\partial \eta }+L_{z} \frac{\partial \psi ^{(2)}}{\partial \eta }=\eta _{10}\frac{\partial ^{2} u_{1z}^{(1)}}{\partial \eta ^{2}},\\ \frac{\partial n_{2}^{(1)}}{\partial T}-V_{p}\frac{\partial n_{2}^{(2)} }{\partial \eta }+L_{x}\frac{\partial u_{2x}^{(2)}}{\partial \eta }+L_{y} \frac{\partial u_{2y}^{(2)}}{\partial \eta }+L_{z}\frac{\partial u_{2z}^{(2)} }{\partial \eta }+L_{z}\frac{\partial }{\partial \eta }\left( n_{2}^{(1)} u_{2z}^{(1)}\right) =0,\\ \frac{\partial u_{2z}^{(1)}}{\partial T}-V_{p}\frac{\partial u_{2z}^{(2)} }{\partial \eta }+u_{2z}^{(1)}L_{z}\frac{\partial u_{2z}^{(1)}}{\partial \eta }-L_{z}\frac{\partial \phi ^{(2)}}{\partial \eta }+L_{z}\frac{\partial \psi ^{(2)} }{\partial \eta }=\eta _{20}\frac{\partial ^{2}u_{2z}^{(1)}}{\partial \eta ^{2}},\\ \frac{\partial ^{2}\psi ^{(1)}}{\partial \eta ^{2}}=\gamma \left[ n_{2} ^{(2)}+\beta \mu n_{1}^{(2)}\right] ,\\ \frac{\partial ^{2}\phi ^{(1)}}{\partial \eta ^{2}}=n_{2}^{(2)}-\alpha \mu n_{1}^{(2)}-(1-\alpha \mu )(\frac{\left[ \phi ^{(1)}\right] ^{2}}{2}-\phi ^{(2)}). \end{array} \right\} \end{aligned}$$
(7)

Also, we obtain the higher-order coefficients of \(\epsilon \) for the momentum equation components along x- and y-directions as

$$\begin{aligned} \left| \begin{array} [c]{c} u_{1x}^{(2)}=\frac{L_{x}V_{p}\beta ^{2}}{\alpha ^{2}\omega _{c1}^{2}}\left( \frac{\alpha }{\beta }\frac{\partial ^{2}\phi ^{(1)}}{\partial \eta ^{2}} +\frac{\partial ^{2}\psi ^{(1)}}{\partial \eta ^{2}}\right) ,\\ u_{2x}^{(2)}=\frac{L_{x}V_{p}}{\omega _{c2}^{2}}\left( \frac{\partial ^{2} \psi ^{(1)}}{\partial \eta ^{2}}-\frac{\partial ^{2}\phi ^{(1)}}{\partial \eta ^{2} }\right) ,\\ u_{1y}^{(2)}=\frac{\beta ^{2}L_{y}V_{p}}{\alpha ^{2}\omega _{c1}^{2}}\left( \frac{\alpha }{\beta }\frac{\partial ^{2}\phi ^{(1)}}{\partial \eta ^{2}} +\frac{\partial ^{2}\psi ^{(1)}}{\partial \eta ^{2}}\right) ,\\ u_{2y}^{(2)}=-\frac{L_{y}V_{p}}{\omega _{c2}^{2}}\left( \frac{\partial ^{2} \phi ^{(1)}}{\partial \eta ^{2}}-\frac{\partial ^{2}\psi ^{(1)}}{\partial \eta ^{2} }\right) . \end{array} \right\} \end{aligned}$$
(8)

Eliminating the second-order perturbed quantities \(n_{1,2}^{(2)} ,u_{1,2x}^{(2)},u_{1,2y}^{(2)},u_{1,2z}^{(2)},\phi ^{(2)}\), and \(\psi ^{(2)}\) by solving Eqs. (7) and (8) with the aid of Eqs. (4) and (6), finally, we get the following KdVB equation:

$$\begin{aligned} \frac{\partial \phi ^{(1)}}{\partial T}+A\phi ^{(1)}\frac{\partial \phi ^{(1)} }{\partial \eta }+B\frac{\partial ^{3}\phi ^{(1)}}{\partial \eta ^{3}} +C\frac{\partial ^{2}\phi ^{(1)}}{\partial \eta ^{2}}=0, \end{aligned}$$
(9)

where A, B, and C represent the nonlinearity, dispersion, and dissipation coefficients, respectively, which are given by

$$\begin{aligned} \left| \begin{array} [c]{c} A=\left( \frac{3L_{z}^{2}\left( \beta \left( 1-\alpha \mu \right) -\beta ^{2}\mu +\alpha \right) }{2\beta \left( \beta \mu +1\right) V_{p}}+\frac{\beta V_{p}^{3}}{2\mu L_{z}^{2}}\frac{\left( \beta \mu +1\right) (1-\alpha \mu )}{\left( \alpha +\beta \right) ^{2}}\right) ,\\ B=\frac{\beta V_{p}^{3}}{2\mu L_{z}^{2}}\frac{\left( \beta \mu +1\right) }{\left( \alpha +\beta \right) ^{2}}\left( 1-\frac{1}{\gamma }\frac{\left( 1-\alpha \mu \right) ^{2}}{\left( \beta \mu +1\right) ^{2}}+\mu \left( 1-L_{z}^{2}\right) \left( \frac{\alpha +\beta }{\beta \mu +1}\right) ^{2}\left( \frac{\mu }{\omega _{c2}^{2}}+\frac{\beta }{\alpha ^{2}\omega _{c1}^{2}}\right) \right) ,\\ C=-\frac{\eta _{10}+\beta \mu \eta _{20}}{2\left( \beta \mu +1\right) }. \end{array} \right\} \end{aligned}$$
(10)

Both the coefficients of nonlinear and dispersive terms are affected also by the same parameters as the phase speed. Figure 2 shows that the nonlinear term can be positive or negative depending on the system parameters. For positive A, A decreases (increases) as \(\theta ,\mu \), and \(\beta \) \(\left( \alpha \right) \) increase (s), while when A becomes negative, its absolute value increases (decreases) as \(\beta \) and \(\mu \) \(\left( \alpha \text { and }\theta \right) \) increase. Figure 3 shows that the dispersive term is affected by the same parameters in an opposite way, where B increases (decreases) as \(\theta ,\mu \), and \(\beta \) (\(\alpha \)) increase(s).

Fig. 2
figure 2

The variation of the nonlinear term A, represented by Eq. (10) at \(\gamma =0.3\) a against \(\alpha \) for different values of \(\beta \) at \(\mu =0.6\) with \(\theta =20\), and b against \(\mu \) for different values of \(\theta \) at \(\alpha =0.5\) with \(\beta =5\)

Full size image
Fig. 3
figure 3

The variation of the dispersive term B, represented by Eq. (10) at \(\gamma =0.3\) a against \(\alpha \) for different values of \(\beta \) at \(\mu =0.6\) with \(\theta =20\), and b against \(\mu \) for different values of \(\theta \) at \(\alpha =0.5\) with \(\beta =3\)

Full size image

These are physical for the DA waves to exist in this magnetized plasma system due to the reasons of both the restoring force that comes from the inertialess electrons pressure, while the inertia is provided by the dust mass. This leads to an increase in the phase velocity as shown in Fig. 1, which in situ leads to affect both the nonlinear and dispersive terms as presented in Figs. 2 and 3, respectively.

To find the solution of KdVB Eq. (9), we use the variable \(\chi =\eta -UT\), where \(\chi \) is the transformed coordinate relative to a reference frame moving with the shock speed U. Integrating Eq. (9) with respect to \(\chi \) leads to

$$\begin{aligned} \frac{\hbox {d}^{2}\phi ^{(1)}}{\hbox {d}\chi ^{2}}+\frac{C}{B}\frac{\hbox {d}\phi ^{(1)}}{\hbox {d}\chi } +\frac{A}{2B}\left( \phi ^{(1)}\right) ^{2}-\frac{U}{B}\phi ^{(1)}=0. \end{aligned}$$
(11)

We use the tanh method to determine the analytical solution of this equation. According to this method, the solution of the KdVB equation takes the form [48]

$$\begin{aligned} \phi ^{(1)}=\frac{U}{A}+\frac{12B}{A}{\text {sech}}^{2}\left( \chi \right) +\frac{12C}{5A}\tanh \left( \chi \right) . \end{aligned}$$
(12)

Moreover, the associated electric field (\(E=-\nabla \phi ^{(1)}\)) [49]with the solution (12) is given by

$$\begin{aligned} E^{(1)}=-\frac{24B}{A}\tanh \left( \chi \right) {\text {sech}}^{2}\left( \chi \right) +\frac{12C}{5A}{\text {sech}}^{2}\left( \chi \right) . \end{aligned}$$
(13)

Figures 4 and 5 present the potential and the associated electric field against \(\chi \), respectively, for different system parameters. The potential includes solitary potential due to the \({\text {sech}}^{2}\left( \chi \right) \) term and shock potential due to the \(\tanh \left( \chi \right) \) term. The shock term is dominant in the presence of viscosity effect and large obliquity angle as shown in Fig. 4a, while the solitary term is dominant as \(\theta \) decreases. Also, as \(\alpha \) increases the potential changes from rarefactive solitary to compressive shock, and finally, it becomes compressive solitary with double layer part as shown in Fig. 4b. Figure 5a, b depicts the associated electric field of the potentials corresponding to Fig. 4a, b, respectively. The electric field spreads as \(\theta \) and \(\alpha \) increase.

Fig. 4
figure 4

The evolution of \(\phi ^{(1)}\) of DA waves represented by Eq. (12) with \(\chi \) at \(\beta =4,\mu =0.6,\eta _{1}=0.5,\eta _{2}=0,\theta =10\), and \(\omega _{c1,2}=0.5\) for different values of a \(\theta \) with \(\alpha =0.3\) and b \(\alpha \) with \(\theta \) \(=20\)

Full size image
Fig. 5
figure 5

The evolution of the associated electric field, \(E^{(1)}\) of DA waves represented by Eq. (13) with \(\chi \) for the potentials those represented by Fig. 5

Full size image

The results obtained from Figs. 4 and 5 are physical because the obliquity angle increase results in the decrease in the nonlinearity with the increase in dispersion which leads to decreasing the soliton amplitude. Small values of protons reside in the positive dust, while larger values of electrons reside in the negative dust; the phase velocity decreases and the rarefactive soliton amplitude increases while the situation is reversed for larger values of protons since the dispersion decreases and the compressive soliton amplitude increases. The associated electric field is affected by the angle, electrons, and protons in the same manner.

These results coincide with those obtained in Refs. [24, 30] where \(\alpha \ \)and \(\beta \) have the same effect on the shock wave phase speed, and in the same manner larger \(\beta \) changes the nonlinear term to be negative as is obtained in Fig. 2. Similarly, \(\alpha \) affects the nonlinear term in the same way and consequently affects the perturbed potential. Also, the results obtained by Sumi et al. [32] represent the same behavior of the same parameter on phase velocity and the perturbed potential in the case of studying DA shock waves in a dusty self-gravitating opposite polarity plasma in the presence of trapped ions.

On the other side, in the absence of dissipative term (C), Eq. (12) is reduced to the following KdV equation:

$$\begin{aligned} \frac{\partial \phi ^{(1)}}{\partial T}+A\phi ^{(1)}\frac{\partial \phi ^{(1)} }{\partial \eta }+B\frac{\partial ^{3}\phi ^{(1)}}{\partial \eta ^{3}}=0, \end{aligned}$$
(14)

The solitary wave solution of the KdV Eq. (14) is given by employing the transformation \(\chi =\left( \eta -UT\right) \) to be represented as [50,51,52]

$$\begin{aligned} \phi ^{(1)}=\phi _{m}sech^{2}\left( \frac{\chi }{\Delta }\right) , \end{aligned}$$
(15)

where the amplitude \(\phi _{m}=\frac{3U}{A}\) and width \(\Delta =\sqrt{\frac{4B}{U}}\). Moreover, the associated electric field of Eq. (15) is given by

$$\begin{aligned} E^{(1)}=\frac{2\phi _{m}}{\Delta }\tanh \left( \frac{\chi }{\Delta }\right) \sec h^{2}\left( \frac{\chi }{\Delta }\right) . \end{aligned}$$
(16)

4 Derivation and solution of the mKdV equation

The nonlinear coefficient of KdV Eq. (14) vanishes at certain sets of critical values, which is approximately equal to zero. This indicates that the KdV equation (14) fails to describe the nonlinear evolution of the perturbation. So, a higher order is needed to describe the system dynamics at the critical value of a certain parameter; we obtain the mKdV equation after neglecting the dissipation in Eqs. (1) by employing the following stretching [51]:

$$\begin{aligned} \left| \begin{array} [c]{c} \eta =\epsilon ^{\frac{1}{2}}(L_{x}x+L_{y}y+L_{z}z-V_{p}t),\\ T=\epsilon ^{\frac{3}{2}}t. \end{array} \right\} \end{aligned}$$
(17)

We then expand the variables \(n_{1,2}\), \(u_{1,2x,1,2y,1,2z},\) \(\psi \), and \(\phi \) in power series of \(\epsilon \) as

$$\begin{aligned} \left| \begin{array} [c]{c} n_{1,2}=1+\epsilon ^{\frac{1}{2}}n_{1,2}^{(1)}+\epsilon n_{1,2}^{(2)} +\epsilon ^{\frac{3}{2}}n_{1,2}^{(3)}+.....,\\ u_{1,2x}=\epsilon u_{1,2x}^{(1)}+\epsilon ^{\frac{3}{2}}u_{1,2x}^{(2)} +\epsilon ^{2}u_{1,2x}^{(3)}+.....,\\ u_{1,2y}=\epsilon u_{1,2y}^{(1)}+\epsilon ^{\frac{3}{2}}u_{1,2y}^{(2)} +\epsilon ^{2}u_{1,2y}^{(3)}+.....,\\ u_{1,2z}=\epsilon ^{\frac{1}{2}}u_{1,2z}^{(1)}+\epsilon u_{1,2z}^{(2)} +\epsilon ^{\frac{3}{2}}u_{1,2z}^{(3)}+.....,\\ \phi =\epsilon ^{\frac{1}{2}}\phi ^{(1)}+\epsilon \phi ^{(2)}+\epsilon ^{\frac{3}{2}}\phi ^{(3)}+.....,\\ \psi =\epsilon ^{\frac{1}{2}}\psi ^{(1)}+\epsilon \psi ^{(2)}+\epsilon ^{\frac{3}{2}}\psi ^{(3)}+.....{{.}} \end{array} \right\} \end{aligned}$$
(18)

By using Eqs. (17,18) in Eq. (1), the values of \(n_{1}^{(1)},n_{2} ^{(1)},u_{1,2x}^{(1)},u_{1,2y}^{(1)},u_{1,2z}^{(1)},\psi ^{(1)}\), and \(V_{p}\) are the same as those derived before in Eqs. (4,5,6). To the next higher order of \(\epsilon \), and by using the values of Eqs. (4,5,6), a set of equations are obtained and can be simplified as

$$\begin{aligned} \left| \begin{array} [c]{c} \frac{\partial n_{1}^{(2)}}{\partial \eta }=\frac{3L_{z}^{4}}{V_{p}^{4}}\left( \frac{\alpha }{\beta }\phi ^{(1)}+\psi ^{(1)}\right) \left( \frac{\alpha }{\beta }\frac{\partial \phi ^{(1)}}{\partial \eta }+\frac{\partial \psi ^{(1)}}{\partial \eta }\right) +\frac{L_{z}^{2}}{V_{p}^{2}}\left( \frac{\partial \psi ^{(2)}}{\partial \eta }+\frac{\alpha }{\beta }\frac{\partial \phi ^{(2)} }{\partial \eta }\right) ,\\ \frac{\partial n_{2}^{(2)}}{\partial \eta }=\frac{3L_{z}^{4}}{V_{p}^{4}}\left( \psi ^{(1)}-\phi ^{(1)}\right) \left( \frac{\partial \psi ^{(1)}}{\partial \eta }-\frac{\partial \phi ^{(1)}}{\partial \eta }\right) +\frac{L_{z}^{2}}{V_{p}^{2} }\left( \frac{\partial \psi ^{(2)}}{\partial \eta }-\frac{\partial \phi ^{(2)} }{\partial \eta }\right) ,\\ u_{1z}^{(2)}=\frac{L_{z}^{3}}{2V_{p}^{3}}\left( \frac{\alpha }{\beta } \phi ^{(1)}+\psi ^{(1)}\right) ^{2}+\frac{L_{z}}{V_{p}}\left( \frac{\alpha }{\beta }\phi ^{(2)}+\psi ^{(2)}\right) ,\\ u_{2z}^{(2)}=\frac{L_{z}^{3}}{2V_{p}^{3}}\left( \psi ^{(1)}-\phi ^{(1)}\right) ^{2}+\frac{L_{z}}{V_{p}}\left( \psi ^{(2)}-\phi ^{(2)}\right) ,\\ \psi ^{(2)}=\frac{\left( 1-\alpha \mu \right) }{\left( \beta \mu +1\right) }\left( \phi ^{(2)}-\frac{3}{2}\left( \phi ^{(1)}\right) ^{2}\right) ,\\ \phi ^{(2)}=-\frac{A}{2}\left( \phi ^{(1)}\right) ^{2}=0. \end{array} \right\} \end{aligned}$$
(19)

Also, we obtain the velocities for the higher-order coefficients of \(\epsilon \) along x- and y-directions to be represented as

$$\begin{aligned} \left| \begin{array} [c]{c} u_{1x}^{(2)}=\frac{\beta ^{2}V_{p}L_{x}}{\alpha ^{2}\omega _{c1}^{2}}\left( \frac{\alpha }{\beta }\frac{\partial ^{2}\phi ^{(1)}}{\partial \eta ^{2}} +\frac{\partial ^{2}\psi ^{(1)}}{\partial \eta ^{2}}\right) +\frac{L_{y}\beta }{\alpha \omega _{c1}}\left( \frac{\alpha }{\beta }\frac{\partial \phi ^{(2)} }{\partial \eta }+\frac{\partial \psi ^{(2)}}{\partial \eta }\right) ,\\ u_{2x}^{(2)}=\frac{-1}{\omega _{c2}}\left( -V_{p}\frac{L_{x}}{\omega _{c2} }\left( \frac{\partial ^{2}\psi ^{(1)}}{\partial \eta ^{2}}-\frac{\partial ^{2}\phi ^{(1)}}{\partial \eta ^{2}}\right) +L_{y}\left( \frac{\partial \psi ^{(2)}}{\partial \eta }-\frac{\partial \phi ^{(2)}}{\partial \eta }\right) \right) ,\\ u_{1y}^{(2)}=-\frac{\beta }{\alpha \omega _{c1}}\left( -\frac{V_{p}\beta L_{y} }{\alpha \omega _{c1}}\left( \frac{\alpha }{\beta }\frac{\partial ^{2}\phi ^{(1)} }{\partial \eta ^{2}}+\frac{\partial ^{2}\psi ^{(1)}}{\partial \eta ^{2}}\right) +L_{x}\left( \frac{\partial \psi ^{(2)}}{\partial \eta }+\frac{\alpha }{\beta }\frac{\partial \phi ^{(2)}}{\partial \eta }\right) \right) ,\\ u_{2y}^{(2)}=-\frac{V_{p}L_{y}}{\omega _{c2}^{2}}\left( \frac{\partial ^{2} \phi ^{(1)}}{\partial \eta ^{2}}-\frac{\partial ^{2}\psi ^{(1)}}{\partial \eta ^{2} }\right) -\frac{L_{x}}{\omega _{ci}}\left( \frac{\partial \phi ^{(2)}}{\partial \eta }-\frac{\partial \psi ^{(2)}}{\partial \eta }\right) . \end{array} \right\} \end{aligned}$$
(20)

To the next higher order of \(\epsilon \), we obtain a set of equations after simplification we get the third-order perturbed quantities in the form

$$\begin{aligned} \left| \begin{array} [c]{c} \frac{\partial n_{1}^{(3)}}{\partial \eta }=\left( \begin{array} [c]{c} \frac{2L_{z}^{2}}{V_{p}^{3}}\left( \frac{\alpha }{\beta }\frac{\partial \phi ^{(1)}}{\partial T}+\frac{\partial \psi ^{(1)}}{\partial T}\right) +\frac{\left( L_{y}^{2}+L_{x}^{2}\right) \beta ^{2}}{\alpha ^{2}\omega _{c1}^{2}}\left( \frac{\alpha }{\beta }\frac{\partial ^{3}\phi ^{(1)}}{\partial \eta ^{3}}+\frac{\partial ^{3}\psi ^{(1)}}{\partial \eta ^{3}}\right) \\ +\frac{15L_{z}^{6}}{2V_{p}^{6}}\left( \frac{\alpha }{\beta }\phi ^{(1)} +\psi ^{(1)}\right) ^{2}\left( \frac{\alpha }{\beta }\frac{\partial \phi ^{(1)} }{\partial \eta }+\frac{\partial \psi ^{(1)}}{\partial \eta }\right) +\frac{3L_{z}^{4}}{V_{p}^{4}}\left( \frac{\alpha }{\beta }\phi ^{(1)}+\psi ^{(1)}\right) \left( \frac{\partial \psi ^{(2)}}{\partial \eta }+\frac{\alpha }{\beta }\frac{\partial \phi ^{(2)}}{\partial \eta }\right) \\ +\frac{3L_{z}^{4}}{V_{p}^{4}}\left( \frac{\alpha }{\beta }\frac{\partial \phi ^{(1)}}{\partial \eta }+\frac{\partial \psi ^{(1)}}{\partial \eta }\right) \left( \psi ^{(2)}+\frac{\alpha }{\beta }\phi ^{(2)}\right) +\frac{L_{z}^{2} }{V_{p}^{2}}\left( \frac{\partial \psi ^{(3)}}{\partial \eta }+\frac{\alpha }{\beta }\frac{\partial \phi ^{(3)}}{\partial \eta }\right) \end{array} \right) ,\\ \frac{\partial n_{2}^{(3)}}{\partial \eta }=\left( \begin{array} [c]{c} \frac{2L_{z}^{2}}{V_{p}^{3}}\left( \frac{\partial \psi ^{(1)}}{\partial T}-\frac{\partial \phi ^{(1)}}{\partial T}\right) +\frac{\left( L_{x} ^{2}+L_{y}^{2}\right) }{\omega _{c2}^{2}}\left( \frac{\partial ^{3}\psi ^{(1)} }{\partial \eta ^{3}}-\frac{\partial ^{3}\phi ^{(1)}}{\partial \eta ^{3}}\right) \\ +\frac{15L_{z}^{6}}{2V_{p}^{6}}\left( \psi ^{(1)}-\phi ^{(1)}\right) ^{2}\left( \frac{\partial \psi ^{(1)}}{\partial \eta }-\frac{\partial \phi ^{(1)} }{\partial \eta }\right) +\frac{3L_{z}^{4}}{V_{p}^{4}}\left( \psi ^{(1)} -\phi ^{(1)}\right) \left( \frac{\partial }{\partial \eta }\psi ^{(2)} -\frac{\partial }{\partial \eta }\phi ^{(2)}\right) \\ +\frac{3L_{z}^{4}}{V_{p}^{4}}\left( \psi ^{(2)}-\phi ^{(2)}\right) \left( \frac{\partial \psi ^{(1)}}{\partial \eta }-\frac{\partial \phi ^{(1)}}{\partial \eta }\right) +\frac{L_{z}^{2}}{V_{p}^{2}}\left( \frac{\partial \psi ^{(3)} }{\partial \eta }-\frac{\partial \phi ^{(3)}}{\partial \eta }\right) \end{array} \right) ,\\ \frac{\partial u_{1z}^{(3)}}{\partial \eta }=\left( \begin{array} [c]{c} \frac{1}{V_{p}}\frac{\partial u_{1z}^{(1)}}{\partial T}+u_{1x}^{(1)} \frac{L_{x}}{V_{p}}\frac{\partial u_{1z}^{(1)}}{\partial \eta }+u_{1y} ^{(1)}\frac{L_{y}}{V_{p}}\frac{\partial u_{1z}^{(1)}}{\partial \eta }\\ +u_{1z}^{(1)}\frac{L_{z}}{V_{p}}\frac{\partial u_{1z}^{(2)}}{\partial \eta }+u_{1z}^{(2)}\frac{L_{z}}{V_{p}}\frac{\partial u_{1z}^{(1)}}{\partial \eta }+\frac{\alpha }{\beta }\frac{L_{z}}{V_{p}}\frac{\partial \phi ^{(3)}}{\partial \eta }+\frac{L_{z}}{V_{p}}\frac{\partial \psi ^{(3)}}{\partial \eta } \end{array} \right) ,\\ \frac{\partial u_{2z}^{(3)}}{\partial \eta }=\left( \begin{array} [c]{c} \frac{1}{V_{p}}\frac{\partial u_{2z}^{(1)}}{\partial T}+u_{2x}^{(1)} \frac{L_{x}}{V_{p}}\frac{\partial u_{2z}^{(1)}}{\partial \eta }+u_{2y} ^{(1)}\frac{L_{y}}{V_{p}}\frac{\partial u_{2z}^{(1)}}{\partial \eta }\\ +u_{2z}^{(1)}\frac{L_{z}}{V_{p}}\frac{\partial u_{2z}^{(2)}}{\partial \eta }+u_{2z}^{(2)}\frac{L_{z}}{V_{p}}\frac{\partial u_{2z}^{(1)}}{\partial \eta }-\frac{L_{z}}{V_{p}}\frac{\partial \phi ^{(3)}}{\partial \eta }+\frac{L_{z} }{V_{p}}\frac{\partial \psi ^{(3)}}{\partial \eta } \end{array} \right) ,\\ \frac{\partial ^{2}\psi ^{(1)}}{\partial \eta ^{2}}=\gamma \left[ n_{2} ^{(3)}+\beta \mu n_{1}^{(3)}\right] ,\\ \frac{\partial ^{2}\phi ^{(1)}}{\partial \eta ^{2}}=n_{2}^{(3)}-\alpha \mu n_{1}^{(3)}+\frac{(1-\alpha \mu )}{6}\left( \phi ^{(1)}\right) ^{3} -(1-\alpha \mu )\phi ^{(1)}\phi ^{(2)}+(1-\alpha \mu )\phi ^{(3)}. \end{array} \right\} \end{aligned}$$
(21)

Also, we obtain the next higher-velocity components along x- and y-directions on employing the next higher-order coefficients of \(\epsilon \) as

$$\begin{aligned} \left| \begin{array} [c]{c} u_{1x}^{(3)}=\frac{\beta }{\alpha \omega _{c1}}\left( -V_{p}\frac{\partial u_{1y}^{(2)}}{\partial \eta }+u_{1z}^{(1)}L_{z}\frac{\partial u_{1y}^{(1)} }{\partial \eta }+L_{y}\frac{\alpha }{\beta }\frac{\partial \phi ^{(3)}}{\partial \eta }+L_{y}\frac{\partial \psi ^{(3)}}{\partial \eta }\right) ,\\ u_{2x}^{(3)}=\frac{-1}{\omega _{c2}}\left( -V_{p}\frac{\partial u_{2y}^{(2)} }{\partial \eta }+u_{2z}^{(1)}L_{z}\frac{\partial u_{2y}^{(1)}}{\partial \eta }-L_{y}\frac{\partial \phi ^{(3)}}{\partial \eta }+L_{y}\frac{\partial \psi ^{(3)} }{\partial \eta }\right) ,\\ u_{1y}^{(3)}=-\frac{\beta }{\alpha \omega _{c1}}\left( -V_{p}\frac{\partial u_{1x}^{(2)}}{\partial \eta }+u_{1z}^{(1)}L_{z}\frac{\partial u_{1x}^{(1)} }{\partial \eta }+L_{x}\frac{\alpha }{\beta }\frac{\partial \phi ^{(3)}}{\partial \eta }+L_{x}\frac{\partial \psi ^{(3)}}{\partial \eta }\right) ,\\ u_{2y}^{(3)}=\frac{1}{\omega _{c2}}\left( -V_{p}\frac{\partial u_{2x}^{(2)} }{\partial \eta }+u_{2z}^{(1)}L_{z}\frac{\partial u_{2x}^{(1)}}{\partial \eta }-L_{x}\frac{\partial \phi ^{(3)}}{\partial \eta }+L_{x}\frac{\partial \psi ^{(3)} }{\partial \eta }\right) . \end{array} \right\} \end{aligned}$$
(22)

Now, combining Eqs. (21)–(22) after simplifying by using Eqs. (19)–(20), we obtain the well-known mKdV equation as follows:

$$\begin{aligned} \frac{\partial \phi ^{(1)}}{\partial T}+F\left( \phi ^{(1)}\right) ^{2} \frac{\partial \phi ^{(1)}}{\partial \eta }+B\frac{\partial ^{3}\phi ^{(1)} }{\partial \eta ^{3}}=0, \end{aligned}$$
(23)

where

$$\begin{aligned} \left| \begin{array} [c]{c} F=\frac{\beta V_{p}^{3}\left( \beta \mu +1\right) }{2\mu L_{z}^{2}\left( \alpha +\beta \right) ^{2}}\left( \frac{15\mu \left( \beta ^{3}\mu ^{3}+1\right) L_{z}^{6}}{2\beta ^{3}V_{p}^{6}}\left( \frac{\alpha +\beta }{\beta \mu +1}\right) ^{4}-\frac{27L_{z}^{4}}{2V_{p}^{4}}\frac{\mu \left( \alpha +\beta \right) ^{2}\left( 1-\alpha \mu \right) }{\beta \left( \beta \mu +1\right) ^{2}}-\frac{(1-\alpha \mu )}{2}\right) ,\\ B=\frac{\beta V_{p}^{3}\left( \beta \mu +1\right) }{2\mu L_{z}^{2}\left( \alpha +\beta \right) ^{2}}\left( 1-\frac{1}{\gamma }\frac{\left( 1-\alpha \mu \right) ^{2}}{\left( \beta \mu +1\right) ^{2}}+\mu \left( L_{x}^{2} +L_{y}^{2}\right) \frac{\left( \alpha +\beta \right) ^{2}}{\left( \beta \mu +1\right) ^{2}}\left( \frac{\mu }{\omega _{c2}^{2}}+\frac{\beta }{\alpha ^{2}\omega _{c1}^{2}}\right) \right) . \end{array} \right\} \end{aligned}$$
(24)

Now, taking the same frame \(\chi =\left( \eta -UT\right) \) as that employed in the KdV solution, the stationary solution of Eq. (24) can be directly given as [51]

$$\begin{aligned} \phi ^{(1)}=\phi _{m}^{(1)}\sec h\left( \frac{\chi }{\delta }\right) \end{aligned}$$
(25)

where the amplitude \(\phi _{m}^{(1)}=\sqrt{\frac{6U}{F}}\) and the width \(\delta =\sqrt{\frac{B}{U}}\) and the electric field associated with this solution is given by

$$\begin{aligned} \left| \begin{array} [c]{c} E^{(1)}=-\nabla \phi ^{(1)},\\ E^{(1)}=\frac{\phi _{m}^{(1)}}{\delta }\tanh \left( \frac{\chi }{\delta }\right) \sec h\left( \frac{\chi }{\delta }\right) . \end{array} \right\} \end{aligned}$$
(26)

Figure 6 represents the changes of the potential (\(\phi ^{(1)}\)) and the associated electric field (\(E^{(1)}\)) against \(\chi \) for various values of \(\alpha \) (\(=Z_{1}/Z_{2}\)). It is depicted that, the solution, Eq. (25) gives only compressive waves, and the amplitude increases as \(\alpha \) increases. This is physical as demonstrated before due to the effect of the electrons on the restoring force and in situ affects the phase velocity which in turn results in the change of the mKdV nonlinear term.

Fig. 6
figure 6

The evolution of a the potential \(\phi ^{(1)}\) represented by Eq. (25) and b the associated electric field, \(E^{(1)}\), represented by Eq. (26) of the DAWs at \(\beta =0.2,\mu =0.6,\eta _{1,2}=0,\theta =20\), and \(\omega _{c1,2}=0.4\) with \(\chi \) for different values of \(\alpha \)

Full size image

5 Bifurcation analysis of the KdVB equation

From Eq. (14), the total energy equation becomes

$$\begin{aligned} H=\frac{1}{2}\left( \frac{\hbox {d}\phi ^{(1)}}{\hbox {d}\chi }\right) ^{2}+V\left( \phi ^{(1)}\right) , \end{aligned}$$
(27)

where \(V\left( \phi ^{(1)}\right) \) is the Sagdeev potential, which is given by

$$\begin{aligned} V\left( \phi ^{(1)}\right) =\frac{A}{6B}\left( \phi ^{(1)}\right) ^{3} -\frac{U}{2B}\left( \phi ^{(1)}\right) ^{2}. \end{aligned}$$
(28)

The variation of \(V\left( \phi ^{(1)}\right) \) with different values of the positive-to-negative dust charges ratio for compressive and rarefactive solitons, depending on \(\beta \) values, is plotted in Fig. 7, where the other variables (\(\mu ,\theta ,\omega _{c1},\omega _{c2},\eta _{10},\eta _{20}\)) are kept fixed. It is shown by increasing \(\alpha \) , the width of the potential well \(V\left( \phi ^{(1)}\right) \) is enhanced for the rarefactive soliton and shrinks for the compressive soliton. This demonstrates that the amplitude of the DA compressive solitary wave decreases by increasing \(\alpha \) as shown in Fig. 7a. It is also seen that the depth of the potential well decreases with increasing values of \(\alpha \). In fact, steeper solitary waves are completely associated with a deeper potential well. The opposite effects appear in the case of rarefactive solitons associated with Fig. 7b. This effect takes place since the nonlinear term behaves in opposite way as it becomes negative (in case of rarefactive solitons) against the increase in \(\alpha \).

Fig. 7
figure 7

The evolution of \(V\left( \phi ^{(1)}\right) \)of DA waves represented by Eq. (28) with \(\phi ^{(1)}\) at \(\mu =0.6,\eta _{1,2}=0,\theta =0,\)and \(\omega _{c1,2}=0.5\) for different values of \(\alpha \) a) at \(\beta =2\) and b) \(\beta =4\)

Full size image

The phase portraits associated with the system of Eq. (11) can be obtained by employing the following transformations:

$$\begin{aligned} \left| \begin{array} [c]{c} \frac{\hbox {d}\phi ^{(1)}}{\hbox {d}\chi }=z,\\ \frac{\hbox {d}}{\hbox {d}\chi }z=\frac{U}{B}\phi ^{(1)}-\frac{A}{2B}\left( \phi ^{(1)}\right) ^{2}-\frac{C}{B}z. \end{array} \right\} \end{aligned}$$
(29)

There are two critical points \(E_{1}(0,0)\) and \(E_{2}(\frac{2U}{A},0)\) for this phase plane. For a chosen set of physical parameters, viz. \(\alpha =0.2\), \(\mu =0.6,\theta =0,U=0.1,\gamma =0.3,\) and \(\omega _{c1}=\omega _{c2}=0.5\), the coefficient matrix of the linearized system (Jacobian matrix) at the critical point, \(E_{1} (0,0)\), satisfies \(J_{E_{1}(0,0)}=-U/B<0\) which gives a saddle node. The coefficient matrix at at the critical point, \(E_{2}(\frac{2U}{A} ,0)\), satisfies \(J_{E_{2}(\frac{2U}{A},0)}=U/B>0\), so it represents a center point.

There are two qualitatively different phase trajectories, namely nonlinear homoclinic trajectory (NHT) and nonlinear periodic (NPT) trajectory when we take \(\eta _{10}=\eta _{20}=0\). These phase trajectories NHT and NPT represent solitary and periodic wave solutions of Eq. (27), respectively. The parameters \(\alpha \), \(\beta \), \(\mu \), and other system parameters affect the formed solitary waves that can be rarefactive or compressive as shown in Fig. 8a, b, respectively.

Fig. 8
figure 8

The phase profile of the KdV equation (14) for a) the compressive DAWs, with \(\beta =2\), and b) the rarefactive DAWs with \(\beta =4\)

Full size image

This is physical due to the effect of \(\beta \) on the phase velocity as shown in Fig. 1 and consequently affects both the magnitude and sign of the nonlinear term. The positive region corresponds to a compressive solitary solution, and the negative region corresponds to a rarefactive solitary solution of the KdV Eq. (14). Therefore, we obtain both compressive and rarefactive DAW solutions of the KdV Eq. (14) for the plasma system.

One can note from Fig. 8 that the phase curve (NPT) is repeated on the same path and one complete cycle corresponds to a wavelength in the physical space. Physically, the pseudoparticle’s speed becomes zero (\(\hbox {d}\phi ^{(1)}/\hbox {d}\chi =0\)); it is reflected as a result of the potential force since(\(-\hbox {d}V\left( \phi ^{(1)}\right) /\hbox {d}\phi ^{(1)}\ne 0\)) and it oscillates between the two points. Therefore, the NPT in the phase plane is a periodic orbit. On the other side, the NHT curve in Fig. 8a emerges from the saddle point, circling anticlockwise around \(\phi ^{(1)}\)axis, and again stops at the saddle point, entering from the upper side. As the analogy, the pseudoparticle starts with zero speed and attains some speed along the \(\phi ^{(1)}\) axis. After maximum speed, its speed decreases and reaches zero at \(\phi ^{(1)}\)= \(\phi _\mathrm{max}^{(1)}\). Furthermore, the pseudoparticle bounces back toward the saddle point as a result of the potential force, where \(-\hbox {d}V\left( \phi ^{(1)}\right) /\hbox {d}\phi ^{(1)}\ne 0\), and gains speed in the opposite direction and returns to rest at the saddle point. In physical space, the electric potential increases from zero (at\(\chi \) = \(-\infty \)), attains a maximum value at \(\chi =0\), and then decreases until it becomes zero (at \(\chi = \infty \)). This potential structure represents the DA compressive soliton and does not repeat [23], while Fig. 8b corresponds to rarefactive DA solitons in which the nonlinear term becomes negative.

6 Nonlinear periodic wave solutions

We follow the same procedure in Refs. [50, 53] and [54] to find the cnoidal wave solution of the obtained KdV Eq. (14) for DA waves. The solution is assumed to be \(\phi ^{\left( 1\right) }\left( \chi \right) \), in which we introduce the same variable transformation \(\chi =\eta -UT\) . Accordingly, Eq. (14) can be written as

$$\begin{aligned} B\frac{\hbox {d}^{3}}{\hbox {d}\chi ^{3}}\Phi +\frac{\hbox {d}}{\hbox {d}\chi }\left( \frac{A}{2}\Phi ^{2} -U\Phi \right) =0, \end{aligned}$$
(30)

where \(\Phi =\phi ^{\left( 1\right) }\left( \chi \right) \). We get some algebraic calculations for evaluating the integration of Eq. (30), which takes the energy balance equation as

$$\begin{aligned} \frac{\hbox {d}^{2}\Phi }{\hbox {d}\chi ^{2}}=-\frac{\hbox {d}W}{\hbox {d}\Phi }, \end{aligned}$$
(31)

where the Sagdeev potential, \(W\left( \Phi \right) \), in this case can be defined as

$$\begin{aligned} W\left( \Phi \right) =\frac{A}{6B}\Phi ^{3}-\frac{U}{2B}\Phi ^{2}+\rho _{0} \Phi -\frac{1}{2}E_{0}^{2}. \end{aligned}$$
(32)

When the potential \(\Phi \) vanishes, both \(\rho _{0}\) and \(E_{0}\) are the density of charge and the electric field, respectively. The potential function \(W\left( \Phi \right) \) has two points of extreme for \(\Phi \), which are defined at \(\partial W/\partial \Phi =0\); these are\(\ \Phi _{1,2}\) and can be given as

$$\begin{aligned} \Phi _{1,2}=\frac{U}{A}\pm \sqrt{\frac{U^{2}}{A^{2}}-\frac{2}{A}\rho _{0}B_{1}}. \end{aligned}$$
(33)

Moreover, for real values, \(U^{2}/A^{2}>2\rho _{0}B/A\) must hold. The zero’s of the potential energy (32), i.e., \(\Phi =z_{1},z_{2},z_{3}\), are given by

$$\begin{aligned} z_{1}=0,z_{2,3}=\frac{3}{A}\left( \frac{U}{2}\pm \sqrt{\frac{U^{2}}{4} -\frac{2A}{3}\rho _{0}B}\right) . \end{aligned}$$
(34)

Now, \(U^{2}/4-2A\rho _{0}B/3\) > 0 must hold to get the shape of the potential well. The positive cnoidal waves are associated with the case of \(\Phi >0\), while the case of negative cnoidal waves is associated with \(\Phi \) \(<0\). Equation (31) is associated with the first integral of the energy that can be inspired by

$$\begin{aligned} \frac{1}{2}\left( \frac{\hbox {d}\Phi }{\hbox {d}\chi }\right) ^{2}+W\left( \Phi \right) =0. \end{aligned}$$
(35)

Using the initial conditions \(\Phi \left( 0\right) =\phi _{0}\) and \(\hbox {d}\Phi \left( 0\right) /\hbox {d}\chi =0\), we can find

$$\begin{aligned} E_{0}^{2}=\frac{A_{1}}{3B_{1}}\Phi _{0}^{3}-\frac{U}{B_{1}}\Phi _{0}^{2} +2\rho _{0}\Phi _{0}. \end{aligned}$$
(36)

Substituting Eqs. (32) and (36) into Eq. (35) and after the factorization process, we have

$$\begin{aligned} \left( \frac{\hbox {d}\Phi }{\hbox {d}\chi }\right) ^{2}=\frac{A}{3B}\left( \phi _{0} -\Phi \right) \left( \Phi -\phi _{1}\right) \left( \Phi -\phi _{2}\right) , \end{aligned}$$
(37)

where

$$\begin{aligned} \phi _{1,2}&=\frac{3}{2}\left[ \frac{U}{A}-\frac{\phi _{0}}{3}\pm \sqrt{\frac{1}{3}\left( \Psi _{1}-\phi _{0}\right) \left( \phi _{0}-\Psi _{2}\right) }\right] ,\\ \Psi _{1,2}&=\frac{U}{A}\pm 2\sqrt{\frac{U^{2}}{A^{2}}-2\rho _{0}\frac{B}{A} }. \end{aligned}$$

Further, the following inequalities \(\Psi _{2}\le \phi _{0}\le \Psi _{1}\) or \(\Psi _{1}\le \phi _{0}\le \Psi _{2}\) in the last relations should also be kept. Moreover, we can get from Eqs. (35) and (37) the following relation:

$$\begin{aligned} U=\frac{A}{3}\left( \phi _{0}+\phi _{1}+\phi _{2}\right) . \end{aligned}$$
(38)

The periodic wave solution of Eq. (35) is given by [50, 55]

$$\begin{aligned} \Phi \left( \chi \right) =\phi _{1}+\psi _{cn}cn^{2}\left( D\chi ,m\right) , \end{aligned}$$
(39)

where cn is the Jacobian elliptic function and the amplitude \(\psi _{cn}=\left( \phi _{0}-\phi _{1}\right) \) and the modulus m (\(0<m<1\)) and D are defined as

$$\begin{aligned} m&=\left( \frac{\phi _{0}-\phi _{1}}{\phi _{0}-\phi _{2}}\right) ^{1/2}, \end{aligned}$$
(40)
$$\begin{aligned} \text {and }D&=\sqrt{\frac{A}{12B}\left( \phi _{0}-\phi _{2}\right) .} \end{aligned}$$
(41)

Physically, the parameter m is the nonlinearity indicator, with the linear limit being \(m\rightarrow 0\) and the extreme nonlinear limit being \(m\rightarrow 1\). The cnoidal solution of Eq. (39) requires the conditions \(\phi _{1}\le \Phi \le \phi _{0}\) and \(\phi _{0}>\) \(\phi _{1}\ge \) \(\phi _{2}\). Furthermore, the cnoidal wave frequency \(\nu \) and the cnoidal wave wavelength \(\lambda \) are defined as

$$\begin{aligned} \nu&=V/\lambda , \end{aligned}$$
(42)
$$\begin{aligned} \lambda&=4\sqrt{\frac{3B}{A\left( \phi _{0}-\phi _{2}\right) }}K\left( m\right) , \end{aligned}$$
(43)

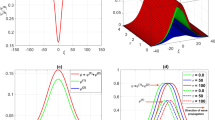
where K(m) is is the first kind of complete elliptic integrals. Figure 9 shows the influence of parameters \(\alpha \), \(\beta \), \(\mu \), and \(\theta \) on basic characteristics of periodic wave solution corresponding to NPT enduring critical point \(C_{0}\). The amplitude of DA periodic waves grows with the increase in \(\alpha \) and \(\mu \) but depletes as \(\theta \) enhances. The periodic wave widths increase also as \(\alpha ,\mu \), and \(\theta \) increase.

Fig. 9
figure 9

The variation of the nonlinear periodic solution of DAWs, Eq. (39), against \(\chi \) with \(\gamma =0.3\) and \(\beta =6\) for different values of a \(\alpha \) at \(\mu =0.5\) and \(\theta =0\), b \(\mu \) at \(\alpha =0.5\) and \(\theta =0\), c) \(\theta \) at \(\alpha =0.5\) and \(\mu =0.5\)

Full size image

This means physically that for lower values of depleted electrons from the positive dust (decrease in \(\alpha \)) or lower values of positive dust density (decrease in \(\mu \)); the restoring force of nonlinear periodic traveling wave decreases which is provided by the electrons pressure. The variation of the profile of the periodic traveling waves with \(\theta \) is examined. It is obvious that the amplitude decreases and the width increases as \(\theta \) increases. Physically, one can predict that as the nonlinear periodic traveling wave approaches the direction perpendicular to the magnetic field, the nonlinear periodic traveling wave disappears where the increase in \(\theta \) causes the increase in the dispersion term coefficient in the nonlinear KdV equation and the periodic traveling wave becomes fatter. Also, the obtained periodic waves are affected by the obliqueness and species densities similarly as presented by Selim et al. [56]. It is noticed that the used plasma system is entirely contained by the magnetic force, an arrangement referred to as magnetic confinement (i.e., the magnetic field makes the nonlinear periodic traveling wave structures in the field direction spikier as demonstrated in Ref. [57].

Now, the soliton solution case [58] can be achieved at \(\phi _{1}=\phi _{2}=0\), in which \(m\rightarrow 1\) and \(\rho _{0}=E_{0}=0\). In this case, \(\psi _{cn}=\phi _{0}=3u_{1}/A=\psi _{m}\), \(D=\sqrt{A\phi _{0} /12B}=\sqrt{u_{1}/4B}=1/\Delta \), Jacobi elliptic function, cn, degenerates to the sech function [59, 60], and then the cnoidal solution, Eq. (24), is reduced to the DA solitary wave solution, Eq. (15).

7 Discussion and conclusions

The reductive perturbation method has been employed to scrutinize small-amplitude DA waves in self-gravitating strongly coupled opposite polarity dust plasma system consisting of strongly coupled inertial positive and negative dust species and inertialess weakly coupled Maxwellian distributed ions, while the electrons are completely depleted to the surface of dust species to make them negatively charged. The KdVB equation has been derived, and its analytical solution is determined using a tanh method. The associated electric field has been also derived and illustrated. In this paper, phase plane analysis of the planar dynamical systems is applied to deal with the KdVB equation. The KdVB equation is reduced to a dynamical system with perturbation on a two-dimensional invariant manifold so that some relations and dynamical system bifurcation methods can be applied to investigate its phase space geometry in detail, which can be used to determine the wave speed for various traveling waves such as periodic and solitary waves in the system. These results will promote the study of numerical solutions and help to seek new analytic solutions of the KdV equation. We point out that the KdV equation may have other oscillatory traveling waves. When a closed trajectory (or a homoclinic trajectory) comes from the Poincaré bifurcation (or a homoclinic bifurcation), the region enclosed by the homoclinic trajectory is compact. It implies that all trajectories and the corresponding traveling waves are bounded. Since these solutions depend on the system parameters, spiral orbits are found to approach the equilibrium within the compact region and its boundary (the periodic orbit), which exactly correspond to oscillatory traveling waves.

Our study may apply to understanding the finite-amplitude localized electrostatic disturbances and nonlinear periodic wave features in different astrophysical environments such as the Earth’s mesosphere, cometary tails, and Jupiter’s magnetosphere [11, 61, 62] where the self-gravitational field effect is presented.