Quantum spin-flavour memory of ultrahigh-energy neutrino

Abstract

There are two types of uncertainties related to the measurements done on a quantum system: statistical and those related to non-commuting observables and incompatible measurements. The latter indicates the quantum system’s inherent nature and is in the scope of the present study. We explore uncertainties related to the interstellar ultrahigh-energy neutrino and introduce a novel concept: quantum spin-flavour memory. Advanced uncertainty measures are entropic measures, and the effect of the quantum memory reduces the uncertainty. The problem in question corresponds to a real physical event: high-energy Dirac neutrinos emitted by some distant source and propagating towards the earth. The neutrino has a finite magnetic moment and interacts with both deterministic and stochastic interstellar magnetic fields. To describe the effect of a noisy environment, we exploit the Lindblad master equation for the neutrino density matrix. Quantum spin-flavour memory is quantified in terms of the generalized Kraus’s trade-off relation. This trade-off relation converts to the equality when quantum memory is absent. We discovered that while most measures of quantum correlations show their irrelevance, the quantum spin-flavour discord is the quantifier of the quantum spin-flavour memory.

1 Introduction

In non-relativistic quantum theory, Heisenberg’s uncertainty principle asserts a limit to the precision of measuring momentum and coordinate of a particle. In a broader sense, Heisenberg’s uncertainty principle concerns any two incompatible measurements of the expectation values of non-commuting operators. We point out the recent interest to the relativistic uncertainty principle (see [1, 2], and references therein). The progress in quantum metrology is related to the entropic uncertainty relation and entropic measures. As distinct from the standard deviations, entropic uncertainty relations are independent of the system’s states to be measured and therefore support the more general formulation of the problem. The critical issue for the quantum measurement and entropic measures are quantum correlations and entanglement. The latter has a certain interplay with thermodynamics. For example, entanglement can be exploited as a resource for producing quantum work [3]. Due to the quantum correlations, measurements performed through the classical device on the quantum systems lead to the entropy production, and the key issue is the spectral property of the system [4, 5]. One can recall other additional facts. Our interest in the present work is about the uncertainty principle in the presence of quantum memory [6,7,8,9,10,11,12,13,14,15,16,17]. As a physical system under study, we consider the ultrahigh-energy neutrino in an interstellar magnetic field [18]. The reason is that neutrinos obey dichotomic left–right helicity and trichotomic lepton flavour (electron, muon, and tau), and when propagating, they can change their type or oscillate. In contrast to the stellar environments, in interstellar space, the matter density is very low and neutrinos can be mainly affected by the neutrino magnetic moment interaction with an interstellar magnetic field. As a result, neutrino spin-flavour oscillations can arise in this case, namely the neutrino can change both its flavour and helicity (see Ref. [18] and references therein). Below, we formulate a concept of quantum spin-flavour memory for investigating this phenomenon.

We consider a model that can mimic a real physical situation when a flux of ultrarelativistic flavour neutrinos emitted deep inside a compact massive astrophysical object (i.e. a core-collapse supernova or a protoneutron object developed from a neutron star merger) propagates to an observer in the Earth. Suppose that along their path from the source to the Earth neutrinos that propagate through highly rarefied space with a stochastic magnetic field, also encounter a dense magnetized and rotating astrophysical object (that can be a pulsar, for instance). The influence of the described above external environments on neutrinos can be considered as a chain of causes of neutrinos’ states change. Two of these state disturbances can be considered as two independent measurements. In particular, in the initial phase of the neutrino propagation deep inside the dense astrophysical object the neutrino undergoes interaction with dense matter. As a result, the left-handed neutrinos can be deflected that creates spin asymmetry in the emitted neutrino flux. This can serve as a “cosmic neutrino filter” inside the astrophysical sources (see [19] for detailed discussions). Predominantly, only nearly sterile right-handed neutrinos survive. This process can be considered as an effective measurement of neutrino spin done with the spin-one-half operator $\sigma _z$. The second “measurement” is provided by the neutrino interaction due to its magnetic moment with the external magnetic field of the second compact astrophysical object and/or by weak interaction of neutrinos with the transversal matter currents which influence neutrinos in the case of possible misalignment of the direction of neutrinos propagation and the rotation axes of the astrophysical object. Both these interactions can initiate the neutrino spin oscillations that can be also (see [20] and [21]) increased to the maximum by the corresponding resonances. These resonant neutrino spin conversions can be considered as another effective measurement of neutrino spin done with the spin-one-half operator that should not be the same as in the case of the first measurement. Thus, in general case this second measurement is done by the spin operator $\sigma _x$.

While “measurements” done on the neutrino and filtering out a particular type of neutrinos occur due to the interaction of neutrino flux with the specific cosmic objects, we exploit projector operators to formulate a problem mathematically. A positive operator-valued measure (POVM) is a set of finite number positive semi-definite operators acting in the Hilbert space. Projecting neutrino states on the particular states mimics the filtering procedure described above. In its most straightforward form, the procedure can be illustrated for qubits. Let $\vert \varphi \rangle =a\vert 0\rangle +b\vert 1\rangle$ be the state of a single qubit. The action of the projector $\hat{\Pi }=\vert n\rangle \langle n\vert$, (in what follows due to the physical interest $\vert n\rangle$ are eigenstates either of z or x components of the neutrino spin), retains only desired filtered post-measurement state $\vert \psi \rangle =\left[ \sqrt{\langle \varphi \vert \hat{\Pi }\vert \varphi \rangle }\right] ^{-1/2}\hat{\Pi }\vert \varphi \rangle$. In the same sense, POVMs can be applied to the neutrino states to describe filtering out a particular type of neutrinos. The elimination of a particular type of neutrinos occurs due to the interaction with specified cosmic objects.

Let $H(\sigma ^z)=-\sum \limits \sigma ^z_i\log _2 \sigma ^z_i$ and $H(\sigma ^x)=-\sum \limits \sigma ^x_i\log _2 \sigma ^x_i$ be Shannon’s entropies for the outcomes of two incompatible measurements done on the quantum spin-1/2 observables $\hat{\sigma }^z$ and $\hat{\sigma }^x$. Here, $\sigma ^z_i=\vert \langle \sigma ^z_i\vert \Psi \rangle \vert ^2$ and $\sigma ^x_i=\vert \langle \sigma ^x_i\vert \Psi \rangle \vert ^2$ are the probability distributions of the measurement outcomes (see the seminal work of David Deutsch [22]), where the state of the system is given by $\vert \Psi \rangle$ and $\vert \sigma _i^z\rangle$, $\vert \sigma _i^x\rangle$ are the eigenstates of the observables. The Kraus’s trade-off relation proved by Maassen and Uffink reads [23, 24]:

$$\begin{aligned} H(\sigma ^z)+H(\sigma ^x)\geqslant -2\log _2c(\sigma ^z,\sigma ^x), \end{aligned}$$

(1)

where $c(\sigma ^z,\sigma ^x)\equiv \max _{ij} \vert \langle \sigma ^z_i \vert \sigma ^x_j\rangle \vert$, and $\vert \sigma ^z_i\rangle , \vert \sigma ^x_j\rangle$ are the eigenvectors of $\hat{\sigma }^z$ and $\hat{\sigma }^x$, respectively. We focus on the bipartite system $\hat{\rho }_{\sigma \nu }$. In what follows, $\nu$ defines the neutrino flavour subspace in the approximation of two neutrino generations ($\nu =\nu _e,\nu _\mu$) and $\sigma$ defines the spin subspace. In the work [9], the theorem was proved that quantifies the correction to the Kraus’s trade-off relation [23, 24]. We adopt this theorem to the ultrahigh-energy neutrino problem:

$$\begin{aligned} S(R\vert \nu )+S(Q\vert \nu )\geqslant -2\log _2 c(R, Q)+S(\sigma \vert \nu )+ \max \left\{ 0, D_{\sigma }(\hat{\rho }_{\sigma \nu })-J_{\sigma }(\hat{\rho }_{\sigma \nu })\right\} . \end{aligned}$$

(2)

Here, $S(R\vert \nu )$ and $S(Q\vert \nu )$ are the conditional von Neumann entropies of the post-measurement states

$$\begin{aligned} S(R\vert \nu )=S(\hat{\rho }_{R\nu })-S(\hat{\rho }_{\nu }),\qquad S(Q\vert \nu )=S(\hat{\rho }_{Q\nu })-S(\hat{\rho }_{\nu }), \end{aligned}$$

(3)

i.e. $S(\hat{\rho }_{R\nu })=-\hat{\rho }_{R\nu }\ln (\hat{\rho }_{R\nu })$, where $\hat{\rho }_{R\nu }$ is the post-measurement density matrix, and two measurements are done on the components of spin $R\equiv \sigma _z$, meaning that POVMs are constructed from eigenvectors $\vert \sigma ^z_j\rangle \equiv \vert r\rangle$:

$$\begin{aligned} \hat{\rho }_{R\nu }=\sum \limits _r\vert r \rangle \langle r \vert _R\otimes Tr_\sigma \left\{ (\varGamma (r)\otimes I_{\nu })\hat{\rho }_{\sigma \nu }\right\} . \end{aligned}$$

(4)

The same is valid for $\hat{\rho }_{Q\nu }$. Post-measurement density matrix $\hat{\rho }_{Q\nu }$ is obtained after measuring x component of the neutrino spin and can be constructed similarly to Eq. (4) by considering $Q\equiv \sigma _x$. The classical correlation term in Eq. (2) is defined as follows:

$$\begin{aligned} J_{\sigma }(\hat{\rho }_{\sigma \nu })=\max _{\varGamma (x)}I(X,\nu ), \end{aligned}$$

(5)

where the mutual information

$$\begin{aligned} I(X,\nu )=S(X)+S(\nu )-S(X\nu ) \end{aligned}$$

(6)

is calculated for the post-measurement state

$$\begin{aligned} \hat{\rho }_{X\nu }=\sum \limits _x\vert x \rangle \langle x \vert _X\otimes Tr_\sigma \left\{ (\varGamma (x)\otimes I_{\nu })\hat{\rho }_{\sigma \nu }\right\} . \end{aligned}$$

(7)

Here, $\varGamma (x)$ is the set of all positive operator-valued measures (POVMs) acting on the spin subspace. Throughout the whole work all the measurements mentioned in the text concern the spin subspace. The last term in Eq. (2) quantifies the quantum discord:

$$\begin{aligned}&D_{\sigma }(\hat{\rho }_{\sigma \nu })=I(\sigma ,\nu )-J_{\sigma }(\hat{\rho }_{\sigma \nu }). \end{aligned}$$

(8)

We note that the right-hand side of Eq. (2) quantifies the lower bound of the uncertainty and contains three terms. The first term quantifies the incompatibility of POVMs acting on the neutrino’s spin. The second term $S(\sigma \vert \nu )$ is the conditional entropy. The third term $\max \left\{ 0, D_{\sigma }(\hat{\rho }_{\sigma \nu })-J_{\sigma }(\hat{\rho }_{\sigma \nu })\right\}$ is related to the quantum discord. The sum of all these three terms on the right-hand side of Eq. (2) defines the lower bound of the uncertainty. We are interested in exploring the case when inequality holds and the lower bound of uncertainty is reduced.

The spin of the neutrino possessed by Alice (the cosmic $\sigma _z$ and $\sigma _x$ measurements) and the flavour that belongs to Bob (the observer at the Earth) are not entirely independent quantum numbers. Bob inherits spin-flavour quantum memory that reduces uncertainties of Alice’s two measurements done on the spin subsystem. We consider the case when after the first measurement, the system undergoes dissipative evolution through the Lindbladian channel. We note that dissipative evolution is relevant for the neutrino evolution in the interstellar space. For details and physical circumstances, we refer to two recent works [19, 25]. Here, we would like to explore robustness of the quantum spin-flavour memory with respect to the Lindbladian evolution. It should be noted that there are quantum information studies of neutrino oscillations (see, for instance, [26]), but in contrast to our present work, they typically do not involve neutrino spin and spin-flavour transitions and dissipative effects. The work is organized as follows: in Sect. 2, we specify the model, in Sect. 3, we discuss the solution of the Lindblad equation, in Sect. 4, we explore the entropic measures, and in Sect. 5, we analyse results and conclude the work.

2 Model

We define the measurement register and the memory through the relations:

$$\begin{aligned}&\hat{\rho }_{R\nu }= \sum \limits _{n}|\psi _{n}\rangle \langle \psi _{n}|\otimes I_{\nu } \hat{\rho }_{\sigma \nu } |\psi _{n}\rangle \langle \psi _{n}|\otimes I_{\nu },\nonumber \\&\hat{\rho }_{Q\nu }= \sum \limits _{n}|\phi _{n}\rangle \langle \phi _{n}|\otimes I_{\nu } \mathcal {\hat{L}}(\hat{\rho }_{R\nu })|\phi _{n}\rangle \langle \phi _{n}|\otimes I_{\nu }. \end{aligned}$$

(9)

The identity operator $I_{\nu }$ acts on the flavour subspace $\nu$, and $|\psi _{1}\rangle =|1\rangle ,~~|\psi _{2}\rangle =|0\rangle$, $|\phi _{1,2}\rangle =\frac{1}{\sqrt{2}}(|0\rangle \pm |1\rangle )$, are the eigenfunctions of the neutrino spin operators $\hat{\sigma }_{z}$, $\hat{\sigma }_{x}$, $c\left( \hat{\sigma }_x,\hat{\sigma }_y\right) =\max \Vert \sqrt{\varGamma _x}\sqrt{\varGamma _y}\Vert$ quantifies incompatibility of POVMs acting on the neutrino’s spin, and $\hat{\varrho }_{\sigma \nu }=\mathcal {\hat{L}}(\hat{\rho }_{\sigma \nu })$ is the Lindbladian trace preserving evolution tackled in the Novikov’s form [27]. Despite abstract character, projection operations have clear physical meaning: the neutrino spins are aligned along (transversely to) the neutrino propagation direction after the first (second) measurement. This polarization effect can be described through POVM spin projectors [28]. Neutrino flux reaching us from such distant sources is affected by galactic and extragalactic magnetic fields. These weak fields can exert a dissipative effect [29]. In what follows, we describe this effect through the dissipative trace-preserving Lindblad equation (for more details we refer to [19]).

We define two helicity basis states for the Dirac neutrino [18, 30, 31] $\vert \nu _{1,s=\pm 1}\rangle$, $\vert \nu _{2,s=\pm 1}\rangle$ with masses $m_1$ and $m_2$. Using the helicity basis states, we define the flavour basis

$$\begin{aligned}&\vert \nu _{e}^{R,L}\rangle =\vert \nu _{1,s=\pm 1}\rangle \cos \theta _\nu +\vert \nu _{2,s=\pm 1}\rangle \sin \theta _\nu ,\nonumber \\&\vert \nu _{\mu }^{R,L}\rangle =\vert \nu _{1,s=\pm 1}\rangle \sin \theta _\nu +\vert \nu _{2,s=\pm 1}\rangle \cos \theta _\nu . \end{aligned}$$

(10)

Here, $\theta _\nu$ is the neutrino mixing angle. The Hamiltonian of the system comprises the several terms:

$$\begin{aligned}&\hat{H}_{eff}=\hat{H}_{vac}+\hat{H}_{mat}+\hat{H}_{B}. \end{aligned}$$

(11)

Here, $\hat{H}_{vac}$ is the vacuum part and terms $\hat{H}_{vac}$, $\hat{H}_{B}$ describe neutrino interaction with the matter and magnetic field, respectively (see for more details [18]). The vacuum part $\hat{H}_{vac}$ explicitly has the form

$$\begin{aligned} {\hat{H}}_{vac}=\omega \begin{pmatrix} -\cos 2 \theta _{\nu } &{}\quad 0 &{}\quad \sin 2 \theta _{\nu } &{}\quad 0 \\ 0 &{}\quad -\cos 2 \theta _{\nu } &{}\quad 0 &{}\quad \sin 2 \theta _{\nu } \\ \sin 2 \theta _{\nu } &{}\quad 0 &{}\quad \cos 2\theta _{\nu } &{}\quad 0 \\ 0 &{}\quad \sin 2 \theta _{\nu } &{}\quad 0 &{}\quad \cos 2\theta _{\nu } \end{pmatrix}, \end{aligned}$$

(12)

with

$$\begin{aligned} \omega = \frac{\varDelta m^2}{4 E_\nu }, \qquad \varDelta m^2 =m_2^2 - m_1^2, \end{aligned}$$

(13)

and $E_\nu$ being the neutrino energy. The neutrino-matter interaction is described by the Hamiltonian

$$\begin{aligned} \hat{H}_{mat}= \frac{G_F }{\sqrt{2}} \begin{pmatrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad n^{(\nu _{e})}_{eff} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad n^{(\nu _{\mu })}_{eff} \end{pmatrix}, \end{aligned}$$

(14)

where $n^{(\nu _{e})}_{eff}= n_e - {n_n}/{2}$ and $n^{(\nu _{\mu })}_{eff}= - {n_n}/{2}$, with the Fermi constant $G_F$, the net electron density $n_e=n_{e^-}-n_{e^+}$ and the neutron density $n_n$. The Hamiltonian of the neutrino interaction with a magnetic field in the flavour basis can be presented as [32]

$$\begin{aligned} \hat{H}_{B}= \begin{pmatrix} \displaystyle -\left( \frac{\mu }{\gamma }\right) _{ee} {B_\parallel } &{}&{} \mu _{ee}B_{\perp } &{}&{} \displaystyle -\left( \frac{\mu }{\gamma }\right) _{ e\mu }{B_\parallel } &{}&{} \mu _{e\mu }B_\perp \\ \mu _{ee}B_\perp &{}&{} \displaystyle -\left( \frac{\mu }{\gamma }\right) _{ee}{B_\parallel } &{}&{} \mu _{e\mu } B_\perp &{}&{} \displaystyle -\left( \frac{\mu }{\gamma }\right) _{e\mu }{B_\parallel } \\ \displaystyle -\left( \frac{\mu }{\gamma }\right) _{e\mu }{B_\parallel } &{}&{} \mu _{e\mu }B_{\perp } &{}&{} \displaystyle -\left( \frac{\mu }{\gamma }\right) _{\mu \mu }{B_\parallel } &{}&{} \mu _{\mu \mu } B_\perp \\ \mu _{e\mu }B_{\perp } &{}&{} \displaystyle -\left( \frac{\mu }{\gamma }\right) _{e\mu }{B_\parallel } &{}&{} \mu _{\mu \mu }B_\perp &{}&{} \displaystyle -\left( \frac{\mu }{\gamma }\right) _{\mu \mu }{B_\parallel } \end{pmatrix}, \end{aligned}$$

(15)

where $B_\parallel$ and $B_\perp$ are the parallel and transverse magnetic field components with respect to the neutrino velocity, and the magnetic moments $\tilde{\mu }_{\ell \ell '}$ and $\mu _{\ell \ell '}$ ($\ell ,\ell '=e,\mu$) are related to those in the mass representation $\mu _{jk}$ ($j,k=1,2$) as follows:

$$\begin{aligned} \mu _{ee}&=\mu _{11} \cos ^2 \theta _{\nu } +\mu _{22} \sin ^2 \theta _{\nu } +\mu _{12} \sin 2\theta _{\nu }, \nonumber \\ \mu _{e\mu }&=\mu _{12}\cos 2\theta _{\nu } + \frac{1}{2} \left( \mu _{22} - \mu _{11}\right) \sin 2\theta _{\nu },\nonumber \\ \mu _{\mu \mu }&=\mu _{11} \sin ^2 \theta _{\nu } +\mu _{22} \cos ^2 \theta _\nu -\mu _{12} \sin 2\theta _{\nu }, \end{aligned}$$

(16)

and

$$\begin{aligned} -\left( \frac{\mu }{\gamma }\right) _{ee}&= \frac{\mu _{11}}{\gamma _{1}}\,\cos ^2 \theta _{\nu } + \frac{\mu _{22}}{\gamma _{2}}\,\sin ^2 \theta _{\nu } + \frac{\mu _{12}}{\gamma _{12}}\,\sin 2\theta _{\nu },\nonumber \\ -\left( \frac{\mu }{\gamma }\right) _{e\mu }&= \frac{\mu _{12}}{\gamma _{12}}\,\cos 2\theta _{\nu } +\frac{1}{2}\left( \frac{\mu _{22}}{\gamma _{2}}-\frac{\mu _{11}}{\gamma _{1}} \right) \sin 2\theta _{\nu },\nonumber \\ -\left( \frac{\mu }{\gamma }\right) _{\mu \mu }&= \frac{\mu _{11}}{\gamma _{1}}\,\sin ^2 \theta _{\nu } +\frac{\mu _{22}}{\gamma _{2}}\,\cos ^2 \theta _{\nu } -\frac{\mu _{12}}{\gamma _{12}}\,\sin 2\theta _{\nu }. \end{aligned}$$

(17)

Here, $\gamma _1$ and $\gamma _2$ are the Lorenz factors of the massive neutrinos, and

$$\begin{aligned} \frac{1}{\gamma _{12}}=\frac{1}{2}\left( \frac{1}{\gamma _1}+\frac{1}{\gamma _2}\right) . \end{aligned}$$

(18)

The problem of the neutrino propagating in the interstellar space can be solved precisely for the constant interstellar matter density and magnetic field (see [18] for details).

3 Solution of the Lindblad equation

Giant magnetic fields generated by cosmic objects impact neutrinos remotely from the sources of the magnetic fields, i.e. in the interstellar space. The stochastic magnetic field includes the effects of interstellar fluctuations, galactic winds, cosmic turbulence, and primordial magnetic field fluctuations. The stochastic magnetic fields exert a dissipative effect on the neutrino spin polarization. Therefore, the evolution of neutrinos in stochastic fields is not unitary and should be described by the Lindblad master equation. We note that the stochastic component of the field is quite strong. In particular, in the centre of galaxy M51, the ratio between stochastic and regular components is on the order of 10$\%$ [33]. The Lindbladian approach for neutrinos is described in detail in recent publications [19, 25].

We prepare the initial state of the system in the mixture of the flavour states:

$$\begin{aligned} \hat{\varrho }(0)= & {} \mathcal {\hat{I}}=a_1\vert \nu _{e}^{L}\rangle \langle \nu _{e}^{L}\vert +a_2\vert \nu _{\mu }^{L}\rangle \langle \nu _{\mu }^{L}\vert \nonumber \\&+a_3\vert \nu _{e}^{R}\rangle \langle \nu _{e}^{R}\vert +a_4\vert \nu _{\mu }^{R}\rangle \langle \nu _{\mu }^{R}\vert , \end{aligned}$$

(19)

and propagate the initial state in the interstellar medium using the Hamiltonian Eq. (11).

The interstellar magnetic field has two contributions: deterministic part $\mathbf {B}$ that enters in Eq. (11) and stochastic magnetic field related to the cosmic dust. The stochastic field is characterized by the mean value $\langle \mathbf {h}(t)\rangle =0$ and the correlation function can be presented in the form $\langle h_\alpha (t)h_\beta (0)\rangle =\delta _{\alpha \beta }\eta B^2 f(t)$, where $\eta =\langle h^2\rangle /B^2$, and f(t) takes the $\delta$-correlator form $f(t)=L_0\delta (t)$ if the correlation length $L_0$ is much less than the neutrino oscillation length $L_{osc}$ (see [25] and references therein). This allows us to rewrite the correlation function $\langle h_\alpha (t)h_\beta (0)\rangle$ in the following form: $\langle h_\alpha (t)h_\beta (0)\rangle = \frac{\delta _{\alpha \beta }W^2}{2\mu _\nu ^2}\,\delta (t)$, where $\mu _\nu$ is a putative value of the neutrino magnetic moment and $W^2=2\eta (\mu _\nu B)^2L_0$ is the dissipation parameter (see below). For the interstellar case, one has $B\simeq 3$ $\mu$G, and $\eta \sim 1$ and $L_0\sim 50$ pc (see [25] and references therein).

We exploit Novikov’s theorem [27] and consider non-perturbative exact master equation for the noise-averaged density matrix (see [34] for a recent literature). The density matrix of the system $\hat{\varrho }$ obeys the Lindblad master equation in the Novikov’s form:

$$\begin{aligned}&\frac{d\hat{\varrho }}{dt}= -i\left[ \hat{H}, \hat{\varrho }\right] - \frac{W^{2}}{2}\left( \hat{\varrho }\hat{V^2} +\hat{V^2}\hat{\varrho }-2\hat{V}\hat{\varrho }\hat{V}\right) . \end{aligned}$$

(20)

The first term in Eq. (20) describes unitary evolution and the second term proportional to $W^2$ is responsible for dissipative effects. We note that the master equation (20) preserves the trace of the density matrix. The dissipator matrix V has the following general form:

$$\begin{aligned} V_{ik} = \left\langle i \right| I_1 \otimes v_2 + I_2 \otimes v_1 \left| k \right\rangle , \end{aligned}$$

(21)

where v is any $2 \times 2$ matrix, and the subscripts 1, 2 denote the action of a matrix on the space of the first and second neutrino, respectively. The matrix v can be expanded into the basis of $2\times 2$ unit matrix and three Pauli matrices:

$$\begin{aligned} v = v_0 I + \mathbf {v} \cdot \mathbf {\sigma }. \end{aligned}$$

(22)

We analytically solve Eq. (20) in the eigenbasis of the Hamiltonian $\hat{H}_{eff}$.

3.1 Diagonalization of the Hamiltonian

The density matrix can be written in different representations. For the specified problem of the neutrino motion in the magnetic field, the most convenient representation is that in the basis of the eigenfunctions of the Hamiltonian in Eq. (11). In the following, we neglect the neutrino interaction with the interstellar matter, which is substantially weaker than both the neutrino interaction with the interstellar magnetic field and the neutrino vacuum oscillation frequency. In the magnetic field Hamiltonian (15), we neglect terms proportional to the longitudinal component of the field due to the large Lorentz factors of ultrahigh-energy neutrinos. Taking the mass basis, the resulting effective Hamiltonian can be written as

$$\begin{aligned} \hat{H}_{\mathrm {eff}}^{\mathrm m} = \begin{pmatrix} -\omega _\nu &{}&{} \mu _{11} B &{}&{} 0 &{}&{} \mu _{12} B \\ \mu _{11} B &{}&{} -\omega _\nu &{}&{} \mu _{12} B &{}&{} 0 \\ 0 &{}&{} \mu _{12} B &{}&{} \omega _\nu &{}&{} \mu _{22} B \\ \mu _{12} B &{}&{} 0 &{}&{} \mu _{22} B &{}&{} \omega _\nu \end{pmatrix}. \end{aligned}$$

(23)

The effective Hamiltonian can be diagonalized in two consecutive steps. At first, we combine the states of the same mass and create the symmetric and antisymmetric combinations of the spin states:

$$\begin{aligned} \nu _{i}^{\pm } = \frac{1}{\sqrt{2}} \left( \psi _{i+} \pm \psi _{i-}\right) , i=1,2. \end{aligned}$$

(24)

The corresponding transformation matrix reads

$$\begin{aligned} T_S = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 &{}&{} 1 &{}&{} 0 &{}&{} 0 \\ 1 &{}&{} -1 &{}&{} 0 &{}&{} 0 \\ 0 &{}&{} 0 &{}&{} 1 &{}&{} 1 \\ 0 &{}&{} 0 &{}&{} 1 &{}&{} -1 \end{pmatrix}, \end{aligned}$$

(25)

or, in terms of $2 \times 2$ blocks,

$$\begin{aligned} T_S = \frac{1}{\sqrt{2}} \begin{pmatrix} \sigma _3 + \sigma _1 &{}&{} 0 \\ 0 &{}&{} \sigma _3 + \sigma _1 \end{pmatrix}, \end{aligned}$$

(26)

where $\sigma _{1,3}$ are Pauli matrices. The Hamiltonian takes the form:

$$\begin{aligned} \begin{pmatrix} -\omega _\nu + \mu _{11} B &{}&{} 0 &{}&{} \mu _{12} B &{}&{} 0 \\ 0 &{}&{} -\omega _\nu - \mu _{11} B &{}&{} 0 &{}&{} -\mu _{12} B \\ \mu _{12} B &{}&{} 0 &{}&{} \omega _\nu + \mu _{22} B &{}&{} 0 \\ 0 &{}&{} - \mu _{12} B &{}&{} 0 &{}&{} \omega _\nu - \mu _{22} B \end{pmatrix}. \end{aligned}$$

(27)

For full diagonalization, we use the following matrix:

$$\begin{aligned} T_{b} = \begin{pmatrix} c_b &{}&{} 0 &{}&{} -s_b&{}&{} 0 \\ 0 &{}&{} c_b &{}&{} 0 &{}&{} s_b \\ s_b &{}&{} 0 &{}&{} c_b &{}&{} 0 \\ 0 &{}&{} -s_b &{}&{} 0 &{}&{} c_b \end{pmatrix}= \begin{pmatrix} c_b I &{}&{} -s_b \sigma _3 \\ s_b \sigma _3 &{}&{} c_b I \end{pmatrix}, \end{aligned}$$

(28)

where $c_b=\cos \theta _{\mathrm B}$ and $s_b=\sin \theta _{\mathrm B}$ with

$$\begin{aligned} \theta _{\mathrm B} = \frac{1}{2} \arctan \left[ \frac{ \mu _{12}B}{\omega _\nu - \frac{1}{2} (\mu _{11} - \mu _{22}) B } \right] . \end{aligned}$$

(29)

The eigenvalues of the Hamiltonian are equal to

$$\begin{aligned} \kappa&= \pm \frac{(\mu _{11} + \mu _{22}) B}{2} \pm \nonumber \\&\sqrt{\left( \omega _\nu - \frac{\mu _{11} - \mu _{22}}{2} B\right) ^2+ (\mu _{12}B)^2}. \end{aligned}$$

(30)

If we set all magnetic moments equal to the same value $\mu _\nu$,

$$\begin{aligned} \mu _{11} = \mu _{22} = \mu _{12} =\mu _\nu , \end{aligned}$$

(31)

then

$$\begin{aligned} \kappa = \pm \left[ \sqrt{ \omega _\nu ^2 + (\mu _\nu B)^2} \pm \mu _\nu B \right] , \end{aligned}$$

(32)

or

$$\begin{aligned} \kappa =\frac{\pm (\omega _{\mathrm N} \pm \omega _{\mathrm B})}{2}, \end{aligned}$$

(33)

where

$$\begin{aligned} \omega _{\mathrm B} = 2\mu _\nu B, \, \omega _{\mathrm N} = 2\sqrt{\omega _\nu ^2 + \omega _{\mathrm B}^2}. \end{aligned}$$

(34)

The “magnetic” angle with these assumptions is

$$\begin{aligned} \theta _{\mathrm B} = \frac{1}{2} \arctan \left[ \frac{\omega _{\mathrm B}}{\sqrt{\omega _{\mathrm N}^2 - \omega _{\mathrm B}^2} }\right] . \end{aligned}$$

(35)

Equations (27) and (28) define the transformations from the mass basis to the basis defined by the Hamiltonian. The full transform is

$$\begin{aligned} T_{\mathrm B} = T_b T_S = \begin{pmatrix} C_{\mathrm B} &{}&{} -S_{\mathrm B} \\ S_{\mathrm B} &{}&{} C_{\mathrm B} \end{pmatrix}, \end{aligned}$$

(36)

where $C_B$, $S_B$ are $2 \times 2$ matrices defined as

$$\begin{aligned} C_{\mathrm B}&= \frac{c_b}{\sqrt{2}} (\sigma _1 + \sigma _3) = \frac{c_b}{\sqrt{2}} \begin{pmatrix} 1 &{}&{} 1 \\ 1 &{}&{} -1 \end{pmatrix}, \end{aligned}$$

(37)

$$\begin{aligned} S_{\mathrm B}&= \frac{s_b}{\sqrt{2}} \sigma _3 (\sigma _1 + \sigma _3) = \frac{s_b}{\sqrt{2}} \begin{pmatrix} 1 &{}&{} 1 \\ -1 &{}&{} 1 \end{pmatrix}. \end{aligned}$$

(38)

The density matrix in the basis of the Hamiltonian $H_{\mathrm {eff}}$ is related to the matrix in the mass and flavour representations by the following formulas:

$$\begin{aligned} \hat{\varrho }^{\mathrm B} = T_{\mathrm B} \hat{\varrho }^{\mathrm m} T_{\mathrm B}^{-1} = (T_{\mathrm B} T_{\mathrm F}) \hat{\varrho }^{\mathrm f} (T_{\mathrm B} T_{\mathrm F})^{-1}, \end{aligned}$$

(39)

where $T_{\mathrm F}$ is the operator relating the density matrices in the flavour and mass representations:

$$\begin{aligned} T_{\mathrm F} = \begin{pmatrix} c_\nu &{}&{} 0 &{}&{} s_\nu &{}&{} 0 \\ 0 &{}&{} c_\nu &{}&{} 0 &{}&{} s_\nu \\ -s_\nu &{}&{} 0 &{}&{} c_\nu &{}&{} 0 \\ 0 &{}&{} -s_\nu &{}&{} 0 &{}&{} c_\nu \end{pmatrix}, \end{aligned}$$

(40)

where $c_\nu = \cos \theta _\nu$, $s_\nu = \sin \theta _\nu$.

3.2 Lindblad equation

The Lindblad master equation is written in the eigenbasis of the Hamiltonian of the neutrino interaction with the magnetic field:

$$\begin{aligned} \frac{d \hat{\varrho }^{\mathrm B}_{nm}}{dt} =&-i \omega _{nm}\hat{\varrho }^{\mathrm B}_{mn} - \frac{w^2}{2} \sum _q\left( \hat{\varrho }^{\mathrm B}_{nq} V^2_{qm} + V^2_{nq} \hat{\varrho }^{\mathrm B}_{qm}\right) \nonumber \\&+ w^2 \sum _{q,s} V_{nq} \hat{\varrho }^{\mathrm B}_{qs} V_{sm}, \end{aligned}$$

(41)

where $\omega _{nm} = E_n - E_m$, $n,m = 1,..,4$. The energy levels of the neutrino in the magnetic field are expressed in Eq. (33), and below, we adopt the following ordering scheme of energy states:

$$\begin{aligned} E_{1,2} = \frac{-\omega _{\mathrm N} \pm \omega _{\mathrm B}}{2}, E_{3,4} = \frac{\omega _{\mathrm N} \pm \omega _{\mathrm B}}{2}. \end{aligned}$$

(42)

The general form of the matrix V reads:

$$\begin{aligned} V_{ik} = \left\langle i \right| I_1 \otimes v_2 + I_2 \otimes v_1 \left| k \right\rangle , \end{aligned}$$

(43)

where v is a $2 \times 2$ matrix defining the interaction with the stochastic part of the magnetic field and acting separately on subspaces spanned by basis components with numbers 1, 2, and 3 4, respectively. Due to this form of the interaction operator, the overall system of 16 linear equations splits into four different subsystems of four linear equations for respective quadrants of the full density matrix.

We write the density matrix as a set of four independent quadrants:

$$\begin{aligned} \hat{\varrho }^{\mathrm B} = \begin{pmatrix} \varrho ^{(11)} &{} \varrho ^{(12)} \\ \varrho ^{(21)} &{} \varrho ^{(22)} \end{pmatrix}, \end{aligned}$$

(44)

where $\varrho ^{(\alpha )}$ is the $2 \times 2$ minors of the density matrix each obeying closed linear equations:

$$\begin{aligned} \frac{d\varrho ^{(ab)}_{ik}}{dt}&= i (\varepsilon ^{ab}\omega _{\mathrm N} - \varepsilon _{ik}\omega _{\mathrm B}) \varrho ^{(ab)}_{ik} \nonumber \\&\quad -\frac{w^2}{2} \sum _l \left( \varrho ^{(ab)}_{il}v^2_{lk}+ v^2_{il}\varrho ^{(ab)}_{lk}\right) \nonumber \\&\quad +w^2 \sum _{l,m} v_{il}\varrho ^{(ab)}_{lm}v_{mk}, \end{aligned}$$

(45)

with $a, b = 1, 2$ representing the quadrant indices as in Eq. (44), and $i, k=1, 2$ the indices inside these quadrants. $\epsilon ^{ab}$ and $\epsilon _{ik}$ are two-dimensional symbols antisymmetric with respect to indices.

The term proportional to $\epsilon ^{ab}$ is the same for all minor elements and therefore

$$\begin{aligned} \varrho ^{(ab)}(t) = e^{i\varepsilon ^{ab}\omega _N t}\bar{\varrho }^{(ab)}(t). \end{aligned}$$

(46)

The matrices $\bar{\varrho }^{(ab)}$ and v are expanded into the linear combinations of the three Pauli matrices and $2 \times 2$ unit matrix:

$$\begin{aligned} \bar{\varrho }^{(ab)} = r^{(ab)}_0 I + \mathbf {r}^{(ab)} \cdot \mathbf {\sigma }, \end{aligned}$$

(47)

where the coefficients are defined by:

$$\begin{aligned} r_i^{(ab)} = \frac{1}{2} \mathrm {Tr}\{ \varrho ^{(ab)}\sigma _i \}, \, \, r_0^{(ab)} = \frac{1}{2} \mathrm {Tr}\{ \varrho ^{(ab)} \}. \end{aligned}$$

(48)

The same expansion we exploit for the matrix v:

$$\begin{aligned} v = v_0 I + \mathbf {v} \cdot \mathbf {\sigma }. \end{aligned}$$

(49)

Using these expansions, one can show that the terms containing $v_0$ do not contribute to the dissipation process, since they are proportional to a unit matrix that commutes with all other matrices, and the second and third terms of Eq. (45) give contributions equal in magnitude but with opposite signs. The vector $\mathbf {v}$ can be represented as

$$\begin{aligned} \mathbf {v} = \vert \mathbf {v} \vert ( \cos \varphi \sin \beta , \sin \varphi \sin \beta , \cos \beta ), \end{aligned}$$

(50)

choosing $\varphi =0$ to make it purely real, and normalizing to unity, which can be done by a proper rescaling of the coefficient $w^2$, one deduces

$$\begin{aligned} \mathbf {v} = (\sin \beta , 0 , \cos \beta ). \end{aligned}$$

(51)

The angle parameter $0<\beta < \pi /2$ defines strength of the dissipation. The dissipation is zero if $\beta =0$ and reaches its maximum value for $\beta =\pi /2$. In the present work, we set $\beta = \pi /4$. After redefining time,

$$\begin{aligned} \tau = 2 w^2 t, \end{aligned}$$

(52)

and frequencies,

$$\begin{aligned} \bar{\omega }_{\mathrm {B,N}} = \frac{\omega _{\mathrm {B,N}} }{2w^2}, \end{aligned}$$

(53)

and using above expansions, through lengthy and rather involved calculations, we deduce the following system of equations for the coefficients $r_i$ of each quadrant

$$\begin{aligned} \frac{d}{d\tau } r_0(\tau )&= 0, \end{aligned}$$

(54)

$$\begin{aligned} \frac{d}{d\tau } r_1 (\tau )&= -c_\beta ^2 r_1(\tau ) + \bar{\omega }_{\mathrm B} r_2(\tau ) + c_\beta s_\beta r_3(\tau ), \end{aligned}$$

(55)

$$\begin{aligned} \frac{d}{d\tau } r_2(\tau )&= - \bar{\omega }_{\mathrm B} r_1(\tau ) -c_\beta ^2 r_2(\tau ), \end{aligned}$$

(56)

$$\begin{aligned} \frac{d}{d\tau } r_3(\tau )&= c_\beta s_\beta r_1(\tau ) -s_\beta ^2 r_3(\tau ), \end{aligned}$$

(57)

where the notations $c_\beta = \cos \beta$, $s_\beta = \sin \beta$ were used.

For solving the linear system, we diagonalize the matrix:

$$\begin{aligned} \mathcal {M} = \begin{pmatrix} - c_\beta ^2 &{}&{} \bar{\omega }_{\mathrm B} &{}&{} s_\beta \cdot c_\beta \\ -\bar{\omega }_{\mathrm B} &{}&{} - c_\beta ^2 &{}&{} 0 \\ s_\beta \cdot c_\beta &{}&{} 0 &{}&{} -s_\beta ^2 \end{pmatrix}, \end{aligned}$$

(58)

and find roots $\{\nu _k\}$ of the cubic polynomial equation. The solution can be represented in the form:

$$\begin{aligned} r_i (\tau ) = \sum _{k=1}^{3} C_{ik} e^{i\nu _k \tau }, \end{aligned}$$

(59)

where the integration constants are given by

$$\begin{aligned} C_{i1}&= \frac{B_{0i} \nu _2 \nu _3 - B_{1i} (\nu _2 + \nu _3) + B_{2i}}{(\nu _1 - \nu _2)(\nu _1 - \nu _3)}, \end{aligned}$$

(60)

$$\begin{aligned} C_{i2}&= \frac{B_{0i} \nu _1 \nu _3 - B_{1i} (\nu _1 +\nu _3) +B_{2i}}{(\nu _2 - \nu _1)(\nu _2 - \nu _3)}, \end{aligned}$$

(61)

$$\begin{aligned} C_{i3}&= \frac{B_{0i} \nu _1 \nu _2 - B_{1i} (\nu _1 + \nu _2) +B_{2i}}{(\nu _3 - \nu _1)(\nu _3 -\nu _2)}, \end{aligned}$$

(62)

where

$$\begin{aligned} B_{0i}&= r_i(0), \, \, \end{aligned}$$

(63)

$$\begin{aligned} B_{1i}&= \sum _k \mathcal {M}_{ik}r_{k}(0), \, \, \end{aligned}$$

(64)

$$\begin{aligned} B_{2i}&= \sum _{kl} \mathcal {M}_{ik} \mathcal {M}_{kl}r_{l}(0). \end{aligned}$$

(65)

4 Entropic measures

After involved calculations, we obtain analytical results for conditional von Neumann entropies. The full spin-flavour density matrix can be written in the corresponding basis in the form:

$$\begin{aligned} \hat{\varrho }= \sum _{\nu \nu ' \sigma \sigma '} \rho ^{(\nu \nu ')}_{\sigma \sigma '} \left| \nu \right\rangle \left| \sigma \right\rangle \left\langle \nu \right| ' \left\langle \sigma \right| '. \end{aligned}$$

(66)

To obtain the reduced flavour density matrix, we take the trace over the spin states

$$\begin{aligned} \hat{\varrho }_{\nu } = \sum _{\sigma } \left\langle \sigma \right| \hat{\varrho }\left| \sigma \right\rangle = \sum _{\nu \nu '}\sum _\sigma \rho ^{(\nu \nu ')}_{\sigma \sigma }\left| \nu \right\rangle \left\langle \nu ' \right| . \end{aligned}$$

(67)

The reduced density matrix in the first line of Eq. (9) is obtained by projecting the matrix on the eigenstates of $\sigma _z$, $\left| 1 \right\rangle$ and $\left| 0 \right\rangle$ (or $\psi _{1,2}$). The result is expressed in terms of the $4 \times 4$ matrices $\rho ^{(\nu \nu ')}_{\sigma \sigma }$

$$\begin{aligned} \hat{\varrho }_{\nu } = \begin{pmatrix} \rho ^{(ee)}_{11} + \rho ^{(ee)}_{00} &{}&{} \rho ^{(e\mu )}_{11} + \rho ^{(e\mu )}_{00} \\ \rho ^{(\mu e)}_{11} + \rho ^{(\mu e)}_{00} &{}&{} \rho ^{(\mu \mu )}_{11} + \rho ^{(\mu \mu )}_{00} \end{pmatrix}. \end{aligned}$$

(68)

The eigenvalues of $\hat{\varrho }_{\nu }$ are

$$\begin{aligned} \lambda ^\nu _{1,2} = \frac{(\varrho ^{(ee)}_\nu + \varrho ^{(\mu \mu )}_\nu ) \pm \sqrt{(\varrho ^{(ee)}_{\nu } - \varrho _{\nu }^{(\mu \mu )})^2 + 4|\varrho _{\nu }^{(e\mu )}|^2 }}{2}, \end{aligned}$$

(69)

where for all pairs $(\nu \nu ')$, $\varrho ^{(\nu \nu ')}_\nu = \varrho ^{(\nu \nu ')}_{11} + \varrho ^{(\nu \nu ')}_{00}$. The reduced spin density matrix is obtained after tracing flavour states:

$$\begin{aligned} \hat{\varrho }_{\sigma } = \sum _{\nu } \left\langle \nu \right| \hat{\varrho }\left| \nu \right\rangle = \sum _{\nu }\sum _{\sigma \sigma } \rho ^{(\nu \nu )}_{\sigma \sigma '}\left| \sigma \right\rangle \left\langle \sigma ' \right| . \end{aligned}$$

(70)

We rewrite $\hat{\varrho }_{\sigma }$ as a $2\times 2$ matrix in the following form:

$$\begin{aligned} \hat{\varrho }_{\sigma } = \begin{pmatrix} \rho ^{(ee)}_{11} + \rho ^{(\mu \mu )}_{11} &{}&{} \rho ^{(ee)}_{10} + \rho ^{(\mu \mu )}_{10} \\ \rho ^{(ee)}_{01} + \rho ^{(\mu \mu )}_{01} &{}&{} \rho ^{(ee)}_{00} + \rho ^{(\mu \mu )}_{00} \end{pmatrix}. \end{aligned}$$

(71)

Eigenvalues $\lambda ^{\sigma }_{1,2}$ of Eq. (71) have the same structure as in Eq. (69) under replacing the elements of the flavour matrix $\hat{\varrho }_\nu$ with the corresponding components of $\hat{\varrho }_\sigma$.

The mutual information between the spin and the flavour is expressed through the eigenvalues of the spin, flavour and full density matrices:

$$\begin{aligned} I(\nu , \sigma )&= -\sum _{i=1}^2 (\lambda ^{\nu }_i\log {\lambda ^{\nu }_i} +\lambda ^{\sigma }_i \log {\lambda ^{\sigma }_i})\nonumber \\&\quad +\sum _{k=1}^4 \lambda _k \log {\lambda _k}, \end{aligned}$$

(72)

where $\lambda _i$, $i=1,..,4$ denote eigenvalues of the full flavour-spin density matrix $\hat{\varrho }$.

The matrix $\hat{\varrho }_{R\nu }$ has the following explicit form:

$$\begin{aligned} \hat{\varrho }_{R\nu } =&\sum _{\nu \nu '}\sum _{\sigma } \varrho ^{(\nu \nu ')}_{\sigma \sigma } \left| \sigma \right\rangle \left| \nu \right\rangle \left\langle \nu ' \right| \left\langle \sigma \right| \nonumber \\&=\sum _{\nu \nu '} \left| \nu \right\rangle \left\langle \nu ' \right| \left( \varrho ^{(\nu \nu ')}_{11}\left| 1 \right\rangle \left\langle 1 \right| + \varrho ^{(\nu \nu ')}_{00} \left| 0 \right\rangle \left\langle 0 \right| \right) , \end{aligned}$$

(73)

and four eigenvalues:

$$\begin{aligned} \lambda ^{R\nu }_{1,2}&= \frac{ (\varrho ^{(ee)}_{11} + \varrho ^{(\mu \mu )}_{11}) \pm \sqrt{(\varrho ^{(ee)}_{11}-\varrho ^{(\mu \mu )}_{11})^2 + 4 |\varrho ^{(e\mu )}_{11}|^2}}{2} , \end{aligned}$$

(74)

$$\begin{aligned} \lambda ^{R\nu }_{3,4}&= \frac{ (\varrho ^{(ee)}_{00} + \varrho ^{(\mu \mu )}_{00}) \pm \sqrt{(\varrho ^{(ee)}_{00}-\varrho ^{(\mu \mu )}_{00})^2 + 4 |\varrho ^{(e\mu )}_{00}|^2}}{2}. \end{aligned}$$

(75)

After projecting on the basis states $\left| \pm \right\rangle = 1/\sqrt{2} (\left| 1 \right\rangle \pm \left| 0 \right\rangle )$ (or $\phi _{1,2}$), the second matrix in Eq. (9) takes the form:

$$\begin{aligned} \hat{\varrho }_{Q\nu } = \sum _{\nu \nu '} \left| \nu \right\rangle \left\langle \nu ' \right| \left( \varrho ^{(\nu \nu ')}_{++}\left| + \right\rangle \left\langle + \right| + \varrho ^{(\nu \nu ')}_{--} \left| - \right\rangle \left\langle - \right| \right) , \end{aligned}$$

(76)

or alternatively

$$\begin{aligned} \hat{\varrho }_{Q\nu } =&\sum _{\nu \nu '} \left| \nu \right\rangle \left\langle \nu ' \right| \frac{ \varrho ^{(\nu \nu ')}_{11} + \varrho ^{(\nu \nu ')}_{00}}{2} \left( \left| 1 \right\rangle \left\langle 1 \right| + \left| 0 \right\rangle \left\langle 0 \right| \right) \nonumber \\&+\sum _{\nu \nu '}\left| \nu \right\rangle \left\langle \nu ' \right| \frac{\varrho ^{(\nu \nu ')}_{10} + \varrho ^{(\nu \nu ')}_{01}}{2} \left( \left| 1 \right\rangle \left\langle 0 \right| + \left| 0 \right\rangle \left\langle 1 \right| \right) . \end{aligned}$$

(77)

The coefficients in Eqs. (76) and (77) are related as

$$\begin{aligned} \rho ^{(\nu \nu ')}_{++}&= \frac{1}{2} \left( \rho ^{(\nu \nu ')}_{11} + \rho ^{(\nu \nu ')}_{00} + \rho ^{(\nu \nu ')}_{10} + \rho ^{(\nu \nu ')}_{01}\right) , \end{aligned}$$

(78)

$$\begin{aligned} \rho ^{(\nu \nu ')}_{--}&= \frac{1}{2} \left( \rho ^{(\nu \nu ')}_{11} + \rho ^{(\nu \nu ')}_{00} - \rho ^{(\nu \nu ')}_{10} - \rho ^{(\nu \nu ')}_{01}\right) . \end{aligned}$$

(79)

The matrix (77) has exactly the same structure as $\hat{\varrho }_{R\nu }$ in the basis $\left| 0 \right\rangle$, $\left| 1 \right\rangle$; therefore, the expressions for the eigenvalues have the form similar to Eqs. (74) and (75):

$$\begin{aligned} \lambda ^{Q\nu }_{1,2}&= \frac{ (\varrho ^{(ee)}_{++} + \varrho ^{(\mu \mu )}_{++}) \pm \sqrt{(\varrho ^{(ee)}_{++}-\varrho ^{(\mu \mu )}_{++})^2 + 4 |\varrho ^{(e\mu )}_{++}|^2}}{2} , \end{aligned}$$

(80)

$$\begin{aligned} \lambda ^{Q\nu }_{3,4}&= \frac{ (\varrho ^{(ee)}_{--} + \varrho ^{(\mu \mu )}_{--}) \pm \sqrt{(\varrho ^{(ee)}_{--}-\varrho ^{(\mu \mu )}_{--})^2 + 4 |\varrho ^{(e\mu )}_{--}|^2}}{2} . \end{aligned}$$

(81)

The conditional entropy from the right-hand side of Eq. (2) is

$$\begin{aligned} S(\sigma \vert \nu ) = S(\hat{\varrho }_{\sigma \nu }) - S(\hat{\varrho }_\nu ), \end{aligned}$$

(82)

and mutual information:

$$\begin{aligned} I(\sigma , \nu ) = S(\hat{\varrho }_\sigma ) - S(\sigma \vert \nu ). \end{aligned}$$

(83)

We calculate the mutual information $I(X, \nu )$ which is required to evaluate the classical correlation according to Eq. (5). At first, we consider $X=\sigma _z$; then, the resulting spin-flavour density matrix is written as

$$\begin{aligned} \hat{\varrho }_{\sigma _z \nu } = \begin{pmatrix} \rho _{11}^{(\nu \nu ')} &{}&{} 0 \\ 0 &{}&{} \rho _{00}^{(\nu \nu ')} \end{pmatrix} = \hat{\varrho }_{R\nu }, \end{aligned}$$

(84)

and the reduced spin matrix:

$$\begin{aligned} \hat{\varrho }_{\sigma _z} = \begin{pmatrix} \rho _{11}^{(ee)} +\rho _{11}^{(\mu \mu )} &{}&{} 0 \\ 0 &{}&{} \rho _{00}^{(ee)} +\rho _{00}^{(\mu \mu )} \end{pmatrix}. \end{aligned}$$

(85)

Similarly, $X=\sigma _x$,

$$\begin{aligned} \hat{\varrho }_{\sigma _x \nu } = \frac{1}{2} \begin{pmatrix} \rho _{11}^{(\nu \nu ')} +\rho _{00}^{(\nu \nu ')} &{}&{} \rho _{10}^{(\nu \nu ')} +\rho _{01}^{(\nu \nu ')} \\ \rho _{10}^{(\nu \nu ')} +\rho _{01}^{(\nu \nu ')} &{}&{} \rho _{11}^{(\nu \nu ')} +\rho _{00}^{(\nu \nu ')} \end{pmatrix} = \hat{\varrho }_{Q\nu }, \end{aligned}$$

(86)

and

$$\begin{aligned} \hat{\varrho }'_{\sigma _x} = \begin{pmatrix} \rho _{++}^{(ee)} +\rho _{++}^{(\mu \mu )} &{}&{} 0 \\ 0 &{}&{} \rho _{--}^{(ee)} +\rho _{--}^{(\mu \mu )} \end{pmatrix} \end{aligned}$$

(87)

in its eigenbasis.

The corresponding mutual information are:

$$\begin{aligned} I(\sigma _z, \nu )&= S(\hat{\varrho }_{\sigma _z})- S(R\vert \nu ), \end{aligned}$$

(88)

$$\begin{aligned} I(\sigma _x, \nu )&= S(\hat{\varrho }_{\sigma _x}) - S(Q\vert \nu ). \end{aligned}$$

(89)

The matrix elements at the initial moment of time in our notations are expressed as

$$\begin{aligned}&\varrho _{11}^{(ee)} (0) = a_3 = \lambda _1, \, \varrho _{00}^{(ee)}(0) = a_1 = \lambda _2, \end{aligned}$$

(90)

$$\begin{aligned}&\varrho _{11}^{(\mu \mu )}(0) = a_4 = \lambda _3, \, \varrho _{00}^{(\mu \mu )} (0) = a_2 = \lambda _4, \end{aligned}$$

(91)

with all non-diagonal elements equal to zero. Therefore, at $t=0$,

$$\begin{aligned}&\lambda ^\nu _1 (0) = \lambda _1 + \lambda _2, \, \lambda ^\nu _2 (0) = \lambda _3 + \lambda _4, \end{aligned}$$

(92)

$$\begin{aligned}&\lambda ^\sigma _1 (0) = \lambda _1 + \lambda _3, \, \lambda ^\sigma _2(0) = \lambda _2 + \lambda _4, \end{aligned}$$

(93)

$$\begin{aligned}&\lambda ^{\sigma _z}_1 (0) = \lambda _1 + \lambda _3, \, \lambda ^{\sigma _z}_2(0) = \lambda _2 + \lambda _4, \end{aligned}$$

(94)

$$\begin{aligned}&\lambda ^{\sigma _x}_1(0) = \frac{1}{2}, \, \lambda ^{\sigma _x}_2(0) = \frac{1}{2},\nonumber \\&\lambda ^{R\nu }_1 (0) = \lambda _1, \, \lambda ^{R\nu }_2 (0) = \lambda _2, \end{aligned}$$

(95)

$$\begin{aligned}&\lambda ^{R\nu }_3 (0) = \lambda _3, \, \lambda ^{R\nu }_4 (0) = \lambda _4,\nonumber \\&\lambda ^{Q\nu }_{1} (0) = \lambda ^{Q\nu }_{2}(0) = \frac{\lambda ^\nu _{1} (0)}{2} = \frac{\lambda _1 + \lambda _2}{2}, \end{aligned}$$

(96)

$$\begin{aligned}&\lambda ^{Q\nu }_{3}(0) = \lambda ^{Q\nu }_{4}(0) = \frac{ \lambda ^\nu _{2}(0)}{2} = \frac{\lambda _3 + \lambda _4}{2}. \end{aligned}$$

(97)

We write down the entropies at the moment of time $t=0$. Below h(x) denotes the binomial entropy $h(x) = -x\log {x} -(1-x)\log {(1-x)}$, where x takes different values from 0 to 1. The arguments used below are

$$\begin{aligned} p_\nu = \lambda _1 + \lambda _2, \end{aligned}$$

(98)

$$\begin{aligned} p_\sigma = \lambda _1 + \lambda _3, \end{aligned}$$

(99)

which correspond to the fractions of electron neutrinos and right-handed neutrinos, respectively. We denote

$$\begin{aligned} S_0 = - \sum _i a_i \log {a_i}. \end{aligned}$$

(100)

The entropies are expressed as

$$\begin{aligned}&S(\hat{\varrho }_{\nu \sigma }) (0) = S_0, \end{aligned}$$

(101)

$$\begin{aligned}&S(\hat{\varrho }_{\nu }) (0) = h(p_\nu ), \end{aligned}$$

(102)

$$\begin{aligned}&S(\hat{\varrho }_{\sigma }) (0) = h(p_\sigma ), \end{aligned}$$

(103)

$$\begin{aligned}&S(\hat{\varrho }_{R\nu }) (0) = S_0 \end{aligned}$$

(104)

$$\begin{aligned}&S(\hat{\varrho }_{Q\nu }) (0) = 1 + h(p_\nu ). \end{aligned}$$

(105)

$$\begin{aligned}&S(\hat{\varrho }_{\sigma _z}) (0) = h(p_\sigma ), \end{aligned}$$

(106)

$$\begin{aligned}&S(\hat{\varrho }_{\sigma _x}) (0) = 1. \end{aligned}$$

(107)

The conditional entropies are

$$\begin{aligned} S(\sigma \vert \nu )(0)&= S_0 - h(p_\nu ), \end{aligned}$$

(108)

$$\begin{aligned} S(R \vert \nu ) (0)&= S_0 - h(p_\nu ), \end{aligned}$$

(109)

$$\begin{aligned} S(Q \vert \nu ) (0)&= 1. \end{aligned}$$

(110)

The mutual information are

$$\begin{aligned} I(\sigma , \nu )(0) \, \,&= h(p_\sigma ) + h(p_\nu ) - S_0, \end{aligned}$$

(111)

$$\begin{aligned} I(\sigma _z, \nu )(0)&= h(p_\sigma ) + h(p_\nu ) - S_0, \end{aligned}$$

(112)

$$\begin{aligned} I(\sigma _x, \nu )(0)&= 0. \end{aligned}$$

(113)

Since the quantum information $I(\sigma _x, \nu )$ is zero, which is the minimum possible value, the classical correlation

$$\begin{aligned} J_\sigma (\hat{\varrho }_{\nu \sigma })(0) = I(\sigma _z, \nu )(0), \end{aligned}$$

(114)

and the discord is zero because of Eqs. (111) and (112). It is easy to see that for a particular choice of the state Eq. (19), the last term in Eq. (2) is always equal to zero. Therefore, taking into account that $S(R\vert \nu )(0) = S(\sigma \vert \nu )(0)$, the entropic uncertainty relation is satisfied at $t=0$:

$$\begin{aligned} S(Q\vert \nu )(0) = -2 \log c(P, Q) = 1. \end{aligned}$$

(115)

5 Results

In what follows, we consider the density matrix for the ultrahigh-energy neutrino in an interstellar magnetic field obtained through the Lindblad equation and the time-dependent uncertainty relations. As in [18], we use putative magnetic moments $\mu _\nu =2.6\times 10^{-12} \mu _{B}$ and $\mu _\nu = 4.5 \times 10^{-12}\mu _B$ with Bohr magneton $\mu _B = 5.79\times 10^{-9}$ eV/G, which correspond to the upper experimental limit on the dipole magnetic moment of neutrinos obtained from observations of red giants in the globular clusters [35]. Thus, the energy of spin-field interaction is $\mu _\nu B \sim 10^{-25}$ eV. The square mass difference is based on solar neutrino observation $\varDelta m^2 = \varDelta m_\mathrm {solar}=7.37 \times 10^{-5}$ eV$^2$, and the vacuum mixing angle is $\sin ^2 \theta _\nu = 0.297$ [36]. As in the previous work, we focus on ultrahigh-energy neutrinos $E_\nu \sim 10^{20}$ eV consistent with Greisen–Zatsepin–Kuz’min (GZK) cut-off for cosmic particles energy [37, 38]. The oscillation energy of the neutrino in this case is of the same order as the interaction with the magnetic field. To illustrate the interplay between the vacuum and magnetic oscillations, we put the vacuum oscillation and magnetic interaction energies to satisfy $\omega _\mathrm {V}/\omega _\mathrm {B}=5$. The stochastic part of the magnetic field $w^2$ is assumed to be equal to 10% of the total value of B as it is discussed in [19] and [25]. The results are obtained in dimensionless time and energy units of Eq. (52), $1/(2w^2)$ corresponding to the unit on the physical time scale, and all frequencies are normalized as in Eq. (53). The dissipation angle is set equal to $\beta = \pi /4$.

In the initial state at $t=0$, only the right-handed electron neutrinos are present (neutrino flux after passing through a spin filter as it is discussed in [19]):

$$\begin{aligned} \hat{\varrho }(0) = \left| \nu _e^R \right\rangle \left\langle \nu _e^R \right| . \end{aligned}$$

(116)

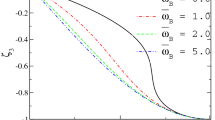
The evolution of the eigenvalues of the full density matrix is shown in Fig. 1.

Fig. 1

Eigenvalues of the full density matrix for the choice of initial condition $\hat{\varrho }^{\mathrm f}(\tau =0) = \mathrm {diag}[1, 0, 0, 0]$ as in Eq. (116). The time scale at the horizontal axis is taken in dimensionless units found by Eq. (52). The corresponding dimensionless frequencies defined as in Eq. (53) for neutrino vacuum oscillations and spin-magnetic field interaction are $\bar{\omega }_{\mathrm V} =5$ and $\bar{\omega }_{\mathrm B}=1$, correspondingly. The stochastic component constitutes 10% of the total magnetic field. The angle parameter is $\beta = \pi /4$ (see Eq. (51)). In real units $\omega _B = \mu _\nu B$, where the interstellar magnetic field is $B = 2.93$ $\mu$G, and $\mu _\nu =2.6\times 10^{-12} \mu _{B}$, with the Bohr magneton $\mu _B = 5.79 \times 10^{-9}$ eV/G. The energy of the spin-field interaction is of the order of $10^{-25}$ eV. The energy of neutrino is of the order $E_\nu \sim 10^{20}$ eV, and the energy of its interaction with the matter is of the order of $10^{-30}$ eV, which can be safely ignored

The eigenvalues of the projected matrices $\hat{\varrho }_{R\nu }$ and $\hat{\varrho }_{Q\nu }$ are shown in Figs. 2 and 3.

Fig. 2

Eigenvalues of the matrix $\hat{\varrho }_{R\nu }$ vs $\tau$ in the same conditions as in Fig. 1

Fig. 3

Eigenvalues of the matrix $\hat{\varrho }_{Q\nu }$ vs $\tau$ in the same conditions as in Fig. 1

We see that after evolving through the Lindbladian channel, the density matrix relaxes, and we observe steady-state oscillations. We plot the entropies required for the calculation of the uncertainty relation. Figure 4 shows the full entropy, as well as the entropies corresponding to the different projected density matrices for the choice of the initial conditions as in Eq. (116). While other entropies exhibit steady-state oscillations with significant amplitude, the reduced density matrix of the spin subsystem becomes constant. This fact shows that spin thermalizes entirely, while the flavour subsystem still possesses coherence. The reason is that the thermal bath, i.e. random magnetic field, is directly coupled to the spin but not to the flavour subsystem. The flavour subsystem experiences the thermalization process only through the spin-flavour oscillation process.

Fig. 4

Dependence of the entropies corresponding to the full ($\hat{\varrho }_{\sigma \nu }$, $\hat{\varrho }_{R\nu }$, $\hat{\varrho }_{Q\nu }$) and reduced ($\hat{\varrho }_\nu$, $\hat{\varrho }_{\sigma }$) matrices on the time parameter $\tau$ for the choice of initial condition as in Eq. (116). Top left corner: the full entropy calculated on the basis of eigenvalues of the full density matrix $\hat{\varrho }_{\sigma \nu }$ expressed by Eq. (66) shown in Fig. 1. The value at $\tau =0$ is 0 and rises as the system thermalizes. Top right corner: entropies of reduced density matrices $\hat{\varrho }_\nu$ and $\hat{\varrho }_\sigma$ expressed by Eqs. (67) and (70), respectively. Bottom: entropies of $\hat{\varrho }_{R\nu }$ (left) and $\hat{\varrho }_{Q\nu }$ (right) calculated with eigenvalues shown in Figs. 2 and 3

The conditional entropies involved in the entropic uncertainty relation are shown in Fig. 5. We see persistent small amplitude oscillations in the steady-state regime.

Fig. 5

Conditional entropies $S(\sigma \vert \nu )$, $S(R\vert \nu )$, and $S(Q\vert \nu )$ as functions of the time parameter $\tau$. The entropies are calculated based on the entropies $S(\hat{\varrho }_{\sigma \nu })$, $S(\hat{\varrho }_{R\nu })$, $S(\hat{\varrho }_{Q\nu })$ and $S(\hat{\varrho }_\nu )$ shown in Fig. 4

The mutual information calculated with these entropies are shown in Fig. 6.

Fig. 6

$\tau$-Dependence of the mutual information defined by Eqs. (83), (88) and (89) for the choice of initial conditions as in Eqs. (116). The equalities follow from the identity of corresponding density matrices due to the specifics of our problem, as it is shown in Eqs. (84) and (86)

According to Eq. (5), the classical correlation is equal to the maximum from the two mutual information $I(\sigma _z, \nu )$ and $I(\sigma _x, \nu )$. As it can be seen, at early stage of evolution, $I(\sigma _x, \nu )>I(\sigma _z)$ and do not coincide with $I(\sigma , \nu )$. This fact confirms that quantum discord is not zero. The classical correlation and discord are shown in Fig. 7. While the classical correlations show thermalized steady-state persistent oscillations, quantum discord shows a more non-trivial behaviour. In the initial state, quantum discord is zero. It becomes nonzero in the transition stage of evolution and tends to zero again after thermalization.

Fig. 7

Classical correlation $J_\sigma (\hat{\varrho }_{\sigma \nu })$ corresponding to the maximal value between $I(\sigma _z, \nu )$ and $I(\sigma _x, \nu )$ and quantum discord $D_\sigma (\hat{\varrho }_{\sigma \nu })$ expressed by Eq. (8), at different values of $\tau$. The time dependence of mutual information is given in Fig. 6

After exploring the particular terms, we analyse the generalized Kraus’s trade-off uncertainty relation Eq. (2). The upper plot in Fig. 8 shows the comparison between entropies and the difference between the discord and classical correlation. The difference between the left- and right-hand sides of Kraus’s trade-off uncertainty relation (2) is shown in the bottom plot. The initial state corresponds to the zero discord. However, discord is generated very promptly, and after propagation on a long distance, discord again decays to zero. In Fig. 8, we see that in Eq. (2), the inequality holds when discord is nonzero, and Eq. (2) turns into equality after discord decays to zero. Thus, we conclude that the discord reduces the lower bound of uncertainty, meaning that condition $D_{EUR}>0$ holds until discord is nonzero, and the maximal value of discord corresponds to the maximum in $D_{EUR}$. After the discord decays to zero, inequality turns into equality $D_{EUR}=0$, meaning that uncertainty reaches its maximum possible value.

Fig. 8

Comparison of different terms in the uncertainty relation (2) (top), and the difference between the left- and the right-hand sides (bottom) at different values of the time parameter $\tau$. $\Lambda$ corresponds to the left-hand side of the uncertainty relation, while $\mathcal {R}[1]$ is the sum of the right-hand side of Eq. (1) and the relative entropy $S(\sigma \vert \nu )$, and $\mathcal {R}[2]$ is the difference between the quantum discord and classical entropy. As it is seen, there is a strict inequality when the system is not thermalized

6 Summary and conclusions

In the present work, we studied ultrahigh-energy neutrino propagation in the interstellar dissipative space. The mathematical problem reduces to the Lindbladian equation written for the density matrix of ultrahigh-energy neutrino. We considered two flavours of neutrino and the effect of spin-flavour oscillations. We obtained the exact analytical solution of the Lindbladian equation and analysed the effect of incompatible invasive measurements and uncertainty relations in particular. Incompatible measurements and corresponding uncertainty relations are still under incisive debate, even for non-relativistic systems. It is known that the best quantifiers of uncertainty are entropic measures which are defined differently and have various interesting features. The concept of a quantum memory was introduced recently and modified in terms of trade-off relation. The trade-off relation contains many terms, such as marginal entropies of the subsystems, quantum, and classical correlation terms. The quantum discord of the ultrahigh-energy neutrino plays the central role in our problem. While marginal entropies show similar behaviour, quantum discord defined through the difference between mutual information and classical correlations shows remarkable features. In the large time interval during the dissipative evolution, quantum discord is nonzero and reduces the uncertainty of incompatible measurements done on the ultrahigh-energy neutrino. This reduction is identified as an effect of the quantum spin-flavour memory hosted by the ultrahigh-energy neutrino.