Abstract
Frames adapted to Kruskal and Novikov coordinate systems are used to compute the energy of the Schwarzschild black/white hole. It turns out that no regularization procedure is necessary if the right hypersurface of simultaneity is used. The importance of using a hypersurface that is consistent with the observers who “measure” the energy is discussed. The effect that the wormhole throat may have on the total energy inside this hypersurface is also discussed; the result shows that this energy becomes the famous \(Mc^2\) only when the throat pinches off completely. The energy of the other universe is calculated. It is shown that, because of reflections at the time and the radial axes of the Kruskal and Novikov frames with respect to the Schwarzschild frame, it is not possible to obtain the energy in both universes “simultaneously.”




Similar content being viewed by others
Data availability
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
Notes
Be aware that the terminology and the definition vary a little in the literature.
By “our universe” we mean the region \(X>0\), including the interior of the black/white hole.
The statement made in Sect. 2.1.3 concerning the divergence of XF can be easily verified from these expressions, which differ from those of our universe only for a minus sign.
This is the same equation as (31.12b) of [18], except for the ± sign in the second term, which is missing in (31.12b).
To see that R diverges, we use (13). In this equation, it is clear that \(R^2\ge r/(2m)-1\). Since r is finite, |R| goes to infinity as m tends to zero.
Because the two terms on the right-hand side of (13) have the same sign, each of these terms has to be finite. In turn, the second term will be finite only if the \(\arccos \sqrt{A}\) goes to zero in such a way that \(R^3\arccos \sqrt{A}\) is finite.
Note that (21) implies
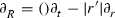 for \(R<0\).
for \(R<0\).
References
J.D. Brown, J.W. York, Phys. Rev. D 47, 1407 (1993). https://doi.org/10.1103/PhysRevD.47.1407
C.C. Chang, J.M. Nester, C.M. Chen, Phys. Rev. Lett. 83, 1897 (1999). https://doi.org/10.1103/PhysRevLett.83.1897
Ṣ Özkurt, S. Aygün, Pramana 88(4), 66 (2017). https://doi.org/10.1007/s12043-017-1367-2
C. Møller, Ann. Phys. 12(1), 118 (1961)
Y.M. Cho, Phys. Rev. D 14, 2521 (1976). https://doi.org/10.1103/PhysRevD.14.2521
Y.M. Cho, Phys. Rev. D 14, 3335 (1976). https://doi.org/10.1103/PhysRevD.14.3335
K. Hayashi, Phys. Lett. B 69(4), 441 (1977). https://doi.org/10.1016/0370-2693(77)90840-1
K. Hayashi, T. Shirafuji, Phys. Rev. D 19, 3524 (1979). https://doi.org/10.1103/PhysRevD.19.3524
J.W. Maluf, Ann. Phys. (Berlin) 525(5), 339 (2013). https://doi.org/10.1002/andp.201200272
J.B. Formiga. The meaning of torsion in teleparallel theories (2020), arXiv: 2004.10788v2
T. Vargas, Gen. Rel. Grav. 36(6), 1255 (2004). https://doi.org/10.1023/B:GERG.0000022386.29438.be
A.A. Sousa, J.S. Moura, R.B. Pereira, Braz. J. Phys 40, 1 (2010)
J.B. Formiga, Ann. Phys. (Berlin) 530(12), 1800320 (2018). https://doi.org/10.1002/andp.201800320
V.C. de Andrade, L.C.T. Guillen, J.G. Pereira, Phys. Rev. Lett. 84, 4533 (2000). https://doi.org/10.1103/PhysRevLett.84.4533
J.W. Maluf, J.F. da Rocha-Neto, T.M.L. Toríbio, K.H. Castello-Branco, Phys. Rev. D 65, 124001 (2002). https://doi.org/10.1103/PhysRevD.65.124001
J.W. Maluf, F.F. Faria, S.C. Ulhoa, Class. Quantum Grav. 24(10), 2743 (2007). https://doi.org/10.1088/0264-9381/24/10/017
J.B. Formiga, Ann. Phys. (Berlin) 532(3), 1900507 (2020). https://doi.org/10.1002/andp.201900507
C.W. Misner, K.S. Thorne, J.A. Wheeler, Gravitation (W.H. Freeman and Company, New York, 1973)
R. Arnowitt, S. Deser, C.W. Misner, Gen. Relativ. Gravit. 40, 1997 (2008). https://doi.org/10.1007/s10714-008-0661-1
Acknowledgements
Victor Gonçalves acknowledges CNPq for financial support.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Appendices
Appendix
The Levi-Civita spin connection of the Kruskal frame
Here, we use the approach developed in [10, 17] to compute the superpotential associated with  . In this approach, one uses a certain coordinate system and at the same time the directions of another coordinate system; for instance, we can use a spherical coordinate system with the frame pointing toward the directions defined by x, y and z. The calculations will be easier to handle in this approach.
. In this approach, one uses a certain coordinate system and at the same time the directions of another coordinate system; for instance, we can use a spherical coordinate system with the frame pointing toward the directions defined by x, y and z. The calculations will be easier to handle in this approach.
From the spherical coordinate system in a flat manifold, we can define the vector components

When the spacetime is curved, we can still use (26) to simplify the expressions by defining the new components  ,
,  ,
,  ,
,  , which allows us to write the frame as
, which allows us to write the frame as

Note that we can raise and lower indices easily:  . It should also be clear that \({\hat{t}}^\mu {\hat{t}}_\mu ={\hat{t}}^a{\hat{t}}_a=1\), \({\hat{r}}^\mu {\hat{r}}_\mu ={\hat{r}}^a{\hat{r}}_a=-1\) and so on.
. It should also be clear that \({\hat{t}}^\mu {\hat{t}}_\mu ={\hat{t}}^a{\hat{t}}_a=1\), \({\hat{r}}^\mu {\hat{r}}_\mu ={\hat{r}}^a{\hat{r}}_a=-1\) and so on.
Comparing Eq. (8) with (27), we find that
where we have used the metric (5) in the last expression.
To calculate the spin connection, we need first the commutation coefficients of  . Since \({\hat{r}}^a\), \({\hat{\theta }}^a\), and \({\hat{\phi }}^a\) depend only on \(\theta \) and \(\phi \), and we are using the coordinates \(x^\mu =(T,X,\theta ,\phi )\), we can calculate them by using (for more details, see section VII of [10])
. Since \({\hat{r}}^a\), \({\hat{\theta }}^a\), and \({\hat{\phi }}^a\) depend only on \(\theta \) and \(\phi \), and we are using the coordinates \(x^\mu =(T,X,\theta ,\phi )\), we can calculate them by using (for more details, see section VII of [10])





To calculate the component (31), we apply  to \({\hat{t}}_\mu \) given by (29). The result is
to \({\hat{t}}_\mu \) given by (29). The result is  , where \(F'\equiv \partial _X F\). From (29), one easily sees that \(\delta ^2_{[\mu }{\hat{\theta }}_{\nu ]}=\delta ^3_{[\mu }{\hat{\phi }}_{\nu ]}=0\). So, the component
, where \(F'\equiv \partial _X F\). From (29), one easily sees that \(\delta ^2_{[\mu }{\hat{\theta }}_{\nu ]}=\delta ^3_{[\mu }{\hat{\phi }}_{\nu ]}=0\). So, the component  can be obtained by applying
can be obtained by applying  to \({\hat{r}}_\nu \). Using (29), we find that
to \({\hat{r}}_\nu \). Using (29), we find that  , where \({\dot{F}}\equiv \partial _T F\). From the expression of \({\hat{r}}_\mu \) in (29), we obtain \(2\delta ^2_{[\mu }{\hat{r}}_{\nu ]}=2F\delta ^1_{[\mu }\delta ^2_{\nu ]}\) and \(2\partial _{[\mu }{\hat{\theta }}_{\nu ]}=-2\left( {\dot{r}}\delta ^0_{[\mu }\delta ^2_{\nu ]}+r' \delta ^1_{[\mu }\delta ^2_{\nu ]} \right) \). Thus, we have
, where \({\dot{F}}\equiv \partial _T F\). From the expression of \({\hat{r}}_\mu \) in (29), we obtain \(2\delta ^2_{[\mu }{\hat{r}}_{\nu ]}=2F\delta ^1_{[\mu }\delta ^2_{\nu ]}\) and \(2\partial _{[\mu }{\hat{\theta }}_{\nu ]}=-2\left( {\dot{r}}\delta ^0_{[\mu }\delta ^2_{\nu ]}+r' \delta ^1_{[\mu }\delta ^2_{\nu ]} \right) \). Thus, we have  . A similar procedure for (34) will lead us to
. A similar procedure for (34) will lead us to  . Now, we use (29) to eliminate the deltas in these expressions. This gives
. Now, we use (29) to eliminate the deltas in these expressions. This gives



Substituting Eqs. (35)–(37) into Eq. (30), and using the fact that \({\dot{F}}/F^2=\left( 1+2m/r\right) FT/(16m^2)\) and \(F'/F^2=-\left( 1+2m/r\right) FX/(16m^2)\), we arrive at

where we have used \({\dot{r}}=-F^2T/(4m)\), \(r'=F^2X/(4m)\) , and \(W_+\equiv 1+2m/r\).
To calculate the coefficients of the Levi-Civita connection in the basis  , we use Eqs. (3) and (38). In this calculation, we only need to focus on the permutation of the elements \(\{{\hat{t}},{\hat{r}},{\hat{\theta }},{\hat{\phi }}\}\). For instance, the term \({\hat{t}}_{[c}{\hat{r}}^{a]}{\hat{t}}_b+{\hat{t}}_{[b}{\hat{r}}^{a]}{\hat{t}}_c-{\hat{t}}_{[b}{\hat{r}}_{c]}{\hat{t}}^a\) can be simplified to \(-2{\hat{t}}_b{\hat{t}}^{[a}{\hat{r}}_{c]}\). Doing the same for the other terms, we obtain
, we use Eqs. (3) and (38). In this calculation, we only need to focus on the permutation of the elements \(\{{\hat{t}},{\hat{r}},{\hat{\theta }},{\hat{\phi }}\}\). For instance, the term \({\hat{t}}_{[c}{\hat{r}}^{a]}{\hat{t}}_b+{\hat{t}}_{[b}{\hat{r}}^{a]}{\hat{t}}_c-{\hat{t}}_{[b}{\hat{r}}_{c]}{\hat{t}}^a\) can be simplified to \(-2{\hat{t}}_b{\hat{t}}^{[a}{\hat{r}}_{c]}\). Doing the same for the other terms, we obtain

From this connection, we can compute all quantities of interest, regardless of the nature of the indices. For instance, if we want  , we can simply change a to \(\lambda \) and use (28). (Note that
, we can simply change a to \(\lambda \) and use (28). (Note that  .).
.).
From (39), (2), (1), and (28), we obtain  , where we have used the fact that \(T^{\lambda a}=0\) (there is no matter field). Finally, integrating
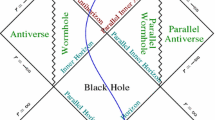
, where we have used the fact that \(T^{\lambda a}=0\) (there is no matter field). Finally, integrating  in the region indicated by a horizontal line on the right side of Fig. 2, and using \(e=32m^3\exp [-r/(2m)]r\sin \theta \), we obtain (9).
in the region indicated by a horizontal line on the right side of Fig. 2, and using \(e=32m^3\exp [-r/(2m)]r\sin \theta \), we obtain (9).
Rights and permissions
About this article
Cite this article
Gonalves, V.R., Formiga, J.B. The black hole energy and the energy of the other universe. Eur. Phys. J. Plus 136, 1063 (2021). https://doi.org/10.1140/epjp/s13360-021-02062-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjp/s13360-021-02062-y




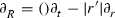 for
for