1 Introduction

Chirality is an asymmetry important in science and technology and confined mainly to the quantum realm. For instance, chirality is commonly associated with the spatial geometry of the atoms composing molecules, the biochemistry of living organisms, and spin properties  [1, 2]. This association with quantum phenomena poses a very natural question: is it possible to identify chiral manifestations arising in phenomena governed by purely classical (that is, not quantum) equations?

The purpose of this paper is to report the observation of chiral structures in a rather unsuspected scenario, namely in the complex but regular way that spikes (i.e., local maxima) of periodic oscillations organize themselves when control parameters are continuously varied in Hartley’s electronic oscillator (Fig. 1), a circuit governed by rate-equations, namely by purely classical (that is, not quantum) equations of motion. Apart from the theoretical novelty, this new nonquantum form of chirality offers interesting opportunities to investigate and to apply hitherto unsuspected properties of complex nonlinear oscillators governed by purely classical equations of motion.

The availability of high-performance computers, combined with fast and reliable numerical methods, allows now the production of cartographic charts summarizing with unprecedented detail the behavior of several millions of individual oscillations and exposing patterns created by oscillations and waveforms when control parameters are tuned continuously. As shown in Figs. 2, 3, and 4, such charts reveal remarkable and unanticipated chiral patterns created collectively by large sets of oscillations and waveforms when control parameters are tuned continuously.

Before proceeding, it is important to emphasize from the outset that the chiral patterns reported here are obtained from computer simulations, and that they cannot be predicted theoretically due to the total absence of an adequate framework to solve analytically systems of coupled nonlinear differential equations. As described below, chiral patterns emerge as a collective property of millions of oscillations. Fortunately, however, they may be validated experimentally.

Fig. 1
figure 1

Schematic diagram of a Hartley’s oscillator with a JFET and a tapped coil as investigated experimentally. See text

Full size image
Fig. 2
figure 2

Stability phases recorded by counting spikes for the voltages and currents \(v_{GS}, v_{GD}, i_1, i_2\). Colors refer to the number of spikes per period, black denotes lack of periodicity (“chaos”). The number of spikes per period depends on the variable used to count them. Parameter circuits, rings, are formed by interconnections of the four “legs” emanating from, e.g., the upper and lower shrimps [19, 21, 22, 24]. Such rings contain chiral structures, shown magnified in Figs. 3 and 4. Capacitances are measured in pF and inductances in \(\mu \)H. Individual panels display the analysis of grids with \(1200\times 1200=1.44\times 10^6\) equally spaced parameter points

Full size image
Fig. 3
figure 3

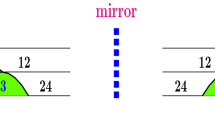
Top row: The leftmost panel, a magnification of box R in Fig. 2, illustrates chiral walls with number of spikes oriented clockwise (after a rotation of 180 degrees) and anticlockwise inside boxes C and A, respectively. Bottom row: Schematic representation of the C and A walls, which are artful images of each other when reflected on a mirror, indicated by the red dashed vertical line. Parabolas contain odd numbers of spikes, arising from spikes additions. Parabolic phases give rise to spikes-doubling cascades. The vertices of each parabola are quint points [17], where five distinct stability phases meet

Full size image
Fig. 4
figure 4

Details of a ring with two pairs of chiral walls. Top row: Walls located on the outer loop of the ring. Bottom row: walls bridging the three legs passing through box M. Chiral walls are needed to ensure proper continuity of the stability phases. X and Y are enantiomers interconnecting the inside and outside of the ring. C and A refer to clockwise or anticlockwise wall orientations. Box R is shown magnified in Fig. 3

Full size image

2 The oscillator of Hartley

Chiral structures were found while studying the inductor-based Hartley’s oscillator, the dual circuit of the more familiar capacitor-based Colpitts oscillator [3, 4]. These two oscillators were introduced in the 1910s, in the early days of transatlantic radiotelephone communications, and which are still used in modern communication systems [3, 4]. Exceedingly complex oscillations generated by Hartley’s oscillator were reported recently in several works [5,6,7,8,9].

The nonlinear oscillator considered here is shown schematically in Fig. 1. It represents an inexpensive N-channel silicon BF245a JFET and the usual tapped coil as studied experimentally by Tchitnga et al. [6]. Neglecting the internal resistance of the coil and using a high-frequency small-signal equivalent of the JFET, the equations governing the circuit are [6, 7]:

$$\begin{aligned} {C_{GS} \frac{dv_{GS}}{dt}}= & {} {-i_1 + i_2 -i_D -i_d}, \end{aligned}$$
(1)
$$\begin{aligned} {C_{GD} \frac{dv_{GD}}{dt}}= & {} {-i_2 +i_d}, \end{aligned}$$
(2)
$$\begin{aligned} {L_1 \frac{di_{1}}{dt}}= & {} {v_{GS}}, \end{aligned}$$
(3)
$$\begin{aligned} {L_2 \frac{di_{2}}{dt}}= & {} {-v_{GS}+v_{GD}+E}, \end{aligned}$$
(4)

where D, S, G refer to the drain, source, and gate of the JFET, respectively, and \(i_D={I_S \left[ \exp \left( {v_{GS}}/{V_T}\right) -1 \right] }\) with

$$\begin{aligned} {i_d}= & {} \left\{ \begin{array}{l l} {0}, &{} \hbox {if }{v_{GS} \le V_c}, \\ {g(v_{GS}-V_c)^2}, &{} \hbox {if }{v_{GD} \le V_c}, \\ {g(v_{GS}-v_{GD})(v_{GS}+v_{GD}-2V_c)}, &{} \hbox {if }{v_{GD} \ge V_c}. \end{array} \right. \end{aligned}$$

In these equations, \(C_{GD}\) stands for the capacitance between gate and drain, \(i_1, i_2\) are the currents across the inductance parts \(L_1\) and \(L_2\), respectively. Here, \(I_S\) is the reverse saturation current flowing through the diode, and \(V_{GS}\) and \(V_{GD}\) are the voltages across the parasitic capacitors \(C_{GS}\) and \(C_{GD}\), respectively, while g is the current gain of the JFET, while E is the bias voltage source. Tchitnga et al. [6] reported finding chaos when using the following parameter values: \(C_{GS} = 3.736\) pF, \(C_{GD} = 3.35\) pF, \(I_S = 33.57\) fA, \(V_c = -1.409\) V, \(V_T = 25\) mV, \(E=2.8\) V, \(g = 1.754\) mAV\(^2\), \(L_1 = 24.5\) \(\mu \)H and \(L_2 = 4\) \(\mu \)H. Here, we investigate what happens if one lets two specific parameters vary while keeping all other parameters fixed at the aforementioned values, namely we classify oscillations for hundreds of millions of \(C_{GD}\) and \(L_2\) values. In experiments, \(C_{GD}\) may be simulated using operational amplifiers. The classification is done using isospike stability diagrams  [10,11,12,13,14,15,16,17,18], the flow version of the isoperiodic stability diagrams commonly used for maps  [19,20,21,22, 24]. Briefly, for a given set of parameters, we numerically integrate the equations of motion recording the number of spikes per period for all periodic oscillations. The number of spikes per period is arguably the simplest possible indicator that may be extracted from nonlinear oscillations. To count oscillation spikes is easy to do in a very reliable way. The fruitful isospike technique to classify complex oscillations is discussed in-depth in recent literature  [10,11,12,13,14,15,16,17,18].

3 Chirality from Hartley’s nonquantum oscillator

Figure 2 shows stability diagrams obtained by counting the number of spikes (i.e., local maxima) of the periodic oscillations for the four independent variables of Hartley’s oscillator. In these diagrams, it is possible to recognize a number of stability rings [25], namely cascades of adjacent closed parameter circuits, which are the objects of interest here.

In Fig. 2, colors are used to represent stability phases characterized by periodic oscillations while black marks parameters for which nonperiodic oscillations (chaos) are found. The number of spikes per period is plotted by “recycling” colors modulo 17. Similarly to the differences familiar from phase-space projections of attractors, the parameter sections in Fig. 2 display distinct aspects of the control parameter space when inspected using different variables. Although the number of spikes per period may differ in distinct panels, the oscillation period measured is always the same, independently of the variable used to record them. Clearly, all four phase diagrams in Fig. 2 produce identical boundaries between phases of periodic oscillations and the black phase representing chaos. Although the shape and extension of the periodic phases agree for all four variables, the number of spikes of individual phases depends significantly on the variable used to determine them.

As can be seen from Fig. 2, rings with multiple adjacent circuits are formed by interconnecting two shrimps  [19,20,21,22,23,24], one upper and one lower shrimp, as indicated in the panel for \(v_{GS}\). Shrimps are complex structures with four main legs displaying infinite successions of spikes-doubling cascades of periodic oscillations in addition to the chaotic phases that follow them. For more details about shrimps, see Refs. [11, 19,20,21,22,23,24], and references therein.

Of interest to us in Fig. 2 are color changes occurring along two stability rings characterized by periodic oscillations, namely along the large ring-shaped structure with boxes M,X,A,C spread along it, and the smaller but similar ring inside box R. As it is clear from the figure, while the \(i_1\) ring displays a homogeneous color, the three others are multicolored, indicating that changes in the number of spikes occur when parameters are tuned along such rings. Transversally, rings are formed by juxtaposition of phases corresponding to spikes-doubling cascades \(u\times 2^n\), where u is a positive integer and \(n=0,1,2,\ldots \), plus a chaotic phase which exists at the “end” of the adjacent period-doubling phases, as discussed elsewhere  [11, 13, 19].

The rings in Fig. 2 are formed by the union of the four main “legs” of two shrimps [19], with three legs interconnected inside and near box M, and the remaining legs forming the large outer loop passing through the small boxes labeled X,A,C. Therefore, longitudinal color changes along rings imply the necessity of having more than one distinct transversal spikes-doubling cascade of the type \(u\times 2^n\), in order for the several distinct colors to be able to match continuously, as spikes keep being continuously added more and more. In other words, the question now is to see how such colors should match each other. The remainder of the paper shows that color changes seen along the rings in Fig. 2 are mediated by two exquisite adding–doubling complex but regular dual structures (shown schematically in the bottom row of Fig. 3), which act as chiral walls separating harmoniously all stability phases of pairs of adjacent spikes-doubling cascades, say \(u\times 2^n\) and \(v\times 2^n\), where \(u,v>0\) are integers.

4 The dual chiral walls

The top row in Fig. 3 shows a magnification of box R in Fig. 2 and illustrates the first and simplest example of dual chiral walls. The two rightmost panels of Fig. 3 show details of the complex but regular walls of spikes that separate the outermost \(5\times 2^n\) and \(6\times 2^n\) cascades. The bottom row of Fig. 3 shows a sketch of the dual unfolding of the first four levels of spikes adding and spikes doubling for the clockwise and anticlockwise oriented chiral walls as reflected by the red dashed vertical line representing a mirror. Parabolas contain odd numbers of spikes, arising from spikes additions. Parabolic phases give rise to spikes-doubling cascades. Such walls mediate color changes between longitudinal segments characterized by periodic oscillations following distinct spikes-doubling cascades, namely \(5\times 2^n\) and \(6\times 2^n\). When juxtaposed, these subtly intricate adding–doubling walls mediate stable oscillations with number of spikes defined by their outermost shells of spikes doubling. Note the fast proliferation of stability phases as the number of spikes grow.

Although a cursory comparison of the two walls may give the impression that their complex unfolding coincides, this is not the case: such walls form a regular and artfully asymmetric chiral pair. To see this, compare cascades \(u\times 2^n\) and \(v\times 2^n\), using the number of spikes where the cascades start, namely (u, v). When rotated to facilitate the comparison, one of the walls seen in Fig. 3 is a (5, 6) wall while the other one is a (6, 5) wall. For easy reference, when \(u<v\) we say that the chiral wall is of type C, clockwise oriented, and when \(u>v\), of type A, anticlockwise. To display two colors, the closed ring in Fig. 3 must obviously contain a pair of chiral walls. The presence of just a single or f an odd number of walls is forbidden because it would be then impossible to match stability phases when circulating along the ring. Thus, closed loops demand the presence of none or of an even number of chiral structures for colors to match, i.e., to harmoniously interconnect distinct spikes-doubling cascades. No chiral doublets exist along the three inner legs interconnecting the two shrimps which are seen on the leftmost ring half. However, changes along inner triplets of legs are possible, as illustrated in Fig. 4.

Figure 4 shows a more elaborated ring, containing two additional color changes than Fig. 3, illustrating the presence of four chiral walls. The top row of Fig. 4 illustrates a situation similar to the one in Fig. 3, but with an additional wall inside box X. As it is known, shrimps have four major legs [19] and box X contains the wall on the leg outside box M, the box which the three other legs cross. Clearly, this is why these two color changes require four chiral walls. On the bottom row, the leftmost panel illustrates walls C and A branching out from a \(6\rightarrow 12\rightarrow \cdots \) cascade. The wall inside box Y arises from a similar branching out, involving the chiral partner located inside box X seen on the top row of Fig. 4. Thus, in contrast to the simpler ring in Fig. 3, here the interconnection of the three stability phases passing through box M involves color changes, namely two distinct spikes-doubling oscillation cascades as parameters are suitably tuned. As before, stability loops of oscillations display only an even number of color changes.

There are several more additional walls mediating cascades along the many filaments seen on the two leftmost panels of Fig. 4. Such filaments are stable phases of periodic oscillation and provide unambiguous evidence of the existence of a myriad of additional chiral walls in the stability diagram of Hartley’s oscillator. In general, it can be difficult to ascertain whether or not the filaments form rings because they get exceedingly thin very fast as parameters are tuned. In this context, an open and rather computer-demanding task is to investigate whether or not chiral walls appear always in pairs in the control parameter space, when rings are not clearly discernible. Be it as it may, chiral walls are also found to exist abundantly over other broad regions of the parameter space (not shown here). Chiral walls were also found in other parameter sections of the control space of Hartley’s oscillator (also not shown here). We see no reason for chiral walls not to exist in the control space of other complex oscillators governed by classical equations of motion.

5 Conclusions and outlook

As summarized schematically at the bottom row of Fig. 3, adding–doubling chiral walls exist in the control parameter planes of Hartley’s electronic oscillator. Such walls mediate distinct spikes-adding and -doubling cascades of stable oscillations of the electronic circuit. The discovery of chiral walls is significant because they arise from Hartley’s oscillator which is governed by classical, i.e., nonquantum, equations of motion. In other words, the chiral asymmetry arising from Hartley’s oscillations is not related to the known chiral asymmetry of quantum origin. Here, subtly intricate and artfully asymmetric structures are found to be active in an unanticipated physical scenario, mediating families of stable classical oscillatory modes and allowing multicolored closed parameter paths in the control space of the oscillator.

As already mentioned, it is important to keep in mind that chiral structures, as well as all other structures seen in Figs. 2, 3, and 4, can be observed only through either computer simulations or experimental work. The reason for this is that these intricate dynamical behaviors are difficult, not to say impossible, to establish theoretically due to the total absence of any adequate framework to obtain analytical solutions over arbitrary parameter ranges for systems of nonlinearly coupled differential equations. Fortunately, chirality produced by classical oscillators is clearly accessible to experimental validation. A number of much more complex parameter paths may be recognized at smaller and smaller scales, particularly in Fig. 2a and d. These more elaborate loops and shrimps will be discussed elsewhere.

From an applied point of view, the existence of chirality in Hartley’s oscillator is a most surprising phenomenon. Chiral fingerprints in a nonquantum system revise current knowledge about the intricate topology of the control space of a prototypical oscillator, and offer opportunities to investigate hitherto unsuspected properties and the whys and wherefores of oscillators governed by totally classical equations of motion. For instance, which phase-space mechanisms are at the origin of chirality at a classical level? It is observed that the unfolding of the dual walls in Fig. 3 depends exclusively on the relative magnitude of the integers u and v where they start. A challenging open question is to understand the underlying dynamical mechanisms leading to the selection of either \(u<v\) or \(u>v\), as well as to the observed order A,C or C,A of the walls spread along rings and filaments. Finally, we briefly mention that we observed chirality in other nonlinear oscillators governed by classical equations of motion, e.g., in two complex chemical oscillators, namely in the Brusselator and in the Belousov–Zhabotinsky reaction, results to be reported in due course. Accordingly, we expect chirality generated by classical equations to be a generic property of a wide class of oscillators and to underly interesting novel applications. An enticing open question is to find a discrete-time dynamical system, a map, able to display chiral structures in the classical world.