1 Introduction

At the very base of any physical theory phenomenological numerical parameters are found; generally assumed space-time independent, they are the fundamental constants. In general not all of them can be considered ranking at the same level and are classified according to the role played in the present vision of Nature. Nowadays Newton’s gravitation constant G, the speed of the light c and Planck constant \(\hbar \) alone are believed universal [1,2,3,4,5,6]. In general the constants are dimensionful but, by algebraically combining them, it is possible to obtain dimensionless quantities; the most famous of these being the fine-structure constant \(\alpha \equiv e^2/(\hbar c)\) with e the positive elementary electric charge. The main reason of the celebrity is to be looked for in the fact that \(\alpha \) gives the strength of the electromagnetic interaction but a role has been played also by its value because the number \(137 \cong \alpha ^{-1}\) has excited the curiosity being a prime number.

The constants c, \(\hbar \) and e represent limiting quantities: they are the natural units for velocity, angular momentum and electric charge. Of course their value depends on the units and on their operational definition. For example, Bridgman [8] showed that the speed of the light can be made infinite by a change of the operational definition; in this way it appears to be the limiting speed of any material object and the speed of a massless particle. Moreover in modern Quantum Field Theory the value of the coupling constants of renormalisable theories is not even constant and depends upon the energy scale.

Historically, by using a heuristic approach, Dirac [9] was the first to conjecture that the physical parameters might be variable, hypothesising that the value of G is time dependent and decreases with a time scale of the order of the age of the Universe. Dirac’s argument and its implication on the Earth’s evolution and temperature were discussed and constraints set on \({\dot{G}}/G\) [5, 7, 10]. Further experimental evidence suggested that G might present oscillations with period \(T_G\approx 6\) yr [11] and induced new theoretical and experimental research to confirm and explain such a putative variation [12,13,14,15,16,17,18]. Data analyses are made difficult by the fact that, in Newton gravitation law, G is always found multiplied to the gravitational masses of the interacting bodies; but these masses are usually changing because of stellar wind and accretion from falling objects [19]. Moreover, precise measurements of G are intrinsically difficult and often comparison between data are made complex by the different experimental methods used [20]. Entangled with this problem is the one related to the constancy of the speed of the light which has profound influence on cosmological theories [21,22,23,24] and in the existence of a privileged frame (see the discussion in [25]).

Astrophysical data analyses have been hinting that \(\alpha \) might be time dependent [26] however additional surveys give a value of \(\varDelta \alpha /\alpha \) compatible with a null value [27, 28]. Further evidence suggests for \(\alpha \) an opposite variation in two different directions of the space and implies a dipolar spatial property [29,30,31]. Of course, if real, there is not any indication to which of the parameters entering \(\alpha \) might cause the variation and an earnest debate is evolving if it is even meaningful to speak of variations for dimensionful parameters [2, 22, 32,33,34].

Recently the idea that the Plank constant might be space dependent has been put forward by Kentosh and Mohageg [35] and Hutchin [36]. Kentosh and Mohageg report a discrepancy on the rate of atomic clocks in orbiting GPS satellites correlated to the distance of the satellite from the Earth; the analyses give the upper limit \(\varDelta \hbar /\hbar <7\times 10^{-3}\).

A survey of 20 years long collected data suggests an annual variation of strong and weak nuclear decay rates [36]; the maximum-minimum points were reported in winter and summer (in northern hemisphere), when Earth is located close to the perihelion—aphelion axis of its orbit. The interpretation is that \(\hbar \) is space dependent. An ad hoc designed pure electromagnetic experiment [36] confirmed the hypothesis setting \(\varDelta \hbar /\hbar \le 29\times 10^{-6}\) across the Earth orbit. The evidence thus is that \(\hbar \) might be space dependent because of a change in the gravitational potential energy in satellite and Earth orbit and/or because of a cosmological dipolar moment. The hypothesis of a dipolar moment is a far reaching one as introduces a privileged direction perhaps to be related, we imagine, to a residual angular momentum of the Universe. New evidence seems to support this possibility. Actually the Universe is constituted by a network of filaments, slender cylindrical structures of galaxies about \(10^8\) light years long and a few \(10^6\) light years of diameter, which appear to be spinning around their axis [37]. Filaments are the largest recognised structures of the Universe; their angular momentum gives a privileged direction to the local space. If future analyses could assess whether the individual angular momenta add up to a net angular momentum would be of paramount importance. But, of course, nothing prevents that the local properties of different volumes of the universe may be different. Back to our own problem, the evidences, although contrasted and not generally accepted, have inspired new theories [38,39,40] and stimulated laboratory experiments [41,42,43,44] to check for the variation of the physical constants.

This paper deals with a theoretical investigation on a pure spatial dependence of \(\hbar \), benchmarking it with a daily variation. Experiments, to be implemented on an Earth based laboratory, are proposed with the goal of setting a constraint on the value of the dimensionless ratio \(\varDelta \hbar /\hbar \). The experiments use a quantum object, for brevity sake referred to as atom, resonantly coupled to a short laser pulse that induces fast oscillations of the wave function of the atom. The atom is let to interact with two equal laser pulses separated by a delay time of the order of hours. Within the assumed hypothesis, we show that the change of the value of \(\hbar \) produces tiny different evolutions of the wave function which can or cannot be observed. In this way a limit to the value of \(\varDelta \hbar /\hbar \) can be set.

2 Model

If real, the variation of \(\hbar \) is small and introduces tiny effects in the evolution of a quantum system and can easily escape observation. Thus it is important to find methods that enhance the dynamics of the atom and, through cumulative effects, produce sizeable results. It is well known that an electromagnetic field, of angular frequency \(\omega _L\) and resonant with an atomic Bohr transition, produces deep and fast oscillations of the wave function between the two coupled states; thus it is natural to study a resonantly coupled laser-atom system to investigate the problem of variation of \(\hbar \). In our treatment to make easy the visualisation of the process, we adopt all simplifying assumptions that permit the understanding of the underlying physics without spoiling it. For the sake of simplicity hereafter we consider a one-electron atom described by the Hamiltonian

$$\begin{aligned} {\hat{H}}_0=\frac{\hat{\varvec{p}}^2}{2m}+U(\varvec{r}) \end{aligned}$$
(1)

with \(U(\varvec{r})\) an effective potential which takes into account the multi-electron nature of the atom.

In general \(U(\varvec{r})\), when describes the intra-atomic potential, is taken spherically symmetric; among the most used forms we find the soft-Coulomb potential

$$\begin{aligned} U_{SC}(r)=-\frac{Q^2}{\sqrt{r^2+a^2}} \end{aligned}$$
(2)

and the Poschl–Teller potential

$$\begin{aligned} U_{PT}(r)=-\frac{U_0}{\cosh ^2(r/a)} . \end{aligned}$$
(3)

By a suitable choice of the free parameters, the energy gap between two bound states or the size of a real atom can be recovered. In both forms the free parameter a is of the order of the Bohr radius \(a_0=5.29\times 10^{-9}\) cm and provides the atomic size [45, 46].

In Ref. [40] a model has been developed that considers the Planck constant as time dependent \(\hbar =\hbar _0f(t)\) with \(\hbar _0\) the nominal value of the Planck constant. The main result is that it is possible to introduce a new time standard

$$\begin{aligned} \tau =\int _0^t f(t') dt' \end{aligned}$$
(4)

which modifies the form of the usual Schrödinger equation into

$$\begin{aligned} i\hbar _0 \frac{\partial }{\partial \tau }\psi (\varvec{r},\tau )= \left\{ {\hat{H}}_0+{\hat{V}}(\varvec{r},\tau )+ \eta (\tau ) [U(\varvec{r})+{\hat{V}}(\varvec{r},\tau )]\right\} \psi (\varvec{r},\tau ) \end{aligned}$$
(5)

where \({\hat{H}}_0\) is the atomic Hamiltonian operator written in terms of \(\hbar _0\) (throughout this paper the index 0 refers to the standard theory), \(U(\varvec{r})\) is the static potential energy experienced by the particle (for example \(U_{SC}\), \(U_{ST}\) or even the Coulomb potential), \({\hat{V}}(\varvec{r},\tau )\) an eventual time dependent interaction energy (such as the one given by the presence of a laser field); moreover:

$$\begin{aligned} \frac{1}{f(\tau )}=1+\epsilon (\tau ) \end{aligned}$$
(6)

and

$$\begin{aligned} \eta (\tau )=\epsilon (\tau )[2+\epsilon (\tau )] . \end{aligned}$$
(7)

Thus, one sees that whenever \(\eta \ll 1\) (practically always), the time dependence of \(\hbar \) introduces a perturbation in the evolution of the particle. The dual role of the potential energy \(U(\varvec{r})\) is note worth: it acts as the potential energy inside \({\hat{H}}_0\), and as a time dependent perturbation in the full Hamiltonian. In this way without interaction the form of the plane wave is not affected by the change of \(\hbar \).

Now, let us assume that \(\hbar \) is position dependent:

$$\begin{aligned} \hbar =\hbar _0g(\varvec{r}) ; \end{aligned}$$
(8)

in the laboratory rest frame we make the ansatz that such a dependence is equivalent to a time dependence with the substitution \(\varvec{r}\rightarrow \varvec{r}(\tau )\) making the use of Eq. (5) possible.

With respect to some inertial frame, such as Virgo super cluster of Galaxies, the motion of an Earth based laboratory is very complex. For example a point at the equator moves with a speed of \(4.6\times 10^2\) m/s with respect to the center of Earth, while the Earth moves around the Sun with a speed of \(3\times 10^4\) m/s while the Sun moves with a speed of \(\sim 10^5\) m/s around the center of the Milk Way which speeds at \(\sim 10^6\) m/s towards a Great Attractor [47] all of this omitting the lunar and planetary perturbations that make the motion of the planets chaotic. Inspired by Heraclitus we may say that no man ever walks under the same sky twice. Things thus standing, the choice of a particular \(\varvec{r}(\tau )\) requires the adoption of a specific model. Motivated by [35, 36] and for definiteness sake, we take into consideration the motion of a laboratory about the Earth polar axis and assume that \(\hbar (\varvec{r})\) depends only on the projection of the laboratory position along a privileged axis here assumed to be the x axis:

$$\begin{aligned} x=R\sin (\omega _E\tau +\phi ) \end{aligned}$$
(9)

with R and \(\omega _E=2\pi /86400\) sec\(^{-1}\) the laboratory distance from the polar axis and Earth angular velocity around it. This is the simplest way to describe a dipolar spatial dependence of \(\hbar \) with respect to some fixed direction and has been suggested in [6] to model a potential spatial dependence of \(\alpha \). According to our hypothesis we make the ansatz that

$$\begin{aligned} f(\tau )=1+\gamma \sin (\omega _E\tau +\phi ) \end{aligned}$$
(10)

with \(\gamma \ll 1\).

2.1 Approximated approach

The smallness of \(\gamma \) can be exploited to simplify the equation and to gain insight on the physics of the process. Thus

$$\begin{aligned} \frac{1}{f(t)}\cong 1-\gamma \sin (\omega _Et+\phi ) \end{aligned}$$
(11)

and

$$\begin{aligned} \eta (\tau )\cong -2\gamma \sin (\omega _E \tau +\phi ) . \end{aligned}$$
(12)

In absence of an external time dependent driving field (i.e. \({\hat{V}}(\varvec{r},\tau )=0\)) the Schrödinger equation becomes:

$$\begin{aligned} i\hbar _0 \frac{\partial }{\partial \tau }\psi (\varvec{r},\tau )\cong \left\{ {\hat{H}}_0-2\gamma U(\varvec{r})\sin (\omega _E\tau +\phi )\right\} \psi (\varvec{r},\tau ) \end{aligned}$$
(13)

the Hamiltonian \({\hat{H}}_0\) describes a freely evolving atom and contains in it all the atomic parameters such as energy levels, time and space scales. The full Hamiltonian is suggestive as, in first approximation, is equivalent to the one of an atom in the presence of a periodic field of angular frequency \(\omega _E\) but of course the period of the equivalent field \(T_E=1\) day is many orders of magnitude longer than any atomic period. As a consequence, the atom initially in an eigenstate of \({\hat{H}}_0\) after a time lapse will be found in a different state; in principle \(\hbar (\varvec{r})\) destroys all quantum correlations and cooperates with other decorrelating effects such as spontaneous decay. Thus the variation of a physical constant shuffles the cards and unveils new Physics. We consider Eq. (13) one of the main results of this Paper.

2.2 Introducing a laser field

The small variation of \(\hbar \) guarantees, in everyday life, the use of the standard Quantum Physics; it is therefore of paramount importance to find a way of speeding up the evolution of the physical system whereby the variation of \(\hbar \) can be revealed. This can be achieved by use of a laser field with photon energy resonant with an atomic transition. In fact the resonance enhances the electron dynamics and induces rapid exchange of electronic population between the coupled levels. Such a configuration has been indicated as particularly favourable to fathom the core laws of quantum mechanics [48,49,50,51,52,53,54,55].

In solving Eq. (5) for an atom in the presence of a laser field of nominal frequency \(\omega _L\), we exploit the resonance condition by taking into account only the two atomic states coupled by the laser which is a standard approximation in the theory of laser-atom interaction [56]; thus the wave function of the atom can be written as

$$\begin{aligned} |\tau \rangle =a_\phi (\tau )|0;1\rangle +b_\phi (\tau )|0;2\rangle \end{aligned}$$
(14)

where \(|0;1\rangle \) and \(|0;2\rangle \) are two orthonormal eigenstates of the bare and unperturbed atom:

$$\begin{aligned} {\hat{H}}_0|0;n\rangle =\hbar _0\omega _n^{(0)}|0;n\rangle , \quad n=1,2 \end{aligned}$$
(15)

which are assumed real and endowed of well defined and opposite parity.

Substitution of \(|\tau \rangle \) into the Schrödinger equation gives the following set of two coupled differential equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} i\hbar _0a_\phi '=\bigl [\hbar _0\omega ^{(0)}_1+\eta (\tau )U^{(0)}_{1,1}\bigr ]a_\phi + \bigl \{V^{(0)}_{1,2}(\tau )+\eta (\tau )V^{(0)}_{1,2}(\tau )\bigr \}b_\phi \\ i\hbar _0b_\phi '=\bigl \{V^{(0)}_{2,1}(\tau )+\eta (\tau ) V^{(0)}_{2,1}(\tau )\bigr \}a_\phi + \bigl [\hbar _0\omega ^{(0)}_2+\eta (\tau )U^{(0)}_{2,2}\bigr ]b_\phi \end{array}\right. } \end{aligned}$$
(16)

with

$$\begin{aligned} U_{m,m}^{(0)}=\langle 0;m|U(r)|0;m\rangle \end{aligned}$$
(17)

and

$$\begin{aligned} V_{m,n}^{(0)}(\tau )=\langle 0; m|{\hat{V}}(\varvec{r}.\tau )|0;n\rangle , \quad m,n=1,2 \end{aligned}$$
(18)

where \(V_{n,n}^{(0)}=0\) is a consequence of the parity of the two states \(|0;n\rangle \). In Eq. (18) of Ref. [40] it is shown that in case of time dependence of \(\hbar \) the laser nominal frequency \(\omega _L\) is changed:

$$\begin{aligned} V^{(0)}_{j,k}=V_0\sin \left( \frac{\omega _L\tau }{f^3(\tau )}\right) \end{aligned}$$
(19)

with \(V_0\) constant. Thus, we see that \(\hbar (\tau )\) enters the equations not only through the obvious \(\eta (\tau )\) but also in tinily chirping the laser frequency.

3 First experiment

The main purpose of our investigation is the setting of an upper limit to the value of \(\gamma \) by solving the system of Eq. (16) with the atom initially in the ground state \(a_\phi (0)=1\) and \(b_\phi (0)=0\). According to our basic hypothesis, the value of \(\hbar \) differs at the two Earth’s positions corresponding to the two stages of the experiment. For convenience sake we describe the different starting instants of the experiment in Eq. (10) by assigning two values to the phase \(\phi \) (\(\varDelta \phi =\pi /12\) corresponds to one hour). At this point of the discussion it is important to select quantities measurable with standard techniques and useful to give information on the variation of \(\hbar \). As it is well known, the resonance condition induces large population exchange between the coupled states with ensuing rapid excitation and de-excitation. But, because of the variation of \(\hbar \), the rate of excitation and de-excitation of the atom is different at different hours of the day and if \(\gamma \) is large enough the quantity \(\varDelta P\equiv |a_{\phi _1}(\tau )|^2-|a_{\phi _2}(\tau )|^2\) becomes sizeable. Thus as a first experiment we propose the study of the ground state population at two different moments of the day.

The particular atom to be used as a probe enters the calculations only through the matrix elements \(U_{m,m}^{(0)}\) and \(V_{m,n}^{(0)}\), thus numerical calculations can be associated to an atom only when these values are assigned. Since our calculations are meant to give a general picture of the behaviour of the atom—and to give free hands to the experimentalist—we choose them in a conservative way [40] and list them in Table 1. From Table 1 we see that the value of \(\omega _L\) describes a three photons resonance; although arbitrary such a choice keeps the atomic energy gap in the optical range and the laser frequency in the near IR range where laser operation is stabler.

Table 1 Value of the relevant parameters entering the calculations
Full size table

The phases \(\phi _1\) and \(\phi _2\) significantly influence \(\varDelta P(\tau )\); since we do not know the orientation of the privileged axis we choose \(\phi _1=0\) because it is the less favourable value for the detection of the effect. Since the laser pulse duration is too short with comparison to one day we are safe in saying that during the first part of the experiment the atom evolves with the nominal value of \(\hbar _0\); in fact a rapid look to Eq. (10) shows that \(\omega _E T<<1\) (T is the pulse duration) and \(f(0)=1\). We arbitrarily choose \(\phi _2=2\pi /12\) meaning that the second branch of the experiment is to be performed after two hours. In Fig. 1, displaying \(\varDelta P(\tau )\), we notice that the difference of population oscillates almost between -1 and 1. So a choice of \(V_0\) and \(\gamma \) exists that makes, at least in principle, observable the variation of \(\hbar \).

Fig. 1
figure 1

Value of \(\varDelta P\equiv |a_{\phi _1}(\tau )|^2-|a_{\phi _2}(\tau )|^2\) for \(\phi _1=0\), \(\phi _2=2\pi /12\) and \(V_0=0.1\) au vs \(\tau \) in units of the laser period; \(\gamma =5\times 10^{-3}\)

Full size image

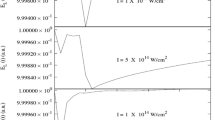
In Fig. 2 we plot the maximum value of \(\varDelta P\) as a function of \(\gamma \) for two different values of \(V_0\) and we notice the interesting result that in the log-log plot the points lies almost in a straight line suggesting a power law dependence of \(\varDelta P\) versus \(\gamma \). At this point, to set a limit for \(\gamma \) is a matter of measuring \(\varDelta P\) and of threshold of the experimental device.

Fig. 2
figure 2

(Color online) Value of \(\varDelta P_{max}\) for \(\phi _1=0\) and \(\phi _2=2\pi /12\) for two values of \(V_0\) in au vs \(\gamma \)

Full size image

4 Second experiment

Accelerated charges emit electromagnetic fields and the distortions of the wave function under the laser driving force imply acceleration of the active electron. It is a well established fact that the radiation emitted by a laser driven atom has a power spectrum containing essentially odd harmonics of \(\omega _L\) and hyper-Raman lines which are predicted by the theory and never observed. The effect is known with the name high order harmonic generation (HHG) [57,58,59]. The radiation carries information on the behaviour of the charge and can be used as a tool for spectroscopy and control of the atoms [60,61,62,63]. It is normal, therefore, to see if the emitted radiation can be used to set a constraint on \(\gamma \). The power spectrum is obtained from the Fourier transform of the atomic dipole moment. For \(V_0=0.5\) au, \(\gamma =2\times 10^{-3}\) and \(\phi =2\pi /12\) the spectrum is shown in Fig. 3; it is paradigmatically resolved in odd and hyper-Raman lines and extends up to the 35th harmonic. A red shift, gradually increasing with the harmonic order, is present and is visible in the inserted zoom. Therefore, the red shift too can be used to set an upper limit to the value of \(\gamma \). Technically to detect the red shift may be easier than to detect a variation of the population dynamics taken with two hours of delay. The experiment should be carried out with a pulse duration T inevitably short with respect to one day but containing many optical cycles to minimize line broadening; in our simulations we used \(T=200T_L\approx 10^{-13}\) s.

Fig. 3
figure 3

Power spectrum of the dipole moment induced by the laser in the second stage of the experiment (\(\phi _2=2\pi /12\)). In the calculations \(V_0=0.5\) au and \(\gamma =2\times 10^{-3}\). A zoom of the Figure is given in the inset to show the red shift in the high frequency part of the spectrum

Full size image
Table 2 Value of the red shift of the 31th harmonic for \(V_0=0.5\) au, \(\phi _1=0\), \(\phi _2=2\pi /12\)
Full size table

5 Parametric Chaos

A by-product not strictly correlated to the problem of setting an upper limit to the value of \(\gamma \) but of some conceptual importance is the emergence of Chaos. We have systematically investigated the possibility of checking the foundations of Quantum Physics by using a laser pulse. The project is realised by making small modifications of the basic laws of Quantum Mechanics and observing how these affect the output of simulations. Always we have seen that even a very tiny modification of the Schrödinger equation produces traits of chaotic nature. This feature is seen after the introduction of a small nonlinearity in the Hamiltonian of the problem [53, 55] which is perhaps to be expected for, but also after introducing a very slow time dependence of the Planck constant which is less obvious as the Schrödinger equation remains linear. In fact in classical domain, where the theory had birth and finds its natural application, Chaos emerges only with nonlinear systems [64]. In general a periodically driven system is chaotic if presents sensitivity to the initial conditions. Insurgence of Chaos is not easy to be detected as it can emerge after a long time lapse. A practical method to unveil Chaos consists in the drawing of a Poincaré section of the time evolution. The Poincaré section is obtained in two steps; first by plotting in the phase space the points of the orbit stroboscopically taken any period of the driver and second by cutting the phase space with a lower dimensionality surface. If the points fill the section, then the system is like to be chaotic. A quantitative method requires the determination of the distance between two orbits starting with very close initial conditions. If the distance D between the two trajectories exponentially diverges as \(D(\tau )\propto e^{\lambda \tau }\) (\(\lambda >0\)) then the motion is chaotic. The parameter \(\lambda \) is called Lyapunov exponent.

The linear Quantum Mechanics cannot show sensitive dependence on the initial conditions, anyhow quantum systems may present sensitive dependence upon small modifications of some physical parameter entering the Hamiltonian. We call this Parametric Chaos. In dealing with two level systems an opportune Poincaré section is given by the trajectory in the Bloch sphere of the quantum averaged Pauli’s matrices (\(n=x,y,z)\): \(\varvec{\sigma }(\tau )=(\sigma _x(\tau ),\sigma _y(\tau ),\sigma _z(\tau ))\) with ; more details are given in Ref. [55] where the technique is fully described.

In Fig. 4 the Poincaré section taken at \(\phi =2\pi /12\) is shown. The number of optical cycles of the pulse has been increased to 1000 because Chaos is an asymptotic feature and may need a long time to appear; the stroboscopic points disperse all over the available space and flag Chaos. For comparison sake in the upper part of the Figure we show the Poincaré section taken at \(\phi =0\) so in the first stage of the experiment the stroboscopic points are situated along a regular curve and do not reveal any chaotic insurgence.

Fig. 4
figure 4

Poincaré section taken at \(\phi _2=2\pi /12\) (second stage of the experiment) after two hours from the first. The Poincaré section at \(\phi _1=0\) is given in the small inset in the right-upper part of the Figure. In the calculations \(V_0=0.5\) au and \(\gamma =1\times 10^{-3}\). The pulse duration is \(T=1000\) oc

Full size image

To go beyond a qualitative indication that chaos has been reached we show the distance \(D(\tau )\) of the points at the two different orbits in the Poincaré section. The complete trajectory would completely fill the plot and be useless, thus we show the distance taken at intervals of 1 oc. in Fig. 5. Even in this granular representation we discern rapid variations of \(D(\tau )\). In the inset of the Figure we show a zoom of all points of \(D(\tau )\) in the time interval \(\tau \in [100.5,104]\) oc. To reveal exponential divergence it is customary to plot \(D(\tau )\) in a base 2 logarithm scale and we follow this convention. Indeed in many time intervals the two trajectories do exponentially diverge. It must be clear, however, that this is not meant to find the Lyapunov exponent like in the standard theory although an equivalent exponent can be found also for the parametric Chaos.

Fig. 5
figure 5

Distance between the Poincaré section taken at \(\phi _1=0\) and \(\phi _2=2\pi /12\) (second stage of the experiment) after two hours from the first. The Poincaré section at \(\phi =0\) is given in the small inset in the right-lower part of the figure. In the calculations \(V_0=0.5\) au and \(\gamma =1\times 10^{-3}\). The pulse duration is \(T=1000\) oc

Full size image

6 Discussion and conclusions

Data from astrophysical and particle physics observations have been published showing that \(\hbar \) may be position dependent and constrain the value of \(\varDelta \hbar /\hbar \). The observations are inhomogeneous and need to be attentively calibrated; new experiments must be designed with the alone aim of observing a variation of \(\hbar \) or of setting an upper limit to \(\varDelta \hbar /\hbar \).

As far as the author knows, there is no cogent conceptual reason demanding that physical constants should not deserve their adjective. Notwithstanding, scientific truth is not based on logic but on experimental evidence and it cannot be ruled out that, after all, a variation of parameters—even dimensionful—may occur and affect experiments. By following a simplicity guideline, we must modify the physical laws and see how measures are affected. If modifications are not experimentally observed then the hypothesis is liable to be incorrect.

In the stream of this reasoning, we propose a viable experiment that is well within today’s technology. The experiment is performed by shining a quantum object with two delayed laser pulses. The wave function of the object evolves differently under the action of the two pulses because the value of the Planck constant is changed. Of course the magnitude of the modifications of the wave functions depends on the size of variation of \(\hbar \) and on the particular observed quantity. We propose two protocols. The first requires the measurement of the difference of population of the ground state of the object in the two moments of the experiment. The second one exploits the well-known HHG and requires the measurement of a red shift of the higher harmonics after a time lapse which we take, conventionally, two hours. The second protocol involves commonly used techniques and might be more easily implemented.

To ground our ideas we refer to the data of Kentosh and Mohageg [35] on a day long variation but, of course, we do not see any impediment to apply the protocols to a one year dependence as in Hutchin [36]. The experiment can be performed on Earth, but foreseeable techniques allow the possibility of using satellites and, in a nearby future, on Moon. The lunar location is rather convenient because has a non-null, albeit small, eccentricity and orbits around Earth with about one month period thus exploring a time range between those of the GPS satellites and one year. Of course the transport and calibration of a power laser is not easy and in the light of this difficulty we have performed calculations with \(V_0=0.1\) au corresponding to a laser intensity of about \(10^{14}\) W cm\(^{-2}\).

Several ansatz are present in the model. To carry out our simulations we have used a non-relativistic formalism previously developed to describe a pure time dependence of the Planck constant: \(\hbar (t)=\hbar _0f(t)\) and neglecting that Earth’s frame is not inertial. The theory introduces the new standard of time \(\tau \) given in Eq. (4) the consequences of which need to be investigated as they might imply a redefinition of the cosmological distance as \(c\tau \ne ct\). This is a crucial point. The main reason of the non-relativistic approach dwells in the desire to single out the presence of \(\hbar \) from other constants, mainly c. Our treatment shows that by introducing the new time variable \(\tau \) a free particle is described by a plane wave; thus the de Broglie hypothesis, which stands at the very base of Quantum Mechanics, is unmodified. Indeed \(\tau \) enters the Schrödinger equation only for interacting particles: in absence of interaction a particle would be described by a pure plane wave or by a wave packet spreading into plane waves. However, the action of \(\tau \) may be assigned to a variation of the speed of the light thus making mandatory a relativistic treatment. It must be stressed that the possibility that the speed of the light might depend on the direction has been object of debate [25, 65,66,67,68].

One by-product of the theory is that slightly modifications of the Schrödinger equation produce evolution with chaotic traits. The surprising thing is that such traits are found even in the present linear theory by a mere change of a parameter. We may assert that a sort of universal, albeit asymptotic, chaotic behaviour is underlying all Nature. Moreover, by extending the concept of Lyapunov exponent, it is possible to define exponentially divergent orbits that are the signature of classical Chaos.

Conceptually, Chaos introduces a non-predictability and a decorrelation in the state of a system that evolves from a well defined initial state. Moreover Eq. (13) shows that no quantum bound state can be considered stable. To remain within the scope of this Paper, from Table 1 we see that Eq. (13) describes a situation equivalent to a particle acted upon by an oscillating field with period \(T_E=1\) day which is too long to give relevant effects in experiments not planned to reveal them.

In conclusion, we have presented two experimental protocols to detect a possible space dependence of \(\hbar \) and given constraints to \(\varDelta \hbar /\hbar \). Moreover, we have analytically shown that the variation of \(\hbar \) is equivalent to a weak, low frequency field, that allows the use of the full mathematical machinery developed for studying time dependent perturbations.