1 Introduction

Electric propulsion (EP), which uses electric energy for thrust production, offers much higher specific impulse \(I_{{{\text{sp}}}}\)Footnote 1 than classic chemical thrusters, dramatically improving the mission mass budget [1]. Hall-effect thruster (HET) [2], due to its relative simplicity and high performance as measured, e.g., by thrust-to-power ratio, for years, has been considered as an alternative for chemical thruster. However, HET as well as other current space engines relying on EP must be optimized further to become indeed attractive.

One of the main issues which should be better understood for HET optimization is relevant to ionization of a propellant and acceleration of the created ions. Although xenon, due to its high ionization cross section and atomic mass, is usually recommended as the propellant of choice for HETs, its scarcity in the Earth's atmosphere makes it very expensive. The global search for cost effective propellant prompted also our team to develop HET which could be fed by another noble gas, namely krypton. Obviously, generating the same specific impulse with a propellant of smaller atomic mass requires to increase the volumetric gas flow rate (vfr) to compensate for less massive particles. Unfortunately, lighter noble gases also have smaller ionization cross sections—despite that, due to increased vfr, ionization efficiency could be kept at the similar level for both type of propellants. However, high vfr results also in a growth of the discharge current and, consequently, of heat loads inside the thruster body. Therefore, for the presented here laboratory model of krypton 0.5 kW class HET, a dedicated radiator has been installed. Moreover, the design also addressed specific requirements for magnetic field topography like increased axial gradient of radial B-field component [3, 4].

One way to achieve higher performance of HET might be to boost its \(I_{{{\text{sp}}}}\), what should improve the mass budget of the mission even further. In HET \(I_{{{\text{sp}}}}\) is a function of a voltage that accelerates ions. Hence, our idea consisted in switching thruster operation to high-voltage regimes. But, as it has been already reported at [5, 6], an increasingly unstable operation of HET was revealed for higher discharge voltage \(U_{{\text{d}}}\)—until the discharge breaks, so discharge stability in a function of \(U_{{\text{d}}}\) should be carefully examined.

The aim of this work was to investigate dynamics of plasma discharge in the HET relying on global thruster characteristics parameterized with discharge voltage. For that, total discharge current as well as ion current were recorded and analyzed. Additionally, the set of parameters for thruster performance assessment was measured.

The paper is organized as follows. First, in Sect. 2, the main principle of HET operation, short prototype description and laboratory of plasma space propulsion (PlaNS laboratory) facility are described. Next, in Sect. 3 a detailed description of the two electric probes which were used to monitor changes in the ion current temporal characteristics are presented and the global concept of experiment and measurement strategy is described.

The main results of these studies are presented in Sect. 4. Finally, in Sect. 5, a discussion with some conclusions is given.

2 Hall-effect thruster (HET) from IPPLM

2.1 Principle of HET operation and short prototype description

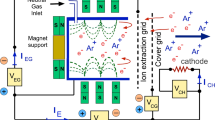
The HET body consists of a magnetic circuit for magnetic field generation of a topography which is controlled by two concentric magnetic coils: inner (hereafter referred to as inn) and outer (out), an anode that is simultaneously a gas distributor, and an internal insulator that constitutes an annular discharge channel in which neutral gas is ionized to maintain plasma. In the presented HET the cathode is placed externally to the thruster body (see the left panel in Fig. 1).

Fig. 1
figure 1

Left: schematic of the HET design with some plasma properties [1]. Middle and right: photographs of the prototype

Full size image

In HET acceleration of ions is enforced by a static electric field induced in plasma with magnetized electrons. Unlike in a gridded ion thruster (GIT), ion current density limitation by its own space charge in HET is mitigated owing to plasma quasi-neutrality. The expelled ions are neutralized downwind the thruster exit plane by electrons produced by the cathode. The resulting plasma jet carrying a momentum produces thrust that is transferred to the thruster body.

In HET, propellant ionization and ion acceleration predominantly take place in a zone in which electric and magnetic fields are mostly orthogonal. Magnetic field is far too weak to modify trajectory of ions accelerated by axial electric field. However, electrons trapped in this zone by magnetic field are subjected to drift azimuthally and may diffuse toward the anode only due to collisions with heavy particles. In these collisions neutral atoms are effectively ionized owing to increased residence time of drifting electrons.

The HET prototype from the IPPLM with a 42 mm mean channel diameter is coupled with a commercial HWPES-250 hollow cathode from HeatWave Labs Inc., which is clearly visible in the photos in Fig. 1.

It is worth noting that, in the case of krypton propellant use and HET operated with increased discharge voltage, the presence of a radiator (as shown in the middle part of Fig. 1) is crucial for an effective heat evacuation from the thruster interior. Our previous research has shown that its size is large enough to reduce temperature of the core and coils sufficiently to operate thruster within the safety limits [4].

2.2 PlaNS laboratory equipment

The presented here HET prototype was from the ground up implemented at the IPPLM and its extensive testing was performed at the PlaNS laboratory, which is furnished with a vacuum facility designed for space environment simulation for the needs of experiments with plasma thrusters. Measurements were taken in 2.5 m3 vacuum chamber equipped with a three-stage pumping system (backing pump, turbo-molecular pump and cryogenic pump), giving an average pumping speed of the facility close to 18 m3/s for krypton and 14 m3/s for xenon. The whole system provides the ultimate pressure inside the chamber in the order of 10–8 mbars when the gas flow is switched off and about 2.5 × 10−5 mbars for 1 mg/s mass flow rate of krypton. The pressure inside the chamber was measured by a Pfeiffer PKR 251 Full Range Gauge and an Oerlikon Leybold Ionivac ITR 90 Gauge (krypton corrected). In order to control gas flow in the anode and cathode gas lines, a Sierra Instruments controller SmartTrak C100L and MicroTrak C101 were applied.

The discharge voltage and cathode keeper voltage were provided by a Sorensen SGI-1000/5 and SGI-800/6 power units (Pus). To supply the cathode heater and coils with current, a Sorensen XG40-21 and two XG20-40 PUs were used.

Discharge current waveforms were captured by a Tektronix TCP0030 current probe while discharge voltage by a Tektronix THDP0200 high-voltage differential probe. Both signals were recorded with a Tektronix DPO410B digital phosphor oscilloscope. The ion current waveforms, as captured by the Faraday probes, were recorded using a GaGe data acquisition card with an increased 12-bit resolution.

During the experiments, the thruster was anchored to a pendulum of the MECARTEX thrust balance (TB), allowing to measure thrust at the level of few mN with 2% accuracy.

The vacuum chamber in PlaNS laboratory was equipped with a homemade driving system allowing for spatially resolved measurements of plasma parameters with different diagnostic probes. The system was composed of a vacuum-compatible rotary and linear driving stage (manufactured by Physik Instrumente GmbH) supported by a stainless steel scaffolding. To measure ion current locally in plasma plume three electric probes were installed at an aluminum arm driven by the system.

3 Ion current collection and data analysis

3.1 Ion probes description

Two types of electric probes have been designed in accordance with recommendations published in papers [7, 8] and subsequently used to collect ion current locally in the expelled plasma. These probes were mounted on the rotary arm, allowing for a rotation of + / − 90° relative to the thruster axis, with center of rotation at the thruster exit plane. The probes were positioned in a far field region of the plasma plume expelled by the thruster—the distance of the probes collectors from the thruster exit plane was 49.4 cm. The Faraday Cup (FC) and the Faraday Probe (FP) arrangement is shown in Fig. 2.

Fig. 2
figure 2

On the left, three electric probes mounted on the rotary arm: FC (left), old laboratory version of FC (center), FP (right). On the right, the ion current density profiles for different probes when thruster was working with 0.8 mg/s anode mass flow rate of krypton, discharge voltage of 600 V and coil current ratio \(I_{{{\text{inn}}}} /I_{{{\text{out}}}}\) = 7.0 A/4.1 A

Full size image

The main part of each homemade probe is the collector, polarized lower than the local plasma potential in order to repel most of incoming electrons and measure only the ion component of the beam (ion saturation regime). It was found independently for each probe that collector voltage of − 15 V with respect to the laboratory ground was sufficient to operate in such regime. The resulting angular ion current distributions obtained by each probe showed good agreement with each other (see Fig. 2). The graph also shows the calculated values of the total ion current \(I_{{{\text{tot}}}}\) and the average value of the discharge current \(I_{{\text{d}}}\).

It is worth mentioning that vent holes were included in the probes design to ensure an effective evacuation of residual gas from the internal regions of the probes during operation.

3.1.1 Faraday cup (FC)

The FC design addresses several important aspects. First of all, the cup design of the collector limits the additional current carried by secondary electrons emitted from the collector surface due to ion bombardment. Additionally, the collimating geometry of the probe allows capturing ions from a well-defined solid angle [8, 9]. Moreover, the collimated FC is less sensitive to low energy charge exchange ions, the density of which depends heavily on the chamber background pressure [10]. Their contribution is most pronounced at large angles—see ion current density profiles in Fig. 2.

Taking into account the typical value of ion current of the order of 0.1 A/cm2 at the thruster channel exit [2, 8] and the distance of 0.5 m between the probe and the channel exit, it was estimated that diameter of a collimator (indicated by a on Fig. 3) greater than 10 mm should allow the measurement of sufficient signal, i.e., in the range of few mA, to be significant with respect to noise. Both collimator and collector (indicated by b on Fig. 3) were made of graphite to minimize secondary electron emission [8, 11]. Cylindrical elements made of PEEK—poly-ethero-ethero-keton (indicated by c on Fig. 3) ensured electric insulation between the collimator and the collector. Besides, the construction allows the probe body to be left at the floating potential.

Fig. 3
figure 3

A CAD model of the FC (left) depicting the 15 mm collimator (a), the 20 mm collector (b) and the electric insulator (c), and the associated electric scheme (right)

Full size image

3.1.2 Faraday probe (FP)

It is known from the literature that a Planar Probe with Guarding Ring is also recommended for HET [7]. The main role of the ring is to keep a flat plasma sheath in front of the probe. Especially the sheath in front of the collector should be flat and uniform, in order to limit edge effects and deviance from the planar ion collection assumption. The collector (indicated by a on Fig. 4) and the ring (indicated by b on Fig. 4) were made of graphite, separated by a distance of 0.5 mm (which should be comparable to the minimum Debye length values expected during measurements) and polarized at the same potential by two separate voltage sources. The collector was biased by a homemade set of 3 V batteries that provide voltage in the range from 3 to 69 V depending on the number of cells used. The ring was biased by a homemade electrically regulated module that provides continuous voltage regulation in the range from − 45 to + 45 V. The shield of this probe, made from graphite and stainless steel, was left at floating potential.

Fig. 4
figure 4

A CAD model of the FP (left) with the collector (a) and the guarding ring (b), and its electric scheme (right)

Full size image

3.2 Ion current oscillations

The ionization instability generates several types of oscillations from which the breathing mode is perhaps the leading one and best known [12]. The current oscillations in this mode are associated with a periodic depletion of the neutral atoms due to ionization inside the discharge channel of the thruster. Since the ionization process is much faster than the refilling of neutral atoms from the anode, the front of the neutral atoms moves inside the discharge channel to the regions of lower magnetic field, associated with a less efficient ionization process. The neutral atom front moves then back to the thruster exhaust, leading to low-frequency oscillations in the 10–30 kHz range. This so-called breathing mode is clearly visible during HET operation, both in the discharge current and in the ion current waveforms.

Several models describing the breathing mode oscillations phenomenon with different levels of complexity have been developed in the last years, e.g., [13, 14]. This type of oscillations can be reproduced by numerical modeling of the discharge in HET using various codes, including the 1D hydrodynamic HETMAN code created at IPPLM by Barral et al. [15]. Nevertheless, the simplest model is based on the Lotka–Volterra equations (so-called prey–predator model) [16]:

$$ \begin{aligned} & \frac{{\partial N_{i} }}{\partial t} + \frac{{N_{i} U_{i} }}{L} = N_{i} N_{n} \xi_{{{\text{ion}}}} , \\ & \frac{{\partial N_{n} }}{\partial t} - \frac{{N_{n} U_{n} }}{L} = - N_{i} N_{n} \xi_{{{\text{ion}}}} , \\ \end{aligned} $$
(1)

where L denotes the length of the ionization zone, N—number density, U—mean axial velocity, the index i stands for ions and n for neutral atoms, and \(\xi_{{{\text{ion}}}}\)—ionization rate coefficient. Neutrals and ions (electrons, cf. plasma quasi-neutrality) play here the role of the prey and predators, respectively. This model assumes that velocities of ions and neutral atoms are constant in time. It assumes also that the plasma is contained in the ionization region in which the spatial variation of all quantities is neglected [17]. The equations have periodic solutions and do not have a simple expression in terms of the usual trigonometric functions, although they are quite tractable.

3.3 Purpose of the experiment

The aim of this experiment was to investigate the dynamics of the discharge and ion currents in a wide range of applied discharge voltages \(U_{{\text{d}}}\), especially for high voltages at which the generation of high \(I_{{{\text{sp}}}}\) was expected. A particular interest was in checking stability of the engine operation under such conditions experimentally. Consequently, the experimental strategy was to study the HET behavior while varying \(U_{{\text{d}}}\). In this purpose, the voltage was progressively increased from 300 to 700 V by steps of 10 V (and sometimes by 5 V); however, the measurements were taken only after temperature equilibrium was achieved [4].

The discharge current as well as the ion current (as captured by two probes positioned at the thruster axis in distance of ~ 0.5 m from its exit plane) was recorded with 50 MHz sampling frequency (25 MHz Nyquist frequency) and acquisition time set to 20 ms. Additionally, the ion beam profile was reproduced (with the use of both probes) by collection of the time averaged ion signals during the diagnostic arm rotation with the aim to assess and compare the total ion current \(I_{{{\text{tot}}}}\) and the beam divergence efficiency \(\eta_{{{\text{div}}}}\) in different operating conditions.

Extensive measurements of HET prototype in our previous experiments had shown which conditions are optimal for its operation, both in terms of stability and performance, see Fig. 5. These conditions were used as a basis for choosing the coil current ratio for the current experiment.

Fig. 5
figure 5

Maps showing the thruster efficiency \(\eta\) for different coil current ratios for two values of discharge voltage − 300 V (left) and 600 V (right); the anode mass flow rate was equal to 0.8 mg/s of Kr while cathode was supplied with 0.17 mg/s. Gray regions indicate unstable thruster operation

Full size image

During the first part of the experiment (referred further as case study I—CSI), the coil current ratio \(I_{{{\text{inn}}}} /I_{{{\text{out}}}}\) was set to 7.0 A/4.0 A while the anode mass flow rate of krypton was set to 0.8 mg/s (0.17 mg/s through the cathode). The experiment related to this case also includes the thrust measurements in the selected conditions. For comparative purposes, the experiment was extended to weaker and stronger magnetic field, i.e., for 6.4 A/3.7 A (referred further as case study II—CSII) and for 7.8 A/4.5 A (referred further as case study III—CSIII). The thruster cross section showing magnetic field magnitude and topography as predicted by simulation in ANSYS Maxwell [18] for three relevant cases is depicted in Fig. 6.

Fig. 6
figure 6

The results of ANSYS simulation (B(z,r) maps) for three settings of coil current ratios. The white rectangles indicate the location of the channel walls and the anode position is marked in red. In the gray region near the inner pole the magnetic field magnitude exceeds 500 Gs

Full size image

Figure 6 shows that, as the current in the coils increases, the strength of the magnetic field increases in the ionization region and the shape of the field lines slightly changes.

3.4 Thrust measurements

During experiments the thruster was mounted on the TB. The thrust measurement cycle consisted of a three minute TB position recording: 1 min of normal thruster operation, 1 min with the thruster switched off and 1 min with calibrating force turned on. After completing this cycle, the thruster was switched on again and its operating parameters were adjusted to the next set point.

An external electromechanical calibrator, using the vertical displacement of a mass sample, generated force of known value parallel to the thrust vector produced by HET. For each step of the thrust measurement cycle, to the TB signal a damped harmonic oscillation function was fitted, allowing for precise read-out of the TB displacement between the steps. The ultimate thrust value was derived from the ratio of these displacements.

It should be mentioned that the repeatability of the calibration impulse was always checked before starting the experiment, and the thrust was always measured in thermally stable conditions to ensure the validity of the results. (Temperature of the magnetic coils never exceeded 500 °C that is a safety limit for coil winding [4].)

3.5 Total ion current calculations

During the measurements of the ion current angular profile, the actual angular position of the electric probes was calculated relying on the simultaneous recording of the triggering signal generated by the diagnostic arm rotary stage. The ion current and trigger signals were continuously recorded as the diagnostic arm was rotating with constant angular velocity of 4.5°/s. The rotation took 40 s to complete. The acquisition card sampling rate was set to 1 kS/s with 100 k recorded points in total. Such values of the arm angular velocity and sampling rate gave ion current angular profile resolution of 0.0045°.

The local ion current density \(j_{i}\) (in A × m−2) was obtained by dividing the measured ion current (in A) at a specific location by the collecting area (in m2) of the probe. In this way, the probe was used to determine the angular distribution of the ion current density \(j_{i} \left( \theta \right)\) generated by HET. Assuming that measurements were taken sufficiently far from the thruster exit plane, i.e., treating the thruster as a point source, and assuming axial symmetry, the measured angular current density distribution could be used to calculate the total ion current \(I_{{{\text{tot}}}}\) from the following formula:

$$ I_{{{\text{tot}}}} = \pi R^{2} \int {j_{i} \left( \theta \right)\sin \theta {\text{d}}\theta } , $$
(2)

where R is the distance between the thruster exit plane and the probe and \(\theta\) the angular position of the probe. The plasma beam divergence is defined as:

$$ \langle \cos \theta\rangle = \pi R^{2} \frac{{\int {j_{i} \left( \theta \right)\sin \theta \cos \theta {\text{d}}\theta } }}{{I_{{{\text{tot}}}} }}, $$
(3)

where the divergence efficiency is such that \(\eta_{{{\text{div}}}} = \langle \cos \theta\rangle^{2}\) [19].

4 Experimental results

The electric probes were used to study dynamics of ion current oscillations when thruster was operated in a wide range of voltages. For comparison of the ion current time-dependent characteristics, three magnetic field topographies induced by three ratios of coil currents were applied identified as cases CSI, CSII and CSIII. The thrust measurements for the needs of specific impulse and the anode efficiency assessment were examined for the CSI.

4.1 Dynamics of oscillations

This section presents the results illustrating the dynamics of the ion currents for three selected discharge voltages and three selected magnetic field topographies identified as CSI, CSII and CSIII.

For the purpose of ion dynamics study, the probes were placed on the thruster axis. The relevant ion signals were collected with resolution of 50 MHz. The breathing mode oscillations, usually well pronounced in the thruster discharge current, were also easily identified in ion current signals as captured by the FC and FP. As it was written in the introduction when HET is operated at increased voltage, the discharge current becomes often unstable and even can be disrupted. This instability may manifest as irregular (highly aperiodic) current oscillations or/and random switches between different oscillating modes. The relevant irregularities can be partially mitigated by magnetic field topography adjustment; however, such control appears to be ineffective if the discharge voltage is too high.

Two different ion current signals as measured by FC in CSI and CSIII are shown in Fig. 7. In the upper part of this figure, the corresponding 20 ms lasting time series for Ud = 650 V are presented. In the central and the bottom panels of the same figure, zoomed in 0.25 ms sections as taken out from the relevant time series are displayed. In the left column, a transition between two modes is clearly visible (zones 1 in red and zone 2 in green). The Fourier spectrum of the time series (normalized to zero mean value and unit variance) that corresponds to zone 2 reveals three harmonics of the breathing mode, at \(f = k \times 27.2\;{\text{kHz}}\) for \(k = 1, 2, 3\), while the spectrum of the zone 1 (in red) shows only one smaller and much broader peak in vicinity of \(f = 27.2\;{\text{kHz}}\). It can be noticed that the mean value of the ion current as calculated for the zone 1 is significantly higher than the ion current mean value obtained for the zone 2, for which the breathing mode dominates. Moreover, the mean value and variance of the current signal depicted in the right column of Fig. 7 and for which the breathing mode is only marginally pronounced are similar to the ones computed for the zone 1. The small share of the breathing mode in the ion current signal of the right column in Fig. 7 is confirmed by its Fourier spectrum which, like the spectrum for zone 1, displays only a single broad peak, however, of frequency \(f = 32.5\;{\text{kHz}}\) that is significantly higher than the main frequency identified for the zone 1—see the bottom part of Fig. 8.

Fig. 7
figure 7

Ion current waveforms as collected by the FC, for \(U_{{\text{d}}} = 650\;{\text{V}}\) in the CSIII (left column) and in the CSI (right column). In the upper panel mean values of ion current are depicted

Full size image
Fig. 8
figure 8

Fast Fourier transform of the FC ion current waveforms collected for \(U_{{\text{d}}} = 650\;{\text{V}}\) in the CSIII (top) and in the CSI (bottom) (These results correspond to Fig. 7)

Full size image

The difference in frequencies is correlated with a difference in coil currents for both cases; however, the detailed relation is to be examined.

In [5], the authors concluded that the breathing mode becomes significant when the discharge voltage increases; however, in that paper the effect of magnetic field had not been examined. In the current study magnetic field was adjusted to search for the best thruster performance in terms of the anode efficiency and high Isp. Nevertheless, B-field variation also results in different dynamics of ion current (as well as discharge current) what is shown in Figs. 7 and 8. The simple relation between the discharge voltage and the share of the breathing mode in the ion current is not valid. Indeed, while for \(U_{{\text{d}}} = 300\;{\text{V}}\) the share of the breathing mode seems to be similar for all three case studies, it is not true for the higher voltages. That is illustrated in Fig. 9 for \(U_{{\text{d}}} = 600\;{\text{V}}\): for CSI and CSII ion current remains relatively smooth and the share of breathing mode is only marginal while for CSIII the breathing mode dominates and transitions between “smooth” and highly oscillating ion current waveform emerge in random.

Fig. 9
figure 9

Selected experimental ion current time traces from FC for a Ud = 300 V and b Ud = 600 V and three different coil current ratios (CSII, CSI and CSIII—from left to right). The bottom panels display a zoom in 0.25 ms sections as taken out from the relevant time series

Full size image

However, in CSI, for just slightly lower \(U_{{\text{d}}} = 550\;{\text{V}}\), the thruster operated stably displaying the strong breathing mode in the ion current signals while for the same voltage in CSII the thruster operation became less stable and switching between quiet and strongly oscillating currents began to appear—see Fig. 10a.

Fig. 10
figure 10

Selected experimental ion current time traces from FC for two discharge voltages a Ud = 550 V, b Ud = 700 V and two different coil current cases (CSI on the left and CSII on the right). The bottom panels display a zoom in 0.25 ms sections as taken out from the relevant time series

Full size image

For \(U_{{\text{d}}} = 700\;{\text{V}}\) the amplitude of the ion current oscillations significantly decreased in comparison with \(U_{{\text{d}}} = 550\;{\text{V}}\) while the leading frequency increased to about 200 kHz. For CSI these fast oscillations seem to be superimposed on the breathing mode while in CSII the breathing mode is hard to be detected—see Fig. 10b.

4.2 Estimation of the main performance parameters

The ion current that should be created if all the neutral atoms were singly ionized can be estimated as \(I_{m} = \dot{V}en_{0}\), where \(\dot{V}\) is the anode volume flow rate in standardized units per second, \(e\) the elementary charge and \(n_{0} \sim 2.67 \times 10^{25} \;{\text{m}}^{ - 3}\) the Loschmidt number. Using \(I_{m}\) as a reference value, it was checked which ratio \(I_{{{\text{tot}},{\text{FP}}}} /I_{m}\) is relevant to the highest thruster performance.

The anode efficiency \(\eta\) was calculated relying on the thrust \(T\), the discharge power \(P_{{\text{d}}}\) and the anode mass flow rate \(\dot{m}_{{\text{a}}}\), as measured during the experiments and according to the equation:

$$ \eta = \frac{{T^{2} }}{{2\dot{m}_{{\text{a}}} P_{{\text{d}}} }}. $$
(4)

The following parameters corresponding to the signals depicted in Fig. 9 are collected in Table 1: discharge voltage \(U_{{\text{d}}}\), electric power \(P_{{\text{d}}}\), current in inner magnetic coil \(I_{{{\text{inn}}}}\), current in outer magnetic coil \(I_{{{\text{out}}}}\), thrust \(T\), anode efficiency \(\eta\), divergence efficiency \(\eta_{{{\text{div}}}}\), current utilization (i.e., total ion current \(I_{{{\text{tot}}}}\) to discharge current \(I_{{\text{d}}}\) ratio) \(I_{{{\text{tot}},{\text{FP}}}} /I_{{\text{d}}}\), ion current ratio \(I_{{{\text{tot}},{\text{FP}}}} /I_{m}\) and the specific impulse \(I_{{{\text{sp}}}}\).

Table 1 Some calculated performances parameters for the three experimental cases related to FP total ion current measurements
Full size table

It can be seen that for selected conditions in Table 1, the highest thrust, specific impulse and anode efficiency of HET were obtained in CSI (\(I_{{{\text{inn}}}} /I_{{{\text{out}}}} = 7.0\;{\text{A}}/4.0\;{\text{A}}\)) at \(U_{{\text{d}}} = 600\;{\text{V}}\) for discharge power of 0.513 kW that is close to the nominal value (of 0.5 kW). Slightly lower performances were obtained for the same discharge voltage at smaller coil current ratio \(I_{{{\text{inn}}}} /I_{{{\text{out}}}} = 6.4\;{\text{A}}/3.7\;{\text{A}}\) resulting in somewhat smaller discharge power. It is visible that the \(\eta_{{{\text{div}}}} , I_{{{\text{tot}},{\text{FP}}}} /I_{m}\) and \(I_{{{\text{tot}},{\text{FP}}}} /I_{{\text{d}}}\) values were relatively stable for the selected set of parameters. It is also worth noting that the largest coil currents ratio (CSIII) does not provide any increase in performance.

4.3 Bifurcation diagrams

Figure 11a presents a FP bifurcation diagram driven by discharge voltage (a control parameter), i.e., a histogram of local extrema that displays evolution of the ion current amplitudes as captured by FP for different discharge voltages during the first part of the experiment (CSI). Red dots represent local minima while the blue ones local maxima of the ion current. A smoothing procedure based on a moving average method was applied to the current waveforms, using a time window of 0.2 µs. The window size of the data set used to search for minima and maxima was set to 100 µs.

Fig. 11
figure 11

a The FP bifurcation diagram, b normalized values of mean discharge current \(I_{{\text{d}}}\), total ion current \(I_{{{\text{tot}}}}\), current utilization \(I_{{{\text{tot}}}} /I_{{\text{d}}}\), discharge power \(P_{{\text{d}}}\) and beam divergence \(\eta_{{{\text{div}}}}\) versus discharge voltage \(U_{{\text{d}}}\), c normalized values of mean discharge current \(I_{{\text{d}}}\), thrust T, discharge power \(P_{{\text{d}}}\) and anode efficiency \(\eta\) versus discharge voltage \(U_{{\text{d}}}\)

Full size image

Additionally, mean value of discharge current \(I_{{\text{d}}}\) and electric power \(P_{{\text{d}}}\) are presented in Fig. 11b, c for the same range of discharge voltage \(U_{{\text{d}}}\). Figure 11b is enriched with the plots displaying variation of current utilization \(I_{{{\text{tot}},{\text{FP}}}}\) and beam divergence \(\eta_{{{\text{div}}}} { }\) while Fig. 11c with thrust \(T\) and the anode efficiency \(\eta\). Prior to ion current integration, a background subtraction with linear trend was applied using the ion current raw signal when the probe was at the farthest position from the thruster axis.

Since thrust measurements are time-consuming, they were limited to selected discharge voltages—that is why in Fig. 11c presented is a data set reduced with respect to that of Fig. 11b. It should also be noted that thrust evaluation relies on a separate series of measurements than CSI recording, so despite the set points of both series corresponded to each other, the thruster behavior was not exactly the same what could be caused, e.g., by discharge channel erosion. The difference is visible in the mean value of discharge current \(I_{{\text{d}}}\) in Fig. 11b, c. The occurrence of a certain hysteresis in the thruster operation is evidenced by other values of \(I_{{\text{d}}}\) as shown in Fig. 12c in blue (CSI) and navy blue (a separate session focused on thrust measurement).

Fig. 12
figure 12

a The beam divergence \(\eta_{{{\text{div}}}}\) versus discharge voltage \(U_{{\text{d}}}\), b the total ion current \(I_{{{\text{tot}},{\text{FP}}}}\) versus discharge voltage \(U_{{\text{d}}}\), c the mean discharge current \(I_{{\text{d}}}\) versus discharge voltage \(U_{{\text{d}}}\)

Full size image

All the values depicted in Fig. 11b, c were normalized with respect to their absolute maxima. The relevant values in maxima were: \(I_{{\text{d}}} = 0.84\;{\text{A}}\) and \(P_{{\text{d}}} = 699\;{\text{W}}\) for Fig. 11b, \(I_{{\text{d}}} = 0.87\;{\text{A}}\) and \(P_{{\text{d}}} = 584\;{\text{WA}}\) for Fig. 11c, while \(T = 13.74\;{\text{mN}}\) (\(I_{{{\text{sp}}}} = 1750\;{\text{s}}\)), \(\eta = 19.6\%\), \(I_{{{\text{tot}},{\text{FP}}}} = 0.52\;{\text{A}}\) and \(\eta_{{{\text{div}}}} = 0.74\) for corresponding subplots.

It could be expected that specific impulse should increase like square root of discharge voltage. However, the alteration in behavior of current oscillations with modification of operating conditions makes this issue more complex. Moreover, uncontrolled variation of the magnetization curve due to growth of the thruster body temperature and consequently of the B-field topography may additionally influence on the current oscillations character.

It is noteworthy that the average discharge current, the calculated total ion current and beam divergence vary relatively slowly in the whole examined \(U_{{\text{d}}}\) range.

Intuitively, it could seem that less oscillating discharge current should be correlated with better thruster performance. Indeed, examining CSI one can notice that better performance of the thruster that was gained at high voltages was also accompanied by a smoother discharge current as well as slightly higher ion current and beam divergence efficiency—see Fig. 11a, b.

In CSI, it has been observed that the highest total ion current appeared at the highest discharge voltages during small amplitude oscillations, but this increase is modest compared to the rest of the cases—see Fig. 12b. In CSII the highest total ion current corresponds to 560 V, it is near the point where the character in the bifurcation diagram changes fundamentally—see Figs. 12b and 13 (top). In Fig. 12a, c it is visible that the \(\eta_{{{\text{div}}}}\), \(I_{{{\text{tot}},{\text{FP}}}}\) and \(I_{{\text{d}}}\) values were relatively stable for all of the measurements.

Fig. 13
figure 13

The bifurcation diagrams (CSII—top and CSIII—bottom)

Full size image

Standard bifurcation diagrams could be enriched with information about population of extrema of a given value identified within relevant time series. It is not only a problem of visualization but also may provide important information how often the system visits its specific states. For that density of extrema on a predefined grid \(U_{{\text{d}}} \times I_{{{\text{d}},{\text{FC}},{\text{FP}}}}\) was calculated—see Figs. 14 and 15. According to the experimental conditions, the voltage resolution was limited to 10 V (5 V in specific cases). For ion currents as captured by FC and FP, the \(I_{{{\text{FC}},{\text{FP}}}}\) resolution was set to 0.035 mA, while for \(I_{{\text{d}}}\) to 0.01 A. The number of discrete intervals resulted from the relevant current ranges, i.e., − 1.0 to 7.0 mA and − 0.5 to 4.5 A, respectively.

Fig. 14
figure 14

Bifurcation diagrams (densities plots) for FC for CSII (top), CSIII (bottom)

Full size image
Fig. 15
figure 15

Bifurcation diagrams (densities plots) in CSI for FP (top), FC (middle), \(I_{{\text{d}}}\) (bottom)

Full size image

While comparing FC bifurcation diagrams for CSI, CSII and CSIII (Figs. 14, 15 middle), one can notice that the same type of narrow branches representing minima and maxima appears if thruster is operated at lower voltages (below 350 V).

For CSI and CSII the same type of sharp transition in the behavior of currents is observed for the highest \(U_{{\text{d}}}\), but the threshold value depends on the strength of the current in the coils—the greater the current, the higher the threshold value voltage. In CSIII the experiment had to be stopped at 650 V not to exceed the HET temperature limitation; however, the sharp transition could be observed around 670 V similarly as for the other cases. An interesting branching between minima and maxima occurs in the middle of the voltage range. It illustrates switching between different modes in the thruster operation which have been identified as zone 1 and zone 2.

An excellent correlation between discharge current and ion current as captured by FP and FC is evident (Fig. 15). The corresponding bifurcation diagrams indicate regions where dramatic changes take place. In both of them, the “belt-like” shapes of the maxima branches are very similar. However, the signal from FC is characterized by a fuzzy branch of low minima, with values often inferior to zero, while the FP signal is very clear, like from \(I_{{\text{d}}}\). The origin of these different behaviors is so far unknown and will require further investigations. However, it seems that it is not an effect of a reduced bandwidth of the FP, because in its PSD a high-frequency component is also present. The bifurcation diagram of \(I_{{\text{d}}}\) is characterized by wider extreme stripes, because the discharge current signal includes not only information about ion current, but also about the dynamics of electron component.

4.4 Power spectrum

The power spectral density (PSD) of the ion current waveforms was determined using the Welch method, after normalizing the signal to zero mean value and unit variance. The 2-ms-long signals were split into ten segments with 50% overlap. The PSD for chosen voltages are shown in Fig. 16. Furthermore, all spectra are summarized in the 2D diagram shown in Fig. 17. Is worth noting that the main peak at f ~ 30 kHz and its harmonics visible in the frequency spectra correspond to BM.

Fig. 16
figure 16

PSD of the ion current waveform for discharge voltages of 300–500 V (top), 550 V and 580 V (middle) and 600–700 V (bottom)

Full size image
Fig. 17
figure 17

PSD of the ion current waveform as a function of the discharge voltage

Full size image

In Fig. 16 (top), it is visible that between 300 and 500 V, the number and intensity of harmonics increases with voltage. With increasing discharge voltage, the regime of ion current oscillations is evolving from a single-harmonic one to a multi-harmonic one. Then, it returns to a single-harmonic behavior after a clear transition at some threshold voltage. For comparison, the PSD before and after transition is shown in Fig. 16 (middle).

For discharge voltages of 580 V and higher, the breathing mode peak becomes very broad and only one indistinct harmonic is visible.

5 Conclusions

In this paper, the influence of operating parameters on the HET performance was examined. Intuitively, it could seem that less oscillating discharge current should be correlated with better thruster performance. Indeed the highest thrust \(T\) and anode efficiency \(\eta\) with insignificantly higher total ion current values were achieved at high-voltage regime (between \(I_{{\text{d}}}\) = 600 V and 680 V) for CSI (\(I_{{{\text{inn}}}} /I_{{{\text{out}}}} = 7.0\;{\text{A}}/4.0\;{\text{A}}\)). It is also worth noting that the largest coil currents ratio (CSIII: \(I_{{{\text{inn}}}} /I_{{{\text{out}}}} = 7.8\;{\text{A}}/4.5\;{\text{A}}\)) does not provide any increase in performance.

It can be concluded from Figs. 7, 8, 9 and 10 that the ion current signal for the lowest voltage (300 V) was smooth and showed oscillations in the range attributable to breathing mode, whereas deep breathing mode oscillations (with higher amplitude) were visible for the middle range of examined voltages, here thruster had tendency to switch between two oscillating modes as described previously as zone 1 and 2. It is worth noting that in zone 2 the number of harmonics in the Fourier spectrum increases with voltage. For the highest values of the examined voltages (the transition value depends of magnetic field strength), the signals show smooth oscillations that exhibit only one indistinct harmonic.

As expected, a strong correlation between discharge current and ion current from the probes was observed. The behavior of current oscillations was changing from single-harmonic to multi-harmonic regime while increasing the discharge voltage, until returning to a single-harmonic regime after a sharp transition at a specific threshold voltage. In the strongest magnetic field configuration, a single-harmonic signal for higher voltages was also observed, but the measurements had to be stopped prematurely due to the high temperature limit (466 °C) of the coils. It means that high-frequency harmonics always disappeared for the highest voltages, after a specific threshold.

Since it is suggested that an increase in the chaotic behavior in the ion current could have a deleterious influence on the thruster efficiency, the data analysis will be further focused on studying the chaotic behavior, in order to search for a possible transition to a chaotic state.