Abstract
In this article we show why flying and rotating beer mats, CDs, or other flat disks will eventually flip in the air and end up flying with backspin, thus, making them unusable as frisbees. The crucial effect responsible for the flipping is found to be the lift attacking not in the center of mass but slightly offset to the forward edge. This induces a torque leading to a precession towards backspin orientation. An effective theory is developed providing an approximate solution for the disk’s trajectory with a minimal set of parameters. Our theoretical results are confronted with experimental results obtained using a beer mat shooting apparatus and a high speed camera. Very good agreement is found.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
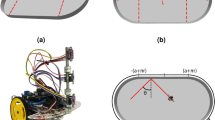
A beer mat (also known as drink coaster) is a commodity most elegantly used to rest a glass on in order to protect a table surface [1]. However, not only for a physicist there are more exciting applications for a beer mat, one of which is to let it fly. Usually, it is a circular piece of cardboard with a diameter of about \({10}\,\hbox {cm}\), though there are also other shapes in use. For the following we will idealise it as a disc with radius r, mass m and negligible thickness, for a sketch see Fig. 1.
If one tries to throw a beer mat, one quickly realises that one can only achieve reasonable flight distances if the mat rotates around the axis perpendicular to it’s circular area, depicted as \(\varvec{D}\) in Fig. 1. The such generated angular momentum stabilises the orientation of the disk via angular momentum conservation preventing chaotic rotations around one of the two other rotation axes of the disc, for which it is known from classical mechanics that rotations around these are in practice unstable, given the relatively small mass of the beer mat.
Now one could expect the mat to fly similarly to a frisbee, i.e. with angular momentum pointing up or down, called ‘sidespin’ from now on, however, it still turns out to be difficult to predict the path of the flying mat: a seemingly random time \(\tau \) after the flight started the mat begins to either turn left or right, depending on it’s direction of rotation, and—if it does not hit ground beforehand—ends up flying with backspin (i.e. with rotation axis pointing sidewards perpendicular to the direction of flight with the upper side rotating against the direction of flight). With a few more experiments one realises that starting the flight with backspin is stable, while a flight with topspin is not.
The observation of the aforementioned seemingly random times \(\tau \) might lead one to hypothesise there to be a chaotic effect in the flight of a beer mat. However, it will turn out that this effect comes from the inability of humans to throw the disk reproducibly.
In principle, the theory of a rotating thin disk moving in air is known. Unfortunately, solving the corresponding equations including effects from turbulence is analytically intractable and even numerically highly demanding. An effective treatment is, therefore, in order by treating the disk as a point-like object to a large extend, which allows one to avoid to solve the full fluid dynamics equations. The closest to the situation we are considering here comes the literature about the flight of a frisbee, see for instance [2,3,4,5,6].Footnote 1 However, a frisbee weighs significantly more and has modified edges to stabilise it’s flight characteristics such that the effects that we will study here are sufficiently suppressed to be neglected.
The aim of this paper is threefold: we will give a qualitative explanation of the observed behaviour in the following Sect. 2. From this section the understanding of the phenomenon should be possible without much expert knowledge. Next, we will derive an effective formalism based on a few assumptions describing the flight of a beer mat. This formalism allows us to make predictions, which can be tested experimentally. Thus, in the third part of this paper we present experimental results. For the experiments to be reproducible we have designed and constructed an apparatus which allows us to throw beer mats with variable angular and forward momentum. A high-speed camera is used to record the mats’ flights and the recordings are used to reconstruct the corresponding flight trajectories. These trajectories are then compared to the predicted trajectories from our effective theory.
Eventually, we compare the experimental results to our theory predictions, after a number of parameters are fitted to the experimental data. The predictions are well confirmed, validating the assumptions the effective theory was built on. This allows us to generalise our findings to other types of disks, which could be tested experimentally.
2 Qualitative discussion
Let us start in a situation where a spinning diskFootnote 2 with its angular momentum \(\varvec{L}\) perpendicular to the disk’s surface is moving through a medium (air) without gravitational force. Drag will cause the disk to orientate itself such that it minimises air resistance by minimising its surface exposed to the airflow. This means the axis \(\varvec{D}\) is perpendicular to the flight direction. Thus, any orientation with slightly tilted rotation axis compared to the situation above will automatically adjust back. In the equilibrium state no torque is available to change the direction of angular momentum.
However, if one now includes the gravitational force pointing into the negative z-direction, the disk will be accelerated downwards. Hence, the airflow approaches it slightly from below (see Fig. 2a). This induces a lifting force \(\varvec{F}^\mathrm {lift}\) upwards [7]. This force now does not attack the disk at its centre, but \(R = \pi r/8\) towards the leading edge [8]. Intuitively, this can be understood by the air stream being broken near the front edge of the disk, so that the lift is acting stronger at the front. Therefore, \(\varvec{F}^\mathrm {lift}\) induces a torque \(\varvec{M} = \varvec{R} \times \varvec{F}^\mathrm {lift}\) which will cause a precession of the disk (Figure 2, C).Footnote 3 The lifting force and, thus, the torque vanishes only in back- or topspin position. But, since the direction of this precession is such that the disk approaches backspin orientation independently of the direction of the angular momentum, the topspin orientation is meta stable and the backspin orientation stable.
Therefore, if the flight of the disk is started not in backspin position, one expects it to perform an oscillation around the backspin position. This oscillation, however, is strongly damped in any real-world experiment.
A secondary but nonetheless important stabilising effect is the Magnus force [10]. Together with drag it is responsible for the aforementioned damping. The Magnus force acts orthogonal to both flight direction and rotation axis \(\varvec{D}\). It does not introduce any torque and, thus, cannot be primarily responsible for the trend towards backspin. However, it can change the flight direction in such a way that backspin is preferred. Imagine the spinning disk simply being dropped without initial spacial velocity and \(\varvec{D}\) pointing in the y-direction, i.e. the leading edge pointing precisely downwards. Once the disk begins to fall, it is accelerated in the x-direction by the Magnus effect.Footnote 4 The sign of this acceleration in x-direction prefers backspin again. Small deviations from backspin can therefore be corrected by the Magnus effect adjusting the flight direction.
3 Effective theory
In this section, we will translate the qualitative arguments developed in the previous section into formulae effectively describing the flight of a beer mat (or any other thin disk). Thereafter, we will test these formulae experimentally in the following section.
Note that this set of equations is not formulated with the goal to explain the reality. Rather it is a means to predict movements with reasonable precision. Terms without an immediate physical intuition have to be read in this light.
3.1 Equations of motions
For a thin disk with radius r and mass m the element of the moment of inertia tensor for rotations around the symmetry axis \(\varvec{D}\) (see Fig. 1) reads \(I_{D} = mr^2/2\). For the other two axes lying in the plane of the disk one finds \(I = I_{D}/2\). We denote the modulus of the velocity of the centre of the disk with \(v = |\varvec{v}|\) and its area with A.
For the angles given in Fig. 1, we will denote \(\omega _0 = {{\dot{\psi }}}\) and assume \(\omega _0\) to be a constant of motion. Our next assumption is that the disk’s area always moves in an orientation with minimised air resistance as explained above, i.e. \(\varvec{v} \perp \varvec{D}\) and starts out in the x-z-plane without loss of generality. The angle \(\theta \in [0,\pi ]\) does not differentiate between top- and backspin, but only together with \(\phi \). In order to describe everything with only a single angle, we introduce \(\vartheta \in [-\pi ,+\pi ]\) such that \(\vartheta = \pm \theta \) with \(\vartheta =+\pi /2\) corresponding to topspin and \(\vartheta \ =-\pi /2\) to backspin. Now the only non-trivial motion is the one described by \(\vartheta \).
As argued in the last section, the acceleration \({\ddot{\vartheta }}\) vanishes for top- and backspin, with backspin the stable state. We expect \({\ddot{\vartheta }}\) to be largest at \(\vartheta = 0\) and symmetric around this point. An easy choice to obtain such a behaviour is a force proportional to \(\cos \vartheta \). Now, there are two contributions to \({\ddot{\vartheta }}\): the first stems from the lifting force \(\varvec{F}^\mathrm {lift}\), which is tilting the disk. We expect the lifting torque to be \(c^\mathrm {pot}_\vartheta \rho r Av^2\) with the density of air \(\rho \) and some dimensionless constant \(c^\mathrm {pot}_\vartheta \). This is the well-known formula for lift combined with a factor r to account for the lever. The second contribution, which reads \(c_\vartheta ^\mathrm {rot} \rho r A^2 \omega _0^2\) with another constant \(c^\mathrm {rot}_\vartheta \), cannot be motivated in such a naive way. It might stem from sub-leading effects, such as the Magnus force, but we introduced it as an a posteriori adjustment to the empirical evidence.
The larger \(\omega _0\), the harder it will be to tilt the disk. The corresponding force must depend on the sign of \({{\dot{\vartheta }}}\), but not on the sign of \(\omega _0\). Thus, we expect \(c_\vartheta ^\mathrm {damp} I \omega _0^2{{\dot{\vartheta }}}\), which is in the form of laminar damping. We assume \({{\dot{\vartheta }}}\) to be relatively small such that damping proportional to \({{\dot{\vartheta }}}^2\) can be neglected.
In summary, for \(\vartheta \) we arrive at the following equation of motion with \(K=\rho r A/I\)
Next we focus on the centre of mass coordinate \(\varvec{x} = (x,y,z)\). The aforementioned condition of minimised air resistance prevents the disk to move in the direction of \(\varvec{D}\). This translates to an effectively reduced gravitational force \(-mg\left( \hat{ \varvec{e}}_z-\varepsilon \varvec{D} \cos \vartheta \right) \). The coefficient \(\cos \vartheta \) takes the dependence of the air resistance in \(\varvec{D}\)-direction on the projected area into account. The case \(\varepsilon =0\) would correspond to a free fall, i.e. the leading edge would be aligned only with the horizontal velocity component and completely ignore the vertical one. Strict alignment would on the other hand imply \(\varepsilon =1\). The truth, as so often, lies somewhere in between.
As before we introduce a damping force with the proportionality constant \(c^\text {damp}_x\) of dimension velocity. Our last assumptions are \(v_y=0\) at \(t=0\) without loss of generality and \(|v_y|\ll |v_x|\) at all times. The latter assumption is not always justified, but usually people throw disks with enough forward momentum that any change of direction is a second-order effect. These assumptions allow to write \(\varvec{D}=\left( 0,\sin \vartheta ,\cos \vartheta \right) ^\top \) significantly simplifying the equations of motion which then read
3.2 Approximate analytic solution
Equations (1) and (2) still form a set of four nonlinear coupled differential equations, but they can be solved numerically much easier and more stably than the full equations of motion described in the appendix. Furthermore they can be approximately solved analytically.
To this end we first assume that \(v\approx v_0=\text {const.}\) over the complete duration of the flight. Then Equation (1) decouples and can be solved independently of the trajectory. We are going to do so in the harmonic approximation about the potential minimum at \(\vartheta =-\pi /2\). It suffices to gain a good understanding of the different stages of the flight. The differential Equation (1) simplifies to
We observe that the system is clearly overdamped in the case of a stable flight (no oscillations are visible). The corresponding stability condition for such a flight reads
In this case we obtain the well-known solution
with \(\lambda \) given by
In the overdamped case \(\lambda \) can be simplified to
by using \(A = \pi r^2\) and \(I=mr^2/4\). Thus, the convergence depends solely on two universal constants \(\lambda _0,\lambda _1\) and the four variables mass, radius, speed and angular speed. It is very remarkable that only the ratio \(v_0/\omega _0\) is relevant.
With these approximations the remaining differential equations can be solved analytically using hypergeometric functions. However, for the sake of gaining intuitive understanding, we approximate even further. With sidespin initial conditions
we focus on the y-component. Exploiting our condition of slow movement in this direction allows us to neglect the damping term. This leaves us with
Using the solution for \(\vartheta \) from Equation (5), we find that there is no acceleration in the y-direction at zero and again at infinite time. In between the acceleration becomes maximal at \(\vartheta =-\pi /4\) with \(|{\ddot{y}}|=g\varepsilon /2\) at the characteristic time scale \(\tau {:}{=}\log 2/\lambda \). In fact, the acceleration is effectively nonzero only for a short time \(t_i\ll \tau \) around \(\tau \) defining two asymptotic regimes: before \(\tau \) we have \({\dot{y}}=0\) and after \({\dot{y}}=\mathrm {const}\ne 0\). The transition between the two regimes takes place exponentially
with some numeric prefactor \(c_2\) of order one depending on the exact form of \(\vartheta \), which can be obtained by evaluating the integral of Eq. (9).
Further details, in particular the discussions of x- and z-components, can be found in “Appendix C”.
4 Experimental method
The beer mat shooting apparatus is picturised in Fig. 3. It consists of two electric motor powered treadmills which can be programmed to move at a given speed up to \({16}\,{\hbox {m}/\hbox {s}}\) forwards or backwards independently of each other. Each of the two treadmills runs around two gears with radius \({10}\,\hbox {mm}\), one of which (the black ones in Fig. 3) is connected to the electro motor. The speed of the treadmills can be inferred by measuring the rotations per minute of the driving gear using a digital laser non-contact photo tachometer. We denote the rotations per minute of the left and the right driving gear by \(u_l\) and \(u_r\), respectively.
A beer mat put between these treadmills is accelerated until the edges assume the speed of the respective treadmill. We have checked with high speed camera videos that an undamaged beer mat does indeed not slip along the treadmills. During acceleration the beer mat is confined vertically between two plastic surfaces.
During operation the apparatus is placed on a table so that the beer mats are shot from a height of \({0.98}\,\hbox {m}\) with the plastic surfaces horizontally aligned. Then, to the level of accuracy required here the apparatus produces reproducible initial flight conditions. All beer mats shot with the same treadmill configuration followed the same trajectory and hit the same point on the floor, up to minor deviations in the order of \({0.1}\,\hbox {m}\).
Flights were recorded using a high speed cameraFootnote 5 with 500 frames per second. Example videos of flights are available in the supplemental material. We used the program TrackerFootnote 6 to extract the coordinates of the beer mat at any given time from the videos. The measurements cover a broad range of different initial velocities and angular momenta. A summary of the recorded and analysed experimental setups is provided in Table 1 of the appendix.
Horizontal position y orthogonal to the initial flight direction in meters against time in seconds. The flight started with initial conditions as in Eq. (8) with \(v_0={2.6}{\hbox {m}/\hbox {s}}\) and \(\omega _0={49}{\hbox {s}}^{-1}\) (corresponding to 7.9 rotations per second). The effective theory fit follows Eq. (10). For details on the numerical simulation see Appendix 6.7. The lengths are not exactly correct due to perspective distortion
5 Results and discussion
For each of the recorded experiments we have analysed the trajectory of the corresponding flight. First, we observe that the angular velocity \(\omega _0\) changes by less than \(10\%\) during the flights.
Next we reconstruct the horizontal position y(t) from the recorded video. We fit the functional form Equation (10) to this data for y(t) for each experimental setup separately and determine the parameters \(c_2\epsilon , t_i\) and \(\tau \). One representative example of such a y-trajectory and the corresponding fit are shown in Fig. 4. The so determined values for the characteristic time \(\tau \) and \(t_i\) are shown in Fig. 5 as functions of \(v_0/\omega _0\). From this Figure one can already read off that stable flights of beer mats longer than \({0.45}\,{\hbox {s}}\) are hardly possible. The detailed fit results are provided in Table 2 of the appendix.
Note that we also solved the full set of differential equations including lift, drag and sub-leading effects numerically, for details see Appendix 6.7. The corresponding y-trajectory is also depicted in Fig. 4 for means of comparison as the purple dash-dotted line.
In Fig. 6 we show \(\lambda \) determined via \(\lambda = \log 2/\tau \) as a function of \((v_0/\omega _0)^2\). In the same Figure we show a fit of Eq. (7) to the data for \(\lambda \) (with \(\rho ={1.25}{\hbox {kg}/\hbox {m}^{3}}\), \(m={5.9}\,{\hbox {g}}\) and \(A=\pi r^2\), \(r={5.3}\,{\hbox {cm}}\)) yielding \(\lambda _0 = {12.4\pm 1.5}\,{\hbox {s}}^{-1}\) and \(\lambda _1 = {10.7\pm 0.7}\,{\hbox {s}}^{-1}\).
Characteristic times \(t_i\) and \(\tau \) derived via a fit of Eq. (10) for a variety of different initial conditions in speed \(v_0\) and angular speed \(\omega _0\)
Note that the statistical error from the fit depicted with errorbars has but a small contribution to the overall error. The total error comes mostly from the fact that the flight of a beer mat is not perfectly reproducible with our apparatus and in principal identical initial conditions lead to slightly different results when repeated several times. This discrepancy between statistical and total error is reflected in the large spread of points totally incompatible with the size of their error bars.
As we mentioned above, \(\omega _0\) does change measurably during the flight, however, not significantly in particular in the phase of the flight relevant for our analysis. Therefore, we think the main assumption for our effective theory of constant \(\omega _0\) is fulfilled well enough, even more so as the effective theory, namely Eqs. (10) (and (C2), (C5) from the appendix), describes the flight trajectories extremely well with fitted parameters. We find our earlier expectations confirmed as indeed \(t_i\ll \tau \) for all flights we investigated. Most importantly, the values of \(\lambda \) are in good agreement with a linear dependence on \(v_0^2/\omega _0^2\) plus a constant.
These values for \(\lambda _0\) and \(\lambda _1\) are universal constants for every system describable by the effective theory. Thus, they should allow us to predict the duration of a stable flight of any rotating and thin enough disk. Just using the constant term \(\propto \lambda _0\) solely depending on the disk’s properties allows one to predict the longest possible stable flight duration. We arrive at some very interesting and astonishingly realistic predictions: recall that a beer mat maintains stability for up to about \({0.45}{\hbox {s}}\). Now a standard playing cardFootnote 7 is expected to reach slightly more than half that time, namely about \({0.24}\,\hbox {s}\), a CD holds out for twice a beer mat’s time or \(\sim {0.8}\,\hbox {s}\), a frisbee for ca. \({0.7}\,\hbox {s}\) (without any aerodynamics due to curvature taken into account) and a discus could in principle fly undisturbed for up to ca. \({16}\,\hbox {s}\). These predictions could be tested experimentally.
We find especially the time estimate for the frisbee very interesting because it is not unrealistic for a mediocre thrower to have the frisbee flip towards backspin in the timespan of about one second though this estimate lies rather on the short side and of course the wing form of a frisbee allows it to remain stable for a much longer time when thrown professionally. The reason is that frisbees have their aerodynamic center very near to their center of mass [2] and, thus, experience much less torque.
6 Summary
In this paper, we have investigated the peculiar flight trajectories of beer mats: independently of their initial conditions, beer mats always tilt into backspin position shortly after being thrown. When thrown by hand, the moment this tilting starts is seemingly random.
We have presented an explanation for this effect and developed an effective theory describing the flight of beer mats, or any thin disk, alongside an experimental investigation of such flights. We used the experimental results to estimate the parameters of the aforementioned effective theory, which describes the data very well. The effective theory then makes universal predictions: for instance, the damping factor \(\lambda \) of the tilting motion must depend linearly on \((v_0/\omega _0)^2\) (the centre-of-mass velocity and the angular speed, respectively) and otherwise only on the disk’s radius, mass and the density of air. This is nicely confirmed by our empirical results.
\(\lambda \) is directly related to the time \(\tau \) via \(\lambda =\log (2)/\tau \). \(\tau \) is the time after take off at which the tilting into backspin orientation becomes visible, i.e. \(\tau \) is the time of stable flight. Its apparent randomness solely stems from the inability to reproduce initial conditions when throwing by hand.
Since the effective theory holds for any thin disk we are also able to predict \(\tau \) for other types of disks like playing cards or CDs, which could be tested experimentally. Frisbees, however, do have different aerodynamic properties than beer mats due to their rounded down edges and, thus, enjoy a significantly extended stable flight time.
Notes
The literature on this topic is sparse and often not published in peer reviewed journals.
The angular momentum is assumed to be large enough to guarantee a stable flight. See appendix 6.11 for more information.
The precession also causes the disk to change its flight direction because it accelerates towards the down-tilted edge. This effect, the so-called fade [9], is well known for frisbees.
This has been visualised many times with a good example of backspin flight in [11].
CR600x2, Optronis Slow-Motion Camera
Even Rick Smith, Jr., the world record holder for farthest card thrown, or a playing card machine gun cannot avoid their cards flying a curve and ending up with backspin after much less than a second [12].
Example videos provided in the supplementary material.
References
beer mat, in Cambridge Advanced Learner’s Dictionary ( Cambridge University Press, 2013) https://dictionary.cambridge.org/dictionary/english/beer-mat
N. M. Kamaruddin, Dynamics and Performance of Flying Discs, Ph.D. thesis (2011), aerodynamic center of frisbees on pp. 104-112 https://search.proquest.com/dissertations-theses/dynamics-performance-flying-discs/docview/1775453524/se-2?accountid=14618
M. Hubbard, S.A. Hummel, Simulation of Frisbee Flight, in 5th Conference on Mathematics and Computers in Sport, edited by G. Cohen ( Sydney, New South Wales, Australia, 2000) http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.196.2540
Erynn J. Schroeder, An Aerodynamic Simulation of Disc Flight, Ph.D. thesis (2015) https://digitalcommons.csbsju.edu/honors_theses/68
R.D. Lorenz, Flight and attitude dynamics measurements of an instrumented Frisbee, Measurement Science and Technology. 16, 738–748 (2005) https://doi.org/10.1088/0957-0233/16/3/017
E. Motoyama, The physics of flying discs, (2002), unpublished manuscript, retrieved online June 11, 2021 http://people.csail.mit.edu/jrennie/discgolf/physics.pdf
H. Schlichting, E. Truckenbrodt, Aerodynamik des Flugzeuges. Erster Band: Grundlagen aus der Strömungsmechanik, Aerodynamik des Tragflügels (Teil I) (Springer-Verlag, Berlin/Heidelberg/New York, 1967) https://doi.org/10.1007/978-3-642-96046-8
I.H. Abbott, A.E. Von Doenhoff, Theory of wing sections, including a summary of airfoil data, Dover books on aeronautical engineering series (Dover Publications, 1959) aerodynamic center derived in chapter 4 https://books.google.de/books?id=DPZYUGNyuboC
Rameka, Explanation of the physics of flying discs, (2009), online blog, visited online June 11, 2021 https://www.dgcoursereview.com/forums/showthread.php?t=2250
G. Magnus, Ueber die Abweichung der Geschosse, und: Ueber eine auffallende Erscheinung bei rotirenden Körpern. Annalen der Phys. 164, 1–29 (1853). https://doi.org/10.1002/andp.18531640102
D. A. Muller, Backspin Basketball Flies Off. Dam, Youtube Video (2015) https://www.youtube.com/watch?v=2OSrvzNW9FE
M. Rober, Playing card machine gun- card throwing trick. Shots, Youtube Video (2018) https://www.youtube.com/watch?v=GYCI58pMGuQ
T. Benson, Modern Lift Equation, (2018) https://wright.nasa.gov/airplane/lifteq.html
E. Hairer, G. Wanner, Solving ordinary differential equations II (Stiff and differential-algebraic problems (Springer, Berlin, 1996) https://archive-ouverte.unige.ch/unige:12344
J.R. Dormand, P.J. Prince, A family of embedded Runge-Kutta formulae. J. Comput. Appl. Math. 6, 19–26 (1980). https://doi.org/10.1016/0771-050X(80)90013-3
E. Hairer, S.P. Nørsett, G. Wanner, Solving Ordinary Differential Equations I: Nonstiff Problems (Springer-Verlag, Berlin, Heidelberg, 1993)
R. Ashino, M. Nagase, and R. Vaillancourt, Behind and beyond the Matlab ODE suite, Comp. Math. Appl. 40, 491 – 512 (2000), Our algorithm ROW23 is called ode23s here. https://doi.org/10.1016/S0898-1221(00)00175-9
K. Levenberg, A method for the solution of certain non-linear problems in least squares. Q. Appl. Mathe. 2, 164–168 (1944) http://www.jstor.org/stable/43633451
D.W. Marquardt, An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 11, 431–441 (1963). https://doi.org/10.1137/0111030
Nonlinear least-squares Fitting, GNU Scientific Library (2019) https://www.gnu.org/software/gsl/doc/html/nls.html
Acknowledgements
This work has been inspired by a trip to Munich in March 2017 with the Physics Show Bonn. We thank all the participants for this inspiration and the very enjoyable time together. We would also like to thank Michael Kortmann who lent us the high speed camera, helped us with the experiments and without whom we three theoreticians would have been completely lost. We thank Karl Maier for very useful discussions on the shooting apparatus’ design. Last but not least we owe huge thanks to the mechanics and electronics labs of the HISKP Bonn and in particular Dirk Lenz for building the beer mat shooting apparatus. This work is supported in part by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) and the NSFC through the funds provided to the Sino-German Collaborative Research Center CRC 110 “Symmetries and the Emergence of Structure in QCD” (DFG Project-ID 196253076 - TRR 110, NSFC Grant No. 12070131001). Our sincere apologies to everyone hit by a beer mat, be it through inaccurate aim or due to us instigating others to perform silly experiments.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Data availability Statement
This manuscript has associated data in a data repository. [Authors’ comment: All the videos analysed for this article and the extracted raw data can be found in https://urldefense.proofpoint.com/v2/url?u=https-3A__uni-2Dbonn.sciebo.de_s_d2Y6V36R0JCstFO&d=DwIDaQ&c=vh6FgFnduejNhPPD0fl_yRaSfZy8CWbWnIf4XJhSqx8&r=7GjDei_PxQva2JNOfHbJQKIolTpKkGdW_4o9-CecCzX9fDPu7SrgsodpYCPByYz6&m=jt2JPHan7diczqYy6gy7n_4zCZRLDEv6szIOJoV9Qyo&s=a6C9jtvrH54wRhuAK0B_55yO8oLpOyGjxmYUflWeCto&e=.]
Supplementary Information
Below is the link to the electronic supplementary material.
Supplementary material 1 (avi 9672 KB)
Supplementary material 2 (avi 3554 KB)
Supplementary material 3 (avi 1537 KB)
Supplementary material 4 (avi 5307 KB)
Appendices
Appendix A: Forces
The equations of motion (EOM) of a rotating rigid body can be derived with well-known techniques. This derivation is given in Appendix 6.1 with the variable convention as in Appendix 6.7. Let us then get our hands on the constraining forces \(F_q\) describing the non-free motion of the disk through air. The challenge is to find forms that are easy (we do not want for example to solve the complete Navier-Stokes equations) and at the same time accurate enough. There are many effective formulae for drag and lift [7] but all of them are only approximations and it is neither clear how well they describe the given problem, nor does one know a priori which are the most significant and which can be neglected. Our numerical simulations helped to identify the most relevant terms as presented here.
The most relevant coordinates are visualised in Fig. 7. A detailed summary of all the coordinates is provided in Appendix 6.7.
In this section, we will use the notation
where i runs over all indices relevant for this component (e.g. \(F_x=F_x^\text {drag}+F_x^\text {lift}\)).
1.1 Derivation of the equations of motion
In what follows we use Lagrange’s formalism because we find it clearer than Newton’s laws or Euler’s equations, though (of course) either approach eventually leads to the same EOM.
The moment of inertia for a flat disk of mass m and radius r is given by
about an axis lying in the plain of the disk and by 2I about the symmetry axis. Thus, the total rotation energy is
Here
denotes the total angular velocity in a basis with diagonal inertia tensor.
The kinetic and potential energies are simply given by \(E_{\text {kin}}=\frac{1}{2} m{\dot{\varvec{x}}}^2\) and \(E_{\text {pot}}=mgz\) respectively. In addition we introduced a torque \(E_{\text {tor}}=\varvec{T}\cdot \varvec{D}\). In the case of a flying disk we have \(\varvec{T}=0\). A nonzero torque however leads to well known precession movements and is thus very helpful for consistency checks. It corresponds to a preferred symmetry axis or a weight attached to the disk on one side.
Putting all these terms together yields the Lagrange function
For a generalised coordinate q exerted to an external constraint force \(F_q\) the Euler-Lagrange-equation reads
As we do not know the drag and lift forces a priori we will denote them by \(F_{\varvec{x},\theta ,\phi ,\psi }\) respectively. This leads to
where we defined
using the orthogonal unit vectors in direction of increasing \(\theta \) and \(\phi \). In the canonical representation this means
In order to simplify further calculations we introduce the reduced quantities corresponding to the respective accelerations
instead of forces. With these terms and the solution of equations (A11) and (A12) for \({\ddot{\phi }}\) and \({\ddot{\psi }}\) the EOMs read
We directly divided the ordinary differential equations (ODEs) of second order into twice as many ODEs of first order. This will be needed for the numerical simulations.
Our notation distinguishes between the time derivative \({\dot{q}}\) of a variable, the auxiliary variable \(p_q\) (in general not equivalent to the canonical momentum) and later the constants of motion \(\varvec{v}_0\) and \(\omega _0\). Even though they might have the same numerical values, they represent different physical concepts.
1.2 Turbulent drag slowing the disk
Generally turbulent drag acts proportionally to the fluid density \(\rho \), the area \(A=\pi r^2\) of the object and its squared velocity. It is always working in the direction opposite to the velocity. In case of translational drag this can be be formulated as
Here \(\alpha \) is the angle of attack. It can be calculated via
The coefficient \(c_x^0\) gives the resistance at zero angle of attack (see Fig. 7) and can be approximated by \(c_x^0\approx 2rd/A\) where d is the thickness of the disk, though choosing \(c_x^0\) slightly larger increases the stability of the simulation significantly. It is not known by how much skin friction increases the coefficient. In contrast the drag coefficient \(c_x^\alpha \approx 1.28\) is known from experiment. It acts on the effective area \(A\sin \alpha \) with a magnitude again proportional to \(\sin \alpha \).
1.3 Laminar drag damping angular momentum
The angular velocities about an axis in the body plane are very low. Due to this it makes sense to consider laminar drag as the main reason for damping of said velocities. The radius of the disk should have cubic influence on this term: two powers from the area, one from the lever. The coefficient is (up to factors \(c_\Phi ^\text {vis}\) and \(c_\Phi ^\text {dyn}\) of order one) composed of the dynamic viscosity of air \(\eta \) and a dynamic term \(|v|r\rho \) reflecting the acceleration of air with a velocity proportional to the distance from the center of rotation, i.e. the radius r, and accumulating more air, the more is passed during flight, thus yielding an additional factor |v|. Put together we receive
There is a skin friction as well, slowing down the rotation about the symmetry axis. It has a much smaller coefficient but is not negligible on long time scales nevertheless. We write
1.4 Lifting force
Lift is the component of the force on the disk acting perpendicular to the movement. Otherwise the formula is quite similar to the turbulent drag. It has a quadratic dependence in \(\varvec{v}\) as well. One finds
where \(\alpha \) and \(\beta \) as defined in (A29) and \(\sin \beta \) is needed for the normalisation of the inner cross-product. The coefficient for thin airfoils has been taken from [13]. As it is known that the lift rapidly drops at about \(\alpha \approx 20^\circ \), we multiplied the coefficient by a sigmoid
with \(\alpha _0=25^\circ \) and \(\sigma =5^\circ \). This form is purely qualitative and might differ from reality significantly. However, it should not be of high relevance because we expect the flight to proceed mostly with a small angle of attack \(\alpha \ll \alpha _0\).
1.5 Lift-induced torque
For a thin airfoil it is known that the aerodynamic center, the point where the lift attacks, lies \(25\%\) behind the leading edge [8], so the lift introduces an additional torque. For a round disk this means an average distance of \(\frac{\pi }{8}r\) from the center of mass to the front [7]. Again we have to project the force onto \(\varvec{D}\). This projection acts in the \(-\varvec{e}\) direction, where
is a unit vector in direction of the leading edge. Putting this together we receive
1.6 Magnus force
The first force that comes in mind when thinking about a rotating object moving through a fluid is the Magnus force [10]. It acts orthogonally to the movement and the angular momentum of the object. In our case the effect is dominated by skin friction and not the movement of air along the rim of the disk, but this should not influence the effect crucially. The resulting force can be written as
with a dimensionless coefficient \(c_x^\text {Magnus}\) of order one.
1.7 Convention for the used variables
For the description of a rotating moving disk we choose Cartesian coordinates \(\varvec{x} = (x,y,z)\) (vectors are printed in bold) to denote the position and spherical coordinates \((\theta ,\,\phi )\) for the orientation of the symmetry axis. The disk rotates about this symmetry axis \(\varvec{D}\) by the angle \(\psi \). A summary is given in Eqs. (A44) and Figure 7.
Appendix B: Numerical simulation
In order to test the considerations from the previous section we solve the system of differential equations numerically. It turns out that this is much more challenging than expected. The results presented here do not describe the flight of a disk quantitatively correctly for several reasons. First of all this is not our goal, at least for now. We are only interested in a numerical verification of our qualitative arguments. In addition we do not know many of the coefficients without experiment, the forces we use are only approximations and it is not clear if we left out relevant terms.
1.1 Algorithms
A huge issue for numerical stability is the region where \(\theta \approx 0\). The two points where \(\theta =0\) exactly are null sets. Therefore, they are protected by a centrifugal barrier and are never reached. This leads to divergent forces \(\sim \sin ^{-3}\theta \). The stability can be improved significantly via coordinate transformations into a system where the polar angle is measured from the axis x, y, or z with the smallest value \(d_i\), i.e. the largest corresponding \(\theta \). For algorithmic details see Appendix 6.10. Fortunately the coordinate transformation leaves the formulae apart from equation (A14) forminvariant. Only the dependence of \(\varvec{D}\) on the angles changes.
Depending on the choice of the coefficients the differential equations sometimes turn out to be stiff [14]. For this reason we implemented two different numeric integrators with adaptive step size. In all physically interesting cases the Dormand-Prince 5(4) algorithm (DOPRI54) [15, 16] gives good results. It is a non-stiff integrator of order 5 that uses an embedded fourth-order integrator for step size correction. In addition we implemented the Rosenbrock-Wanner 2(3) algorithm (ROW23) [17] of order two with third order step size correction. It is suitable for stiff ODEs being A- and L-stable. We cross checked the correctness of the usually faster DOPRI54 with the stable ROW23.
1.2 Results
If not mentioned otherwise explicitly, the following results all use the parameters from equations (B4) and (B5) in Appendix 6.11. We tried to keep the values as near to the ones of a beer mat as possible, but we had to guess several values. This is especially critical for \(c_x^0\), \(c_x^\text {Magnus}\) and \(c_\Phi ^\text {dyn}\) where we did not find good literature values, but a strong dependency of the flight behaviour.
We did not attempt any fine tuning of these parameters, on the contrary, we restricted ourself to integer or inverse integer values, because we are mostly interested in the qualitatively correct behaviour. It is an important stability test that minor changes in the parameters do not significantly change the picture as a whole. Otherwise our predictions might not be valid on a mountain with thinner air, on a hot or humid day, or for a slightly thicker disk. For these reasons, our numerical simulations do not match the experimental data exactly (see Figs. 11 and 4). Nevertheless they provide a reasonably good approximation capturing all the important features and providing a proof that we identified the relevant forces.
Figure 8 shows the trajectory of a disk with all the relevant forces given in Sect. 1 included. We chose to shift the angles by \(\pi /2\) and \(3\pi /2\) respectively, so that the zero-line marks backspin. In addition we normalised the azimuthal angle \(\phi \) to the flight direction \(\phi _0\). One clearly sees that the disk converges to backspin orientation. The time scale of about half a second on which this happens is realistic. Once backspin has been reached, the disk remains in this orientation for any simulated duration. It is also interesting to observe that \(\phi \) reaches the vicinity of its target value much earlier than \(\theta \). While \(\theta \) is smoothly and monotonously increasing, \(\phi \) reaches an orientation of minimised air resistance practically immediately. Afterwards \(\phi \) overshoots its final value and continues a with a smooth convergence. This overshooting is caused by the positive angle of attack and is crucial for the convergence towards backspin.
Next we show that \(F_\Phi ^\text {lift}\) is indeed the force responsible for always converging to backspin. In Fig. 9 we visualise the time evolution in absence of this force. In this case the polar angle \(\theta \) does not change and the azimuthal angle \(\phi \) does not carry any meaning at \(\theta =0\). In other words, there is no torque and the orientation remains as it is without ever reaching backspin. As there is no difference in the initial conditions leading to the Figs. 8 and 9 respectively other than \(c_\Phi ^\text {lever}\), we can conclude that it is this effect that leads to backspin as the only preferred orientation.
Let us conclude with an example of coefficients chosen in such a way that the orientation of the disk does not converge at all. For this we show the time evolution without the Magnus effect and the drag at zero angle of attack in Fig. 10. The system does not converge because damping and gravitational acceleration just balance each other. Instead it oscillates about the backspin orientation. Again we find that \(F_\Phi ^\text {lift}\) leads to a preference of this orientation, thus we do not need the Magnus effect in principle to explain the qualitative trend. From this and other simulations we find, however, that it is crucial for the stability.
1.3 Details on the coordinate transformation
Here, we denote the spherical coordinates with reference to \(x_k\) by \((\theta _k,\,\phi _k)\). I.e. in the usual case we use \(z\equiv x_3\) and have \((\theta ,\,\phi )\equiv (\theta _3,\,\phi _3)\). Then equation (A14) generalises to
Then a coordinate transformation from the initial axis \(x_i\) to the final one \(x_f\) in given in Algorithm 1. The formulae for \(\theta \) and \(\phi \) are simply the geometrical definitions. The derivatives of these formulae directly lead to the equations for \(p_{\theta }={\dot{\theta }}\) and \(p_{\phi }={\dot{\phi }}\).

1.4 Parameters used in the numerical simulation
The coefficients listed in equation (B4) reproduce the values of a beer mat as accurately as possible while setting the maximum number of coefficients to zero and without fine tuning. The nonzero coefficients are
We deliberately chose to trade some accuracy in the description for better qualitative understanding by removing all the terms that are not needed to describe the investigated effect.
The relevant starting parameters have been set, again reproducing the experimental setup as realistically as possible, to
We checked that different initial angles do not influence the long term behaviour by repeating the simulation several times with \(\varvec{D}\) sampled randomly from a uniform distribution on the unit sphere.
Appendix C: The x- and z-components in the effective theory
In the main article we solve the differential equation obtained from the effective theory only for the y-component of the trajectory (see Eq. (10)). This coordinate shows the most remarkable behaviour because it is dominated by two very distinct regimes and the time scale \(\tau \) of the rotation features prominently in the curve. Nevertheless the x- and z-components are of interest as well and we are going to investigate them here closely.
The differential equation
is easily solvable for x by integration.
Last but not least we investigate the vertical component z following the differential equation
Here, we introduced a dependence of the damping coefficient \(c^\text {damp}_x(\vartheta )\) on the angle \(\vartheta \). We do not make any predictions about the nature of this dependence other than the damping being larger parallel to \(\varvec{D}\) than orthogonal to \(\varvec{D}\), writing \(c^\text {damp}_x(0) {=}{:}c^{\parallel }_xxc^{\perp }_x {:}{=}c^\text {damp}_x(\pm \pi /2)\).
For convenience let us define the time scale \(\tau _z{:}{=}\frac{m}{c^{\parallel }_x A}\) and the coefficient \(c^\text {rel}_x{:}{=}c^{\parallel }_x/c^{\perp }_x\). As always we start with side spin. Similarly to the considerations of the y-component we can split the dynamics into two stages that have to be connected smoothly. In the first one (\(t\ll \tau \)) we use \(\cos ^2\vartheta \approx 1\) and \(c^\text {damp}_x(\vartheta )\approx c^{\parallel }_x\), in the second one (\(t\gg \tau \)) the other extreme \(\cos ^2\vartheta \approx 0\) and \(c^\text {damp}_x(\vartheta )\approx c^{\perp }_x\) applies. In both stages, the differential equation is easily solvable and we use the same transition function as in equation (10) to obtain
where we assumed \(\tau _z<\tau \) which we find to hold for realistic experiments.
Horizontal position in initial flight direction x (left) and vertical position z (right) in meters against time in seconds. The flight started with initial conditions as in Eq. (8) with \(h={98}\,{\hbox {cm}}\), \(v_0={2.6}\,{\hbox {m}/\hbox {s}}\) and \(\omega _0={49}{\hbox {rad}/\hbox {s}}\) (corresponding to 7.9 rotations per second). The fit follows Eq. (C2) and Eq. (C5) respectively. For details on the numerical simulation, see Sect. 6.7. The lengths are not exactly correct due to perspective distortion
In Fig. 11 we visualise both x- and z-components of the same real flight presented in Fig. 4 of the main article. We find that as before the experimental data is very well matched by the effective theory. The results obtained via first principle numerical simulations (see Sec. 6.7) provide a decent approximation of the real course of flight by following the correct trend.
Appendix D: Experimental setups and fit results
The different setups used for the experimental analysis of the beer mats’ flights are listed in Table 1. The corresponding fit results can be found in Table 2. The fit has been done using the Levenberg-Marquardt algorithm [18, 19]. Reference [20] provides a comprehensible explanation of the uncertainty estimation.
Appendix E: Flight with zero angular momentum
It is quite instructive to understand the unstable flight of a non-rotating disk because the influence of forces leading to precession otherwise can be observed directly. We find that the disk orientation undergoes a spontaneous symmetry breaking by tilting either slightly up- or downwards.Footnote 8 Once it has a finite angle of attack \(\alpha \), the lift-induced torque tends to increase \(\alpha \). This leads to a rapid rotation and an acceleration towards the original tilting; if the movement started with an upwards tilt, the beer mat flies up, otherwise it flies down. At the same time the movement decelerates due to large drag whenever the angle of attack is different from zero.
We now have to distinguish between the two possibilities explicitly. In the case of downwards tilt the disk flies a steep downwards curve and crashes into the floor. Successive shots hit the same place in very good approximation. There is no significant sidewards deviation from the original flight direction. This trajectory leads to the clustering in the lower central region of Fig. 12.
If, on the other hand, the disk is tilted upwards initially, it flies upwards much as a mirror image of the downwards trajectory. However, as it does not hit anything on its way, it decelerates up to some point of maximum height and nearly zero total velocity. From this point it simply falls down and minor influences can cause the disk to fall somewhere on a semicircle as can be seen in the upper half of Fig. 12.
The essential lesson from this experiment is that we can proof the existence of the lift-induced torque, or in other words show that the lift indeed attacks not in the center of mass but somewhere to the front of it.
A curios reader might wonder whether upwards and downwards movements are equally likely. We repeated the experiment several times and counted the number of beer mats in the lower cluster as well as the number of beer mats in the upper semicircle. It turns out that roughly two thirds of the beer mats chose the upper trajectory and landed in the semi-circle and only one third flew downwards. A \(\chi ^2\)-test revealed that the probability of both trajectories being equally likely lies at \(p={3} \times 10^{-8}\). Again it is clear that gravity breaks the symmetry explicitly. As the disks are accelerated downwards starting in a neutral position, it is more likely for them to end up with a positive angle of attack.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ostmeyer, J., Schürmann, C. & Urbach, C. Beer mats make bad frisbees. Eur. Phys. J. Plus 136, 769 (2021). https://doi.org/10.1140/epjp/s13360-021-01732-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjp/s13360-021-01732-1