Multiplicative inverse with quantum search algorithm under π/18 phase rotation

Abstract

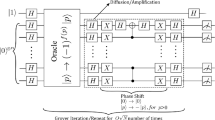
A quantum search algorithm with phase shift of π/18 is proposed to find a multiplicative inverse of an equation in an unsorted database. The unitary operator $Q{\text{ }}$ ($Q{\text{ = }}I_{t} U^{{ - 1}} I_{0} U$) is operated repeatedly on the initial state with $\left\lfloor {9\sqrt {{N \mathord{\left/ {\vphantom {N M}} \right. \kern-\nulldelimiterspace} M}} } \right\rfloor$ times to find a marked item successfully. At least 99.81% of the probability of success could be achieved by this proposed quantum search algorithm with time complexity $O\left( {\sqrt {{N \mathord{\left/ {\vphantom {N M}} \right. \kern-\nulldelimiterspace} M}} } \right)$. Compared with four typical algorithms, the proposed search algorithm has better performance to find out a match in terms of success probability with the same time complexity $O\left( {\sqrt {{N \mathord{\left/ {\vphantom {N M}} \right. \kern-\nulldelimiterspace} M}} } \right)$.

Appendices

Appendix A

In this appendix, Eq. (12) can be deduced. The required number of iterations can be calculated as follows,

$$ R = {\text{CI}}\left( {\frac{{{\pi \mathord{\left/ {\vphantom {\pi {2 - \theta }}} \right. \kern-\nulldelimiterspace} {2 - \theta }}}}{{2\theta }}} \right), $$

(24)

where ${\text{CI}}(x)$ represents the integer closest to x.

Let $\sin ^{2} \theta = {M \mathord{\left/ {\vphantom {M N}} \right. \kern-\nulldelimiterspace} N} = \lambda$, Eq. (24) becomes

$$ \begin{aligned} R &= {\text{CI}}\left( {\frac{{\arccos \sqrt {{M \mathord{\left/ {\vphantom {M N}} \right. \kern-\nulldelimiterspace} N}} }}{{2\arcsin \sqrt {{M \mathord{\left/ {\vphantom {M N}} \right. \kern-\nulldelimiterspace} N}} }}} \right) \\ & = {\text{CI}}\left( {\frac{{\arccos \sqrt \lambda }}{{2\arcsin \sqrt \lambda }}} \right). \\ \end{aligned} $$

(25)

Equation (24) implies that ${\text{R}} \le \left\lfloor {{\pi \mathord{\left/ {\vphantom {\pi {4\theta }}} \right. \kern-\nulldelimiterspace} {4\theta }}} \right\rfloor$(26), and assume that $M \le {N \mathord{\left/ {\vphantom {N 2}} \right. \kern-\nulldelimiterspace} 2}$ for the moment, the following condition would be obtained.

$$ \theta \ge \sin \theta = \sqrt {\frac{M}{N}} . $$

(26)

Combining Eq. (26) with Eq. (27), the upper bound on the number of iteration required is

$$ R \le \left\lfloor {\frac{\pi }{4}\sqrt {\frac{N}{M}} } \right\rfloor . $$

(27)

In conclusion, according to Eqs. (25) and (28), (12)$R = {\text{CI}}\left( {\frac{{\arccos \sqrt \lambda }}{{2\arcsin \sqrt \lambda }}} \right){\text{ = }}\left\lfloor {\frac{\pi }{4}\sqrt {\frac{N}{M}} } \right\rfloor$ in Sect. 2.1 can be taken.

Appendix B

In this appendix, a derivation is given to Eq. (17) in Sec. 3. By observing that $M \ll N$, we have $\sin \theta = \sqrt {{M \mathord{\left/ {\vphantom {M N}} \right. \kern-\nulldelimiterspace} N}} \approx \theta$, and $\arcsin (\sin ({\phi \mathord{\left/ {\vphantom {\phi 2}} \right. \kern-\nulldelimiterspace} 2})\sin \theta ) \approx \sin ({\phi \mathord{\left/ {\vphantom {\phi 2}} \right. \kern-\nulldelimiterspace} 2})\sin \theta$, so the following form can be taken,

$$ R = \left\lfloor {\frac{\pi }{{4\arcsin (\sin ({\phi \mathord{\left/ {\vphantom {\phi 2}} \right. \kern-\nulldelimiterspace} 2})\sin \theta )}}} \right\rfloor \approx \left\lfloor {\frac{\pi }{{4\sin ({\phi \mathord{\left/ {\vphantom {\phi 2}} \right. \kern-\nulldelimiterspace} 2})\sin \theta }}} \right\rfloor . $$

(28)

when $\phi = {\pi \mathord{\left/ {\vphantom {\pi {18}}} \right. \kern-\nulldelimiterspace} {18}}$, Eq. (29) becomes

$$ R \approx \left\lfloor {\frac{\pi }{{4\sin ({\phi \mathord{\left/ {\vphantom {\phi 2}} \right. \kern-\nulldelimiterspace} 2})\sin \theta }}} \right\rfloor \approx \left\lfloor {9\sqrt {\frac{N}{M}} } \right\rfloor . $$

(29)

So Eq. (17) can be deduced.

Appendix C

In this appendix, calculation expressions about the success probability and the number of iterations of five algorithmic schemes are shown as follows (Table

Table 2 Calculation expressions of the proposed algorithm with four different algorithms ($\sin \theta = {M \mathord{\left/ {\vphantom {M N}} \right. \kern-\nulldelimiterspace} N}$)

2).