Probabilistic analysis of random nonlinear oscillators subject to small perturbations via probability density functions: theory and computing

Abstract

We study a class of single-degree-of-freedom oscillators whose restoring function is affected by small nonlinearities and excited by stationary Gaussian stochastic processes. We obtain, via the stochastic perturbation technique, approximations of the main statistics of the steady state, which is a random variable, including the first moments, and the correlation and power spectral functions. Additionally, we combine this key information with the principle of maximum entropy to construct approximations of the probability density function of the steady state. We include two numerical examples where the advantages and limitations of the stochastic perturbation method are discussed with regard to certain general properties that must be preserved.

1 Introduction

Many problems arising in physics and engineering lead to differential equations whose data (initial/boundary conditions, forcing term and/or coefficients) must be set from experimental information that involves, what is usually termed, epistemic (or reducible) randomness [1]. Although this type of uncertainty can possibly be reduced by improved measurements or improvements in the modelling process, there is another uncertainty source often met in mathematical modelling of real-world problems called aleatory (or irreducible) randomness, which comes from the intrinsic variability of the phenomenon to be modelled. This approach leads to formulate random/stochastic differential equations [2, 3]. Apart from answering fundamental questions about existence, uniqueness, continuous dependence of the solution with respect to model parameter or stability, solving a random differential equation means not only to calculate, exact or approximately, its solution, which is a stochastic process, but also to determine its main statistical information like the expectation or the variance. However, a more ambitious goal is to calculate the finite distribution functions (usually termed the fidis) of the solution, being the first probability density function the main fidis since by integration one can calculate any one-dimensional moment (so including the mean and the variance), and also the probability that the solution lies within an interval of specific interest [2]. In real-world applications of physics or engineering, this fact is a key point since it allows us to calculate relevant information such as, for example, the probability that the position of an oscillator lies within two specific values where it is under control, the probability of buckling of a tower subject to extreme loads, etc.

In the realm of stochastic vibratory systems, many problems can be directly formulated through differential equations of the form ${\mathcal {L}}[Y(t)]=Z(t)$, where ${\mathcal {L}}[\cdot ]$ is a linear operator and Z(t) is a stochastic external source, which acts upon the system producing random vibrations. For example, the model ${\mathcal {L}}[Y(t)]= Z(t)$, where ${\mathcal {L}}[Y(t)]:=\frac{\mathrm {d}^2Y(t)}{\mathrm {d}t^2} + 2\beta \frac{\mathrm {d}Y(t)}{\mathrm {d}t} +\omega _0^2 Y(t)$, has been used, from the original contribution [4], to describe the effect on earthbound structures of earthquake-type disturbances being Y(t) the relative horizontal displacement of, for example, the roof of a building with respect to the ground [5]. Additionally, many vibratory systems are described by nonlinear equations, say ${\mathcal {N}}[Y(t)]=Z(t)$, where the nonlinear operator is defined in terms of a small perturbation $\epsilon$, ${\mathcal {N}}[\cdot ;\epsilon ]$. For example, in the case of the foregoing model the following general equation

$$\begin{aligned} \frac{\mathrm {d}^2Y(t)}{\mathrm {d}t^2} + 2\beta \frac{\mathrm {d}Y(t)}{\mathrm {d}t} +\omega _0^2 (Y(t)+\epsilon h(Y(t))) = Z(t),\quad t>0, \end{aligned}$$

(1)

where h, that is independent of $\epsilon$, is a nonlinear function of the unknown, and Y(t) has also been extensively applied. In most contributions, the nonlinear term h has a polynomial form [6]. For example, for $h(Y(t))=Y^3(t)$, model (1) corresponds to Duffing oscillator, which physically models an elastic pendulum whose spring’s stiffness violates Hooke’s law [7].

The goal of this paper is to tackle the stochastic study of oscillators of form (1) in the case that the nonlinear term h is a transcendental function using a polynomial approximation, based on Taylor’s expansions, and then to apply the stochastic perturbation method to approximate the main statistical functions of the steady state. Afterwards, we take advantage of the principle of maximum entropy (PME), in order to determine approximations of the probability density function (p.d.f.) of the stationary solution. To conduct our study, we have chosen a general form of the pendulum equation

$$\begin{aligned} \frac{\mathrm {d}^2Y(t)}{\mathrm {d}t^2} + 2\beta \frac{\mathrm {d}Y(t)}{\mathrm {d}t} +\omega _0^2 (Y(t)+\epsilon \sin (Y(t))) = Z(t),\quad t>0, \end{aligned}$$

(2)

where we will assume that $\beta >0$, the external source, Z(t), is defined via zero-mean Gaussian stationary stochastic process, which corresponds to an important case in the analysis of vibratory systems [8, 9]. In Sect. 2, we will obtain the main theoretical results throughout. Afterwards, in Sect. 3, we perform a numerical analysis through two examples, with criticism about the validity of the results obtained via the stochastic perturbation method. Conclusions are drawn in Sect. 4.

2 Probabilistic analysis

This section is devoted to study, from a probabilistic standpoint, the steady state of model (2). It is important to point out that the non-perturbated associated model

$$\begin{aligned} \frac{\mathrm {d}^2Y(t)}{\mathrm {d}t^2} + 2\beta \frac{\mathrm {d}Y(t)}{\mathrm {d}t} +\omega _0^2 Y(t) = Z(t),\quad t>0, \end{aligned}$$

(3)

has a steady-state solution provided $\beta >0$ and regardless of the value of $\omega _0^2$. For the sake of completeness, in “Appendix A”, we discuss about this issue in the general setting that Z(t) is a stationary Gaussian process and also in connection with the examples presented later. Firstly, in Sect. 2.1, we will apply the stochastic perturbation method to approximate its stationary solution, which is a random variable. Secondly, in Sect. 2.2, we will perform a stochastic analysis addressed to obtain the main statistical functions of the stationary solution. In particular, we will obtain the first one-dimensional moments and the correlation function.

2.1 Stochastic perturbation expansion

In the case of model (2), the method of perturbation consists in expanding the unknown, Y(t), in terms of a formal power series of the perturbative parameter $\epsilon$, which is assumed to have a small value ($|\epsilon | \ll 1$),

$$\begin{aligned} Y(t) = \sum _{n\ge 0} Y_n(t) \epsilon ^n, \end{aligned}$$

(4)

where the coefficients $Y_n(t)$ need to be determined. The idea of the perturbation method is to impose that expansion (4) satisfies the nonlinear differential equation (2), which does not have a closed-form solution, in order to obtain a set of exactly solvable equations whose unknowns are the coefficients $Y_n(t)$. As this reasoning leads to an infinite cascade system for $Y_n(t)$, in practice only a few terms of the expansion are considered, and so the method provides an approximation of the solution. This technique is usually applied by truncating expansion (4) to the first-order approximation

$$\begin{aligned} {\widehat{Y}}(t) = Y_0(t)+\epsilon Y_1(t), \end{aligned}$$

(5)

since as $\epsilon$ is small, the terms associated with higher powers ($Y_n(t)\epsilon ^n$, $n=2,3,\ldots$) in the series expansion can usually be neglected. This fact determines the legitimacy of the approximation only for a small range for the values of parameter $\epsilon$, which is consistent with the initial assumption that $\epsilon$ is a small parameter [10]. It is important to point out that, as already reported in [2, Ch. 7], no proof is available to show that the stochastic process Y(t) given in (4) converges in the mean square sense (or other probabilistic convergences), while some restrictive convergence conditions have been established in the deterministic framework [11]. Therefore, the convergence of Y(t) can be formulated in terms of strong hypotheses about its sample behaviour, which, in practice, results in very restrictive assumptions. Based on these facts, we here will apply the stochastic perturbation method by checking its validity with regard that some important statistical properties are preserved.

On the other hand, to derive a solvable family of differential equations after applying the perturbation method to model (2), we will also use a double approximation for the nonlinear term $\sin (Y(t))$. Specifically, we first apply a truncation of its Taylor’s series

$$\begin{aligned} \sin (Y(t)) \approx \sum _{m= 0}^M \dfrac{(-1)^{m}}{(2m+1)!} (Y(t))^{2m+1} , \end{aligned}$$

(6)

and secondly, we approximate Y(t) using (5), i.e.

$$\begin{aligned} \sin (Y(t)) \approx \sin ({\widehat{Y}}(t)) \approx \sum _{m= 0}^M \dfrac{(-1)^{m}}{(2m+1)!} (Y_0(t)+\epsilon Y_1(t))^{2m+1}. \end{aligned}$$

(7)

Substituting expansions (7) and (5) into (2), and equating terms with the same power of $\epsilon$, leads to the two following linear differential equations

$$\begin{aligned} \begin{array}{lcccl} \epsilon ^0 &{}: &{} \dfrac{\mathrm {d}^2Y_0(t)}{\mathrm {d}t^2} + 2\beta \dfrac{\mathrm {d}Y_0(t)}{\mathrm {d}t} + \omega _0^2 Y_0(t) &{}=&{} Z(t),\\ \epsilon ^1 &{} : &{}\dfrac{\mathrm {d}^2Y_1(t)}{\mathrm {d}t^2} + 2\beta \dfrac{\mathrm {d}Y_1(t)}{\mathrm {d}t} + \omega _0^2 Y_1(t) &{}=&{} \displaystyle \omega _0^2 \left( \sum _{m= 0}^M \dfrac{(-1)^{m+1}}{(2m+1)!} (Y_0(t))^{2m+1} \right) , \end{array} \end{aligned}$$

(8)

that can be solved in cascade. Although the method can be applied for any order of truncation associated with the Taylor’s expansion (6), in practice the value of M is set when the approximations obtained with M and $M+1$ are very closed with reference to a prefixed error or tolerance. In our subsequent analysis, we will consider $M= 2$ (that corresponds to a Taylor’s approximation of order 5, $\sin (Y(t)) \approx Y(t)-1/3!(Y(t))^3+1/5!(Y(t))^5$), since, as we shall show later, the approximations of the main statistics of the solution stochastic process do not significantly change with respect to $M= 1$ (that corresponds to a Taylor’s approximation of order 3, $\sin (Y(t)) \approx Y(t)-1/3!(Y(t))^3$). Summarizing, we have performed a double truncation. The first one, based on Taylor expansion for the nonlinear term ($\sin (Y(t))$), and the second one, when applying the stochastic perturbation expansion given in expression (5). (This latter approximation is fixed in our analysis at order 1 in $\epsilon$, as it is usually done in the literature.) Notice that the order M of the Taylor truncation is independent of the order of truncation applied for the perturbation method.

As previously indicated, we are interested in the stochastic analysis of the stationary solution or steady state. Based upon the linear theory of Laplace transformation [12], the solutions $Y_0(t)$ and $Y_1(t)$ are given by

$$\begin{aligned} Y_0(t)=\int _{0}^{\infty }g(s)Z(t-s){{\,\mathrm{d\textit{s}}\,}}, \end{aligned}$$

(9)

and

$$\begin{aligned} Y_1(t)=\omega _0^2 \sum _{m= 0}^M \int _{0}^{\infty } g(s) \dfrac{(-1)^{m+1}}{(2m+1)!} (Y_0(t-s))^{2m+1}{{\,\mathrm{d\textit{s}}\,}}, \end{aligned}$$

(10)

where for the underdamped case ($\frac{\beta ^2}{\omega _0^2}<1$),

$$\begin{aligned} g(t)= \left\{ \begin{array}{cll} \left( \omega _0^2-\beta ^2\right) ^{-\frac{1}{2}}{{\,\mathrm{e}\,}}^{-\beta t}\sin \left( \left( \omega _0^2-\beta ^2\right) ^{\frac{1}{2}}t\right) , &{} \quad \text {if} &{} \, \, t> 0,\\ 0, &{} \quad \text {if} &{} \, \, t\le 0. \end{array} \right. \end{aligned}$$

(11)

Physically this situation corresponds to the case that the oscillator approaches zero oscillating about this value [13]. Finally, we point out that the integrals defining $Y_0(t)$ and $Y_1(t)$ in (9) and (10) must be interpreted in the mean square sense [2, Ch. 4].

2.2 Constructing approximations of the first moments of the stationary solution

It is important to point out that the solution of model (2) is not Gaussian, so in order to probabilistically describe the stationary solution, the approximations of the mean and the variance (or more generally, the correlation) functions are not enough. This fact motivates that this subsection is addressed to construct reliable approximations of higher moments of the stationary solution [represented by the first-order approximation (5)]. This key information will be used in the next section to obtain approximations of the p.d.f., which in turns permits to obtain any one-dimensional moment of the stationary solution.

Specifically, in the subsequent development we will compute any statistical moments of odd order, ${\mathbb {E}}\left[ ({\widehat{Y}}(t))^{2i+1}\right]$, $i=0,1,2,\ldots$, the second-order moment, ${\mathbb {E}}\left[ ({\widehat{Y}}(t))^{2}\right]$, the correlation function, $\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau )$, the variance, ${\mathbb {V}}\left[ {\widehat{Y}}(t)\right]$, and the spectral density function, $S_{{\widehat{Y}}\!(t)}(f)$.

As indicated in Sect. 1, we shall assume that the stochastic external source, Z(t), is a stationary Gaussian stochastic process centred at the origin, i.e. ${\mathbb {E}}\left[ Z(t)\right] =0$, being $\varGamma _{ZZ}(\tau )$, its correlation function. Notice that the hypothesis ${\mathbb {E}}\left[ Z(t)\right] =0$ is not restrictive since otherwise we can work, without loss of generality, with the process ${\tilde{Z}}(t)=Z(t)-{\mathbb {E}}\left[ Z(t)\right]$, whose mean is null.

The mean of the first-order approximation is calculated taking the expectation operator in (5) and using its linearity,

$$\begin{aligned} {\mathbb {E}}\left[ {\widehat{Y}}(t)\right] ={\mathbb {E}}\left[ Y_0(t)\right] +\epsilon {\mathbb {E}}\left[ Y_1(t)\right] . \end{aligned}$$

(12)

To compute ${\mathbb {E}}\left[ Y_0(t)\right]$, we take the expectation operator in (9), then we first apply the commutation of the expectation and the mean square integral [2, Eq. (4.165), p. 104] and, secondly, we use that ${\mathbb {E}}\left[ Z(t)\right] =0$,

$$\begin{aligned} {\mathbb {E}}\left[ Y_0(t)\right] = {\mathbb {E}}\left[ \int _{0}^{\infty }g(s)Z(t-s){{\,\mathrm{d\textit{s}}\,}}\right] =\int _{0}^{\infty }g(s){\mathbb {E}}\left[ Z(t-s)\right] {{\,\mathrm{d\textit{s}}\,}}= 0. \end{aligned}$$

(13)

To compute ${\mathbb {E}}\left[ Y_1(t)\right]$, we take the expectation operator in (10) (recall that we take $M=2$) and we again apply the commutation between the expectation and the mean square integral as well as the integral representation of $Y_0(t)$ given in (9),

$$\begin{aligned} \begin{aligned} {\mathbb {E}}\left[ Y_1(t)\right]&={\mathbb {E}}\left[ -\omega _0^2\int _{0}^{\infty }\!\!g(s) Y_0(t-s){{\,\mathrm{d\textit{s}}\,}}+ \frac{\omega _0^2}{3!} \int _{0}^{\infty }\!\! g(s) (Y_0(t-s))^3{{\,\mathrm{d\textit{s}}\,}}\right. \\&\quad \left. -\frac{\omega _0^2}{5!}\int _{0}^{\infty }\!\!g(s) (Y_0(t-s))^5{{\,\mathrm{d\textit{s}}\,}}\right] \\&= -\omega _0^2\int _{0}^{\infty }\!\!g(s)\int _{0}^{\infty }\!\!g(s_1) {\mathbb {E}}\left[ Z(t-s-s_1)\right] {{\,\mathrm{d\textit{s}}\,}}_1 {{\,\mathrm{d\textit{s}}\,}}\\&\quad \, + \frac{\omega _0^2}{3!} \int _{0}^{\infty }\!\! g(s)\int _{0}^{\infty }\!\! g(s_1) \int _{0}^{\infty }\!\! g(s_2) \int _{0}^{\infty }\!\! g(s_3)\\&\qquad {\mathbb {E}}\left[ Z(t-s-s_1)Z(t-s-s_2)Z(t-s-s_3)\right] {{\,\mathrm{d\textit{s}}\,}}_3{{\,\mathrm{d\textit{s}}\,}}_2{{\,\mathrm{d\textit{s}}\,}}_1 {{\,\mathrm{d\textit{s}}\,}}\\&\quad \, - \frac{\omega _0^2}{5!} \int _{0}^{\infty }\!\! g(s) \int _{0}^{\infty }\!\! g(s_1) \int _{0}^{\infty }\!\! g(s_2) \int _{0}^{\infty }\!\! g(s_3) \int _{0}^{\infty }\!\! g(s_4) \int _{0}^{\infty }\!\! g(s_5)\\&\qquad {\mathbb {E}}\left[ Z(t-s-s_1)Z(t-s-s_2)\right. \\&\quad \, \cdot \left. Z(t-s-s_3)Z(t-s-s_4)Z(t-s-s_5)\right] {{\,\mathrm{d\textit{s}}\,}}_5{{\,\mathrm{d\textit{s}}\,}}_4{{\,\mathrm{d\textit{s}}\,}}_3{{\,\mathrm{d\textit{s}}\,}}_2{{\,\mathrm{d\textit{s}}\,}}_1 {{\,\mathrm{d\textit{s}}\,}}. \end{aligned} \end{aligned}$$

(14)

Now, observe that

$$\begin{aligned} {\mathbb {E}}\left[ Z(t-s-s_1)Z(t-s-s_2) Z(t-s-s_3)Z(t-s-s_4)Z(t-s-s_5)\right] =0, \end{aligned}$$

since Z(t) is a zero-mean Gaussian process [2, Eq. (2.101), p. 28]. Then, from (14) one gets

$$\begin{aligned} {\mathbb {E}}\left[ Y_1(t)\right] =0. \end{aligned}$$

(15)

Substituting (15) and (13) into (12), one obtains

$$\begin{aligned} {\mathbb {E}}\left[ {\widehat{Y}}(t)\right] = {\mathbb {E}}\left[ Y_0(t)\right] +\epsilon {\mathbb {E}}\left[ Y_1(t)\right] = 0. \end{aligned}$$

(16)

To obtain the second-order moment, ${\mathbb {E}}\left[ ({\widehat{Y}}(t))^2\right]$, we square expression (5), but retaining up to the first-order approximation in the parameter $\epsilon$,

$$\begin{aligned} {\mathbb {E}}\left[ ({\widehat{Y}}(t))^2\right] ={\mathbb {E}}\left[ (Y_0(t))^2\right] +2\epsilon {\mathbb {E}}\left[ Y_0(t)Y_1(t)\right] . \end{aligned}$$

(17)

To calculate ${\mathbb {E}}\left[ (Y_0(t))^2\right]$, we substitute expression (9) and apply Fubini’s theorem,

$$\begin{aligned} \begin{array}{ccl} {\mathbb {E}}\left[ (Y_0(t))^2\right] &{}=&{} \displaystyle {\mathbb {E}}\left[ \left( \int _{0}^{\infty } g(s) Z(t-s) {{\,\mathrm{d\textit{s}}\,}}\right) \left( \int _{0}^{\infty } g(s_1) Z(t-s_1) {{\,\mathrm{d\textit{s}}\,}}_1 \right) \right] \\ &{} = &{} \displaystyle \int _{0}^{\infty } g(s) \int _{0}^{\infty } g(s_1){\mathbb {E}}\left[ Z(t-s)Z(t-s_1)\right] {{\,\mathrm{d\textit{s}}\,}}_1{{\,\mathrm{d\textit{s}}\,}}. \end{array} \end{aligned}$$

(18)

Now, ${\mathbb {E}}\left[ Z(t-s)Z(t-s_1)\right]$ can be expressed in terms of the correlation function, $\varGamma _{ZZ}(\cdot )$, ${\mathbb {E}}\left[ Z(t-s)Z(t-s_1)\right] =\varGamma _{ZZ}(t-s_1-(t-s))=\varGamma _{ZZ}(s-s_1)$. Then, (18) writes

$$\begin{aligned} {\mathbb {E}}\left[ (Y_0(t))^2\right] =\int _{0}^{\infty } g(s) \int _{0}^{\infty } g(s_1)\varGamma _{ZZ}(s-s_1){{\,\mathrm{d\textit{s}}\,}}_1{{\,\mathrm{d\textit{s}}\,}}. \end{aligned}$$

(19)

Observe that the correlation function is a deterministic function of a single variable, since Z(t) is a stationary process. To calculate the term ${\mathbb {E}}\left[ Y_0(t) Y_1(t)\right]$ in (17), we substitute the expressions of $Y_0(t)$ and $Y_1(t)$ given in (9) and (10) (recall that we take $M=2$) and apply Fubini’s theorem,

$$\begin{aligned}&{\mathbb {E}}\left[ Y_0(t)\,Y_1(t)\right] = \displaystyle {\mathbb {E}}\left[ Y_0(t) \left( -\omega _0^2\int _{0}^{\infty }\!\!g(s) Y_0(t-s){{\,\mathrm{d\textit{s}}\,}}+ \frac{\omega _0^2}{3!} \int _{0}^{\infty }\!\! g(s) (Y_0(t-s))^3{{\,\mathrm{d\textit{s}}\,}}\right. \right. \nonumber \\&\qquad \left. \left. -\frac{\omega _0^2}{5!}\int _{0}^{\infty }\!\!g(s) (Y_0(t-s))^5{{\,\mathrm{d\textit{s}}\,}}\right) \right] \nonumber \\&\quad = \displaystyle \int _{0}^{\infty }g(s){\mathbb {E}}\left[ Y_0(t)\left( -\omega _0^2 Y_0(t-s) + \frac{\omega _0^2}{3!}(Y_0(t-s))^3-\frac{\omega _0^2}{5!}(Y_0(t-s))^5\right) \right] {{\,\mathrm{d\textit{s}}\,}}\nonumber \\&\quad = \displaystyle -\omega _0^2\int _{0}^{\infty }\!\!g(s)\int _{0}^{\infty }\!\!g(s_1)\int _{0}^{\infty }\!\!g(s_2) {\mathbb {E}}\left[ Z(t-s_1)Z(t-s-s_2)\right] {{\,\mathrm{d\textit{s}}\,}}_2 {{\,\mathrm{d\textit{s}}\,}}_1 {{\,\mathrm{d\textit{s}}\,}}\nonumber \\&\qquad \displaystyle + \frac{\omega _0^2}{3!} \int _{0}^{\infty }\!\! g(s) \int _{0}^{\infty }\!\! g(s_1) \int _{0}^{\infty }\!\! g(s_2) \int _{0}^{\infty }\!\! g(s_3)\int _{0}^{\infty }\!\! g(s_4)\nonumber \\&\quad \qquad {\mathbb {E}}\left[ Z(t-s_1)Z(t-s-s_2)Z(t-s-s_3)\right. \nonumber \\&\qquad \displaystyle \cdot \left. Z(t-s-s_4)\right] {{\,\mathrm{d\textit{s}}\,}}_4{{\,\mathrm{d\textit{s}}\,}}_3{{\,\mathrm{d\textit{s}}\,}}_2{{\,\mathrm{d\textit{s}}\,}}_1 {{\,\mathrm{d\textit{s}}\,}}\nonumber \\&\qquad \displaystyle - \frac{\omega _0^2}{5!} \int _{0}^{\infty }\!\! g(s) \int _{0}^{\infty }\!\! g(s_1) \int _{0}^{\infty }\!\! g(s_2) \int _{0}^{\infty }\!\! g(s_3) \int _{0}^{\infty }\!\! g(s_4) \int _{0}^{\infty }\!\! g(s_5) \int _{0}^{\infty }\!\! g(s_6) \nonumber \\&\quad \qquad {\mathbb {E}}\left[ Z(t-s_1)Z(t-s-s_2)\right. \nonumber \\&\qquad \displaystyle \cdot \left. Z(t-s-s_3)Z(t-s-s_4)Z(t-s-s_5)Z(t-s-s_6)\right] {{\,\mathrm{d\textit{s}}\,}}_6{{\,\mathrm{d\textit{s}}\,}}_5{{\,\mathrm{d\textit{s}}\,}}_4{{\,\mathrm{d\textit{s}}\,}}_3{{\,\mathrm{d\textit{s}}\,}}_2{{\,\mathrm{d\textit{s}}\,}}_1 {{\,\mathrm{d\textit{s}}\,}}.\nonumber \\ \end{aligned}$$

(20)

Now, we express the expectations that appear in the above integrals in terms of the correlation function, $\varGamma _{ZZ}(\cdot )$, taking into account that Z(t) is stationary. For the first expectation, one gets

$$\begin{aligned} {\mathbb {E}}\left[ Z(t-s_1)Z(t-s-s_2)\right] =\varGamma _{ZZ}(s_1-s-s_2). \end{aligned}$$

(21)

To calculate the other two expectations, we will apply the symmetry in the subindexes and the Isserlis–Wick theorem [14], which provides a formula to express the higher-order moments of a zero-mean multivariate normal vector, say $(Y_1, \ldots , Y_n )$, in terms of its correlation matrix

$$\begin{aligned} {\mathbb {E}}\left[ Y_1 \cdots Y_n \right] =\sum _{p\in P_n^2} \prod _{\{ i,j\}\in p} {\mathbb {E}}\left[ Y_i Y_j \right] = \sum _{p\in P_n^2} \prod _{\{ i,j\}\in p} \varGamma (Y_i, Y_j ), \end{aligned}$$

where $\varGamma (Y_i, Y_j )$ stands for the correlation of vector $(Y_i,Y_j)$. The sum is over all distinct ways of partitioning the set of indexes $\{ 1,2,\ldots ,n \}$ into pairs $\{ i,j\}$ (the set of these pairs is denoted by $P_n^2$), and the product is over these pairs. In our case, we apply this result taking into account that Z(t) is a zero-mean stationary Gaussian process. To determine the second expectation in (20), we will denote $u_1=t-s_1$, $u_2=t-s-s_2$, $u_3=t-s-s_3$ and $u_4=t-s-s_4$ to facilitate the presentation of our computations

$$\begin{aligned} \begin{aligned}&{\mathbb {E}}\Big [Z(t-s_1)Z(t-s-s_2)Z(t-s-s_3)Z(t-s-s_4)\Big ] \\&\quad = {\mathbb {E}}\left[ Z(u_1)Z(u_2)\right] {\mathbb {E}}\left[ Z(u_3)Z(u_4)\right] \\&\qquad +{\mathbb {E}}\left[ Z(u_1)Z(u_3)\right] {\mathbb {E}}\left[ Z(u_2)Z(u_4)\right] +{\mathbb {E}}\left[ Z(u_1)Z(u_4)\right] {\mathbb {E}}\left[ Z(u_2)Z(u_3)\right] \\&\quad = \varGamma _{ZZ}(u_2-u_1)\varGamma _{ZZ}(u_4-u_3)+\varGamma _{ZZ}(u_3-u_1)\varGamma _{ZZ}(u_4-u_2)\\&\qquad +\varGamma _{ZZ}(u_4-u_1)\varGamma _{ZZ}(u_3-u_2) \\&\quad = \varGamma _{ZZ}(s_1-s-s_2)\varGamma _{ZZ}(s_3-s_4)+\varGamma _{ZZ}(s_1-s-s_3) \varGamma _{ZZ}(s_2-s_4)\\&\qquad +\varGamma _{ZZ}(s_1-s-s_4) \varGamma _{ZZ}(s_2-s_3). \end{aligned} \end{aligned}$$

Then, the second integral in (20) can be computed as

$$\begin{aligned}&\displaystyle \int _{0}^{\infty }\!\! g(s) \int _{0}^{\infty }\!\! g(s_1) \int _{0}^{\infty }\!\! g(s_2) \int _{0}^{\infty }\!\! g(s_3)\int _{0}^{\infty }\!\! g(s_4)\nonumber \\&\qquad {\mathbb {E}}\left[ Z(t-s_1)Z(t-s-s_2)Z(t-s-s_3) Z(t-s-s_4)\right] {{\,\mathrm{d\textit{s}}\,}}_4{{\,\mathrm{d\textit{s}}\,}}_3{{\,\mathrm{d\textit{s}}\,}}_2{{\,\mathrm{d\textit{s}}\,}}_1 {{\,\mathrm{d\textit{s}}\,}}\nonumber \\&\quad \displaystyle = \int _{0}^{\infty }\!\! g(s) \int _{0}^{\infty }\!\! g(s_1) \int _{0}^{\infty }\!\! g(s_2) \int _{0}^{\infty }\!\! g(s_3)\int _{0}^{\infty }\!\! g(s_4) \left( \varGamma _{ZZ}(s_1-s-s_2)\varGamma _{ZZ}(s_3-s_4) \right. \nonumber \\&\qquad \displaystyle +\varGamma _{ZZ}(s_1-s-s_3) \varGamma _{ZZ}(s_2-s_4)\nonumber \\&\qquad \left. +\varGamma _{ZZ}(s_1-s-s_4) \varGamma _{ZZ}(s_2-s_3) \right) {{\,\mathrm{d\textit{s}}\,}}_4{{\,\mathrm{d\textit{s}}\,}}_3{{\,\mathrm{d\textit{s}}\,}}_2{{\,\mathrm{d\textit{s}}\,}}_1 {{\,\mathrm{d\textit{s}}\,}}\nonumber \\&\quad \displaystyle = 3 \int _{0}^{\infty }\!\! g(s) \int _{0}^{\infty }\!\! g(s_1) \int _{0}^{\infty }\!\! g(s_2) \int _{0}^{\infty }\!\! g(s_3)\int _{0}^{\infty }\!\! g(s_4)\nonumber \\&\qquad \varGamma _{ZZ}(s_1-s-s_2)\varGamma _{ZZ}(s_3-s_4) {{\,\mathrm{d\textit{s}}\,}}_4{{\,\mathrm{d\textit{s}}\,}}_3{{\,\mathrm{d\textit{s}}\,}}_2{{\,\mathrm{d\textit{s}}\,}}_1 {{\,\mathrm{d\textit{s}}\,}}. \end{aligned}$$

(22)

Notice that we have taken advantage of the symmetry of the correlation function, $\varGamma _{ZZ}(\cdot )$, to express the last multidimensional integral. The third expectation in (20) can be analogously calculated

$$\begin{aligned}&{\mathbb {E}}\Big [Z(t-s_1)Z(t-s-s_2)Z(t-s-s_3)Z(t-s-s_4)Z(t-s-s_5)Z(t-s-s_6)\Big ] \nonumber \\&\quad = \varGamma _{ZZ}(s_1-s-s_2)\varGamma _{ZZ}(s_3-s_4)\varGamma _{ZZ}(s_5-s_6) \nonumber \\&\qquad + \varGamma _{ZZ}(s_1-s-s_2)\varGamma _{ZZ}(s_3-s_5)\varGamma _{ZZ}(s_4-s_6) \nonumber \\&\qquad + \varGamma _{ZZ}(s_1-s-s_2)\varGamma _{ZZ}(s_3-s_6)\varGamma _{ZZ}(s_4-s_5) \nonumber \\&\qquad + \varGamma _{ZZ}(s_1-s-s_3)\varGamma _{ZZ}(s_2-s_4)\varGamma _{ZZ}(s_5-s_6) \nonumber \\&\qquad + \varGamma _{ZZ}(s_1-s-s_3)\varGamma _{ZZ}(s_2-s_5)\varGamma _{ZZ}(s_4-s_6) \nonumber \\&\qquad + \varGamma _{ZZ}(s_1-s-s_3)\varGamma _{ZZ}(s_2-s_6)\varGamma _{ZZ}(s_4-s_5) \nonumber \\&\qquad + \varGamma _{ZZ}(s_1-s-s_4)\varGamma _{ZZ}(s_2-s_3)\varGamma _{ZZ}(s_5-s_6) \nonumber \\&\qquad + \varGamma _{ZZ}(s_1-s-s_4)\varGamma _{ZZ}(s_2-s_5)\varGamma _{ZZ}(s_3-s_6) \nonumber \\&\qquad + \varGamma _{ZZ}(s_1-s-s_4)\varGamma _{ZZ}(s_2-s_6)\varGamma _{ZZ}(s_3-s_5) \nonumber \\&\qquad + \varGamma _{ZZ}(s_1-s-s_5)\varGamma _{ZZ}(s_2-s_3)\varGamma _{ZZ}(s_4-s_6) \nonumber \\&\qquad + \varGamma _{ZZ}(s_1-s-s_5)\varGamma _{ZZ}(s_2-s_4)\varGamma _{ZZ}(s_3-s_6) \nonumber \\&\qquad + \varGamma _{ZZ}(s_1-s-s_5)\varGamma _{ZZ}(s_2-s_6)\varGamma _{ZZ}(s_3-s_4) \nonumber \\&\qquad + \varGamma _{ZZ}(s_1-s-s_6)\varGamma _{ZZ}(s_2-s_3)\varGamma _{ZZ}(s_4-s_5) \nonumber \\&\qquad + \varGamma _{ZZ}(s_1-s-s_6)\varGamma _{ZZ}(s_2-s_4)\varGamma _{ZZ}(s_3-s_5) \nonumber \\&\qquad + \varGamma _{ZZ}(s_1-s-s_6)\varGamma _{ZZ}(s_2-s_5)\varGamma _{ZZ}(s_3-s_4). \end{aligned}$$

(23)

Then, substituting (22) and (23) into (20), and taking again the advantage of the symmetry of the correlation function, $\varGamma _{ZZ}(\cdot )$, to simplify the representation of the last multidimensional integral, one obtains

$$\begin{aligned}&{\mathbb {E}}\left[ Y_0(t)Y_1(t)\right] = -\omega _0^2\int _{0}^{\infty }\!\!\!g(s)\int _{0}^{\infty }\!\!\! g(s_1)\int _{0}^{\infty }\!\!\! g(s_2)\varGamma _{ZZ}(s_1-s-s_2){{\,\mathrm{d\textit{s}}\,}}_2{{\,\mathrm{d\textit{s}}\,}}_1{{\,\mathrm{d\textit{s}}\,}}\nonumber \\&\quad + \frac{\omega _0^2}{2}\int _{0}^{\infty }\!\!\! g(s)\int _{0}^{\infty }\!\!\! g(s_1)\int _{0}^{\infty }\!\!\! g(s_2)\int _{0}^{\infty }\!\!\! g(s_3)\int _{0}^{\infty }\!\!\! g(s_4)\nonumber \\&\qquad \varGamma _{ZZ}(s_1-s-s_2)\varGamma _{ZZ}(s_3-s_4){{\,\mathrm{d\textit{s}}\,}}_4{{\,\mathrm{d\textit{s}}\,}}_3{{\,\mathrm{d\textit{s}}\,}}_2{{\,\mathrm{d\textit{s}}\,}}_1{{\,\mathrm{d\textit{s}}\,}}\nonumber \\&\quad - \frac{\omega _0^2}{8}\int _{0}^{\infty }\!\!\! g(s)\int _{0}^{\infty }\!\!\! g(s_1)\int _{0}^{\infty }\!\!\! g(s_2)\int _{0}^{\infty }\!\!\! g(s_3)\int _{0}^{\infty }\!\!\! g(s_4)\int _{0}^{\infty }\!\!\! g(s_5)\int _{0}^{\infty }\!\!\! g(s_6)\varGamma _{ZZ}(s_1-s-s_2)\nonumber \\&\quad \cdot \varGamma _{ZZ}(s_3-s_4)\varGamma _{ZZ}(s_5-s_6){{\,\mathrm{d\textit{s}}\,}}_6{{\,\mathrm{d\textit{s}}\,}}_5{{\,\mathrm{d\textit{s}}\,}}_4{{\,\mathrm{d\textit{s}}\,}}_3{{\,\mathrm{d\textit{s}}\,}}_2{{\,\mathrm{d\textit{s}}\,}}_1{{\,\mathrm{d\textit{s}}\,}}. \end{aligned}$$

(24)

So, substituting expressions (19) and (24) into (17), we obtain an explicit approximation of the second-order moment for the approximation ${\widehat{Y}}(t)$,

$$\begin{aligned}&{\mathbb {E}}\left[ ({\widehat{Y}}(t))^2\right] =\int _{0}^{\infty }\!\!\! g(s)\int _{0}^{\infty }\!\!\! g(s_1)\varGamma _{ZZ}(s-s_1){{\,\mathrm{d\textit{s}}\,}}_1{{\,\mathrm{d\textit{s}}\,}}\nonumber \\&\quad +2\epsilon \,\Bigg (-\omega _0^2\int _{0}^{\infty }\!\!\!g(s)\int _{0}^{\infty }\!\!\! g(s_1)\int _{0}^{\infty }\!\!\! g(s_2)\varGamma _{ZZ}(s_1-s-s_2){{\,\mathrm{d\textit{s}}\,}}_2{{\,\mathrm{d\textit{s}}\,}}_1{{\,\mathrm{d\textit{s}}\,}}\nonumber \\&\quad + \frac{\omega _0^2}{2}\int _{0}^{\infty }\!\!\! g(s)\int _{0}^{\infty }\!\!\! g(s_1)\int _{0}^{\infty }\!\!\! g(s_2)\int _{0}^{\infty }\!\!\! g(s_3)\int _{0}^{\infty }\!\!\! g(s_4)\varGamma _{ZZ}(s_1-s-s_2)\nonumber \\&\qquad \varGamma _{ZZ}(s_3-s_4){{\,\mathrm{d\textit{s}}\,}}_4{{\,\mathrm{d\textit{s}}\,}}_3{{\,\mathrm{d\textit{s}}\,}}_2{{\,\mathrm{d\textit{s}}\,}}_1{{\,\mathrm{d\textit{s}}\,}}\nonumber \\&\quad - \frac{\omega _0^2}{8}\int _{0}^{\infty }\!\!\! g(s)\int _{0}^{\infty }\!\!\! g(s_1)\int _{0}^{\infty }\!\!\! g(s_2)\int _{0}^{\infty }\!\!\! g(s_3)\int _{0}^{\infty }\!\!\! g(s_4)\int _{0}^{\infty }\!\!\! g(s_5)\int _{0}^{\infty }\!\!\! g(s_6)\varGamma _{ZZ}(s_1-s-s_2)\nonumber \\&\cdot \varGamma _{ZZ}(s_3-s_4)\varGamma _{ZZ}(s_5-s_6){{\,\mathrm{d\textit{s}}\,}}_6{{\,\mathrm{d\textit{s}}\,}}_5{{\,\mathrm{d\textit{s}}\,}}_4{{\,\mathrm{d\textit{s}}\,}}_3{{\,\mathrm{d\textit{s}}\,}}_2{{\,\mathrm{d\textit{s}}\,}}_1{{\,\mathrm{d\textit{s}}\,}}\Bigg ). \end{aligned}$$

(25)

Now, we compute the third-order moment of ${\widehat{Y}}(t)$, using the first-order approximation with respect to the perturbative parameter $\epsilon$,

$$\begin{aligned} {\mathbb {E}}\left[ ({\widehat{Y}}(t))^3\right] ={\mathbb {E}}\left[ (Y_0(t))^3\right] +3\epsilon {\mathbb {E}}\left[ (Y_0(t))^2 Y_1(t)\right] . \end{aligned}$$

(26)

By reasoning analogously as in the calculation of the foregoing statistical moments, we obtain

$$\begin{aligned} {\mathbb {E}}\left[ (Y_0(t))^3\right] =\int _{0}^{\infty }\!\!\! g(s)\int _{0}^{\infty }\!\!\! g(s_1)\int _{0}^{\infty }\!\!\! g(s_2){\mathbb {E}}\left[ Z(t-s)Z(t-s_1)Z(t-s_2)\right] {{\,\mathrm{d\textit{s}}\,}}_2 {{\,\mathrm{d\textit{s}}\,}}_1 {{\,\mathrm{d\textit{s}}\,}}=0,\nonumber \\ \end{aligned}$$

(27)

and

$$\begin{aligned} {\mathbb {E}}\left[ (Y_0(t))^2 Y_1(t)\right]&= \int _{0}^{\infty }\!\!\! g(s){\mathbb {E}}\left[ Y_0^2(t)\left( -\omega _0^2 Y_0(t-s) + \frac{\omega _0^2}{3!}(Y_0(t-s))^3\right. \right. \nonumber \\&\quad \left. \left. -\frac{\omega _0^2}{5!}(Y_0(t-s))^5\right) \right] {{\,\mathrm{d\textit{s}}\,}}=0. \end{aligned}$$

(28)

We here omit the details of these calculations since they are somewhat cumbersome and they can easily inferred from our previous developments. Then, substituting (27) and (28) into (26), we obtain

$$\begin{aligned} {\mathbb {E}}\left[ ({\widehat{Y}}(t))^3\right] ={\mathbb {E}}\left[ (Y_0(t))^3\right] +3\epsilon {\mathbb {E}}\left[ (Y_0(t))^2 Y_1(t)\right] =0. \end{aligned}$$

In general, it can be straightforwardly shown that the statistical moments of odd order are null,

$$\begin{aligned} {\mathbb {E}}\left[ ({\widehat{Y}}(t))^{2n+1}\right] =0, \quad n=0,1,2,\dots \end{aligned}$$

(29)

The correlation function of ${\widehat{Y}}(t)$, using the approximation of first-order with respect to the perturbative parameter $\epsilon$, is given by

$$\begin{aligned} \varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau )= & {} {\mathbb {E}}\left[ {\widehat{Y}}(t){\widehat{Y}}(t+\tau )\right] ={\mathbb {E}}\left[ Y_0(t)Y_0(t+\tau )\right] \nonumber \\&+\epsilon \left( {\mathbb {E}}\left[ Y_0(t)Y_1(t+\tau )\right] +{\mathbb {E}}\left[ Y_1(t)Y_0(t+\tau )\right] \right) . \end{aligned}$$

(30)

The first term of (30) corresponds to the correlation function of $Y_0(t)$. It is determined, in terms of the correlation function $\varGamma _{ZZ}(\cdot )$, by applying Fubini’s theorem and the stationarity of Z(t),

$$\begin{aligned} \begin{aligned} {\mathbb {E}}\left[ Y_0(t)Y_0(t+\tau )\right]&= \int _{0}^{\infty }g(s)\int _{0}^{\infty }g(s_1){\mathbb {E}}\left[ Z(t-s)Z(t+\tau -s_1)\right] {{\,\mathrm{d\textit{s}}\,}}_1 {{\,\mathrm{d\textit{s}}\,}}\\&= \int _{0}^{\infty }g(s)\int _{0}^{\infty }g(s_1)\varGamma _{ZZ}(\tau -s_1+s){{\,\mathrm{d\textit{s}}\,}}_1 {{\,\mathrm{d\textit{s}}\,}}. \end{aligned} \end{aligned}$$

(31)

The two last expectations on the right-hand side of (30), correspond to the cross-correlation function of $Y_0(t)$ and $Y_1(t)$. They can be expressed explicitly in terms of the correlation function $\varGamma _{ZZ}(\cdot )$,

$$\begin{aligned}&{\mathbb {E}}\left[ Y_0(t)Y_1(t+\tau )\right] \nonumber \\&\quad = \int _{0}^{\infty }g(s){\mathbb {E}}\left[ Y_0(t)\left( -\omega _0^2 Y_0(t+\tau -s) + \frac{\omega _0^2}{3!}(Y_0(t+\tau -s))^3\right. \right. \nonumber \\&\qquad \left. \left. -\frac{\omega _0^2}{5!}(Y_0(t+\tau -s))^5\right) \right] {{\,\mathrm{d\textit{s}}\,}}\nonumber \\&\quad =-\omega _0^2\int _{0}^{\infty }\!\!\! g(s)\int _{0}^{\infty }\!\!\! g(s_1)\int _{0}^{\infty }\!\!\! g(s_2)\varGamma _{ZZ}(s_1+\tau -s-s_2){{\,\mathrm{d\textit{s}}\,}}_2{{\,\mathrm{d\textit{s}}\,}}_1{{\,\mathrm{d\textit{s}}\,}}\nonumber \\&\qquad \, +\frac{\omega _0^2}{2}\int _{0}^{\infty }\!\!\! g(s)\int _{0}^{\infty }\!\!\! g(s_1)\int _{0}^{\infty }\!\!\! g(s_2)\int _{0}^{\infty }\!\!\! g(s_3)\int _{0}^{\infty }\!\!\! g(s_4)\nonumber \\&\qquad \quad \varGamma _{ZZ}(s_1+\tau -s-s_2)\varGamma _{ZZ}(s_3-s_4){{\,\mathrm{d\textit{s}}\,}}_4{{\,\mathrm{d\textit{s}}\,}}_3{{\,\mathrm{d\textit{s}}\,}}_2{{\,\mathrm{d\textit{s}}\,}}_1{{\,\mathrm{d\textit{s}}\,}}\nonumber \\&\qquad \, -\frac{\omega _0^2}{8}\int _{0}^{\infty }\!\!\!g(s)\int _{0}^{\infty }\!\!\! g(s_1)\int _{0}^{\infty }\!\!\! g(s_2)\int _{0}^{\infty }\!\!\! g(s_3)\int _{0}^{\infty }\!\!\! g(s_4)\int _{0}^{\infty }\!\!\! g(s_5)\int _{0}^{\infty }\!\!\! g(s_6)\nonumber \\&\qquad \quad \varGamma _{ZZ}(s_1+\tau -s-s_2)\nonumber \\&\qquad \, \cdot \varGamma _{ZZ}(s_3-s_4)\varGamma _{ZZ}(s_5-s_6){{\,\mathrm{d\textit{s}}\,}}_6{{\,\mathrm{d\textit{s}}\,}}_5{{\,\mathrm{d\textit{s}}\,}}_4{{\,\mathrm{d\textit{s}}\,}}_3{{\,\mathrm{d\textit{s}}\,}}_2{{\,\mathrm{d\textit{s}}\,}}_1{{\,\mathrm{d\textit{s}}\,}}\end{aligned}$$

(32)

and

$$\begin{aligned}&{\mathbb {E}}\left[ Y_1(t)Y_0(t+\tau )\right] \nonumber \\&\quad = \int _{0}^{\infty }g(s){\mathbb {E}}\left[ Y_0(t+\tau )\left( -\omega _0^2 Y_0(t-s) + \frac{\omega _0^2}{3!}(Y_0(t-s))^3-\frac{\omega _0^2}{5!}(Y_0(t-s))^5\right) \right] {{\,\mathrm{d\textit{s}}\,}}\nonumber \\&\quad =-\omega _0^2\int _{0}^{\infty }\!\!\!g(s)\int _{0}^{\infty }\!\!\!g(s_1)\int _{0}^{\infty }\!\!\!g(s_2)\varGamma _{ZZ}(s_1-\tau -s-s_2){{\,\mathrm{d\textit{s}}\,}}_2{{\,\mathrm{d\textit{s}}\,}}_1{{\,\mathrm{d\textit{s}}\,}}\nonumber \\&\qquad \, +\frac{\omega _0^2}{2}\int _{0}^{\infty }\!\!\!g(s)\int _{0}^{\infty }\!\!\!g(s_1)\int _{0}^{\infty }\!\!\!g(s_2)\int _{0}^{\infty }\!\!\!g(s_3)\int _{0}^{\infty }\!\!\!g(s_4)\nonumber \\&\qquad \quad \varGamma _{ZZ}(s_1-\tau -s-s_2)\varGamma _{ZZ}(s_3-s_4){{\,\mathrm{d\textit{s}}\,}}_4{{\,\mathrm{d\textit{s}}\,}}_3{{\,\mathrm{d\textit{s}}\,}}_2{{\,\mathrm{d\textit{s}}\,}}_1{{\,\mathrm{d\textit{s}}\,}}\nonumber \\&\qquad \, -\frac{\omega _0^2}{8}\int _{0}^{\infty }\!\!\!g(s)\int _{0}^{\infty }\!\!\!g(s_1)\int _{0}^{\infty }\!\!\!g(s_2)\int _{0}^{\infty }\!\!\!g(s_3)\int _{0}^{\infty }\!\!\!g(s_4)\int _{0}^{\infty }\!\!\!g(s_5)\int _{0}^{\infty }\!\!\!g(s_6)\nonumber \\&\qquad \quad \varGamma _{ZZ}(s_1-\tau -s-s_2)\nonumber \\&\qquad \, \cdot \varGamma _{ZZ}(s_3-s_4)\varGamma _{ZZ}(s_5-s_6){{\,\mathrm{d\textit{s}}\,}}_6{{\,\mathrm{d\textit{s}}\,}}_5{{\,\mathrm{d\textit{s}}\,}}_4{{\,\mathrm{d\textit{s}}\,}}_3{{\,\mathrm{d\textit{s}}\,}}_2{{\,\mathrm{d\textit{s}}\,}}_1{{\,\mathrm{d\textit{s}}\,}}. \end{aligned}$$

(33)

From expressions (31)–(33), we observe that the correlation function, $\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau )$, given by (30), only depends on the difference $\tau$ between two different instants, t and $t+\tau$ (as it has been anticipated in the notation in (30)). This fact together with ${\mathbb {E}}\left[ {\widehat{Y}}(t)\right] =0$ (see (16)) allows us to say that the first-order approximation, ${\widehat{Y}}(t)$, given in (5) and obtained via the perturbation technique, is a stationary stochastic process. Additionally, it is clear that the covariance function of the steady state coincides with the correlation function, i.e. ${\mathbb {C}}\mathrm {ov}\left[ {\widehat{Y}}(t_1), {\widehat{Y}}(t_2)\right] = \varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau )$, where $\tau =|t_1-t_2|$ and, also the variance matches the second-order moment, which in turn can be calculated evaluating the correlation function at the origin,

$$\begin{aligned} {\mathbb {V}}\left[ {\widehat{Y}}(t)\right] = {\mathbb {E}}\left[ {\widehat{Y}}(t)^2\right] =\varGamma _{{\widehat{Y}}{\widehat{Y}}}(0). \end{aligned}$$

(34)

From the correlation function, $\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau )$, it is straightforward to also determine the power spectral density function (or simply, the power spectrum) of ${\widehat{Y}}(t)$

$$\begin{aligned} S_{{\widehat{Y}}\!(t)}(f)= \int _{-\infty }^{\infty }{{\,\mathrm{e}\,}}^{-\mathrm {i} f\tau }\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau )\mathrm {d}\tau , \end{aligned}$$

(35)

here, $\mathrm {i}=\sqrt{-1}$ is the imaginary unit and f is the angular frequency. Observe that, $S_{{\widehat{Y}}\!(t)}(f)$ is the Fourier transform of the correlation function of ${\widehat{Y}}(t)$. This function plays a key role to describe the distribution of power into frequency components composing a signal represented via stationary stochastic process [15].

3 Numerical examples

In the previous section, we have obtained approximations of the main statistical moments of the steady state of problem (2). In this section, we combine this key information, together with the PME technique, to construct approximations of the p.d.f. of the stationary solution. We will show two examples where important stochastic processes play the role of the external source, Z(t), in problem (2). In the first example, we will take as Z(t) the white Gaussian noise, while in the second one, the Ornstein–Uhlenbeck stochastic process will be considered. Since the validity of perturbation method is restricted to small values of the perturbative parameter $\epsilon$, the numerical experiments are carried out with criticism to this key point taking into account that the numerical approximations must retain certain universal properties such as the positivity of even-order statistical moments (for any stochastic process) and the symmetry of the correlation and power spectral functions; the correlation function reaches its maximum value at the origin and the positivity of the spectral function, in the case of stationary stochastic processes. Of course, additional properties about other statistical functions could also be added to further check the consistency of the numerical results obtained via the stochastic perturbation method.

For the sake of completeness, down below we revise the main definitions and results about the PME method and the power spectral function that will be used throughout the two numerical examples.

As detailed in [16], the PME is an efficient method to determine the p.d.f., $f_Y(y)$, of a random variable, say Y, constrained by the statistical information available (domain, expectation, variance, symmetry, kurtosis, etc.) on Y. The method consists in determining $f_Y(y)$ such that it maximizes the so-called Shannon’s entropy (also referred to as differential entropy), which is given by ${\mathcal {S}}\left\{ f_{Y} \right\} = - \int _{y_1}^{y_2}f_{Y}(y)\log (f_{Y}(y)) {{\,\mathrm{d\textit{y}}\,}}$, subject to a number of constraints, which are usually defined by the N first moments, say $a_n$, $n=1,2, \ldots ,N$, of the random variable Y together with the normalization condition, $\int _{y_1}^{y_2}f_{Y}(y) {{\,\mathrm{d\textit{y}}\,}}=1$. In this context, the admissible set of solutions is then defined by ${\mathcal {A}}=\{ f_Y:[y_1,y_2] \longrightarrow {\mathbb {R}}: \int _{y_1}^{y_2} y^n f_{Y}(y){{\,\mathrm{d\textit{y}}\,}}=a_n, \, n=0,1,\ldots ,N\}$. Notice that $n=0$ corresponds to the normalization condition (i.e. the integral of the p.d.f. is one) and that the rest of the restrictions are defined by the statistical moments, ${\mathbb {E}}\left[ Y^n \right] =a_n$, $n=1,2,\ldots ,N$. It can be seen, by applying the functional version of Lagrange multipliers associated with ${\mathcal {A}}$, that

$$\begin{aligned} f_{Y}(y) = \mathbbm {1}_{[y_1,y_2]}(y){{\,\mathrm{e}\,}}^{-\sum _{i=0}^{N}\lambda _i y^i},\qquad \mathbbm {1}_{[y_1,y_2]}(y) = \left\{ \begin{array}{ccl} 1, &{} &{} y\in [y_1,y_2],\\ 0, &{} &{} y\notin [y_1,y_2]. \end{array} \right. \end{aligned}$$

(36)

In practice, the Lagrange multipliers, $\lambda _i$, $i=0,1,\ldots ,N$, are determined by numerically solving the following system of $N+1$ nonlinear equations defined by the constraints

$$\begin{aligned} \int _{y_1}^{y_2} y^n \mathbbm {1}_{[y_1,y_2]}(y){{\,\mathrm{e}\,}}^{-\sum _{i=0}^{N}\lambda _i y^i} {{\,\mathrm{d\textit{y}}\,}}=a_n, \qquad n=0,1,\ldots ,N. \end{aligned}$$

(37)

In words, the PME method selects, among all the p.d.f.’s that satisfy the constraints given by the available statistical information, the one that maximizes the Shannon or differential entropy as a measure of randomness. This can be naively interpreted as looking for the p.d.f. which maximizes the uncertainty from the minimal quantity of information [16].

In the examples, we will also calculate the power spectral density function $S_{{\widehat{Y}}\!(t)}(f)$ defined in (35). Using the Euler identity ${{\,\mathrm{e}\,}}^{\mathrm {i} x}=\cos (x)+ \mathrm {i} \sin (x)$, it is easy to check that, for any stationary process, the power spectral density is an even function,

$$\begin{aligned} S_{{\widehat{Y}}\!(t)}(f)= \int _{-\infty }^{\infty } \cos (f \tau ) \varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau ) \mathrm {d}\tau = 2\int _{0}^{\infty } \cos (f \tau ) \varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau ) \mathrm {d}\tau =S_{{\widehat{Y}}\!(t)}(-f). \end{aligned}$$

(38)

This property is also fulfilled by the correlation function, $\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau )=\varGamma _{{\widehat{Y}}{\widehat{Y}}}(-\tau )$ [2, Ch. 3]. Moreover, the correlation function reaches its maximum at the origin, i.e. $|\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau )| \le \varGamma _{{\widehat{Y}}{\widehat{Y}}}(0)$ [2, Ch. 3], while it can be proved that the power spectral function is non-negative, $S_{{\widehat{Y}}\!(t)}(f)\ge 0$ [15]. To reject the possible spurious approximations obtained via the stochastic perturbation method, we will check in our numerical experiments whether all these properties are preserved. We will also take advantage of the approximations of the power spectral density and of the correlation function to obtain the two following important parameters associated with a stationary stochastic process, the noise intensity (${\mathcal {D}}$) and the correlation time (${\hat{\tau }}$), respectively, defined by

$$\begin{aligned} {\mathcal {D}}= \int _{0}^{\infty } \varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau ) \mathrm {d}\tau = \frac{1}{2} S_{{\widehat{Y}}\!(t)}(0), \qquad {\hat{\tau }} = \frac{\int _{0}^{\infty } \varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau ) \mathrm {d}\tau }{\varGamma _{{\widehat{Y}}{\widehat{Y}}}(0)}=\frac{{\mathcal {D}}}{\varGamma _{{\widehat{Y}}{\widehat{Y}}}(0) }. \end{aligned}$$

(39)

Notice that the value of ${\mathcal {D}}$ comes from evaluating $S_{{\widehat{Y}}\!(t)}(f)$ at $f=0$ in (38). So, the noise intensity is defined as the area beneath the correlation function $\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau )$, while the correlation time is a standardized noise intensity [17]. The parameters ${\mathcal {D}}$ and ${\hat{\tau }}$ indicate how strongly the stochastic process is correlated over the time.

In both examples, the numerical results that we shall show correspond to third-order Taylor’s approximations of the nonlinear term $\sin (Y(t))$ in (7), since we have checked that no significant differences are obtained using fifth-order Taylor’s approximations.

Example 1

Let us consider as external source the stochastic process $Z(t)=\xi (t)$, where $\xi (t)$ is a white Gaussian noise, i.e. is a stationary Gaussian stochastic process with zero mean, ${\mathbb {E}}\left[ Z(t) \right] =0$, and flat power spectral density, $S_{Z(t)}(f)=\frac{N_0}{2}$, for all f. Then, its correlation function is given by $\varGamma _{ZZ}(\tau )=\frac{N_0}{2}\delta (\tau )$, where $\delta (\tau )$ is the Dirac delta function. We will take the following data for the parameters involved in model (2), $\omega _0=1$, $\beta =\frac{5}{100}$ and $N_0=\frac{1}{100}$ (that satisfy the conditions of “Appendix A”, so ensuring the existence of the steady-state solution), so the nolinear random oscillator is formulated by

$$\begin{aligned} \frac{\mathrm {d}^2Y(t)}{\mathrm {d}t^2} + \frac{1}{10}\frac{\mathrm {d}Y(t)}{\mathrm {d}t}+Y(t)+\epsilon \sin (Y(t)) = \xi (t),\quad t>0. \end{aligned}$$

(40)

We will now take advantage of the results derived in Sect. 2.2, to calculate the following statistical information of the first-order approximation, ${\widehat{Y}}(t)$, obtained via the perturbation method and given in (5): (1) the moments up to order 3, i.e. ${\mathbb {E}}\left[ ({\widehat{Y}}(t))^i\right]$, $i=1,2,3$; (2) the variance, ${\mathbb {V}}\left[ {\widehat{Y}}(t)\right]$, and (3) the correlation function, $\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau )$. We will use this information to compute approximations, first of the p.d.f. of ${\widehat{Y}}(t)$, using the PME, and, secondly, of the spectral density function of ${\widehat{Y}}(t)$.

From expression (29), in particular, we know that ${\mathbb {E}}\left[ {\widehat{Y}}(t)\right]$ and ${\mathbb {E}}\left[ ({\widehat{Y}}(t))^3\right]$ are null. For the second-order moment, ${\mathbb {E}}\left[ ({\widehat{Y}}(t))^2\right]$, using expression (25) we obtain

$$\begin{aligned} {\mathbb {E}}\left[ ({\widehat{Y}}(t))^2\right] =\frac{1}{40}-\frac{12641}{512000}\epsilon . \end{aligned}$$

This value is also the variance since ${\mathbb {E}}\left[ {\widehat{Y}}(t)\right] =0$. On the other hand, as ${\mathbb {E}}\left[ ({\widehat{Y}}(t))^2\right]$ is always positive, we can obtain the following bound for the perturbative parameter, $\epsilon <1.01258$. Although this value bounds the validity of the perturbation method, down below we show that is a conservative bound.

To this end, we will compare the mean and standard deviation (sd) of ${\widehat{Y}}(t)$ obtained via the perturbation method and the ones computed by Kloeden–Platen–Schurz algorithm [3]. The results are shown in Table 1. We can observe that both approximations are accurate for $\epsilon = 0$ (which corresponds to the linearization of model (2)), $\epsilon =0.01$ and $\epsilon =0.1$. But significant differences in the standard deviation are revealed for $\epsilon = 0.5$ and $\epsilon =1$.

Table 1 Comparison between stochastic perturbation method and Kloeden–Platen–Schurz algorithm for different values of $\epsilon$ with regard to the approximations of the mean and the standard deviation (sd) of the steady state. Example 1

According to expressions (30)–(33), the approximation of the correlation function is given by

$$\begin{aligned} \varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau ) = {\left\{ \begin{array}{ll} \dfrac{{{\,\mathrm{e}\,}}^{-\tau /20}\left( 399\left( 5107200+12641\epsilon (-399+10\tau ) \right) \cos \left( \frac{\sqrt{399}\tau }{20}\right) +\sqrt{399}(5107200-12641\epsilon (599+3990\tau ))\sin \left( \frac{\sqrt{399}\tau }{20}\right) \right) }{81510912000}, &{} \text {if }\tau > 0,\\ -\dfrac{{{\,\mathrm{e}\,}}^{\tau /20}\left( 399(-5107200+12641\epsilon (399+10\tau ))\cos \left( \frac{\sqrt{399}\tau }{20}\right) +\sqrt{399}(5107200+12641\epsilon (-599+3990\tau ))\sin \left( \frac{\sqrt{399}\tau }{20}\right) \right) }{81510912000}, &{} \text {if }\tau < 0,\\ \dfrac{1}{40}-\dfrac{12641}{512000}\epsilon , &{} \text {if }\tau = 0. \end{array}\right. }\nonumber \\ \end{aligned}$$

(41)

Notice that, in full agreement with expression (34), it is satisfied that

$$\begin{aligned} {\mathbb {E}}\left[ ({\widehat{Y}}(t))^2\right] ={\mathbb {V}}\left[ {\widehat{Y}}(t)\right] =\varGamma _{{\widehat{Y}}{\widehat{Y}}}(0)=\frac{1}{40}-\frac{12641}{512000}\epsilon . \end{aligned}$$

In Fig. 1, we show the graphical representation of the correlation function, $\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau )$, plotted from the expression (41) and using different values of the perturbative parameter $\epsilon$. To emphasize this dependence on the parameter $\epsilon$, hereinafter we will denote this function by $\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau , \epsilon )$. In Fig. 1a, we observe that the approximations of the $\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau , \epsilon )$ deteriorate as $\epsilon$ increases in full agreement with the results obtained in Table 1. The deterioration of the approximations as $\epsilon$ increases can also be confirmed by checking that the general property $|\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau )|\le \varGamma _{{\widehat{Y}}{\widehat{Y}}}(0)$ for the correlation function [18] does not fulfil for $\epsilon =0.5$ and $\epsilon =1$ (see Fig. 1a). In contrast, for smaller values of $\epsilon = 0, 0.01,0.1\}$ this property holds. Notice that the correlation function for $\epsilon = 0$ and $\epsilon = 0.01$ is quite similar, as expected. For the sake of clarity, we have plotted these results in Fig. 1b. Finally, in Fig. 1c we show $\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau , \epsilon )$ as a surface varying $(\tau , \epsilon )\in [-20,20]\times [0,0.1]$.

Fig. 1

Correlation function $\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau ,\epsilon )$ of ${\widehat{Y}}(t)$. a and b: 2D representation of $\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau ,\epsilon )$ for fixed values of $\epsilon$. c: 3D representation of $\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau ,\epsilon )$ for $\epsilon \in [0,0.1].$ Example 1

Now, we compute the approximation of the p.d.f., $f_{{\widehat{Y}}(t)}(y)$, of the steady state, using the PME. Therefore, according to the PME the p.d.f. is sought in the form

$$\begin{aligned} f_{{\widehat{Y}}(t)}(y) = {{\,\mathrm{e}\,}}^{-1 - \lambda _0 - \lambda _1 y - \lambda _2 y^2 - \lambda _3 y^3}, \end{aligned}$$

where in our case, $\lambda _0$, $\lambda _1$, $\lambda _2$ and $\lambda _3$ are determined numerically solving system (37) with $a_0=1$, $a_1=0$, $a_2=\frac{1}{40}-\frac{12641}{512000}\epsilon$. In Table 2, we show the values of $\lambda _0$, $\lambda _1$, $\lambda _2$ and $\lambda _3$ and the corresponding domain $[y_1,y_2]$ for the following values of the perturbative parameter $\epsilon \in \{ 0, 0.01, 0.1\}$. The domain has been determined using the Bienaymé–Chebyshev inequality $[\mu -k\sigma , \mu +k\sigma ]$ (in our case $\mu =0$) with $k=10$. This guarantees the $99\%$ of the probability is contained in the above interval $[\mu -k\sigma , \mu +k\sigma ]$ regardless of the distribution of the corresponding random variable [14]. In Fig. 2, we compare the graphical representations of the p.d.f, $f_{{\widehat{Y}}(t)}(y)$. From them, we can observe that the plots are quite similar.

Table 2 Values for $\lambda _i$, $i\in \{0,1,2,3\}$ and the domain $[y_1,y_2]$ obtained via the PME method, for $\epsilon \in \{0, 0.01, 0.1\}$. Example 1

Fig. 2

Approximate p.d.f., $f_{{\widehat{Y}}(t)}(y)$, of steady state, ${\widehat{Y}}(t)$, for $\epsilon \in \{0, 0.01, 0.1\}$. Example 1

To complete our numerical analysis, in Fig. 3 we show a graphical representation of the power spectral density for $\epsilon \in \{0, 0.01,0.1\}$. We observe that the approximation obtained via the stochastic perturbation method is able to retain the properties of symmetry and positivity of the power spectral density for $\epsilon \in \{0, 0.01\}$; however, positivity begins to slightly fail for $\epsilon =0.1$, therefore restricting the validity of the results provided by the stochastic perturbation method. In Table 3, the noise intensity (${\mathcal {D}}$) and the correlation time (${\hat{\tau }}$) have been calculated for $\epsilon \in \{0, 0.01\}$.

Fig. 3

Power spectral density of the approximation solution ${\widehat{Y}}(t)$, $S_{{\widehat{Y}}(t)}(f)$, for $\epsilon \in \{0, 0.01,0.1\}$. Example 1

Example 2

In this second example, let us consider the Ornstein–Uhlenbeck stochastic process to play the role of the external source, Z(t). So, it is defined as the stationary solution of the Langevin equation

$$\begin{aligned} \dfrac{\mathrm {d}Z(t)}{\mathrm {d}t} + \alpha Z(t) = \sigma \dfrac{\mathrm {d}W(t)}{\mathrm {d}t},\quad \alpha > 0, \end{aligned}$$

where W(t) is the Wiener process [3]. Notice that $\alpha > 0$ is a necessary and sufficient condition to have a stationary solution. Z(t) satisfies the hypotheses so that the stochastic perturbation method can be applied, i.e. is a zero-mean stationary Gaussian stochastic process, being $\varGamma _{ZZ}(\tau )=\sigma ^2{{\,\mathrm{e}\,}}^{-\alpha |\tau |}$ its correlation function. We take the following values for the parameters in Eq. (2), $\omega _0=1$, $\beta =1/100$, $\sigma =1/100$ and $\alpha =1/2$ (thus, according to “Appendix A”, it ensures the existence of the steady-state solution). So, in this case, the nonlinear random oscillator is given by

$$\begin{aligned} \frac{\mathrm {d}^2Y(t)}{\mathrm {d}t^2} + \frac{1}{50}\frac{\mathrm {d}Y(t)}{\mathrm {d}t}+Y(t)+\epsilon \sin (Y(t)) = Z(t),\quad t>0. \end{aligned}$$

(42)

We will now apply the same steps as in Example 1 to obtain approximations of the main statistical functions of the approximate stochastic solution ${\widehat{Y}}(t)$. First, we will determine the three first statistical moments. From expression (29), ${\mathbb {E}}\left[ {\widehat{Y}}(t)\right]$ and ${\mathbb {E}}\left[ {\widehat{Y}}^3(t)\right]$ are null. For the second-order moment, ${\mathbb {E}}\left[ {\widehat{Y}}^2(t)\right]$, using expression (17) we obtain

$$\begin{aligned} {\mathbb {E}}\left[ {\widehat{Y}}^2(t)\right] =\frac{13}{6300}-\frac{465955883861}{126023688000000}\epsilon . \end{aligned}$$

(43)

From this expression, we can obtain a rough bound for $\epsilon$, since ${\mathbb {E}}\left[ {\widehat{Y}}^2(t)\right] > 0$. In this case, $\epsilon <0.558098$. To check that our second-order moment approximation is consistent, we will compare it with the random linear oscillator obtained when $\epsilon \rightarrow 0$ [2, Example 7.2],

$$\begin{aligned} \frac{\mathrm {d}^2Y(t)}{\mathrm {d}t^2} + \frac{1}{50}\frac{\mathrm {d}Y(t)}{\mathrm {d}t}+Y(t) = Z(t),\quad t>0. \end{aligned}$$

Notice that, according to (34), expression (43) is also the variance of ${\widehat{Y}}(t)$, ${\mathbb {V}}\left[ {\widehat{Y}}(t)\right]$.

In Fig. 4, we can observe that for t large enough (corresponding in the limit as $t \rightarrow \infty$ to the steady state), the second-order moment of the random linear equation approaches to our approximation for $\epsilon = 0$. Observe in the plot that the ${\mathbb {E}}\left[ Y^2(t) \right] \rightarrow 0.00206349 \approx \frac{13}{6300}$ as $t \rightarrow \infty$, in accordance with (43).

Table 3 Values for ${\mathcal {D}}$ and ${\hat{\tau }}$, defined in (39), for $\epsilon \in \{0, 0.01\}$. Example 1

Fig. 4

Comparison of second-order moments between linear and nonlinear random oscillator for small values of $\epsilon$ and t large (corresponding to the steady state). Example 2

Once we have obtained the mean, ${\mathbb {E}}\left[ {\widehat{Y}}(t)\right]$ and the standard deviation (sd), $\sqrt{{\mathbb {V}}\left[ {\widehat{Y}}(t)\right] }$, of ${\widehat{Y}}(t)$ via the perturbation method, we compare them with the ones computed by the Kloeden–Platen–Schurz algorithm. The results are shown in Table 4. We can observe that both approximations are accurate for $\epsilon \in \{0, 0.01, 0.1\}$; however, significant differences in the standard deviation are shown for $\epsilon = 0.5$, thus showing the perturbation method does not provide acceptable approximations.

Table 4 Comparison of the mean and the standard deviation (sd) between the stochastic perturbation method and the Kloeden–Platen–Schurz algorithm for different values of $\epsilon$. Example 2

The approximation of the correlation function, $\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau )$, using (30) together with expressions (31)–(33), is given by

$$\begin{aligned} \varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau ) = {\left\{ \begin{array}{ll} f_1(\tau ), &{} \text {if }\tau < 0, \\ f_2(\tau ), &{} \text {if }\tau > 0,\\ \dfrac{13}{6300}-\dfrac{465955883861}{126023688000000}\epsilon , &{} \text {if} \,\, \tau =0, \\ \end{array}\right. } \end{aligned}$$

(44)

where

$$\begin{aligned} f_1(\tau )&= -\frac{{{\,\mathrm{e}\,}}^{\tau /100}}{298974181793219856000000}\left( 19286265625 {{\,\mathrm{e}\,}}^{\frac{49 \tau }{100}} (1585962845 \epsilon {-}992186496)\right. \nonumber \\&\quad \left. + \sqrt{1111} \sin \left( \frac{3 \sqrt{1111} \tau }{100}\right) (317192569 (28243342050 \tau -3197833091) \epsilon \right. \nonumber \\&\quad +466418810254320000)\nonumber \\&\quad \left. +1111 \cos \left( \frac{3 \sqrt{1111} \tau }{100}\right) (317192569 (22036350 \tau +3050020523) \epsilon \right. \nonumber \\&\quad \left. -538069558062960000)\right) \end{aligned}$$

(45)

and

$$\begin{aligned} \begin{aligned} f_2(\tau )&= \frac{{{\,\mathrm{e}\,}}^{-\frac{\tau }{2}}}{298974181793219856000000}\left( 1111 \cos \left( \frac{3 \sqrt{1111} \tau }{100}\right) (317192569 (22036350 \tau \right. \\&\quad -3050020523) \epsilon +538069558062960000)\\&\quad +{{\,\mathrm{e}\,}}^{\frac{49 \tau }{100}} \left( \sqrt{1111} \sin \left( \frac{3 \sqrt{1111} \tau }{100}\right) (466418810254320000\right. \\&\quad \left. -317192569 (28243342050 \tau +3197833091) \epsilon )\right) \\&\quad \left. -19286265625 (1585962845 \epsilon -992186496)\right) . \end{aligned} \end{aligned}$$

(46)

Then, we can check that property (34) holds.

In Fig. 5, we show the graphical representations of the correlation function, given by expression (44), for different values of the perturbative parameter $\epsilon$. First, in Fig. 5a, we can observe that for $\epsilon =0.1$ and 0.2 the property $|\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau )|\le \varGamma _{{\widehat{Y}}{\widehat{Y}}}(0)$ is not fulfilled, so showing the perturbation method does not provide reliable approximations for such values of $\epsilon$. For the other values of $\epsilon$, we have represented the correlation function (see Fig. 5b). One observes that $\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau , \epsilon )$ for $\epsilon \in \{0, 0.01\}$ are quite similar. Finally, in Fig. 5c we show $\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau , \epsilon )$ as a surface varying $(\tau , \epsilon )\in [-20,20]\times [-0.01,0.01]$.

Fig. 5

Correlation function $\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau ,\epsilon )$ of ${\widehat{Y}}(t)$. a and b: 2D representation of $\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau ,\epsilon )$ for fixed values of $\epsilon$. c: 3D representation of $\varGamma _{{\widehat{Y}}{\widehat{Y}}}(\tau ,\epsilon )$ for $\epsilon \in [-0.01,0.01].$ Example 2

Now, we will obtain the approximation of the p.d.f. in the form $f_{{\widehat{Y}}(t)}(y)={{\,\mathrm{e}\,}}^{-1 - \lambda _0 - \lambda _1 y - \lambda _2 y^2 - \lambda _3 y^3}$ using the PME. The values of $\lambda _0$, $\lambda _1$, $\lambda _2$ and $\lambda _3$ are shown in Table 5 together with the domain $[y_1,y_2]$ for the following values of the perturbative parameter $\epsilon \in \{ 0, 0.01, 0.1\}$. As in Example 1, the intervals $[y_1,y_2]$ have been computed using the Bienaymé–Chebyshev inequality.

In Fig. 6, we compare the graphical representations of the p.d.f., $f_{{\widehat{Y}}(t)}(y)$. From them, we can observe that the approximations are very similar.

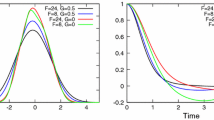
To complete our numerical example, we have calculated graphical representations of the power spectral density, $S_{{\widehat{Y}}(t)}(f)$, of the ${\widehat{Y}}(t)$. In Fig. 7, we show two plots. Panel left corresponds to $\epsilon \in \{0,0.01\}$, and panel right to $\epsilon \in \{0,0.001\}$. We observe that the property of symmetry breaks down when $\epsilon$ increases, while positivity is retained. In Table 6, ${\mathcal {D}}$ and ${\hat{\tau }}$ have been calculated for $\epsilon \in \{0, 0.001\}$.

Table 5 Values of $\lambda _i$, $i=\{0,1,2,3\}$ and the domain $[y_1,y_2]$ obtained via PME, for $\epsilon =0$ and 0.01. Example 2

4 Conclusions

In this paper, we have studied a class of stochastic nonlinear oscillators, whose nonlinear term is defined via a transcendental function. We have assumed that the oscillator is excited by a zero-mean stationary Gaussian process. Since the nonlinear term is affected by a small parameter, to conduct our probabilistic analysis, we have approximated the nonlinear term using a Taylor’s polynomial, and then, we have applied the stochastic perturbation method to obtain the main statistical moments of the stationary solution. After this theoretical analysis, we have carried out numerical examples where the stochastic excitation is driven by two important stochastic processes, the Gaussian white noise and the Ornstein–Uhlenbeck processes. Since a key point when applying the perturbation method is the accuracy of the approximations in terms of the size of the perturbative parameter, from the numerical results obtained in the two examples, we have performed a critical analysis checking whether some important general properties of the statistics associated with the stationary solution are correctly preserved. To better checking the accuracy of the approximations of the mean and the standard deviation via the perturbation method, we have compared them with the ones calculated by means of an accurate numerical scheme, showing good agreement for certain sizes of the perturbative parameter. This comparative analysis includes the linear case obtained when the perturbative parameter is null. In this limit case, the results are also fully consistent. Summarizing, our study shows, by means of a class of stochastic nonlinear oscillators, that the double approximation Taylor-perturbation method is able to approximate the statistics of the stationary solution. Additionally, we have taken advantage of the above computed statistics, in combination with the principle of maximum entropy, to construct reliable approximations of the density of the steady state. Our analysis has been performed with criticism with regard to the size of the perturbative parameter, as required when applying the stochastic perturbation method. Our approach can be useful to study other stochastic nonlinear oscillators whose small perturbations affect a transcendental functions with the additional advantage of computing the density of the stationary solution. In our future works, we plan to tackle this type of problems for other stochastic nonlinear oscillators that have not been analysed yet.

Fig. 6

P.d.f. of ${\widehat{Y}}(t)$, $f_{{\widehat{Y}}(t)}(y)$, for $\epsilon =0$ and 0.01. Example 2

Fig. 7

Power spectral density, $S_{{\widehat{Y}}(t)}(f)$, of ${\widehat{Y}}(t)$. Panel left: $\epsilon \in \{0,0.01\}$. Panel right: $\epsilon \in \{0,0.001\}$. Example 2

Table 6 Values for ${\mathcal {D}}$ and ${\hat{\tau }}$, defined in (39), for $\epsilon \in \{0, 0.001\}$. Example 2

Appendix: Existence of the steady-state solution

Notice that the linearized equation associated with (2) is

$$\begin{aligned} \frac{\mathrm {d}^2Y(t)}{\mathrm {d}t^2} + 2\beta \frac{\mathrm {d}Y(t)}{\mathrm {d}t} +\omega _0^2 Y(t) = Z(t), \end{aligned}$$

and using the classical change of variable ${\mathbf {Y}}=(Y_1(t), Y_2(t))^{\top }=(Y(t),\frac{\mathrm {d}Y(t)}{\mathrm {d}t})^{\top }$ can be written as

$$\begin{aligned} \frac{\mathrm {d}{\mathbf {Y}}(t)}{\mathrm {d}t}=\left( \begin{array}{cc} 0 &{} 1 \\ -\omega _0^2 &{} -2\beta \end{array} \right) {\mathbf {Y}}(t) + \left( \begin{array}{c} 0\\ 1 \end{array} \right) Z(t), \end{aligned}$$

(47)

i.e.

$$\begin{aligned} \mathrm {d}{\mathbf {Y}}(t)=\left( \begin{array}{cc} 0 &{} 1 \\ -\omega _0^2 &{} -2\beta \end{array} \right) {\mathbf {Y}}(t)\mathrm {d}t + \left( \begin{array}{c} 0\\ 1 \end{array} \right) Z(t)\mathrm {d}t. \end{aligned}$$

(48)

In the case that $Z(t)=\xi (t)$ is the white noise (a zero mean, Gaussian and stationary process), i.e. $\xi (t)={\dot{W}}(t)$ (W(t) is the Wiener process), equation (48) writes

$$\begin{aligned} \mathrm {d}{\mathbf {Y}}(t)= & {} \left( \begin{array}{cc} 0 &{} 1 \\ -\omega _0^2 &{} -2\beta \end{array} \right) {\mathbf {Y}}(t)\mathrm {d}t + \left( \begin{array}{c} 0\\ 1 \end{array} \right) {\dot{W}}(t)\mathrm {d}t, \\ \mathrm {d}{\mathbf {Y}}(t)= & {} \left( \begin{array}{cc} 0 &{} 1 \\ -\omega _0^2 &{} -2\beta \end{array} \right) {\mathbf {Y}}(t)\mathrm {d}t + \left( \begin{array}{c} 0\\ 1 \end{array} \right) \mathrm {d}W(t), \end{aligned}$$

it is well known that it has a stationary or steady-state solution if the real parts of the eigenvalues of matrix

$$\begin{aligned} {\mathbf {F}}=\left( \begin{array}{cc}0 &{} 1\\ omega_0^2 &{} -2\beta \end{array}\right) \end{aligned}$$

are negative (in other words, ${\mathbf {F}}$ is a Hurwitz matrix). Assuming $\beta > 0$, it is easy to check that this condition fulfils since the spectrum os ${\mathbf {F}}$ is given by

$$\begin{aligned} \sigma ({\mathbf {F}})=\left\{ \lambda _1=-\beta + \sqrt{\beta ^2-\omega _0^2}, \lambda _2=-\beta - \sqrt{\beta ^2-\omega _0^2}\right\} , \end{aligned}$$

and $\text {Re}(\lambda _1)=\text {Re}(\lambda _2)=-\beta <0$ ($\text {Re}(\cdot )$ denotes the real part). Observe that in the underdamped case $(\beta ^2/\omega _0^2<1)$, $\lambda _1$ and $\lambda _2$ are complex conjugate. This fact is used in Example 1 where $\beta =\frac{1}{20}>0$ to guarantee the existence of the steady-state solution. In the more general case that Z(t) in (47) is such that satisfies a state-space stochastic differential equation (SDE) of the form

$$\begin{aligned} \mathrm {d}Z(t)=r_1 Z(t) \mathrm {d}t + r_2 \mathrm {d}W(t), \end{aligned}$$

(49)

model (47) together with (49) can be written as

$$\begin{aligned} \left\{ \begin{array}{lll} \mathrm {d}Y_1(t) &{} = &{} Y_2(t)\mathrm {d}t, \\ \mathrm {d}Y_2(t) &{} = &{} -\omega _0^2 Y_1(t)\mathrm {d}t - 2\beta Y_2(t)\mathrm {d}t + Z(t)\mathrm {d}t, \\ \mathrm {d}Z(t) &{} = &{} r_1 Z(t) \mathrm {d}t + r_2 \mathrm {d}W(t). \end{array} \right. \end{aligned}$$

(50)

This system is of the form

$$\begin{aligned} \mathrm {d}{\tilde{\mathbf {Y}}}(t)={\tilde{\mathbf {F}}}{\tilde{\mathbf {Y}}}(t)\mathrm {d}t+{\tilde{\mathbf {G}}} \mathrm {d}W(t), \end{aligned}$$

(51)

where

$$\begin{aligned} {\tilde{\mathbf {Y}}}(t)=\left( \begin{array}{c} Y_1(t)\\ Y_2(t)\\ Z(t) \end{array} \right) ,\quad {\tilde{\mathbf {F}}}=\left( \begin{array}{ccc} 0&{}\quad 1&{}\quad 0\\ omega_0^2&{}\quad -2\beta &{}\quad 1\\ 0&{}\quad 0&{}\quad r_1 \end{array} \right) ,\quad {\tilde{\mathbf {G}}}=\left( \begin{array}{c} 0\\ 0\\ r_2 \end{array} \right) . \end{aligned}$$

(52)

The well-known results about the existence of a steady-state solution of Itô SDEs then apply to study the larger dimensional system (50) [or equivalently (51) and (52)]. As a consequence, it is enough to check that the real parts of all the eigenvalues of matrix ${\tilde{\mathbf {F}}}$ are negative. In this case,

$$\begin{aligned} \sigma ({\tilde{\mathbf {F}}})=\left\{ \lambda _1=r_1, \lambda _2=-\beta + \sqrt{\beta ^2-\omega _0^2}, \lambda _3=-\beta - \sqrt{\beta ^2-\omega _0^2}\right\} . \end{aligned}$$

Hence, since $\beta >0$, it is sufficient that $r_1<0$. Notice that in Example 2, Z(t) is the Ornstein–Uhlenbeck process and $r_1=-\alpha <0$ (since $\alpha >0$), so the existence of the steady state is also guaranteed. Finally, it is interesting to point out that in the general case that Z(t) is a (zero mean) stationary Gaussian process (like the white noise and Ornstein–Uhlenbeck processes in Examples 1 and 2, respectively), it is possible to use state-space representations of form (51) to reduce a (stationary) Gaussian process-driven ordinary differential equation of the form

$$\begin{aligned} \frac{\mathrm {d}{\mathbf {Y}}(t)}{\mathrm {d}t}={\mathbf {F}}{\mathbf {Y}}(t)+{\mathbf {G}} Z(t), \end{aligned}$$

as (47) into a larger-dimensional ordinary differential equation driven by white noise, i.e. a linear Itô SDE. This can be done when the spectral density of the covariance function of Z(t) is a rational function.