1 Introduction

Muon tomography [1,2,3] is a valuable imaging technique that allows quick scanning of cargo containers, it takes advantage of muons, particles that make up the constant natural background of cosmic particles. When traversing media, muons are deviated from their original trajectories due to multiple Coulomb scattering. Since the intensity of the scattering strictly depends on the atomic number and the geometry of the objects traversed, it is possible to infer the content of a volume and distinguish materials with different compositions by tracking the muons traversing it.

The goal of the TECNOMUSE project is to design and build a muon tomography scanner based on multi-gap resistive plate chambers (MRPC) detectors [4,5,6,7]. Through the interactions of the muons in the detectors, it is possible to infer the scattering angle of each muon traversing the volume and consequently to reconstruct a tomographic image of its content with a contrast depending on the atomic number of the materials encountered. The goal of the project is to infer the presence of unexpected and potentially harmful objects and materials inside cargo containers.

As shown in Table 1, many detection strategies and technologies have been used for muon tomography. The main advantage of MRPCs and the rationale of their choice for the TECNOMUSE project are high spatial resolution (below 1 mm [11]), high time resolution (better than 600 ps [12]), allowing time-of-flight (ToF) measurement for momentum estimation, and high efficiency for muons (above 90% from preliminary tests on the TECNOMUSE detectors—not reported in this article). Furthermore, MRPCs make possible to cover wide surfaces because of their small cost per unit of area.

Differently from other groups focused on the study of MRPC for muon tomography [13,14,15], the TECNOMUSE project aims to develop a complete scanner based on MRPC.

In this work, the performance of the TECNOMUSE scanner is preliminary evaluated via Monte Carlo simulations. The image reconstruction has been carried out by means of algorithms specifically developed for muon tomography [2, 3]. Different simulations have been developed with the aim to assess the detection capabilities and imaging performance.

2 Detector design and Monte Carlo simulations

2.1 The TECNOMUSE system

The TECNOMUSE system is based on MRPC [4, 5] detectors placed above and below the volume to be scanned to reconstruct the muon tracks traversing the detector from which it infers the content of the volume itself.

Inside the detectors, developed by General Tecnica [17] (a company that already realized the RPC detectors for ATLAS [18] and ARGO projects [19]), there is a mixture of gases (namely 94.7% C\(_{2}\)H\(_{2}\)F\(_{4}\), 5.0% C\(_{4}\)H\(_{10}\) and 0.3% SF\(_{6}\)) specifically tailored for the application with the aim to avoid UV-photons quenching and, consequently, the widening of the discharge and the occurrence of streamers at low voltages. Moreover, being the sulfur fluoride component of the gas mixture, an electronegative gas, it reduces the occurrences of avalanches at high voltages [6, 7].

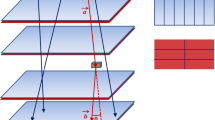
In its prototypical design, the scanner assembly has been realized by stacking three cargo containers in a self-supporting and modular structure (see Fig. 1) that proved to be useful in the development and test stages. The detectors have been placed inside the upper and lower containers in order to realize the muon tracer, while the central container has been used to place the unknown materials to detect.

As many as 36 detectors with different characteristics and sizes have been produced and arranged on the top, bottom and lateral faces of the upper and lower containers. The main characteristics of the detector are given in Table 2.

The main detection section of the scanner, as shown in Fig. 1, is composed of six couples of detectors, each one composed by three-by-three crossed detectors, placed on the top and bottom faces of the upper and lower container, respectively (the blue and green detectors). The crossed detectors are necessary to obtain both the x and y coordinate of the impact of the muons (from detectors arranged along the y- and x-axis, respectively). The z coordinate is inferred from the position of the chamber. Each read-out plane is segmented in strips of 1.4 cm pitch.

The vertical spacing between the detectors (about 2.5 m) is required to allow the incoming muons momentum estimation, which will be available in further developments of the scanner. In the following simulations, only interactions occurring in these horizontal RPCs are considered, since they take into account the preliminary geometry of the tomograph. For the sake of clarity, this choice does not affect the evaluation of the imaging performance since vertical RPCs (the red and yellow ones) only detect wide scattering angle interactions, which compose a small fraction of the total interactions.

Table 1 Approaches to muon tomography and detection techniques
Full size table
Fig. 1
figure 1

Rendering of the TECNOMUSE scanner, showing the geometry of the detectors

Full size image
Table 2 Characteristics of the MRPC detectors in the TECNOMUSE scanner
Full size table

2.2 Monte Carlo simulations

With the aim to obtain a preliminary quantitative and qualitative characterization of the performance of the TECNOMUSE scanner a series of Monte Carlo simulations have been developed. Simulations are indeed able to provide very useful information to model the behavior of the detector, to select the hardware solutions and to better define the detection geometries, allowing for a continuous improvement of the system during its realization. In this specific case, they have been very useful to define the overall geometry and to implement and test the algorithms developed for the tomographic reconstruction of the content of the scanning volume. For this reason, Monte Carlo simulations based on the Geant4 toolkit [20]—largely used in High Energy Physics—have been developed. The simulations were performed taking into account both the performance of the MRPC detectors and the overall geometry of the scanner, together with all the experimental features of the actual scenario.

With the aim to simplify the accurate reproduction of the geometrical layout of detectors, containers and other complex geometries, and to facilitate the execution of the simulations, these have been developed by taking advantage of the GATE software [21]. GATE, indeed, allows to model the geometries, the sources and the time in an easier and more efficient way than Geant4, even if it uses the Geant4 kernel for simulation [22]. Beyond the geometries and the materials, the Monte Carlo simulations have allowed to accurately reproduce the Physics and the behavior of the cosmic muons from both the angular and energetic standpoints [23, 24]. Moreover, the physical response of the MRPC detectors to the muons have been taken into account since the gas mixture and their volume has been correctly modeled in the simulations to produce an accurate intrinsic efficiency of the MRPC detectors. The simulated results are indeed quantitatively accurate with respect to the actual response of the detectors.

By means of the simulations, it has been possible to simulate different kinds of materials and shapes inside the central container (the one to be scanned). The tests performed on the objects located in the middle container allowed to evaluate the imaging performance of the system.

The simulations were developed before the realization of the scanner, but they have been remodeled in order to fulfill the new requirements resulting from the experimental development, so to be the most reliable possible.

3 Performance evaluation of the TECNOMUSE scanner

3.1 Muon tomography imaging

The principle on which muon tomography relies is multiple Coulomb scattering, which explains how the muons traversing an object are scattered with a deviation angle that has a Gaussian distribution around zero and a standard deviation calculated as follows: [2, 3]:

$$\begin{aligned} \sigma \ \approx \ \frac{13.6 \ \text{ MeV/c }}{p}\sqrt{\frac{L}{L_{0}}} \end{aligned}$$
(1)

where p is the particle momentum, L is the thickness of the traversed object, and \(L_{0}\) is the radiation length of the material the object itself is made of, which is related with the atomic number Z.

The software for the reconstruction of tomographic images that starts from the interaction points of the muons in the detectors to assess the scattering density (SD, which is proportional to the mean square deviation angle of muons, i.e., \(\sigma ^2\), passing through a unit depth of that material) has been made conforming to the algorithm developed by Schultz et al. [2, 3]. The algorithm has been modified to be geometry-independent and suitable to the detectors used in the TECNOMUSE project.

The results and images reported in this article have been obtained from tomographic reconstructions and analyses performed by using MATLAB 2017b.

In order to evaluate the imaging performance of the scanner, some Monte Carlo simulations have been performed with different geometries and materials in the scanning volume inside the middle container.

Unlike other imaging techniques (e.g., nuclear medical imaging such as PET or SPECT), for which consolidated procedures for evaluating imaging features exist (e.g., NEMA protocols [25]), there are no guidelines to assess imaging performance in muon tomography.

In this section, several simulated geometries are presented, each tailored to evaluate a different imaging performance.

3.2 Spatial resolution and voxel size

In order to evaluate the spatial resolution of the system, the object inside the scan volume has a geometry borrowed from nuclear imaging, namely the so-called “bar-phantom”.

The bar phantom, as shown in Fig. 2a, is made of a series of vertically placed square slab with 25 cm side and different thickness, namely 0.5 cm, 1 cm, 2 cm and 3 cm. The spacing between the slabs is the same as the thickness.

Tomographic reconstruction have been executed taking into account different voxel sizes in order to evaluate the best trade-off between spatial resolution and voxel size, since the latter implicates the time for the imaging reconstruction.

Images show the projection of tomographic reconstruction after an acquisition of about 4 and 8 min at sea level given the aforementioned counting efficiency, corresponding to about 12,000 tracks and 24,000 muon tracks, respectively. While the reconstruction with 5-cm voxel size does not allow to recognize (as expected) none of the section of the phantom, those with 2 cm and 1 cm allow to recognize the 2-cm bars. The 1-cm reconstruction, due to the higher level of noise, does not make the 1-cm pattern distinguishable, and it does not add any further detail to the 2-cm pattern.

Taking into account also the times needed for the reconstruction with a single, 2.60GHz, core processor, shown in Table 3, it appears that there are no advances in using 1-cm voxel size.

In a real scenario, fast reconstruction algorithms are mandatory to avoid any delay in image reconstruction, which could impact and slow down the overall inspection time.

Since the minimum recognizable thickness of the bar-phantom is in both cases 2 cm (it confirms the result in [26]), it can be inferred that this value is the spatial resolution of the system.

The following analyses have been executed with 2-cm voxel size in order to obtain the best trade-off between image quality and time for its realization.

3.3 Counting efficiency and count rate

As mentioned above, the design of the scanner with the three stacked containers is a prototypical one and also the size and geometry of the MRPC detectors have been chosen to prove the feasibility of the detector.

In fact, the detection area providing planar positional information is given by the sole intersection of the blue and green detectors (see Fig. 1), for an overall area of 176 \(\times \) 176 cm\(^{2}\) on the four planes perpendicular to the vertical axis.

For this reason, the solid angle of acceptance for this design is just 0.22sr. Taking into account the detection efficiency of the four MRPCs, this provides a count-rate of about 48 Hz (i.e., about 2900 counts per minute).

Fig. 2
figure 2

a Three-dimensional view of the bar-phantom. Starting from the upper-right sector and going counter-clockwise, bar with 0.5, 1, 2 and 3 cm pitch. Tomographic reconstruction with b 5 cm, c 2 cm and d 1 cm voxel size with about and 12,000 and 24,000 muon tracks. The grayscale represents SD values from 0 to 100

Full size image
Table 3 Time needed to a single-core CPU to reconstruct an image of 12,000 muon tracks with the specified voxel size
Full size table
Fig. 3
figure 3

Image of the grid for the evaluation of the FoV. The red circle highlights the useful FoV reached in the reconstruction. The grayscale represents SD values from 0 to 100

Full size image

3.4 Field-of-view

By design, the detector efficiency in term of counting is better at the center of the horizontal plane of detection since it is possible to collect more tracks with respect to the edge of the plane. In fact, muons impinging the edges of the detectors in the upper container can be scattered by the objects in the scanning volume outside the area covered by the detectors in the lower container, resulting in a lost track, which is not recorded by the system. In order to evaluate the influence of the detection geometry on the field-of-view (FoV), a grid has been simulated. The grid is made of a series of concentric square each one 5-cm-thick spaced of 5 cm with a maximum side of 170 cm. The squares are connected by a cross having the same thickness.

Figure 3 shows that the outer corners of the grid are not recognizable, and the features are clearly distinguishable up to 99 cm from the center, that is, the radius of the circle defining the use of the FoV of the scanner in this configuration. Although this size could not be enough for the scanning of a complete container, it is important to stress that the TECNOMUSE scanner is in a prototypical geometry in this phase.

3.5 Volume recognition

Two simulations have been made to evaluate the capability of the system in the identification of the volumes depending on the time and their sizes. The first has been made simulating a series of Tungsten slabs with a 10 cm \(\times \) 10 cm face and variable thicknesses from 5 to 100 mm. The reconstruction of the slabs is shown in Fig. 4a, for acquisition time from 4 to 20 min.

All the images of the slabs are visible since 4 min but those with the smaller thickness becomes more evident only after 16-min acquisition. The results show that 4-min acquisition is enough to provide, even though quite weakly, an information proving the presence of high Z materials, especially if the thickness is sufficient. Increasing the acquisition time, the square shape becomes more recognizable and the signal is less noisy. The improvement is clearer for the thicker slabs (in which the contrast increase from 62 to 82%) with respect to thinner slabs (for the 20 mm one the contrast only increase from 15 to 20%).

Fig. 4
figure 4

Tomographic reconstruction of a slabs and b cubes with different sizes at different acquisition time. The grayscale represents SD values from 0 to 100

Full size image

The other simulation is made by simulating cubes with different sides from 0.5 to 10 cm, as shown in Fig. 4b. Differently from the slabs, that are all visible since 4-min acquisition, the cubes are different since the volume of each one is not enough to produce a sufficient contrast. As the acquisition time increases, in addition to a better definition of the shapes, the number of visible cubes also increases, although the smallest cube visible is the 20 mm one. This result is in accordance with the one highlighted in Sect. 3.2. The signal from smaller cubes, since the voxel size is 2 cm, is not distinguishable from the noise after 20 min, too. It is important to stress that beyond the choice of the voxel size, the signal from cubes is proportional to the third power of the side and, for this reason, the signal from a 1-cm-side cube is just one eighth of the signal of a 2-cm-side cube. It follows that detecting very small objects is practically impossible with the aforementioned acquisition times.

It is important to stress that the detection of so small objects is beyond the scope of muon tomography; in practice, due to the limited amount of time for the scanning of the container, the goal of the technique is not the identification of very small volumes, but volumes of at least 1000 cubic centimeters [27, 28].

3.6 Elemental composition

In order to assess the capability to differentiate object made of materials of different atomic number, a simulation involving cubes of progressively increasing Z has been made. Analogously to the simulations of the slabs and cubes, in this one, a series of 10-cm-side cubes but made of different materials, namely water, aluminum (\(Z=13\)), iron (\(Z=26\)), silver (\(Z=47\)), tungsten (\(Z=74\)) and lead (\(Z=82\)) have been simulated. They have been placed along a circumference with the atomic number ascending clockwise.

The results are shown in Fig. 5. The green color indicates low atomic number and, progressively, yellow and red indicate higher atomic numbers. Until aluminum, there are no evidence of red dots (indicating high scattering density) that starts from iron and progressively increase with the atomic number. The image has been made taking into account muon interactions occurring in about 25 min at sea level.

Fig. 5
figure 5

Detail of the reconstruction of the cubes composed of different materials. The topmost cube is composed of water, and aluminum (\(Z=13\)), iron (\(Z=26\)), silver (\(Z=47\)), tungsten (\(Z=74\)) and lead (\(Z=82\)) are placed clockwise. The color scale represents SD values from 0 to 110 with three intervals: green (low Z, SD from 0 to 37), yellow (medium Z, SD from 37 to 73) and red (high Z, SD from 73 to 110

Full size image
Fig. 6
figure 6

Reconstruction in the case of a real scenario, taking into account also the scanner structure (i.e., the containers), a before and b after the application of the threshold filter. The grayscale represents SD values from 0 to 100

Full size image

3.7 Simulation in a real scenario

In order to assess the performance of the scanner in a real scenario, a simulation taking into account also the structure of the TECNOMUSE tomograph is reported.

In fact, the presence of the structure of the containers is expected to be an additional source of noise to the image and its contribution has to be evaluated. To evaluate the effect of the structure of the containers on the reconstructed images, additional simulations have been made.

From the comparison between Figs. 5 and 6a, it is clear the contribution due to the structure of the containers, mostly made by iron bar at their bottom and several millimeters of iron on their ceiling. The structure produces a series of scattered and spurious points that produces an homogeneous cloud of noise around the main signal.

In order to partially suppress these noisy contributions, a simple filter based on a threshold between the voxel value and the values from the first neighbors, reported in Eq. 2, allows to suppress most of those spurious counts. \(\mathrm{SD}_{x,y,z}\) is the value of the scattering density for a voxel and if the sum of its neighbors is smaller than a certain fraction (the threshold \(\tau \)) of the voxel value, then the value is set to zero. It implies that only counts in a neighborhood composing a continuous volume remain after the filter.

$$\begin{aligned} \text{ If: } \quad \sum _{i=x-1}^{i=x+1} \sum _{j=y-1}^{j=y+1} \sum _{k=z-1}^{k=z+1} \mathrm{SD}_{i,j,k} - \mathrm{SD}_{x,y,z} < \tau \cdot \mathrm{SD}_{x,y,z} \quad \text{ then: } \quad \mathrm{SD}_{x,y,z}=0 \end{aligned}$$
(2)

The result of the reconstruction after the application of the filter with threshold \(\tau =20\%\) is shown in Fig. 6b. It is clear that most of the signal is suppressed and the content of the scanning volume becomes clearer.

4 Conclusions

In this work, through different Monte Carlo simulations, it has been possible to assess and define the imaging performance of the prototypical design of the TECNOMUSE scanner for muon tomography.

The results have been useful for the study and the optimization of the tomograph, its detectors, and the algorithms for tomographic reconstruction. As shown in Sects. 3.2, 3.4, 3.5 and 3.6, volume reconstruction and elemental composition recognition are feasible with the current detection geometry and the developed algorithms.

For the feasibility in a real scenario, the main improvement to be made is the refinement of the detection geometry to improve counting efficiency (see Sect. 3.3) and avoid undesired noise from the structure itself (see Sect. 3.7).

The first can be achieved by scaling the size of the detectors of at least a 2.5 factor to obtain an estimate count-rate of 10,000 tracks per min or by reducing the vertical spacing between the detectors (losing any ToF possibility). The latter will be obtained by substituting the three stacked containers with a dedicated structure that allows for the installation of the detectors on the top and bottom of the inspection volume, without any other interfering mechanical structures.