Effects of geometric frustration in Kitaev chains

Abstract

We study the topological phase transitions of a Kitaev chain frustrated by the addition of a single long-range hopping. In order to study the topological properties of the resulting legged-ring geometry (Kitaev tie model), we generalize the transfer matrix approach through which the emergence of Majorana edge modes is analyzed. We find that geometric frustration gives rise to a topological phase diagram in which non-trivial phases alternate with trivial ones at varying the range of the hopping and the chemical potential. Robustness to disorder of non-trivial phases is also proven. Moreover, geometric frustration effects persist when translational invariance is restored by considering a multiple-tie system. These findings shed light on an entire class of experimentally realizable topological systems with long-range couplings.

1 Introduction

Topological quantum matter and Majorana quasiparticles have attracted growing interest from the scientific community. Because of their peculiar properties, Majorana’s excitations are believed to be relevant for the fault-tolerant quantum computation[1,2,3], whose realization represents a fundamental step toward the implementation of the forthcoming quantum computers.

Majorana’s states have been predicted to exist as zero-energy edge modes in various condensed matter systems and some evidences have come from experiments conducted on proximity-coupled semiconducting nanowires or ferromagnetic atomic chains on a superconducting substrate [4,5,6]. These findings suggest that a topological phase can be synthesized by combining conventional s-wave superconductors with nanostructured materials presenting strong spin–orbit interaction and/or magnetic properties. Resorting to an appropriate fine-tuning of the system parameters, these superconducting heterostructures can exhibit a topological phase transition, the non-trivial phase being characterized by the emergence of topological superconductivity.

A minimal model of topological superconductivity has been introduced by Kitaev in his seminal work [7]. The Kitaev model consists of spinless fermions confined to a one-dimensional lattice and subject to a p-wave superconducting pairing. In view of its simplicity, the Kitaev model has become an established paradigm in studying the topological phase transitions and various generalization of such model have appeared, for example, to describe coupled nanowires (e.g., the Kitaev ladder) [8,9,10,11,12]. The generalizations of the Kitaev model allow to test the robustness of the topological phase with limited computational effort and are often used to get insights into the response of real devices. Operation of real devices is often affected by the detrimental effects of impurities or system’s imperfections and thus an important issue is testing the robustness of the topological phase to these effects. In order to prove to what extent a topological phase is preserved in the presence of system’s imperfections, disordered Kitaev models have been studied [13,14,15,16,17,18]. The outcome of these studies evidences that the topological phase is essentially immune to a moderate disorder, which is an expected property of the topological matter.

Recently, extended models of Kitaev chain with finite and infinite range in the hopping and pairing parameters have been considered [19,20,21,22]. While these models are relevant in mathematical physics, the interest for long-range Kitaev models is mainly motivated by the fact that they are realizable, at least in principle, in photonic or in cold atoms systems using the powerful trick of the synthetic dimensions. However, the possibility to implement these models in condensed matter systems appears to be very challenging.

Despite these general difficulties, in [23] it has been identified a special class of long-range Kitaev models (the so-called Kitaev tie models) that can be realized in a condensed matter context. In particular, it has been proposed that the original Kitaev chain model can be modified to include an additional hopping term with arbitrary range (see Fig. 1), being the latter situation realizable in flexible ballistic conductors or in chains of iron atoms arranged to form a legged ring on the surface of a superconducting material with strong spin–orbit coupling (e.g., lead). While the latter experimental method requires precise positioning of atoms on a surface by using the same technique and materials used in [6], the former can be implemented by using single-walled carbon nanotubes where superconducting proximity effect can be easily implemented [24,25,26]. Moreover, in order to implement the geometry required for the realization of a Kitaev tie model, nanotube loops similar to those described in Ref. [27] can be used. Interestingly, the range of the extra hopping of the Kitaev tie model is controlled by the diameter of the nanotube loop, which on its turn can be altered by means of nanomanipulators inside the chamber of a scanning electron microscope (SEM). The latter technique allows repeatable modifications of the nanotube loop diameter, while maintaining almost unaffected the remaining device parameters.

According to the aforementioned arguments, the experimental implementation of the Kitaev tie model appears to be a promising platform to test the interplay between topology and long-range effects. A preliminary study of these effects has been reported in [23] where a first indication about the topological phase diagram has been provided. In that context, the relevant concept of topological frustration has been introduced. Topological frustration phenomenon shares similarities with the geometric frustration effects which are well known in magnetism [28]. Despite this analogy, less is known about the geometric frustration on the topological phase transitions and filling this vacancy represents one of the main goals of this work. Before proceeding further with the presentation, it is useful to precise the concept of topological frustration.

It is a known fact that a Kitaev chain with periodic boundary conditions does not present unpaired Majorana modes, while, when Dirichlet boundary conditions are considered, unpaired Majorana states may nucleate at the system edges. The above situation is reminiscent of the fact that a topological system can exhibit unpaired topological states when an interface with a topologically trivial material (e.g., the vacuum) is created. A topological system can be subject to a peculiar frustration condition in which a competition between the presence and the absence of unpaired Majorana states is established. The occurrence of this peculiar frustration is favored in topological systems with non-trivial lattice connectivity and the resulting phenomenon is here referred to as topological frustration. Since the topological frustration is determined by the lattice connectivity (i.e., by the system’s geometry), throughout this work we use the notion of geometric frustration as a synonym.

Once the notion of topological frustration has been specified, we observe that a Kitaev tie model represents the simplest realization of a topological frustrated system. Indeed, a Kitaev tie, being shaped in the form of a legged ring, realizes an intermediate condition between a Kitaev ring and a Kitaev chain. Under this condition, unpaired Majorana modes nucleate or not depending on the number of lattice sites forming the ring. However, once a system configuration has been assigned, the presence of unpaired Majorana states is hardly anticipable. Due to this, a Kitaev tie presents a rich topological phase diagram whose investigation requires the use of several theoretical tools.

Indeed, the additional long-range hopping of the Kitaev tie model causes the breaking of the translational invariance and, for this reason, the topological properties of the system cannot be studied by means of a topological bulk index Q [29]. Thus, alternative approaches are needed.

In order to characterize topological systems with broken translational invariance (e.g., due to disorder effects), real space methods based on non-commutative geometry [30] and on the wavefunction properties [18, 31] have appeared in the literature. In particular, the transfer matrix (TM) method, which is well known in optics [32], has been widely used to study one-dimensional systems [22, 33, 34] and is suited to reveal the emergence of localized Majorana zero-energy states.

In this work, we provide a comprehensive analysis of the topological phase diagram of a Kitaev tie by using complementary and diverse theoretical tools. In particular, we use a generalization of the TM method proposed in Ref. [18, 31] and adapted to describe systems hosting long-range hopping terms. Moreover, the energy spectrum analysis, already reported in Ref. [23], is here complemented by the computation of the Majorana polarization (MP) proposed in Ref. [35]. All these approaches provide similar topological phase diagrams showing the nucleation of non-trivial regions inside trivial ones when the chemical potential $\mu$ and the parameter d, controlling the hopping range, are varied. Comparing information obtained by using different techniques, we are able to demonstrate that the topological frustration strongly perturbs the energy spectrum of the system and the morphology of the topological phase boundaries reflects this perturbation.

We also show that the topological phases of the Kitaev tie model are robust against the detrimental effects of disorder. Moreover, in order to study topological frustration effects in a translational-invariant system, we propose a multiple-tie model in which the topological phase transitions can be studied by using the bulk invariant, i.e., the Majorana number. In this context, we demonstrate that topological frustration effects persist even in a translational-invariant system.

The paper is organized as follows. In Sect. 2, we introduce the Kitaev tie Hamiltonian, while its topological phase transitions are discussed in Sect. 3. In particular, the transfer matrix method is discussed in Sect. 3.1, while the Majorana polarization is introduced in Sect. 3.2. A comparison between the topological phase diagrams obtained by using the transfer matrix method and the Majorana polarization is also presented. In Sect. 4, we investigate the robustness of the topological phases against the disorder. To this purpose, disordered realizations of the Kitaev tie model are considered. A translational-invariant topologically frustrated system is presented in Sect. 5, where a multiple-tie model is investigated. There the topological phase diagram is obtained by using the Pfaffian invariant. Conclusions are given in Sect. 6. A comparison between the transfer matrix method, the Majorana polarization and the spectral analysis is reported in Appendix A. The effect of the long-range hopping strength and the bulk-edge correspondence for a multiple-tie system are discussed in Appendices B and C, respectively.

2 The Kitaev tie model

A Kitaev chain perturbed by the addition of a single long-range hopping linking two distant lattice sites can be rearranged in the form of tie (Fig. 1). The tight-binding Hamiltonian of the resulting system, which is here referred to as Kitaev tie, is given by:

$$\begin{aligned} H=H_K+H_d \end{aligned}$$

(1)

where $H_K$ is the usual Kitaev chain Hamiltonian [7]:

$$\begin{aligned} H_K=\sum _{j=1}^{L-1}\left( -tc^\dagger _{j}c_{j+1}+\varDelta c^\dagger _{j+1}c^\dagger _{j}+h.c.\right) -\mu \sum _{j=1}^L c^\dagger _{j}c_{j} \end{aligned}$$

(2)

written in terms of creation/annihilation fermionic operators $c^\dagger _j/c_j$; t and $\varDelta$ are the hopping and the superconducting pairing amplitudes between nearest neighbor sites, while $\mu >0$ is the chemical potential; $H_d$ is the knot Hamiltonian linking the two sites d and $L-d+1$:

$$\begin{aligned} H_d=-t_d\left( c^\dagger _{d}c_{L-d+1}+h.c.\right) , \end{aligned}$$

(3)

where $t_d$ is the hopping amplitude linking two distant sites. The range of the extra hopping, controlled by d, is varied to change the length of the legs (see Fig. 1). A previous analysis of the Kitaev tie energy spectrum in [23] has already shown a frustration of the system emerging from a competition between localized edge modes and hybridized modes along the ring. Moreover, the breakdown of translational invariance symmetry leads to a system with no bulk associated [36] since the long-range-hopping Hamiltonian $H_d=\sum _{k,q} c^\dagger _{k}V_{kq}c_q$, written in momentum representation, couples all k-modes via the single particle potential $V_{kq}=t_d\left[ e^{ikd}e^{-iq(L-d+1)}+e^{-iqd}e^{ik(L-d+1)}\right]$. Thus, the topological phase transitions have to be analyzed by using real space methods. Accordingly, in next section, we generalize the TM method introduced in Ref. [18] to the peculiar geometry of the Kitaev tie model.

Fig. 1

a Schematic of the Kitaev tie model. It is obtained by adding a long-range coupling to the Kitaev chain. The resulting system is a legged ring (b), which admits the tight-binding description schematized in (c)

3 Topological phase diagram of a Kitaev tie

3.1 Transfer matrix approach with a long-range hopping and the boundary invariant

Topological properties of finite-sized systems are usually described in terms of geometric indices also known as topological invariants Q, whose definition is strictly connected to the bulk of the system in which periodic boundary conditions are considered. The bulk-edge correspondence, then, can be invoked in order to calculate the number of zero-energy edge modes [36]. However, the topological properties of the frustrated system considered here cannot be addressed by means of the momentum-space properties. Thus, we base our analysis on the TM approach which provides information on the boundary invariant.

Starting from the Kitaev tie Hamiltonian, we make the change of basis from the fermionic operators $c_n$, $c_n^{\dagger }$ of Eq. (1) to Majorana operators $a_n=c_n+c^{\dagger }_n$, $b_n=i(c^{\dagger }_n-c_n)$ which satisfy the relations: $a^{\dagger }_n=a_n$, $b^{\dagger }_n=b_n$, $\{a_n,a_m\}=2\delta _{n,m}$, $\{b_n,b_m\}=2\delta _{n,m}$. In this new basis, the Hamiltonian reads:

$$\begin{aligned} H_M=H_K^{'}+H_d^{'} \end{aligned}$$

(4)

where

$$\begin{aligned} H^{'}_K= & {} -\frac{i}{2} \sum _{j=1}^{L-1}\left[ t_- a_jb_{j+1}-t_+ b_ja_{j+1}\right] -\frac{i}{2}\mu \sum _{j=1}^{L}a_jb_j\nonumber \\ H^{'}_d= & {} -\frac{i}{2}t_d\left( a_db_{L-d+1}+a_{L-d+1}b_d\right) , \end{aligned}$$

(5)

while $t_\pm =t\pm \varDelta$. The TM can be obtained by means of the Heisenberg equations of motion for the Majorana operators. Imposing the zero-energy constraint ($\omega =0$) for Majorana modes, two decoupled equations for the components of the Majorana wavefunctions $a_j$ and $b_j$ are obtained:

$$\begin{aligned} \left[ a_j,H_M\right] =t_-b_{j+1}+t_+b_{j-1}+\mu b_j+t_d\left( \delta _{\alpha ,j}b_{\beta }+\delta _{\beta ,j}b_\alpha \right) =0 \end{aligned}$$

(6)

$$\begin{aligned} \left[ b_j,H_M\right] =t_-a_{j-1}+t_+a_{j+1}+\mu a_j+t_d\left( \delta _{\alpha ,j}a_{\beta }+\delta _{\beta ,j}a_\alpha \right) =0, \end{aligned}$$

(7)

where the shortened notation $\alpha =d$ and $\beta =L-d+1$ has been introduced. The space evolution of the $a_j$ Majorana mode is controlled by the following equation:

$$\begin{aligned} x_{j+1}= A x_j+\delta _{\alpha ,j}\left( \begin{array}{cc} -\frac{t_d}{t_+}a_\beta \\ 0 \end{array} \right) +\delta _{\beta ,j}\left( \begin{array}{cc} -\frac{t_d}{t_+}a_\alpha \\ 0 \end{array} \right) \end{aligned}$$

(8)

where

$$\begin{aligned} A=\left( \begin{array}{cc} -\frac{\mu }{t_+}&{}-\frac{t_-}{t_+}\\ 1&{}0\\ \end{array} \right) ,&\ \ x_j=\left( \begin{array}{cc} a_j\\ a_{j-1}\\ \end{array} \right) . \end{aligned}$$

(9)

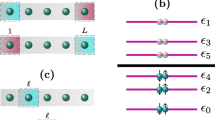
In the absence of the extra hopping term connecting the sites $\alpha$ and $\beta$, the model reduces to the standard Kitaev chain and the TM connecting $x_{1}$ and $x_{L+1}$ is simply given by $A^{L}$ (see panel (a) of Fig. 2). The TM for the b-mode has an identical structure with the change $t_-\rightarrow t_+$.

When the Kitaev tie model is analyzed, the lattice sites $j=\alpha$ and $j=\beta$ are linked by the long-range hopping and thus the transfer matrix of the system cannot be reduced to a product of A matrices. For these reasons, the derivation of the transfer matrix of a Kitaev tie model requires a more involved procedure.

Fig. 2

Sketch of the transfer matrix method (TM): a for a Kitaev chain and b for a Kitaev tie. The transfer matrix representation of a Kitaev tie model presented in (b) can be visualized by separating the legs and the ring region as shown in panel (c). The operators loop structure induced by the extra hopping term presents a complicated internal structure, which is reminiscent of the interference phenomena of the wavefunction along the ring

Panel (c) of Fig. 2 schematically shows TM structure of a Kitaev tie model. In particular, the tie geometry introduces an operators loop structure in the TM equations which is reminiscent of the interference processes of the wavefunction. To determine the TM of the Kitaev tie, first we focus on Eq. (8) by taking $j=\alpha$ and $j=\beta$. Consequently, the following non-local relations are obtained:

$$\begin{aligned} x_{\alpha +1}= & {} \tilde{A} x_{\alpha }+\varGamma _{1} x_{\beta +1}+ \varGamma _{2} x_\beta , \end{aligned}$$

(10)

$$\begin{aligned} x_{\beta +1}= & {} \tilde{A} x_{\beta }+\varGamma _{1} x_{\alpha +1}+ \varGamma _{2} x_\alpha , \end{aligned}$$

(11)

where the following auxiliary matrices have been introduced:

$$\begin{aligned} \tilde{A}= & {} \left( \begin{array}{cc}\frac{t_d^2-\mu ^2}{\mu t_+} &{}-\frac{t_-}{t_+}\\ 1&{}0 \end{array} \right) , \end{aligned}$$

(12)

$$\begin{aligned} \varGamma _1= & {} \left( \begin{array}{cc}\frac{t_d}{\mu }&{}0\\ 0&{}0 \end{array} \right) ,\quad \varGamma _2=\left( \begin{array}{cc}0&{}\frac{t_dt_-}{\mu t_+}\\ 0&{}0 \end{array} \right) . \end{aligned}$$

(13)

Interestingly, the two terms $\varGamma _1$ and $\varGamma _2$ appear because of the long-range hopping. Using now the relations $x_{\alpha }=A^{k}x_1$ and $x_{\beta }=A^{p}x_{\alpha +1}$ with $k=\alpha -1$ and $p=L-2\alpha$, Eqs. (10)–(11) can be recast in the following form:

$$\begin{aligned}&x_{\alpha +1}= \left( \mathbb {I}-\varGamma _2 A^p\right) ^{-1} \left( \tilde{A} A^k x_1+ \varGamma _1 x_{\beta +1}\right) \end{aligned}$$

(14)

$$\begin{aligned}&x_{\beta +1}= \left( \tilde{A}A^p+\varGamma _1\right) x_{\alpha +1}+\varGamma _2 A^k x_1. \end{aligned}$$

(15)

Substituting the expression for $x_{\alpha +1}$ given in Eq. (14) into Eq. (15), one easily gets the relation:

$$\begin{aligned} x_{\beta +1}=G x_{1}, \end{aligned}$$

(16)

where G is an appropriate matrix operator. Multiplying both sides of Eq. (16) by acting with the operator $A^{k}$ and using the relation $x_{L+1}=A^{k} x_{\beta +1}$, the following result is derived:

$$\begin{aligned} x_{L+1}=T x_1. \end{aligned}$$

(17)

Here, $T=(\mathbb {I}-R)^{-1}S$ is the transfer matrix of the legged-ring model with

$$\begin{aligned} R= & {} A^k \left( \tilde{A}A^p+\varGamma _1\right) \left( \mathbb {I}-\varGamma _2 A^p\right) ^{-1} \varGamma _1 A^{-k} \\ S= & {} A^k\left( \tilde{A}A^p+\varGamma _1\right) \left( \mathbb {I}-\varGamma _2 A^p\right) ^{-1}\tilde{A}A^k+A^k\varGamma _2A^k. \end{aligned}$$

Once the TM is known, the topological phase transitions can be analyzed by imposing the localization requirement of the Majorana modes, which corresponds to the equation $a_{L+1}=T_{11}a_1+T_{12}a_0$ complemented by the open boundary condition $a_{L+1}=a_0=0$. This conditions implies $T_{11}=0$.

For finite-size systems, the ground state degeneracy, expected in thermodynamic limit, is broken by an exponentially small energy splitting. The latter is originated by a weak overlap between the wavefunctions tails of Majorana modes localized at opposite edges. Due to this the condition $T_{11}=0$, which has been derived under the assumption of decoupled Majorana modes, cannot be exactly met. Thus, for systems of finite size, the condition $T_{11}=0$ has to be substituted by the weaker one $T_{11}<\lambda$, with $\lambda$ a suitable cutoff value. We have numerically verified that topological regions of the phase diagram can be easily discriminated from trivial ones by using the cutoff value $\lambda =10^{-7}$.

The phase diagram obtained by the condition above is shown in panel (a) of Fig. 3 for a tie of 121 sites at varying the chemical potential $\mu$ and the extra hopping range, controlled by d. Topological phases (blue regions) nucleate inside trivial regions (white regions). Moreover, the number of non-trivial phases increases, when the circumference of the ring is reduced (d is increased), i.e., when the system approaches a perturbed Kitaev chain limit, which is reached for $d=60$. The interstitial character of the topological phase is more evident for small values of the parameter d since, in this case, the system is similar to a ring with very short legs. The figure indicates the intricate behavior which may occur in the frustrated case, including re-entrant phases.

Fig. 3

Topological phase diagram of a Kitaev tie ($L = 121$) in the $d-\mu$ plane. The model parameters have been fixed as: $t_d=1$, $\varDelta = 0.02$ in units of t. Panel a is obtained with the Majorana transfer matrix method ($T_{11}<10^{-7}$), while Majorana polarization has been used to obtain panel (b). In panel c is reported the topological phase diagram obtained by the gap closing of the lowest energy eigenvalue. The red dots of panel b correspond to four selected values of the extra hopping range controlled by the parameter d ($d=1$, 3, 40, 59) for which the polarization is plotted in Fig. 4. Blue (white) regions represent topological (trivial) phases

Fig. 4

Majorana polarization (MP) of the Kitaev tie (blue curves) for the values of d corresponding to the red dots of Fig. 3. The cases of a Kitaev ring ($d=1$, panel (a)), a quasi-Kitaev ring ($d=3$, panel (b)), $d=40$, panel (c) and of a perturbed Kitaev chain ($d=59$, panel (d)) are shown. The red curves in each panel represent the MP of a Kitaev chain of the same size $L=121$. The numbered black circles are the selected minima and maxima at which we evaluate the local Majorana polarization shown in Fig. 5

Such phase diagram can be contrasted with the one derived by the energy spectrum shown in Fig. 3 (panel (c)) and the Majorana polarization in panel (b). In the first case, the topological phase transitions are signaled by the gap closing events indicating the existence of zero-energy edge modes. The phase diagram of Fig. 3 (panel (c)) accounts for the spectral properties of the system and agrees well with the phase diagram obtained by the boundary invariant (Fig. 3a). A similar topological phase diagram is obtained by using the Majorana polarization (Fig. 3b), which is presented in the next subsection. The qualitative agreement among the phase diagrams obtained by different approaches is clearly evident. However, distinct methods highlight complementary properties of the topological phase and thus a strict quantitative agreement is not expected. Different methods indeed capture different features of the system. For instance, the transfer matrix method provides a measure of the spatial localization of the edge modes, while the spectrum analysis is sensitive to the eigenvalues of the energy. Majorana polarization, on the other hand, captures the eigenstates symmetry in the Nambu space. Despite these differences, topological phase diagrams obtained by using different methods present an interstitial structure of the topological phase. When this structure is explored without introducing cutoffs (see Appendix A), the estimators of the topological phase present very similar behavior and show a consistent picture of the topological phase diagram.

3.2 Majorana polarization

Another quantity that permits to evaluate the topological phase diagram is the Majorana polarization (MP) [35, 35, 37,38,39]. This is a topological order parameter, analogous to the local density of states (LDOS), which measures the quasiparticles weight in the Nambu space.

Let us introduce the Nambu representation $\varPsi =(c_1,c_1^\dagger ,...,c_L,c_L^\dagger )^T$. Accordingly, the Hamiltonian in Eq. (1) can be written in the Bogoliubov–de-Gennes form:

$$\begin{aligned} H=\frac{1}{2}\varPsi ^\dagger H_{BdG}\varPsi \end{aligned}$$

(18)

where $H_{BdG}$ is a $2 L\times 2L$ matrix being L the number of lattice sites. The eigenstates of $H_{BdG}$ are expressed in the electron–hole basis as $\psi ^{(m)}=(e_1^{(m)},h_1^{(m)},...,e_L^{(m)},h_L^{(m)})^T$ and the local Majorana polarization is defined as:

$$\begin{aligned} P_M(n)=\int _{-\infty }^\infty P_M(\omega ,n) d\omega \end{aligned}$$

(19)

where

$$\begin{aligned} P_M(\omega ,n)=2\sum _{m}\delta (\omega -\epsilon _m)e^{(m)*}_nh_n^{(m)} \end{aligned}$$

is the density of MP and $e_n^{(m)}$ ($h_n^{(m)}$) refers to the m-th eigenstate, while n is a site index. If a state $\psi ^{(m)}$ belongs to the particle or hole sector, i.e., $h_n^{(m)}=0$ or $e_n^{(m)}=0$ $\forall$ n, the $P_M$ is indeed zero. On the other hand, the Majorana polarization $P_M=\sum _{n=1}^{L/2}P_M(n)$ of a genuine Majorana state is $\pm 1$. We also note that the system has to satisfy the constraint: $P_M^{tot}=\sum _{n=1}^{L}P_M(n)=0$, because free Majorana monopole cannot exist. In panel (b) of Fig. 3, we show the topological phase diagram obtained by evaluating the Majorana polarization of the legged-ring system ($t_d\ne 0$) measured in units of the Majorana polarization of the Kitaev chain ($t_d=0$) with the same system length $L=121$. We recover qualitatively the same phase diagram of panel (a) with alternating trivial/non-trivial phases.

The effect of geometric frustration is also analyzed in Fig. 4 where we show the MP as a function of the chemical potential by varying the range of the extra hopping: $d=1$ (Kitaev ring), 3, 40, 59 (perturbed Kitaev chain). The case of a Kitaev chain of 121 sites (red curves) is also plotted for comparison. Going from the Kitaev ring limit (panel (a)) to the perturbed Kitaev chain limit (panel(d)), the MP mean value increases favoring the non-trivial regime. On the other hand, the alternation of local minima and maxima keeps track of the geometric frustration of the system induced by the long-range hopping. The phenomenology of the frustration is clear when looking at Fig. 5 where the real space Majorana polarization is plotted in correspondence of the minima and maxima of Fig. 4 (indicated by the black circles). The size of the circles is proportional to the absolute values of the local MP, while blue and red colors refer to positive and negative values of the MP, respectively. As shown, the minima of Fig. 4 correspond to hybridized Majorana states and the hybridization becomes stronger when d is smaller. This is clearly seen in the extreme case of a Kitaev ring (panel (a)) where the polarization is uniformly distributed throughout the system. On the other hand, local maxima correspond to Majorana modes localized at the system’s legs. A similar analysis can be performed by studying the wavefunction along the chain as done in Fig. 5 of Ref. [23]. Also in that case, localized modes have been identified at the system legs and it has been found that the localization properties are strongly affected by interference phenomena controlled by d.

Up to now, we have considered the case of uniform hopping $t_d=t$. The case $t_d \ne t$, reported in Appendix B for completeness, shows a phase diagram similar to the one obtained for the homogeneous case.

Fig. 5

Real space Majorana polarization for the system parameters corresponding to the numbered black circles (1, 2) of Fig. 4. Panels a, b, c and d follow the same order of panels of Fig. 4. The model parameters have been fixed as: $t = t_d = 1$, $\varDelta = 0.02$ and $L = 121$

4 Disorder effects

We have demonstrated that the topological regions of the phase diagram of a Kitaev tie model are surrounded by trivial areas. The presence of trivial regions for $\mu <2$ is peculiar to the proposed model and, indeed, it is not expected in the phase diagram of a Kitaev chain. Thus, the emergence of trivial regions in the phase diagram of a Kitaev tie model is direct consequence of the topological frustration effect induced by the perturbation due to the long-range hopping. This observation suggests that topological phases of the Kitaev tie model should be as immune to disorder as the topological phase of the original Kitaev chain model. In order to verify the above conclusion, disordered realizations of the Kitaev tie model have to be studied. There are several options to include disorder effects in Eq. 1. Here we confine our attention to those appearing directly related to a recognizable physical origin. Topological systems are usually realized by using nanowires in proximity coupling with superconductors. Typically, the nanowire–superconductor coupling, which is responsible for the induced superconductivity inside the nanowire, can be prone to unwanted spatial variations along the wire. These inhomogeneities can be modeled as random couplings. Accordingly, it is quite reasonable to infer that the induced superconductivity along the nanowire takes a stochastic character which can be included in the Kitaev tie model by considering a random site-dependent pairing potential. Disorder, however, can be of endogen origin. Typically, the growth process of a nanowire requires the delicate control of several process parameters. Under this condition, compositional gradient along the nanowire may originate a space-dependent effective mass of the charge carriers, which is a well-known effect in semiconducting heterostructures. Within the framework of a discrete description, effective mass gradient and random doping along the nanowire can be modeled by including site-dependent random hopping integrals in the Kitaev tie model. This conclusion is equally applicable to the case of flexible one-dimensional conductors, such as the single-wall carbon nanotubes. The latter systems are typically homogeneous from the chemical viewpoint even though they are not immune to modifications of the hopping integrals induced by local bending effects and interaction with the substrate. The aforementioned sources of disorder are simultaneously present in real systems and their relative relevance is in general hardly anticipable. Thus, in the following, we study two distinct conditions, characterized by the presence of one source of disorder at the time. When disordered realizations of the Kitaev tie model are considered, the existence of Majorana modes is pinpointed by gap closing events in the energy spectrum. This condition can be monitored by studying the smallest subgap energy eigenvalue as a function of the chemical potential, while fixing different values for the disorder strength. Disorder strength is quantified by the variance of the uniform distributed random variable representing the site-dependent pairing potential or the site-dependent hopping integral. In order to study disorder effects, single disorder realizations are analyzed and we have checked that the corresponding behavior does not differ too much from the typical behavior deduced from the analysis of a relevant number of independent random realizations. From the experimental viewpoint, the disorder contribution to the Hamiltonian is typically due to a precise impurity pattern, which is responsible for sample-specific signatures. For this reason, studying the device response to a single disorder realization seems to be more appropriate than using an ensemble average (involving several disordered realizations). The latter strategy is particularly appropriate when mesoscopic samples are considered.

Fig. 6

Lowest energy eigenvalues as a function of the chemical potential $\mu$ for different values of the disorder strength. A system’s size of $L=121$ lattice sites has been considered. Panels a–c: pairing disorder has been introduced by considering a random site-dependent pairing potential generated by a uniform probability distribution defined in the interval ($\varDelta -\delta$, $\varDelta +\delta$). Panels d–f: hopping disorder has been obtained by considering a random site-dependent hopping integral generated by a uniform probability distribution defined in the interval ($t-\tau$, $t+\tau$). For each panel, a single disorder realization is considered. The remaining model parameters have been fixed as: $t = 1$, $\varDelta = 0.02$

Results of this analysis are reported in Fig. 6a–f. In particular, in Fig. 6a–c, the effect of a random superconducting coupling is studied by considering random values of the site-dependent pairing potential. The disordered Hamiltonian is described by $H'=H+H^{dis}$, with H defined in Eq. 1 and $H^{dis}= \sum _{j=1}^{L-1} \delta _j^{dis} c^\dagger _{j+1} c^\dagger _j+ h.c.$. Here, $\delta _j^{dis}$ represents a random pairing fluctuation with uniform distribution in the interval ($-\delta$, $\delta$). The effect of random hopping integrals is reported in Fig. 6d–f, where disorder is introduced by generating uniformly distributed random values of the site-dependent hopping integrals. In this case, the disordered Hamiltonian is $H'=H+H^{dis}$ with $H^{dis}= \sum _{j=1}^{L-1} \tau _j^{dis} c^\dagger _j c_{j+1}+h.c.$ and $\tau _j^{dis}$ a random hopping fluctuation with uniform distribution in the interval ($-\tau$, $\tau$). When disorder is induced by a random pair potential (Fig. 6a–c), depending on the legs’ length d and on the chemical potential, two distinct situations are realized: (i) the gap closing events are pinned to specific values of the chemical potential which are insensitive to the disorder’s strength; (ii) the gap closing events are displaced by disorder toward different chemical potential values. For the considered disorder strength, we never observe the disappearance of a topological region induced by disorder. Probably, the mentioned condition is almost reached in Fig. 6a, where two topological phases (i.e., two gap closing points separated by a trivial phase) tend to merge as the disorder strength is increased. The merging condition, which is not reached, is probably the prelude to the gap opening and the disappearance of the two topological phases. It is worth mentioning here that the maximum disorder strength considered in Fig. 6a–c is comparable with the mean value of the pairing potential $\varDelta$. The latter condition corresponds to an extremely disordered system, which is not expected in realistic experimental conditions. A similar phenomenology can be observed by studying disorder effects induced by random values of the hopping integral (Fig. 6d–f). Here, although the effects of disorder constitute a small perturbation compared to the previous case, a similar phenomenology is observed. This observation suggests that random hopping is more effective in perturbing the topological phase then a random superconducting pairing. From the above analysis, we conclude that realistic values of the disorder strength only produce a reshaping of the topological phase boundaries, while preserving the interstitial nature of the topological phases. The latter are robust features of the topological frustration phenomenon.

5 Building of a topological frustrated translational-invariant system

Fig. 7

Panel a: The multiple-tie system with N unit cells. The red square is the n-th unit cell. Panel b: topological phase diagram in $\mu -d$ plane of the model given by the Majorana number $Q_M$. The topological (trivial) phases correspond to the blue (white) regions. The parameters have been fixed as: $L=121$, $\varDelta =0.02$, $t=1$

In this section, we consider a multiple-tie system which is the simplest model to recover translational invariance while still having geometric frustration in the single unit cell. Beyond the theoretical interest, such a model can describe the multiple loops geometry sometimes observed in carbon nanotubes [27, 40]. Thus, we define a multiple-tie system with N unit cells each of which having a tie of fixed size L (see Fig. 7 panel (a)). In the thermodynamic limit $N \rightarrow \infty$, translational invariance is recovered. The physical properties of the translational-invariant system can be studied in momentum representation. To this purpose, we implement periodic boundary conditions $c_{j,N+1}^\dagger =c_{j,1}^\dagger$ and perform the Fourier transform of the fermionic operators:

$$\begin{aligned} c_{j,n}^\dagger =\frac{1}{\sqrt{N}} \sum _k c_{j,k}^\dagger e^{-ikn} \end{aligned}$$

where $k\in [-\pi ,\pi ]$ is the wave vector, j is the intracell site index, while n labels the unit cell with $n=1,\dots , N$. The multiple-tie Hamiltonian can be written in the momentum space as:

$$\begin{aligned} H_{MK}(k)=H_{c}(k)+H_{ic}(k), \end{aligned}$$

(20)

where $H_c$ and $H_{ic}$ are given by:

$$\begin{aligned} H_c(k)= & {} \frac{1}{2}\left[ -t\sum _{j=1}^{L-1}\sum _k\left( c_{j,k}^{\dagger } c_{j+1,k}+c_{j,-k}^{\dagger } c_{j+1,-k}+h.c.\right) \right. \nonumber \\&+\varDelta \sum _{j=1}^{L-1}\sum _k\left( c_{j+1,k}^{\dagger } c^{\dagger }_{j,-k}+c_{j+1,-k}^{\dagger } c_{j,k}^{\dagger }+h.c.\right) \nonumber \\&\left. -t_d\sum _k\left( c^\dagger _{\alpha ,k}c_{\beta ,k}+c^\dagger _{\alpha ,-k}c_{\beta ,-k}+h.c.\right) -\mu \sum _{j=1}^L\sum _k\left( c_{j,k}^{\dagger } c_{j,k}+c_{j,-k}^{\dagger } c_{j,-k}\right) \right] \nonumber \\ H_{ic}(k)= & {} \frac{1}{2}\sum _{k} \left[ -t\left( c_{1,k}^{\dagger } c_{L,k}e^{-ik}+c_{1,-k}^{\dagger } c_{L,-k}e^{ik}+h.c.\right) \right. \nonumber \\&\left. +\varDelta \left( c_{1,k}^{\dagger } c^{\dagger }_{L,-k} e^{-ik}+c_{1,-k}^{\dagger } c_{L,k}^{\dagger } e^{ik}+h.c.\right) \right] . \end{aligned}$$

(21)

Due to the translational invariance, one can compute the topological bulk invariant corresponding to the Majorana number introduced by Kitaev [7]. Let us first introduce the Majorana operators in k-space: $a_{j,k}=c_{j,k}+c_{j,-k}^\dagger ,\ \ b_{j,k}=(c_{j,k}-c_{j,-k}^\dagger )/i$ in terms of which the Hamiltonian becomes:

$$\begin{aligned} H_{MK}=\frac{i}{2}\varPsi ^\dagger _M\left[ \mathcal {H}+(\tau _1 e^{ik}+\tau _2 e^{-ik}+h.c.)\right] \varPsi _M \end{aligned}$$

where $\varPsi _M=(a_{1,-k},b_{1,-k},\dots ,a_{L,-k},b_{L,-k})^T$ and $a^\dagger _{j,k}=a_{j,-k}$, $b^\dagger _{j,k}=b_{j,-k}$. In the new basis, $\mathcal {H}$, $\tau _1$ and $\tau _2$ are $2L \times 2L$ matrices whose structure is defined by Eq. (21). The Majorana number, is defined as:

$$\begin{aligned} Q_M=\mathrm {Sign}\left[ \mathrm {Pf} M(0) \right] \mathrm {Sign}\left[ \mathrm {Pf} M(\pi ) \right] , \end{aligned}$$

(22)

where $\mathrm {Pf}M(0)$ or $\mathrm {Pf}M(\pi )$ represent the Pfaffians of the Hamiltonian $M(k)=\mathcal {H}+(\tau _1 e^{ik}+\tau _2 e^{-ik}+h.c.)$ evaluated at the points $k=0$ or $k=\pi$ in the momentum space. The computation proceeds as follows. We first reduce the Hamiltonian to the canonical form $M'=U M U^T$ by means of an orthogonal $2L \times 2L$ matrix U whose rows are the eigenvectors of M. After the transformation, the Hamiltonian takes the form:

$$\begin{aligned} M'=\begin{pmatrix} 0&{}\lambda _1&{}&{}&{}\\ -\lambda _1&{}0\\ &{}&{}&{}.\\ &{}&{}&{}&{}.\\ &{}&{}&{}&{}&{}.\\ &{}&{}&{}&{}&{}&{}0&{}\lambda _{2L}\\ &{}&{}&{}&{}&{}&{}-\lambda _{2L}&{}0\\ \end{pmatrix}, \end{aligned}$$

(23)

whose Pfaffian $\mathrm {Pf} M'=\lambda _1 \dots \lambda _{2L}$ can be easily calculated. Then, using the Pfaffian property $\mathrm {Pf}(UMU^T)=\mathrm {det}[U]\mathrm {Pf}(M)$, the Majorana number can be recast in the form:

$$\begin{aligned} Q_M=\mathrm {Sign}\left[ \frac{\mathrm {Pf} M'(0)}{\mathrm {det}(U)} \right] \mathrm {Sign}\left[ \frac{\mathrm {Pf} M'(\pi )}{\mathrm {det}(U)} \right] , \end{aligned}$$

(24)

which is evaluated numerically.

Panel (b) of Fig. 7 shows the phase diagram in $d-\mu$ plane of a multiple-tie system when the single unit cell has size $L=121$. The topological phases correspond to $Q_M=-1$ (blue regions) while the trivial phases correspond to $Q_M=1$ (white regions). We note that the trivial/non-trivial phases sequence is still present for values of the chemical potential close to the value $\mu =2t$ where the topological phase transition is expected for a Kitaev chain. The presence of trivial phases close before $\mu =2t$ is essentially due to the frustration of the single unit cell. Bulk-edge correspondence is explicitly proven for a system of reduced size in Appendix C.

6 Conclusions

We have presented an analysis of the topological phase diagram of a Kitaev chain affected by geometric frustration caused by the presence of a long-range hopping (Kitaev tie). Due to the breaking of the translational invariance, we have based our analysis on a real space method which exploits a generalization of the transfer matrix approach. Using the transfer matrix, we have studied the emergence of localized Majorana modes at the system’s legs. We have found that the geometric frustration gives rise to an interstitial-like behavior of the topological phase diagram in which non-trivial phases nucleate inside trivial ones at varying the chemical potential and the range of the extra hopping. We have demonstrated that non-trivial phases become dominant when the perturbed Kitaev chain limit (i.e., large values of parameter d) is considered. The same interstitial-like character of the topological phase diagram emerges when the gap closing and the Majorana polarization methods are considered. The disorder effects on the topological regions have also been investigated and the results show that localized edge modes are robust against hopping and pairing random realizations. Finally, we have analyzed a multiple-tie system in which translational invariance coexists with frustration effects. We have shown that the geometric frustration is reduced but still present for chemical potential values close to the critical value of the unperturbed Kitaev chain. Moreover, the bulk-edge correspondence of the multiple-tie system has been proven.

The aforementioned findings suggest that topological frustration could be a relevant ingredient to design proof-of-principle nanodevices. Using these systems, Hamiltonian models with long-range couplings could be studied in a condensed matter context. In this respect, flexible nanowires, such as, e.g., carbon nanotubes, are the main testbed to prove the topological frustration physics described in this work.

Appendices

Appendix A: Comparison between transfer matrix, Majorana polarization and spectral analysis.

We compare the transfer matrix method, the Majorana polarization and the spectral analysis in defining the phase diagram of a Kitaev tie of $L=121$ sites. Selected values of the long-range hopping positions (namely, $d=10$, 30, 50) are considered, while the remaining parameters have been fixed as done in Fig. 3. In Fig. 8, we compare the behavior of the complement of the Majorana polarization ($1-|P_M|$), the first element of the transfer matrix and the lowest energy eigenvalue. The presence of unpaired Majorana modes is related to small or vanishing values of the mentioned estimators. All plots clearly show the topological frustration phenomenon which is signaled by an oscillating behavior of the estimators as a function of the chemical potential $\mu$. Interestingly, the agreement between distinct methods is improved when high values of d are considered. Good agreement is obtained when the perturbed-chain limit is reached (see panel (c)).

Fig. 8

Comparison among the complement of the Majorana polarization (red curve), the first element of the transfer matrix (green curve) and lowest energy eigenvalue (blue curve) as a function of the chemical potential $\mu$. Kitaev tie models with $d=10$ (panel (a)), $d=30$ (panel (b)) and $d=50$ (panel (c)) are considered. The remaining parameters have been fixed as done in Fig. 3

Appendix B: Effect of the hopping strength

In the main text, we have shown the effect of geometric frustration by varying the range of the extra hopping. Here we investigate the effect of changing the amplitude of long-range hopping by setting $t_d\ne t$. This analysis is performed in Fig. 9. Since the transfer matrix and MP methods provide compatible results, we restrict our analysis to the Majorana polarization. Panel (a) of Fig. 9 shows that for $t_d/t=0.5$ the extent of non-trivial phases is increased compared to the homogeneous case ($t_d=t=1$) reported in Fig. 3 (panel (b)). In particular, panel (b) of Fig. 9 shows the Majorana polarization as a function of chemical potential for $t_d=1$ and $t_d=0.5$ when $d=3$. When the strength of the extra hopping is fixed to $t_d=0.5$, the Majorana polarization manifests a tendency to increase as long as $\mu <1.6$, while an opposite tendency is detected for $\mu >1.6$.

Fig. 9

a Topological phase diagram in the $\mu -d$ plane for $t/t_d=0.5$. b Majorana polarization as a function of chemical potential $\mu$ for $t_d=1$ (green curve) and $t_d=0.5$ (orange curve). The other parameters are: $t=1$, $\varDelta =0.02$, $d=3$, $L=121$

Appendix C: Bulk-edge correspondence for a multiple-tie system

In this Appendix, we show bulk-edge correspondence for a multiple-tie system made of 30 unit cells. In particular, in Fig. 10a, we show the phase diagram of the translational-invariant multiple-tie system having 20 sites per unit-cell. The phase diagram has been obtained by exploiting the band topological invariant. It shows a checkerboard pattern which is reminiscent of the topological frustration of the single unit cell. Panel (b) of Fig. 10 shows the lowest energy eigenvalues corresponding to the red horizontal cut of panel (a). The correspondence between trivial and non-trivial phases is clearly visible in Fig. 10b. In order to get further insight, in panels (c)–(f), we show the localization properties of the wavefunction for a trivial/topological phase sequence moving the chemical potential along the red line of Fig. 10a. This analysis directly shows that localized states correspond to the gapless points in Fig. 10b, while trivial states correspond to the gapped ones. The above results explicitly prove the bulk-edge correspondence for a multiple-tie system.

Fig. 10

a Topological phase diagram of a multiple-tie system of 30 unit cells and 20 sites per unit cell obtained by the Majorana number Q. The topological (trivial) phases correspond to the blue (white) regions. b Energy eigenvalues of the system as a function of chemical potential $\mu$ corresponding to the horizontal red cut of panel (a). The other parameters have been fixed as: $\varDelta =0.02$, $t=1$. c–f Amplitude of the lowest energy modes of the multiple-tie system with $N=30$ unit cells and with $L=20$ sites per unit cell, as a function of the lattice index j. Different panels refer to distinct values of the chemical potential $\mu$ belonging to the red line of panel (a)