Shape-driven optofluidic rotational actuation

Abstract

In the present work, we report light-induced rotation of millimeter-sized objects driven by their non-symmetric shape. The light-induced torque is originated by the thermal gradient on different sides of the teeth of star-shaped objects floating on liquid surfaces that leads to unbalanced surface tension due to the Marangoni effect. The dependence of the angular rotation on the number of teeth is demonstrated. The angular velocity is linearly dependent on the light intensity and follows a simple time behavior typical of objects moving under fluid friction.

Graphic abstract

1 Introduction

The interest in transforming light energy into mechanical work is increased in the last two decades leading to broad and deep investigations mainly focused on optical manipulation of small particles, cells and even atoms [1,2,3,4] with the aim of studying physical processes occurring at microscopic scale. Based on these investigations, a wide range of microdevices have also being developed for a variety of applications mainly concerned with biotechnology [2, 3]. On the other hand, a significant but limited number of reports can be found on optical manipulation of objects at macroscale (see for instance ref(s). [4,5,6,7]), due to the difficulty of finding the conditions where light-induced forces are strong enough to produce a mechanical work overcoming the friction dissipation. Nevertheless light-induced actuation of millimeter–centimeter-sized objects may have several potential applications such as, for instance, in remote control of mini-robots or mini-devices operating in fluid environment. In this case, one possible approach to make effective the transformation of light energy into mechanical work is the exploitation of the Marangoni effect [8, 9]: It consists of the onset of unbalanced forced at solid–fluid interface due to a gradient of the surface tension caused by differences in composition or temperature. As a matter of fact, using light it is possible to create a temperature gradient on macroscopic objects exploiting either asymmetric light absorption of the illuminated system or asymmetric thermal distribution of the adsorbed energy due to the asymmetric shape of the object.

In a previous work, we have exploited asymmetric illumination on or around a centimeter-sized object [10, 11] to make it escaping from the irradiated area with a translational motion, while in a more recent paper we have demonstrated that a non-symmetric illumination is able to induce a mechanical torque on millimeter-sized objects characterized by a symmetric star shape, leading them to rotate [12].

We demonstrate here that the same result can be obtained by uniform illumination of asymmetric star-shaped objects. The investigation of the light-induced rotation has been carried out reporting how rotation is affected by the different shapes of the object and by light intensity.

The basic concept is the following. Considering a black object floating on a non-absorbing liquid, it can be uniformly heated by a Gaussian laser beam having any wavelength in the visible spectrum and a spot size approximately overlapping the whole object. The absorbed heat is partially transferred to the solid–water interface and, due to the asymmetric shape of the object, a non-uniform temperature field is obtained connected to a non-uniform decrease of the surface tension along the object contour. This unbalance of the forces applied on the liquid–solid interfaces produces a nonzero torque (capillary torque) that gives rise to a rotational motion [13]. All the reported data confirm that thermal gradient induced by light absorption is the origin of the process that makes the Marangoni effect coming into action.

2 Experimental results

We have already pointed out that in a uniformly absorbing (black painted) symmetric star the capillary torque is always zero [12]. On the other hand, in Ref. [13] the authors point out that at a microscopic scale the torque is different from zero in case of non-symmetric shape. We take advantage of this result and apply it to non-symmetric stars on a macroscopic scale. A six-tooth asymmetric star is sketched in Fig. 1a, and all the analyzed shapes are also shown in Fig. 1b.

Fig. 1

a Sketch of a non-symmetric six-tooth star. b Shape of the five asymmetrical stars used in our experiments

Using this figure, we can derive the analytical expression of the nonzero torque acting on the star following the same arguments reported in Ref. [13]. In doing this calculation, we assume that a liquid–air–solid contact line forms along the saw-toothed contour of any star. In the absence of heating, the temperature is uniform, and each element of the contact line experiences the same force per unit length resulting in a zero net force and torque. In the presence of heating induced by light absorption, a non-uniform temperature field develops with temperature decreasing from the center of the star with radial symmetry as simulated in Fig. 2. This thermal gradient gives rise to a surface tension gradient along the star contour. Looking at Fig. 1a, for uniform illumination we can assume that points A and D have the same temperature $(T_{A} = T_{D} )$ being at the same distance from the star center O, different from the temperature in B, $T_{B}$. Therefore, along the lines AB and DB there is a gradient of surface tension. Considering that the length $AB \ne DB$, this results in unbalanced forces causing a nonzero total torque $\vec{\tau }$. In order to calculate the temperature distribution and the consequent torque we used COMSOL heat transfer module. The heat source is assumed to be at the star top surface.

Fig. 2

Temperature distribution after 30 s of irradiation. Due to the asymmetric shape of the star, a nonzero total torque is generated (Eq. (1). The arrow indicates the direction of rotation

The mechanical torque exerted by the capillary forces during irradiation is given by [13]:

$$ \vec{\tau }_{L} = \int \vec{r} \wedge {\text{d}}\vec{F} = \int \vec{r} \wedge \hat{n}\gamma \left( T \right){\text{d}}s, $$

(1)

where $\vec{r}$ is the position vector with the origin in the center of the star, $ds$ a generic contact line element and $\gamma \left( T \right)$ the surface tension of the liquid–air interface at the local temperature $T$ in $\vec{r}$. We can separate the total torque into two contributes $\vec{\tau }_{AB}$ and $\vec{\tau }_{DB}$ coming from each single tooth contour and rewrite the mechanical torque for a star with N teeth as:

$$ \vec{\tau }_{L} = N\left( {\vec{\tau }_{AB} + \vec{\tau }_{DB} } \right). $$

(2)

As an example, by assuming that the temperature variations along the liquid–air–solid contact line are smooth enough to be well approximated by linear profiles, for a six-tooth star such as the one sketched in Fig. 1a the expression for the light-induced torque becomes:

$$ \vec{\tau }_{L} = \hat{z}\Delta \gamma ab\left( {1 - \cos \pi /3} \right), $$

(3)

where $\hat{z}$ is the unit vector pointing out of the plane of Fig. 1, $\Delta \gamma = \gamma \left( {T_{B} } \right) - \gamma \left( {T_{A} } \right)$ is the surface tension difference between the outer (B) and inner (A and D) vertices (see Fig. 1a), T_B and T_A are the corresponding temperatures, and $a$ and $b$ are two sides of the triangle forming each tooth as highlighted in Fig. 1a. The typical linear dimensions in the stars are $a\sim 10\,{\text{mm}}, b\sim 3\,{\text{mm}}$. Stars thickness is d = 100 μm. Five asymmetric stars, with a number of teeth ranging from 3 to 7, were used in order to investigate how different geometries affect the stars motion. The used shapes are shown in Fig. 1b. The number of teeth was increased from three to seven keeping one side of each single tooth oriented toward the stars center and the other touching a virtual circle centered in the stars center. To avoid linear displacements, the floating stars are drilled in the center and forced to rotate around a metallic vertical pin. Stars are made by Mylar and black painted in a second time.

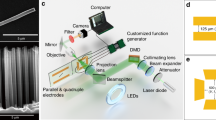
In this way, the angle $\widehat{{{\text{BOA}}}}$ ranges from 120 to ~ 51 degrees, whereas the angle $\widehat{{{\text{BDO}}}}$ is always equal to zero. The experimental setup is reported in Fig. 3. A CW argon laser, with a Gaussian profile and an expanded beam waist of 6 mm, operating at λ = 514 nm was used to irradiate the star floating on the surface of a fluid contained in a vessel, and the light-induced star motion was recorded by a digital camera. The depth of the liquid was 0.8 cm, and the diameter of the vessel was 7 cm. In order to reduce the surface tension and make the effect easily observable with the available laser powers, we used a 60/40 in weight mixture of water and ethanol [14]. In Fig. 4, the number of revolutions (1 revolution = 2π rad) versus time is shown for our five stars set. Each star begins its rotation by slowly increasing its angular velocity until a maximum stationary value is reached. For a constant value of impinging power (P = 70 mW), the angular velocity clearly depends on the number of teeth being higher for the stars having the higher number.

Fig. 3

Experimental setup used in our experiments

Fig. 4

Revolutions as function of time for our stars set at the fixed irradiation power of 70mW

We also investigated the dependence of the angular velocity on the impinging power by using the faster rotating seven-tooth star. For each value of the incident power, we digitally tracked the star rotations as a function of time and derived the rotational speed by a linear regression of the asymptotic region. The results are reported in Fig. 5. As can be seen, the rotational speed increases linearly with increasing the incident power. In our experiments, the maximum observed speed was ω = 0.55 rad/s for an incident power of 0.14 W.

Fig. 5

Angular velocity versus the incident power P for a seven-tooth star. Measurements correspond to the steady-state maximum value reached at each light power. The continuous line represents the best linear fit

It is also useful to report the angular displacement and the corresponding angular velocity vs time in the same figure as shown in Fig. 6 for the seven-tooth star. Figures 4, 5 and 6 clearly show the achievement of a steady-state constant value for the angular velocity with a characteristic time shorter and shorter as the teeth number increases.

Fig. 6

Angular displacement vs time (left y axis and filled triangles) and the corresponding angular velocity for a seven-tooth star (right y axis and open triangles). The continuous line represents the data fit made by using Eq. (5). (P = 70 mW and λ = 514 nm)

3 Discussion

All these results can be easily discussed starting from the simple motion equation for a rigid body in the presence of friction:

$$ I\dot{\omega } + \zeta \omega = \tau_{L} , $$

(4)

where I is the moment of inertia of the star, $\zeta$ a dissipative constant and $\tau_{L}$ the torque induced by the impinging light. The well-known solution is given by:

$$ \omega \left( t \right) = \frac{{\tau_{L} }}{\zeta }\left( {1 - e^{{ - \frac{\zeta t}{I}}} } \right). $$

(5)

First of all, we find that the steady-state angular velocity ($t \to \infty )$ is proportional to the driving torque. Since according to Eq. (1) the torque is proportional to the number of teeth, this is in agreement with the experimental data shown in Fig. 4 where the slope of the curve increases for increasing number of teeth. We notice the excellent quantitative fit with Eq. (5) of the experimental data concerning $\omega \left( t \right)$ reported in Fig. 6. This makes possible to get further information. For this purpose, it is necessary to evaluate the moment of inertia of the asymmetric star. By using a common method, the moment of inertia of the star $I$ can be calculated as difference between the moment of inertia of the right angle triangle OBC ($I_{{{\text{OBC}}}}$) minus the one of the right angle triangle ABC ($I_{{{\text{ABC}}}}$), thus giving the effective moment of inertia of the triangle OAB with respect to an orthogonal axis in O. The moment of inertia of the star is then obtained by multiplying by the number of teeth N. By looking at Fig. 1a, we have:

$$ I = N\left( {I_{{{\text{OBC}}}} - I_{{{\text{ABC}}}} } \right) = \frac{N}{12}\sigma dba\cos \left( \alpha \right)\left( {b^{2} + ab\sin \left( \alpha \right) + a^{2} } \right), $$

(6)

with $\sigma$ being the mass density of the star’s material. With the following experimental parameters, $\overline{{{\text{BC}}}}$ = 7.8 mm, $\overline{{{\text{OC}}}} = \overline{{{\text{BC}}}} \tan \left( \alpha \right)$ = 6.2 mm, $\overline{{{\text{AC}}}} = \overline{{{\text{OC}}}} - \overline{{{\text{BC}}}} \tan \left( {\alpha^{\prime}} \right)$ = 3.2 mm, $\sigma = 1.35 \times 10^{3} \,{\text{Kg/m}}^{3}$ (density of Mylar), d = 100 µm and N = 7 (number of teeth), we obtain: $I\sim 4 \times 10^{ - 10} \,{\text{Kg}}/{\text{m}}^{2}$. The experimental data concerning the angular velocity reported in Fig. 6 have been fitted using Eq. (5) with the values $\tau_{L} = 5.0 \times 10^{ - 11} {\text{N}}\,{\text{m}}$ and $\zeta = 2.0 \times 10^{ - 10} \,{\text{N}}\,{\text{m}}\,{\text{s}}$. From the exponential term of Eq. (5), we get the characteristic time needed to reach the steady-state value, and it is given by $\tau = \frac{I}{\zeta }\sim 2 s$. The mirror asymmetry due to the stars design determines the sign of the rotational velocity: As expected, if the stars are reversed upside down, they rotate in the opposite direction. The linear relationship between angular velocity and illumination power reported in Fig. 5, already observed in similar system at a microscopic scale [10], can be roughly explained as follows. For the sake of simplicity, we assume that the star is very thin, and the thermo-diffusion equation can be simplified to a 2D case. This assumption is justified because the star thickness is much less than the star in-plane characteristic dimensions. The heating of the star is due to the absorption of light by its upper (dark) surface and is supposed to be linearly dependent on the light power; then, the corresponding term in the heat transfer equation is given by $\beta I_{{{\text{h }}}\nu}$ where $\beta$ is constant and $I_{{{\text{h}}}\upnu }$ the light intensity. Cooling of the star occurs at the bottom surface, in contact with the fluid. The heat flux at the star bottom surface is proportional to the temperature difference between the star surface and fluid, $\eta \left( {T_{{{\text{ambient}}}} - T} \right)$, where $\eta =$ h/c_pρd being $h$ the convective heat transfer coefficient, $c_{p}$ the specific heat, $\rho$ the mass density and $d$ the star thickness. The equation for the star temperature changes then reads:

$$ \frac{\partial T}{{\partial t}} = \alpha \nabla_{2D}^{2} T + \beta I_{{{\text{h}}}\upnu } + \eta \left( {T_{{{\text{ambient}}}} - T} \right), $$

(7)

$\alpha = k/\left( {c_{p} \rho } \right)$ here is the thermal diffusivity coefficient and $k$ the thermal conductivity. By introducing the variable $\tilde{T} = T - T_{{{\text{ambient}}}}$, we rewrite the equation as

$$ \frac{{\partial \tilde{T}}}{\partial t} - \alpha \nabla_{2D}^{2} \tilde{T} + \eta \tilde{T} = \beta I_{{{\text{h}}}\upnu } . $$

(8)

Now it is clearly seen that $\tilde{T}\left( {r,t} \right)\sim I_{{{\text{h}}}\upnu }$. The surface tension dependence on the temperature for a small temperature change can be approximated as $\gamma \left( T \right) \approx \gamma \left( {T_{{{\text{ambient}}}} } \right) + \frac{d\gamma }{{dT}}\left( {T\left( {r,t} \right) - T_{{{\text{ambient}}}} } \right)$. We speculate that there is a linear dependence between the actual temperature profile along the star’s teeth and the temperature rise estimated from the Eq. (8). This reasonable assumption, confirmed by our numerical simulations (see supplementary information), means that the surface tension change, and therefore the induced torque on the star, is linearly proportional to the light intensity magnitude $I_{{{\text{h}}}\upnu }$. Finally, from Eq. (3) it follows that the rotational velocity is also linearly dependent on the light intensity as reported in Fig. 6. After the end of irradiation, an unexpected behavior is observed: The motion stops for a while and after that restarts anticlockwise for a few seconds. This backflow effect, similar to the one observed for symmetric stars [12], is always present in our investigated shapes; it leads to an oscillating behavior clockwise and anticlockwise by switching ON and OFF the CW irradiation as shown for example in Fig. 7 for a five-tooth star.

Fig. 7

Clockwise and anticlockwise rotations of a five-tooth asymmetric star under alternate (ON/OFF) CW irradiation (P = 70 mW and λ = 514 nm)

The origin of this backflow effect is actually very simple: It comes from surface waves reflected from the vessel walls. This can be proved by putting on the liquid surface many small floating tracking particles: During irradiation, the particles are pushed away from the star, and when the illumination ends, they tend to go back to their starting position. The final effect is the backward star’s rotation. Finally, we would like to underline the thermal origin of the described phenomena by mentioning the following observation: On a white painted star, almost no rotation was detected, demonstrating that heating plays the fundamental role in the observed phenomenon. Visualizations 1 and 2 connected with Fig. 8 show a comparison between a black painted star and a white painted one. The two stars behave in a very different way: The black painted one rotates much faster than the other. Please note s by 3 × due to our video board settings.

Fig. 8

Black (a) and white (b) painted stars respond in a completely different way to the laser irradiation (see visualizations 1 and 2)

4 Conclusions

In conclusion, in this work we have demonstrated the rotation of millimeter-sized objects of asymmetric star shape floating on fluids caused by uniform light absorption. The experimental data are in agreement with a model that takes into account the light-induced change of the surface tension along the star profile (Marangoni effect) and the force unbalance due to the asymmetric shape. The steady-state angular velocity is found to be proportional to the number of teeth of the star and on the driving light intensity.