Skip to main content

Advertisement

SpringerLink
Log in

Anti-plane surface and interfacial waves influenced by layer reinforcement in Piezo-Electro-Magnetic structures with surface energy

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

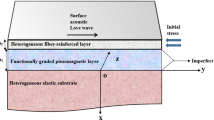
The electro-magnetic coupling parameter which is absent in monolithic piezoelectric materials is a unique property of the composite Piezo-Electro-Magnetic(PEM) materials that enhance the applicability of these composites in magnetic field probes, electric packaging, biotechnological applications, etc. In surgical process of joining bones, the freshly developed bone is softer than the mature bone, and thus the mechanical properties of this soft bone becomes important in the success of the surgery. Hence, these kinds of structures having a soft material reinforced at the surface or interface are the prime motivation of this study. In the present work, the propagation of Anti-plane wave is discussed in two models, namely a PEM half-space with a thin elastic layer reinforced at the free surface - Model\(-1\) and two imperfectly bonded PEM half-spaces with a thin elastic layer reinforced at the interface - Model\(-2\). The presence of imperfectness(mechanical, electrical, and magnetic) at the interface gives rise to the discontinuity of displacement and electric & magnetic potential which result in imperfect signal communications affecting the performance of sensing devices. The Gurtin−Murdoch approach is used to derive the surface strain energy density, surface stress tensor, and surface kinetic energy density accounting for the reinforced elastic layer. Admissible boundary/interface conditions relating to the propagation of Anti-plane wave are defined for Electrically Open-Magnetically Open (EOMO) and Electrically Short-Magnetically Short (ESMS) boundaries/interfaces. Using these conditions, the dispersion relation for the propagating Anti-plane wave in both models and the mechanical-electro-magnetic boundaries/interfaces are derived. The impact of the electro-magnetic coupling parameter, imperfectness parameter, and reinforcement of soft & stiff elastic layer on the dispersion relation of Anti-plane wave is numerically computed and portrayed graphically. The data of two dissimilar PEM composites and surface/interface elastic layer of Iron, Gold, and Aluminum with different crystallographic directions constituting soft and stiff reinforcement are considered for numerical and graphical purposes. The electromechanical efficiency of the models are discussed through electromechanical coupling parameter. Moreover, the Cut-Off frequencies of both the models are portrayed graphically for the three data of soft reinforcement of surface/interface layer.

Graphic Abstract

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. J.L. Bleustein, A new surface wave in piezoelectric materials. Appl. Phys. Lett. 13(12), 412–413 (1968). https://doi.org/10.1063/1.1652495

    Article  ADS  Google Scholar 

  2. Chaki MS, Eremeyev VA, Singh AK (2020) Surface and interfacial anti-plane waves in micropolar solids with surface energy. Mathematics and Mechanics of Solids p 1081286520965646, 10.1177/1081286520965646

  3. M. Dehghan, F. Ebrahimi, On wave dispersion characteristics of magneto-electro-elastic nanotubes considering the shell model based on the nonlocal strain gradient elasticity theory. Europ. Phys. J. Plus 133(11), 466 (2018). https://doi.org/10.1140/epjp/i2018-12304-7

    Article  ADS  Google Scholar 

  4. F. Dell’Isola, A. Madeo, L. Placidi, Linear plane wave propagation and normal transmission and reflection at discontinuity surfaces in second gradient 3d continua. ZAMM-J. Appl. Math. Mech./Zeitschrift für Angewandte Mathematik und Mechanik 92(1), 52–71 (2012). https://doi.org/10.1002/zamm.201100022

    Article  ADS  MathSciNet  MATH  Google Scholar 

  5. Du J, Cheng X, Wang J (2008) Surface acoustic waves propagating in magnetoelectro-elastic material structures. In: 2008 IEEE International Frequency Control Symposium, IEEE, pp 135–138

  6. F. Ebrahimi, A. Dabbagh, M.R. Barati, Wave propagation analysis of a size-dependent magneto-electro-elastic heterogeneous nanoplate. Europ. Phys. J. Plus 131(12), 1–18 (2016). https://doi.org/10.1140/epjp/i2016-16433-7

    Article  Google Scholar 

  7. V.A. Eremeyev, G. Rosi, S. Naili, Surface/interfacial anti-plane waves in solids with surface energy. Mech. Res. Commun. 74, 8–13 (2016). https://doi.org/10.1016/j.mechrescom.2016.02.018

    Article  Google Scholar 

  8. S. Ghahnavieh, S. Hosseini-Hashemi, K. Rajabi, A higher-order nonlocal strain gradient mass sensor based on vibrating heterogeneous magneto-electro-elastic nanoplate via third-order shear deformation theory. Europ. Phys. J. Plus 133(12), 518 (2018). https://doi.org/10.1140/epjp/i2018-12338-9

    Article  ADS  Google Scholar 

  9. S. Guha, A.K. Singh, Effects of initial stresses on reflection phenomenon of plane waves at the free surface of a rotating piezothermoelastic fiber-reinforced composite half-space. Int. J. Mech. Sci. (2020). https://doi.org/10.1016/j.ijmecsci.2020.105766

    Article  Google Scholar 

  10. S. Guha, A. Singh, A. Das, Analysis on different types of imperfect interfaces between two dissimilar piezothermoelastic half-spaces on reflection and refraction phenomenon of plane waves. Waves Random Complex Media (2019). https://doi.org/10.1080/17455030.2019.1610198

    Article  Google Scholar 

  11. X. Guo, P. Wei, L. Li, Q. Tang, Influences of mechanically and dielectrically imperfect interfaces on the reflection and transmission waves between two piezoelectric half spaces. Int. J. Solid Struct. 63, 184–205 (2015). https://doi.org/10.1016/j.ijsolstr.2015.02.050

    Article  Google Scholar 

  12. M.E. Gurtin, A.I. Murdoch, A continuum theory of elastic material surfaces. Arch. Ration. Mech. Anal. 57(4), 291–323 (1975). https://doi.org/10.1007/BF00261375

    Article  MathSciNet  MATH  Google Scholar 

  13. L.L. Ke, Y.S. Wang, J. Yang, S. Kitipornchai, The size-dependent vibration of embedded magneto-electro-elastic cylindrical nanoshells. Smart Mater. Struct. 23(12), 125036 (2014). https://doi.org/10.1088/0964-1726/23/12/125036

    Article  Google Scholar 

  14. J.Y. Li, M.L. Dunn, Micromechanics of magnetoelectroelastic composite materials: average fields and effective behavior. J. Intell. Mater. Syst. Struct. 9(6), 404–416 (1998). https://doi.org/10.1177/1045389X9800900602

    Article  Google Scholar 

  15. Y. Li, P. Wei, Q. Tang, Reflection and transmission of elastic waves at the interface between two gradient-elastic solids with surface energy. Europ. J. Mech./Solids 52, 54–71 (2015). https://doi.org/10.1016/j.euromechsol.2015.02.001

    Article  ADS  MathSciNet  MATH  Google Scholar 

  16. G.S. Murty, A theoretical model for the attenuation and dispersion of stoneley waves at the loosely bonded interface of elastic half spaces. Phys. Earth Planet. Inter. 11(1), 65–79 (1975)

    Article  ADS  MathSciNet  Google Scholar 

  17. C.W. Nan, Magnetoelectric effect in composites of piezoelectric and piezomagnetic phases. Phys. Rev. B 50(9), 6082 (1994). https://doi.org/10.1103/PhysRevB.50.6082

    Article  ADS  Google Scholar 

  18. R. Ogden, D. Steigmann, Plane strain dynamics of elastic solids with intrinsic boundary elasticity, with application to surface wave propagation. J. Mech. Phys. Solid 50(9), 1869–1896 (2002). https://doi.org/10.1016/S0022-5096(02)00006-6

    Article  ADS  MathSciNet  MATH  Google Scholar 

  19. C. Othmani, H. Zhang, C. Lü, F. Takali, Effects of initial stresses on the electromechanical coupling coefficient of sh wave propagation in multilayered pzt-5h structures. Europ. Phys. J. Plus 134(11), 551 (2019). https://doi.org/10.1140/epjp/i2019-12891-7

    Article  ADS  Google Scholar 

  20. L. Placidi, G. Rosi, I. Giorgio, A. Madeo, Reflection and transmission of plane waves at surfaces carrying material properties and embedded in second-gradient materials. Math. Mech. Solid 19(5), 555–578 (2014). https://doi.org/10.1177/1081286512474016

    Article  MathSciNet  MATH  Google Scholar 

  21. A. Singh, S. Singh, R. Kumari, A. Ray, Impact of point source and mass loading sensitivity on the propagation of an sh wave in an imperfectly bonded fgppm layered structure. Acta Mechanica 231(6), 2603–2627 (2020a). https://doi.org/10.1007/s00707-020-02659-x

    Article  MathSciNet  MATH  Google Scholar 

  22. A.K. Singh, S. Guha, Reflection of plane waves from the surface of a piezothermoelastic fiber-reinforced composite half-space. Mech. Adv. Mater. Struct. (2020). https://doi.org/10.1080/15376494.2020.1736697

    Article  Google Scholar 

  23. A.K. Singh, R. Kumari, G. Dharmender, Green’s function analysis of mass loading sensitivity on the shear wave propagation induced by a point source in piezo-electro-magnetic structure. Mech. Based Design Struct. Mach. (2020b). https://doi.org/10.1080/15397734.2020.1809455

    Article  Google Scholar 

  24. A.K. Singh, P. Rajput, M.S. Chaki, Analytical study of love wave propagation in functionally graded piezo-poroelastic media with electroded boundary and abruptly thickened imperfect interface. Waves Random Complex Media (2020c). https://doi.org/10.1080/17455030.2020.1779387

    Article  Google Scholar 

  25. T.L. Wu, J.H. Huang, Closed-form solutions for the magnetoelectric coupling coefficients in fibrous composites with piezoelectric and piezomagnetic phases. Int. J. Solid. Struct. 37(21), 2981–3009 (2000). https://doi.org/10.1016/S0020-7683(99)00116-X

    Article  MATH  Google Scholar 

  26. L. Xu, X. Wang, H. Fan, Anti-plane waves near an interface between two piezoelectric half-spaces. Mech. Res. Commn. 67, 8–12 (2015). https://doi.org/10.1016/j.mechrescom.2015.04.006

    Article  Google Scholar 

Download references

Acknowledgements

The authors gratefully acknowledge the support Indian Institute of Technology (Indian School of Mines) Dhanbad, India, for providing Senior Research Fellowship to Ms. Sonam Singh, along with the best facilities for carrying out this research work.

Author information

Authors and Affiliations

  1. Indian institute of Technology (Indian School of Mines), Dhanbad, India

    Sonam Singh & A. K. Singh

Authors
  1. Sonam Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. K. Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. K. Singh.

Ethics declarations

Funding

The authors gratefully acknowledge the support of Council of Scientific & Industrial Research (CSIR)[Grant No.25(0265)/17/ EMR-II] for providing the necessary equipment to carry out this research work.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Availability of data and material

The data regarding the material have been taken from the works of Ke et al. [13], Du et al. [5] Eremeyev et al. [7] and Xu et al. [26].

Code availability

Not Applicable

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Singh, S., Singh, A.K. Anti-plane surface and interfacial waves influenced by layer reinforcement in Piezo-Electro-Magnetic structures with surface energy. Eur. Phys. J. Plus 136, 312 (2021). https://doi.org/10.1140/epjp/s13360-021-01288-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-021-01288-0

Search

Navigation