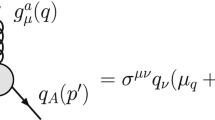Abstract
A new estimate of the one loop contributions of the standard model to the chromomagnetic dipole moment (CMDM) \(\hat{\mu }_q(q^2)\) of quarks is presented with the aim to address a few disagreements arising in previous calculations. The most general case with arbitrary \(q^2\) is considered and analytical results are obtained in terms of Feynman parameter integrals and Passarino-Veltman scalar functions, which are then expressed in terms of closed form functions when possible. It is found that while the QCD contribution to the static CMDM (\(q^2=0\)) is infrared divergent, which agrees with previous evaluations and stems from the fact that this quantity has no sense in perturbative QCD, the off-shell CMDM (\(q^2\ne 0\)) is finite and gauge independent, which is verified by performing the calculation for arbitrary gauge parameter \(\xi \) via both a renormalizable linear \(R_\xi \) gauge and the background field method. It is thus argued that the off-shell \(\hat{\mu }_q(q^2)\) can represent a valid observable quantity. For the numerical analysis we consider the region 30 GeV\(<\Vert q\Vert<\) 1000 GeV and analyze the behavior of \(\hat{\mu }_q(q^2)\) for all the standard model quarks. It is found that the CMDM of light quarks is considerably smaller than that of the top quark as it is directly proportional to the quark mass. In the considered energy interval, both the real and imaginary parts of \(\hat{\mu }_t(q^2)\) are of the order of \(10^{-2}-10^{-3}\), with the largest contribution arising from the QCD induced diagrams, though around the threshold \(q^2=4m_t^2\) there are also important contributions from diagrams with Z gauge boson and Higgs boson exchange.








Similar content being viewed by others
Data Availability Statement
This manuscript has associated data in a data repository. [Authors’ comment: All data included in this manuscript are available upon request by contacting with the corresponding author.]
Notes
From now on, all the corresponding loop functions appearing in the contributions to \(a_q\left( q^2\right) \), denoted by calligraphy letters, will be presented in terms of Feynman parameter integrals, Passarino-Veltman scalar functions and closed form results in Appendices A.1, A.2, and A.3, respectively, including the results for \(q^2=0\).
References
S. Laporta, E. Remiddi, Phys. Lett. B 379, 283 (1996). https://doi.org/10.1016/0370-2693(96)00439-X
S.R. Moore, K. Whisnant, B.L. Young, Phys. Rev. D 31, 105 (1985). https://doi.org/10.1103/PhysRevD.31.105
F. Jegerlehner, Acta Phys. Polon. B 49, 1157 (2018). https://doi.org/10.5506/APhysPolB.49.1157
A. Czarnecki, M. Skrzypek, Phys. Lett. B 449, 354 (1999). https://doi.org/10.1016/S0370-2693(99)00076-3
M. Lindner, M. Platscher, F.S. Queiroz, Phys. Rep. 731, 1 (2018). https://doi.org/10.1016/j.physrep.2017.12.001
M. Pospelov, A. Ritz, Ann. Phys. 318, 119 (2005). https://doi.org/10.1016/j.aop.2005.04.002
A. Czarnecki, W.J. Marciano, Adv. Ser. Direct. High Energy Phys. 20, 11 (2009). https://doi.org/10.1142/9789814271844_0002
A. Moyotl, A. Rosado, G. Tavares-Velasco, Phys. Rev. D 84, 073010 (2011). https://doi.org/10.1103/PhysRevD.84.073010
H. Novales-Sánchez, M. Salinas, J.J. Toscano, O. Vázquez-Hernández, Phys. Rev. D 95(5), 055016 (2017). https://doi.org/10.1103/PhysRevD.95.055016
C.F. Chang, P.Q. Hung, C.S. Nugroho, V.Q. Tran, T.C. Yuan, Nucl. Phys. B 928, 21 (2018). https://doi.org/10.1016/j.nuclphysb.2018.01.007
V. Keus, N. Koivunen, K. Tuominen, JHEP 09, 059 (2018). https://doi.org/10.1007/JHEP09(2018)059
H. Gisbert, J. Ruiz Vidal, Phys. Rev. D 101(11), 115010 (2020). https://doi.org/10.1103/PhysRevD.101.115010
A.I. Hernández-Juárez, A. Moyotl, G. Tavares-Velasco, Phys. Rev. D 98(3), 035040 (2018). https://doi.org/10.1103/PhysRevD.98.035040
R. Martinez, M.A. Perez, N. Poveda, Eur. Phys. J. C 53, 221 (2008). https://doi.org/10.1140/epjc/s10052-007-0457-6
R. Gaitan, E.A. Garces, J.H.M. de Oca, R. Martinez, Phys. Rev. D 92(9), 094025 (2015). https://doi.org/10.1103/PhysRevD.92.094025
J.I. Aranda, D. Espinosa-Gómez, J. Montaño, B. Quezadas-Vivian, F. Ramírez-Zavaleta, E.S. Tututi, Phys. Rev. D 98(11), 116003 (2018). https://doi.org/10.1103/PhysRevD.98.116003
Q.H. Cao, C.R. Chen, F. Larios, C.P. Yuan, Phys. Rev. D 79, 015004 (2009). https://doi.org/10.1103/PhysRevD.79.015004
L. Ding, C.X. Yue, Commun. Theor. Phys. 50, 441 (2008). https://doi.org/10.1088/0253-6102/50/2/32
A. Aboubrahim, T. Ibrahim, P. Nath, A. Zorik, Phys. Rev. D 92(3), 035013 (2015). https://doi.org/10.1103/PhysRevD.92.035013
R. Martinez, M.A. Perez, O.A. Sampayo, Int. J. Mod. Phys. A 25, 1061 (2010). https://doi.org/10.1142/S0217751X10048159
T. Ibrahim, P. Nath, Phys. Rev. D 84, 015003 (2011). https://doi.org/10.1103/PhysRevD.84.015003
V. Khachatryan et al., Phys. Rev. D 93(5), 052007 (2016). https://doi.org/10.1103/PhysRevD.93.052007
A.M. Sirunyan et al., Phys. Rev. D 100(7), 072002 (2019). https://doi.org/10.1103/PhysRevD.100.072002
A. Czarnecki, B. Krause, Phys. Rev. Lett. 78, 4339 (1997). https://doi.org/10.1103/PhysRevLett.78.4339
I.B. Khriplovich, Phys. Lett. B 173, 193 (1986). https://doi.org/10.1016/0370-2693(86)90245-5
I.B. Khriplovich, Yad. Fiz. 44, 1019 (1986)
E.P. Shabalin, Sov. J. Nucl. Phys. 28, 75 (1978)
E.P. Shabalin, Yad. Fiz. 28, 151 (1978)
I.D. Choudhury, A. Lahiri, Mod. Phys. Lett. A 30(23), 1550113 (2015). https://doi.org/10.1142/S0217732315501138
A.M. Sirunyan et al., Eur. Phys. J. C 79(11), 886 (2019). https://doi.org/10.1140/epjc/s10052-019-7387-y
A.I. Davydychev, P. Osland, L. Saks, Phys. Rev. D 63, 014022 (2001). https://doi.org/10.1103/PhysRevD.63.014022
J.M. Cornwall, Phys. Rev. D 26, 1453 (1982). https://doi.org/10.1103/PhysRevD.26.1453
J.M. Cornwall, J. Papavassiliou, Phys. Rev. D 40, 3474 (1989). https://doi.org/10.1103/PhysRevD.40.3474
D. Binosi, J. Papavassiliou, Phys. Rep. 479, 1 (2009). https://doi.org/10.1016/j.physrep.2009.05.001
A. Denner, G. Weiglein, S. Dittmaier, Nucl. Phys. B 440, 95 (1995). https://doi.org/10.1016/0550-3213(95)00037-S
A. Pilaftsis, Nucl. Phys. B 487, 467 (1997). https://doi.org/10.1016/S0550-3213(96)00686-4
V. Shtabovenko, R. Mertig, F. Orellana, Comput. Phys. Commun. 207, 432 (2016). https://doi.org/10.1016/j.cpc.2016.06.008
H.H. Patel, Comput. Phys. Commun. 197, 276 (2015). https://doi.org/10.1016/j.cpc.2015.08.017
W. Hollik, J.I. Illana, S. Rigolin, C. Schappacher, D. Stockinger, Nucl. Phys. B 551, 3 (1999). https://doi.org/10.1016/S0550-3213(99)00396-X ([Erratum: Nucl. Phys. B 557, 407-409 (1999)])
Z. Hioki, K. Ohkuma, Eur. Phys. J. C 65, 127 (2010). https://doi.org/10.1140/epjc/s10052-009-1204-y
J.F. Kamenik, M. Papucci, A. Weiler, Phys. Rev. D 85, 071501 (2012). https://doi.org/10.1103/PhysRevD.85.071501 ([Erratum: Phys. Rev. D 88, 039903 (2013)])
W. Bernreuther, Z.G. Si, Phys. Lett. B 725, 115 (2013). https://doi.org/10.1016/j.physletb.2013.06.051 ([Erratum: Phys. Lett. B 744, 413-413 (2015)])
Km. Cheung, Phys. Rev. D 53, 3604 (1996). https://doi.org/10.1103/PhysRevD.53.3604
P. Haberl, O. Nachtmann, A. Wilch, Phys. Rev. D 53, 4875 (1996). https://doi.org/10.1103/PhysRevD.53.4875
S. Larin, J. Vermaseren, Phys. Lett. B 303, 334 (1993). https://doi.org/10.1016/0370-2693(93)91441-O
G. Prosperi, M. Raciti, C. Simolo, Prog. Part. Nucl. Phys. 58, 387 (2007). https://doi.org/10.1016/j.ppnp.2006.09.001
M. Tanabashi et al., Phys. Rev. D 98(3), 030001 (2018). https://doi.org/10.1103/PhysRevD.98.030001
T. Hahn, M. Perez-Victoria, Comput. Phys. Commun. 118, 153 (1999). https://doi.org/10.1016/S0010-4655(98)00173-8
A. Denner, S. Dittmaier, L. Hofer, Comput. Phys. Commun. 212, 220 (2017). https://doi.org/10.1016/j.cpc.2016.10.013
J. Aranda, T. Cisneros-Pérez, J. Montaño, B. Quezadas-Vivian, F. Ramírez-Zavaleta, E. Tututi, e-print arxiv: 2009.05195 [hep-ph] (2020)
Acknowledgements
We acknowledge support from Consejo Nacional de Ciencia y Tecnología and Sistema Nacional de Investigadores. Partial support from Vicerrectoría de Investigación y Estudios de Posgrado de la Benémerita Universidad Autónoma de Puebla is also acknowledged.
Author information
Authors and Affiliations
Corresponding author
Analytic results for the loop functions
Analytic results for the loop functions
We now present the results for the loop functions appearing in the contributions to the CMDM of quarks discussed in Sect. 2 in term of Feynman parameter integrals, Passarino-Veltman scalar functions, and closed form functions. For sake of completeness we also include the results for \(q^2=0\).
1.1 Feynman parameter integrals
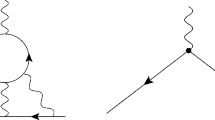
We note that this calculation was done via the unitary gauge as the result are gauge independent, which was explicitly verified via the Passarino-Veltman reduction scheme. Therefore, in the EW sector we only computed by this method the Feynman diagrams (a) through (c) of Fig. 3.
We introduce the definition \(r_{a,b}=m_a/m_b\) and present the loop functions for the QCD contributions to the CMDM of quarks. Feynman diagram 2(a) yields the loop function [Eq. (9)]:
whereas Feynman diagram 2(b) gives [Eq. (14)]:
which for \(q^2=0\) reduces to
As far as the EW contributions to the CMDM of quarks are concerned, the Feynman diagram with photon exchange of Fig. 3a gives [Eq. (17)]:
whereas the Z boson exchange diagram gives [Eq. (23)]
and
where \(\varDelta _Z=m_q^2 (u-1)^2+m_Z^2 u+q^2 v(u+v-1)\) and \(\mu \) is the scale of dimensional regularization, which cancels out after integration.
For \(q^2=0\), the last two loop functions give:
and
As for the W boson exchange contribution of diagram 3(b), it is given by [Eq. (28)]:
with the following result for \(q^2=0\):
where \(\varDelta _W= u \left( m_{q}^2 (u-1)+m_W^2\right) -m_{q^\prime }^2 (u-1)+q^2 v(u+v-1)\). Again this calculation was done via the unitary gauge.
Finally, for the Higgs contribution [Eq. (30)] we obtain:
which for \(q^2=0\) reduces to
1.2 Passarino-Veltman results
We now present the above results in terms of Passarino-Veltman scalar integrals, where we use the standard notation for the two- and three-point scalar functions. Our calculation was done via a renormalizable linear \(R_\xi \) gauge and the BFM to verify that the dependence on the \(\xi \) gauge parameter drops out. The loop functions are thus gauge independent and read
where we define \(\eta (x,y)=\sqrt{x^2-4y^2}\). Also
and
1.3 Closed form results
We also present the explicit solutions for the two-point scalar functions in terms of closed form functions. Below \(C_0\left( m_i^2,m_j^2,q^2;m_k,m_l,m_n\right) \) stands for a three-point Passarino-Veltman scalar function.
and
Rights and permissions
About this article
Cite this article
Hernández-Juárez, A.I., Moyotl, A. & Tavares-Velasco, G. New estimate of the chromomagnetic dipole moment of quarks in the standard model. Eur. Phys. J. Plus 136, 262 (2021). https://doi.org/10.1140/epjp/s13360-021-01239-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjp/s13360-021-01239-9